Abstract
The sign least mean square with reweighted L1-norm constraint (SLMS-RL1) algorithm is an attractive sparse channel estimation method among Gaussian mixture model (GMM) based algorithms for use in impulsive noise environments. The channel sparsity can be exploited by SLMS-RL1 algorithm based on appropriate reweighted factor, which is one of key parameters to adjust the sparse constraint for SLMS-RL1 algorithm. However, to the best of the authors’ knowledge, a reweighted factor selection scheme has not been developed. This paper proposes a Monte-Carlo (MC) based reweighted factor selection method to further strengthen the performance of SLMS-RL1 algorithm. To validate the performance of SLMS-RL1 using the proposed reweighted factor, simulations results are provided to demonstrate that convergence speed can be reduced by increasing the channel sparsity, while the steady-state MSE performance only slightly changes with different GMM impulsive-noise strengths.
1. Introduction
Adaptive filtering algorithms have been widely applied for multipath channel estimation, especially in broadband wireless systems [1,2,3,4,5,6,7], where the broadband signals are vulnerable to multipath fading as well as additive noises [8,9,10]. Hence, channel state information (CSI) is necessary for coherent demodulation [11]. Based on the classical Gaussian noise model, second-order statistics based least mean square (LMS) algorithm has been widely used to estimate channels due to its simplicity and robustness [1,2]. However, the performance of LMS is usually degraded by impulsive noise [12], which is common in broadband wireless systems and can be described by the Gaussian mixture noise model (GMM) [13]. Thus, it is necessary to develop robust channel estimation algorithms in the presence of GMM impulsive noise. In [1], a standard sign least mean square (SLMS) algorithm was proposed to suppress impulsive noise. In [14], Jiang et al. proposed a sophisticated robust matched filtering algorithm in -space to realize time delay estimation (TDE) and joint delay-Doppler estimation (JDDE) for target localization. On the other hand, wireless channels can be often modeled as sparse or cluster-sparse and hence many of channel coefficients are zero [15,16,17,18,19]. However, standard SLMS algorithm does not exploit sparse channel structure information, while some potential performance gain could be obtained by adopting advanced adaptive channel estimation algorithms.
To exploit channel sparsity as well as to mitigate GMM impulsive noises, some state-of-the-art channel estimation algorithms using linear programming [20,21] and Bayesian learning [22] have been investigated. However, these algorithms often have high computational complexity. It is well known that the fast channel estimation algorithm is one of important factors to design wireless communication systems. Hence, a fast adaptive sparse channel estimation algorithm, i.e., SLMS with reweighted L1-norm constraint (SLMS-RL1) algorithm was proposed in [23]. In our previous work, we focused on the convergence analysis without considering the reweighted factor selection, where the empirical parameter is set as [6]. However, the reweighted factor is one of critical parameters to balance estimation performance and sparsity exploitation. To this end, this paper proposes a Monte-Carlo (MC) based selection method to select suitable reweighted factor for SLMS-RL1 algorithm. Numerical simulations are provided to evaluate the performance of the SLMS-RL1 algorithm using the proposed reweighted factor.
The rest of the paper is organized as follows. In Section 2, we introduce GMM noise model and review of SLMS-RL1 algorithm. By analyzing the convergence performance of LMS-RL1 algorithm, the important problem of the reweighted factor selection is point out. In Section 3, the MC-based selection method is proposed to select an appropriate reweighted factor for SLMS-RL1 algorithm. In Section 4, numerical simulations are provided to demonstrate the effectiveness of SLMS-RL1 with the proposed reweighted factor. Finally, Section 5 concludes this paper.
2. Problem Formulation
2.1. Review of SLMS-RL1 Algorithm
Consider an additive noise interference channel, which is modeled by the unknown N-length finite impulse response (FIR) vector at discrete time index . The ideal received signal is expressed as
where is the input signal vector of the most recent input samples; is an -dimensional column vector of the unknown system that we wish to estimate, and is impulsive noise which can be described by Gaussian mixture model (GMM) [13] distribution as
where denotes impulsive-noise strength and denotes the Gaussian distributions with zero mean and variance , and the is the mixture parameter to control the impulsive noise level. According to Equation (2), one can find that stronger impulsive noises can be described by larger noise variance as well as larger mixture parameter . According to Equation (2), variance of GMM is obtained.
Note that will reduce to Gaussian noise model if . The objective of the adaptive channel estimation is to perform adaptive estimate of with limited complexity and memory given sequential observation in the presence of additive GMM noise . According to Equation (1), instantaneous estimation error can be written as
where is the estimator of at iteration .
To obtain the optimal channel estimation, one can construct the -norm minimization problem as
where denotes -norm operator which is defined as . That is to say, the main function of is to find the total number of nonzero coefficients. However, solving the -norm minimization is a Non-Polynomial (NP) hard problem. Hence, it is necessary to introduce an approximate -norm minimization function so that Equation (5) is solvable. On the adaptive sparse channel estimation, reweighted -norm (RL1) minimization has a better performance than -minimization that is usually employed in compressive sensing [24]. It is due to the fact that a properly RL1 can approximate the -norm more accurate than -norm. Hence, one approach to enforce the sparsity of the solution for the sparse SLMS algorithm is to introduce the RL1 penalty term in thee cost function as RL1-LAE which considers a penalty term proportional to the RL1 of the coefficient vector. Hence, the cost function Equation (5) can be revised as
where is the weight associated with the penalty term and elements of the diagonal reweighted matrix are devised as
where being some positive number and hence for . The update equation can be derived by differentiating (6) with respect to the FIR channel vector . Then, the resulting update equation is
where . Notice that in Equation (8), since , one can get , where denotes sign function, i.e., for , for .
2.2. Problem Formulation
Define the misalignment channel vector as and as the second moment matrix of , Equation (4) can be rewritten as . To verify the performance, the convergence analysis of SLMS-RL1 algorithm is derived via mean convergence and excess MSE. Based on independent assumptions, in [23], the authors derive that SLMS-RL1 is stable if
where denotes the maximal eigenvalue of . Then the mean estimation error is derived as
where and . Similarly, excess mean square error (MSE) is approximated as
where and are defined as
and
respectively. Here, denotes -norm constraint. Both mean estimation error and excess MSE imply that the reweighted factor adjusts performance of SLMS-RL1 algorithm. Hence, it is necessary to develop effective method to choose agreeable reweighted factor for further reinforce the proposed SLMS-RL1 algorithm.
3. Reweighted Factor Selection for SLMS-RL1 Algorithm
MC-based reweighted factor selection method is developed for SLMS-RL1 algorithm in different SNR regimes, impulsive-noise strength , mixture parameters as well as channel sparsity . For achieving average performance, independent Monte-Carlo runs are adopted. The simulation setup is configured according to the typical broadband wireless communication system [10]. The signal bandwidth is 50 MHz located at the central radio frequency of 2.1 GHz. The maximum delay spread of . Hence, the maximum length of channel vector is . In addition, each dominant channel tap follows random Gaussian distribution as which is subject to and their positions are randomly decided within . To evaluate SLMS-RL1 algorithm using different factors, we adopt the average mean square error (MSE) metric which is defined as
where and are the actual signal vector and reconstruction vector, respectively; denotes mathematical expectation operator. The received SNR is defined as , where is the received power of the pseudo-random (PN) binary sequence for training signal. Detailed parameters for computer simulation are listed in Table 1.

Table 1.
Simulation parameters.
| Parameters | Values |
|---|---|
| Training signal structure | Pseudo-random Binary sequences |
| Channel length | |
| No. of nonzero coefficients | |
| Distribution of nonzero coefficient | Random Gaussian distribution |
| Received SNR | |
| GMM noise distribution | , , |
| Step-size | |
| Regularization parameters for sparse penalties | |
| Thresholds of the SLMS-RL1 algorithms |
First of all, MC based reweighted factor selection method is performed in Figure 1 and Figure 2. Average MSE curves of the SLMS-RL1 algorithm are depicted under two SNR regimes, i.e., . To confirm the effectiveness of the proposed method, standard SLMS [1] is considered as a performance benchmark. As we discussed in Section 2, one can see that the MSE performance of SLMS-RL1 algorithms depends highly on the reweighted factor . In these two figures, the lowest MSE performance of SLMS-RL1 is achieved when reweighted factor is set as 0.005 in two SNR regimes. On the one hand, too big reweighted factor may suppress noise excessively and hence it result in lossy exploitation of channel sparsity. On the other hand, a too small reweighted factor may mitigate noise insufficiently and it causes inefficient exploitation of channel sparsity. Therefore, suitable reweighted factor could balance the noise suppression and channel sparsity exploitation.
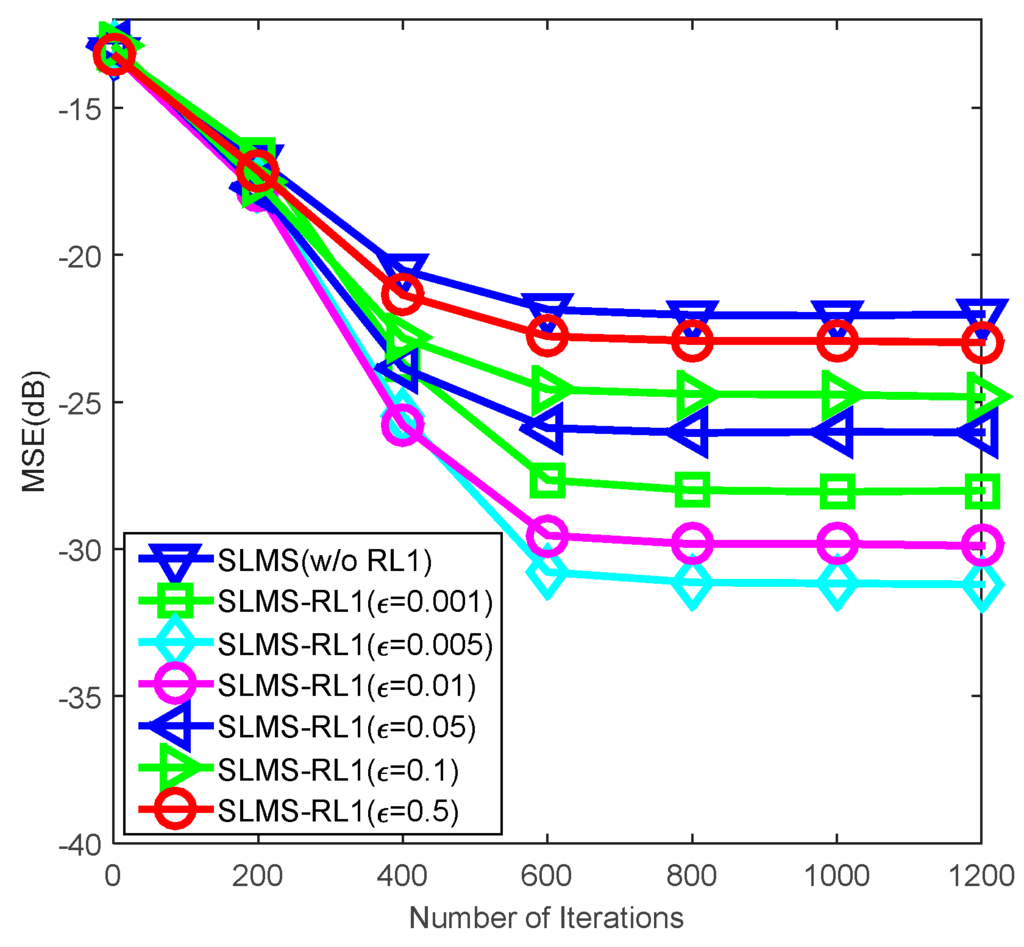
Figure 1.
Monte Carlo simulations averaging for evaluating sign least mean square with reweighted L1-norm constraint (SLMS-RL1) algorithm over 1000 runs with respect to reweighted factors in the scenarios of mixture parameter , impulsive-noise strength , channel length , channl sparsity and .
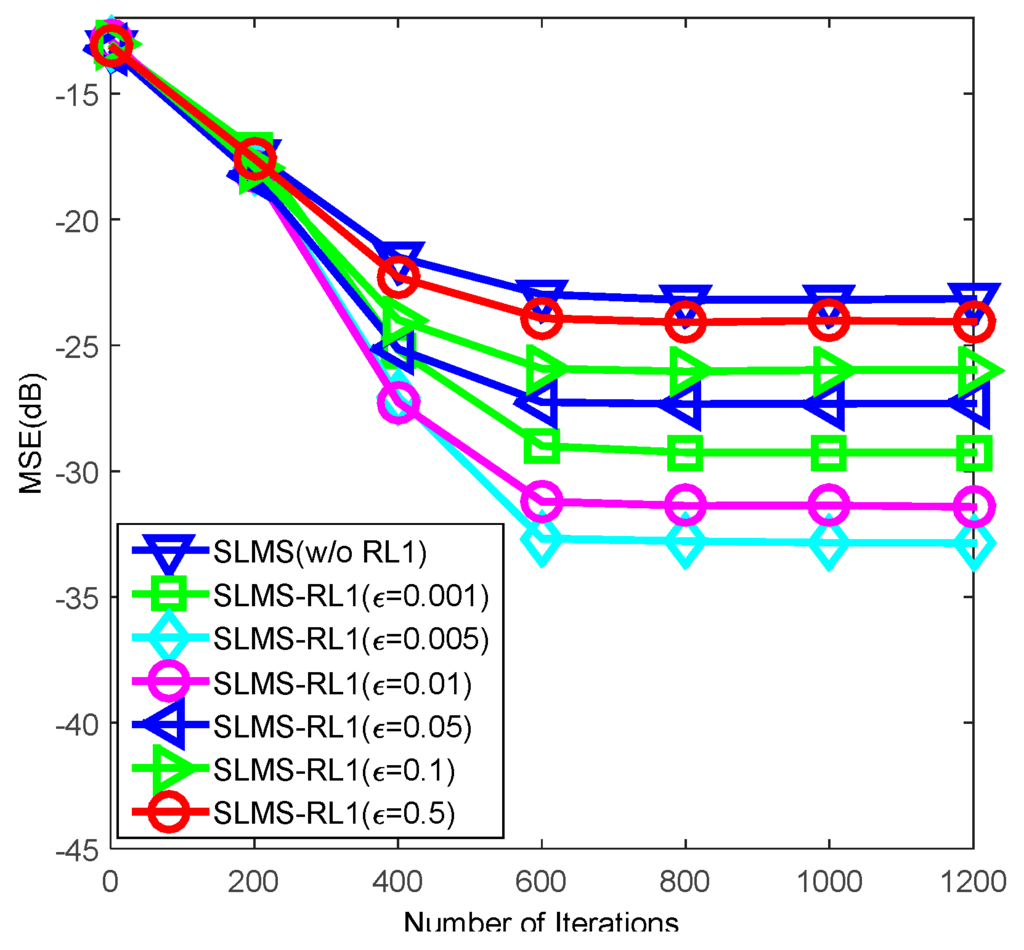
Figure 2.
Monte Carlo simulations averaging for evaluating SLMS-RL1 algorithm over 1000 runs with respect to reweighted factors in the scenarios of mixture parameter , impulsive-noise strength , channel length , channl sparsity and .
4. Numerical Simulations
In this section, three examples are given to verify the performance of SLMS-RL1 algorithm by using proposed reweighted factor in the scenarios of = 10 dB, impulsive-noise strength , mixture parameters as well as channel sparsity . For achieving average performance, independent Monte-Carlo runs are adopted as well. Detailed parameters for computer simulation are listed in Table 2.

Table 2.
Simulation parameters.
| Parameters | Values |
|---|---|
| Training signal structure | Pseudo-random Binary sequences |
| Channel length | |
| No. of nonzero coefficients | |
| Distribution of nonzero coefficient | Random Gaussian distribution |
| Received SNR | |
| GMM noise distribution ( controls impulsive noise strength) | , , |
| Step-size | |
| Regularization parameters for sparse penalties | |
| Threshold of the SLMS-RL1 |
In the first example, average MSE curves of different algorithms are depicted in Figure 3. Under the certain circumstance, channel sparsity, , GMM noise with impulsive-noise parameter as well as mixture parameter , one can find that proposed SLMS-RL1 algorithm can achieve at least 5 dB and 10 dB performance gain in contrast to SLMS algorithm and LMS-type algorithms, respectively. Because SLMS algorithm does not exploit the channel sparsity while LMS-type algorithms do not stable under GMM noise environments. Hence, the proposed SLMS-RL1 can exploit channel sparsity and can keep stability in the presence of GMM noises.
In the second example, average MSE curves of SLMS-RL1 algorithm with respect to channel sparsity are depicted in Figure 4. Under the certain circumstance, e.g., , GMM noise with impulsive-noise parameter as well as mixture parameter , one can find that that convergence speed of SLMS-RL1 depends on channel sparsity () while steady-state MSE curves of corresponding algorithms are very close. For different channel sparsity, in other words, the adaptive sparse algorithms may differ from conventional compressive sensing based sparse channel estimation algorithms [15], [16], [25], [26] which depend highly on channel sparsity. Hence, SLMS-RL1 using MC-based reweighted factor is expected to deal with different sparse channels stably even non-sparse cases.
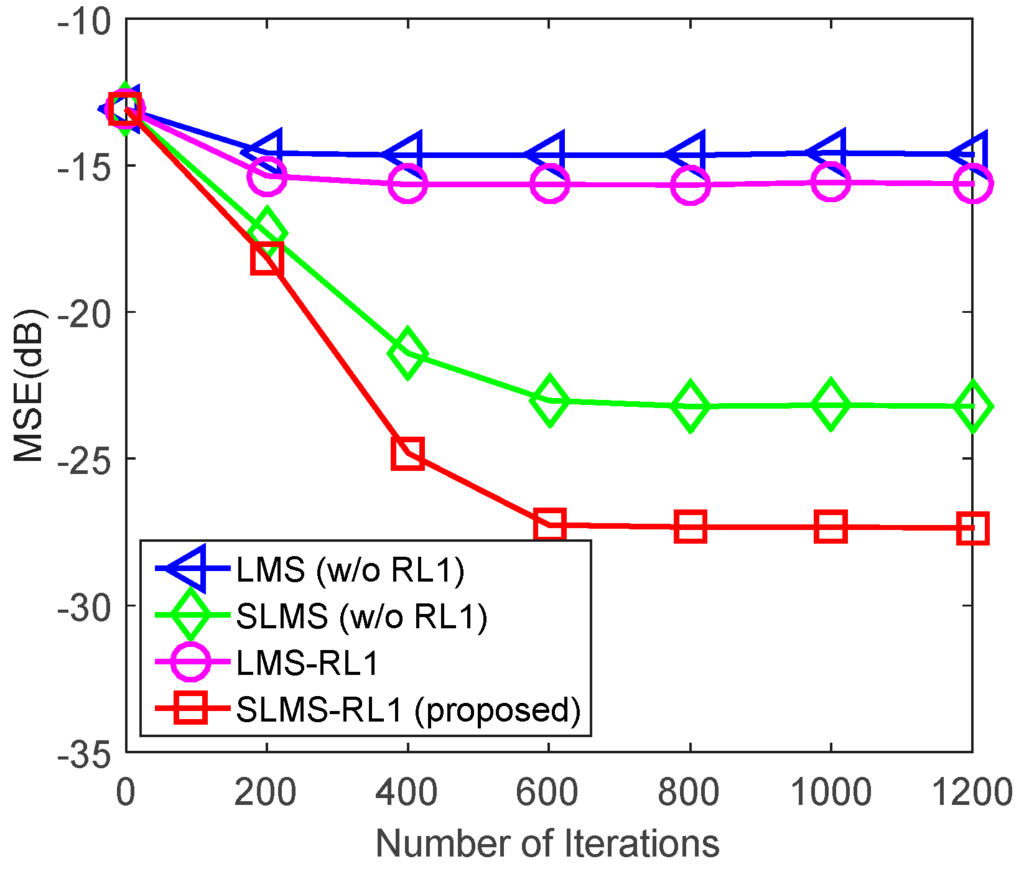
Figure 3.
Monte Carlo simulations averaging for different algorithms over 1000 runs in the scenarios of mixture parameter , impulsive-noise strength , channel length , channl sparsity and .
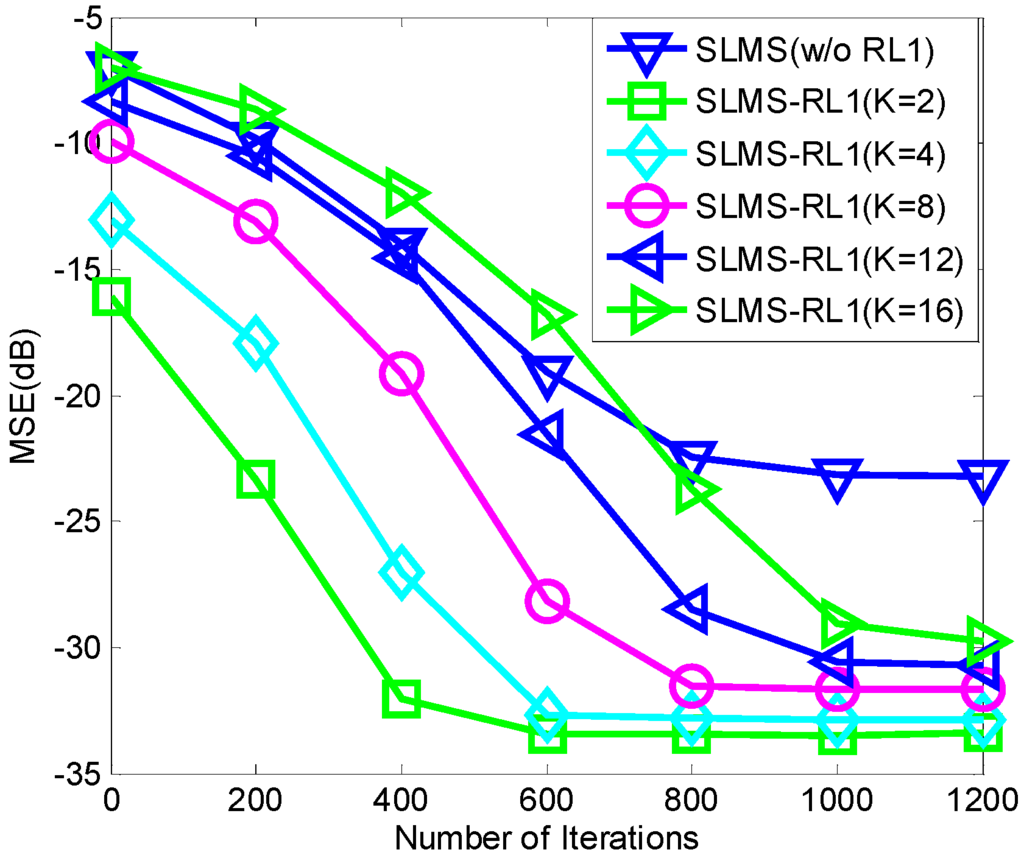
Figure 4.
Monte Carlo simulations averaging for evaluating SLMS-RL1 algorithm over 1000 runs with respect to channel sparsity in the scenarios of mixture parameter , impulsive-noise strength , channel length , and .
In the third example, average MSE curves of SLMS-RL1 algorithm using reweighted selected factor with respect to impulsive-noise strength are depicted in Figure 5. In addition, average MSE curves of the algorithm with respect to mixture parameter are depicted in Figure 6. In the two figures, one can see that SLMS-RL1 algorithm using is stable for different GMM noises with impulsive-noise strength parameters as well as mixture parameters . The main reason of SLMS-RL1 algorithm is that sign function is utilized to mitigate the GMM impulsive noise. It is worth noting that SLMS-RL1 algorithm may be deteriorated by the enlarging the mixture parameter of impulsive noise. In practical application scenarios, the mixture parameter is very small (less than 0.1). Hence, the proposed reweighted factor for SLMS-RL1 is stable for GMM impulsive-noise.
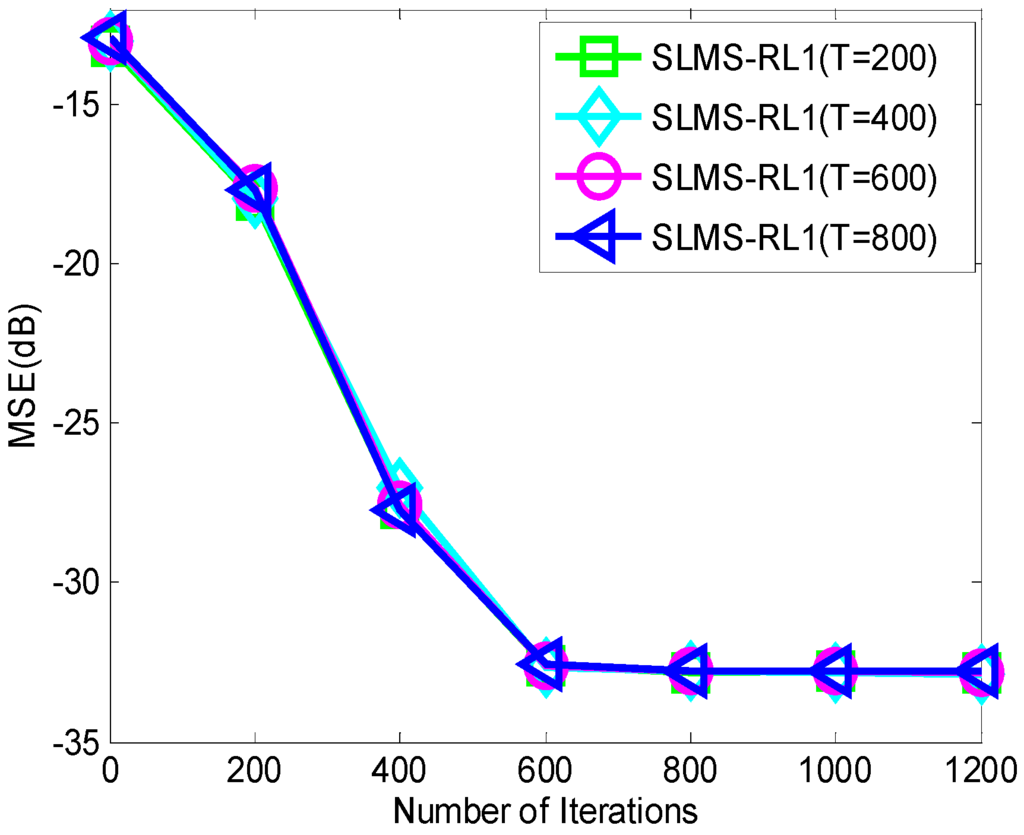
Figure 5.
Monte Carlo simulations averaging for evaluating SLMS-RL1 over 1000 runs with respect to impulsive-noise strength in the scenarios of mixture parameter , channel length , channel sparsity and .
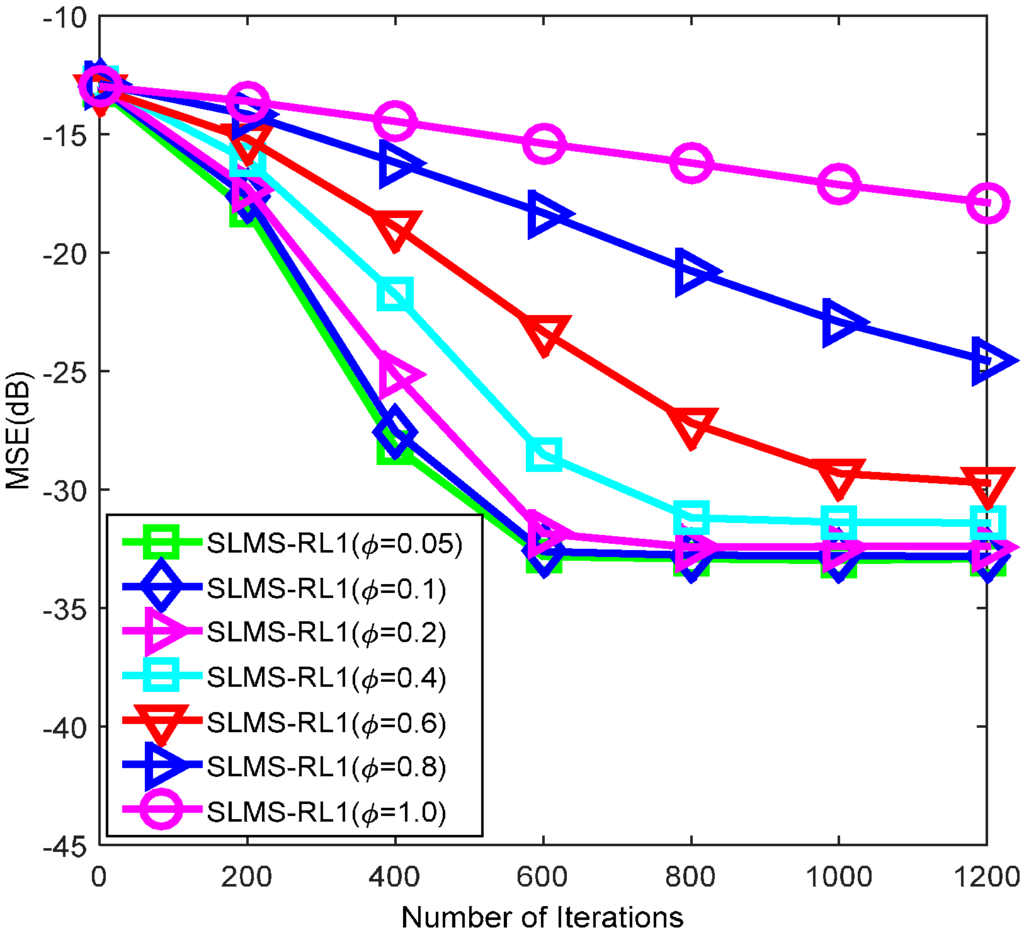
Figure 6.
Monte Carlo simulations averaging for evaluating SLMS-RL1 over 1000 runs with respect to mixture parameter in the scenarios of impulsive-noise strength , channel length , channel sparsity , and .
5. Conclusions
In this paper, we propose a Monte-Carlo based reweighted factor selection method so that the SLMS-RL1 algorithm can exploit channel sparsity efficiently. Simulation results are provided to illustrate our findings. First of all, SLMS-RL1 can achieve the lowest MSE performance by selecting the reweighted factor as in different SNR regimes. Secondly, the convergence speed of SLMS-RL1 can be reduced by increasing the channel sparsity . At last, the steady-state MSE performance of SLMS-RL1 does not change considerably under different GMM impulsive-noise strength . In other words, SLMS-RL1 algorithm using the reweighted factor is stable under different GMM impulsive noises.
Acknowledgments
The authors would like to extend their appreciation to the anonymous reviewers for their constructive comments. This work was supported in part by the Japan Society for the Promotion of Science (JSPS) research grants (No. 26889050, No. 15K06072), and the National Natural Science Foundation of China grants (No. 61401069, No. 61271240).
Author Contributions
We proposed the reweighted factor selection method for sign least mean square with reweighted L1-norm constraint (SLMS-RL1) algorithm under Gaussian mixture noise model. Tingping Zhang drafted this paper including theoretical work and computer simulation. Guan Gui checked the full paper in writing and presentation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sayed, A.H. Adaptive Filters; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Haykin, S.S. Adaptive Filter Theory, Prentice Hall, Upper Saddle River, NJ, USA, 1996.
- Yoo, J.; Shin, J.; Park, P. Variable step-size affine projection aign algorithm. IEEE Trans. Circuits Syst. Express Br. 2014, 61, 274–278. [Google Scholar]
- Chen, B.; Zhao, S.; Zhu, P.; Principe, J.C. Quantized kernel recursive least squares algorithm. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1484–1491. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Zhao, S.; Zhu, P.; Principe, J.C. Quantized kernel least mean square algorithm. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 22–32. [Google Scholar] [CrossRef] [PubMed]
- Taheri, O.; Vorobyov, S.A. Sparse channel estimation with LP-norm and reweighted L1-norm penalized least mean squares. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 2864–2867.
- Gendron, P.J. An empirical Bayes estimator for in-scale adaptive filtering. IEEE Trans. Signal Process. 2005, 53, 1670–1683. [Google Scholar] [CrossRef]
- Adachi, F.; Kudoh, E. New direction of broadband wireless technology. Wirel. Commun. Mob. Comput. 2007, 7, 969–983. [Google Scholar] [CrossRef]
- Raychaudhuri, B.D.; Mandayam, N.B. Frontiers of wireless and mobile communications. Proc. IEEE 2012, 100, 824–840. [Google Scholar] [CrossRef]
- Dai, L.; Wang, Z.; Yang, Z. Next-generation digital television terrestrial broadcasting systems: Key technologies and research trends. IEEE Commun. Mag. 2012, 50, 150–158. [Google Scholar] [CrossRef]
- Adachi, F.; Garg, D.; Takaoka, S.; Takeda, K. Broadband CDMA techniques. IEEE Wirel. Commun. 2005, 12, 8–18. [Google Scholar] [CrossRef]
- Shao, M.; Nikias, C.L. Signal processing with fractional lower order moments: Stable processes and their applications. Proc. IEEE 1993, 81, 986–1010. [Google Scholar] [CrossRef]
- Middleton, D. Non-Gaussian noise models in signal processing for telecommunications: New methods and results for class A and class B noise models. IEEE Trans. Inf. Theory 1999, 45, 1129–1149. [Google Scholar] [CrossRef]
- Jiang, X.; Zeng, W.-J.; So, H.C.; Rajan, S.; Kirubarajan, T. Robust matched filtering in lp-space. IEEE Trans. Signal Process. Unpublished work. 2015. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Lu, Z.; Yuen, C.; Member, S.; Wang, Z. Super-resolution sparse MIMO-OFDM channel estimation based on spatial and temporal correlations. IEEE Commun. Lett. 2014, 18, 1266–1269. [Google Scholar] [CrossRef]
- Dai, L.; Wang, Z.; Yang, Z. Compressive sensing based time domain synchronous OFDM transmission for vehicular communications. IEEE J. Sel. Areas Commun. 2013, 31, 460–469. [Google Scholar]
- Qi, C.; Wu, L. Optimized pilot placement for sparse channel estimation in OFDM systems. IEEE Signal Process. Lett. 2011, 18, 749–752. [Google Scholar] [CrossRef]
- Gui, G.; Peng, W.; Adachi, F. Sub-Nyquist rate ADC sampling-based compressive channel estimation. Wirel. Commun. Mob. Comput. 2015, 15, 639–648. [Google Scholar] [CrossRef]
- Gui, G.; Zheng, N.; Wang, N.; Mehbodniya, A.; Adachi, F. Compressive estimation of cluster-sparse channels. Prog. Electromagn. Res. C 2011, 24, 251–263. [Google Scholar] [CrossRef]
- Jiang, X.; Kirubarajan, T.; Zeng, W.-J. Robust sparse channel estimation and equalization in impulsive noise using linear programming. Signal Process. 2013, 93, 1095–1105. [Google Scholar] [CrossRef]
- Jiang, X.; Kirubarajan, T.; Zeng, W.J. Robust time-delay estimation in impulsive noise using lp-correlation. In Proceedings of the IEEE Radar Conference (RADAR), Ottawa, ON, Canada, 29 April–3 May 2013; pp. 1–4.
- Lin, J.; Member, S.; Nassar, M.; Evans, B.L. Impulsive noise mitigation in powerline communications using sparse Bayesian learning. IEEE J. Sel. Areas Commun. 2013, 31, 1172–1183. [Google Scholar] [CrossRef]
- Zhang, T.; Gui, G. IMAC: Impulsive-mitigation adaptive sparse channel estimation based on Gaussian-mixture model. Available online: http//arxiv.org/abs/1503.00800 (accessed on 14 September 2015).
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted L1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Bajwa, W.U.; Haupt, J.; Sayeed, A.M.; Nowak, R. Compressed channel sensing: A new approach to estimating sparse multipath channels. Proc. IEEE 2010, 98, 1058–1076. [Google Scholar] [CrossRef]
- Tauböck, G.; Hlawatsch, F.; Eiwen, D.; Rauhut, H. Compressive estimation of doubly selective channels in multicarrier systems: Leakage effects and sparsity-enhancing processing. IEEE J. Sel. Top. Signal Process. 2010, 4, 255–271. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).