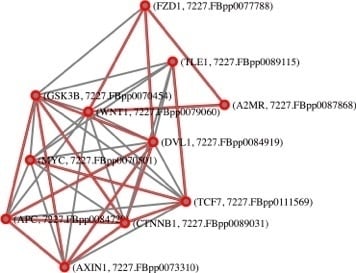
Natalie 2.0: Sparse Global Network Alignment as a Special Case of Quadratic Assignment †
Abstract
:1. Introduction
1.1. Previous Work
1.2. Contribution
2. Preliminaries
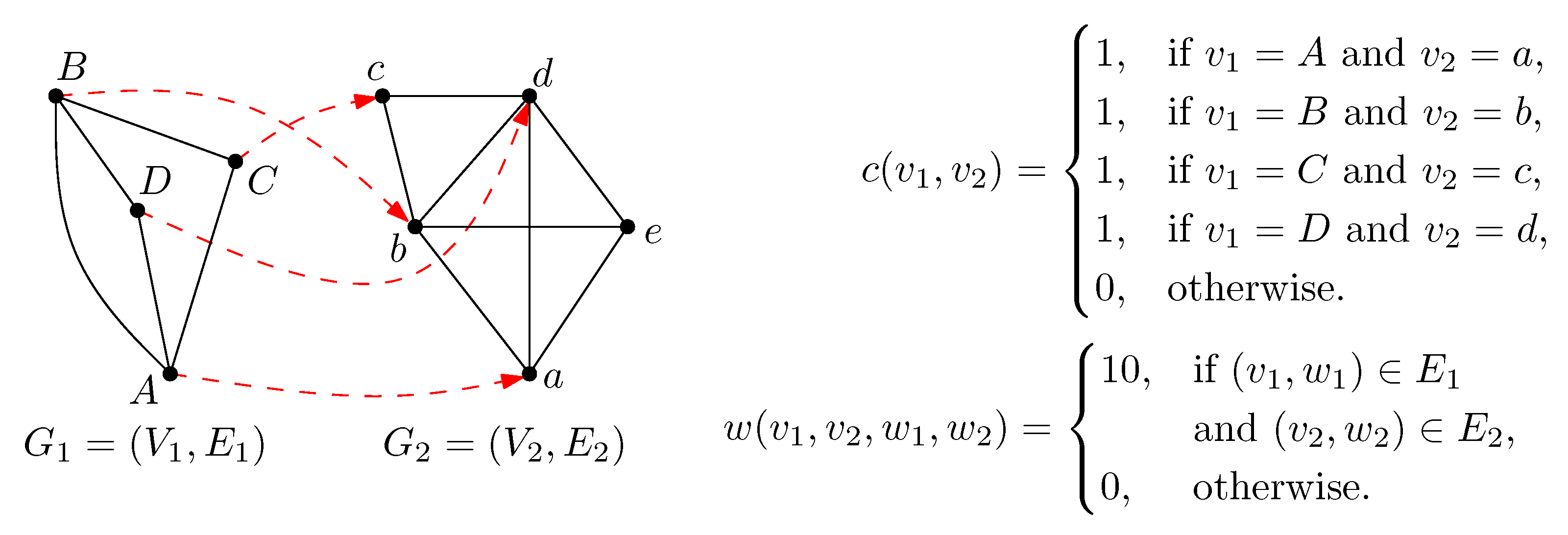
3. Methods
3.1. Solving Strategies
3.1.1. Subgradient Optimization
| Algorithm 1: SubgradientOpt |
|
3.1.2. Dual Descent
| Algorithm 2: DualDescent |
|
3.1.3. Overall Method
| Algorithm 3: Natalie |
|
4. Experimental Evaluation
| Species | Nodes | Annotated | Interactions |
|---|---|---|---|
| cel (c) | 5948 | 4694 | 23,496 |
| sce (s) | 6018 | 5703 | 131,701 |
| dme (d) | 7433 | 6006 | 26,829 |
| rno (r) | 8002 | 6786 | 32,527 |
| mmu (m) | 9109 | 8060 | 38,414 |
| hsa (h) | 11,512 | 9328 | 67,858 |
4.1. Topological Measures
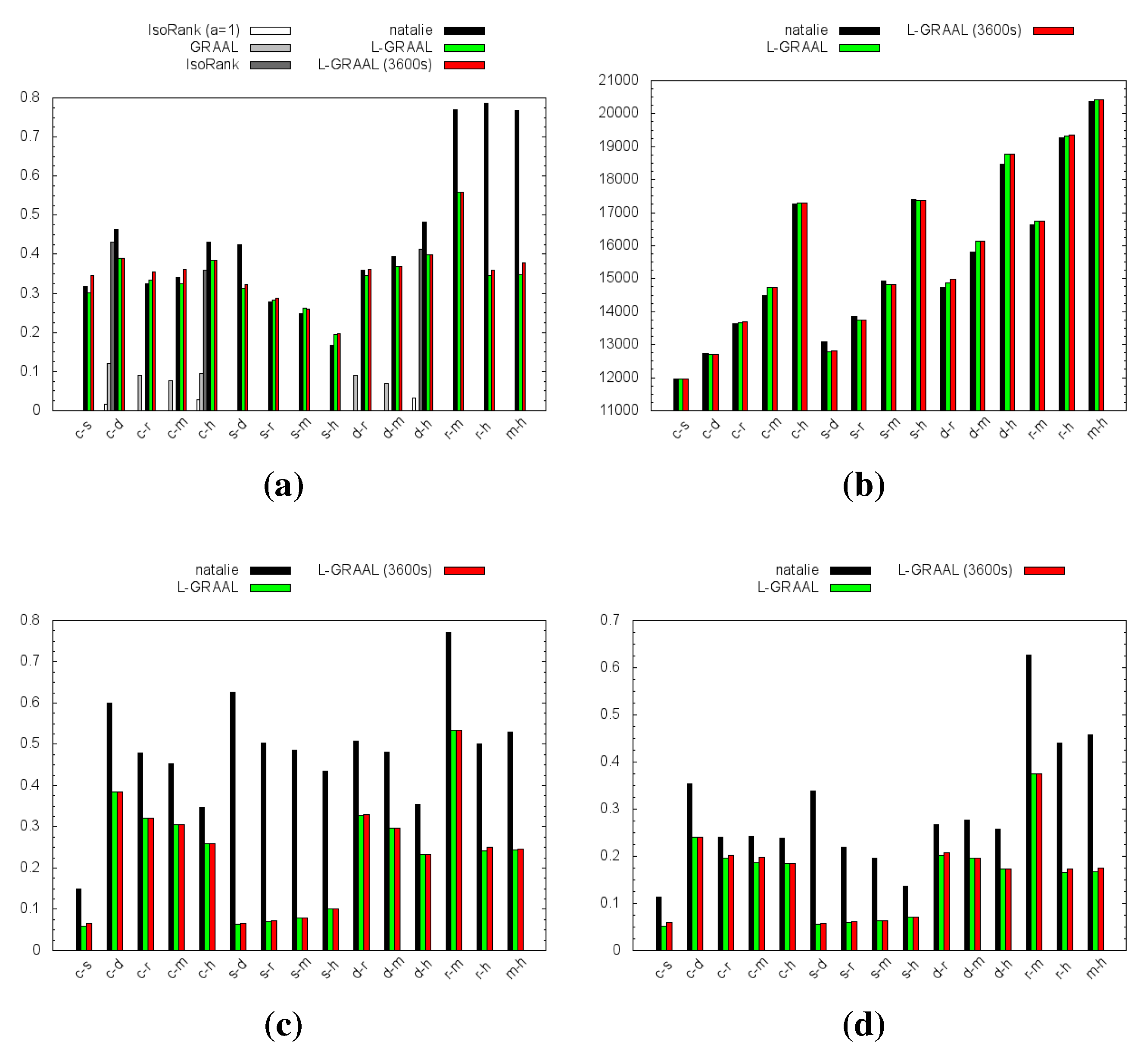
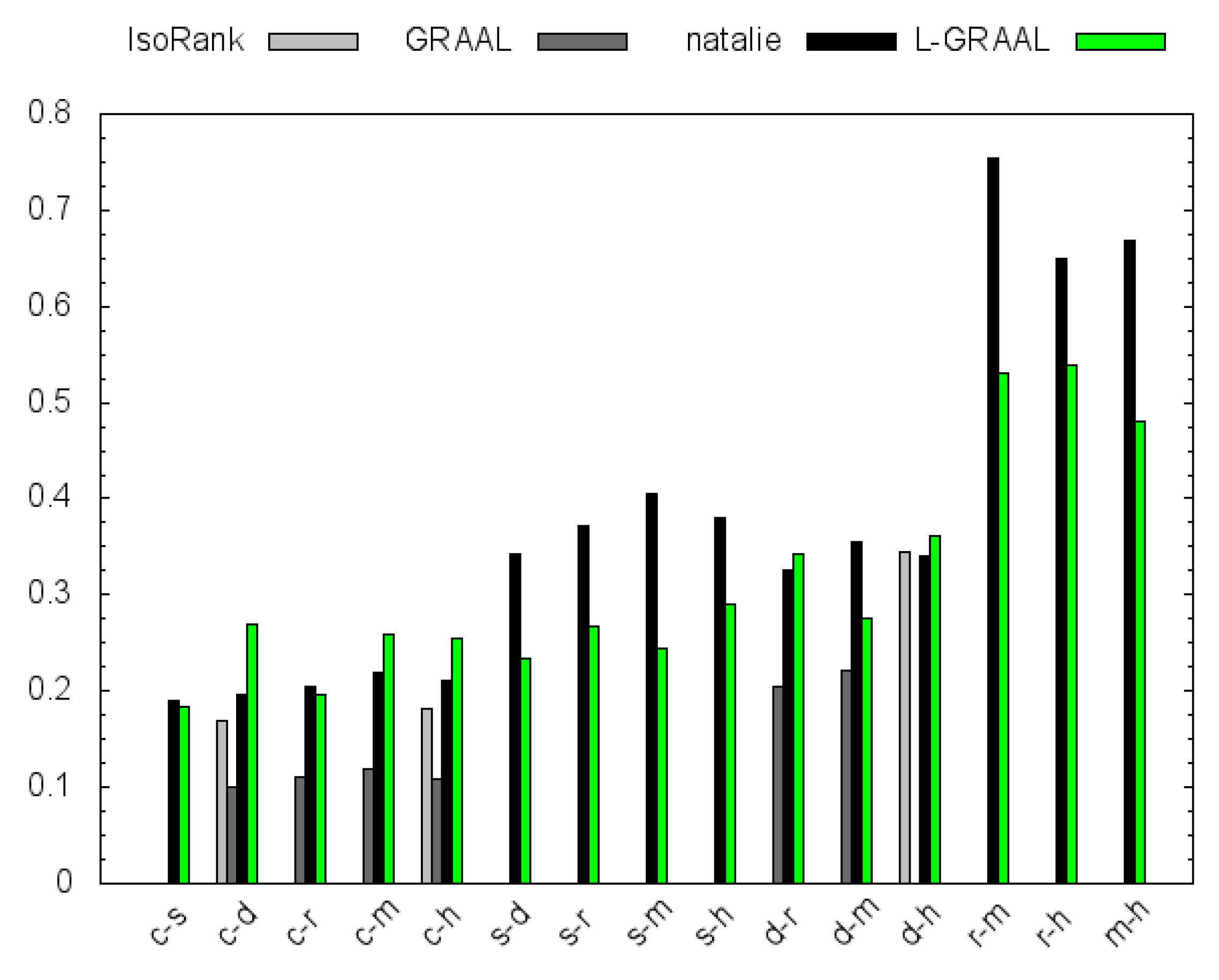
4.2. GO Similarity
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Szklarczyk, D.; Franceschini, A.; Wyder, S.; Forslund, K.; Heller, D.; Huerta-Cepas, J.; Simonovic, M.; Roth, A.; Santos, A.; Tsafou, K.P.; et al. STRING v10: Protein-protein interaction networks, integrated over the tree of life. Nucleic Acids Res. 2015, 43. [Google Scholar] [CrossRef] [PubMed]
- Sharan, R.; Ideker, T. Modeling cellular machinery through biological network comparison. Nat. Biotechnol. 2006, 24, 427–433. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Goto, S.; Hattori, M.; Aoki-Kinoshita, K.F.; Itoh, M.; Kawashima, S.; Katayama, T.; Araki, M.; Hirakawa, M. From genomics to chemical genomics: New developments in KEGG. Nucleic Acids Res. 2006, 34. [Google Scholar] [CrossRef] [PubMed]
- Alon, U. Network motifs: Theory and experimental approaches. Nat. Rev. Genet. 2007, 8, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Elmsallati, A.; Clark, C.; Kalita, J. Global alignment of protein-protein interaction networks: A survey. IEEE/ACM Trans. Comput. Biol. Bioinf. 2015, 99. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Xu, J.; Berger, B. Global alignment of multiple protein interaction networks with application to functional orthology detection. Proc. Natl. Acad. Sci. USA 2008, 105, 12763–12768. [Google Scholar] [CrossRef] [PubMed]
- Klau, G.W. A new graph-based method for pairwise global network alignment. BMC Bioinf. 2009, 10. [Google Scholar] [CrossRef] [PubMed]
- Kuchaiev, O.; Milenkovic, T.; Memisevic, V.; Hayes, W.; Przulj, N. Topological network alignment uncovers biological function and phylogeny. J. R. Soc. Interface 2010, 7, 1341–54. [Google Scholar] [CrossRef] [PubMed]
- Patro, R.; Kingsford, C. Global network alignment using multiscale spectral signatures. Bioinformatics 2012, 28, 3105–3114. [Google Scholar] [CrossRef] [PubMed]
- Neyshabur, B.; Khadem, A.; Hashemifar, S.; Arab, S.S. NETAL: A new graph-based method for global alignment of protein-protein interaction networks. Bioinformatics 2013, 29, 1654–1662. [Google Scholar] [CrossRef] [PubMed]
- Aladağ, A.E.; Erten, C. SPINAL: Scalable protein interaction network alignment. Bioinformatics 2013, 29, 917–924. [Google Scholar] [CrossRef] [PubMed]
- Chindelevitch, L.; Ma, C.Y.; Liao, C.S.; Berger, B. Optimizing a global alignment of protein interaction networks. Bioinformatics 2013, 29, 2765–2773. [Google Scholar] [CrossRef] [PubMed]
- Hashemifar, S.; Xu, J. HubAlign: An accurate and efficient method for global alignment of protein-protein interaction networks. Bioinformatics 2014, 30, i438–i444. [Google Scholar] [CrossRef] [PubMed]
- Vijayan, V.; Saraph, V.; Milenković, T. MAGNA++: Maximizing accuracy in global network alignment via both node and edge conservation. Bioinformatics 2015, 31. [Google Scholar] [CrossRef] [PubMed]
- Clark, C.; Kalita, J. A multiobjective memetic algorithm for PPI network alignment. Bioinformatics 2015, 31, 1988–1998. [Google Scholar] [CrossRef] [PubMed]
- Malod-Dognin, N.; Przulj, N. L-GRAAL: Lagrangian graphlet-based network aligner. Bioinformatics 2015, 31, 2182–2189. [Google Scholar] [CrossRef] [PubMed]
- Natalie 2.0. Available online: http://software.cwi.nl/natalie (accessed on 15 November 2015).
- El-Kebir, M.; Brandt, B.W.; Heringa, J.; Klau, G.W. NatalieQ: A web server for protein-protein interaction network querying. BMC Syst. Biol. 2014, 8. [Google Scholar] [CrossRef] [PubMed]
- NatalieQ. Available online: http://www.ibi.vu.nl/programs/natalieq/ (accessed on 15 November 2015).
- Karp, R.M. Reducibility Among Combinatorial Problems. In Complexity of Computer Computations; Miller, R.E., Thatcher, J.W., Eds.; Plenum Press: New York, NY, USA, 1972; pp. 85–103. [Google Scholar]
- Lawler, E.L. The quadratic assignment problem. Manage Sci. 1963, 9, 586–599. [Google Scholar] [CrossRef]
- Adams, W.P.; Johnson, T. Improved linear programming-based lower bounds for the quadratic assignment problem. DIMACS Ser. Discr. Math. Theor. Comput. Sci. 1994, 16, 43–77. [Google Scholar]
- Kuhn, H.W. The Hungarian method for the assignment problem. Naval Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Munkres, J. Algorithms for the assignment and transportation problems. SIAM J. Appl. Math. 1957, 5, 32–38. [Google Scholar] [CrossRef]
- Edmonds, J.; Karp, R.M. Theoretical improvements in algorithmic efficiency for network flow problems. J. ACM 1972, 19, 248–264. [Google Scholar] [CrossRef]
- Edmonds, J. Path, trees, and flowers. Can. J Math 1965, 17, 449–467. [Google Scholar] [CrossRef]
- Guignard, M. Lagrangean relaxation. Top 2003, 11, 151–200. [Google Scholar] [CrossRef]
- Held, M.; Karp, R.M. The traveling-salesman problem and minimum spanning trees: Part II. Math. Progr. 1971, 1, 6–25. [Google Scholar] [CrossRef]
- Caprara, A.; Fischetti, M.; Toth, P. A heuristic method for the set cover problem. Oper. Res. 1999, 47, 730–743. [Google Scholar] [CrossRef]
- Egerváry Research Group on Combinatorial Optimization. LEMON Graph Library. Available online: http://lemon.cs.elte.hu/ (accessed on 15 November 2015).
- Ashburner, M.; Ball, C.A.; Blake, J.A.; Botstein, D.; Butler1, H.; Cherry, J. M.; Davis, A.P.; Dolinski, K.; Dwight, S.S.; Eppig, J.T.; et al. Gene Ontology: Tool for the unification of biology. Nat. Genet. 2000, 25, 25–29. [Google Scholar] [CrossRef] [PubMed]
- Couto, F.M.; Silva, M.J.; Coutinho, P.M. Measuring Semantic Similarity between Gene Ontology Terms. Data Knowl. Eng. 2007, 61, 137–152. [Google Scholar] [CrossRef]
- Wohlers, I.; Andonov, R.; Klau, G.W. Algorithm Engineering for optimal alignment of protein structure distance matrices. Optim. Lett. 2011, 5, 421–433. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Kebir, M.; Heringa, J.; Klau, G.W. Natalie 2.0: Sparse Global Network Alignment as a Special Case of Quadratic Assignment. Algorithms 2015, 8, 1035-1051. https://doi.org/10.3390/a8041035
El-Kebir M, Heringa J, Klau GW. Natalie 2.0: Sparse Global Network Alignment as a Special Case of Quadratic Assignment. Algorithms. 2015; 8(4):1035-1051. https://doi.org/10.3390/a8041035
Chicago/Turabian StyleEl-Kebir, Mohammed, Jaap Heringa, and Gunnar W. Klau. 2015. "Natalie 2.0: Sparse Global Network Alignment as a Special Case of Quadratic Assignment" Algorithms 8, no. 4: 1035-1051. https://doi.org/10.3390/a8041035
APA StyleEl-Kebir, M., Heringa, J., & Klau, G. W. (2015). Natalie 2.0: Sparse Global Network Alignment as a Special Case of Quadratic Assignment. Algorithms, 8(4), 1035-1051. https://doi.org/10.3390/a8041035