Improving CLOPE’s Profit Value and Stability with an Optimized Agglomerative Approach
Abstract
:1. Introduction
2. The CLOPE Algorithm
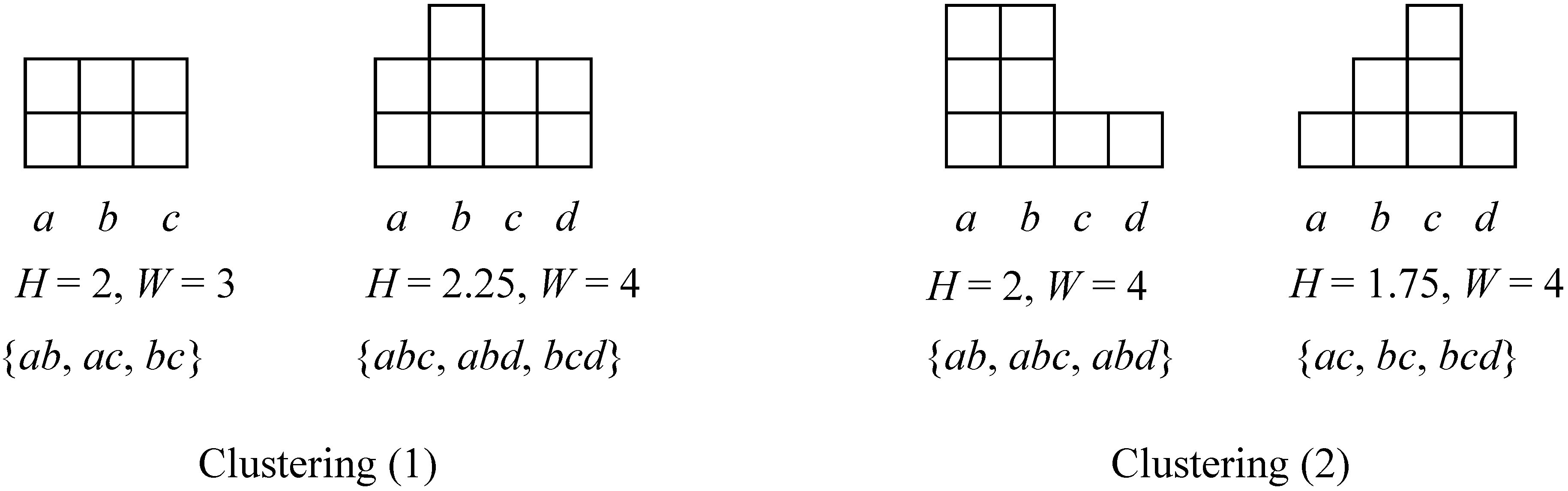
2.1. Terminologies
- (1)
- The size is the total number of attributes in cluster c, defined as:
- (2)
- The width is the total number of different attributes in cluster c, defined as:
- (3)
- The height is the ratio between the size and the width, defined as:
- (4)
- The number of transactions in cluster c, defined as .
2.2. Problem Discovery
3. The Optimized Agglomerative Approach
3.1. Extension from CLOPE
3.2. Optimization on Traditional Agglomerative Approach

| Algorithm 1 Agg-CLOPE |
/*Phase 1 - Initialization*/ 1: while not end of the database file 2: read the next transaction t; 3: ci←t; V←ci; 4: end while /*Phase 2 - Iteration*/ 5: do 6: merged=false; GM=0; 7: for i=0 to V.size 8: for j=i+1 to V.size 9: if(Di,j>GM) 10: GM=Di,j; clear(E); E.add(i, j); 11: clear(ci.L ); ci.L.add(j); 12: clear(cj.L ); cj.L.add(i); 13: else if(Di,j==GM) 14: E.add(i, j);.ci.L.add(j);cj.L.add(i); 15: end if 16: end for 17: end for 18: if (E.size>0) 19: for each distinct c in E 20: LinkMerge(c); 21: End For 22: clear(E); clear(M); merged=true; 23: end if 24: while(merged) |
| Algorithm 2 LinkMerge |
Parameter: c is a cluster(vertex) in cluster graph G 1: If(c is not merged) 2: for each k in c.L 3: LinkMerge(ck); 4: End For 5: End If |
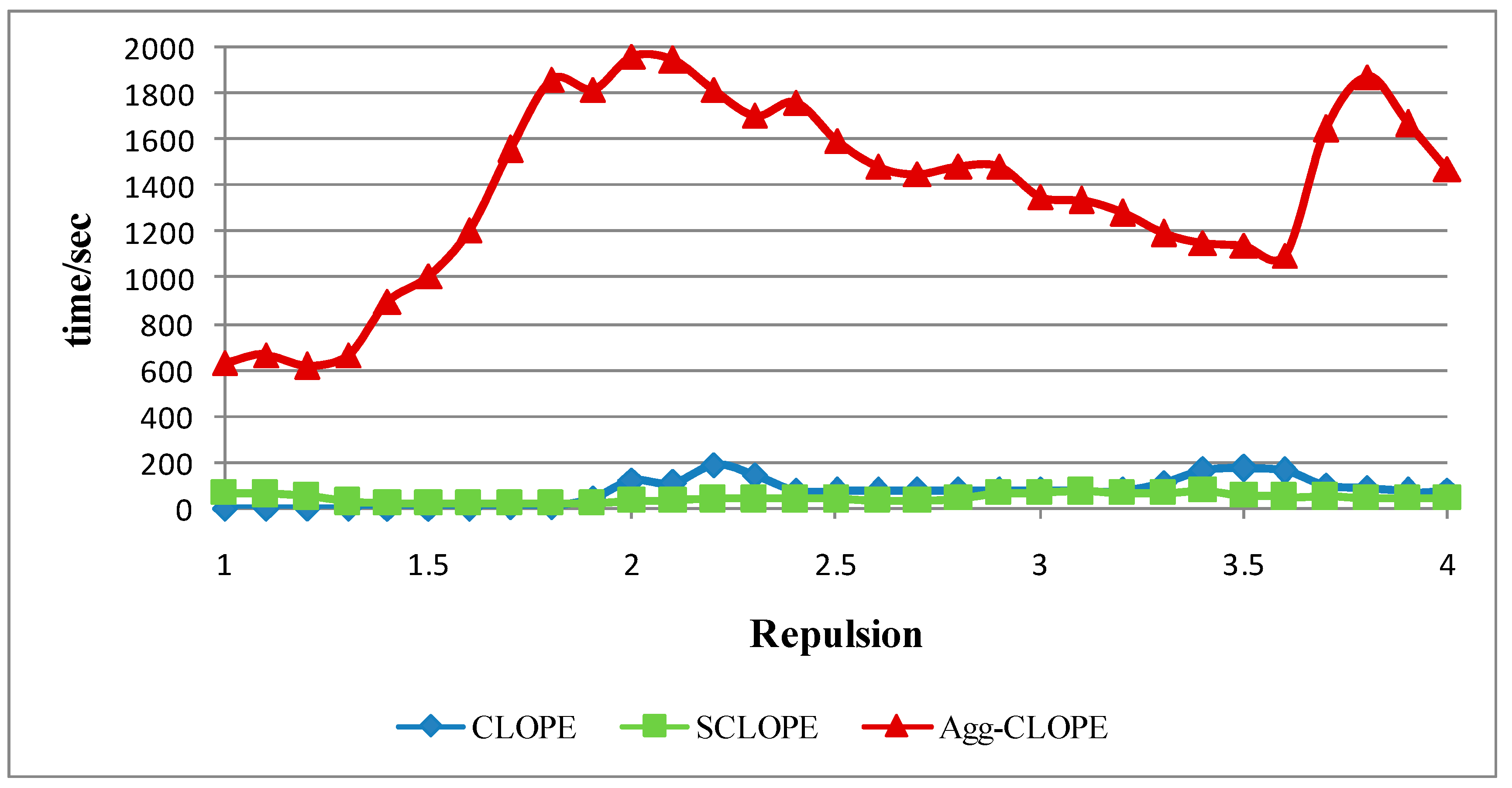
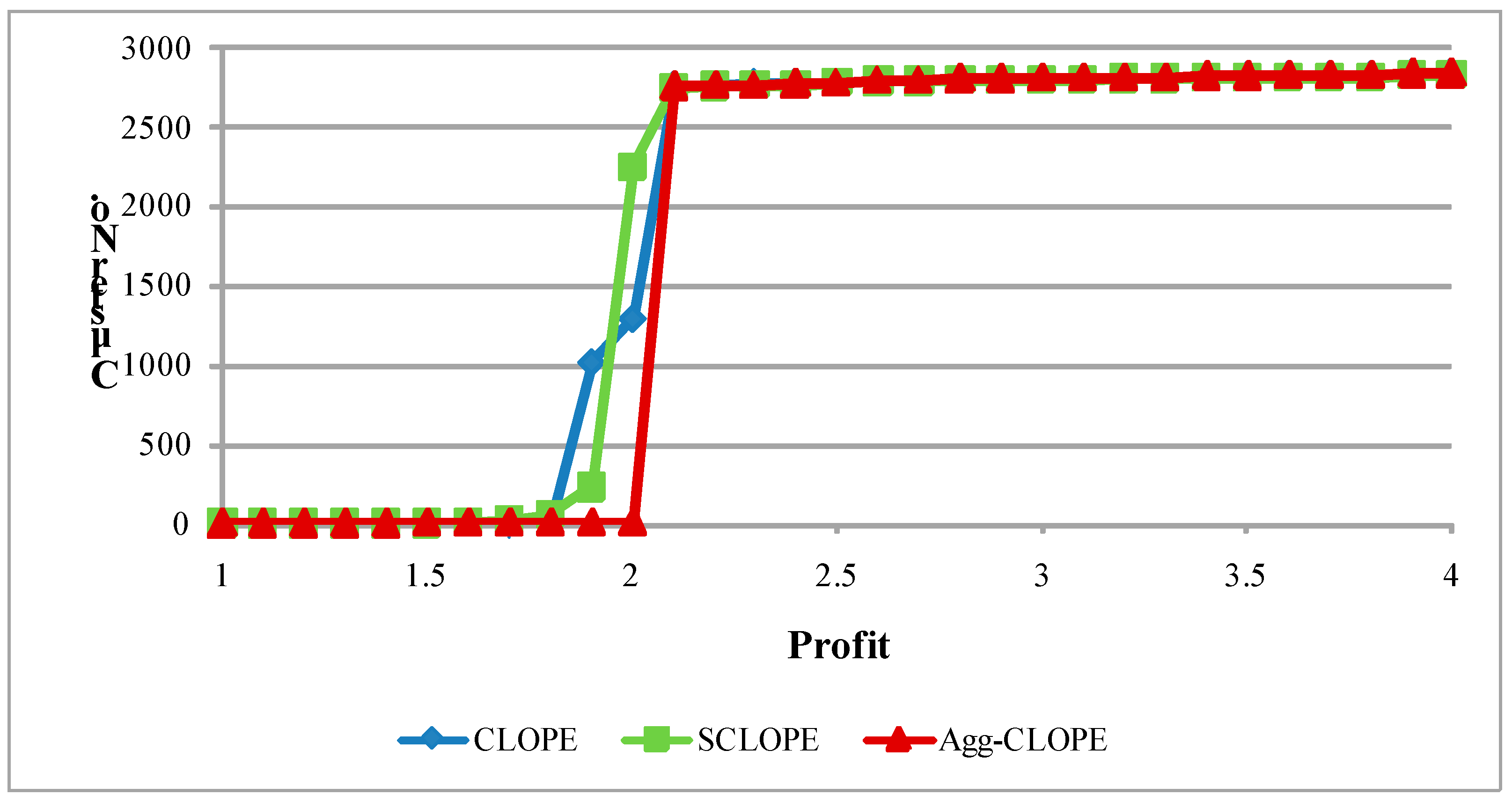
4. Experimental Results
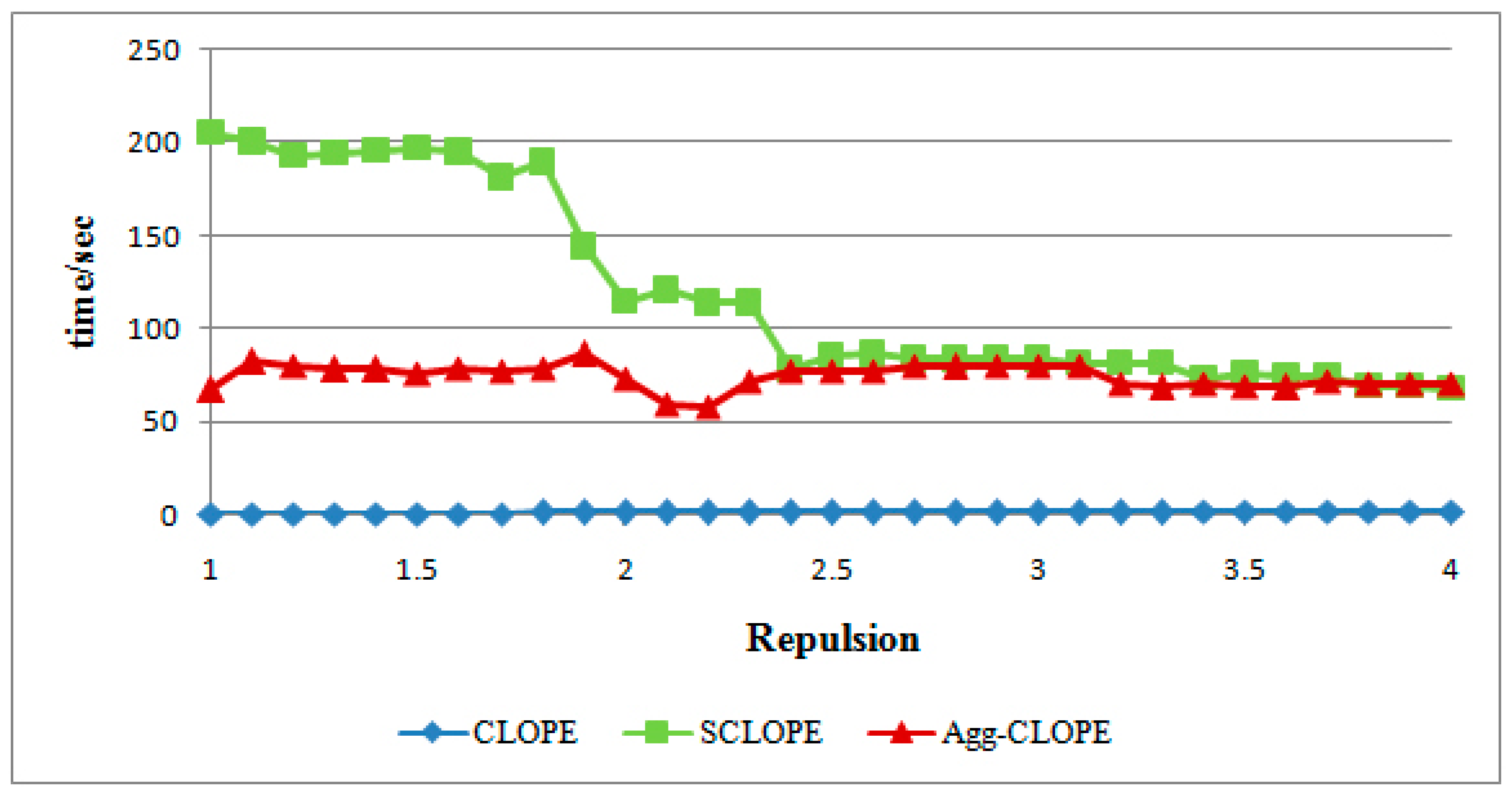
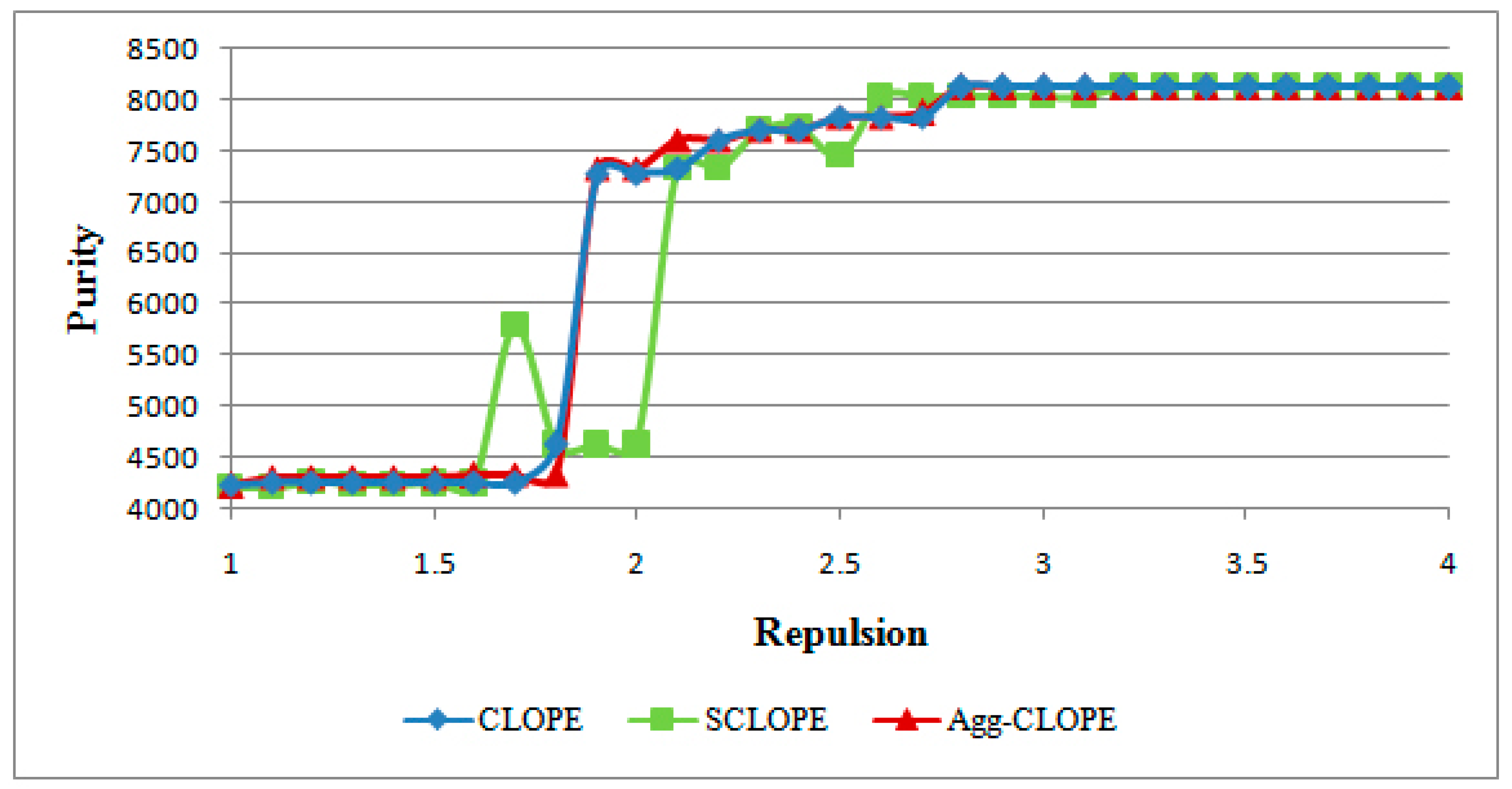
4.1. The Mushroom Dataset
| r | CLOPE | SCLOPE | Agg-CLOPE | r | CLOPE | SCLOPE | Agg-CLOPE |
|---|---|---|---|---|---|---|---|
| 1.0 | 745.6473 | 1698.0084 | 1791.9966 | 2.6 | 2.2697 | 2.4834 | 2.5242 |
| 1.2 | 343.3131 | 649.052 | 731.0381 | 2.8 | 0.9636 | 1.2427 | 1.2429 |
| 1.4 | 149.1631 | 270.5546 | 300.6443 | 3.0 | 0.4784 | 0.6134 | 0.6141 |
| 1.6 | 68.7164 | 108.0098 | 123.7143 | 3.2 | 0.2375 | 0.3034 | 0.3034 |
| 1.8 | 41.9501 | 48.5129 | 50.9582 | 3.4 | 0.1065 | 0.1499 | 0.1499 |
| 2.0 | 20.6140 | 20.0634 | 21.7069 | 3.6 | 0.0529 | 0.074 | 0.0741 |
| 2.2 | 9.4386 | 9.6683 | 10.4227 | 3.8 | 0.0262 | 0.0366 | 0.0366 |
| 2.4 | 5.1001 | 4.4739 | 5.1279 | 4.0 | 0.0141 | 0.0181 | 0.0181 |


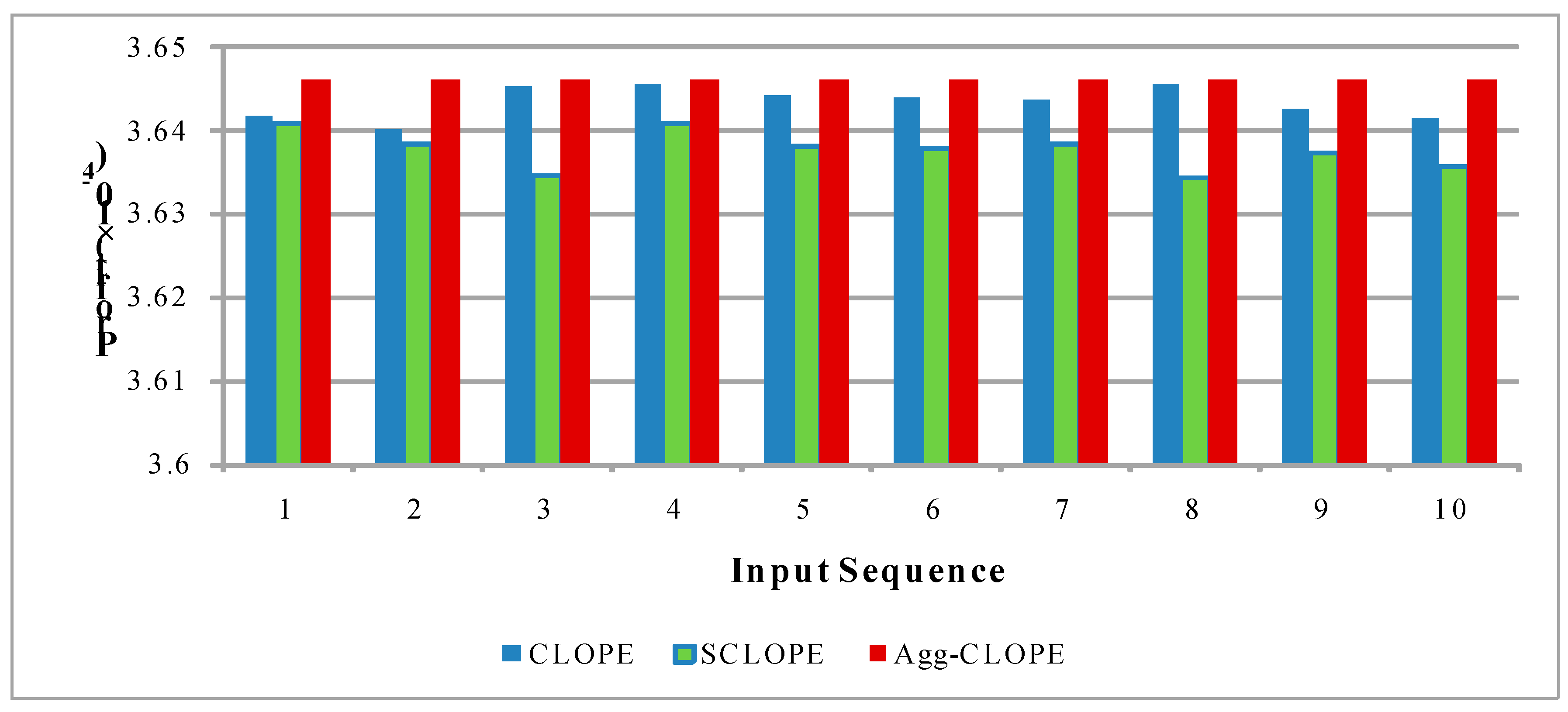
4.2. The Splice-junction Gene Sequences Dataset
| r | CLOPE | SCLOPE | Agg-CLOPE | r | CLOPE | SCLOPE | Agg-CLOPE |
|---|---|---|---|---|---|---|---|
| 1.0 | 398.0057 | 671.4143 | 790.0327 | 2.6 | 1.9059 × 10−3 | 1.9066 × 10−3 | 1.9086 × 10−3 |
| 1.2 | 201.1890 | 256.7411 | 263.9993 | 2.8 | 8.3294 × 10−4 | 8.3264 × 10−4 | 8.3408 × 10−4 |
| 1.4 | 47.9589 | 81.7548 | 88.2186 | 3.0 | 3.6453 × 10−4 | 3.6395 × 10−4 | 3.6459 × 10−4 |
| 1.6 | 16.0532 | 28.5838 | 29.4792 | 3.2 | 1.5947 × 10−4 | 1.5921 × 10−4 | 1.5960 × 10−4 |
| 1.8 | 4.9876 | 9.3903 | 9.8508 | 3.4 | 6.9867 × 10−5 | 6.9718 × 10−5 | 6.9912 × 10−5 |
| 2.0 | 1.0539 | 0.1744 | 3.2666 | 3.6 | 3.0626 × 10−5 | 3.0527 × 10−5 | 3.0643 × 10−5 |
| 2.2 | 0.0100 | 9.9808 × 10−3 | 0.0100 | 3.8 | 1.3428 × 10−5 | 1.3379 × 10−5 | 1.3443 × 10−5 |
| 2.4 | 4.3660 × 10−3 | 4.3463 × 10−3 | 4.3731 × 10−3 | 4.0 | 5.8913 × 10−6 | 5.8686 × 10−6 | 5.8998 × 10−6 |

5. Conclusion
- (1)
- We might specify an additional parameter to limit the number of iterative rounds so that the algorithm would terminate earlier.
- (2)
- We might specify the upper or lower bound to limit the number of clusters produced by the algorithm, which might also stop the iteration ahead of time.
- (3)
- We might apply this algorithm on a distributed environment such as MapReduce framework so that the input dataset can be divided into smaller parts and executed on multiple machines in parallel.
Acknowledgements
Author Contributions
Conflicts of Interest
References
- He, Z.Y.; Xu, X.F.; Deng, S.C. A cluster ensemble method for clustering categorical data. Inf. Fusion 2005, 6, 143–151. [Google Scholar] [CrossRef]
- Gibson, D.; Kleiberg, J.; Raghavan, P. Clustering categorical data: An approach based on dynamic systems. In Proceedings of the VLDB’98, New York, NY, USA, 24–27 August 1998.
- Guha, S.; Rastogi, R.; Shim, K. A robust clustering algorithm for categorical attributes. In Proceedings of the ICDE’99, Sydney, Australia, 23–26 March 1999.
- Wang, K.; Xu, C.; Liu, B. Clustering transactions using large items. In Proceedings of the CIKM’99, Kansas City, MI, USA, 2–6 November 1999.
- He, Z.; Xu, X.; Deng, S. Squeezer: An efficient algorithm for clustering categorical data. J. Comp. Sci. Tech. 2002, 17, 611–624. [Google Scholar] [CrossRef]
- Yang, Y.; Guan, S.; You, J. CLOPE: A fast and effective clustering algorithm for transactional data. In Proceedings of the KDD’02, Edmonton, AB, Canada, 23–23 July 2002.
- Barbará, D.; Li, Y.; Couto, J. COOLCAT: An entropy-based algorithm for categorical clustering. In Proceedings of the CIKM’02, McLean, VA, USA, 4–9 November 2002.
- Ong, K.L.; Li, W.Y.; Ng, W.K. SCLOPE: An algorithm for clustering data streams of categorical attributes. In LCNS 3181: Knowledge-Based Intelligent Information and Engineering Systems; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3181, pp. 209–218. [Google Scholar]
- Yap, P.H.; Ong, K.L. σ-SCLOPE: Clustering categorical streams using attribute selection. In LCNS 3682: Knowledge-Based Intelligent Information and Engineering Systems; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3682, pp. 929–935. [Google Scholar]
- Aggarwal, C.C.; Han, J.W.; Wang, J.Y.; Yu, P.S. A framework for clustering evolving data streams. In Proceedings of the VLDB’03, Berlin, Germany, 9–12 September 2003.
- Han, J.W.; Pei, J.; Yin, Y.W. Mining frequent patterns without candidate generation. ACM Sigmod Rec. 2000, 29, 1–12. [Google Scholar] [CrossRef]
- Li, J.; Gao, X.B.; Jiao, L.C. A fuzzy CLOPE algorithm and its optimal parameter choice. J. Electr. 2006, 23, 384–388. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The elements of statistical learning: Data mining, inference, and prediction, 2nd ed.; Springer Verlag: New York, NY, USA, 2009; Volume 2, pp. 520–528. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Le, J.; Wang, M. Improving CLOPE’s Profit Value and Stability with an Optimized Agglomerative Approach. Algorithms 2015, 8, 380-394. https://doi.org/10.3390/a8030380
Li Y, Le J, Wang M. Improving CLOPE’s Profit Value and Stability with an Optimized Agglomerative Approach. Algorithms. 2015; 8(3):380-394. https://doi.org/10.3390/a8030380
Chicago/Turabian StyleLi, Yefeng, Jiajin Le, and Mei Wang. 2015. "Improving CLOPE’s Profit Value and Stability with an Optimized Agglomerative Approach" Algorithms 8, no. 3: 380-394. https://doi.org/10.3390/a8030380
APA StyleLi, Y., Le, J., & Wang, M. (2015). Improving CLOPE’s Profit Value and Stability with an Optimized Agglomerative Approach. Algorithms, 8(3), 380-394. https://doi.org/10.3390/a8030380





