Identification of Dual-Rate Sampled Hammerstein Systems with a Piecewise-Linear Nonlinearity Using the Key Variable Separation Technique
Abstract
:1. Introduction
2. The Description of the Dual-Rate Hammerstein System
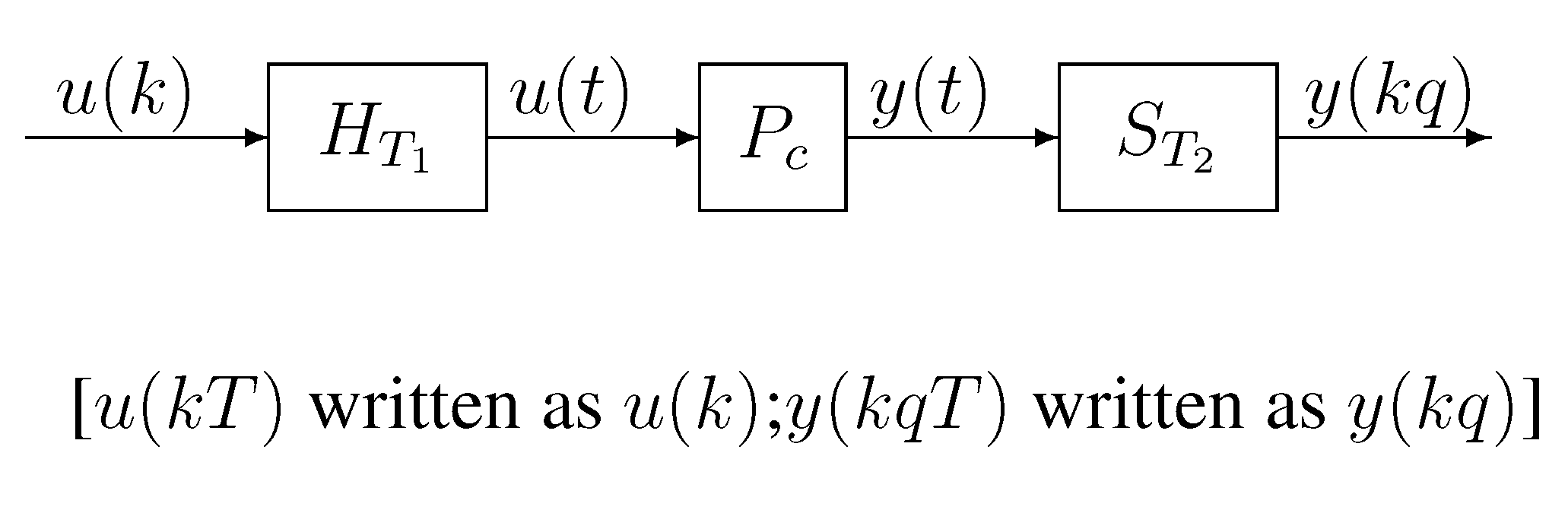
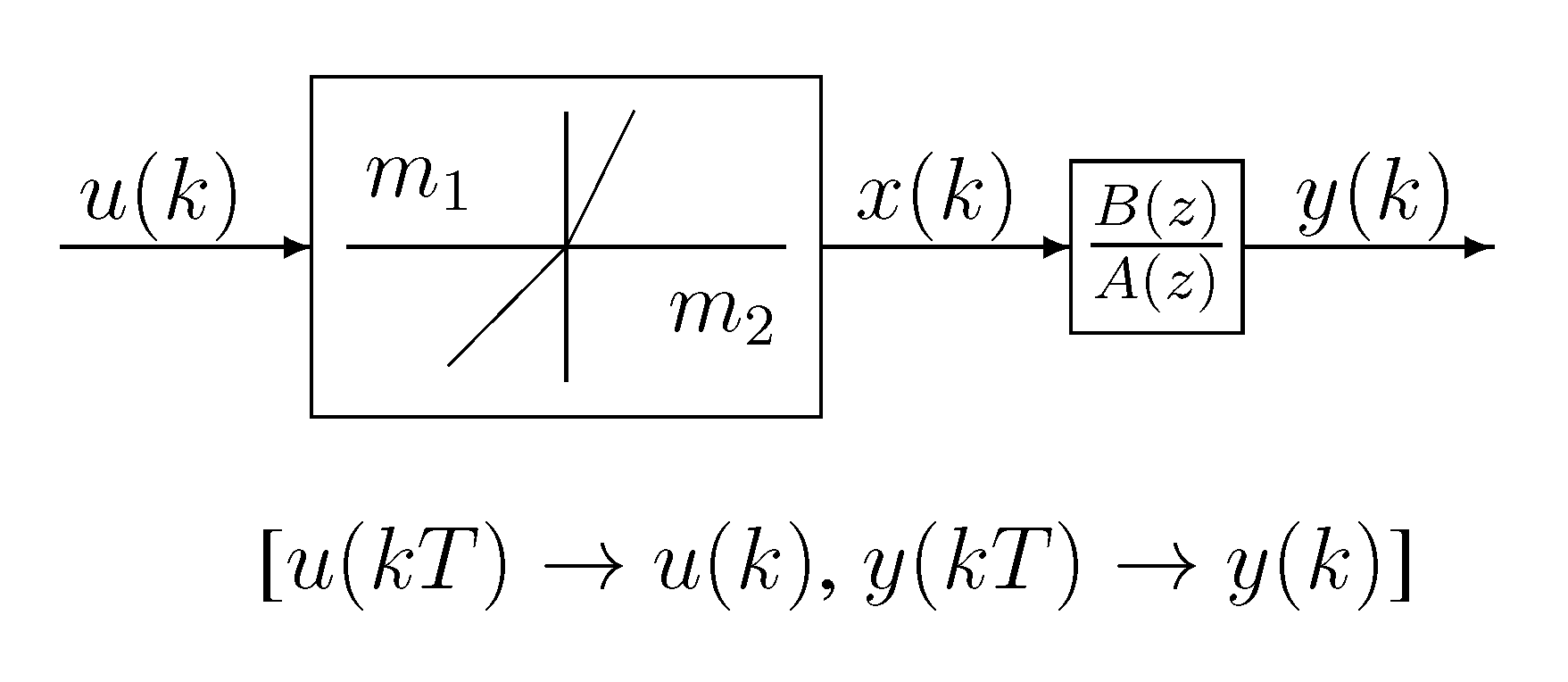
- For the dual-rate Hammerstein system in this paper, all of the input data {u(k) : k = 0, 1, 2, …} are measurable; only a part of the output data {y(kq) : k = 0, 1, 2, …} can be measured, where q ≥ 2 is a positive integer. Intersample outputs (missing outputs) {y(kq − i) : k = 0, 1, 2, …, 0 < i < q} are unknown. Because there exist unavailable outputs y(kq − i) in the information vector ϕ(kq), with kq − i not equaling the integer multiples of q, the single-rate model in Equation (5) cannot be used as the identification model for the dual-rate system.
- Moreover, the single-rate model in Equation (5) contains the products of the parameters of the nonlinear block and the linear block, i.e., the output of the model is a bilinear function about the parameter vectors and M, and a standard least squares method cannot be directly applied to the model.
3. The Dual-Rate Identification Model of the Hammerstein System
4. The Dual-Rate/Single-Rate Parameter Estimation
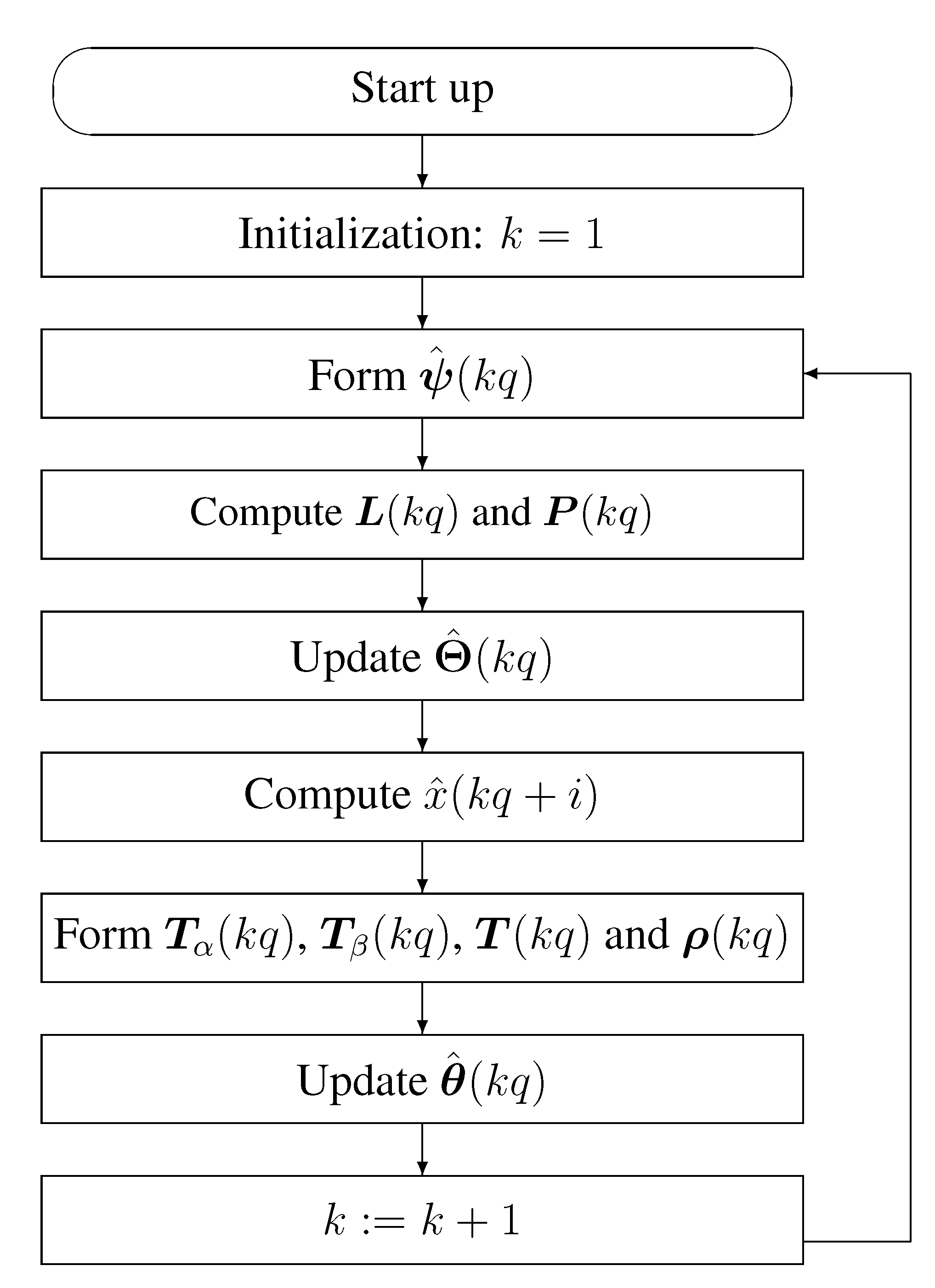
- Step 1. To initialize, let k = 1 and (0) = 1nq+n+2/p0, and P(0) = p0I, (kq) = 0; u(k) = 0; y(k) = 0, for k ≤ 0, p0 = 106.
- Step 4. Update the dual-rate parameter estimate by Equation (14).
- Step 5. Compute by Equation (18).
- Step 7. Update the single-rate parameter estimate by Equation (26).
- Step 8. Increase k by one and go to Step 2.
5. The Convergence Analysis
6. Experiment
| σ2 | 0.502 | 1.002 | ||||||
|---|---|---|---|---|---|---|---|---|
| t | 100 | 1000 | 2000 | 3000 | 100 | 1000 | 2000 | 3000 |
| = 1.5000 | 1.64510 | 1.49306 | 1.48069 | 1.48674 | 1.64332 | 1.47369 | 1.45489 | 1.46773 |
| =−1.0000 | −1.10137 | −1.00671 | −0.98836 | −0.99494 | −1.07085 | −0.98956 | −0.96557 | −0.98115 |
| = 0.6000 | 0.44924 | 0.56619 | 0.58761 | 0.60112 | 0.46040 | 0.54639 | 0.58138 | 0.60706 |
| = 0.0900 | −0.02088 | 0.04436 | 0.07612 | 0.08695 | −0.07241 | 0.04529 | 0.09448 | 0.10813 |
| = −0.4000 | −0.10421 | −0.33348 | −0.35710 | −0.36657 | −0.13676 | −0.33817 | −0.35584 | −0.36336 |
| = −0.2100 | −0.16787 | −0.18590 | −0.20263 | −0.20855 | −0.14399 | −0.16044 | −0.19223 | −0.20651 |
| =−0.7400 | −0.70650 | −0.75683 | −0.74221 | −0.73669 | −0.77498 | −0.75709 | −0.72961 | −0.72063 |
| = 0.1225 | 0.15543 | 0.14357 | 0.12683 | 0.12660 | 0.18953 | 0.13963 | 0.11305 | 0.11506 |
| =0.0000 | 18.97213 | 4.54356 | 2.51473 | 1.76071 | 18.54456 | 5.34749 | 3.71454 | 2.84976 |
| σ2 | 0.502 | 1.002 | ||||||
|---|---|---|---|---|---|---|---|---|
| t | 100 | 1000 | 2000 | 3000 | 100 | 1000 | 2000 | 3000 |
| = 1.5000 | 1.64332 | 1.47369 | 1.45489 | 1.46773 | 1.64510 | 1.49306 | 1.48069 | 1.48674 |
| =−1.0000 | −1.07085 | −0.98956 | −0.96557 | −0.98115 | −1.10137 | −1.00671 | −0.98836 | −0.99494 |
| = 0.2000 | −0.13036 | 0.18131 | 0.18225 | 0.16469 | −0.16282 | 0.13686 | 0.15786 | 0.15793 |
| =−0.3500 | −0.28358 | −0.40123 | −0.36730 | −0.34446 | −0.21271 | −0.36634 | −0.35419 | −0.34545 |
| = 0.8000 | 0.33046 | 0.72731 | 0.76196 | 0.77122 | 0.28415 | 0.70397 | 0.74542 | 0.75947 |
| = 0.6000 | 0.36387 | 0.50014 | 0.56053 | 0.58345 | 0.40609 | 0.51357 | 0.55673 | 0.57349 |
| =0.0000 | 30.68012 | 6.56738 | 3.93705 | 2.92556 | 33.17133 | 6.90524 | 4.02630 | 3.13498 |
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Igbida, N.; Karami, F.; Ta, T.N.N. Discrete collapsing sandpile model. Nonlinear Anal. 2014, 99, 177–189. [Google Scholar] [CrossRef]
- Zaslavski, A.J. Stability of a turnpike phenomenon for approximate solutions of nonautonomous discrete-time optimal control systems. Nonlinear Anal. 2014, 100, 1–22. [Google Scholar] [CrossRef]
- Chen, J.; Lv, L.X.; Ding, R.F. Multi-innovation stochastic gradient algorithms for dual-rate sampled systems with preload nonlinearity. Appl. Math. Lett. 2013, 26, 124–129. [Google Scholar] [CrossRef]
- Chen, J. Several gradient parameter estimation algorithms for dual-rate sampled systems. J. Frankl. Inst. 2014, 351, 543–554. [Google Scholar] [CrossRef]
- Kumbasar, E.P.A.; Aydin, H.; Ondogan, Z.; Ozcelik, M.; Ondogan, E.N. Automatic indigo measurement system as part of a dosing system for indigo Dyeing. Fibres Text. East. Eur. 2006, 14, 86–90. [Google Scholar]
- Ding, J.; Ding, F.; Liu, X.P.; Liu, G. Hierarchical least squares identification for linear SISO systems with dual-rate sampled-data. IEEE Trans. Automat. Control 2011, 56, 2677–2683. [Google Scholar] [CrossRef]
- Liu, Y.J.; Ding, F.; Shi, Y. An efficient hierarchical identification method for general dual-rate sampled-data systems. Automatica 2014, 50, 962–973. [Google Scholar] [CrossRef]
- Huang, J.; Shi, Y.; Huang, H.N.; Li, Z. l2-l∞ filtering for multirate nonlinear sampled-data systems using T-S fuzzy models. Digit. Signal Proc. 2013, 23, 418–426. [Google Scholar] [CrossRef]
- Haber, R.; Keviczky, L. Nonlinear System Identification-Input-Output Modeling Approach; Kluwer Academic Publishers: Dorchrecht, The Netherlands; Boston, MA, USA; London, UK, 1999. [Google Scholar]
- Vörös, J. Parameter identification of Wiener systems with multisegment piecewise-linear nonlinearities. Syst. Control Lett. 2007, 56, 99–105. [Google Scholar] [CrossRef]
- Chidambaram, M. Computer Control of Processes; CRC Press: New York, NY, USA, 2001. [Google Scholar]
- Wang, D.Q.; Chu, Y.Y.; Yang, G.W.; Ding, F. Auxiliary model-based recursive generalized least squares parameter estimation for Hammerstein OEAR systems. Math. Comput. Model. 2010, 52, 309–317. [Google Scholar] [CrossRef]
- Vörös, J. Iterative algorithm for parameter identification of Hammerstein systems with two-segment nonlinearities. IEEE Trans. Automat. Control 1999, 44, 2145–2149. [Google Scholar] [CrossRef]
- Vörös, J. Identification of Hammerstein systems with time-varying piecewise-linear chatacteristics. IEEE Trans. Circuits Syst. II 2005, 52, 865–869. [Google Scholar] [CrossRef]
- Vörös, J. Identification of nonlinear cascade systems with time-varying backlash. J. Electr. Eng. 2011, 62, 87–92. [Google Scholar] [CrossRef]
- Deng, K.P.; Ding, F. Newton iterative identification method for an input nonlinear finite impulse response system with moving average noise using the key variables separation technique. Nonlinear Dyn. 2014, 76, 1195–1202. [Google Scholar] [CrossRef]
- Li, J.H. Parameter estimation for Hammerstein CARARMA systems based on the Newton iteration. Appl. Math. Lett. 2013, 26, 91–96. [Google Scholar] [CrossRef]
- Wang, C.; Tang, T. Recursive least squares estimation algorithm applied to a class of linear-in-parameters output error moving average systems. Appl. Math. Lett. 2014, 29, 36–41. [Google Scholar] [CrossRef]
- Salimifard, M.; Jafari, M.; Dehghani, M. Identification of nonlinear MIMO block-oriented systems with moving average noises using gradient based and least squares based iterative algorithms. Neurocomputing 2012, 94, 22–31. [Google Scholar] [CrossRef]
- Ding, F.; Liu, X.P.; Yang, H.Z. Parameter identification and intersample output estimation for dual-rate systems. IEEE Trans. Syst. Man Cybern. Part A 2008, 38, 966–975. [Google Scholar] [CrossRef]
- Ding, F.; Liu, X.P.; Liu, G. Identification methods for Hammerstein nonlinear systems. Digit. Signal Proc. 2011, 21, 215–238. [Google Scholar] [CrossRef]
- Goodwin, G.C.; Sin, K.S. Adaptive Filtering, Prediction and Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Ding, F.; Chen, T. Hierarchical least squares identification methods for multivariable systems. IEEE Trans. Automat. Control 2005, 50, 397–402. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.-Y.; Wang, X.-D.; Wang, D.-Q. Identification of Dual-Rate Sampled Hammerstein Systems with a Piecewise-Linear Nonlinearity Using the Key Variable Separation Technique. Algorithms 2015, 8, 366-379. https://doi.org/10.3390/a8030366
Wang Y-Y, Wang X-D, Wang D-Q. Identification of Dual-Rate Sampled Hammerstein Systems with a Piecewise-Linear Nonlinearity Using the Key Variable Separation Technique. Algorithms. 2015; 8(3):366-379. https://doi.org/10.3390/a8030366
Chicago/Turabian StyleWang, Ying-Ying, Xiang-Dong Wang, and Dong-Qing Wang. 2015. "Identification of Dual-Rate Sampled Hammerstein Systems with a Piecewise-Linear Nonlinearity Using the Key Variable Separation Technique" Algorithms 8, no. 3: 366-379. https://doi.org/10.3390/a8030366
APA StyleWang, Y.-Y., Wang, X.-D., & Wang, D.-Q. (2015). Identification of Dual-Rate Sampled Hammerstein Systems with a Piecewise-Linear Nonlinearity Using the Key Variable Separation Technique. Algorithms, 8(3), 366-379. https://doi.org/10.3390/a8030366





