On String Matching with Mismatches
Abstract
:1. Introduction
1.1. Pattern Matching with Mismatches
1.2. Pattern Matching with K Mismatches
1.3. Our Results
- An algorithm for pattern matching with mismatches and wild cards that runs in time, where g is the number of non-wild card positions in the pattern; see Section 2.2.1.
- A randomized algorithm that approximates the Hamming distance for every alignment, when wild cards are present, within an ϵ factor in time with high probability; see Section 2.3.
- An algorithm for pattern matching with k mismatches, without wild cards, that runs in time; this algorithm is simpler and has a better expected run time than the one in [11]; see Section 2.2.3.
- An algorithm that tests if the Hamming distance is less than k for a subset of the alignments, without wild cards, at a cost of time per alignment, using only additional memory; see Section 2.2.2.
- A Las Vegas algorithm for the k mismatches problem with wild cards that runs in time with high probability; see Section 2.4.3.
2. Materials and Methods
2.1. Some Definitions
2.2. Deterministic Algorithms
| Algorithm 1: |
 |
2.2.1. Pattern Matching with Mismatches
2.2.2. Pattern Matching with K Mismatches
2.2.3. An Time Algorithm for K Mismatches
| Algorithm 2: Subset k mismatches() |
 |
| Algorithm 3: Knapsack k mismatches() |
 |
2.3. Approximate Counting of Mismatches
| Algorithm 4: |
 |
2.4. A Las Vegas Algorithm for K Mismatches
2.4.1. The 1 Mismatch Problem
- Compute for . Note that will be zero if and P match (assuming that a wild card can be matched with any character). . Thus, this step can be completed with three convolution operations.
- Compute for , where (for . Like Step 1, this step can also be completed with three convolution operations.
- Let if , for . Note that if the Hamming distance between and P is exactly one, then will give the position in the text where this mismatch occurs.
- If for any i (), and if , then we conclude that the Hamming distance between and P is exactly one.
2.4.2. The Randomized Algorithms of [17]
2.4.3. A Las Vegas Algorithm
| Algorithm 7: |
 |
3. Results
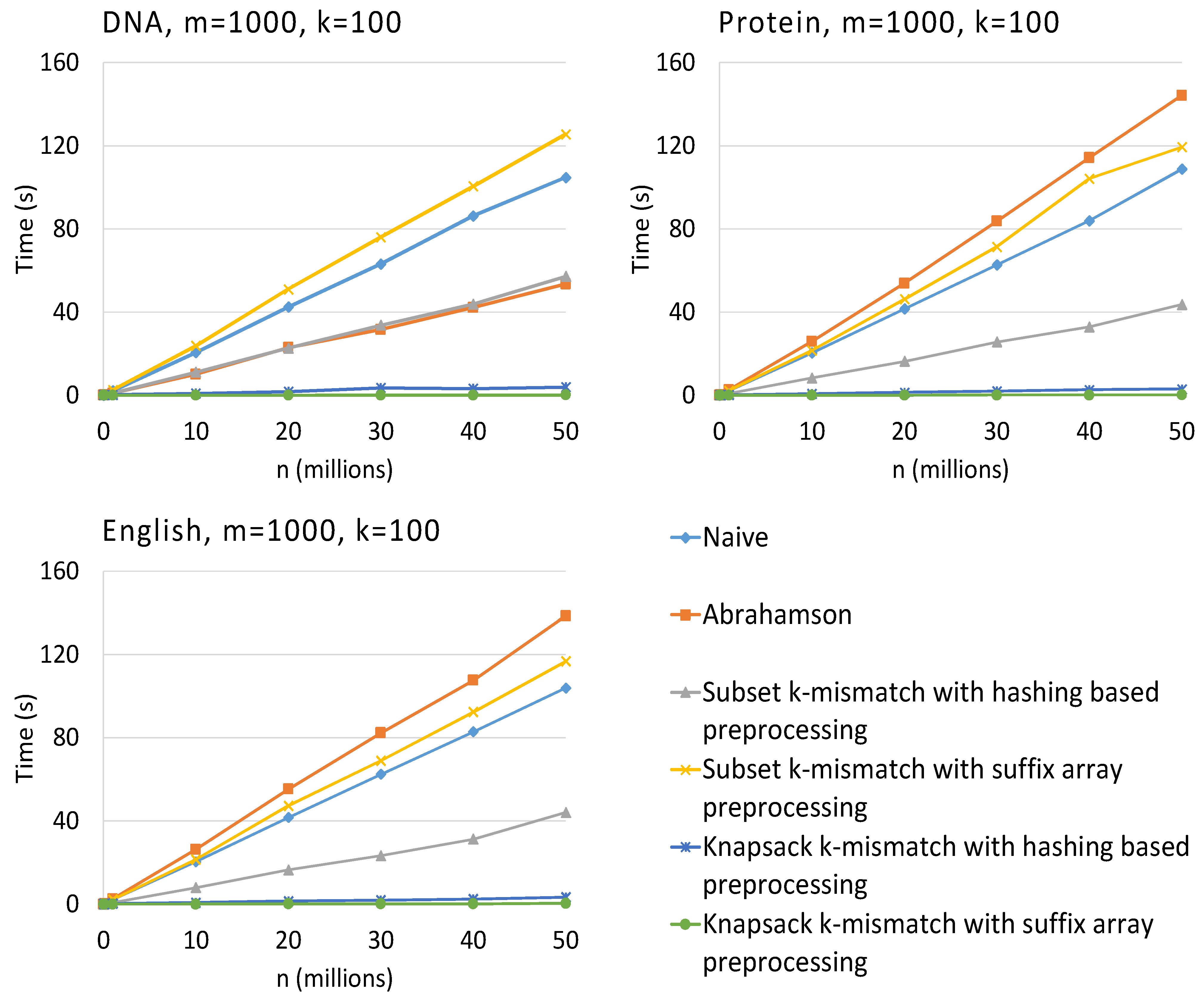
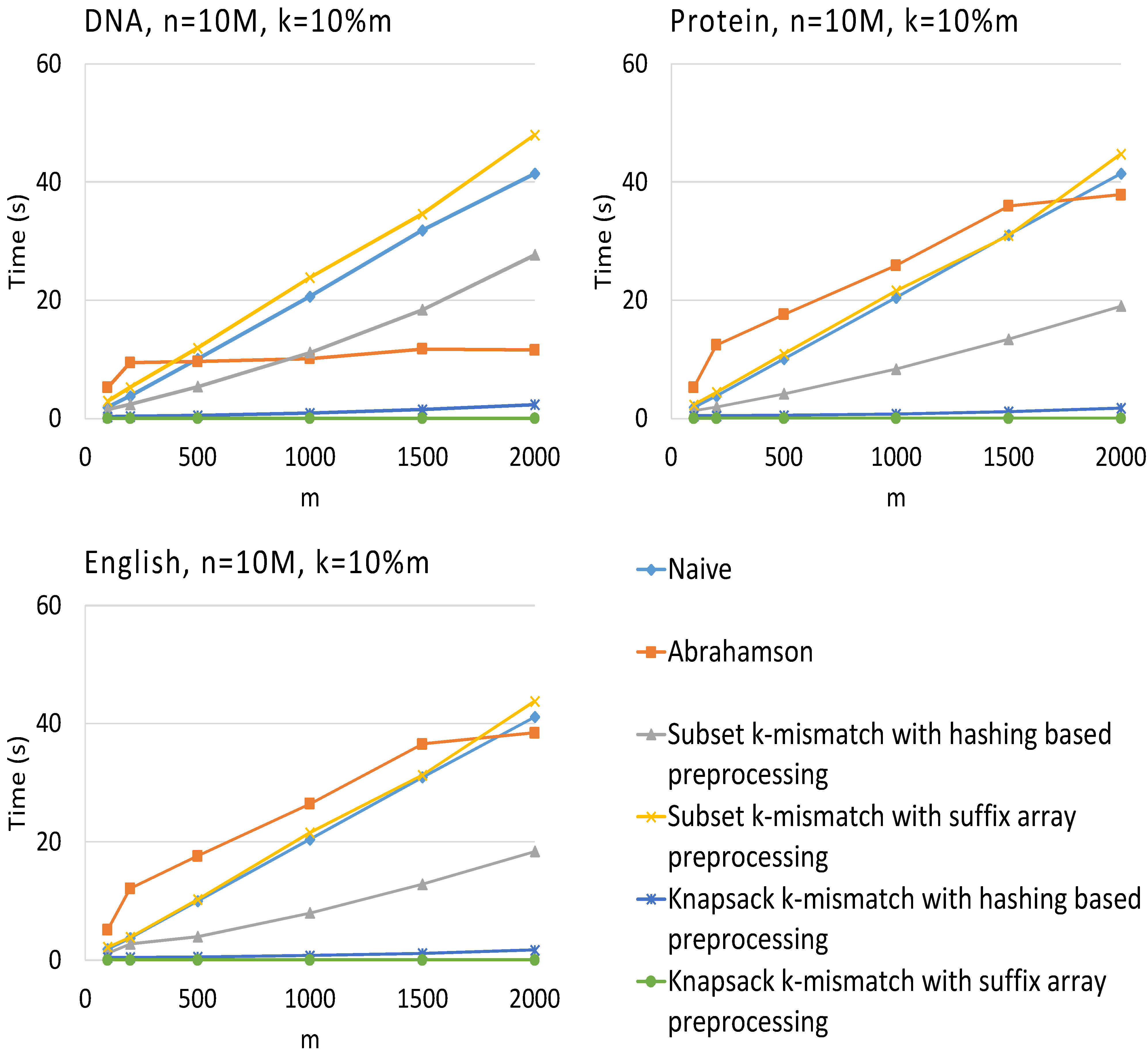

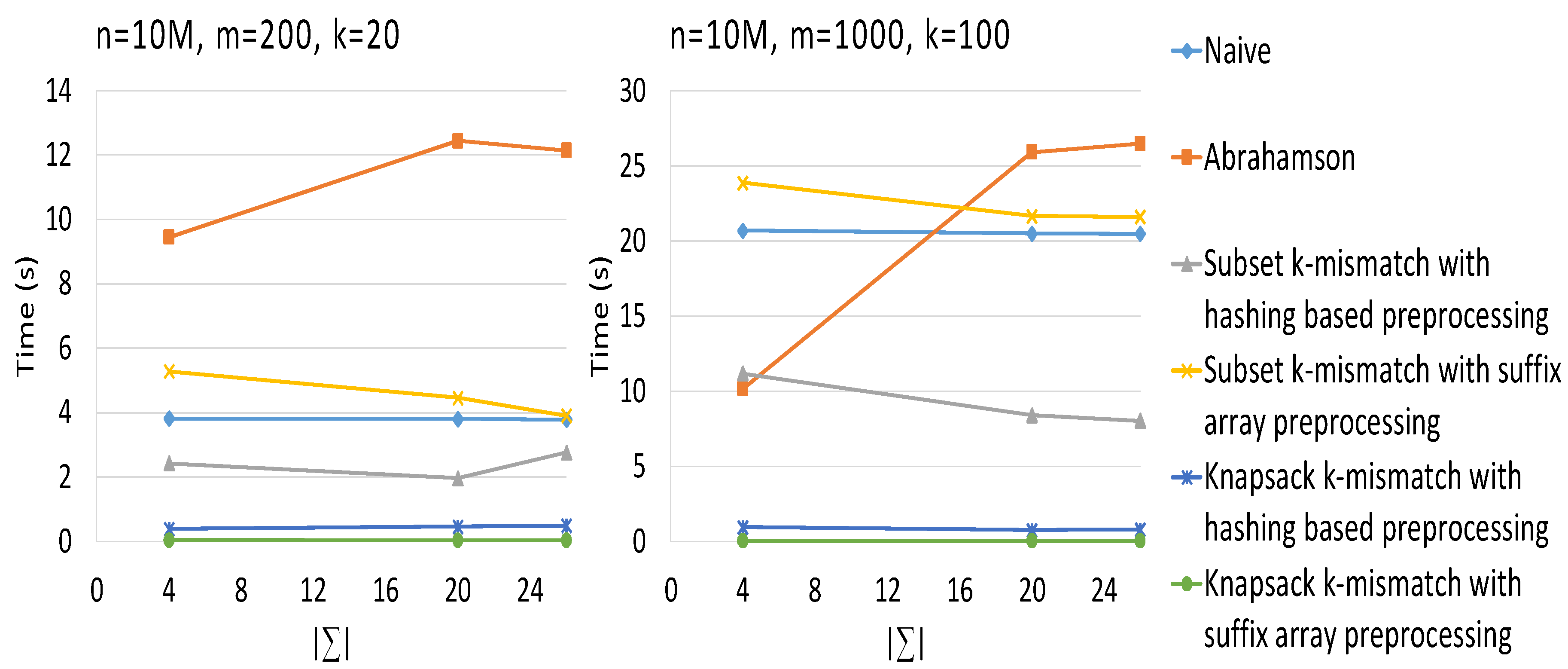
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Knuth, D.E.; Morris, J.H., Jr.; Pratt, V.R. Fast Pattern Matching in Strings. SIAM J. Comput. 1977, 6, 323–350. [Google Scholar] [CrossRef]
- Aho, A.V.; Corasick, M.J. Efficient string matching: An aid to bibliographic search. Commun. ACM 1975, 18, 333–340. [Google Scholar] [CrossRef]
- Fischer, M.J.; Paterson, M.S. String-Matching and Other Products; Technical Report MAC-TM-41; Massachusetts Institute of Technology Cambridge Project MAC: Cambridge, MA, USA, 1974. [Google Scholar]
- Indyk, P. Faster Algorithms for String Matching Problems: Matching the Convolution Bound. In Proceedings of the 39th Symposium on Foundations of Computer Science, Palo Alto, CA, USA, 8–11 November 1998; pp. 166–173.
- Kalai, A. Efficient pattern-matching with don't cares. In Proceedings of the thirteenth annual ACM-SIAM symposium on Discrete algorithms; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. SODA ’02. pp. 655–656. [Google Scholar]
- Clifford, P.; Clifford, R. Simple deterministic wildcard matching. Inf. Process. Lett. 2007, 101, 53–54. [Google Scholar] [CrossRef]
- Cole, R.; Hariharan, R.; Indyk, P. Tree pattern matching and subset matching in deterministic O(n log3 n)-time. In Proceedings of the Tenth Annual ACM-SIAM Symposium on Discrete Algorithms, Baltimore, MD, USA, 17–19 January 1999; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. SODA '99. pp. 245–254. [Google Scholar]
- Navarro, G. A guided tour to approximate string matching. ACM Comput. Surv. 2001, 33, 31–88. [Google Scholar] [CrossRef]
- Navarro, G.; Raffinot, M. Flexible Pattern Matching in Strings–Practical on-Line Search Algorithms for Texts and Biological Sequences; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Abrahamson, K. Generalized String Matching. SIAM J. Comput. 1987, 16, 1039–1051. [Google Scholar] [CrossRef]
- Amir, A.; Lewenstein, M.; Porat, E. Faster algorithms for string matching with k mismatches. J. Algorithms 2004, 50, 257–275. [Google Scholar] [CrossRef]
- Atallah, M.J.; Chyzak, F.; Dumas, P. A randomized algorithm for approximate string matching. Algorithmica 2001, 29, 468–486. [Google Scholar] [CrossRef]
- Karloff, H. Fast algorithms for approximately counting mismatches. Inf. Process. Lett. 1993, 48, 53–60. [Google Scholar] [CrossRef]
- Clifford, R.; Efremenko, K.; Porat, B.; Porat, E. A black box for online approximate pattern matching. In Combinatorial Pattern Matching; Springer: Berlin Heidelberg, Germany, 2008; pp. 143–151. [Google Scholar]
- Porat, B.; Porat, E. Exact and Approximate Pattern Matching in the Streaming Model. In Proceedings of the (FOCS '09) 50th Annual IEEE Symposium on Foundations of Computer Science; 2009; pp. 315–323. [Google Scholar]
- Porat, E.; Lipsky, O. Improved sketching of Hamming distance with error correcting. In Combinatorial Pattern Matching; Springer: Berlin Heidelberg, Germany, 2007; pp. 173–182. [Google Scholar]
- Clifford, R.; Efremenko, K.; Porat, E.; Rothschild, A. k-mismatch with don't cares. In Algorithms–ESA 2007; Springer: Berlin Heidelberg, Germany, 2007; pp. 151–162. [Google Scholar]
- Clifford, R.; Efremenko, K.; Porat, B.; Porat, E.; Rothschild, A. Mismatch Sampling. Inf. Comput. 2012, 214, 112–118. [Google Scholar] [CrossRef]
- Landau, G.M.; Vishkin, U. Efficient string matching in the presence of errors. In Proceedings of the 26th Annual Symposium on Foundations of Computer Science, Portland, OR, USA, 21–23 October; 1985; pp. 126–136. [Google Scholar]
- Galil, Z.; Giancarlo, R. Improved string matching with k mismatches. SIGACT News 1986, 17, 52–54. [Google Scholar] [CrossRef]
- Clifford, R.; Efremenko, K.; Porat, E.; Rothschild, A. From coding theory to efficient pattern matching. In Proceedings of the Twentieth Annual ACM-SIAM Symposium on Discrete Algorithms, New York, New York, USA, 4–6 January, 2009; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009. SODA '09. pp. 778–784. [Google Scholar]
- Clifford, R.; Porat, E. A filtering algorithm for k-mismatch with don't cares. Inf. Process. Lett. 2010, 110, 1021–1025. [Google Scholar] [CrossRef]
- Fredriksson, K.; Grabowski, S. Combinatorial Algorithms; Springer-Verlag: Berlin, Germany, 2009; Chapter Fast Convolutions and Their Applications in Approximate String Matching; pp. 254–265. [Google Scholar]
- Chernoff, H. A Measure of Asymptotic Efficiency for Tests of a Hypothesis Based on the Sum of Observations. Ann. Math. Stat. 1952, 2, 241–256. [Google Scholar] [CrossRef]
- Kasai, T.; Lee, G.; Arimura, H.; Arikawa, S.; Park, K. Linear-Time Longest-Common-Prefix Computation in Suffix Arrays And Its Applications; Springer-Verlag: Berlin, Germany, 2001; pp. 181–192. [Google Scholar]
- Bender, M.; Farach-Colton, M. The LCA Problem Revisited. In LATIN 2000: Theoretical Informatics; Gonnet, G., Viola, A., Eds.; Springer: Berlin, Germany, 2000; Volume1776, pp. 88–94. [Google Scholar]
- Ferragina, P.; Manzini, G. Opportunistic data structures with applications. In Proceedings of the IEEE 41st Annual Symposium on Foundations of Computer Science, Redondo Beach, CA, USA, 12–14 November; 2000; pp. 390–398. [Google Scholar]
- Frigo, M.; Johnson, S.G. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef]
- Rajasekaran, S.; Nicolae, M. An elegant algorithm for the construction of suffix arrays. J. Discrete Algorithms 2014, 27, 21–28. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicolae, M.; Rajasekaran, S. On String Matching with Mismatches. Algorithms 2015, 8, 248-270. https://doi.org/10.3390/a8020248
Nicolae M, Rajasekaran S. On String Matching with Mismatches. Algorithms. 2015; 8(2):248-270. https://doi.org/10.3390/a8020248
Chicago/Turabian StyleNicolae, Marius, and Sanguthevar Rajasekaran. 2015. "On String Matching with Mismatches" Algorithms 8, no. 2: 248-270. https://doi.org/10.3390/a8020248
APA StyleNicolae, M., & Rajasekaran, S. (2015). On String Matching with Mismatches. Algorithms, 8(2), 248-270. https://doi.org/10.3390/a8020248




