The Auxiliary Problem Principle with Self-Adaptive Penalty Parameter for Multi-Area Economic Dispatch Problem

Abstract

The auxiliary problem principle is a powerful tool for solving multi-area economic dispatch problem. One of the main drawbacks of the auxiliary problem principle method is that the convergence performance depends on the selection of penalty parameter. In this paper, we propose a self-adaptive strategy to adjust penalty parameter based on the iterative information, the proposed approach is verified by two given test systems. The corresponding simulation results demonstrate that the proposed self-adaptive auxiliary problem principle iterative scheme is robust in terms of the selection of penalty parameter and has better convergence rate compared with the traditional auxiliary problem principle method.

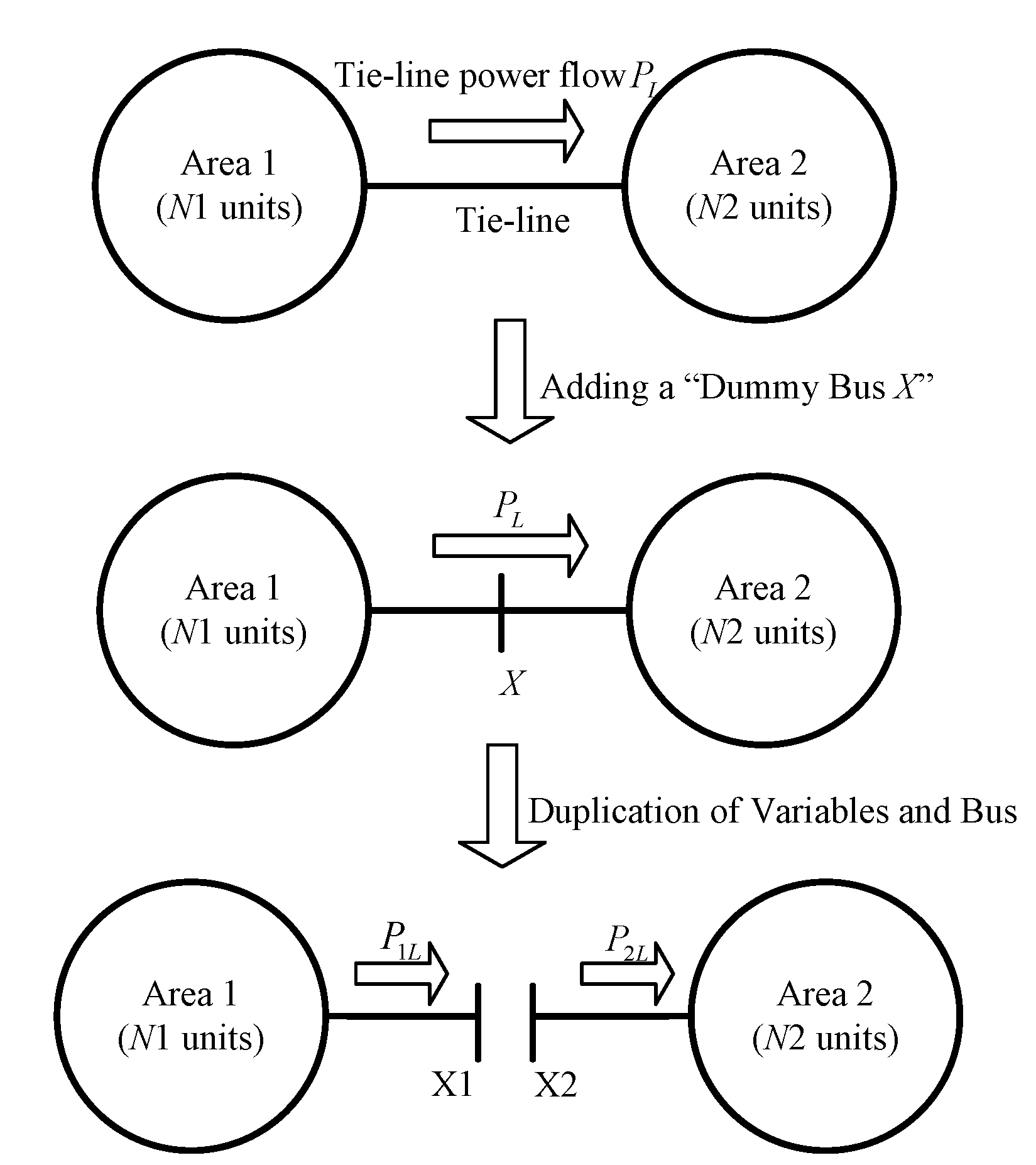
1. Introduction

The aim of economic dispatch (ED) problem in power systems field is to determine the allocation of real power outputs for the generating units economically while satisfying corresponding physical and operational constraints [1]. With the growing scale of power systems, traditional centered ED algorithm is inclined to bring many problems like disaster of dimensionality, bottleneck of network communication. Furthermore, the modern power systems are composed of numerous sub-networks interconnected by tie-lines, each sub-network has its own energy management system (EMS) and most data in sub-network is treated confidentially and used internally. Thus, it is necessary to propose a distributed algorithm and each sub-network only exchanges its boundary information with its neighbor sub-networks, rather than exchanging all data with all sub-networks in power systems.

Wei Yan proposed a new decomposition-coordination interior point method (DIPM) to tackle the multi-area optimal reactive power flow problem [2]. Actually, the proposed DIPM is parallel distributed algorithm. However, DIPM needs a coordinator server which communicates with all sub-systems for exchanging required information, a great deal of data interchange will lead to communication bottlenecks. Approximate Newton directions method is applied to address multi-area optimal power flow problem [3,4], the upside is that it allows the EMS in each sub-network to operate its system independently while obtaining an optimal coordinated but decentralized solution; the downside is that it is limited by strict condition which is a difficult requirement to meet in practice.

Auxiliary problem principle (APP) has been originally introduced by Cohen in 1980 [5], this method has been extensive applied in power systems field, such as daily generation scheduling optimization [6], unit commitment [7] and distributed optimal power flow [8,9]. However, APP method has a major drawback: it is very sensitive to the value of related penalty parameter, i.e., the convergence performance of APP will be poor if penalty parameter is selected improperly. Meanwhile, the suitable penalty parameter varies with different systems, it is impossible to obtain a generic penalty parameter in advance. In this paper, we propose a self-adaptive APP for solving multi-area economic dispatch (MAED) problem, the key is that penalty parameter is allowed to vary per iteration according to the iterate information for better convergence performance.

The rest of this paper is organized as follows. In section 2, we give the formulation of the multi-area economic dispatch problem. Then, section 3 describes the traditional auxiliary problem principle. After that, we propose a self-adaptive APP iterative scheme in section 4, during which the corresponding penalty parameter c is allowed to adjust based on the iterate message. In section 5, two test systems are given to verify the effectiveness of the proposed method, and we conclude in section 6.

2. The Formulation of Multi-Area Economic Dispatch

2.1. The Traditional MAED Formulation

The aim of MAED is to minimize the total production cost while satisfying various physical and operational constraints [10]. In this section, we employ a two-area economic dispatch formulation to illustrate the MAED problem.

The objective function F, which represents total generator fuel cost of two areas, can be written as

$$\begin{array}{l}\min \text{}F={\displaystyle {\sum }_{m=1}^2{\displaystyle {\sum }_{n=1}^{N_m}{f}_{mn}\left(P_{mn}\right)}}\\ ={\displaystyle {\sum }_{m=1}^2{\displaystyle {\sum }_{n=1}^{N_m}\left(a_{mn}{P}_{mn}^2+b_{mn}{P}_{mn}+c_{mn}\right)}}\end{array}$$

(1)

where P_mn is the real power output of the nth generating unit in area m. f_mn(P_mn) is the fuel cost function of the nth generating unit in area m and is usually expressed as a quadratic function without considering valve-point effect, the corresponding cost coefficients for f_mn(P_mn) are given as a_mn, b_mn, c_mn. N_m represents there are N_m generating units in area m. In addition, the objective function is minimized and subjected to the following physical constraints [11,12].

1) Real power balance constraints without considering transmission loss

$${\displaystyle {\sum }_{n=1}^{N_1}{P}_{1n}=P_{1D}+P_L}$$

(2)

$${\displaystyle {\sum }_{n=1}^{N_2}{P}_{2n}=P_{2D}-P_L}$$

(3)

where P_mD is the total demand in area m; P_L is the tie-line real power transfer between area 1 and area 2. P_L is positive when power flow transfers from area 1 to area 2. By contrast, P_L is negative when power flow transfers from area 2 to area 1.

2) Tie-line capacity constraints

$$\left|P_L\right|<P_{L,\max }$$

(4)

where P_L,max is the maximum tie-line power flow between area 1 and area 2.

3) Real power generation capacity constraints

$$P_{mn,\min }<P_{mn}<P_{mn,\max }$$

(5)

where P_mn,min and P_mn,max are the minimum and maximum generation limits of the nth generating unit n in area m.

2.2. Area-based Decentralization for MAED

Kim proposed a coarse-grained distributed optimal power flow method in [13]. Inspired by this idea, we add a “dummy bus X” between area1 and area 2, the corresponding variable for this “dummy bus” is tie-line power flow P_L. By duplicating the “dummy bus” as X1 and X2, we get two separated systems as shown in Fig. 1. Meanwhile, P_L is duplicated as P_1L and P_2L, i.e., a new consistency constraint $P_{1L}-P_{2L}=0$ is introduced. Then the equivalent form of traditional MAED problem can be expressed as follows.

$$\begin{array}{l}\min \text{}F={\displaystyle {\sum }_{m=1}^2{\displaystyle {\sum }_{n=1}^{N_m}{f}_{mn}\left(P_{mn}\right)}}\\ subjectto:{\displaystyle {\sum }_{n=1}^{N_1}{P}_{1n}=P_{1D}+P_{1L}}\\ {\displaystyle {\sum }_{n=1}^{N_2}{P}_{2n}=P_{2D}-P_{2L}}\\ P_{mn,\min }<P_{mn}<P_{mn,\min }\\ \left|P_{1L}\right|<P_{L,\max }\\ \left|P_{2L}\right|<P_{L,\max }\\ P_{1L}-P_{2L}=0\end{array}$$

(6)

For convenience, the compact form of problem (6) is expressed as follows.

$$\begin{array}{l}\min \text{}f\left(x_1\right)+g\left(x_2\right)\\ subjectto:x_1\in {\mathrm{\Omega }}_1,x_2\in {\mathrm{\Omega }}_2\\ \mathrm{\Theta }\left(x_1,x_2\right)\equiv A{x}_1+B{x}_2=0\end{array}$$

(7)

where $f\left(x_1\right)$ and $g\left(x_2\right)$ are total fuel cost in area 1 and area 2 respectively; $x_1={\left(P_{1,1},P_{1,2},\cdots ,P_{1,N_1},P_{1L}\right)}^T$ and $x_2={\left(P_{2,1},P_{2,2},\cdots ,P_{2,N_2},P_{2L}\right)}^T$ are the vectors of corresponding control variables in area 1 and area 2; ${\mathrm{\Omega }}_1$ and ${\mathrm{\Omega }}_2$ are feasible regions representing operational constraints on x₁ and x₂; equation $\mathrm{\Theta }\left(x_1,x_2\right)$ represents the new introduced consistency constraint, during which A and B are given matrices.

Figure 1. Decentralization of an interconnected power system.

Figure 1. Decentralization of an interconnected power system.

3. Auxiliary Problem Principle for MAED Problem

As shown in (7), it is clear that there is a coupling relationship between adjacent areas through the consistency constraint $\mathrm{\Theta }\left(x_1,x_2\right)$. In this section, with the concept of augmented lagrangian relaxation method and auxiliary problem principle, we will discuss how to divide the original problem (7) into independent sub-problems with the consistency constraint decoupled.

3.1. Augmented Lagrangian Relaxation Method

In this section, we first employ augmented lagrangian relaxation method to deal with the consistency constraint $\mathrm{\Theta }\left(x_1,x_2\right)$. Then, the problem (7) can be rewritten as follows.

$$\begin{array}{l}\min \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}f\left(x_1\right)+g\left(x_2\right)-{\lambda }^T\left(A{x}_1+B{x}_2\right)+\frac{c}{2}{\Vert A{x}_1+B{x}_2\Vert }^2\\ subjectto:x_1\in {\mathrm{\Omega }}_1\\ x_2\in {\mathrm{\Omega }}_2\end{array}$$

(8)

where $\lambda$ is the Lagrangian multiplier for $\mathrm{\Theta }\left(x_1,x_2\right)$; c>0 is the given penalty factor. $\Vert x\Vert =\sqrt{x^{T}x}$ denotes the Euclidean norm of vector x.

In addition, problem (8) is equivalent to solving a saddle-point problem via the following iterative scheme:

$\left(x_1^{k+1},x_2^{k+1}\right)$ is obtained by solving

$$\left(x_1^{k+1},x_2^{k+1}\right)=\arg \min \left\{f\left(x_1\right)+g\left(x_2\right)-{\lambda }^{T,k}\left(A{x}_1+B{x}_2\right)+\frac{c}{2}{\Vert A{x}_1+B{x}_2\Vert }^2|x_1\in {\mathrm{\Omega }}_1,x_2\in {\mathrm{\Omega }}_2\right\}$$

(9)

then, ${\lambda }^{k+1}$ is obtained by updating

$${\lambda }^{k+1}={\lambda }^k-c\left(A{x}_1^{k+1}+B{x}_2^{k+1}\right)$$

(10)

3.2. Auxiliary Problem Principle

In this section, we take advantage of auxiliary problem principle to cope with the non-separable quadratic term $\frac{c}{2}{\Vert A{x}_1+B{x}_2\Vert }^2$. The iterative scheme APP for solving problem (8) can be expressed as follows [14,15].

Step1. Compute

$$x_1^{k+1}=\arg \min \left\{f\left(x_1\right)-{\lambda }^{T,k}A{x}_1+\frac{c}{2}{\Vert A{x}_1+B{x}_2^k\Vert }^2+\frac{\beta -c}{2}{\Vert A{x}_1-A{x}_1^k\Vert }^2|x_1\in {\mathrm{\Omega }}_1\right\}$$

(11)

Step2. Compute

$$x_2^{k+1}=\arg \min \left\{g\left(x_2\right)-{\lambda }^{T,k}B{x}_2+\frac{c}{2}{\Vert A{x}_1^k+B{x}_2\Vert }^2+\frac{\beta -c}{2}{\Vert B{x}_2-B{x}_2^k\Vert }^2|x_2\in {\mathrm{\Omega }}_2\right\}$$

(12)

Step3. Lagrange multiplier updating

$${\lambda }^{k+1}={\lambda }^k-\epsilon \left(A{x}_1^k+B{x}_2^k\right)$$

(13)

Step4. Check the stop criterion. If

$$\max \left(\Vert {\lambda }^k-{\lambda }^{k+1}\Vert ,\Vert A{x}_1^k-A{x}_1^{k+1}\Vert ,\Vert B{x}_2^k-B{x}_2^{k+1}\Vert \right)<\eta$$

(14)

then stop. If not k=k+1, go to Step1.

where β is given APP parameter and ε denotes step size. The sufficient condition for convergence of APP iterative scheme is given as follow [13].

$$\epsilon <2c<\beta$$

(15)

Furthermore, experience on applications has illustrated that, for the given penalty parameter c, the selection of parameters β and ε has a significant influence on convergence performance of APP iterative scheme. Ren has pointed that APP iterative scheme can get the best convergence performance when $\beta \to 2c$ and $\epsilon =c$ [16]. Moreover, kim has pointed that convergence performance of APP was reliable with the choice [13]:

$$\epsilon \text{=}\frac{\beta }{2}\text{=}c$$

(16)

As a result, for the best convergence performance, we choice the APP parameters satisfying $\epsilon \text{=}c\text{=}\beta /2$ in this paper.

4. Auxiliary Problem Principle Method with Self-Adaptive Penalty Parameter

Although, the intrinsic relationship between parameters β, ε and c has been discussion in section 3.2, how to achieve proper parameters for APP proved to be a challenge. Experience on applications has shown that the convergence results depend on the selection of penalty parameter c; hence, it is important to estimate a proper penalty parameter. Inspired by Bingsheng He’s modified alternating direction method [17], we proposed a self-adaptive APP which makes progress in the choice of penalty parameter.

4.1. Motivation

Bingsheng He proposed a modified alternating direction method to deal with problem (8). To be more exact, this method adjusts the penalty parameter c based on the iterate message [17].

Now we give the details on how to adjust the penalty parameter c for better convergence performance. In fact, the solution of problem (8) is equivalent to finding a zero point e(w^k):

$$e\left(w^k\right)=\left[\begin{array}{l}{e}_{x_1}\left(w^k\right)\hfill \\ e_{x_2}\left(w^k\right)\hfill \\ e_{\lambda }\left(w^k\right)\hfill \end{array}\right]=\left[\begin{array}{l}{x}_1^k-P_{\mathrm{\Omega }1}\left\{x_1^k-\left[\nabla f\left(x_1^k\right)-A^T{\lambda }^k\right]\right\}\hfill \\ x_2^k-P_{\mathrm{\Omega }2}\left\{x_2^k-\left[\nabla g\left(x_2^k\right)-B^T{\lambda }^k\right]\right\}\hfill \\ A{x}_1^k+B{x}_2^k\hfill \end{array}\right]$$

(17)

where

$$w=\left(\begin{array}{l}{x}_1\hfill \\ x_2\hfill \\ \lambda \hfill \end{array}\right),W={\mathrm{\Omega }}_1\times {\mathrm{\Omega }}_2\times R^r,w^k\in W$$

(18)

$P_{\mathrm{\Omega }}(·)$ is the projection on Ω. $\nabla f(·)$ and $\nabla g(·)$ denote the gradient of $f(·)$ and $g(·)$ respectively.

Equation (17) offers us an inspiration on how to adjust penalty parameter c. For the sake of balance, we should adjust the penalty parameter c such that $\Vert e_{x_1}\left(w^k\right)\Vert \approx \Vert e_{x_2}\left(w^k\right)\Vert \approx \Vert e_{\lambda }\left(w^k\right)\Vert$, but it is always difficult to achieve. Fortunately, if we use alternating direction method to deal with problem (8), then we will find that [17]:

$$e_{x_2}\left(w^k\right)=x_2^k-P_{\mathrm{\Omega }2}\left\{x_2^k-\left[\nabla g\left(x_2^k\right)-B^T{\lambda }^k\right]\right\}=0$$

(19)

Now, we only need to adjust the penalty parameter c such that $\Vert e_{x_1}\left(w^k\right)\Vert \approx \Vert e_{\lambda }\left(w^k\right)\Vert$, it is relatively easy to be achieved. To be more exact, for an iterate $w^k$, if $\Vert e_{x_1}\left(w^k\right)\Vert \ll \Vert e_{\lambda }\left(w^k\right)\Vert$, we should increase penalty parameter c. By contrast, if $\Vert e_{x_1}\left(w^k\right)\Vert \gg \Vert e_{\lambda }\left(w^k\right)\Vert$, we should decrease penalty parameter c.

4.2. Self-Adaptive Penalty Parameter for Two-Area Economic Dispatch Problem

Inspired by Bingsheng He’s idea, we employ the concept of balance to adjust penalty parameter c during APP’s iteration. However, it is difficult to achieve a balance between $\Vert e_{x_1}\left(w^k\right)\Vert$, $\Vert e_{x_2}\left(w^k\right)\Vert$ and $\Vert e_{\lambda }\left(w^k\right)\Vert$ directly, so we first give Lemma 1 which gives a basic convergence property for APP iterative scheme and is useful for further analysis about how to adjust penalty parameter.

Lemma 1 

Let sequence {w^k} is generated by the iterative scheme APP and w^* is the solution of problem (8). Then we have

$${\Vert w^k-w^{*}\Vert }_M^2-{\Vert w^{k+1}-w^{*}\Vert }_M^2\ge {\Vert w^k-w^{k+1}\Vert }_M^2$$

(20)

where

$$w=\left(\begin{array}{l}{x}_1\hfill \\ x_2\hfill \\ \lambda \hfill \end{array}\right),M=\left(\begin{array}{lll}\left(\beta -c\right)A^{T}A\hfill & -c{A}^{T}B\hfill & 0\hfill \\ -c{B}^{T}A\hfill & \left(\beta -c\right)B^{T}B\hfill & 0\hfill \\ 0\hfill & 0\hfill & \frac{1}{c}{I}_m\hfill \end{array}\right)$$

(21)

The M-norm ${\Vert x\Vert }_M$ is denoted by $\sqrt{x^{T}Mx}$.

Proof. 

Solving optimization problem (11) and (12) is equivalent to solving $\left(x_1^{k+1},x_2^{k+1}\right)$ which satisfies [18]

$$\begin{array}{l}f\left(x_1\right)-f\left(x_1^{k+1}\right)+{\left(x_1-x_1^{k+1}\right)}^T\\ \left\{\left(\beta -c\right)A^T\left(A{x}_1-A{x}_1^k\right)+c{A}^T\left(A{x}_1+B{x}_2^k\right)-A^T{\lambda }^k\right\}\ge 0,\forall x_1\in {\mathrm{\Omega }}_1\end{array}$$

(22)

$$\begin{array}{l}g\left(x_2\right)-g\left(x_2^{k+1}\right)+{\left(x_2-x_2^{k+1}\right)}^T\\ \left\{\left(\beta -c\right)B^T\left(B{x}_2-B{x}_2^k\right)+c{B}^T\left(A{x}_1^k+B{x}_2\right)-B^T{\lambda }^k\right\}\ge 0,\forall x_2\in {\mathrm{\Omega }}_2\end{array}$$

(23)

and using ${\lambda }^{k+1}={\lambda }^k-c\left(A{x}_1^{k+1}+B{x}_2^{k+1}\right)$, we get

$$\begin{array}{l}f\left(x_1\right)+g\left(x_2\right)-f\left(x_1^{k+1}\right)-g\left(x_2^{k+1}\right)+\\ {\left(w-w^{k+1}\right)}^T\left\{F\left(w^{k+1}\right)+M\left(w^{k+1}-w^k\right)\right\}\ge 0,\forall w\in W\end{array}$$

(24)

Setting w=w^* in (24), we get,

$$\begin{array}{l}{\left(w^{*}-w^{k+1}\right)}^{T}M\left(w^{k+1}-w^k\right)\\ \ge f\left(x_1^{k+1}\right)+g\left(x_2^{k+1}\right)-f\left(x_1^{*}\right)-g\left(x_2^{*}\right)+{\left(w^{k+1}-w^{*}\right)}^{T}F\left(w^{k+1}\right)\end{array}$$

(25)

where

$$F\left(w\right)=\left(\begin{array}{l}-A^T\lambda \hfill \\ -B^T\lambda \hfill \\ A{x}_1+B{x}_2\hfill \end{array}\right)$$

(26)

Using the concept of variational inequality [18], solving optimization problem (8) is equivalent to solving w^* which satisfies

$$f\left(x_1\right)+g\left(x_2\right)-f\left(x_1^{*}\right)-g\left(x_2^{*}\right)+{\left(w-w^{*}\right)}^{T}F\left(w^{*}\right)\ge 0,\forall w\in W$$

(27)

In fact, F is monotone operator [19]. We have,

$${\left(w^{k+1}-w^{*}\right)}^{T}F\left(w^{k+1}\right)\ge {\left(w-w^{*}\right)}^{T}F\left(w^{*}\right)$$

(28)

Combing (25) and (28), we get

$$\begin{array}{l}{\left(w^{*}-w^{k+1}\right)}^{T}M\left(w^{k+1}-w^k\right)\ge 0\\ \Rightarrow {\left(w^{*}-w^k+w^k-w^{k+1}\right)}^{T}M\left(w^{k+1}-w^k\right)\ge 0\\ \Rightarrow {\left(w^{*}-w^k\right)}^{T}M\left(w^{k+1}-w^k\right)\ge {\left(w^k-w^{k+1}\right)}^{T}M\left(w^k-w^{k+1}\right)\end{array}$$

(29)

Using (29), we get,

$$\begin{array}{l}{\Vert w^k-w^{*}\Vert }_M^2-{\Vert w^{k+1}-w^{*}\Vert }_M^2\\ ={\Vert w^k-w^{*}\Vert }_M^2-{\Vert w^k-w^{*}-(w^k-w^{k+1})\Vert }_M^2\\ =2{\left(w^{*}-w^k\right)}^{T}M\left(w^{k+1}-w^k\right)-{\Vert w^k-w^{k+1}\Vert }_M^2\\ \ge 2{\Vert w^k-w^{k+1}\Vert }_M^2-{\Vert w^k-w^{k+1}\Vert }_M^2\\ ={\Vert w^k-w^{k+1}\Vert }_M^2\end{array}$$

(30)

Based on above discussion, the proof of Lemma 1 is completed.

Furthermore, (20) can be rewritten as follow.

$${\Vert v^k-v^{*}\Vert }_N^2-{\Vert v^{k+1}-v^{*}\Vert }_N^2\ge {\Vert v^k-v^{k+1}\Vert }_N^2$$

(31)

where

$$v=\left(\begin{array}{l}A{x}_1\hfill \\ B{x}_2\hfill \\ \lambda \hfill \end{array}\right),N=\left(\begin{array}{lll}\left(\beta -c\right)I\hfill & -cI\hfill & 0\hfill \\ -cI\hfill & \left(\beta -c\right)I\hfill & 0\hfill \\ 0\hfill & 0\hfill & \frac{1}{c}{I}_m\hfill \end{array}\right)$$

(32)

It is clear that (31) is Fejér monotone, so we get [20]

$$\underset{k\to \infty }{\lim }\Vert A{x}_1^{k+1}-A{x}_1^k\Vert =0,\underset{k\to \infty }{\lim }\Vert B{x}_2^{k+1}-B{x}_2^k\Vert =0,\underset{k\to \infty }{\lim }\Vert {\lambda }^{k+1}-{\lambda }^k\Vert =0$$

(33)

Interestingly, (33) is consistent with APP’s stop criterion, so it is clear that if ${\Vert w^k-w^{k+1}\Vert }_M^2\to 0$, then w^k+1 can be denoted by w^*. Hence, the magnitude of ${\Vert w^k-w^{k+1}\Vert }_M^2$ can measure the error between w^k and w^*.

According to β=2c which is described in (16), we get,

$${\Vert w^k-w^{k+1}\Vert }_M^2={\Vert \left(A{x}_1^{k+1}-A{x}_1^k\right)-\left(B{x}_2^{k+1}-B{x}_2^k\right)\Vert }_c^2+{\Vert {\lambda }^{k+1}-{\lambda }^k\Vert }_{\frac{1}{c}}^2$$

(34)

Now, for the sake of balance, we only need to adjust penalty parameter c such that ${\Vert \left(A{x}_1^{k+1}-A{x}_1^k\right)+\left(B{x}_2^{k+1}-B{x}_2^k\right)\Vert }_c\approx {\Vert {\lambda }^{k+1}-{\lambda }^k\Vert }_{\frac{1}{c}}$.

4.3. The Extension of Self-Adaptive Penalty Parameter for MAED Problem

Problem (7) is the two-area economic dispatch model. Apparently, Problem (7) can be easily extended to N-area system. By denoting $\mathrm{\Theta }\left(x_i,x_j\right)\equiv A_{ij}{x}_i+B_{ij}{x}_j=0$ for the consistency constraint between area i and area j, the corresponding lagrangian multiplier and penalty parameter for $\mathrm{\Theta }\left(x_i,x_j\right)$ are defined as ${\lambda }_{ij}$ and c_ij. In consideration of the most complex case, each area exchanges active power with all the other areas, a general formulation for the N-area model of MAED can be expressed as follows:

$$\begin{array}{l}\min \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\displaystyle \sum _{i=1}^n{f}_i\left(x_i\right)+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n\left({\lambda }_{ij}^T\left(A_{ij}{x}_i+B_{ij}{x}_j\right)+\frac{c_{ij}}{2}{\Vert A_{ij}{x}_i+B_{ij}{x}_j\Vert }^2\right)}}}\\ subjectto:x_i\in {\mathrm{\Omega }}_{i}i=1,2,\cdots ,n\end{array}$$

(35)

For solving problem (35), the corresponding APP iterative scheme can be expressed as follows. $\left(x_1^{k+1},x_2^{k+1},\cdots ,x_n^{k+1}\right)$ is obtained by solving

$$\begin{array}{l}\left(x_1^{k+1},x_2^{k+1},\cdots ,x_n^{k+1}\right)=\arg \min \{{\displaystyle \sum _{i=1}^n{f}_i\left(x_i\right)}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n({\lambda }_{ij}^{k,T}\left(A_{ij}{x}_i+B_{ij}{x}_j\right)+\frac{c_{ij}}{2}\left({\Vert A_{ij}{x}_i^k+B_{ij}{x}_j\Vert }^2+{\Vert A_{ij}{x}_i+B_{ij}{x}_j^k\Vert }^2\right)}}\\ +\frac{{\beta }_{ij}-c_{ij}}{2}\left({\Vert A_{ij}{x}_i-A_{ij}{x}_i^k\Vert }^2+{\Vert B_{ij}{x}_j-B_{ij}{x}_j^k\Vert }^2\right))|x_i\in {\mathrm{\Omega }}_i,i=1,2,\cdots ,n\}\end{array}$$

(36)

then, ${\lambda }_{ij}^{k+1}$ is obtained by updating

$${\lambda }_{ij}^{k+1}={\lambda }_{ij}^k-c_{ij}\left(A_{ij}{x}_i^{k+1}+B_{ij}{x}_j^{k+1}\right),i,j=1,2,\cdots ,nandj>i$$

(37)

Like the proof of Lemma 1 and (31), taking advance of the concept of variational inequality to deal with (36) and using (37), it is easy to get

$${\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n{\Vert v_{ij}^k-v_{ij}^{*}\Vert }_{N_{ij}}^2}}-{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n{\Vert v_{ij}^{k+1}-v_{ij}^{*}\Vert }_{N_{ij}}^2}}\ge {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n{\Vert v_{ij}^k-v_{ij}^{k+1}\Vert }_{N_{ij}}^2}}$$

(38)

where

$$v_{ij}=\left(\begin{array}{l}{A}_{ij}{x}_i\hfill \\ B_{ij}{x}_j\hfill \\ {\lambda }_{ij}\hfill \end{array}\right),N_{ij}=\left(\begin{array}{lll}\left({\beta }_{ij}-c_{ij}\right)I\hfill & -c_{ij}I\hfill & 0\hfill \\ -c_{ij}I\hfill & \left({\beta }_{ij}-c_{ij}\right)I\hfill & 0\hfill \\ 0\hfill & 0\hfill & \frac{1}{c_{ij}}I\hfill \end{array}\right),i,j=1,2,\cdots ,nandj>i$$

(39)

For the sake of balance, we only need to adjust penalty parameter such that

$${\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n{\Vert \left(A_{ij}{x}_i^{k+1}-A_{ij}{x}_i^k\right)-\left(B_{ij}{x}_j^{k+1}-B_{ij}{x}_j^k\right)\Vert }_{c_{ij}}^2}}\approx {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i+1}^n{\Vert {\lambda }_{ij}^{k+1}-{\lambda }_{ij}^k\Vert }_{\frac{1}{c_{ij}}}^2}}$$

(40)

In order to achieve balance in (40), we have to create a coordinator server which communicates with all sub-systems for exchanging required information. However, it is impossible for practical applications. In fact, achieving the balance in (40) provided that

$${\Vert \left(A_{ij}{x}_i^{k+1}-A_{ij}{x}_i^k\right)-\left(B_{ij}{x}_j^{k+1}-B_{ij}{x}_j^k\right)\Vert }_{c_{ij}}^2\approx {\Vert {\lambda }_{ij}^{k+1}-{\lambda }_{ij}^k\Vert }_{\frac{1}{c_{ij}}}^2,i,j=1,2,\cdots ,nandj>i$$

(41)

The corresponding self-adaptive strategy for adjusting penalty parameter can be expressed as follows.

$$c_{ij}=\{\begin{array}{l}0.5\frac{c_{ij}}{r_{ij}^{k+1}}if{r}_{ij}^{k+1}>10\hfill \\ 2c_{ij}if{r}_{ij}^{k+1}<0.1\hfill \\ c_{ij}otherwise\hfill \end{array}$$

(42)

where

$$r_{ij}^{k+1}=\frac{{\Vert \left(A_{ij}{x}_i^{k+1}-A_{ij}{x}_i^k\right)-\left(B_{ij}{x}_j^{k+1}-B_{ij}{x}_j^k\right)\Vert }_{c_{ij}}}{{\Vert {\lambda }_{ij}^{k+1}-{\lambda }_{ij}^k\Vert }_{\frac{1}{c_{ij}}}},i,j=1,2,\cdots ,nandj>i$$

(43)

It is clear that the proposed SAPP only uses existing information to adjust penalty parameter, no extra information is needed. In addition，in comparison with the optimization problem (36), the calculation cost of (42) and (43) is slight and can be neglected. Therefore, the proposed SAPP scheme is implementable for practical applications.

5. Simulation Results

In this section, we employ two test systems to verify the effectiveness of the proposed self-adaptive APP iterative scheme (SAPP) which is compared with traditional APP iterative scheme. Throughout this paper, stop criterion is set to be $\eta ={10}^{-4}$, the initial lagrangian multiplier is set to be ${\lambda }_{ij}=0$, the maximum iteration kmax is set to be 100 and the intrinsic relationship between APP’s parameters β_ij, ε_ij and c_ij is set to be c_ij=ε_ij=β_ij/2.

5.1. Test System 1

This system is composed of four generating units without considering valve-point effect and transmission loss, and all data about generating unit is strict from [21]. The total load demand for test system 1 is 800MW. In details, all generating units are divided into two areas. Area 1 includes 2 generating units and the corresponding load demand accounts for 70% of the total load demand. Area 2 consists of 2 generating units and makes up 30% of the total load demand. The maximum power flow between area 1 and area 2 is 200 MW.

5.2. Test System 2

This system is constituted of ten generators; valve-point effect and transmission loss are neglected here. The total load demand is set to be 2700 MW. Moreover, test system 2 is divided into three areas as shown in Fig. 2. Area 1 consists of four generating units; area 2 is comprised of three generating units; area 3 is made up of four generating units. The load demand in area 1 accounts for 50% of the total load demand, the corresponding proportion for area 2 and area 3 are both 25%. The generating unit data with three different fuel options has been taken from [22]. In this paper, we take the fuel option 1 as the fuel cost. In addition, there are three tie-lines in this system and the limits for tie-lines are all set to be 100MW.

Figure 2. Test system 2, three-area power system.

Figure 2. Test system 2, three-area power system.

5.3. Simulation Analysis

Table I and table II reflect the convergence information of test system 1 and test system 2 respectively. The first column gives initial value of penalty parameter. The second and third columns indicate total number of iterations when the corresponding iterative scheme satisfies stop criterion. The fourth column shows total cost as objective function for MAED problem. Simulation results demonstrate that the APP is sensitive to the selection of initial penalty parameter, if penalty parameter is chosen too big or too small, APP need more number of iteration to reach the optimum. By contrast, the proposed SAPP has better stability in convergence with different penalty parameter, and has better convergence rate.

6. Conclusion

Auxiliary problem principle is one of the attractive approaches to solve multi-area economic dispatch problem and has been applied in many other fields in power systems. However, its convergence performance is significantly influenced by the selection the penalty parameter. In this paper, we propose a self-adaptive APP iterative scheme, which allow the penalty parameter increase or decrease according to iterative information. Simulation results illustrate that the proposed SAPP is superior to the traditional APP in terms of stability in convergence.

Table 1. Comparison of results for test system 1.

Penalty parameter	Number of iterations		Total cost ($/h)
	APP	SAPP
102	Fail to convergence with maximum iteration 100	6	7.7549×103
101	Fail to convergence with maximum iteration 100	6
100	Fail to convergence with maximum iteration 100	6
10-1	Fail to convergence with maximum iteration 100	6
10-2	15	7
10-3	45	10
10-4	Fail to convergence with maximum iteration 100	14
10-5	Fail to convergence with maximum iteration 100	17
10-6	Fail to convergence with maximum iteration 100	21

Table 1. Comparison of results for test system 1.

Penalty parameter	Number of iterations		Total cost ($/h)
	APP	SAPP
102	Fail to convergence with maximum iteration 100	6	7.7549×103
101	Fail to convergence with maximum iteration 100	6
100	Fail to convergence with maximum iteration 100	6
10-1	Fail to convergence with maximum iteration 100	6
10-2	15	7
10-3	45	10
10-4	Fail to convergence with maximum iteration 100	14
10-5	Fail to convergence with maximum iteration 100	17
10-6	Fail to convergence with maximum iteration 100	21

Table 2. Comparison of results for test system 2.

Penalty parameter	Number of iterations		Total cost ($/h)
	APP	SAPP
102	Fail to convergence with maximum iteration 100	46	718.0707
101	Fail to convergence with maximum iteration 100	31
100	Fail to convergence with maximum iteration 100	27
10-1	Fail to convergence with maximum iteration 100	27
10-2	Fail to convergence with maximum iteration 100	11
10-3	31	23
10-4	Fail to convergence with maximum iteration 100	23
10-5	Fail to convergence with maximum iteration 100	31
10-6	Fail to convergence with maximum iteration 100	28

Table 2. Comparison of results for test system 2.

Penalty parameter	Number of iterations		Total cost ($/h)
	APP	SAPP
102	Fail to convergence with maximum iteration 100	46	718.0707
101	Fail to convergence with maximum iteration 100	31
100	Fail to convergence with maximum iteration 100	27
10-1	Fail to convergence with maximum iteration 100	27
10-2	Fail to convergence with maximum iteration 100	11
10-3	31	23
10-4	Fail to convergence with maximum iteration 100	23
10-5	Fail to convergence with maximum iteration 100	31
10-6	Fail to convergence with maximum iteration 100	28