The Lobe Fissure Tracking by the Modified Ant Colony Optimization Framework in CT Images

Abstract

Chest computed tomography (CT) is the most commonly used technique for the inspection of lung lesions. However, the lobe fissures in lung CT is still difficult to observe owing to its imaging structure. Therefore, in this paper, we aimed to develop an efficient tracking framework to extract the lobe fissures by the proposed modified ant colony optimization (ACO) algorithm. We used the method of increasing the consistency of pheromone on lobe fissure to improve the accuracy of path tracking. In order to validate the proposed system, we had tested our method in a database from 15 lung patients. In the experiment, the quantitative assessment shows that the proposed ACO method achieved the average F-measures of 80.9% and 82.84% in left and right lungs, respectively. The experiments indicate our method results more satisfied performance, and can help investigators detect lung lesion for further examination.

1. Introduction

The lung tissue is composed by alveolus, bronchial tubes and blood vessels. Because the densities of air in alveolus and bronchial tubes are lower and cannot pass through by X-ray, the Hounsfield unit (HU) is also lower in CT images as shown for the gray regions [1,2]. Otherwise, owing to the high density of blood in vessels, the HU is higher as shown for the white regions in Figure 1a. However, when we change the CT image to gray-level image, the lobe fissure is not very obvious as shown for the yellow arrow in Figure 1a. It may cause the segmentation faults for the lobes separation in clinical experiments.

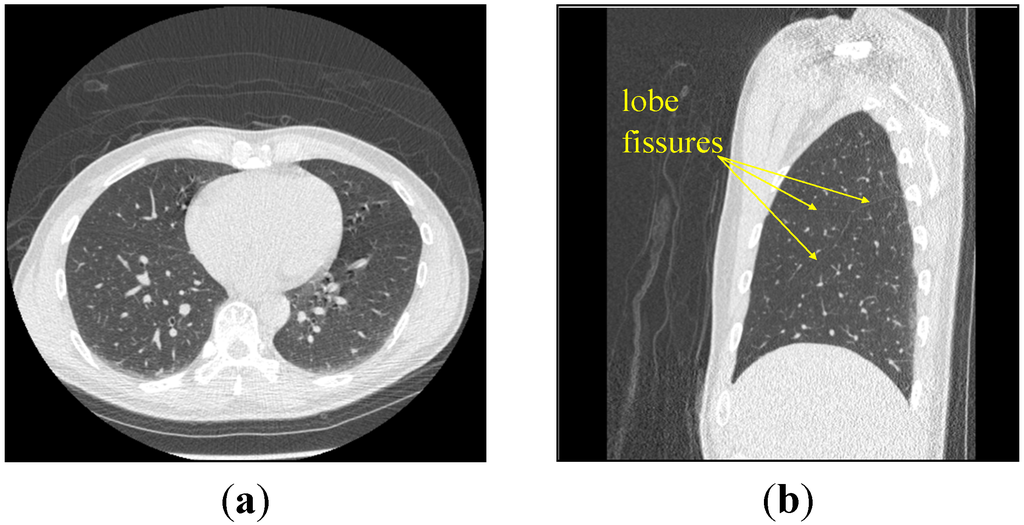
Figure 1. The lung CT image for (a) axial slice (whole lung) and (b) sagittal slice (right lung). Whole information of lung lobe is more suitable than axial views or coronal view.

Figure 1. The lung CT image for (a) axial slice (whole lung) and (b) sagittal slice (right lung). Whole information of lung lobe is more suitable than axial views or coronal view.

About the researches for lobe segmentation, all of them were first to improve the lobe fissure by different methods to facilitate the following analyses [3,4,5,6]. Wang et al. [4] used the proposed transformation called “ridge map” to enhance the appearance of fissure. Lassen et al. [5] used a pre-clustering method based on the distributions of bronchial tubes and blood vessels, and segmented the lobe fissure by the watershed transform. In the above researches of lobe fissure, most of them were focused on the axial view in CT images. However, the imaging structure of axial view cannot display the whole information of lung lobe, as shown in Figure 1a; it will increase the difficulty of lobe fissure tracking. In this paper, we focused on the sagittal view in CT slices. Although the lobe fissures are still ambiguous on sagittal view, as shown in Figure 1b; the whole information of lung lobe is more suitable than axial views or coronal view.

In this study, we try to use a high-performance tracking framework to obtain the vague lobe fissure on the sagittal view in CT slices. In order to provide accuracy, we modified an algorithm from ant movements in the natural world called the ant colony algorithm (ACA) [7,8,9,10,11,12,13]. The ant colony algorithm (ACA) is a method to process the optimized problem. It also can be applied to this study to assist the tracking framework of lobe fissure. We also add several evaluation rules to increase the number of walking by the ants on the lobe fissure. Let the pheromone on the lobe fissure become more and more to make the ants follow the candidate paths. Finally, all the ants may follow one optimal path, which has the highest pheromone level. The lobe fissure will be obtained correctly to assist the corresponding studies.

2. Related Works

2.1. Ant Colony Algorithm

The ant colony algorithm (ACA) is a method to process the optimized problem. This theory was proposed by Dorigo [8,9,10]. The main idea of ACA is that when ants work together, they will find a best path to walk by leaving pheromones. Then, we can use this principle to solve some real optimized problems. Dorigo’s theories are:

(1)

The ant will choose the path with higher pheromone levels.

(2)

For the shorter path, the accumulation rate of pheromone is faster than other paths.

(3)

The ants can communicate with each other with pheromones.

Therefore, the ants do not rely on the help of vision, and only use pheromones to find an optimized path from the starting point to destination. Because ants will leave pheromones on visited paths, the paths with a high concentration of pheromones will be visited again by other ants and the shortest path will be found. Hence, the ACA uses a positive feedback method to effectively solve the optimized problem.

Based on the principle of ACA, we can try to increase the amount of walking by the ants on the lobe fissure. Let the pheromone on the lobe fissure become more and more. When the concentration of pheromone on the lobe fissure is increased, the gray-level of lobe fissure will be enhanced and obtained to assist the following segmentation of lung structure.

2.2. Robinson Filter and Kirsch Filter

In this study, we also applied two powerful filters to enhance the region edges, such as Robinson filter and Kirsch filter [14]. Robinson filter and Kirsch filter are the compass masks. In their methods, each point of the image is used by the convolution algorithm with eight parts, as shown in Figure 2 and Figure 3. The maximum response of each part is produced only corresponding to a certain given edge direction. The maximum of all of the eight directions can be regarded as the output of the image edge amplitude. The serial numbers of the part with the maximum response are the codes of edge direction.

Figure 2. The masks of Robinson filter.

Figure 2. The masks of Robinson filter.

Figure 3. The masks of Kirsch filter.

Figure 3. The masks of Kirsch filter.

3. Tracking Framework for Lobe Fissure Based on Modified ACO Algorithm

In this section, we will show the proposed tracking framework for lobe fissure based on the modified ant colony optimization (ACO) algorithm.

3.1. Data Acquisition

In this paper, the 15 lung CT cases with 3D continuous images were acquired from China Medical University Hospital, Taiwan. The CT scanner is a 64 Slices Volume CT Scanner (GE Healthcare, Waukesha, WI, USA). In each case, there are 520 DICOM images and the image size is 512 × 512. The values of window center and width are −600 and 1600, respectively; slice thickness is 0.625 mm; pixel spacing: 1 pixel = 0.677734 × 0.677734 mm². In the experiment, we will first change all testing cases to sagittal view by our proposed system. Then, the proposed ACO framework will be applied into all testing cases to obtain the lobe fissures.

3.2. Design of the Modified ACO Method

The modified ant colony optimization (ACO) algorithm is used to track the lobe fissures in lung CT images. The idea of ACO is that the ants will find a best path to walk by their pheromone. The procedure of modified ACO algorithm is listed in Figure 4, where R is the number of path-tracking rounds and N is the number of ants. First, the input images are transferred to the sagittal slices from each axial CT cases. Second, we marked two points to be the start and end points on the boundary of lung; the ants can use the initial pheromone table to search and create the candidate paths. In each round, the pheromone table will be updated by the updating rules and the local optimal path will also be found. Last, the lobe fissure is the final optimal path through R rounds and N ants. Figure 5 shows the flowchart of proposed system.

Figure 4. The procedure of modified ACO algorithm.

Figure 4. The procedure of modified ACO algorithm.

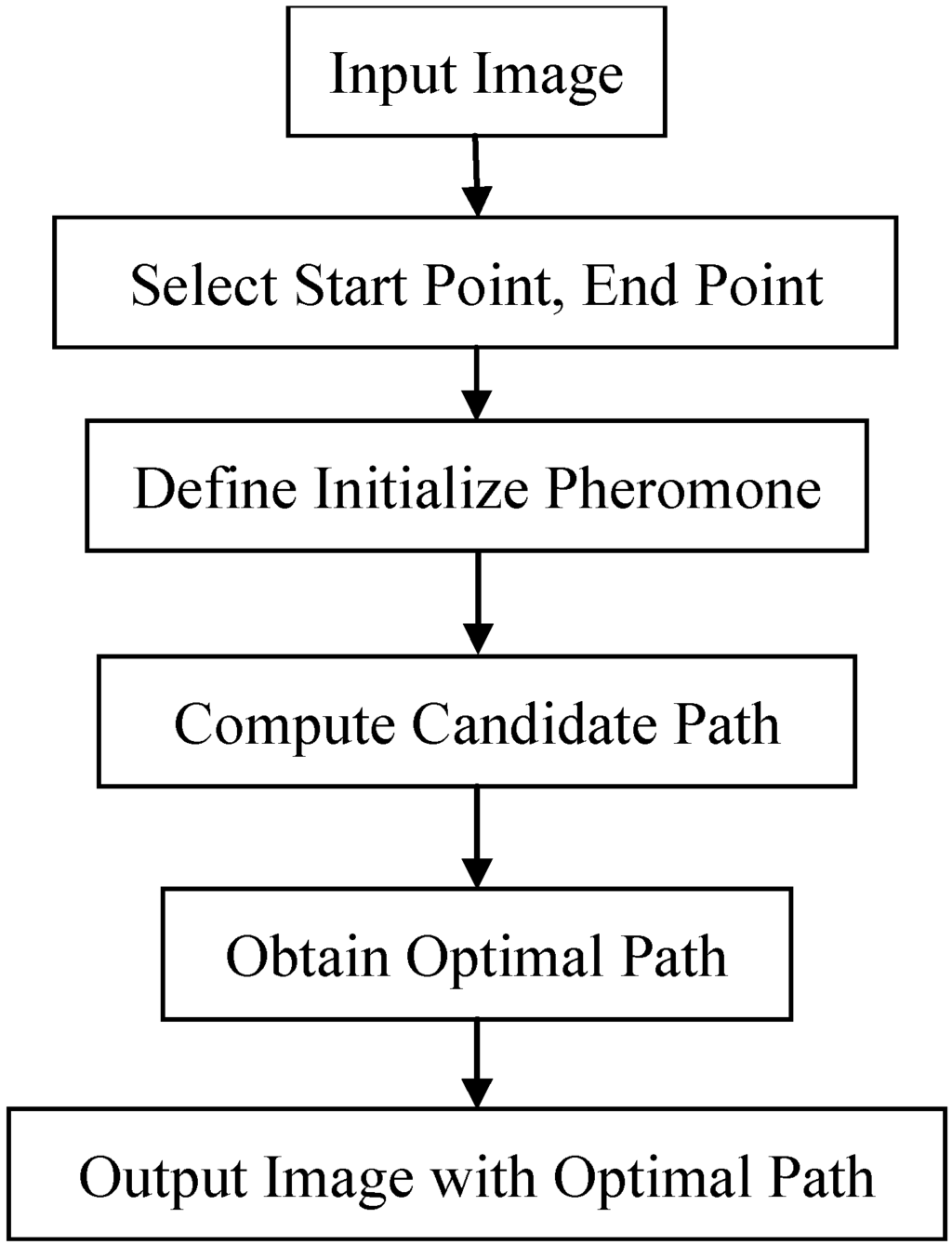
Figure 5. The flowchart of proposed ACO framework.

Figure 5. The flowchart of proposed ACO framework.

3.3. Define the Initial Pheromone

Figure 6a,d are the original sagittal views of lung CT images. We can see that the intensity of lobe fissure is higher than the lung region, but is lower than the lung tubes. Therefore, we use Otsu’s method [15] to be a location map to find out lung tubes, as shown in Figure 6b,e. The initialized pheromone can be set by the intensity function (IF):

$$IF(I)=\alpha {\left(\frac{(\max (I)-I(x,y))}{\max (I)}\right)}^k$$

(1)

Where I(x,y) is the intensity of image I, max(I) is the maximum intensity in the image, and k is a positive constant that can control the intensity [16]. Figure 6c,f show the example results by the intensity function. The intensity function can increase contrast of image; the weak edges on the image can be enhanced. According to the definition of intensity function, a corresponding pheromone table PHM can be created as:

$$PHM(x,y)=\frac{I{F}_i(x,y)}{\max (I{F}_i)}$$

(2)

Where i of pheromone table is the number of images, IF_i is the i-th processing by the intensity function. The location map (LM) is defined as:

$$LM(x,y)=\frac{\max (OtsuMethod)-OtsuMethod(x,y)}{\max (OtsuMethod)}$$

(3)

Figure 6. The examples for the definition of initial pheromone: (a,d) The sagittal view of a lung CT image; (b,e) after Otsu’s method; (c,f) after intensity function.

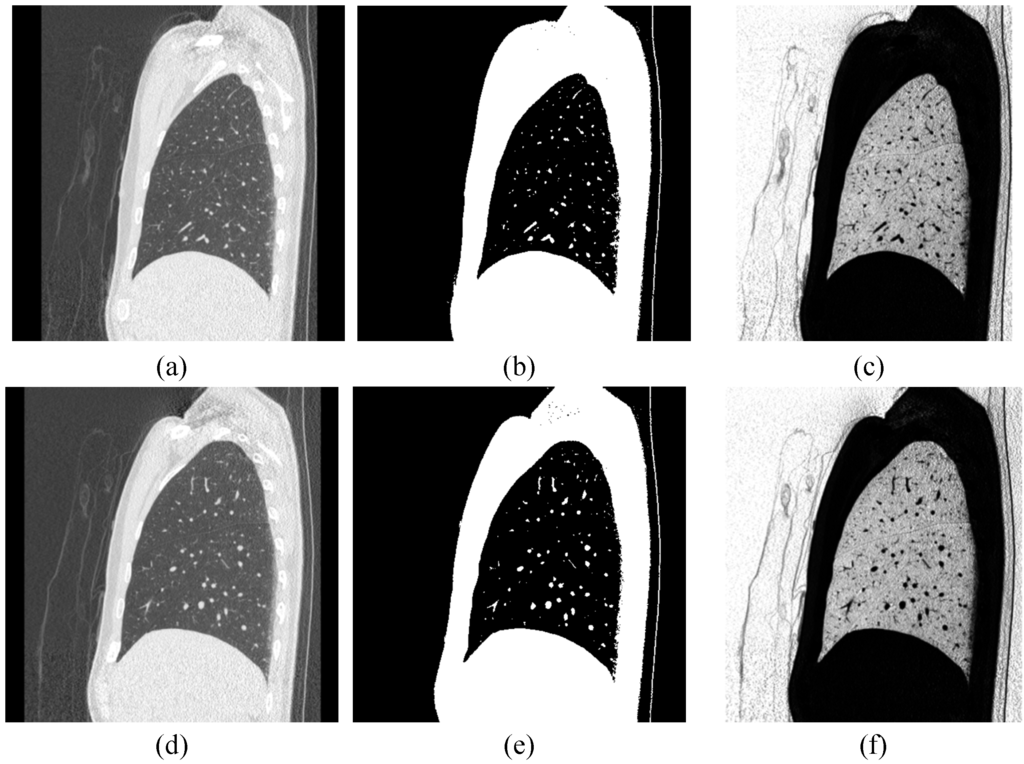
Figure 6. The examples for the definition of initial pheromone: (a,d) The sagittal view of a lung CT image; (b,e) after Otsu’s method; (c,f) after intensity function.

3.4. Edge Enhancement

In the proposed ACO procedure, we use Robinson filter and Kirsch filter to assist increasing the efficiency of proposed methods. In our study, the amplitude of Robinson filter (RFA) on the lobe fissure is lower than other regions of lung, as shown in Figure 7a,b. The amplitude of Kirsch filter (KFA) of lobe fissure is almost high, as shown in Figure 7e,f. Figure 7c,d show the orientation of Robinson filter (RFO); Figure 7g,h show the orientation of Kirsch filter (KFO). Because the identified lobe fissures always have the same direction, the shortest path may not be the optimal in proposed ACO algorithm. In order to avoid this problem, we define the equation to find the optimal path in each round. RFO and KFO have eight directions in each processing result. We denote RFO of the path as Path_RFO, and KFO of the path as Path_KFO. C_RFO and C_KFO are the counts of Path_RFO and Path_KFO to correspond with eight directions. Moreover, the path amplitudes of RFA and KFA are denoted as Path_RFA and Path_KFA, respectively. Those can calculate the count number of the maximum direction with two amplitude results of compass filters, and determine lobe fissure correctly.

$$\begin{array}{c}{C}_{RFO}=count(Pat{h}_{RFO})\\ C_{KFO}=count(Pat{h}_{KFO})\\ Robinson\times Kirsch=\frac{sum(Pat{h}_{RFA})}{sum(Pat{h}_{KFA})\times \max (C_{RFO})\times \max (C_{KFO})}\end{array}$$

(4)

Figure 7. Examples of edge enhancement after (a,b) the amplitude of Robinson filter (RFA); (c,d) the orientation of Robinson filter (RFO); (e,f) the amplitude of Kirsch filter (KFA); (g,h) the orientation of Kirsch filter (KFO).

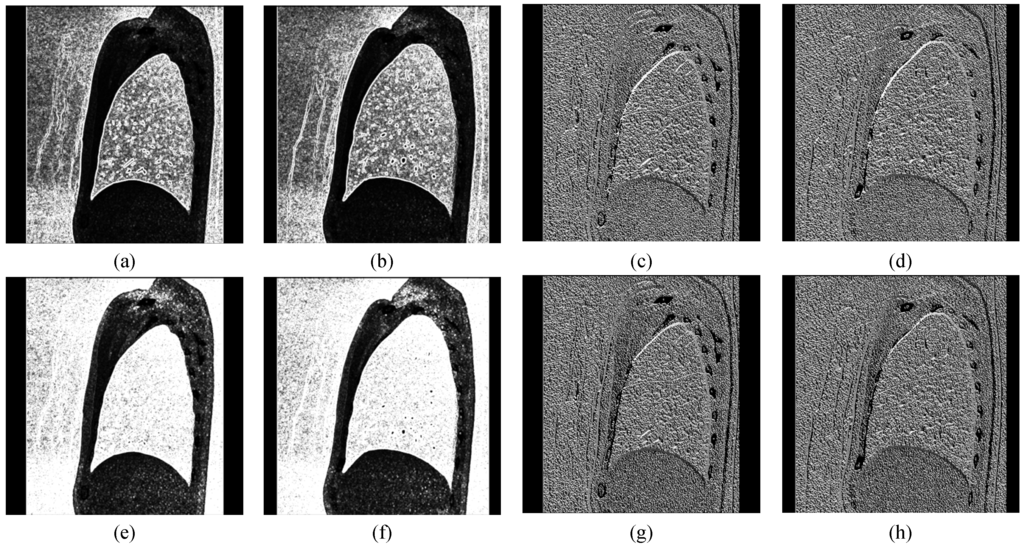
Figure 7. Examples of edge enhancement after (a,b) the amplitude of Robinson filter (RFA); (c,d) the orientation of Robinson filter (RFO); (e,f) the amplitude of Kirsch filter (KFA); (g,h) the orientation of Kirsch filter (KFO).

3.5. The Updating Rule of Pheromone

In the proposed ACO procedure, we have two updating rules (the local and global rules) to assist ants in choosing the optimal path by updating the pheromone table (PHM). When the tracking procedure of each ant is completed, we can use the local rules to update the pheromones. Then, the end of each round is updated by the global rules. In the local rules, the evaporated pheromone is defined as:

$$PHM(x,y)=PHM(x,y)\times (1-\mathsf{\rho })$$

(5)

and the completed path of pheromone is enhanced by:

$$PHM(x,y)=\max (CompletePath(PHM))\times \mathsf{\rho }$$

(6)

Where α and ρ are probability values to enhance the pheromone in PHM table by the global rules and local rules, respectively. In the global rules, the evaporated pheromone is defined as:

$$PHM(x,y)=PHM(x,y)\times (1-\mathsf{\alpha })$$

(7)

and the optimal path of pheromone is enhanced by:

$$PHM(x,y)=\frac{\mathsf{\alpha }}{PHM(x,y)}$$

(8)

3.6. Optimal Path Detection

According to Euclidean distance formula, the distance D_i is 8-neighbor of I(x₁,y₁) to I(x₂,y₂). The parameter i can provide the direction information that can be calculated as following:

$$D_i=\sqrt{{(neighbo{r}_i-IF(x,y))}^2}$$

(9)

Then, we used two ant movement (AM) steps to create a new direction for each ant. Especially in random step, that can be eight random directions, or be only a chosen direction, which is controlled by q. The other one is to compute τ_i to find out the minimum of D_i and intensity function. The parameter τ_i means the ant choose i-th direction to be a new direction, which is controlled by p. The parameters, p and q, are probability values to control the path direction during ant moving. T_p and T_q are the thresholds of p and q, respectively. V is a vector connecting end point that is used to avoid the ant movement entering an infinite loop. The ant movement (AM) function is defined as:

$$\begin{array}{l}A{M}_i=\{\begin{array}{l}\begin{array}{cc}{\tau }_i=\min (\frac{D_i}{PHM}),& \hspace{0.17em}if p>T_p\end{array}\\ \begin{array}{cc}\left[RandomStep\right]\hspace{0.17em},& \hspace{1em}if p\end{array}\le T_p\end{array}\\ \begin{array}{cc}\left[Random\hspace{0.17em}Step\right]:\hspace{1em}\{\begin{array}{l}V,\hspace{1em}\hspace{1em}\hspace{1em}if q>T_q\\ Random, if q\le T_q\end{array}& \end{array}\end{array}$$

(10)

Finally, when ants completed all paths from start point to end point, we can choose the shortest one to be the optimal path. The optimal path (OP) is defined as:

$$OP=\min (\frac{P(A{M}_i)}{Robinson\times Kirsch})$$

(11)

Where P(AM_i) is the path length of AM_i. Through the completed framework of proposed ACO method, the optimal path of lobe fissure can be detected by N ants with R rounds, as shown in Figure 8 and Figure 9.

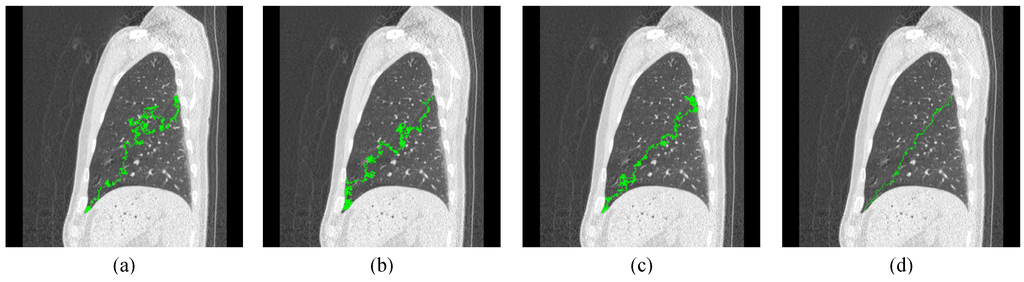
Figure 8. The first example for optimal path of ant movement with N = 10, where (a) R = 1; (b) R = 2; (c) R = 3; and (d) R = 5.

Figure 8. The first example for optimal path of ant movement with N = 10, where (a) R = 1; (b) R = 2; (c) R = 3; and (d) R = 5.

Figure 9. The second example for optimal path of ant movement with N = 10, where (a) R = 1; (b) R = 2; (c) R = 3; and (d) R = 5.

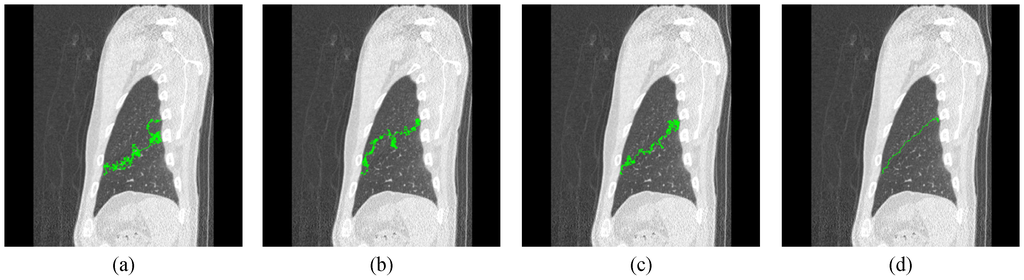
Figure 9. The second example for optimal path of ant movement with N = 10, where (a) R = 1; (b) R = 2; (c) R = 3; and (d) R = 5.

4. Experimental Results

In the experiments, we have tested fifteen 3D lung CT cases, and there are more than 500 continuous images in each case. The experimental procedure is shown in Figure 10. We first prepared the initial pheromone table and location map that can train the ant where the lung tubes or noise are. Second, we used Robinson filter and Kirsch filter to assist the edge enhancement to track the optimal path. Then, we used the updating rules to change the pheromone and detect the optimal path for the lobe fissures. In the testing procedure, we had set some parameters and the values of parameters are listed in Table 1. Two experimental results for the left and right lung CT images by the proposed ACO framework are shown in Figure 11 and Figure 12.

Figure 10. The details of proposed ACO framework for lung fissure tracking.

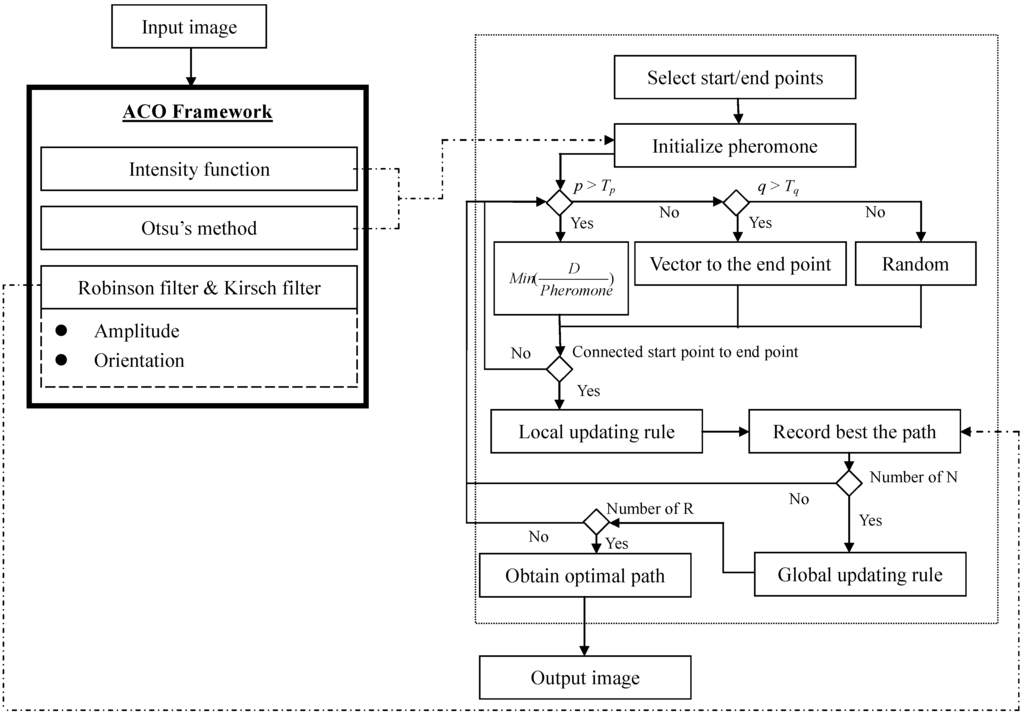
Figure 10. The details of proposed ACO framework for lung fissure tracking.

Table 1. The values of parameters for the proposed ACO framework.

ACO	Intensity Function	Updating Rules
R = 5	α = 605	α = 0.8
N = 10	k = 4	ρ = 0.6
Tp = 0.5	-	-
Tq = 0.8	-	-

Table 1. The values of parameters for the proposed ACO framework.

ACO	Intensity Function	Updating Rules
R = 5	α = 605	α = 0.8
N = 10	k = 4	ρ = 0.6
Tp = 0.5	-	-
Tq = 0.8	-	-

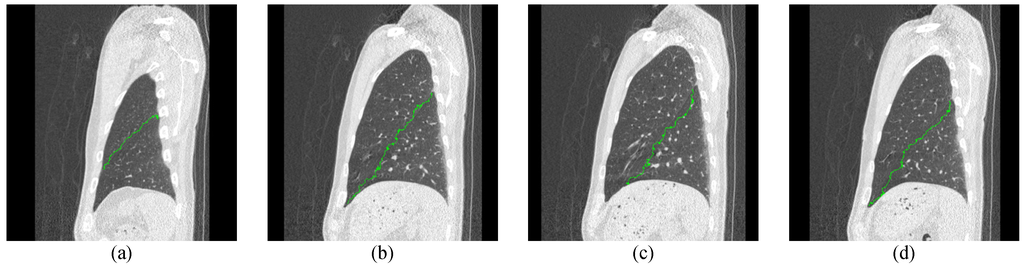
Figure 11. The first experimental result for the left lung CT by the proposed ACO framework.

Figure 11. The first experimental result for the left lung CT by the proposed ACO framework.

Figure 12. The second experimental result for the right lung CT by the proposed ACO framework.

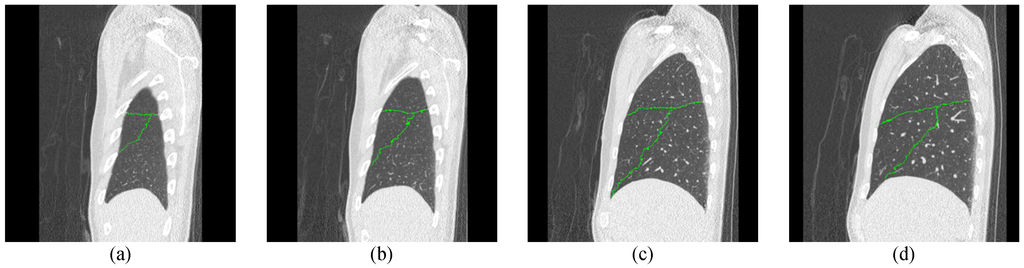
Figure 12. The second experimental result for the right lung CT by the proposed ACO framework.

In the analysis of system performance, we set the obtained lobe fissure by the proposed system to be LF_ACO, and the artificial fissure path by the professional physician to be LF_P. Ideally, these two parameters are compared with each other. However, the path widths of LF_ACO and LF_P are a single pixel. If we compared LF_ACO and LF_P directly, the results of performance may be inaccurate and unsatisfactory. Therefore, we applied the statistical conception of trustful region for lobe fissure comparison, shown in Figure 13. The conception of trustful region here is to broaden the widths of LF_ACO and LF_P from 1 pixel to 5 pixels, respectively. Then we can obtain the trustful region of LF_ACO and LF_P, that are TR(LF_ACO) and TR(LF_P). If the points on TR(LF_ACO) are located in TR(LF_P), we can say that the points belonged to the path of lobe fissure. It can avoid the fault that only compared LF_ACO and LF_P by 1-pixel width.

Figure 13. The conception of trustful region for lobe fissure tracking.

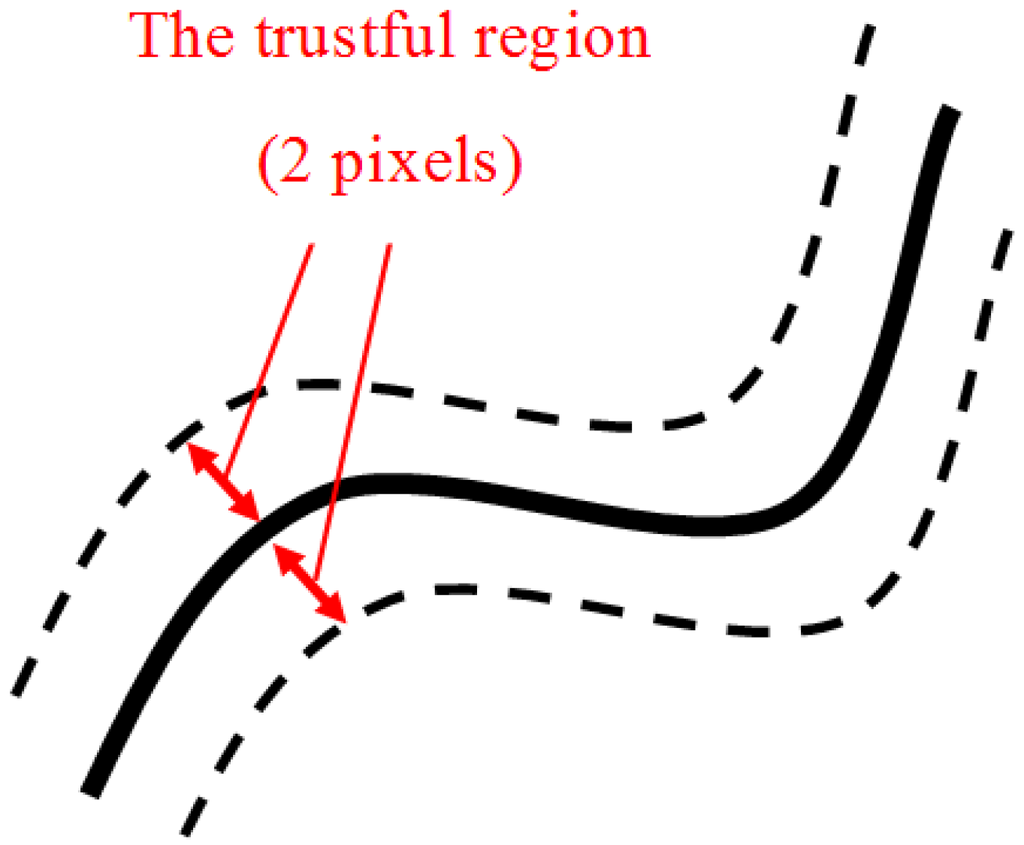
Figure 13. The conception of trustful region for lobe fissure tracking.

In the analysis of performance metric, the precision, recall and F-measure [17,18,19,20] are used to analyze the performance of the proposed ACO method. These metric functions are defined:

$$precision=\frac{TLF}{TLF+FRLF}$$

(12)

$$recall=\frac{TLF}{TLF+FLF}$$

(13)

$$F\_measure=\frac{2\times (precision\times recall)}{precision+recall}$$

(14)

The relationship of three parameters FLF, TLF, and FRLF is shown in Figure 14. These are defined as:

• The value of false lobe fissure (FLF): the TR(LF_ACO) is not overlapped on the trustful region of TR(LF_P);
• The value of true lobe fissure (TLF): the TR(LF_ACO) is overlapped on the trustful region of TR(LF_P);
• The value of false real lobe fissure (FRLF): the TR(LF_P) is not overlapped on the trustful region of TR(LF_ACO);

Figure 14. The relationship of parameters: false lobe fissure (FLF), true lobe fissure (TLF), and false real lobe fissure (FRLF).

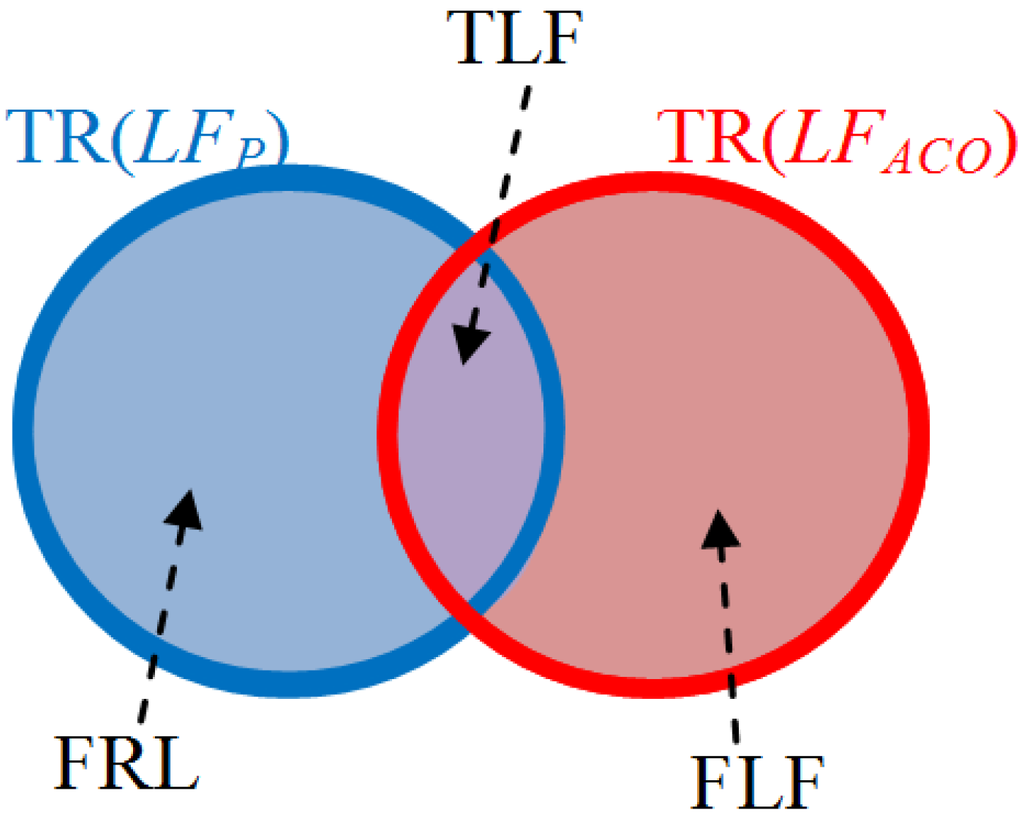
Figure 14. The relationship of parameters: false lobe fissure (FLF), true lobe fissure (TLF), and false real lobe fissure (FRLF).

According to the analyzed results (as listed in Table 2 and Table 3), the mean values of precision, recall and F-measure that can be achieved are 78.26%, 83.89% and 80.9% on all left-lung cases, and 79.68%, 86.34% and 82.84% on all right-lung cases, respectively. We can observe that the value of recall is almost always larger than precision, because the cyclic paths would be happened when the ants move in some unclear lung CT cases. We also obtain that the metric values in right lung are larger than in the left lung. This is because the heartbeat may cause the scanning error of lung CT. However, the quantitative assessment shows that the proposed ACO method achieved the average F-measures of 80.9% and 82.84% for left and right lung cases, respectively. The higher F-measure means that the proposed ACO method for lobe fissure tracking is practicable.

Table 2. The experimental results of precision, recall and F-measure by the proposed ACO method for 15 left lung cases.

Case	Lung	Mean (%)
		Precision	Recall	F-measure
1	Left	88.7	81.79	85.1
2	Left	70.39	76.52	73.33
3	Left	78.65	84.95	81.68
4	Left	79.94	79.99	79.96
5	Left	83.77	87.51	85.6
6	Left	75.66	85.84	80.43
7	Left	82.21	89.4	85.65
8	Left	74.4	81.7	77.88
9	Left	76.09	84.36	80.01
10	Left	76.83	88.58	82.29
11	Left	72.13	81.62	76.58
12	Left	86.65	84.15	85.38
13	Left	71.38	79.37	75.16
14	Left	79.4	84.05	81.66
15	Left	77.72	88.5	82.76
Average		78.26	83.89	80.9

Table 2. The experimental results of precision, recall and F-measure by the proposed ACO method for 15 left lung cases.

Case	Lung	Mean (%)
		Precision	Recall	F-measure
1	Left	88.7	81.79	85.1
2	Left	70.39	76.52	73.33
3	Left	78.65	84.95	81.68
4	Left	79.94	79.99	79.96
5	Left	83.77	87.51	85.6
6	Left	75.66	85.84	80.43
7	Left	82.21	89.4	85.65
8	Left	74.4	81.7	77.88
9	Left	76.09	84.36	80.01
10	Left	76.83	88.58	82.29
11	Left	72.13	81.62	76.58
12	Left	86.65	84.15	85.38
13	Left	71.38	79.37	75.16
14	Left	79.4	84.05	81.66
15	Left	77.72	88.5	82.76
Average		78.26	83.89	80.9

Table 3. The experimental results of precision, recall and F-measure by the proposed ACO method for 15 right lung cases.

Case	Lung	Mean (%)
		Precision	Recall	F-measure
1	Right	80.32	85.73	82.94
2	Right	75.75	87.11	81.03
3	Right	78.46	83.97	81.12
4	Right	74.95	76.9	75.91
5	Right	77.06	85.45	81.04
6	Right	76.04	87.2	81.24
7	Right	86.06	86.01	86.03
8	Right	78.19	87.41	82.54
9	Right	85.56	86.06	85.81
10	Right	83.85	89.95	86.79
11	Right	79.24	88.27	83.51
12	Right	86.26	90.03	88.1
13	Right	75.81	86.63	80.86
14	Right	80.56	88.91	84.53
15	Right	77.15	85.49	81.11
Average		79.68	86.34	82.84

Table 3. The experimental results of precision, recall and F-measure by the proposed ACO method for 15 right lung cases.

Case	Lung	Mean (%)
		Precision	Recall	F-measure
1	Right	80.32	85.73	82.94
2	Right	75.75	87.11	81.03
3	Right	78.46	83.97	81.12
4	Right	74.95	76.9	75.91
5	Right	77.06	85.45	81.04
6	Right	76.04	87.2	81.24
7	Right	86.06	86.01	86.03
8	Right	78.19	87.41	82.54
9	Right	85.56	86.06	85.81
10	Right	83.85	89.95	86.79
11	Right	79.24	88.27	83.51
12	Right	86.26	90.03	88.1
13	Right	75.81	86.63	80.86
14	Right	80.56	88.91	84.53
15	Right	77.15	85.49	81.11
Average		79.68	86.34	82.84

5. Discussion

In this paper, we have used several parameters to initialize and process our proposed system, as shown in Table 1. Some parameter values are meaningful, such as N and R. The parameter N is number of ants; we used 10 ants to track the candidate path through their pheromone in PHM table (pheromone table) in each round. In our experiment, the result of N > 10 is similar to N = 10. Besides, if the number of ants (N) is too large, the system performance will be decreased. Therefore, we set parameter N is 10 in our study. Second, R is the number of path-tracking rounds. We can see the experimental results in Figure 8 and Figure 9; the optimal path can be obtained in the fifth round. However, if R > 5, the results are the same as R = 5. Therefore, with consideration to performance, we set the parameter R is 5. The other parameters, p, q, α and ρ are probability parameters, p and q are used to control the path direction during ant moving, α and ρ are used to enhance the pheromone in PHM table by the global rules and local rules, respectively. These parameters, p, q, α and ρ, are expired values in our experiments.

Besides, we have no comparison with other methods. The reason is most researches of lobe fissure were focused on the axial slices in CT. However, the imaging structure of axial view cannot display the whole information of lung lobe. Besides, the lobe fissure in axial slice is not a clear line; it may be an irregular region. The proposed ACO method is an ant-tracking algorithm. If the tracking path is not similar to a line or curve, we cannot define the start and end points to initialize our system. Hence, the proposed method cannot apply to an axial slice, and we only focus on sagittal view to obtain the lobe fissures on left lung and right lung, respectively. Through this proposed method, most of the lobe fissures can still be obtained and the metric values are also satisfied according to the results in Table 2 and Table 3. Therefore, this performance of proposed method in this study can also be proved.

6. Conclusions

In this study, we focused on the vague lobe fissure in CT images, and proposed a tracking framework based on the modified ant colony optimization (ACO) algorithm to enhance the lobe fissure. Several evaluation rules are used to increase the number of walking by the ants on the lobe fissure, and then the pheromone on the lobe fissure would be increased. Finally, the optimal lobe fissure will be obtained to assist the segmentation procedures on the future work. In the experiment, the quantitative assessment shows that the proposed ACO method achieved the average F-measures of 80.9% and 82.84% in left and right lungs, respectively. The experiments indicate that our method has a more satisfied performance, and can help to detect lung lesion for further examination.

However, the experiments indicate our method results in more satisfied performance in most cases. The values of parameters for the proposed ACO framework may be become the variations of proposed system performance. As we said that the lobe fissure in CT images is very ambiguous, therefore we must to use several enhancement rules to help the ACO algorithm. In the future, we can apply some AI (artificial intelligence) module, such as fuzzy, neural network, genetic algorithm, etc., to train the necessary parameters. Let the proposed system become more powerful.