Neural Networks for Muscle Forces Prediction in Cycling
Abstract
:1. Introduction
2. Methods and Techniques
- Definition of a kinematic model to evaluate the position of every segment of the leg involved in the gesture;
- Definition of the inverse dynamics to evaluate the muscular torque for every joint;
- Calculation of the muscular forces through the data obtained with the two previous steps.
2.1. Biomechanical Model Identification

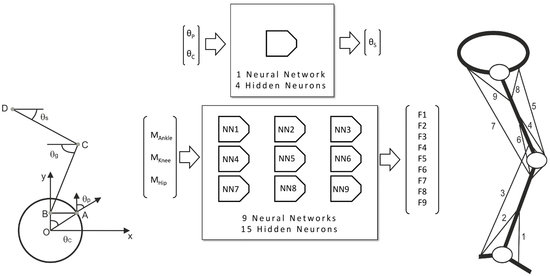
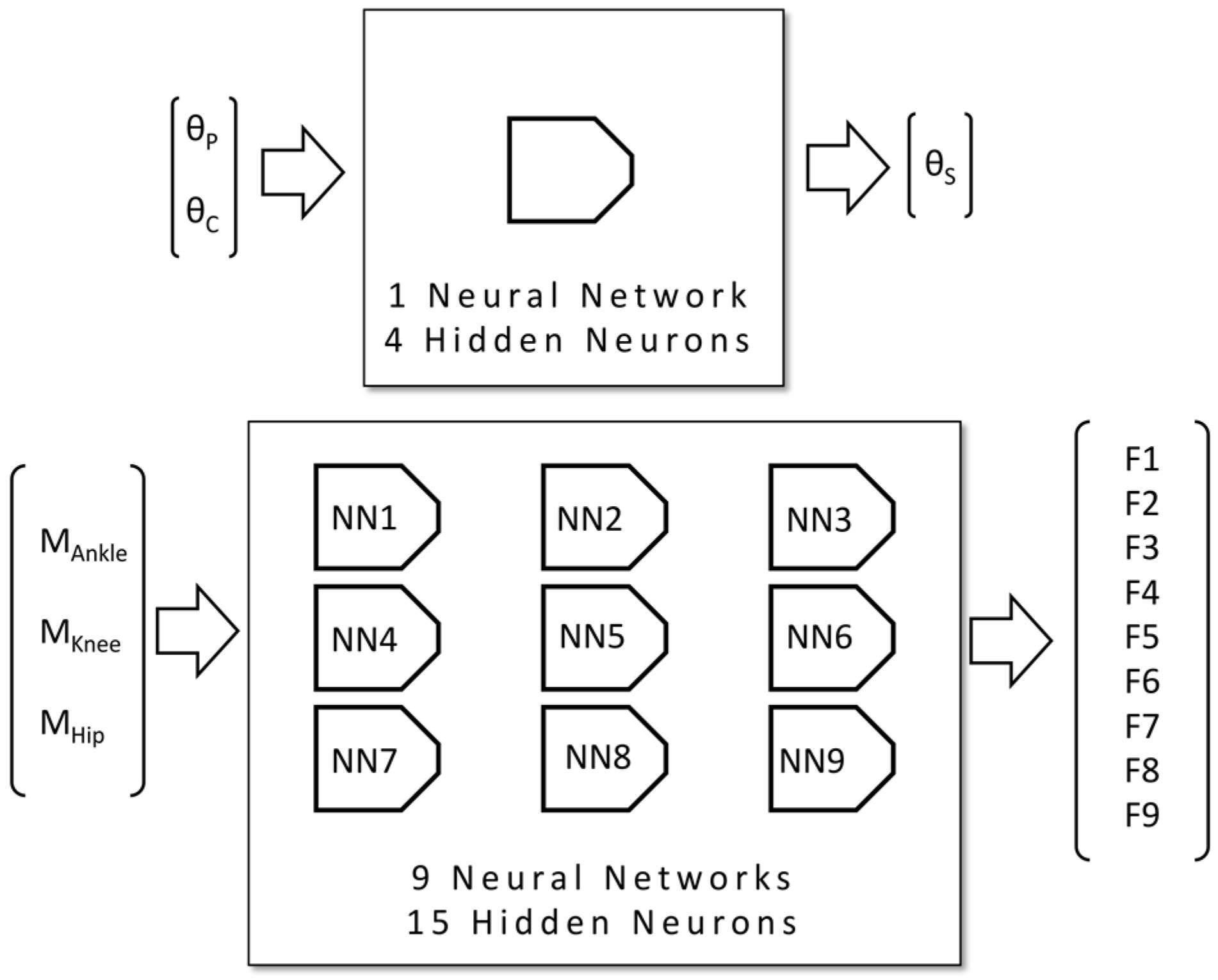
2.2. Neural Network Design
- Calculation of the relative rotational angle between the frame of the bicycle and the thigh, θS;
- Estimation of muscle forces.

2.3. Bland-Altman Plots
- The 1.96 σdiff boundary for the difference distribution, pointing out how much the two methods spread.
- The regularity of the distribution along the mean axis, to identify variable-related error patterns.
- The symmetry of the distribution around the zero, addressing systematic bias of the measurements.
2.4. Experimental Protocol and Validation
- Training and validation set of NNs using data obtained previously by a deterministic optimization algorithm.
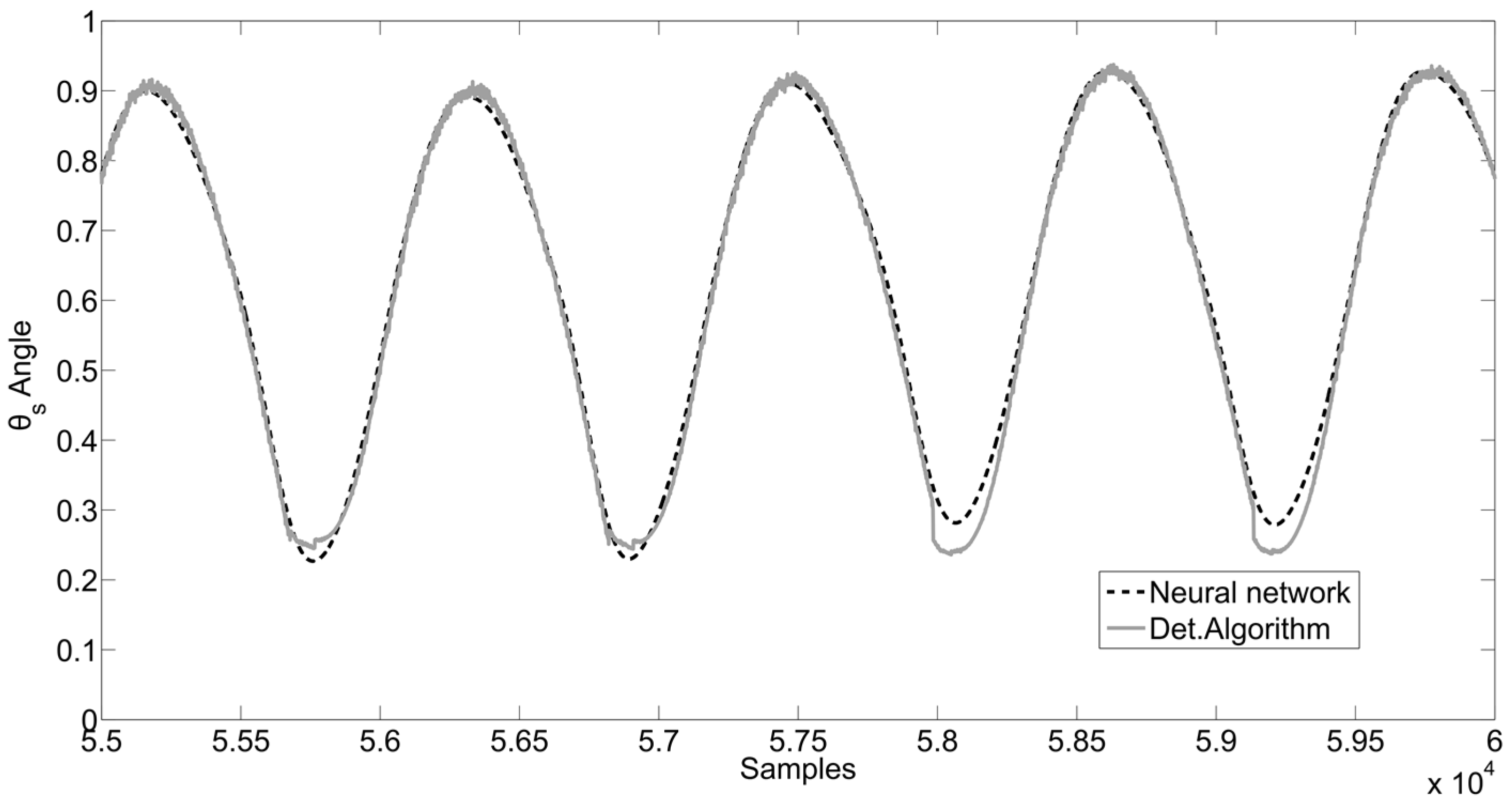
- Plot analysis between the signals obtained by NNs and signals obtained by the optimization algorithm, and the evaluation of the RMSE and RMSE Standard Deviation.
- Validation of the experimental protocol analyzing Bland-Altman plots extrapolating 1180 random samples from each muscle forces signals.
3. Results and Discussion
| Output | NN topology | Number of inputs | Number of neurons in the hidden layer | Training set (Samples) | Validation set (Samples) |
|---|---|---|---|---|---|
| θS angle | 1 MISO | 2 | 4 | 7,050 | 118,000 |
| Muscle Forces | 9 MISO | 3 | 15 | 2,360 | 118,000 |
| Subject | RMS Error % | Standard Deviation Error |
|---|---|---|
| 1 | 0.085% | 2.68 × 10−4 |
| 2 | 0.134% | 7.35 × 10−4 |
| 3 | 0.077% | 4.53 × 10−4 |
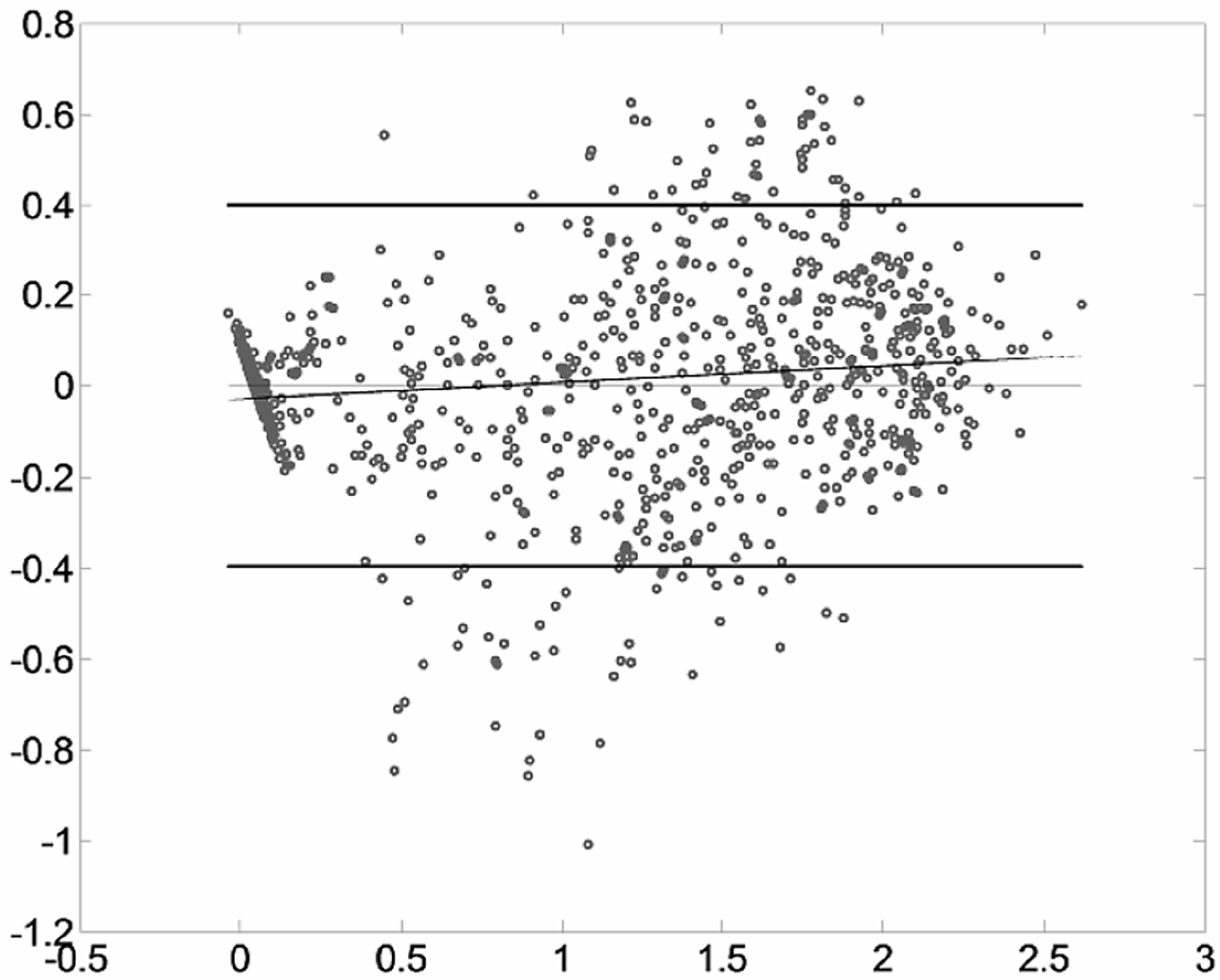
| Muscle | Upper Boundary | Lower Boundary | Normalized Boundary |
|---|---|---|---|
| TA | 0.1573 | −0.1577 | 0.6707 |
| SO | 0.6296 | −0.6341 | 0.0786 |
| GA | 0.5829 | −0.5845 | 0.4660 |
| VA | 0.1203 | −0.1212 | 0.0794 |
| RF | 0.3996 | −0.3967 | 0.4155 |
| BFs | 0.08088 | −0.08076 | 0.6616 |
| BFl | 0.7286 | −0.7266 | 0.1354 |
| IL | 0.2739 | −0.2748 | 0.1873 |
| GLM | 0.9368 | −0.9251 | 0.1311 |
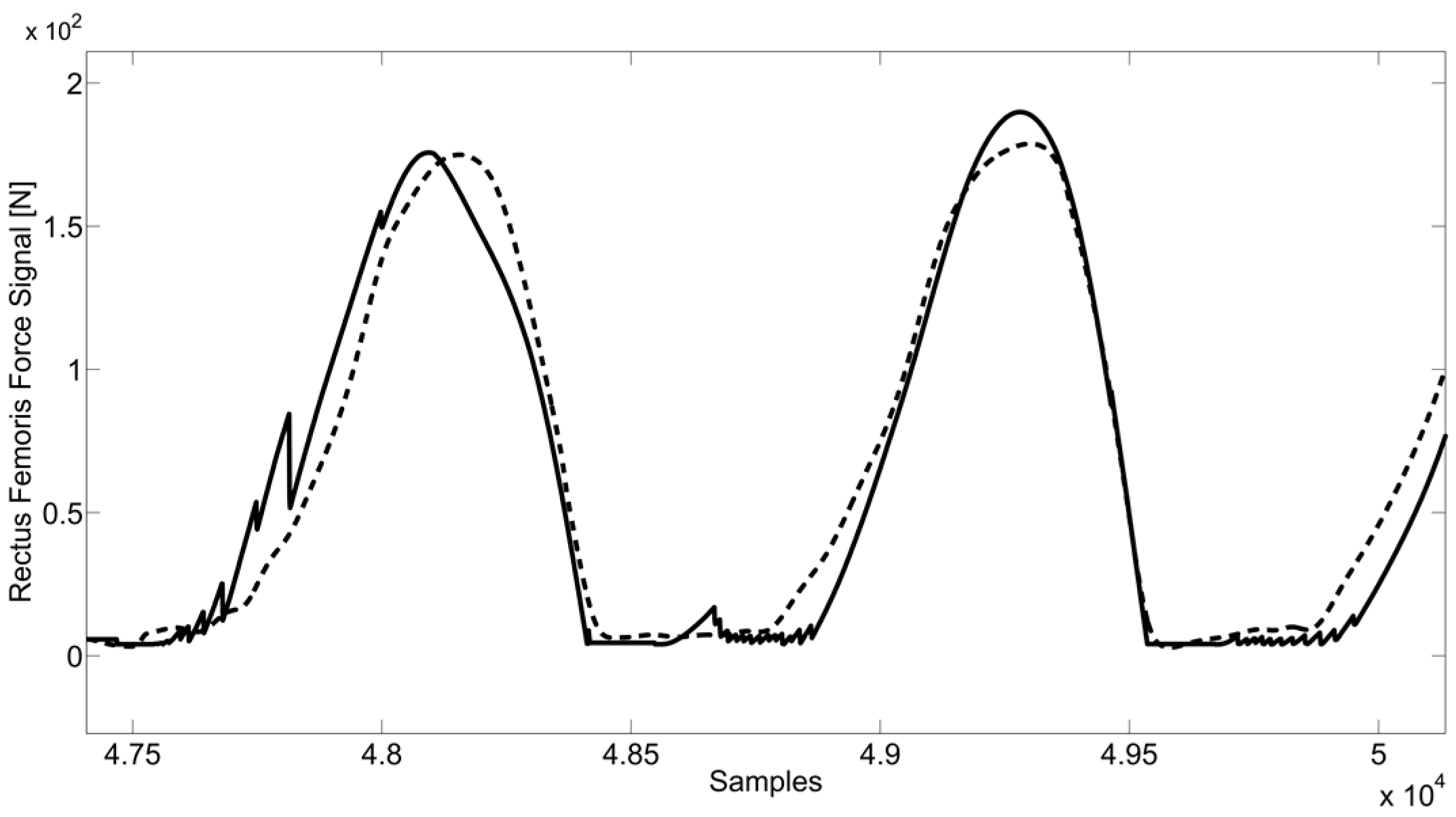
4. Conclusions and Future Developments
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Erdemir, A.; McLean, S.; Herzog, W.; van den Bogert, A.J. Model-based estimation of muscle forces exerted during movements. Clin. Biomech. 2007, 22, 131–154. [Google Scholar] [CrossRef] [PubMed]
- Pandy, M.G.; Andriacchi, T.P. Muscle and joint function in human locomotion. Annu. Rev. Biomed. Eng. 2010, 12, 401–433. [Google Scholar] [CrossRef] [PubMed]
- Hughes, R.E.; An, K.N. Monte Carlo simulation of a planar shoulder model. Med. Biol. Eng. Comput. 1997, 35, 544–548. [Google Scholar] [CrossRef] [PubMed]
- Dorn, T.W.; Schache, A.G.; Pandy, M.G. Muscular strategy shift in human running: Dependence of running speed on hip and ankle muscle performance. J. Exp. Biol. 2012, 25, 1944–1956. [Google Scholar] [CrossRef] [PubMed]
- Ingram, D.; Müllhaupt, P.; Terrier, A.; Farron, A. Dynamical Biomechanical Model of the Shoulder for Muscle-Force Estimation. In Proceedings of 4th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics, Rome, Italy, 24–27 June 2012.
- Aeberhard, M.; Michellod, Y.; Mullhaupt, P.; Terrier, A.; Pioletti, D.P.; Gillet, D. Dynamical Biomechanical Model of the Shoulder: Null Space Based Optimization of the Overactuated System. In Proceedings of Robotics and Biomimetics ROBIO 2008 IEEE International Conference, Bangkok, Thailand, 22–25 February 2009.
- Terrier, A.; Aeberhard, M.; Michellod, Y.; Mullhaupt, P.; Pioletti, D.P.; Farron, A.; Gillet, D. A musculoskeletal shoulder model based on pseudo-inverse and null-spact5e optimization. Med. Eng. Phys. 2010, 32, 1050–1056. [Google Scholar] [CrossRef] [PubMed]
- Mughal, A.M.; Kamran, I. 3D Bipedal Model for Biomechanical Sit-to-Stand Movement with Coupled Torque Optimization and Experimental Analysis. In Proceedings of Systems Man and Cybernetics (SMC) 2010 IEEE International Conference, Istanbul, Turkey, 10–13 October 2010.
- Ferry, M.; Martin, L.; Termoz, N.; Côté, J.; Prince, F. Balance control during an arm raising movement in bipedal stance: Which biomechanical factor is controlled? Biol. Cybern. 2004, 91, 104–114. [Google Scholar] [CrossRef] [PubMed]
- Castronovo, A.M.; Conforto, S.; Schmid, M.; Bibbo, D.; D’Alessio, T. How to assess performance in cycling: The multivariate nature of influencing factors and related indicators. Front. Physiol. 2013, 4, 116. [Google Scholar] [CrossRef] [PubMed]
- Watson, M.; Bibbo, D.; Duffy, C.R.; Riches, P.E.; Conforto, S.; Macaluso, A. Validity and reliability of an alternative method for measuring power output during 6s all out cycling. J. Appl. Biomech. 2014, 30, 598–603. [Google Scholar] [CrossRef] [PubMed]
- De Marchis, C.; Schmid, M.; Bibbo, D.; Castronovo, A.M.; D’Alessio, T.; Conforto, S. Feedback of mechanical effectiveness induces adaptations in motor modules during cycling. Front. Comput. Neurosci. 2013, 7, 1–12. [Google Scholar] [CrossRef] [PubMed]
- De Marchis, C.; Schmid, M.; Bibbo, D.; Bernabucci, I.; Conforto, S. Inter-individual variability of forces and modular muscle coordination in cycling: A study on untrained subjects. Hum. Mov. Sci. 2013, 32, 1480–1494. [Google Scholar] [CrossRef] [PubMed]
- De Marchis, C.; Castronovo, A.M.; Bibbo, D.; Schmid, M.; Conforto, S. Muscle Synergies are Consistent when Pedaling under Different Biomechanical Demands. In Proceedings of the 34th IEEE-EMBS Conference, San Diego, CA, USA, 28 August–1 September 2012; Volume 1, pp. 3308–3311.
- Bibbo, D.; Conforto, S.; Gallozzi, C.; D’Alessio, T. Combining electrical and mechanical data to evaluate muscular activities during cycling. WSEAS Trans. Biol. Biomed. 2006, 5, 339–346. [Google Scholar]
- Prilutsky, B.I. Coordination of two-and one-joint muscles: Functional consequences and implications for motor control. Mot. Control 2000, 4, 1–44. [Google Scholar]
- Prilutsky, B.I.; Zatsiorsky, V.M. Optimization-based models of muscle coordination. Exerc. Sp. Sci. Rev. 2002, 30, 32. [Google Scholar] [CrossRef]
- Bottasso, C.L.; Prilutsky, B.I.; Croce, A.; Imberti, E.; Sartirana, S. A numerical procedure for inferring from experimental data the optimization cost functions using a multibody model of the neuro-musculoskeletal system. Multibody Syst. Dyn. 2006, 16, 123–154. [Google Scholar] [CrossRef]
- D’Alessio, T.; Conforto, S. Extraction of the envelope from surface EMG signals: An adaptive procedure for dynamic protocols. IEEE Eng. Med. Biol. Mag. 2001, 6, 55–61. [Google Scholar] [CrossRef]
- Conforto, S.; D’Alessio, T.; Pignatelli, S. Optimal rejection of movement artefacts from myoelectric signals by means of a wavelet filtering procedure. J. Electromyogr. Kinesiol. 1999, 9, 47–57. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Chen, T.P.; Chen, H. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems. IEEE Trans. Neural Netw. 1995, 6, 911–917. [Google Scholar] [CrossRef] [PubMed]
- Leshno, M.; Lin, V.Y.; Pinkus, A.; Schocken, S. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Netw. 1993, 6, 861–867. [Google Scholar] [CrossRef]
- Chen, T.P.; Chen, H. Approximations of continuous functional by neural networks with application to dynamic systems. IEEE Trans. Neural Netw. 1993, 4, 910–918. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.P.; Chen, H.; Liu, R.W. Approximation capability in C (Rn) by multilayer feedforward networks and related problems. IEEE Trans. Neural Netw. 1995, 6, 25–30. [Google Scholar] [CrossRef] [PubMed]
- Tamura, S.; Tateishi, M. Capabilities of a four-layered feedforward neural network: Four layers versus three. IEEE Trans. Neural Netw. 1997, 8, 251–255. [Google Scholar] [CrossRef] [PubMed]
- De Villiers, J.; Barnard, E. Backpropagation neural nets with one and two hidden layers. IEEE Trans. Neural Netw. 1993, 4, 136–141. [Google Scholar] [CrossRef] [PubMed]
- Razavi, S.; Tolosn, B.A.; Burn, D.H. Numerical assessment of metamodelling strategies in computationally intensive optimization. Environ. Modell Softw. 2011, 34, 67–86. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Krejcar, O.; Penhaker, M.; Janckulik, D.; Motalova, L. Performance Test of Multiplatform Real Time Processing of Biomedical Signals. In Proceedings of 8th IEEE International Conference on Industrial Informatics, Osaka, Japan, 13–16 July 2010.
- Van den Bogert, A.J.; Geijtenbeek, T.; Even-Zohar, O.; Steenbrink, F.; Hardin, E.C. A real-time system for biomechanical analysis of human movement and muscle function. Med. Biol. Eng. Comput. 2013, 51, 1069–1077. [Google Scholar] [CrossRef] [PubMed]
- Bland, M.J.; Altman, D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Lam, A.; Chen, D.; Chiu, R.; Chui, W.S. Comparison of IOP measurements between ORA and GAT in normal Chinese. Optom. Vis. Sci. 2007, 84, 909–914. [Google Scholar] [CrossRef] [PubMed]
- De Leva, P. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Prilutsky, B.I.; Gregor, R.J. Strategy of coordination of two- and one-joint leg muscles in controlling an external force. Mot. Control 1997, 1, 92–116. [Google Scholar]
- Crowninshield, R.D.; Brand, R.A. A physiologically based criterion of muscle force prediction in locomotion. J. Biomech. 1981, 14, 793–801. [Google Scholar] [CrossRef]
- Dul, J.; Johnson, J.E.; Schiavi, R.; Townsend, M.A. Muscular synergism—II. A minimum-fatigue criterion for load sharing between synergistic muscles. J. Biomech. 1984, 17, 675–684. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training feed forward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network Toolbox 7. Available online: http://www.mathworks.cn/products/techkitpdfs/8511.pdf (accessed on 15 August 2014).
- Capizzi, G.; Coco, S.; Giuffrida, C.; Laudani, A. A neural network approach for the differentiation of numerical solutions of 3-D electromagnetic problems. IEEE Trans. Magn. 2004, 2, 953–956. [Google Scholar] [CrossRef]
- Fulginei, F.R.; Salvini, A.; Parodi, A.M. Learning optimization of neural networks used for MIMO applications based on multivariate functions decomposition. Inverse Probl. Sci. Eng. 2012, 20, 29–39. [Google Scholar] [CrossRef]
- Bland, M.J.; Altman, D. Validating scales and indexes. BMJ Br. Med. J. 2002, 324, 606. [Google Scholar] [CrossRef]
- Bibbo, D.; Conforto, S.; Schmid, M.; D’Alessio, T. A Wireless Integrated System to Evaluate Efficiency Indexes in Real Time during Cycling. In Proceedings of the 4th European Conference of the International Federation for Medical and Biological Engineering IFMBE Proceedings, Antwerp, Belgium, 23–27 November 2008; Volume 22, pp. 89–92.
- Conforto, S.; Sciuto, S.A.; Bibbo, D.; Scorza, A. Calibration of a Measurement System for the Evaluation of Efficiency Indexes in Bicycle Training. In Proceedings of the 4th European Conference of the International Federation for Medical and Biological Engineering IFMBE Proceedings, Antwerp, Belgium, 23–27 November 2008; Volume 22, pp. 106–109.
- Bibbo, D.; Conforto, S.; Bernabucci, I.; Carli, M.; Schmid, M.; D’Alessio, T. Analysis of Different Image-Based Biofeedback Models for Improving Cycling Performances. In Proceedings of SPIE 2012 the International Society for Optical Engineering, San Francisco, CA, USA, 9–10 January 2012; p. 829503.
- Fulginei, F.R.; Salvini, A.; Pulcini, G. Metric-topological-evolutionary optimization. Inverse Probl. Sci. Eng. 2012, 20, 41–58. [Google Scholar] [CrossRef]
- Coco, S.; Laudani, A.; Pulcini, G.; Fulginei, F.R.; Salvini, A. Shape optimization of multistage depressed collectors by parallel evolutionary algorithm. IEEE Trans. Magn. 2012, 48, 435–438. [Google Scholar] [CrossRef]
- Laudani, A.; Fulginei, F.R.; Lozito, G.M.; Salvini, A. Swarm/flock optimization algorithms as continuous dynamic systems. Appl. Math. Comput. 2014, 243, 670–683. [Google Scholar] [CrossRef]
- Laudani, A.; Fulginei, F.R.; Salvini, A.; Schmid, M.; Conforto, S. CFSO3: A new supervised swarm-based optimization algorithm. Math. Probl. Eng. 2013, 2013, 560614. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cecchini, G.; Lozito, G.M.; Schmid, M.; Conforto, S.; Fulginei, F.R.; Bibbo, D. Neural Networks for Muscle Forces Prediction in Cycling. Algorithms 2014, 7, 621-634. https://doi.org/10.3390/a7040621
Cecchini G, Lozito GM, Schmid M, Conforto S, Fulginei FR, Bibbo D. Neural Networks for Muscle Forces Prediction in Cycling. Algorithms. 2014; 7(4):621-634. https://doi.org/10.3390/a7040621
Chicago/Turabian StyleCecchini, Giulio, Gabriele Maria Lozito, Maurizio Schmid, Silvia Conforto, Francesco Riganti Fulginei, and Daniele Bibbo. 2014. "Neural Networks for Muscle Forces Prediction in Cycling" Algorithms 7, no. 4: 621-634. https://doi.org/10.3390/a7040621
APA StyleCecchini, G., Lozito, G. M., Schmid, M., Conforto, S., Fulginei, F. R., & Bibbo, D. (2014). Neural Networks for Muscle Forces Prediction in Cycling. Algorithms, 7(4), 621-634. https://doi.org/10.3390/a7040621