Power Cable Fault Recognition Based on an Annealed Chaotic Competitive Learning Network
Abstract
:1. Introduction
2. Related Research
2.1. SupportVector Machine
2.2. Particle Swarm Optimization Algorithm (PSO)
2.3. Improved Particle Swarm Optimization-Support Vector Machine (IPSO-SVM) Method

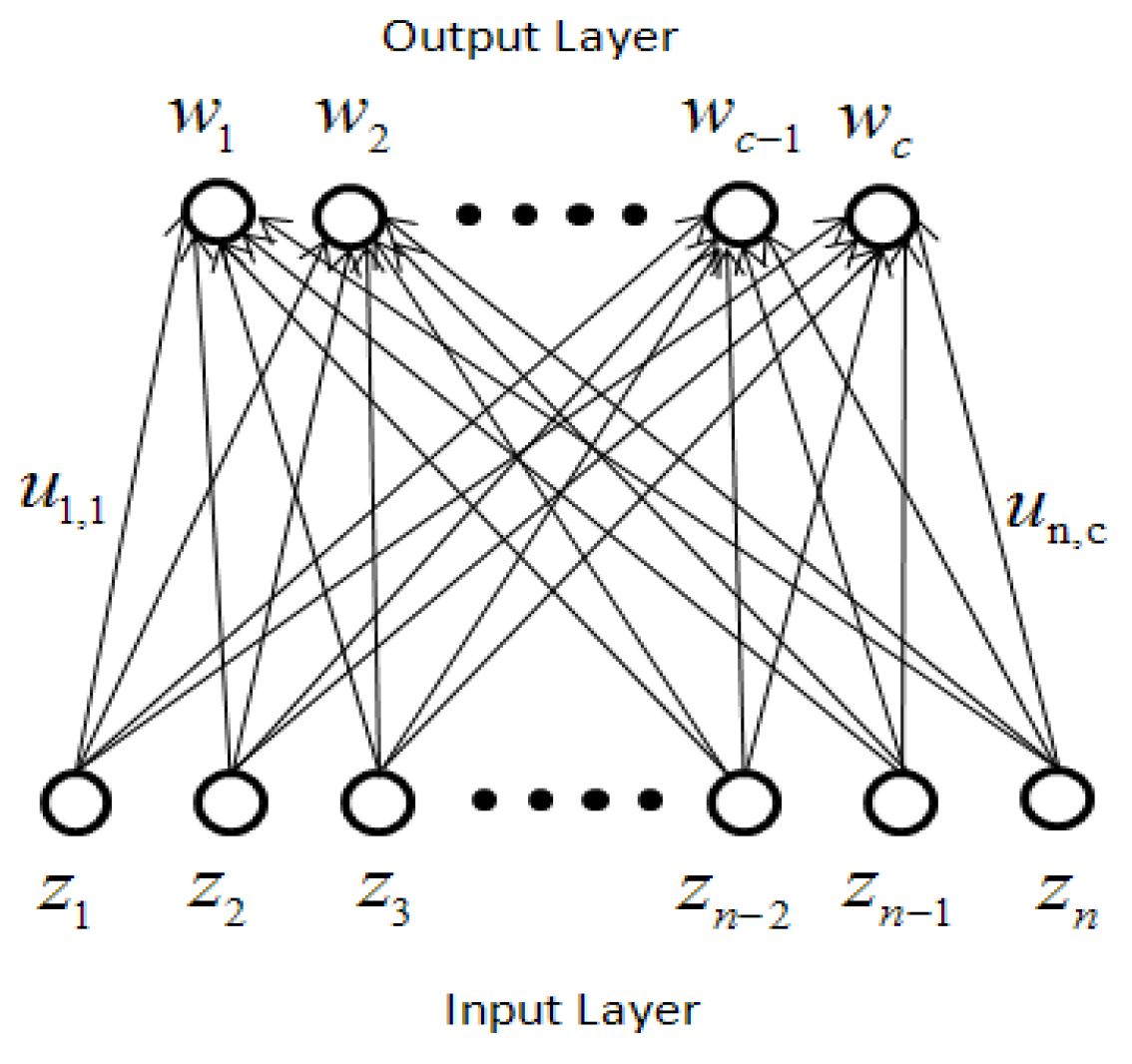
2.4. Competitive Learning Network
2.5. Annealed Chaotic Function
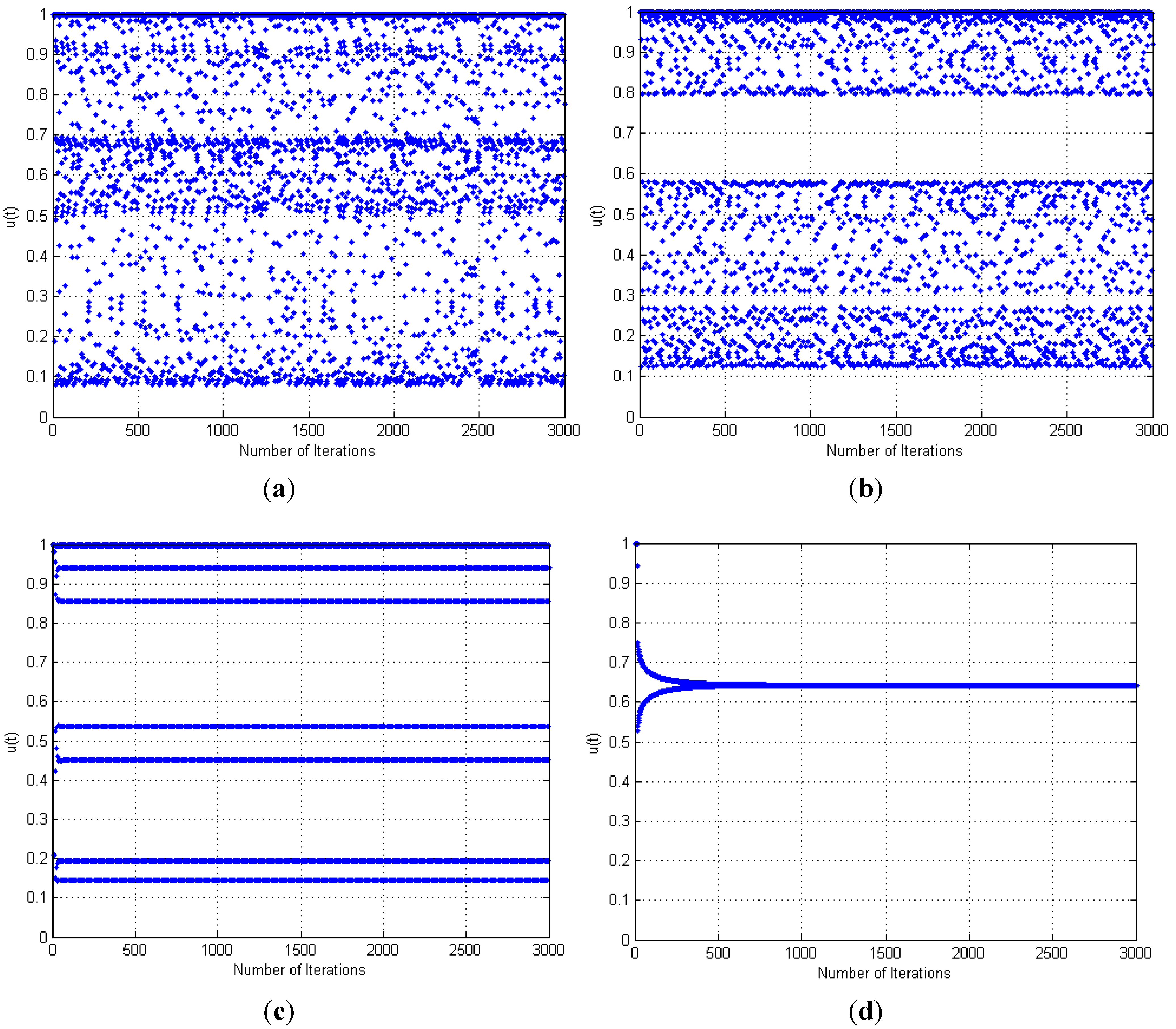
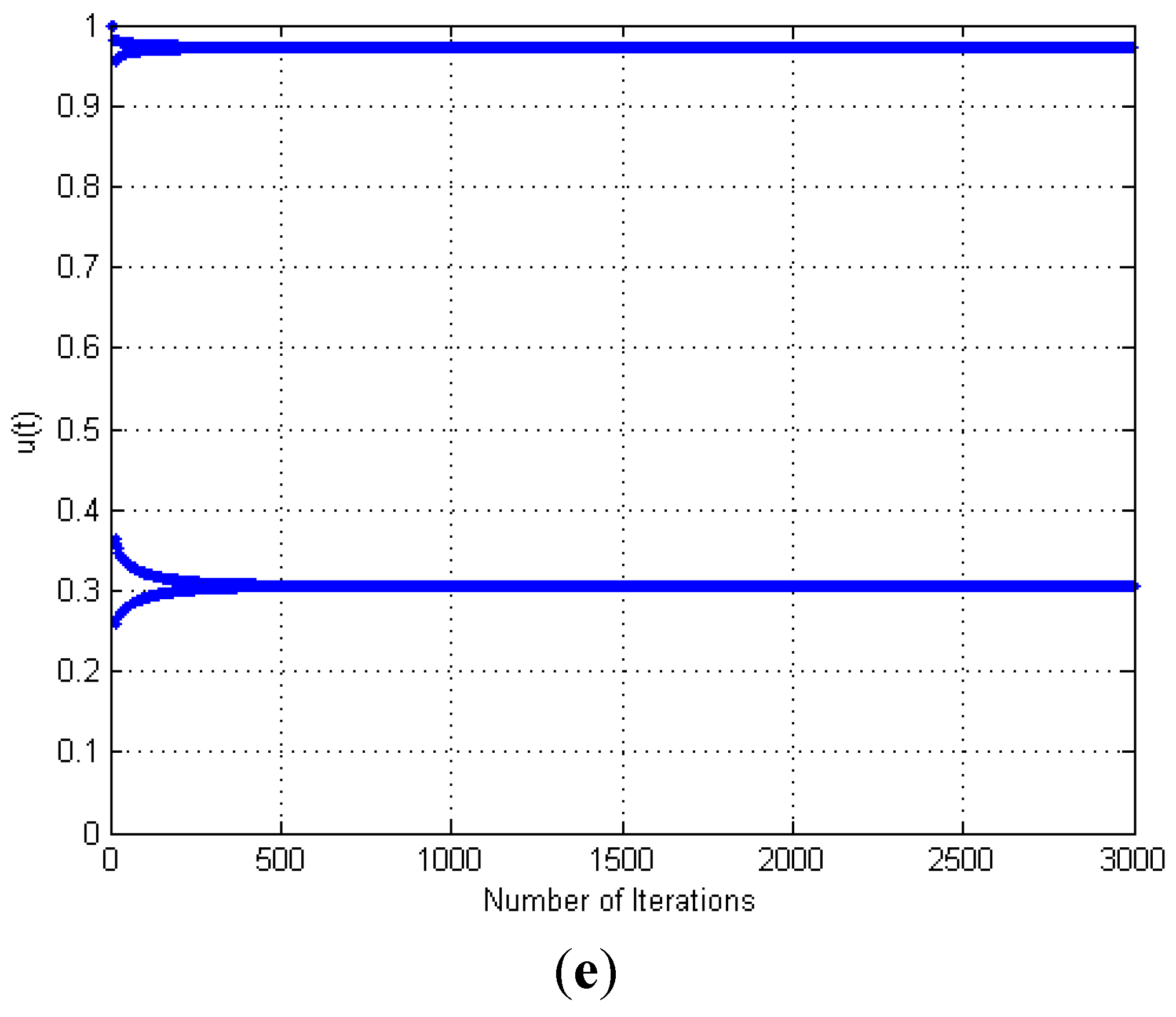
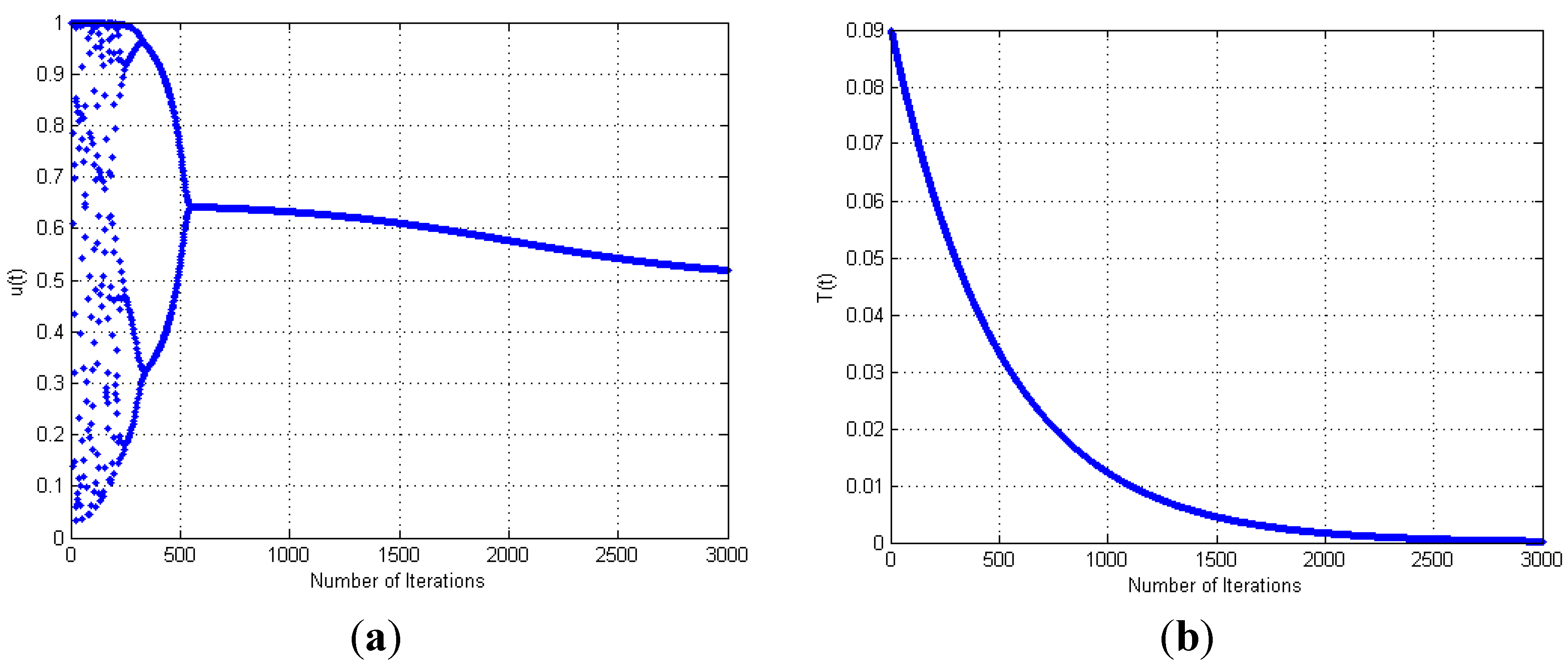
3. Annealed Chaotic Competitive Learning Network
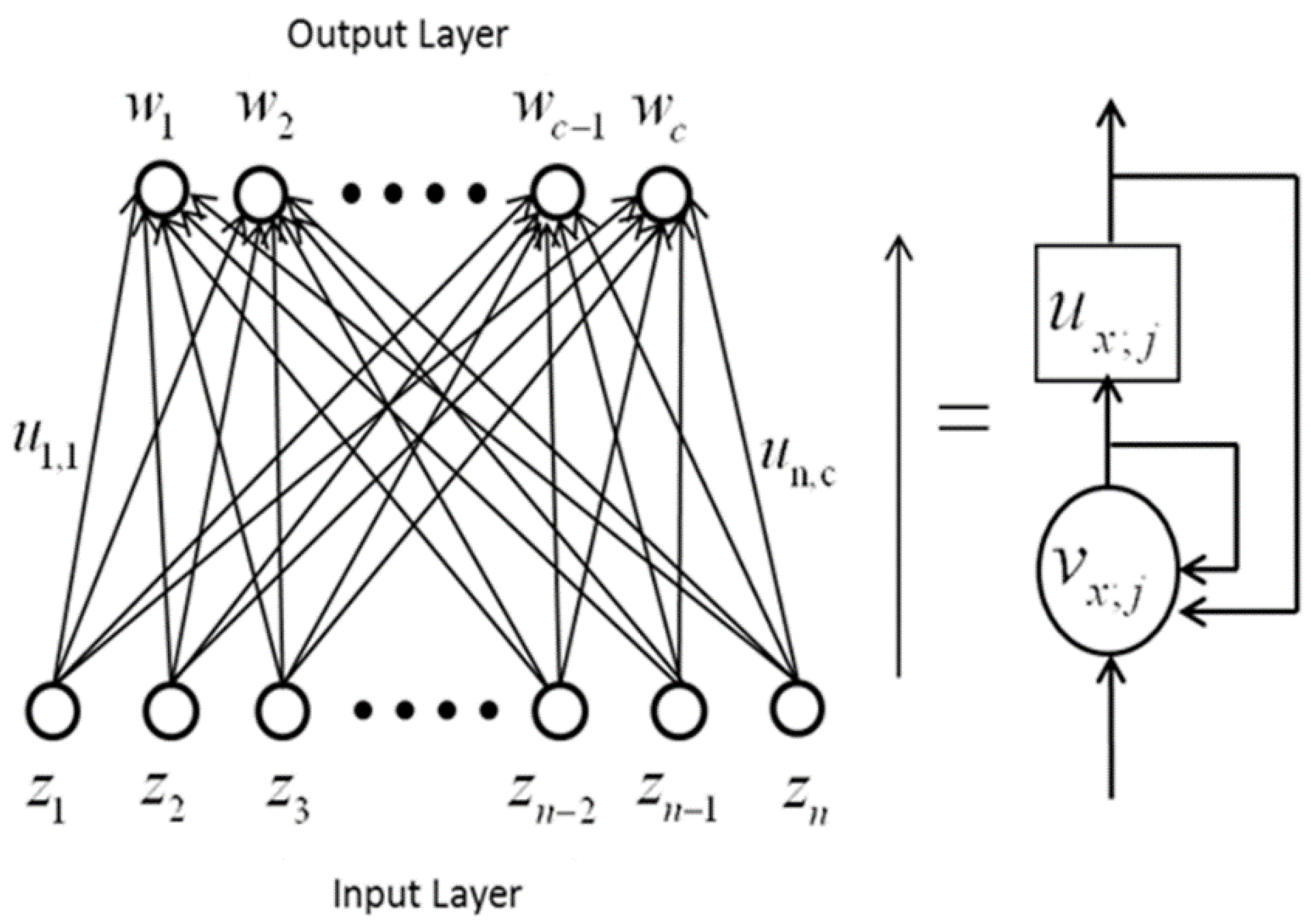
4. The Application of the ACCLN to Power Cable Fault
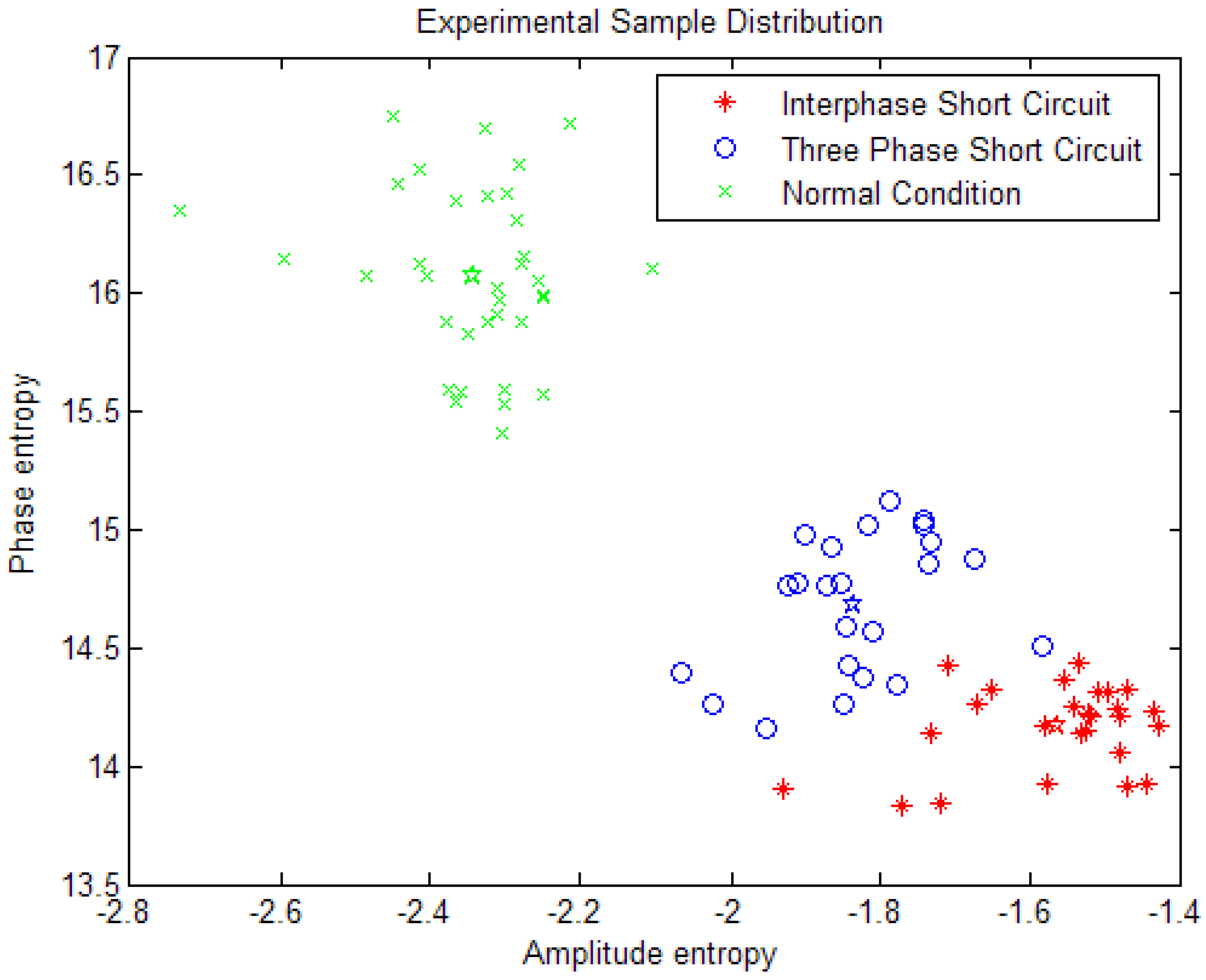
4.1. The Experimental Platform

| Fault types | Training samples | Test samples | Total sample number |
|---|---|---|---|
| interphase short circuit | 9 | 7 | 16 |
| three phase short circuit | 8 | 5 | 13 |
| normal condition | 15 | 10 | 25 |
| Total | 32 | 22 | 54 |
4.2. Performance of the IPSO-SVM Algorithm

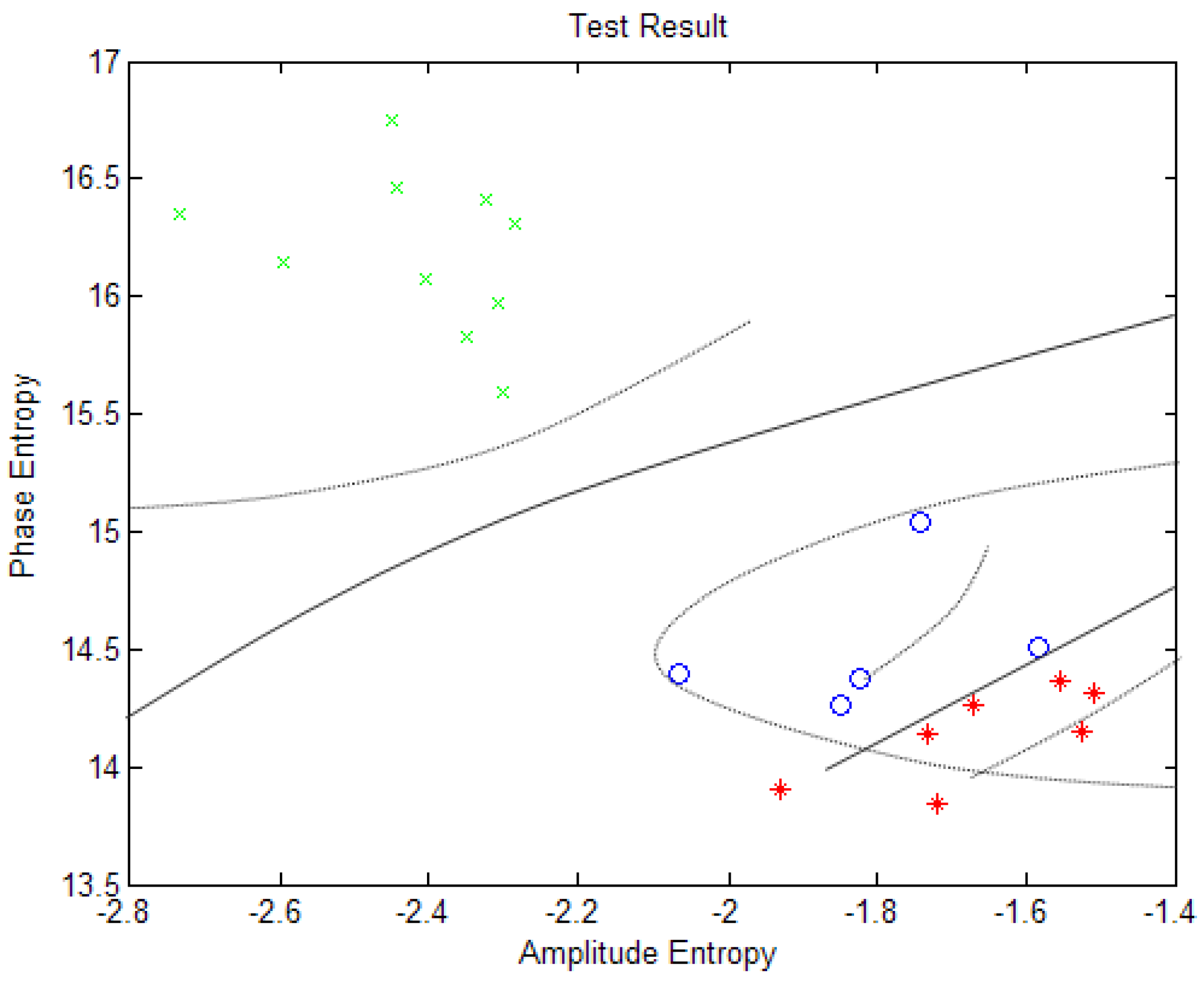
4.3. Power Cable Fault is Processed by the ACCLN Method


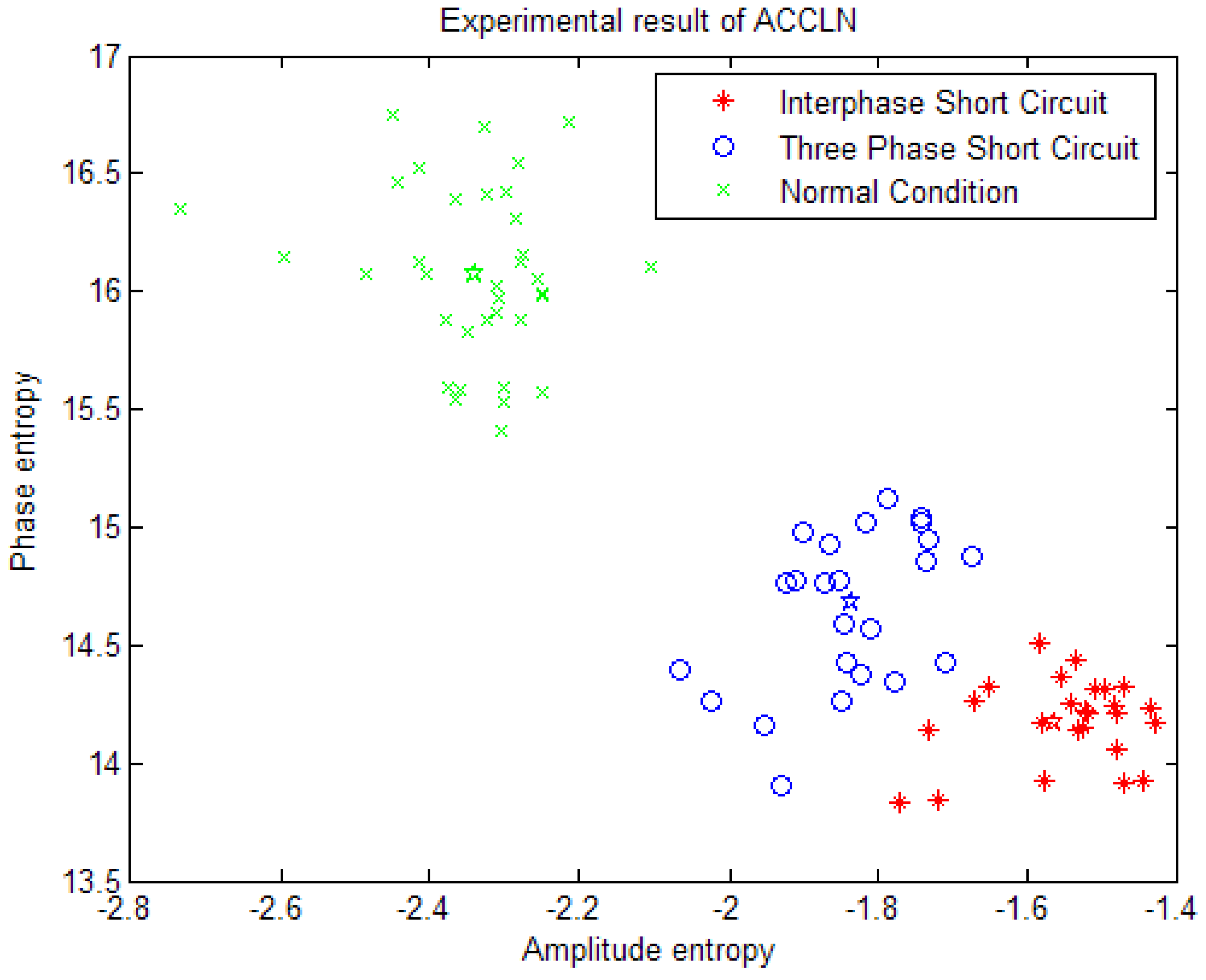
 ” indicates normal condition of power cable, 25 samples. The blue “
” indicates normal condition of power cable, 25 samples. The blue “  ” indicates the power cable of three-phase short circuit, 13 samples. The red “
” indicates the power cable of three-phase short circuit, 13 samples. The red “  ” indicates the power cable of interphase short fault, 16 samples. The different colors “☆” corresponds to each cluster-center.
” indicates the power cable of interphase short fault, 16 samples. The different colors “☆” corresponds to each cluster-center.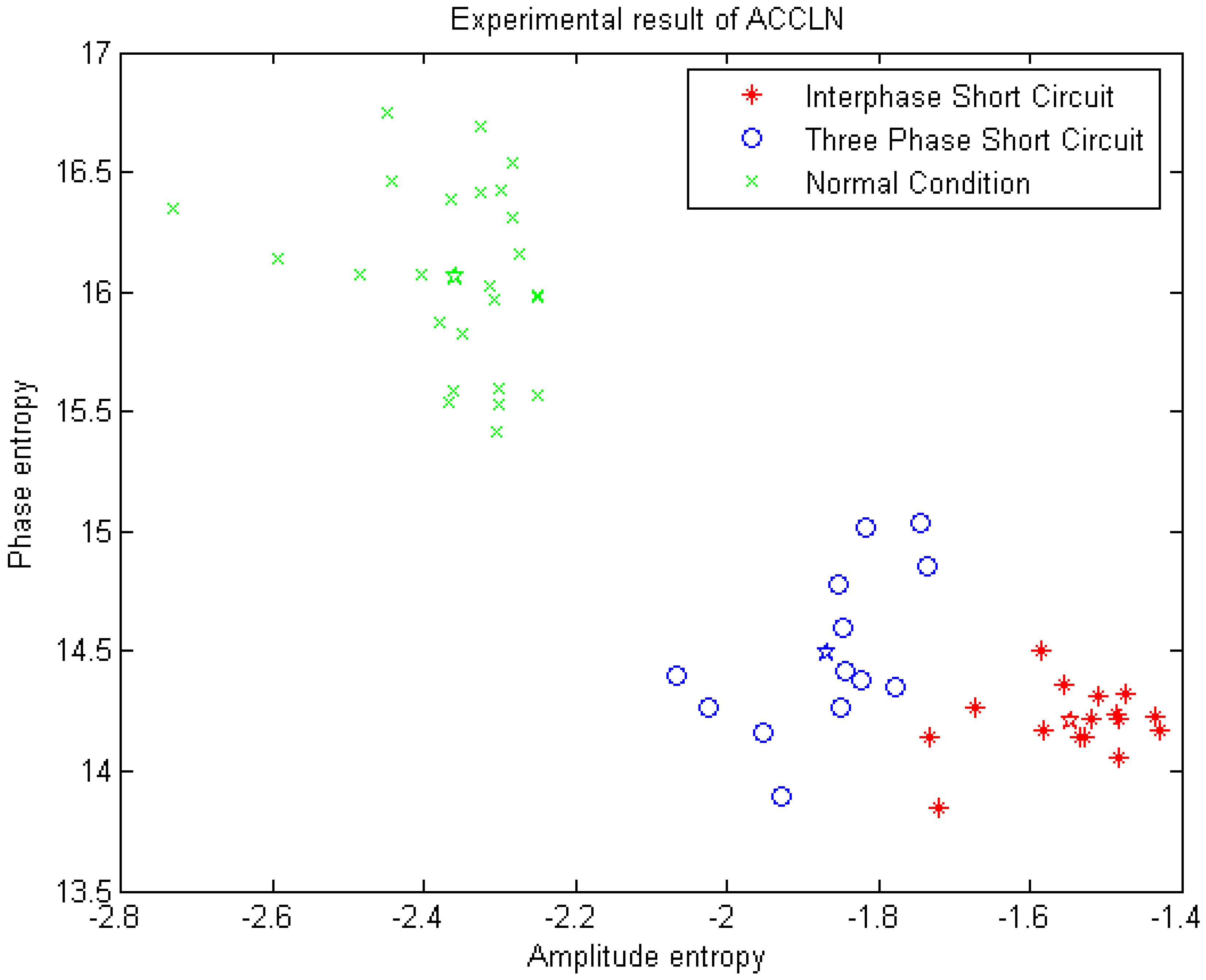
| Algorithm | Recognition Accuracy | Training Time |
|---|---|---|
| ACCLN | 96.2% | 0.032 |
| IPSO-SVM | 90.7% | 0.0523 |
| SVM | 87.0% | 0.0575 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, M.; Stathaki, T. Online fault recognition of electric power cable in coal mine based on the minimum risk neural network. J. Coal Sci. Eng. 2008, 14, 492–496. [Google Scholar] [CrossRef]
- Ratnaweera, A.; Halgamuge, S. Self-Organizing Hierarchical Particle Swarm Optimizer with Time-Varying Acceleration Coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Chen, P.; Zhao, C.H.; Li, J.; Liu, Z.M. Solving the Economic Dispatch in Power System via a Modified Genetic Particle Swarm Optimization. In Proceedings of the 2009 International Joint Conference on Computational Sciences and optimization, Sanya, Hainan, China, 24–26 April 2009; pp. 201–204.
- Gao, S.; Zhang, Z.Y.; Cao, C.G. Particle Swarm Optimization Algorithm for the Shortest Confidence Interval Problem. J. Computer. 2012, 7, 1809–1816. [Google Scholar] [CrossRef]
- Fronza, L.; Sillitti, A.; Succi, G. Failure prediction based on log files using Random Indexing an Support Vector Machines. J. Syst. Softw. 2013, 86, 2–11. [Google Scholar] [CrossRef]
- Liu, H.; Li, S. Decision fusion of sparse representation and support vector machine for SAR image target recognition. Neurocomputing 2013, 113, 97–104. [Google Scholar] [CrossRef]
- Yang, X.; Yu, Q.; He, L.; Guo, T. The one-against-all partition based binary tree support vector machine algorithms for multi-class classification. Neurocomputing 2013, 113, 1–7. [Google Scholar] [CrossRef]
- Zhang, J.-M.; Liang, S. Research on Fault Location of Power Cable with Wavelet Analysis. In Proceedings of the IEEE Digital Manufacturing and Automation, Zhangjiajie, Hunan, China, 5–7 August 2011; pp. 956–959.
- Jiang, J.A.; Chen, C.-S.; Liu, C.-W. A new protection scheme for fault detection, direction discrimination, classification, and location in transmission lines. IEEE Trans. Power Deliv. 2003, 18, 34–42. [Google Scholar] [CrossRef]
- Gnatenko, M.A.; Shupletsov, A.V.; Zinoviev, G.S.; Weiss, H. Measurement system for quality factors and quantities of electric energy with possible wavelet technique utilization. In Proceedings of the 8th Russian-Korean International Symposium on Science and Technology, Tomsk Polytechnic University, Tomsk, Russia, 26 June–3 July 2004; pp. 325–328.
- Li, B.; Shen, Y. Electric Heating Cable Fault Locating System Based on Neural Network. In Proceedings of the IEEE International Conference on Natural Computation, Tianjin, China, 14–16 August 2009; pp. 43–47.
- Wang, M.; Li, X. Power Cable Fault Recognition Using the Improved PSO-SVM Algorithm. Appl. Mech. Mater. 2013, 427–429, 830–833. [Google Scholar] [CrossRef]
- Cai, G.-L.; Shao, H.-J. Synchronization-based approach for parameter identification in delayed chaotic network. Chin. Phys. B 2010, 19, 1056–1074. [Google Scholar]
- Uchiyama, T.; Arbib, M.A. Color Image Segmentation using competitive learning. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 1197–1206. [Google Scholar] [CrossRef]
- Lin, J.; Tsai, C. An Annealed Chaotic Competitive Learning Network with Nonlinear Self-feedback and Its Application in Edge Detection. Neural Process. Lett. 2001, 13, 55–69. [Google Scholar] [CrossRef]
- Lu, S.W.; Shen, J. Artificial neural networks for boundary extraction. In Proceedings of the IEEE International Conference on SMC, Beijing, China, 14–17 October 1996; pp. 2270–2275.
- Xiang, W.; Zhou, Z. Camera Calibration by Hybrid Hopfiled Network and self-Adaptive Genetic Algorithm. Meas. Sci. 2012, 12, 302–308. [Google Scholar]
- Wright, A.H. Genetic Algorithms for Real Parameter Optimization. In Foundations of Genetic Algorithms; Rawlins, G.J.E., Ed.; Morgan Kaufmann: Missoula, Montana, 1991; pp. 205–218. [Google Scholar]
- Lin, J.-S.; Liu, S. Classification of Multispectral Images Based on a Fuzzy-Possibilistic Neural Network. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2002, 32, 499–506. [Google Scholar]
- Zhang, C.; Liu, Y.; Zhang, H.; Huang, H. Research on the Daily Gas Load Forecasting Method Based on Support Vector Mechine. J. Comput. 2011, 6, 2662–2667. [Google Scholar] [CrossRef]
- Al-Geelani, N.A.; Piah, M.A.M.; Adzis, Z.; Algeelani, M.A. Hybrid regrouping PSO based wavelet neural networks for characterization of acoustic signals due to surface discharges on H.V. insulators. Appl. Soft Comput. J. 2013, 13, 78–87. [Google Scholar] [CrossRef]
- Maldonado, Y.; Castillo, O.; Melin, P. Particle swarm optimization of interval type-2 fuzzy systems for FPGA applications. Appl. Soft Comput. J. 2013, 13, 456–465. [Google Scholar] [CrossRef]
- Hamta, N.; Fatemi Ghomi, S.M.T.; Jolai, F.; Akbarpour Shirazi, M. A hybrid PSO algorithm for a multi-objective assembly line balancing problem with flexible operation times, sequence-dependent setup times and learning effect. Int. J. Prod. Econ. 2013, 141, 357–365. [Google Scholar] [CrossRef]
- Qi, F.; Xie, X.; Jing, F. Application of improved PSO-LSSVM on network threat detection. Wuhan Univ. J. Nat. Sci. 2013, 18, 418–426. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Azarkish, M.; Sadeghnejad-Barkousaraie, A. Solving a multi-objective job shop scheduling problem with sequence-dependent setup times by a Pareto archive PSO combined with genetic operators and VNS. Int. J. Adv. Manuf. Technol. 2011, 53, 733–750. [Google Scholar] [CrossRef]
- Lin, J.-S. Annealed chaotic neural network with nonlinear self-feedback and its application to clustering problem. Patten Recognit. 2001, 34, 1093–1104. [Google Scholar] [CrossRef]
- Tsai, C.; Liaw, C. Polygonal approximation using an annealed chaotic Hopfield network. In Proceedings of the IEEE International Workshop on Cellular Neural Networks and Their Application, Hsinchu, Taiwan, 28–30 May 2005; pp. 122–125.
- Chen, L.; Kazuyaki, A. Chaotic Simulated Annealing by a Neural Network Model with Transient Chaos. Neural Netw. 1995, 8, 915–930. [Google Scholar] [CrossRef]
- George, A.; Katerina, T. Simulating annealing and neural networks for chaotic time series forecasting. Chaotic Model. Simul. 2012, 1, 81–90. [Google Scholar]
- Atsalakis, G.; Skiadas, C. Forecasting Chaotic time series by a Neural Network. In Proceedings of the 8th International Conference on Applied Stochastic Models and Data Analysis, Vilnius, Lithuania, 30 June–3 July 2008; pp. 77–82.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, X.; Wang, M.; Lin, J.-S.; Li, X. Power Cable Fault Recognition Based on an Annealed Chaotic Competitive Learning Network. Algorithms 2014, 7, 492-509. https://doi.org/10.3390/a7040492
Qin X, Wang M, Lin J-S, Li X. Power Cable Fault Recognition Based on an Annealed Chaotic Competitive Learning Network. Algorithms. 2014; 7(4):492-509. https://doi.org/10.3390/a7040492
Chicago/Turabian StyleQin, Xuebin, Mei Wang, Jzau-Sheng Lin, and Xiaowei Li. 2014. "Power Cable Fault Recognition Based on an Annealed Chaotic Competitive Learning Network" Algorithms 7, no. 4: 492-509. https://doi.org/10.3390/a7040492
APA StyleQin, X., Wang, M., Lin, J.-S., & Li, X. (2014). Power Cable Fault Recognition Based on an Annealed Chaotic Competitive Learning Network. Algorithms, 7(4), 492-509. https://doi.org/10.3390/a7040492





