Modeling Dynamic Programming Problems over Sequences and Trees with Inverse Coupled Rewrite Systems
Abstract
:1. Introduction
- Mapping from concrete to abstract
- is always the easier way.
1.1. Motivation
1.2. Overview
- describe optimization problems on a declarative level of abstraction, where fundamental ideas are not obscured by implementation detail, and relationships between similar problems are transparent and can be exploited;
- implement algorithmic solutions to these problems in a systematic or even automated fashion, thus liberating algorithm designers from error-prone coding and tedious debugging work, enabling re-use of tried-and-tested components, and overall, enhancing programmer productivity and program reliability.
1.3. Previous Work
1.4. Article Organization
| ICORE/Grammar | Dim. | Problem addressed | In Section | Page |
|---|---|---|---|---|
| EditDistance | 2 | simple edit distance/alignment | 4.2 | 77 |
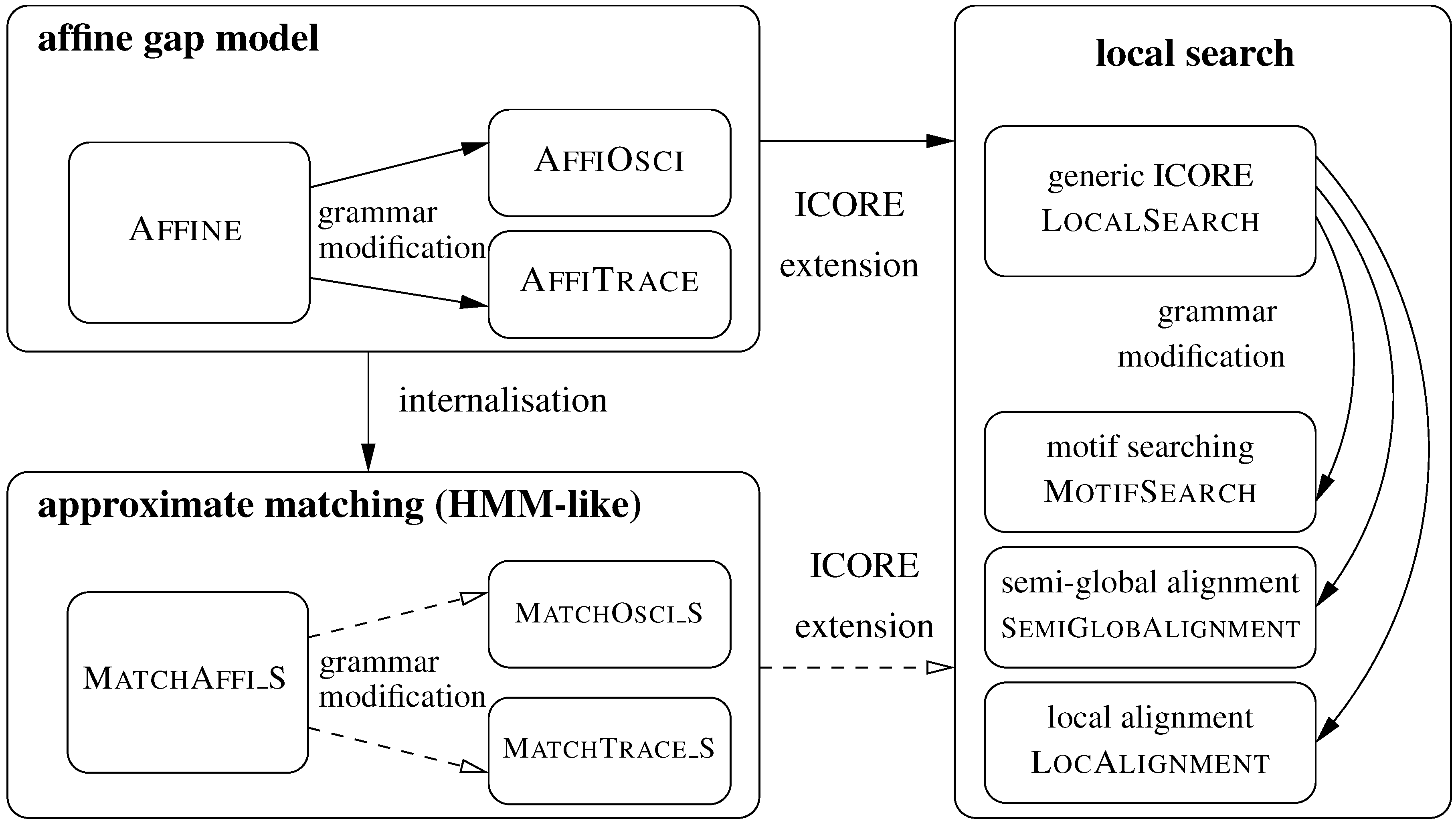
| Affine | 2 | edit distance, affine gaps | 5.1 | 82 |
| AffiOsci | 2 | oscillating affine gaps | 5.1 | 84 |
| AffiTrace | 2 | sequence traces, affine gaps | 5.1 | 84 |
| LocalSearch | 2 | generic local alignment | 5.2 | 85 |
| MotifSearch | 2 | short in long alignment | 5.2.1. | 86 |
| SemiGlobAlignment | 2 | semi-global alignment | 5.2.2. | 86 |
| LocalAlignment | 2 | local alignment | 5.2.3. | 86 |
| MatchSeq_S | 1 | hardwired sequence matching | 5.3.1. | 88 |
| MatchAffi_S | 1 | same with affine gap model | 5.3.1. | 88 |
| MatchSeq_S | 1 | profile HMM | 5.3.2. | 88 |
| with position-specific scores | ||||
| RNAfold | 1 | RNA folding | 6.3 | 93 |
| StructAli | 2 | struct. Alignment prototype | 6.4 | 97 |
| SimultaneousFolding | 2 | generalized fold and align | 6.5 | 98 |
| ExactConsensusStructure | 2 | exact consensus structure | 6.5.2. | 98 |
| for two RNA sequences | ||||
| Sankoff | 2 | simultaneous fold and align | 6.5.3. | 99 |
| S2SGeneric | 2 | covariance model, generic | 6.6.1. | 101 |
| S2SExact | 2 | match RNA sequence | 6.6.2. | 100 |
| to target structure | ||||
| Match_S2S_r | 2 | exact local motif matcher | 6.6.4. | 103 |
| Match_S2S_r’ | 1 | motif matcher, hard coded | 6.6.4. | 104 |
| SCFG | 1 | stochastic context free grammar | 6.3 | 93 |
| CovarianceModel_r | 1 | covariance model, hard coded | 6.6.5. | 106 |
| TreeAlign | 2 | classical tree alignment | 7.2 | 111 |
| TreeAliGeneric | 2 | tree alignment protoype + variants | 7.2.2. | 113 |
| OsciSubforest | 2 | tree ali. with oscillating gaps | 7.2.2. | 117 |
| TreeEdit | 2 | classical tree edit | 7.3 | 119 |
| RNATreeAli | 2 | RNA structure alignment | 7.5 | 127 |
2. A Motivating Example
replacement of ‘A’ by ‘A’,
replacement of ‘C’ by ‘A’,
deletion of ‘G’,
replacement of ‘T’ by ‘T’,
replacement of ‘A’ by ‘A’,
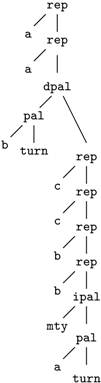
insertion of ‘G’This edit script is represented by the term
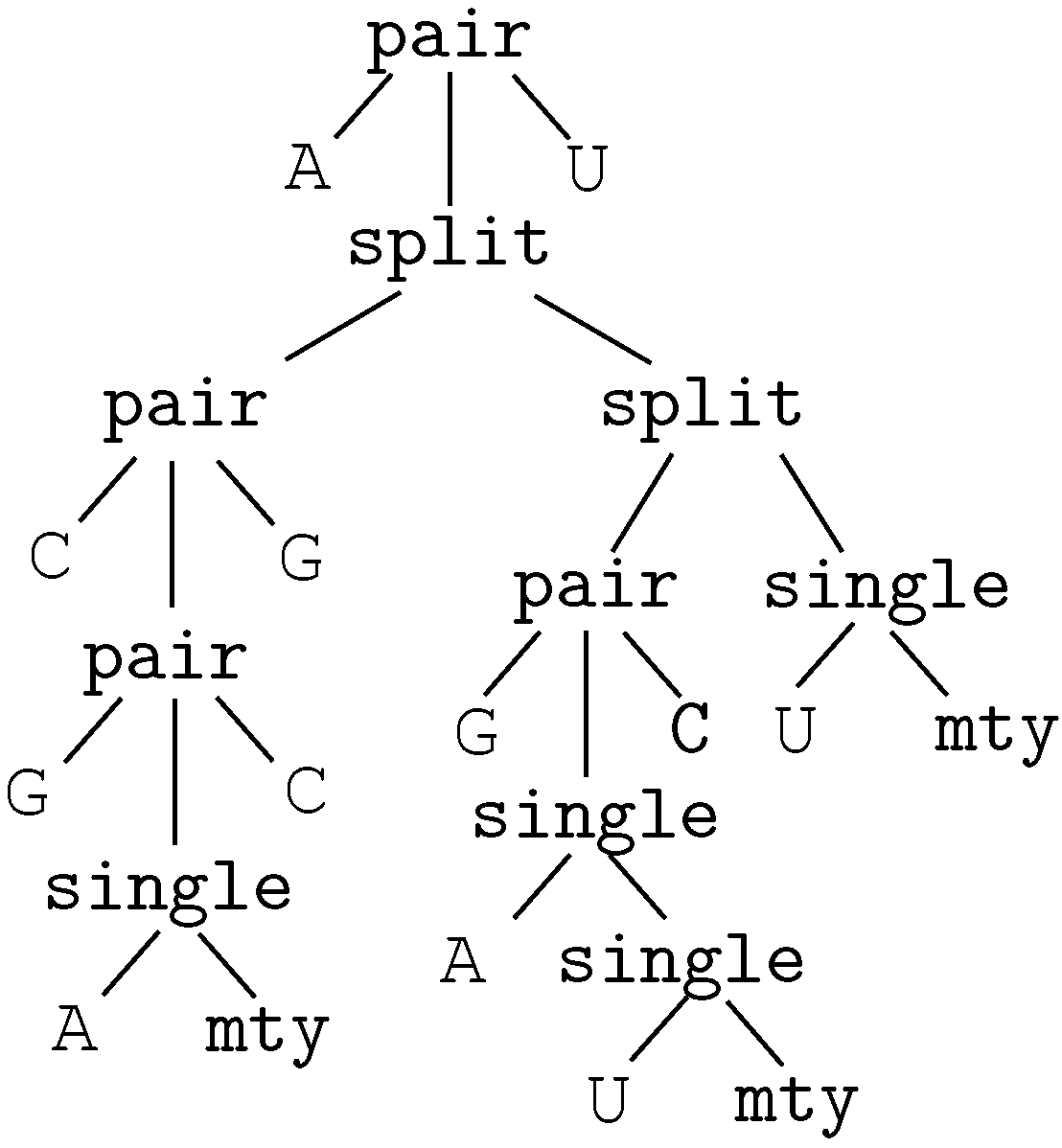
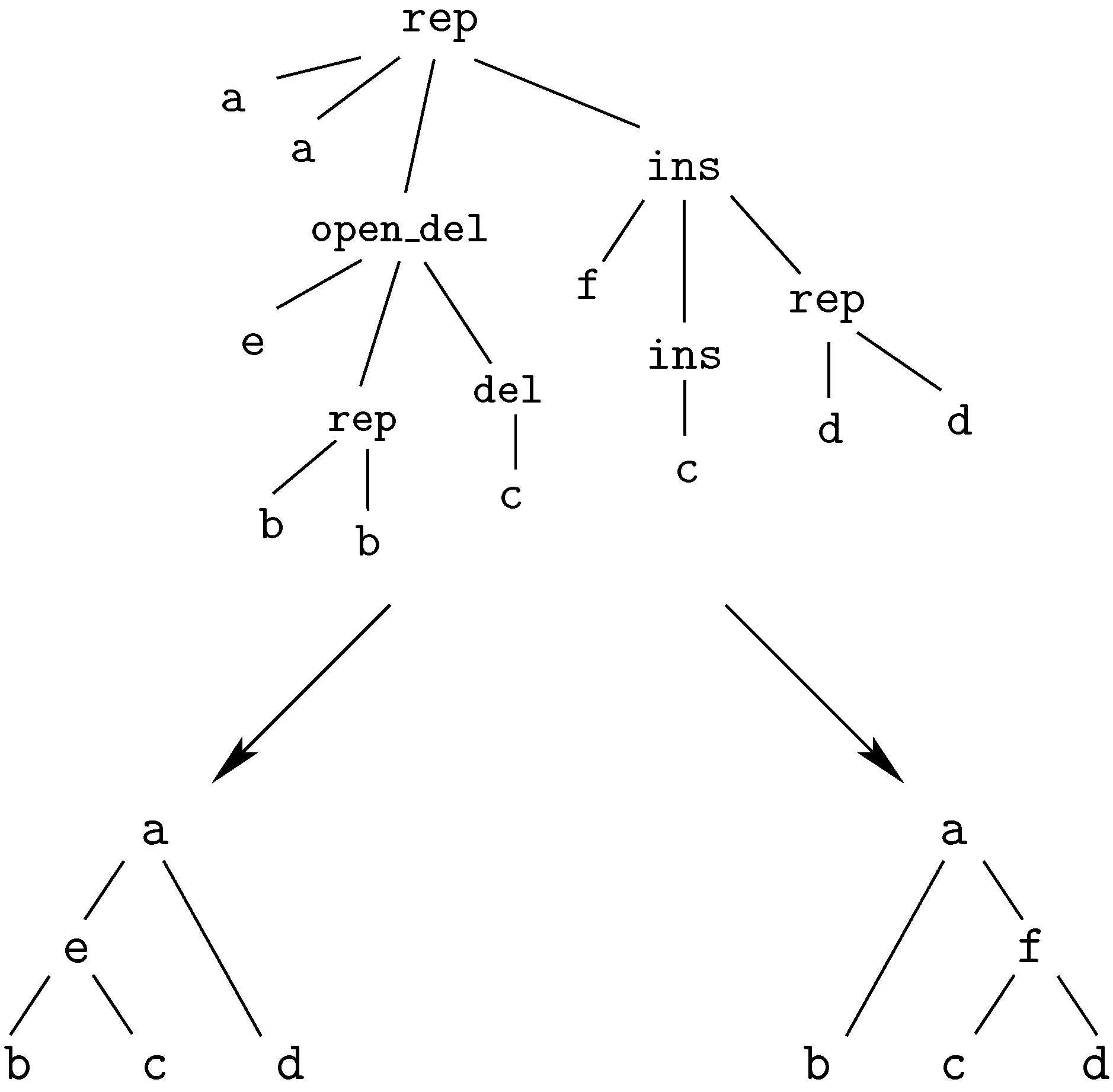
rep(A,A,rep(C,A,del(G,rep(T,T,rep(A,A,ins(G,mty))))))
We call these terms core terms, as they represent the search space of candidate solutions. A visually better representation of this edit script would be an alignment of the two sequences, in this case
A C G T A -
A A - T A GA term representing an edit script contains in some sense the two input sequences: U is the concatenation of the first arguments of and of . V is the concatenation of the second arguments of and the first arguments of . This projection is formally expressed with two term rewrite systems:
3. Machinery
3.1. Variables, Signatures, Alphabets, Terms and Trees
- Let be a set of sorts. Sorts are names or placeholders for abstract data types.
- We assume the existence of countably infinite sets of variables for every sort α of . The union of all is denoted by V.
- We assume a finite -sorted signature F. An -sorted signature is a set of function symbols together with a sort declaration for every f of F. Here and n is called the arity of f. Function symbols of arity 0 are called constant symbols.
- A signature F may include an alphabet , which is a designated subset of the nullary function symbols (constant symbols) in F. Where the distinction matters, the function symbols in are called characters, and the other function symbols are called operators.
- denotes the set of well-typed terms over F and V. It is the union of the sets for α in that are inductively defined as follows:
- each variable of is a term of ,
- if f is a function symbol of F with sort declaration and for all , then is in .
is called the term algebra over F and V. The set of variables appearing in a term t is denoted by , and its sort by such that when . - denotes the set of ground terms of , where .
- A substitution σ maps a set of variables to a set of terms, preserving sorts. The application of a substitution σ to a term t replaces all variables in t for which σ is defined by their images. The result is denoted .
- Terms and trees: We adopt a dual view on terms as trees. A term can be seen as a finite rooted ordered tree, the leaves of which are labeled with constant symbols or variables. The internal nodes are labeled with function symbols of arity greater than or equal to 1, such that the outdegree of an internal node equals the arity of its label. Note that alphabet characters, being nullary function symbols, can only occur at the leaves of a tree.
- A position within a term can be represented as the sequence of positive integers that describe the path from the root to that position (the path is given in Dewey’s notation). We denote by the subterm of t at position p and the replacement of in t by u.
3.2. Rewrite Systems
- A rewrite rule is an oriented pair of terms, denoted , such that and . Because of the last requirement, generally is not a legal rewrite rule, and rewrite rules cannot be reversed without generating unbound variables. Furthermore, we disallow , as such a rule would allow to rewrite any term, while is perfectly legal.
- A term rewrite system R is a finite set of such rewrite rules. The rewrite relation induced by R, written , is the smallest relation closed under context and substitution containing each rule of R. In other words, a term t rewrites to a term u, written , if there exist a position p in t, a rule in R and a substitution σ such that and . is the reflexive transitive closure of .
- In the sequel, we will consider term rewrite systems with disjoint signatures. We say that R is a term rewrite system with disjoint signatures if it is possible to partition F into two subsets ζ and Σ such that for each rule of R, the left-hand side ℓ belongs to , and the right-hand side r belongs to . In this manuscript, ζ is called the core signature, and Σ the satellite signature. Ground terms of are called core terms. ζ and Σ can both contain an associative binary operator, denoted and respectively (see below).In practice, core signatures may share function symbols with satellite signatures (possibly not with the same arity). Often, they share the alphabet. By convention, when a shared symbol occurs in a rewrite rule, it belongs to the signature ζ on the left-hand side, and to Σ on the right-hand side. Elsewhere, symbols of ζ will be subscripted for clarity.
- Syntactic conditions: Rewrite rules may have associated syntactic conditions for their applicability, as inIn our framework, these conditions will only refer to characters from a finite alphabet. This is merely a shorthand against having to write too many similar rules, and does not contribute computational power. It must not be confused with general conditional term rewriting as in , where the rule is applicable if x and y can be rewritten to a joint reduct by the given rewrite system.
3.3. Rewriting Modulo Associativity
3.4. Tree Grammars
- F is the signature,
- N is a set of non-terminal symbols, disjoint from F, where each element is assigned a sort.
- Z is the starting non-terminal symbol, with , and
- P is a set of productions of the form , where , , and X and t have the same sort.
3.5. Algebras
- Given signature F, an F-algebra A associates a carrier set (i.e., a concrete data type) with each sort symbol in F, and a function of the corresponding type with each . denotes the value obtained by evaluating term t under the interpretation given by algebra A. Often, we shall provide several algebras to evaluate terms.
- An objective function is a function ϕ, where M is the domain of multisets (bags) over some carrier set in a given algebra. (Multiple carrier sets give rise to one overloaded instance of ϕ on each carrier set.) Typically, ϕ will be minimization or maximization, but summation, enumeration, or sampling are also common. Our objective functions are defined on multisets rather than sets, as we want to model problems such as finding all co-optimal solutions of a problem instance.
- An F-algebra augmented by an objective function for multisets over each of its carrier sets is called an evaluation algebra.
4. Inverse Coupled Rewrite Systems
4.1. ICORE Definitions
- a set V of variables,
- a core signature ζ, and k satellite signatures , such that . (Function symbols of ζ are disjoint from all , except for a possible shared alphabet.)
- k term rewrite systems with disjoint signatures, , which all have the same left-hand sides in . (Those systems are called the satellite rewrite systems.)
- optionally a tree grammar over the core signature ζ,
- an evaluation algebra A for the core signature ζ, including an objective function ϕ.
- (start of a coupled derivation),
- , ..., (end of a coupled derivation),
- for each e, (step in a coupled derivation), there exists a rule projection such that rewrites modulo associativity to with the rule and all rewrites apply simultaneously at the same place. In other words, for each i, there is a term , a position in and a substitution such that , , , and all operator symbols in ℓ have the same initial position in c.
- c is recognized by the tree grammar: , and
- c has a coupled rewriting into all inputs: .
4.2. ICORE Pseudocode

- ICORE, grammar and algebra names are written in small Capitals.
- Signatures have three- or four-letter names in ITA LICS.
- Sort names have an inital upper-case letter.
- Operators are written in typewriter font.
- Concrete alphabet symbols are written in typewriter font, such as A, +.
- Variables refer to alphabet characters, to (sub-)terms in rewrite rules (that may undergo further rewriting), and to values derived from core terms in some algebra.
- The variable w is reserved for multisets of candidate values, on which objective functions operate.
4.3. An ICORE Exercise
aaBBccbb aa bBCCBb AABBccbb aabbccbb
aa ccbbAA aaCCb bAA AA ccbbAA aaccbbaawhere the capital letters indicate the palindrome choices, and the small letters the matched characters. Note that "AABB" marks two adjacent palindromes of length 2 in the third case. Of course, there are many more candidates which must be considered to find the minimum. □
4.4. Why Rewriting the Wrong Way?
5. ICOREs for Sequence Analysis
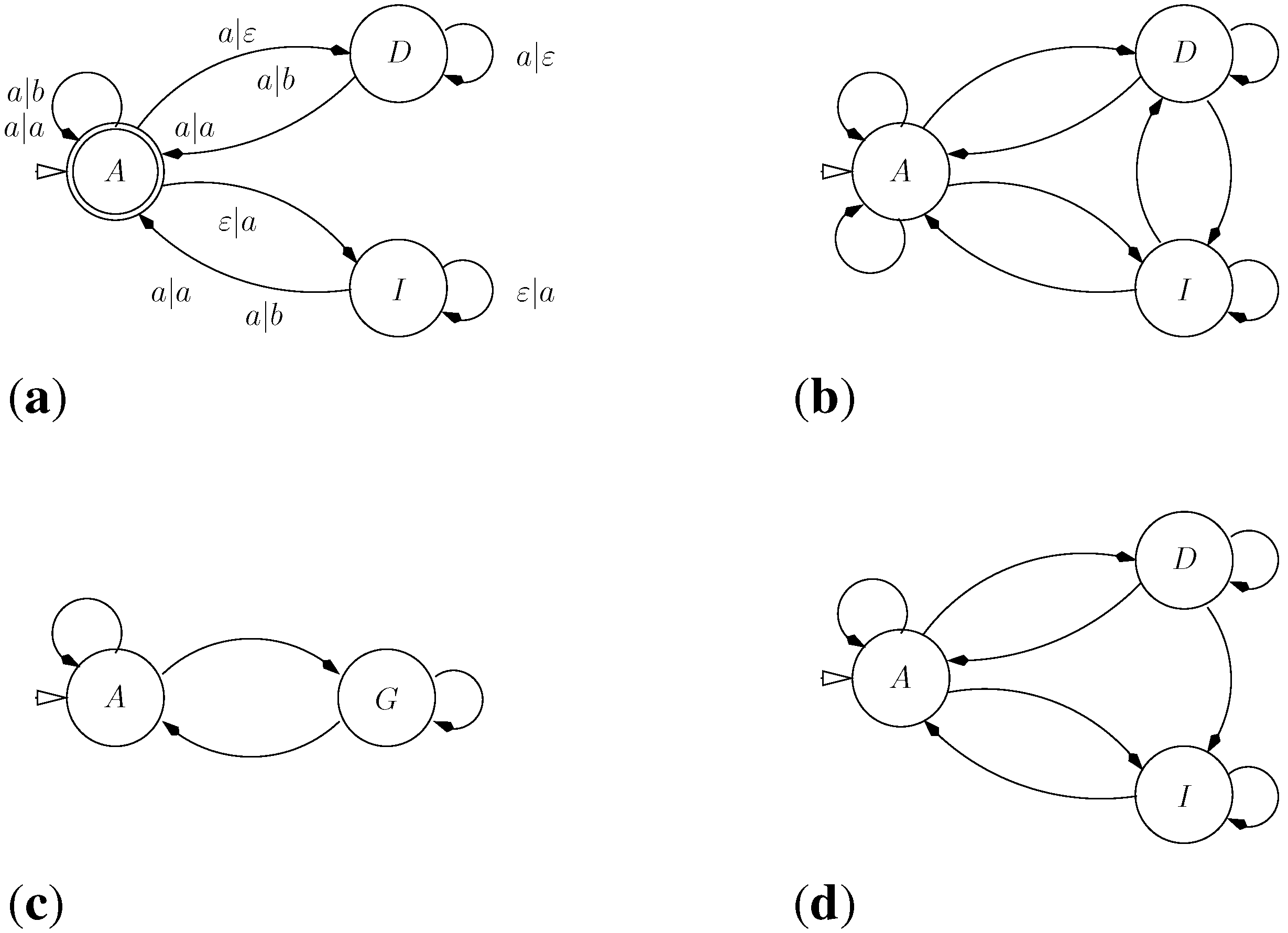
5.1. Sequence Comparison with an Affine Gap Model
5.1.1. Standard Affine Gap Model

G C - - - T G T C C A
| | | | |
A C G A A T G - - C AOn the other side, a term such as is banned by the grammar because the gap extension has no preceding gap opening. It does not correspond to a legal alignment in the affine gap model. A borderline example is a term such as , because the “same” gap contains two gap opening operations. Many formulations of affine gap alignment allow for this case–it will never score optimally, so why care. However, should we be interested also in near-optimal solutions, it is more systematic to keep malformed candidates out of the search space. Our grammar rules out this candidate solution. □
5.1.2. Variants of the Affine Gap Model: Oscillating Gaps and Traces
AACC--TT AA--CCTT AA-CC-TT AAC-C-TT AAC--CTT
|| || || || || || || || || ||
AA--GGTT AAGG--TT AAG--GTT AA-G-GTT AA-GG-TT

5.2. From Global Comparison to Local Search

5.2.1. Motif Searching
5.2.2. Semi-Global Alignment
5.2.3. Local Alignment

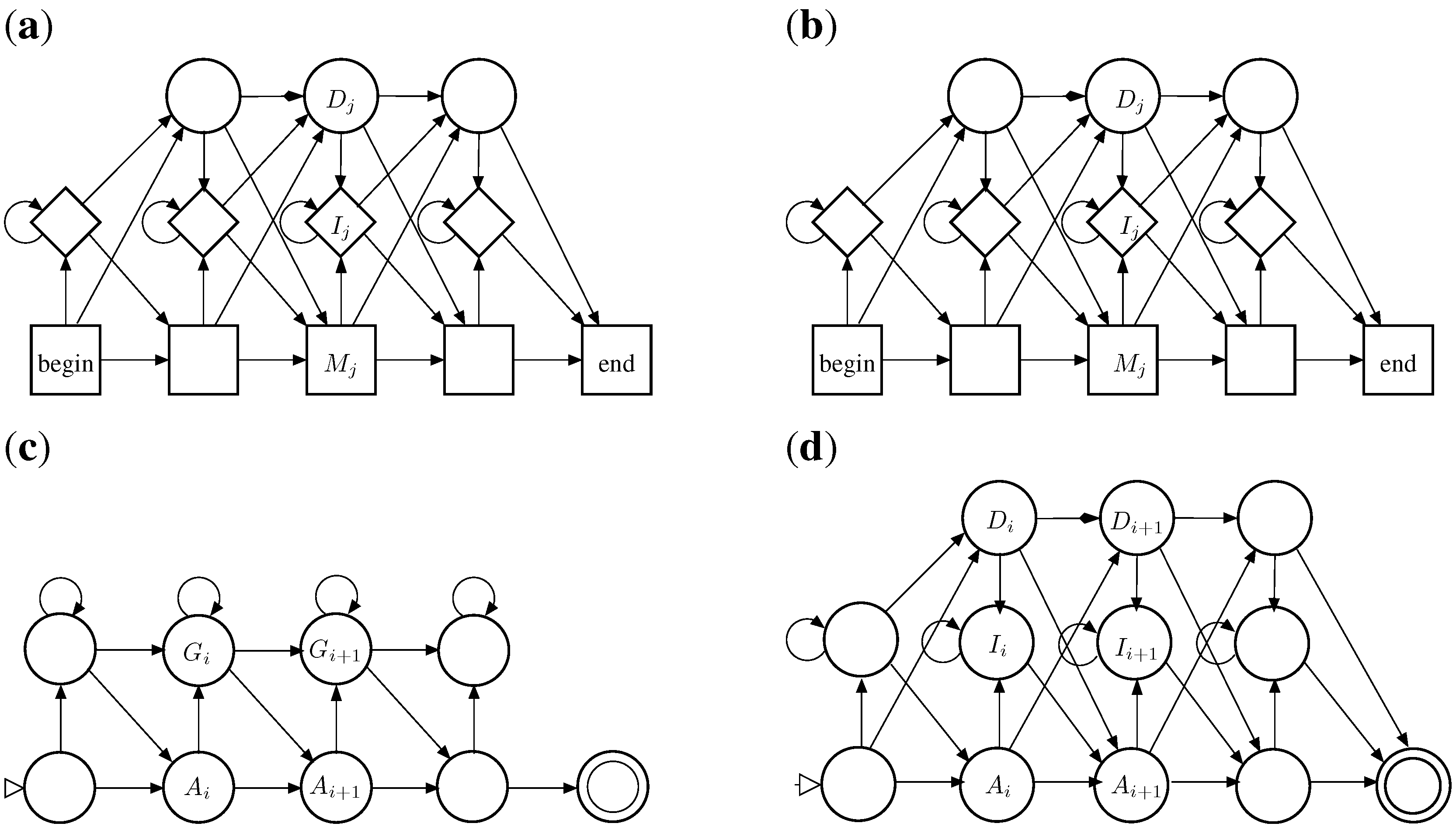
5.3. Approximate Motif Matching and HMMs
5.3.1. Approximate Matching

5.3.2. From Approximate Matching to Profile HMMs
- HMMs are normally described as Moore machines, which emit symbols on states, independent of transitions. In our grammar, "emissions" are associated with the transitions: symbol is generated on transition into from to . In this sense, they are closer to Mealy machines.
- In a profile HMM, the target model is built from a multiple sequence alignment, rather than from a single sequence. In the target S, the “characters” now are columns from that alignment. Each matching state of the HMM (square state) is a position in the target sequence.
- Scoring parameters in HMMs are position-specific. This implies that the scoring algebra of the ICORE should take into account the position in the core term: In , column is represented simply by i, which is used to look up the score parameter for this position.
6. ICOREs for RNA Secondary Structure Analysis
6.1. RNA Structure Analysis Overview
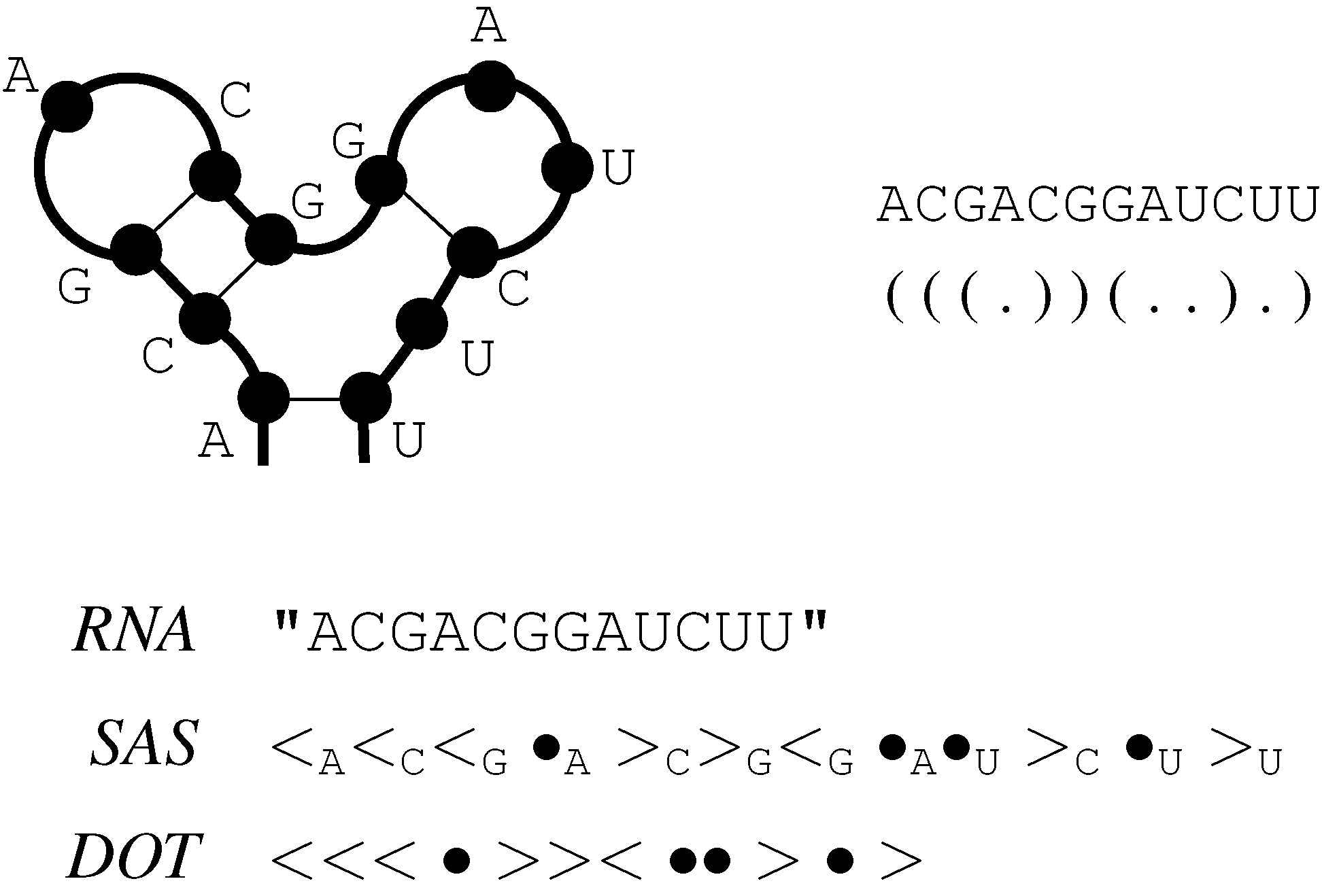
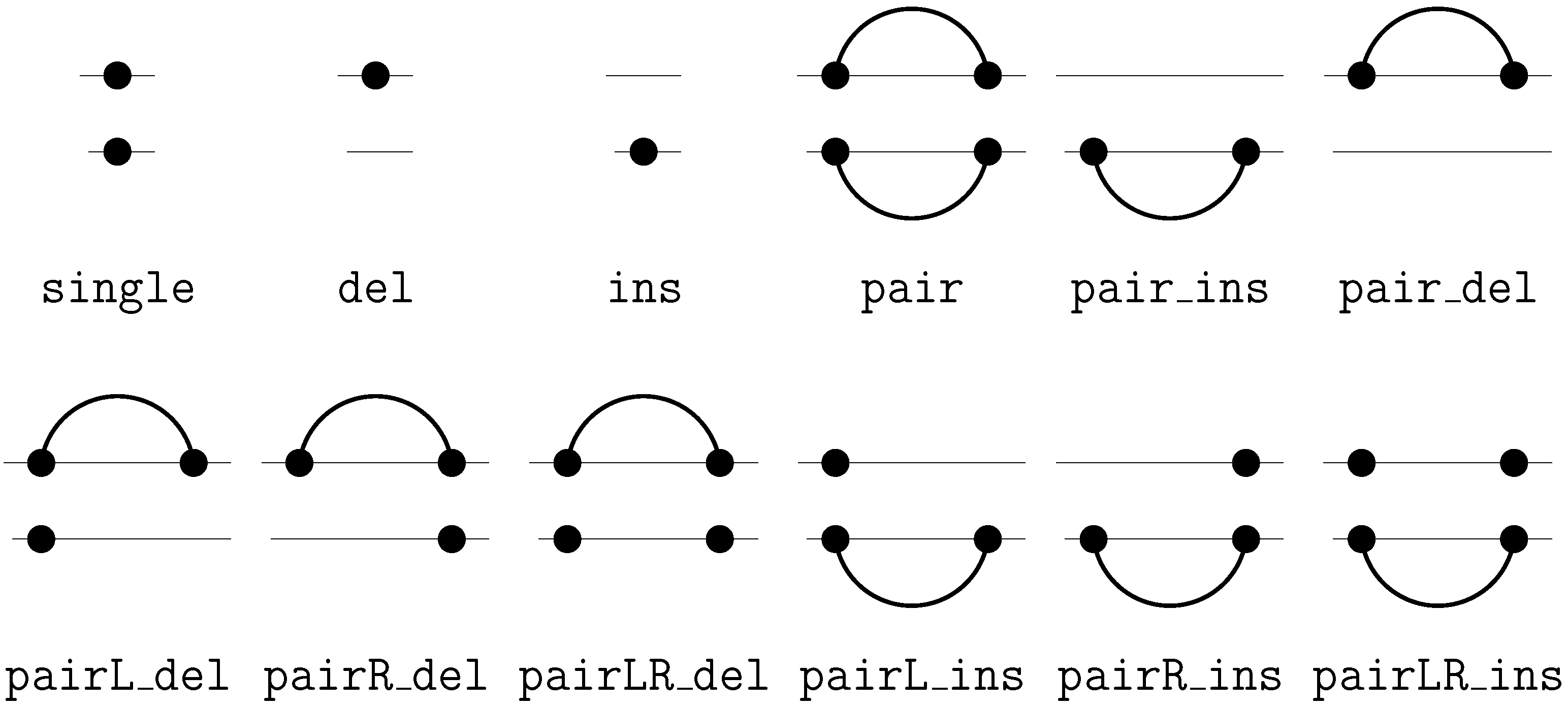
6.2. Satellite Signatures for RNA Sequences and Structures
6.3. RNA Folding

- Algebra BPmax implements base pair maximization as our objective function, as it is done in the Nussinov algorithm.
- Algebra DotPar serves to visualize predicted structures as strings in a dot-bracket notation. Used by itself in a call to RNAfold(DotPar, s), this algebra would enumerate the full candidate space for input s. Normally, it is used in a product with other algebras (cf. Section 8), where it reports optimal candidates.
6.4. Structural Alignment
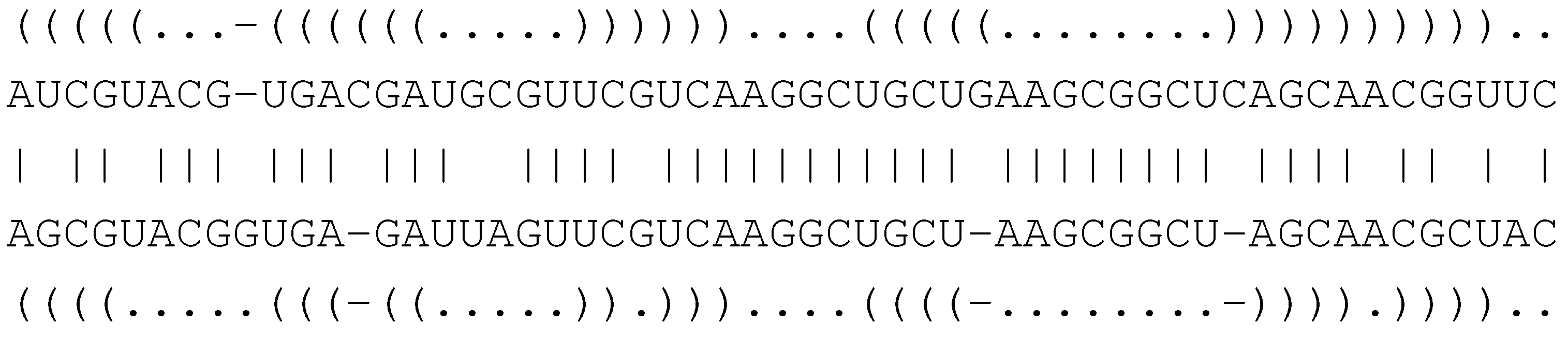
6.4.1. Core Signature and Grammar for Structural Alignment
( . - - ) ( )
A G - - U C G
| | | |
A G C C U C A
( ( ) . ) . .

6.4.2. Structural Alignment in the Prism of Tree Alignment
6.5. The Sankoff Algorithm for Simultaneous Alignment and Folding, with Variations


6.5.1. Structural Alignment without Given Structures
6.5.2. Exact Consensus Structure
G A U A G A U A G A U A
( . ) . . . ( ) . . . .
C A G U C A G U C A G UFor example, the first core term rewrites as "GAUA""CAGU". In contrast, the core term
6.5.3. The Sankoff Algorithm
G-UCC -GUCC
(.).. .(..)
AUUG- AUU-GThis is exactly the model used in the Sankoff algorithm. Intuitively, it merges the ideas of sequence alignment with those of RNA structure prediction [5]. With the ICORE formalism, this is literally what happens: We obtain the ICORE Sankoff by augmenting ExactConsensusStructure with the indel rules from EditDistance.
6.6. Sequence-to-Structure Alignment and RNA Family Modeling
6.6.1. A Generic Structure Matcher
6.6.2. Generic Exact Structure Matching

6.6.3. From Generic to Hard-Coded Structure Matching
6.6.4. A Structural Matcher for Exact Search
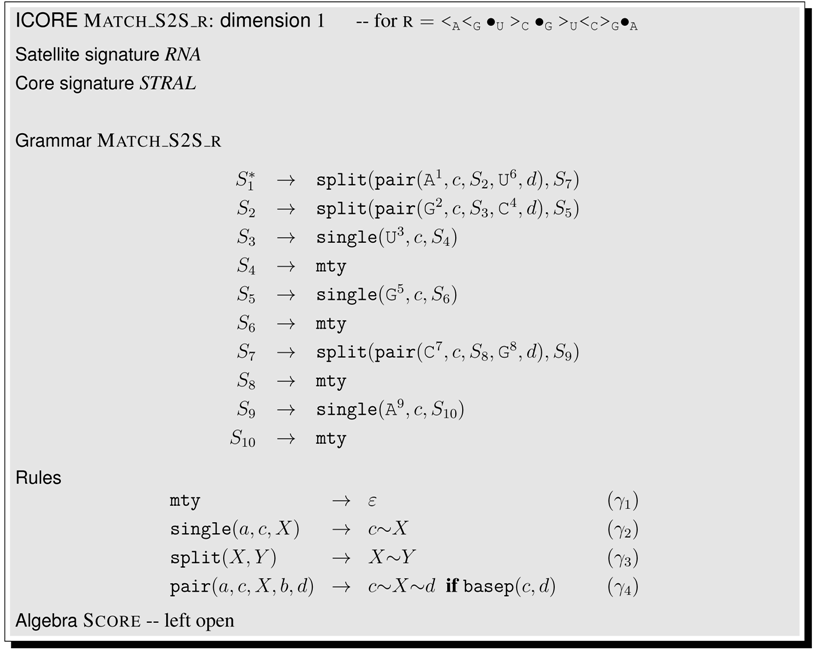
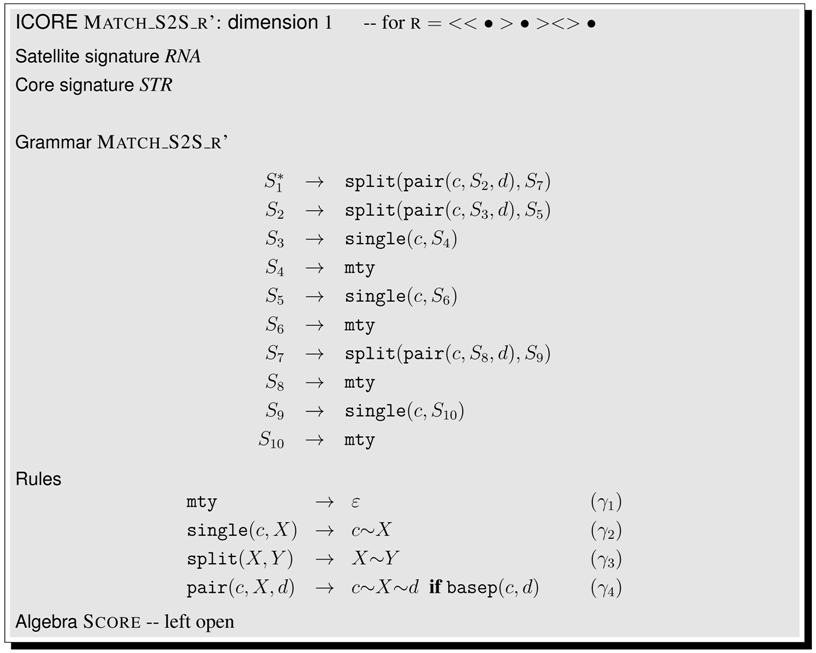
6.6.5. A Structural Matcher for Covariance Models
| - <<•>•><−>• | −− <<•>•>-<−>• | −− -<-<•>•><>• |

6.7. Conclusion on ICOREs for RNA Analysis
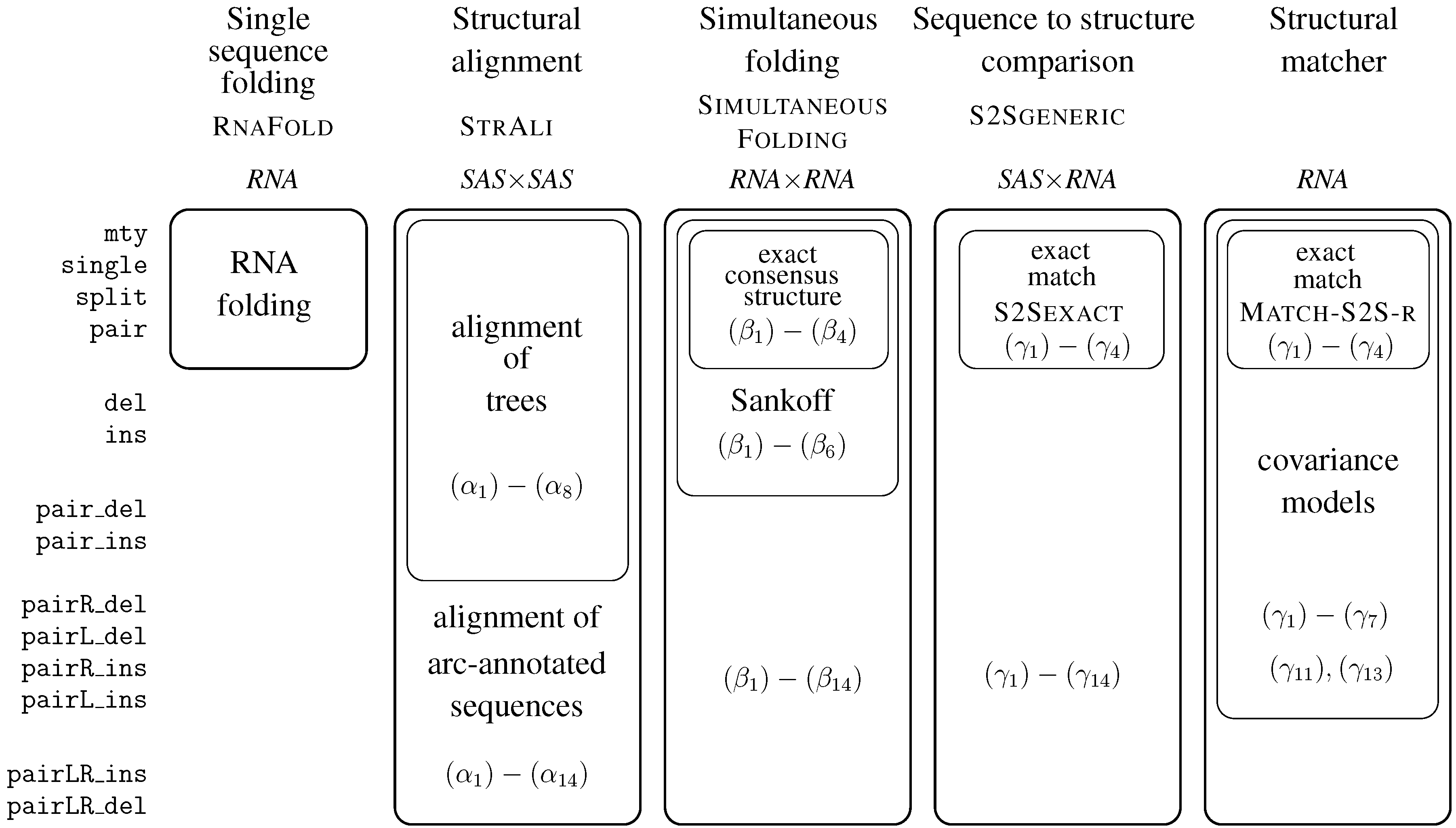
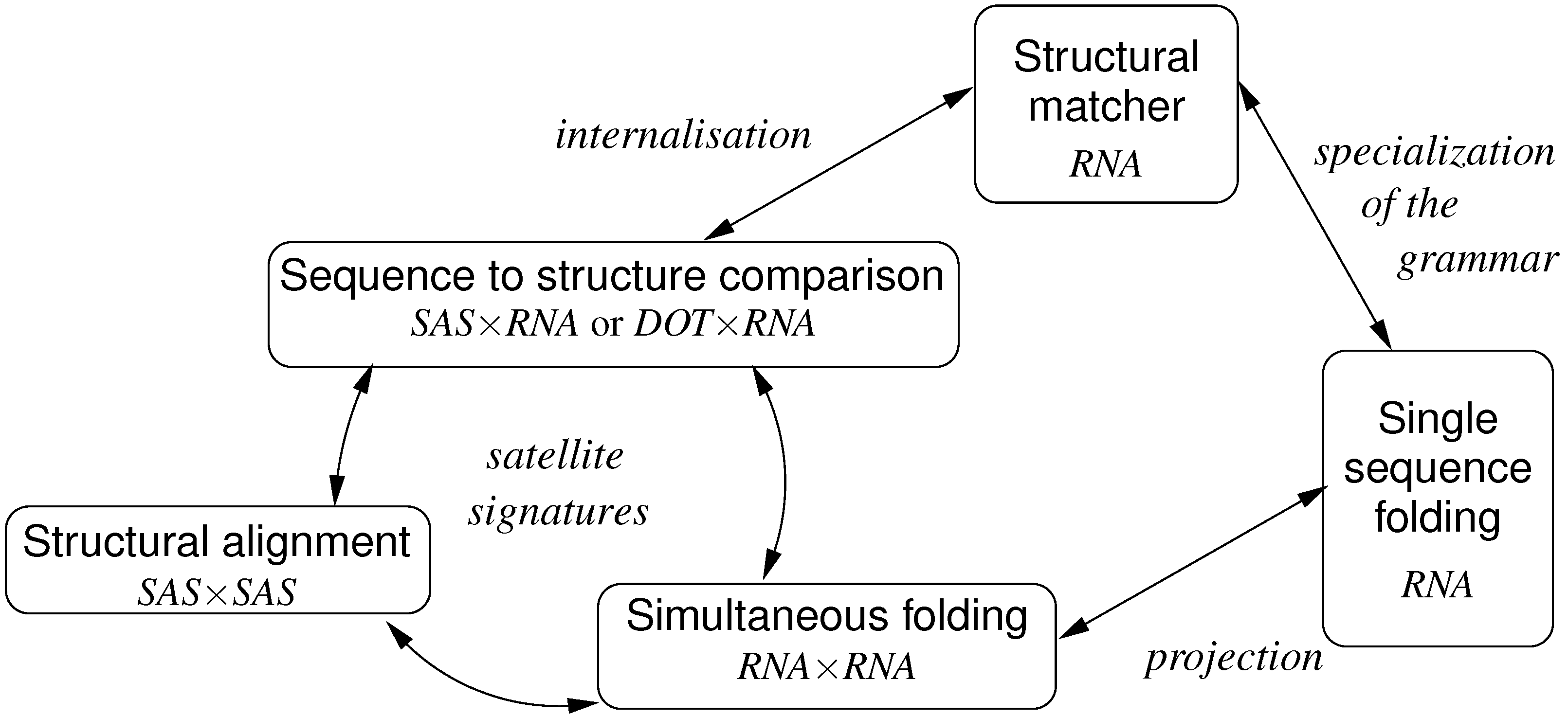
7. Tree Comparison and Related Problems
7.1. Notations and Signatures
7.2. Tree Alignment
7.2.1. Classical Tree Alignment

7.2.2. Tree Alignment with Affine Gap Scoring

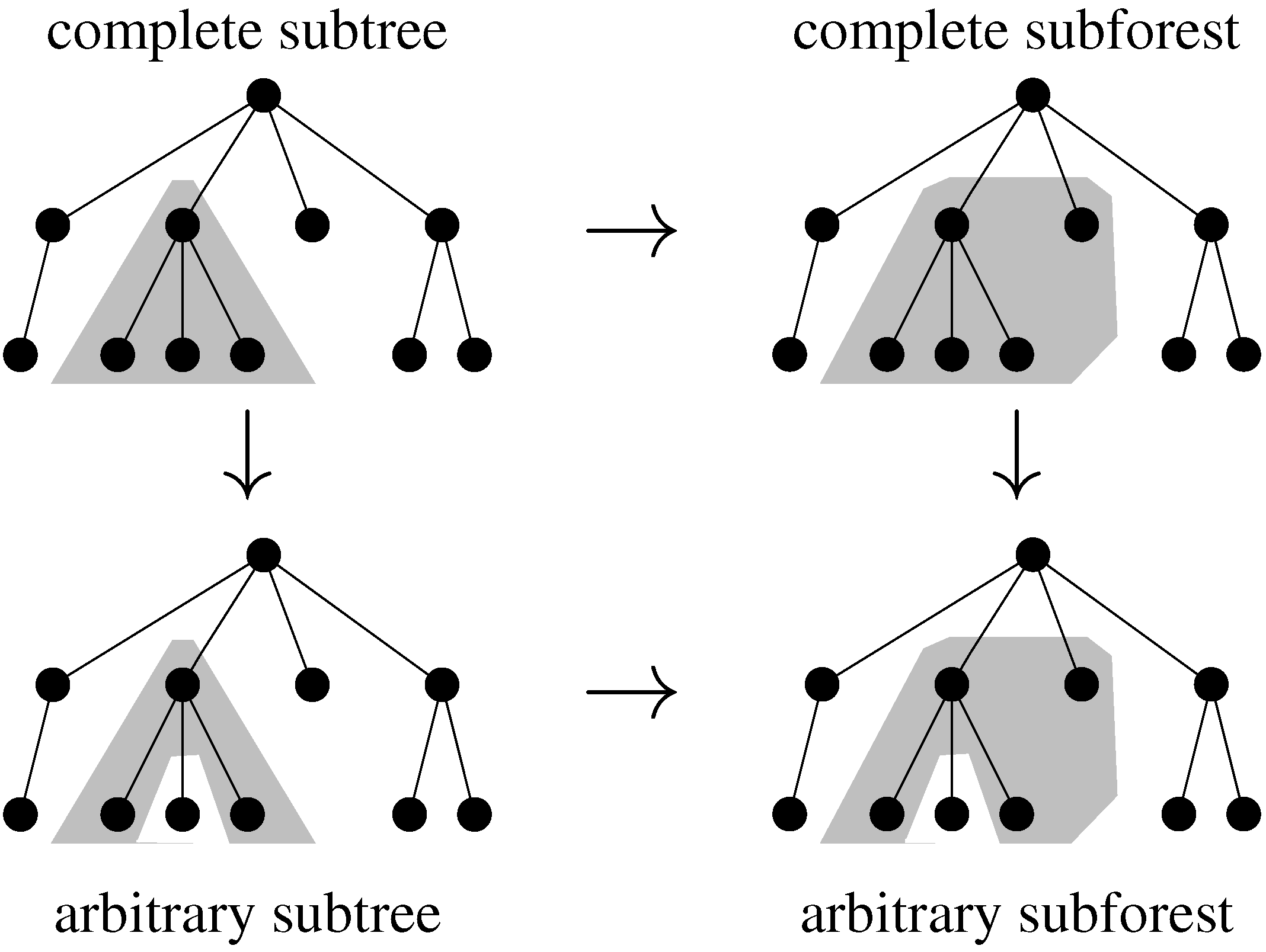




7.3. Classical Tree Edit Distance

- -
- If a occurs in and b in :
- -
- if a is not in :
- -
- if b is not in :
7.4. Variations on Tree Edit Distance and Alignment of Trees
7.5. Tree Alignment under a Generalized Edit Model
- Both satellite signatures are F.
- The core signature contains a single sort, the constant operator symbol , the alphabet of the satellite signatures (if any) as nullary operators, and operators: . The arity of and of is the cardinality s of .
- For each edit operation , we have two rewrite ruleswhere .
- The scoring algebra is
- The grammar accepts all core terms.
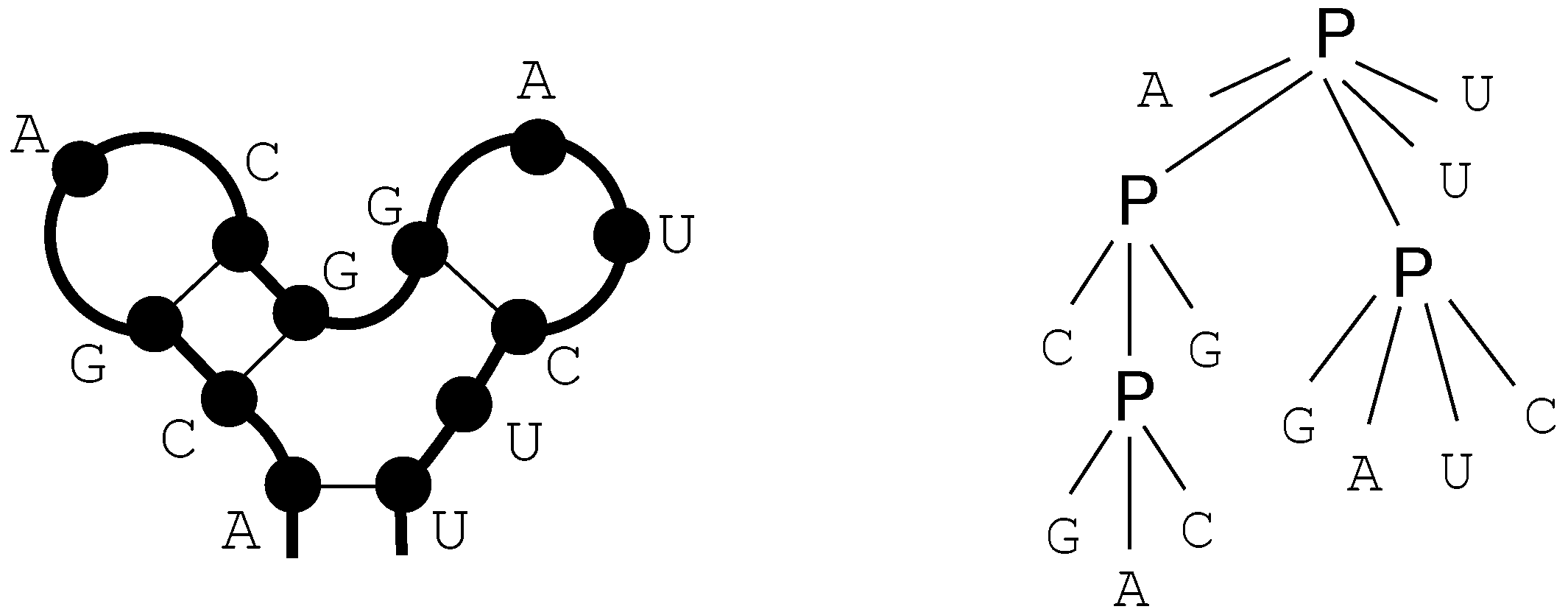

ACGCAGUGGACACUCGU ACGAGUGGACACUCCGU
(((.(((....)))))) ((((((....))).)))An meaningful tree alignment should probably choose indels for both ‘C’-bulges, and match the rest of the structures, as in
ACGCAGUGGACACU-CGU
(((.(((....)))-)))
(((-(((....))).)))
ACG-AGUGGACACUCCGUThe penalty of two indels can make this alignment submerged in the suboptimal candidate space. Better results can be expected with an additional edit operation such as
8. Evaluation Algebras and Their Products
| Algebra Product | Computes | Remark |
|---|---|---|
| A | optimal score under A | |
| B | optimal score under B | |
| optimal under lexicographic | ||
| order on | ||
| C | size of candidate space | avoids exponential explosion! |
| score and number of co-optimal | ||
| candidates under A | ||
| score and number of co-optimal | ||
| candidates under () | ||
| P | representation of all candidates | complete enumeration! |
| , | score and representation | also known as |
| of co-optimal candidates | co-optimal backtrace | |
| D | classification attributes | all candidates’ attributes |
| of all candidates | (useless by itself) | |
| , | optimal score within each | “classified” DP |
| class as assigned by D | ||
| , | opt. score and candidate | |
| for each class | ||
| size of each class | ||
| (number of candidates) |
9. Relation with Other Formal Models

9.1. “Classical” ADP Algorithms Seen as ICOREs
9.2. Letter Transducers Seen as ICOREs
- a finite set of states Q
- a set of initial states,
- an input alphabet
- an output alphabet and
- a weighted transition relation
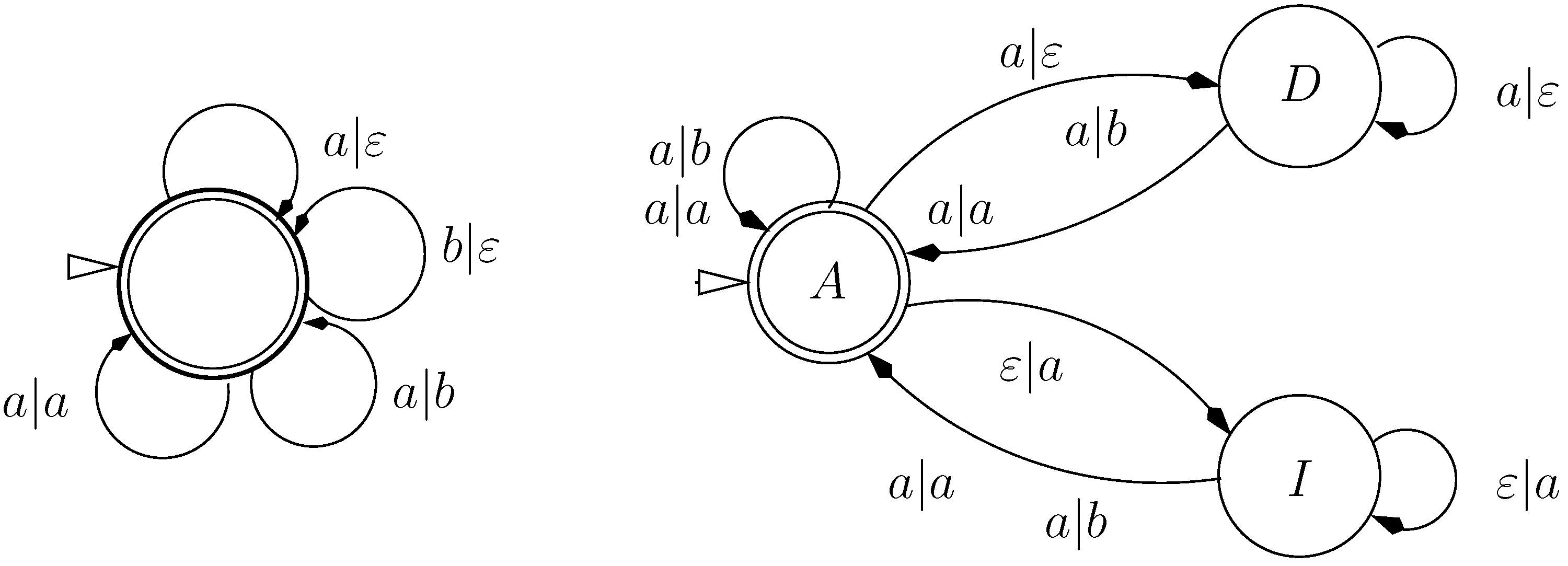

- ,
- t belongs to the language of the grammar
- t evaluates to α
9.3. Multi-Tape S-Attribute Grammars
9.4. Relations between Turing Machines and ICOREs
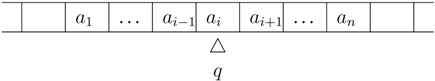

9.5. A Trade-off between Grammar and Rewrite Rules
10. Conclusions
10.1. ICOREs as a Declarative Specification Framework
- In the introduction to this article, we informally stated that the Sankoff algorithm for consensus structure prediction can bee seen as running two RNA folding and one sequence alignment algorithm simultaneously. In creating the Sankoff ICORE, we literally copied twice the rules from RNAfold and imported two rules from EditDistance–this was the complete Sankoff specification.
- We feel that our description of covariance model construction in three steps, going from RNAfold via Sankoff and S2SExact to CM_r is more systematic than what we find in the literature, and in particular, it points out the role of RNAfold as a model architecture in covariance model design. One could start from a different model architecture, but then proceed in the same fashion.
- The generic covariance model S2SGeneric, the Sankoff-variant SimFold and the generalized tree edit model exemplified by RNATreeAli are new algorithmic problems and deserve further investigation in their own right.
- The definition of the search space is independent of any scoring algebra. We can experiment with altermative models, we can refine rules and/or grammar, for example to eliminate mal-formed candidates from the search space (rather than tricking with . We can test how the size of the search space is affected by design decisions, independent of scoring. We can worry about (non-)ambiguity of our problem decomposition by studying properties of the grammar.
- When it comes to evaluating candidates, we can formulate arbitrary algebras over the given signature. For each, we need to prove that it satisfies Bellman’s Principle. Fortunately, this is independent of the search space and how it is constructed.
- Rewrite systems and algebras can be combined correctly in a modular fashion, bringing to bear the software engineering principles of component re-use and ease of modification.
- Finally, as seen in Section 8, the ability to define product operations on algebras and produce refined analyses from simpler ones is also due to the perfect separation of search space and evaluation of candidates.
10.2. Research Challenges in ICORE Implementation
- Search space construction: Grammar and rewrite rules must be used jointly to construct the search space by an interleaved enumeration of core terms and their rewriting towards the input. This is inherently a top-down process.
- Rewriting modulo associativity: where required, this contributes an implementation challenge of its own to the above.
- Generating recurrences: Candidate evaluation by an algebra is simple, but is inherently a bottom-up process, which must be amalgamed with search space construction. This amalgamation takes the form of dynamic programming recurrences which must be generated.
- Tabulation design: In order to avoid exponential explosion due to excessive recomputation of intermediate results, tabulation is used. This involves decisions on what to tabulate, and how to efficiently map sub-problems to table entries.
- Repeat analysis: A special challenge arises from the fact that ICOREs allow for non-linear rewrite rules. A variable may be duplicated on the righthand side of a rule. Two copies of a core term naturally rewrite to identical sub-terms in a satellite, and the implementation must take care to exploit this fact.
- Table number, dimension and size: While tabulating every intermediate result would be mathematically correct and asymptotically optimal, space efficiency requires careful analysis of the number of dynamic programming tables, their dimensions and sizes.
- Product optimizations: Certain tasks are conveniently expressed as algebra products, but for competitive code, they require more efficient techniques than the generic implementation of a product algebra. Two cases in point are full backtracing (for near-optimal solutions) and stochastic sampling (based on a stochastic scoring algebra). For combinatorial optimization problems on trees, no such techniques have been reported, and an implementation of ICOREs will have to cover new ground in this respect.
- A purist might say that the signature declarations are actually redundant, as they can be inferred from the rewrite rules, as well as from the algebras.
- A programming language designer would argue that a certain degree of redundancy is necessary, to safeguard against user errors and allow the compiler to give helpful error messages.
- A software engineer would point to the need to work with evolving programs, e.g., to have a signature where not all operators are used in a particular rewrite system, but are already included for a planned refinement.
Acknowledgments
Conflicts of Interest
Glossary
| symbols | used for |
| signatures | |
| evaluation algebras | |
| variables for alphabet characters | |
| variables for core terms | |
| values of core terms under some algebra | |
| w | multiset of subterms or their values |
| subterm variables in rules |
| notions | meaning | defined in section |
| V | set of variables | Machinery |
| term algebra over signature F and variable set V | Machinery | |
| ∼ | associative operator | any signature where needed |
| ϵ | neutral element with ∼ | wherever ∼ is |
| tree grammar over some F | Machinery | |
| language of , subset of | Machinery | |
| value of term t under algebra A | Machinery | |
| various alphabets | where needed |
| Example | convention | used for |
| Hamming | small capitals | ICORE names |
| RNAstruct | small capitals | grammar names |
| Score | small capitals | evaluation algebra names |
| three/four capital letters, italics | signature names | |
| typewriter font | signature operators | |
| ‘a’, ‘b’, ‘<’ | symbols in single quotes, typewriter font | concrete alphabet symbols |
References
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, UK, 1957. [Google Scholar]
- Gusfield, D. Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Needleman, S.B.; Wunsch, C.D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 1970, 48, 443–453. [Google Scholar] [CrossRef]
- Smith, T.F.; Waterman, M.S. Identification of common molecular subsequences. J. Mol. Biol. 1981, 147, 195–197. [Google Scholar] [CrossRef]
- Sankoff, D. Simultaneous solution of the RNA folding, alignment and protosequence problems. SIAM J. Appl. Math. 1985, 45, 810–825. [Google Scholar] [CrossRef]
- Ferch, M.; Zhang, J.; Höchsmann, M. Learning cooperative assembly with the graph representation of a state-action space. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, EPFL lausanne, Switzerland, 30 September–4 October 2002.
- Reis, D.; Golgher, P.; Silva, A.; Laender, A. Automatic web news extraction using tree edit distance. In Proceedings of the 13th International Conference on World Wide Web, ACM, New York, NY, USA, 17–22 May, 2004; pp. 502–511.
- Searls, D.B. Investigating the linguistics of DNA and definite clause grammars. In Proceedings of the North American Conference on Logic Programming; Lusk, E., Overbecck, R., Eds.; MIT Press: Cambridge, MA, USA, 1989; pp. 189–208. [Google Scholar]
- Searls, D.B. The Computational Linguistics of Biological Sequences. In Artificial Intelligence and Molecular Biology; Hunter, L., Ed.; AAAI/MIT Press: Cambridge, MA, USA, 1993; pp. 47–120. [Google Scholar]
- Searls, D.B. Linguistic approaches to biological sequences. CABIOS 1997, 13, 333–344. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre. A grammar-based unification of several alignment and folding algorithms. AAAI Intell. Syst. Mol. Biol. 1996, 4, 143–154. [Google Scholar]
- Knuth, D.E. Semantics of context free languages. Theory Comput. Syst. 1968, 2, 127–145. [Google Scholar] [CrossRef]
- Giegerich, R.; Meyer, C.; Steffen, P. A discipline of dynamic programming over sequence data. Sci. Comput. Program. 2004, 51, 215–263. [Google Scholar] [CrossRef]
- Giegerich, R.; Steffen, P. Challenges in the compilation of a domain specific language for dynamic programming. In Proceedings of the 2006 ACM Symposium on Applied Computing, Dijon, France, 23–27 April, 2006; Haddad, H., Ed.;
- Höner zu Siederdissen, C. Sneaking around concatMap: efficient combinators for dynamic programming. In Proceedings of the 17th ACM SIGPLAN International Conference on Functional Programming, Copenhagen, Denmark, 10–12 September, 2012; ACM: New York, NY, USA, 2012. ICFP ’12. pp. 215–226. [Google Scholar]
- Sauthoff, G.; Möhl, M.; Janssen, S.; Giegerich, R. Bellman’s GAP-A language and compiler for dynamic programming in sequence analysis. Bioinformatics 2013, 29, 551–560. [Google Scholar] [CrossRef] [PubMed]
- Baader, F.; Nipkow, T. Term Rewriting and All That; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Ohlebusch, E. Advanced Topics in Term Rewriting; Springer: New York, NY, USA, 2002. [Google Scholar]
- Gotoh, O. An improved algorithm for matching biological sequences. J. Mol. Biol. 1982, 162, 705–708. [Google Scholar] [CrossRef]
- Durbin, R.; Eddy, S.R.; Krogh, A.; Mitchison, G. Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Giegerich, R. Explaining and controlling ambiguity in dynamic programming. In Proceedings of the Combinatorial Pattern Matching; Springer: New York, NY, USA, 2000; pp. 46–59. [Google Scholar]
- Nussinov, R.; Pieczenik, G.; Griggs, J.; Kleitman, D. Algorithms for loop matchings. SIAM J. Appl. Math. 1978, 35, 68–82. [Google Scholar] [CrossRef]
- Baker, J.K. Trainable grammars for speech recognition. J. Acoust. Soc. Am. 1979, 65, 54–550. [Google Scholar] [CrossRef]
- Sakakibara, Y.; Brown, M.; Hughey, R.; Mian, I.; Sjölander, K.; Underwood, R.; Haussler, D. Recent Methods for RNA Modeling Using Stochastic Context-Free Grammars. In Combinatorial Pattern Matching 1994, Asilomar, CA, USA, June 5–8, 1994; pp. 289–306.
- Dowell, R.; Eddy, S. Evaluation of several lightweight stochastic context-free grammars for RNA secondary structure prediction. BMC Bioinf. 2004, 5, 71. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Lin, G.; Ma, B.; Zhang, K. A general edit distance between RNA structures. J. Comput. Biol. 2002, 9, 371–388. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Wang, L.; Zhang, K. Alignment of trees – An alternative to tree edit. Theor. Comput. Sci. 1995, 143, 137–148. [Google Scholar] [CrossRef]
- Macke, T.J.; Ecker, D.J.; Gutell, R.R.; Gautheret, D.; Case, D.A.; Sampath, R. RNAMotif, an RNA secondary structure definition and search algorithm. Nucleic Acids Res. 2001, 29, 4724–4735. [Google Scholar] [CrossRef] [PubMed]
- Reeder, J.; Reeder, J.; Giegerich, R. Locomotif: from graphical motif description to RNA motif search. Bioinformatics 2007, 23, i392. [Google Scholar] [CrossRef] [PubMed]
- Eddy, S.R.; Durbin, R. RNA sequence analysis using covariance models. Nucleic Acids Res. 1994, 22, 2079–2088. [Google Scholar] [CrossRef] [PubMed]
- Giegerich, R.; Höner zu Siederdissen, C. Semantics and ambiguity of stochastic RNA family models. IEEE/ACM Trans. Comput. Biol. Bioinf. 2011, 8, 499–516. [Google Scholar] [CrossRef] [PubMed]
- Gardner, P.; Daub, J.; Tate, J.; Nawrocki, E.; Kolbe, D.; Lindgreen, S.; Wilkinson, A.; Finn, R.; Griffiths-Jones, S.; Eddy, S.; et al. Rfam: Updates to the RNA families database. Nucleic Acids Res. 2009, 37, D136. [Google Scholar] [CrossRef] [PubMed]
- Rosselló, F.; Valiente, G. An algebraic view of the relation between largest common subtrees and smallest common supertrees. Theor. Comput. Sci. 2006, 362, 33–53. [Google Scholar] [CrossRef]
- Chawathe, S. Comparing hierarchical data in external memory. In Proceedings of the 25th International Conference on Very Large Data Bases, San Francisco, CA, USA; 1999; pp. 90–101. [Google Scholar]
- Touzet, H. Tree edit distance with gaps. Inf. Process. Lett. 2003, 85, 123–129. [Google Scholar] [CrossRef]
- Zhuozhi Wang, K.Z. Alignment between Two RNA Structures. In Mathematical Foundations of Computer Science; 25–29 August 2001; Budapest; pp. 690–702. [Google Scholar]
- Backofen, R.; Chen, S.; Hermelin, D.; Landau, G.M.; Roytberg, M.A.; Weimann, O.; Zhang, K. Locality and gaps in RNA comparison. J. Comput. Biol. 2007, 14, 1074–1087. [Google Scholar] [CrossRef] [PubMed]
- Jansson, J.; Hieu, N.T.; Sung, W.K. Local gapped subforest alignment and its application in finding RNA structural motifs. J. Comput. Biol. 2006, 13, 702–718. [Google Scholar] [CrossRef] [PubMed]
- Schirmer, S.; Giegerich, R. Forest Alignment with Affine Gaps and Anchors. In Combinatorial Pattern Matching; Springer: New York, NY, USA, 2011; pp. 104–117. [Google Scholar]
- Dulucq, S.; Touzet, H. Decomposition algorithms for the tree edit distance problem. J. Discrete Algorithms 2005, 3, 448–471. [Google Scholar] [CrossRef]
- Erik Demaine, Shay Mozes, B.R.; Weimann, O. An optimal decomposition algorithm for tree edit distance. ACM Trans. Algorithms 2009, 6. [Google Scholar] [CrossRef]
- Sauthoff, G.; Janssen, S.; Giegerich, R. Bellman’s GAP: A declarative language for dynamic programming. In Proceedings of the 13th International ACM SIGPLAN Symposium on Principles and Practices of Declarative Programming, Odense, Denmark, July 20–22, 2011; ACM: New York, NY, USA, 2011. PPDP ’11. pp. 29–40. [Google Scholar]
- Searls, D.B.; Murphy, K.P. Automata-theoretic models of mutation and alignment. In Proceedings of the ISMB, 1995; Rawlings, C.J., Clark, D.A., Altman, R.B., Hunter, L., Lengauer, T., Wodak, S.J., Eds.; pp. 341–349.
- Huet, G.; Lankford, D. On theUniform Halting Problem for Term Rewriting Systems. Technical Report, Rapport Laboria 283, IRIA. 1978. [Google Scholar]
- Powell, W.B. Approximate Dynamic Programming: Solving the Curses of Dimensionality; Wiley-Interscience: New York, NY, USA, 2007. [Google Scholar]
- Voß, B.; Giegerich, R.; Rehmsmeier, M. Complete probabilistic analysis of RNA shapes. BMC Biol. 2006, 4, 5. [Google Scholar] [CrossRef] [PubMed]
- Sedgewick, R. Algorithms; Addison-Wesley: Reading, MA, USA, 2002. [Google Scholar]
- Cormen, T.; Leiserson, C.; Rivest, R. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Braßel, B.; Hanus, M.; Peemöller, B.; Reck, F. KiCS2: A new compiler from curry to haskell. In Proceedings of the 20th International Workshop on Functional and (Constraint) Logic Programming; Springer: New York, NY, USA, 2011; pp. 1–18. [Google Scholar]
- Thompson, S. Haskell: The Craft of Functional Programming; Addison Wesley: Boston, MA, USA, 2011. [Google Scholar]
- Eisner, J.; Filardo, N.W. Dyna: Extending Datalog for modern AI. Datalog 2.0; Furche, T., Gottlob, G., Grasso, G., de Moor, O., Sellers, A., Eds.; Springer: New York, NY, USA, 2011. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Giegerich, R.; Touzet, H. Modeling Dynamic Programming Problems over Sequences and Trees with Inverse Coupled Rewrite Systems. Algorithms 2014, 7, 62-144. https://doi.org/10.3390/a7010062
Giegerich R, Touzet H. Modeling Dynamic Programming Problems over Sequences and Trees with Inverse Coupled Rewrite Systems. Algorithms. 2014; 7(1):62-144. https://doi.org/10.3390/a7010062
Chicago/Turabian StyleGiegerich, Robert, and H´el'ene Touzet. 2014. "Modeling Dynamic Programming Problems over Sequences and Trees with Inverse Coupled Rewrite Systems" Algorithms 7, no. 1: 62-144. https://doi.org/10.3390/a7010062
APA StyleGiegerich, R., & Touzet, H. (2014). Modeling Dynamic Programming Problems over Sequences and Trees with Inverse Coupled Rewrite Systems. Algorithms, 7(1), 62-144. https://doi.org/10.3390/a7010062




