1. Introduction
Matrix equations are frequently encountered in control theory applications, like model-order reduction or linear-quadratic optimal control problems, involving dynamical linear systems that represent a variety of physical phenomena or chemical processes [
1]. In this paper, we address the solution of Lyapunov equations and algebraic/differential Riccati equations (AREs/DREs), involving dense coefficient matrices, via the matrix sign function [
2]. This iterative method exhibits a number of appealing properties, such as numerical reliability, high concurrency and scalability and a moderate computational cost of
floating-point arithmetic operations (flops) per iteration, where
n denotes the number of the states of the dynamical linear system. Therefore, the solution of matrix equations with
n of
and larger asks for the use of high performance architectures, often parallel computers, as well as efficient concurrent implementations.
The PLiC (Parallel Library in Control) and PLiCMR (Parallel Library in Control and Model Reduction) packages [
3,
4] offer numerical tools, based on the matrix sign function, for the solution of very large-scale matrix equations (
n of
and larger) on message-passing architectures. However, the interface to the routines in these packages is complex, especially by the need to initially distribute the data matrices and collect the results at the end of the computation. Furthermore, the use of these libraries requires access to a message-passing platform (e.g., a cluster of computers).
The last few years have witnessed a rapid evolution in the number and computational power of the processing units (cores) featured in general-purpose CPUs, and an increasing adoption of GPUs as hardware accelerators in scientific computing. A number of efforts have demonstrated the remarkable speed-up that these systems provide for the solution of dense and sparse linear algebra problems. Among these, a few works targeted the numerical solution of matrix equations, which basically can be decomposed into primitive linear algebra problems, using this class of hardware [
5,
6,
7,
8,
9]. In this paper, we review the rapid solution of Lyapunov equations, AREs and DREs, on multicore processors, as well as GPUs, making the following specific contributions:
We collect and update a number of previous results distributed in the literature [
5,
6,
7,
8,
9], which show that the matrix sign function provides a common and crucial building block for the efficient parallel solution of these three types of matrix equations on multicore CPUs, hybrid CPU-GPU systems and hybrid platforms with multiple GPUs.
We extend the single-precision (SP) experiments previously reported in [
5,
6,
7] with double-precision (DP) data. This is especially relevant, as DP solutions are required in practical control theory applications. While modifying the original codes to operate with DP data was relatively straight-forward, several parameters of the implementations needed to be carefully optimized to compensate for the higher cost of the communications when DP matrices were involved. Among other parameters, algorithmic block-sizes, the depth of look-ahead strategies and the adoption of multilevel blocking techniques are architecture- and precision-dependent parameters that had to be experimentally retuned to attain high performance.
We experimentally compare the efficiency of the solvers using two generations of GPUs with diverging approaches to exploit ample data-parallelism. In particular, the NVIDIA K20 features a high number of cores (2496) and low frequency (706 MHz), while each GPU in the NVIDIA S2050 presents a lower number of cores (448), but operates at higher frequency (1150 MHz). None of our previous work [
5,
6,
7,
8,
9] reported data with the newer NVIDIA K20.
We follow the general design framework for the solution of Lyapunov equations and DREs on multi-GPU platforms, extending these ideas to implement and evaluate a new ARE solver that leverages the presence of multiple GPUs in a hybrid platform.
Overall, we provide a clear demonstration that commodity hardware, available in current desktop systems, offers sufficient computational power to solve large-scale matrix equations, with 5,000–10,000. These methods are thus revealed as appealing candidates to replace and complement more cumbersome message-passing libraries for control theory applications.
The rest of the paper is structured as follows. In
Section 2, we revisit the matrix sign function, which is the parallel building block underlying our Lyapunov equation and ARE solvers described in the first two subsections there; the third subsection then addresses the solution of the DRE using the matrix-sign function-based Lyapunov solver just introduced. Several implementation details for the different solvers/equations are provided in
Section 3. One of the major contributions of this paper, namely the experimental evaluation of double-precision implementations of these solvers, using state-of-the-art multi-core and many-core platforms, follows in
Section 4, and a few concluding remarks close the paper in
Section 5.
2. Matrix Sign Function-Based Solvers
The sign function method [
2] is an efficient numerical tool to solve Lyapunov, Sylvester and Riccati equations, with dense coefficient matrices, on parallel message-passing computers [
3,
4], as well as on hardware accelerators [
10]. The convenience of the sign function method is based on two properties: First, it is composed of well-known basic linear algebra operations that exhibit a high degree of concurrency. Moreover, high performance implementations for parallel architectures of these operations are included in linear algebra libraries, like BLAS (Basic Linear Algebra Subprograms) and LAPACK (Linear Algebra PACKage), and their extension for GPUs, CUBLAS (CUDA BLAS) from NVIDIA and for message-passing platforms, e.g., ScaLAPACK (Scalable LAPACK). Second, it is an iterative algorithm that presents a fast convergence rate that is asymptotically quadratic.
Several schemes have been proposed in the literature to compute the sign function. Among them, the Newton iteration, illustrated in Algorithm 1—GESINE below, exhibits a remarkable simplicity and efficiency.
| Algorithm 1: GESINE: |
| |
| |
| repeat |
| |
| |
| until |
The most time-consuming operation in Algorithm 1—GESINE is the inversion of . Given a square matrix, A, of order n, this operation renders the cost of the algorithm as flops per iteration. The cubic computational cost in the matrix dimension is inherited by all solvers described next.
To avoid stagnation of the iteration, we set , where ε stands for the machine precision, and perform one additional iteration step after the stopping criterion is satisfied. Due to the asymptotic quadratic convergence rate of the Newton iteration, this is usually enough to reach the attainable accuracy.
2.1. Solution of Lyapunov Equations
Algorithm 2—
GECLNC, presented below, illustrates a variant of the sign function method for the solution of a Lyapunov equation of the form:
where
is c-stable (
i.e., all its eigenvalues have a negative real part),
and
is the desired solution.
| Algorithm 2: GECLNC: |
| , |
| |
| repeat |
| Compute the rank-revealing QR (rank-revealing QR (RRQR)) decomposition |
| |
| |
| |
| |
| until |
On convergence, after iterations, is a full (row-)rank approximation of S, so that .
In practice, the scaling factor,
, is used to accelerate the convergence rate of the algorithm, (
i.e., to reduce the number of required iterations). In our case, we set:
Furthermore, we choose
and perform an extra step after the convergence criterion is satisfied. Note that the number of columns of
is doubled at each iteration and, in consequence, the computational and storage costs associated with its update increase with each iteration. This growth can be controlled by computing a RRQR (rank-revealing QR) factorization, which introduces a relatively low overhead. This approach reports important gains when the number of iterations needed for convergence is large, or when the number of columns of
B is large. The RRQR decomposition can be obtained by means of the traditional QR factorization with column pivoting [
11], plus a reliable rank estimator. Note that
is not accumulated, as it is not needed in subsequent computations. This reduces the cost of computing the RRQR significantly.
2.2. Solution of Algebraic Riccati Equations
The sign function method can also be employed to compute the stabilizing solution of an algebraic Riccati equation (ARE) of the form:
where
F,
G,
Q and the solution,
, is symmetric and satisfies that
is c-stable.
In particular, the solution to the ARE can be obtained from the c-stable invariant subspace of the Hamiltonian matrix [
12]:
which can be extracted by first obtaining the matrix sign function of
H:
and then solving the over-determined system:
Algorithm 3—
GECRSG below summarizes the above steps to solve the ARE in Equation (
2) with this method.
| Algorithm 3: GECRSG: |
| |
| Apply Algorithm 1—GESINE to compute |
| Solve for X |
2.3. Solution of Differential Riccati Equations
The matrix sign function can also be applied in combination with the Rosenbrock method for the solution of an autonomous symmetric differential Riccati equation (DRE) [
13] of the form:
where
,
,
,
and
. Here, we assume that the coefficient matrices are piecewise continuous locally bounded matrix-valued functions, which ensures the existence and uniqueness of the solution to Equation (
6); see, e.g., Theorem 4.1.6 in [
1].
The application of the Rosenbrock method of order one to an autonomous symmetric DRE of the form Equation (
6) yields:
where
and
; see [
14,
15] for details. In addition, we assume:
,
,
,
,
,
, with
p,
m,
. If we denote
, then the Lyapunov Equation (
7) results in:
where
. The procedure that is obtained from this elaboration is presented in Algorithm 4—
ROS1. Observing that rank
, we can use the sign function method to solve Equation (
8), as illustrated in Algorithm 2—
GECLNC (see
Section 2.1).
| Algorithm 4: ROS1: |
| |
| for to |
| |
| |
| Apply Algorithm 2—GECLNC to obtain , a low-rank approximation to |
| the solution of |
| |
| end for |
Note that, since we obtain the low rank factor of the solution of Equation (
8), the cost associated with the updates of both
and
is drastically decreased, and thus, the most time-consuming operation in Algorithm 4—
ROS1 is the solution of Equation (
8),
i.e., the execution of Algorithm 2—
GECLNC.
3. High Performance Implementations
In this section, we briefly review several high performance implementations for the solution of the matrix equations in the study. In particular, we describe Lyapunov, ARE and DRE solvers based on Algorithm 2—GECLNC, Algorithm 3—GECRSG and Algorithm 4—ROS1, respectively. These algorithms require the computation of the sign function and, therefore, inversion of a large dense matrix, which in all cases represents the most expensive operation from the computational point of view.
In the next two subsections, we describe an efficient and reliable numerical method for matrix inversion and the parallelization techniques applied in each platform: multi-core, hybrid CPU-GPU systems and hybrid multi-GPU platforms. In
Section 3.3, we then discuss some additional details on the parallel solution of matrix equations.
3.1. Matrix Inversion
Traditional matrix inversion via Gaussian elimination requires the computation of the LU factorization of the matrix and the solution of two triangular linear systems. This method presents two drawbacks when implemented in parallel architectures: the process is partitioned into three consecutive stages, and the solution of the linear systems involves triangular matrices (impairing load-balance).
| Algorithm 5: GJEBLK: |
Partition A → ![Algorithms 06 00857 i001]() , where ATL is 0 × 0 and ABR is n × n , where ATL is 0 × 0 and ABR is n × n |
| while m(ATL) < m(A) do |
| Determine block size b |
| Repartition |
![Algorithms 06 00857 i002]() |
![Algorithms 06 00857 i003]() |
| Continue with |
![Algorithms 06 00857 i004]() |
| end while |
On the other hand, matrix inversion via the Gauss-Jordan elimination method (GJE) is mathematically equivalent and presents the same arithmetic cost to/as the Gaussian-based counterpart, but computes the inverse in a single stage, does not require to operate with triangular matrices and casts the bulk of the computations in terms of coarse-grain highly parallel operations (matrix-matrix products). Algorithm 5—
GJEBLK, presented above, illustrates a blocked version of the matrix inversion GJE-based algorithm using a FLAME (Formal Linear Algebra Methods Environment) notation [
16]. There,
stands for the number of rows of the matrix. We believe the rest of the notation to be intuitive; for further details, see [
16]. A description of the unblocked version called from inside the blocked one can be found in [
17]; for simplicity, we hide the application of pivoting during the factorization, but details can be found there, as well.
3.2. Parallel Implementations of the Gauss-Jordan Elimination Algorithm
Three high performance implementations were developed for the matrix inversion, one for each class of target platform: general-purpose multicore processor, hybrid CPU-GPU systems and hybrid multi-GPU platforms. Using these implementations, we can obtain parallel and efficient solvers for each matrix equation and architecture under study.
Multicore processors. The multicore routines rely on high-performance multi-threaded implementations of BLAS that efficiently exploit the hardware concurrency (superscalar/pipelined processing of instructions, SIMD (Single Instruction Multiple Data) floating-point units, multiple cores, etc.) on this type of architecture. The key to success here is the use of a highly-efficient implementation of the matrix-matrix product to perform the updates of the corresponding blocks in Algorithm 5—GJEBLK, as well as a correct evaluation of the algorithmic block size. Some additional performances can be regained by replacing the unblocked algorithm that factorizes the panel at each iteration by a blocked implementation.
Hybrid CPU-GPU systems. These implementations exploit the massively parallel architecture of the GPU to reduce the time-to-response of costly data-parallel computations (e.g., large matrix-matrix products), while operations that feature a reduced computational cost or present fine-grain parallelism are executed on the CPU.
In matrix inversion via GJE (see Algorithm Algorithm 5—
GJEBLK), all operations are performed on the GPU, except for the factorization of panel
, which is done on the CPU. Assuming that the complete matrix initially lies in the GPU memory, this panel is transferred to the CPU at the beginning of each iteration and processed there, and the results are sent back to the GPU. This version benefits from the use of architecture-specific parallel BLAS, like Intel’s MKL (Math Kernel Library) for the CPU and NVIDIA’s CUBLAS for the GPU. Additionally, these implementations include several common optimization techniques:
Padding adds rows at the bottom of the matrix until their number is a multiple of 32. Padding slightly increases the memory requirements, but not the computational cost, as we do not access/operate with the elements in these rows. On the other hand, the GPU-memory accesses are notoriously accelerated due to coalescing.
Look-ahead advances the computation of operations in the critical path. In our case, a key element in this path is the column panel factorization performed at each step of the algorithm. To advance this computation, we partition the update of into two parts: the first b columns of this block (which will form blocks in the next iteration) are first updated. Next, while this part is transferred to the CPU and factorized there, the rest of the elements of the matrix are updated in the GPU.
Recursive blocking detaches the block sizes used by the GPU and CPU. While the GPU usually attains high performance using a large algorithmic block-size, the CPU requires a smaller value for this parameter. Furthermore, the unblocked algorithm that factorizes is replaced by a blocked implementation, which uses an inner algorithmic block-size.
More details on these techniques can be found in [
18].
Hybrid multi-GPU systems. Hybrid CPU-GPU implementations offer remarkable performance, but the dimension of the problems that can be tackled with them is constrained by the size of the GPU memory (typically, 4–6 Gbytes). Hybrid implementations that combine a CPU with multiple GPUs partially overcome this problem, since, as the number of GPUs grows, the aggregated size of the memory is also increased. The use of several GPUs also increments the computational power of the platform and, thus, can potentially reduce the execution time.
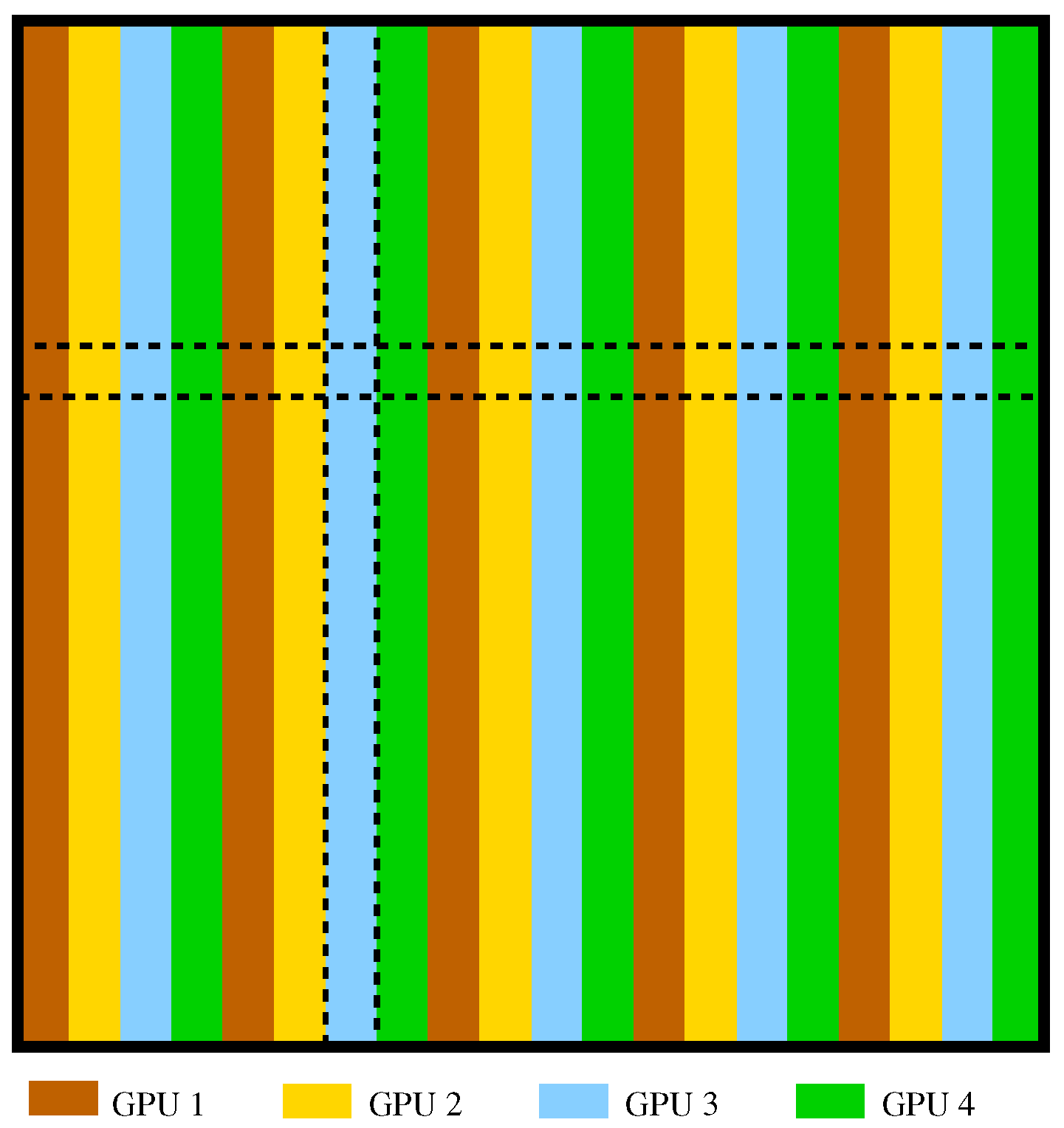
The implementations for this type of platform extend the hybrid CPU-GPU codes, while dealing with several difficulties, particularly, load balancing and data transfers. In general, the data layout exerts a relevant impact on load-balance and data transfers. However, the special properties of the GJE algorithm allow us to rely on a simple block cyclic data distribution, as shown in
Figure 1. The matrix is partitioned there into blocks of columns, which are then distributed cyclically among the GPUs.
Figure 1.
Data distribution between graphics processing units (GPUs) for the multi-GPU implementation (example with four GPUs).
Figure 1.
Data distribution between graphics processing units (GPUs) for the multi-GPU implementation (example with four GPUs).
Additionally, in the multi-GPU codes, some operations that are performed are merged, reducing the number of invocations to BLAS kernels and avoiding the computation of small to moderate matrix-matrix products that offer a poor performance on the GPUs. In particular, the update of
can be performed with a single matrix-matrix product. These and other features of this version are detailed in [
19].
3.3. Parallel Matrix Equations Solvers
The optimization of the matrix equation solvers is not restricted to the matrix inversion routines and, by extension, the calculation of the matrix sign function. All the phases of Algorithm 2—GECLNC, Algorithm 3—GECRSG and Algorithm 4—ROS1 were carefully optimized for the different platforms.
In the case of the Lyapunov solver, high performance linear algebra kernels from BLAS and LAPACK were employed to execute most of the additional computations that appear in Algorithm 2—GECLNC (QR factorization, matrix-matrix products, computation of the scaling factor, convergence test, etc.). OpenMP directives were also employed to parallelize other minor computations, like matrix addition and matrix scaling.
The ARE solvers build matrix H in parallel and employ OpenMP directives to efficiently compute the matrix addition and scaling required for the update of . Besides, multi-threaded routines from BLAS and LAPACK were used to solve the over-determined system in the last stage of the method.
In the DRE solvers, the computation of the low rank factor for the solution, , dramatically reduces the computational cost of all steps. Thus, the total cost of the algorithm basically boils down to that required by the solver of the Lyapunov equations. Once more, multi-threaded BLAS and LAPACK kernels and OpenMP directives were employed to parallelize some minor computations, like matrix additions and matrix norm computations. The updates of and require several matrix-matrix products, matrix additions and scalings that are computed on the CPU. Although matrix-matrix products of large matrices are suitable for the GPU architecture, the dimensions of B and are usually too small to amortize the cost of data transfers.
4. Experimental Results
We evaluate the performance of the implementations using two problems from the
Oberwolfach Model Reduction Benchmark Collection [
20]. For the STEEL problem, we employ two instances,
steel and
steel. For both cases,
and
. The order of the system is
for
steel and
for
steel; for the FLOW_METER the dimensions are
,
,
.
Experiments are performed on two different platforms. The first platform,
Kepler, is equipped with an Intel Sandy Bridge-E i7-3930K processor at 3.2 GHz, 24 GB of RAM, and is connected to an NVIDIA Tesla K20 via a PCI-e bus. The second platform,
S2050, consists of two Intel Xeon QuadCore E5440 processors at 2.83 GHz, with 16 GB of RAM, connected to an NVIDIA Tesla S2050 (four NVIDIA M2050 GPUs) via two PCI-e buses. Platform
Kepler is employed to evaluate the multicore and hybrid CPU-GPU kernels, while the multi-GPU kernels are evaluated in
S2050. (More details on the platforms are offered in
Table 1.)
Table 1.
Hardware platforms employed in the experimental evaluation.
Table 1.
Hardware platforms employed in the experimental evaluation.
| Platform | Processors | #proc. | #cores | Frequency | L2 cache | Memory |
|---|
| (per proc.) | (GHz) | (MB) | (GB) |
|---|
| Kepler | Intel i7-3930 | 1 | 6 | 13.2 | 1.5 | 24 |
| NVIDIA K20 | 1 | 2,496 | 0.71 | – | 5 |
| S2050 | Intel E5440 | 2 | 4 | 2.83 | 6 | 16 |
| NVIDIA S2050 | 4 | 448 | 11.15 | – | (3 × 4)12 |
A multi-threaded version of the Intel MKL library (version 10.3.9) provides the necessary LAPACK and BLAS kernels for the CPU and NVIDIA CUBLAS (version 5.0) for the GPU computations. Experiments are performed in double precision arithmetic.
Table 2 shows the results obtained for the Lyapunov equation solvers. (Hereafter, the subindices,
cpu,
gpu, or
mgpu, identify the target platform as CPU, hybrid CPU-GPU and hybrid multi-GPU, respectively). The use of the GPU reports important gains for all the problems evaluated. The difference between the performance of GECLNC
_gpu and GECLNC
_cpu grows with the problem dimension. In particular, GECLNC
_gpu is 30% faster than GECLNC
_cpu for the solution of the smallest problem, but 4.4× faster for
FLOW_METER, the largest problem tackled. The comparison among GECLNC
_gpu and GECLNC
_mgpu shows that the multi-GPU kernel offers high performance for smaller problems, which decays for larger problems. This can be explained by two main characteristics of the NVIDIA devices employed. On the one hand, the number of computational units in NVIDIA K20 is larger than the aggregated number of computational cores in the four GPUs of NVIDIA S2050. This difference, of about 500 computational units, renders NVIDIA K20 more suitable for large problems. On the other hand, the cores in NVIDIA S2050 work at a higher frequency, which is a key factor for moderate/small problems. As a result, GECLNC
_mgpu is 25% and 12% faster than GECLNC
_gpu for benchmarks
STEEL and
STEEL, respectively, but 12% slower for
FLOW_METER. In summary, the GPU-based variants reported gains between 1.85× and 4.4×.
Table 2.
Execution time (in seconds) for the solution of Lyapunov equations.
Table 2.
Execution time (in seconds) for the solution of Lyapunov equations.
| GECLNC_cpu | GECLNC_gpu | GECLNC_mgpu |
|---|
| STEEL | 1.35 | 0.99 | 0.73 |
| STEEL | 26.92 | 8.01 | 6.79 |
| FLOW_METER | 154.30 | 34.86 | 40.53 |
Table 3 summarizes the results for the solution of algebraic Riccati equations. Note that the codes to build the matrix,
(column 2), and solve the over-determined system (column 3) are similar for the three implementations evaluated. Columns 4–9 report the time dedicated to compute the sign function and the total execution time for each variant. In this case, GECRSG
_gpu obtains the best result for problems
STEEL and
STEEL, and clearly outperforms the CPU and multi-GPU implementation. The large computational cost of the solution of the ARE and the large number of computational units in the NVIDIA K20 explains this behavior. The storage requirements of problem
FLOW_METER exceed the memory in NVIDIA K20, and consequently, the corresponding equation cannot be solved with GECRSG
_gpu. On the other hand, the solution of this benchmark is accelerated by a factor of 4.5× using GECRSG
_mgpu.
Finally,
Table 4 shows the execution time obtained for the solution of differential Riccati equations using the matrix sign function-based Lyapunov solver. We solve the DREs in the time interval
, using a step size of length
. Two values are reported for each implementation: the time to compute the sign function (Fsign) and the total execution time. Most of the time, approximately 97% is dedicated to the sign function method (
i.e., the Lyapunov solver). The ROS1
_gpu implementation attains the best execution time for problems
STEEL and
STEEL, while it is slightly slower than ROS1
_mgpu for the larger problem. In all the cases, ROS1
_gpu clearly outperforms the multi-core variant, due to the large computational cost of the algorithm and its large parallelism.
Table 3.
Execution time (in seconds) for the solution of algebraic Riccati equations.
Table 3.
Execution time (in seconds) for the solution of algebraic Riccati equations.
| | System | GECRSG_cpu | | GECRSG_gpu | | GECRSG_mgpu |
|---|
| Fsign | Total | | Fsign | Total | | Fsign | Total |
|---|
| STEEL | 0.03 | 0.28 | 15.38 | 17.04 | | 5.34 | 6.64 | | 15.48 | 16.17 |
| STEEL | 0.45 | 12.03 | 505.96 | 545.36 | | 109.26 | 129.68 | | 162.75 | 188.86 |
| FLOW_METER | 1.37 | 72.79 | 2945.08 | 3173.54 | | – | – | | 533.25 | 689.26 |
Table 4.
Execution time (in seconds) for the solution of differential Riccati equations.
Table 4.
Execution time (in seconds) for the solution of differential Riccati equations.
| ROS1_mc | | ROS1_gpu | | ROS1_mgpu |
|---|
| Fsign | Total | | Fsign | Total | | Fsign | Total |
|---|
| STEEL | 5.23 | 5.28 | | 3.93 | 3.98 | | 2.53 | 2.70 |
| STEEL | 189.98 | 190.66 | | 45.05 | 45.73 | | 21.19 | 23.01 |
| FLOW_METER | 1952.50 | 1954.77 | | 404.54 | 406.82 | | 258.56 | 251.75 |
5. Conclusions
We have addressed the solution of three types of Lyapunov matrix equations, algebraic Riccati equations and differential matrix equations, that arise in control theory applications. A collection of implementations were evaluated for each solver targeting three different target platforms: multicore CPU, a hybrid system equipped with a multicore CPU and a GPU and a platform composed of a multicore CPU connected to several GPUs. All the routines make intensive use of high performance kernels from linear algebra libraries, like Intel’s MKL and NVIDIA’s CUBLAS, and parallel interfaces, like OpenMP.
Numerical results employing three benchmarks, extracted from the Oberwolfach Model Reduction Benchmark Collection, show the efficiency attained by the parallel solvers. The hybrid implementations that exploit the use of a single GPU report remarkable performance, being more than four-times faster than their corresponding multicore counterparts for large problems. However, their applicability is limited by the size of the GPU memory. This limitation is partially overcome in the multi-GPU implementations, where the amount of aggregated memory is larger.
 , where ATL is 0 × 0 and ABR is n × n
, where ATL is 0 × 0 and ABR is n × n