Abstract
We develop an efficient multicore algorithm, PMS6MC, for the -motif discovery problem in which we are to find all strings of length l that appear in every string of a given set of strings with at most d mismatches. PMS6MC is based on PMS6, which is currently the fastest single-core algorithm for motif discovery in large instances. The speedup, relative to PMS6, attained by our multicore algorithm ranges from a high of 6.62 for the (17,6) challenging instances to a low of 2.75 for the (13,4) challenging instances on an Intel 6-core system. We estimate that PMS6MC is 2 to 4 times faster than other parallel algorithms for motif search on large instances.
1. Introduction
Motifs are patterns found in biological sequences. These common patterns in different sequences help in understanding gene functions, and lead to the design of better drugs to combat diseases. Several versions of the motif search problem have been studied in the literature. In this paper, we consider the version known as the Planted Motif Search (PMS), or motif search problem. In PMS, given n input strings and two integers l and d, we aim to find all the strings M of length l (also referred to as l-mers) that are substrings of every input sequence (We use the terms sequence and string interchangeably in this paper) with at most d mismatches. The d-neighborhood of an l-mer s is defined to be the set of all the strings that differ from s in at most d positions. So, for an l-mer M to be motif for n input strings, there has to be a substring in each of those n input strings that is in the d-neighborhood of M.
The PMS problem is known to be NP-hard [2]. Consequently, PMS is often solved by approximation algorithms that do not guarantee to produce every motif present in the input. Exact algorithms for PMS, on the other hand, have exponential worst-case complexity but find every motif. MEME (Multiple EM for Motif Elicitation) [3], which is one of the most popular approximation algorithms for PMS, is based on the expectation minimization technique. MEME outputs the probability that each character is present in each motif and one can take the characters with highest probability in each position to construct the desired motif with an acceptable range of error. GibbsDNA [4] also calculates the same probability matrix of each character in different motif positions using Gibbs sampling. CONSENSUS [5] first aligns the input sequences using statistical measures and then tries to extract the motifs. Randomized algorithms are also proposed for PMS. Buhler and Tompa [6] proposed an algorithm where they group the input l-mers based on k randomly chosen positions out of the total l positions. With a high probability, many instances of the desired motif belong to the group that has a large number of these k-mers. Local search strategies such the one proposed by Price et al. [7], which searches d-neighborhood of some l-mers from the input, also have been used to find motifs. MULTIPROFILER [8] and ProfileBranching [7] are two algorithms that use local search. Some approximation algorithms for PMS first map the PMS problem to a graph problem and then apply well-studied approximation techniques to solve that graph problem. The WINNOWER algorithm [9], proposed by Pevzner and Sze, constructs a graph in which each node represents an l-mer and two nodes are connected by an edge iff those two l-mers differ in at most positions. The problem of finding motifs then reduces to that of finding large cliques in this graph. Although exact algorithms have worst-case exponential complexity, for many small instances of interest they are able to find all motifs within a reasonable amount of time using a modern computer. MITRA [10] is an exact algorithm for PMS that uses a modified trie called Mismatch trie to spell out the motifs one character at a time. SPELLER [11], SMILE [12], RISO [13], and RISOTTO [14] all use some form of suffix tree to direct motif discovery with RISOTTO being the fastest of these. CENSUS [15] first creates a trie with all l-mers from the input. The trie is then traversed keeping track of the number of mismatches with the currently generated motif in the nodes. Entire branches of the trie can be pruned off if the number of mismatches becomes more than d. Voting algorithms such as [16] use an indicator array of size equal to the number of all possible strings of length l. For each l-mer in the d-neighborhood of every l-mer from the input, the corresponding entry in the array is set. The entries that have been set by every input sequence or has “votes" from every input sequence are the motifs. As the number of possible strings of length l grows exponentially with l, this approach becomes infeasible even for small values of l. Kauska and Pavlovic [17] designed an algorithm to output motif stems i.e., a superset of motifs using regular expression. However, the number of possible motifs that can be generated from this superset might be very large. They also don’t provide a mechanism to select the actual motifs. As a result, the stemming approach is difficult to assess. The PMS series of algorithms (PMS1-PMS6, PMSP, and PMSPrune) solve PMS instances relatively fast using a reasonable amount of storage for data structures. PMS1, PMS2 and PMS3 [18] first sorts the d-neighborhood of input l-mers using radix sort and then intersects them to find the motifs. PMS4 [19] proposes a very general technique to reduce the run time of any exact algorithm by examining only k input sequences out of total n input sequences. It relies on the fact that if there is a motif, it will be present in those k input sequences as well. PMSP [20] extends this idea further by only examining the d-neighborhood of the l-mers from the first input sequence. PMSPrune [20] improves upon PMSP by using dynamic programming branch-and-bound algorithm while exploring the d-neighborhoods. Pampa [21] uses wildcards to first determine the motif patterns and then does a exhaustive search within possible mappings of the pattern to find the motifs. PMS5 [22] improves other algorithms from PMS series by efficiently computing the intersection of the d-neighborhood of l-mers without generating the entire d-neighborhoods for all the l-mers. PMS6 [23], which is the fastest algorithm in the series, is almost two times as fast as PMS5. This algorithm gets its speedup over PMS5 by grouping l-mers whose d-neighborhood computation follows a similar process.
Since exact algorithms for motif search are compute intensive, it is natural to attempt parallelization that reduce the observed run time. Dasari, Desh and Zubair [24] have proposed a multi-core motif search algorithm that is based on the voting approach. They followed this work with another parallel algorithm for Graphics Processing Units (GPUs) [25]. Their GPU algorithm is based on examining the branches of a suffix tree in parallel.
In this paper, we develop a multi-core version of PMS6 by generating and processing many d-neighborhoods in parallel. In Section 2 we introduce some notations and definitions used throughout the paper and also describe the PMS6 algorithm in detail. The techniques used to develop PMS6MC are described in Section 3. The performance of PMS6MC is compared to that of other parallel motif search algorithms and PMS6 in Section 5.
2. PMS6
2.1. Notations and Definitions
We use the same notations and definitions as in [22]. An l-mer is simply any string of length l. r is an l-mer of s iff (a) r is an l-mer and (b) r is a substring of s. The notation denotes an l-mer r of s. The Hamming distance, , between two equal length strings s and t is the number of places where they differ and the d-neighborhood, , of a string s, is . Let . It is easy to see that , where Σ is the alphabet in use. We also define to be . For a set of triples C, we define as . We note that x is an motif of a set S of strings if and only if (a) and (b) every has an l-mer (called an instance of x) whose Hamming distance from x is at most d. The set of motifs of S is denoted .
2.2. Overview
PMS6, which is presently the fastest exact algorithm to compute for large , was proposed by Bandyopadhyay, Sahni and Rajasekaran [23]. This algorithm (Algorithm 1) first computes a superset, , of the motifs of S. This superset is then pruned to by the function , which examines the l-mers in one by one determining which are valid motifs. This determination is done in a brute force manner.
| Algorithm 1: PMS6 [23]. |
PMS6()
// Determine a superset of motifs
for each
{
for to
{
;
;
for each and
{
Compute for ;
if
{
Create the class
with ;
Add to ;
}
else add to class ;
}
for each class in
if then
else ;
if break;
}
// Prune
;
}
|
To compute , PMS6 examines triples , where x is an l-mer of and y and z are l-mers of and , respectively for some fixed k. These triples are first partitioned into equivalence classes based on the number of positions in the l-mers of a triple that are of each of 5 different types (see below). Next, we compute the for all triples by classes. This two step process is elaborated below.
- Step 1: Form Equivalence Classes. Classify each position i of the triple , into one of the following five types [22]:
- Type 1: .
- Type 2: .
- Type 3: .
- Type 4: .
- Type 5: .The triples of l-mers such that , and are partitioned into classes where denotes the type j positions in the triple (for .
- Step 2: Compute for all triples by classes. For each class , the union, , of for all triples in that class is computed. We note that the union of all s is the set of all motifs of x, , and .
2.3. Computing
Let be a triple in and let w be an l-mer in . Then is the number of positions of Type i, for the triple . Each may be decomposed as below for all [22]:
- = number of Type 1 positions i such that .
- () = number of Type 2 positions i such that ().
- () = number of Type 3 positions i such that ().
- () = number of Type 4 positions i such that ().
- (, ) = number of Type 5 positions i such that )(,).
As the distance of w has to be less than or equal to d from each of x, y and z, the following equations result.
- All variables are non-negative integers.
Given a 10-tuple solution to this ILP, we may generate all l-mers w in as follows:
- Each of the l positions in w is classified as being of Type 1, 2, 3, 4, or 5 depending on the classification of the corresponding position in the l-mers x, y, and z (see Section 2.2).
- Select of the Type 1 positions of w. If i is a selected position, then, from the definition of a Type 1 position, it follows that . Also from the definition of , these many Type 1 positions have the same character in w as in x, y, and z. So, for each selected Type 1 position i, we set . The remaining Type 1 positions of w must have a character different from (and hence from and ). So, for a 4-character alphabet there are 3 choices for each of the non-selected Type 1 positions of w. As there are ways to select positions out of positions, we have different ways to populate the Type 1 positions of w, where .
- Select positions I and different positions J from the Type 2 positions of w. For each , set and for each , set . Each of the remaining Type 2 positions of w is set to a character different from the characters in x, y, and z. So, if k is one of these remaining Type 2 positions, . We set to one of the 2 characters of our 4-letter alphabet that are different from and . Hence, we have ways to populate the Type 2 positions in w, where .
- Type 3 and Type 4 positions are populated using a strategy similar to that used for Type 2 positions. The number of ways to populate Type 3 positions is , where and that for Type 4 positions is , where .
- To populate the Type 5 Positions of w, we must select the Type 5 positions, k, that will be set to , the Type 5 positions, k, that will be set to , and the Type 5 positions, k, that will be set to . The remaining Type 5 positions, k, of w are set to the single character of the 4-letter alphabet that differs from , , and . We see that the number of ways to populate the Type 5 positions is .
The preceding strategy to generate generates l-mers w for each 10-tuple . While every generated l-mer is in , some l-mers may be the same. Computational efficiency is obtained by computing for all in the same class concurrently by sharing the loop overheads as the same loops are needed for all in a class. Algorithm 2 gives the pseudocode to compute by classes.
As an example, lets say we have 3 input strings , and and we are asked to find motifs i.e., motifs of length 3 with at most 1 mismatch. Also, the l-mer is denote by . In this particular case, and hence for example. For the triplet , i.e., for the triplet we have . Hence it belongs to the class . For the triplet i.e., we have and it belongs to class . After evaluating all 8 triplets, we will end up having class . We then need to find and to compute . To computer , we need to compute . We can evaluate that , and and subsequently we have . Similarly, we can see that and hence . Run-time may be reduced by pre-computing data that do not depend on the string set S. So, for a given pair , there are 5-tuples . For each of the 5-tuples, we can pre-compute all 10-tuples () that are solutions to the ILP. For each 10-tuple, we can pre-compute all combinations (i.e., selections of positions in w). The pre-computed 10-tuple solutions for each 5-tuple are stored in a table with entries and indexed by and the pre-computed combinations for the 10-tuple solutions are stored in a separate table. By storing the combinations in a separate table, we can ensure that each is stored only once even though the same combination may be needed by many 10-tuple solutions.
| Algorithm 2: Compute [23]. |
ClassBd()
Find all ILP solutions with parameters
for each solution ()
{
← first combination for this solution;
for i = 0 to (# combinations)
{
for each triplet in
{
Generate ws for ;
Add these ws to ;
}
← next combination in Gray code order;
}
}
return
|
We store pre-computed combinations as vectors. For example, a Type 1 combination for and could be stored as indicating that the first and third Type 1 positions of w have a character different from what x, y, and z have in that position while the character in the second Type 1 position is the same as in the corresponding position of x, y, and z. A Type 2 combination for and could be stored as indicating that the character in the first Type 2 position of w comes from the third l-mer, z, of the triplet, the second Type 2 position of w has a character that is different from any of the characters in the same position of x and z and the third and fourth Type 2 positions of w have the same character as in the corresponding positions of x. Combinations for the remaining position types are stored similarly. As indicated by our pseudocode of Algorithm 2, combinations are considered in Gray code order so that only two positions in the l-mer being generated change from the previously generated l-mer. Consequently, we need less space to store the combinations in the combination table and less time to generate the new l-mer. An example of a sequence of combinations in Gray code order for Type 2 positions with is {0012, 0021,0120,0102,0201,0210,1200,1002,1020, 2010, 2001, 2100}. Note that in going from one combination to the next only two positions are swapped.
2.4. The Data Structure Q
We now describe the data structure Q that is used by PMS6. This is a reasonably simple data structure that has efficient mechanisms for storing and intersection. In the PMS6 implementation of [23], there are three arrays in Q; a character array, , for storing all l-mers, an array of pointers, ,which points to locations in the character array and a bit array, , used for intersection. There is also a parameter which determines how many characters of l-mers are used for indexing into array. As there are 4 possibilities for a character, for p characters can vary from 0 to . The number of characters, p, to be used for indexing into , is set when Q is initialized. During the first iteration of PMS6, for , l-mers in are stored in . After all s are computed, is sorted in-place using Most Significant Digit radix sort. After sorting, duplicate l-mers are adjacent to each other. Also, l-mers that have the same first p characters and hence are in the same bucket are adjacent to each other as well in . By a single scan through , duplicates are removed and the pointers in are set to point to different buckets in . During the remaining iterations, for , all s generated are to be intersected with Q. This is done by using the bit array . First, while computing , each l-mer is searched for in Q. The search proceeds by first mapping the first p characters of the l-mer to the corresponding bucket and then doing a binary search inside within the region pointed to by the bucket pointer. If the l-mer is found, its position is set in . Once all l-mers are marked in the , is compacted by removing the unmarked l-mers by a single scan through the array. The bucket pointers are also updated during this scan.
For larger instances, the size of is such that we don’t have sufficient memory to store in Q. For these larger instances, in the iteration, we initialize a Bloom filter using the l-mers in rather than storing these l-mers in Q. During the next iteration (k = 2), we store, in Q, only those l-mers that pass the Bloom filter test (i.e., the Bloom filter’s response is “Maybe"). For the remaining iterations, we do the intersection as for the case of small instances. Using a Bloom filter in this way reduces the number of l-mers to be stored in Q at the expense of not doing intersection for the second iteration. Hence at the end of the second iteration, we have a superset of (Algorithm 1) of the set we would have had using the strategy for small instances. Experimentally, it was determined that the Bloom filter strategy improves performance for challenging instances of size (19,7) and larger. As in [22], PMS6 uses a partitioned Bloom filter of total size 1GB. From Bloom filter theory [26] we can determine the number of hash functions to use to minimize the filter error. However, we need to minimize the run time rather than the filter error. Experimentally, [23] determined that the best performance was achieved using two hash functions with the first one being bytes 0–3 of the key and the second being the product of bytes 0–3 and the remaining bytes (byte 4 for (19,7) instances and bytes 4 and 5 for (21,8) and (23,9)instances).
3. PMS6MC
3.1. Overview
PMS6MC exploits the parallelism present in the PMS6 algorithm. First, there is outer-level parallelism where the motif search for many x’s from can be carried out in parallel (i.e., several iterations of the outer for loop of Algorithm 1 are run in parallel). Second, there is inner-level parallelism where the individual steps of the inner for loop of Algorithm 1 are done in parallel using multiple threads. Outer-level parallelism is limited by the amount of memory available. We have designed PMS6MC to be flexible in terms of its memory and thread requirements. The total number of threads can be set depending on the number of cores and available memory of the system. The threads are grouped into thread blocks. Each thread block operates on a different x from . So, for example, if we use a total of t threads and 4 thread blocks, then our code does 4 iterations of the outer for loop in parallel with each iteration (or thread block) being assigned to threads. The threads assigned to a thread block cooperate to find the motifs corresponding to a particular x. The threads use the primitive function to synchronize. This function can be implemented using the thread library synchronization mechanism available under different operating systems. We denote thread block i as while the threads within thread block i are denoted by . Figure 1 shows a diagram of the steps in PMS6MC.
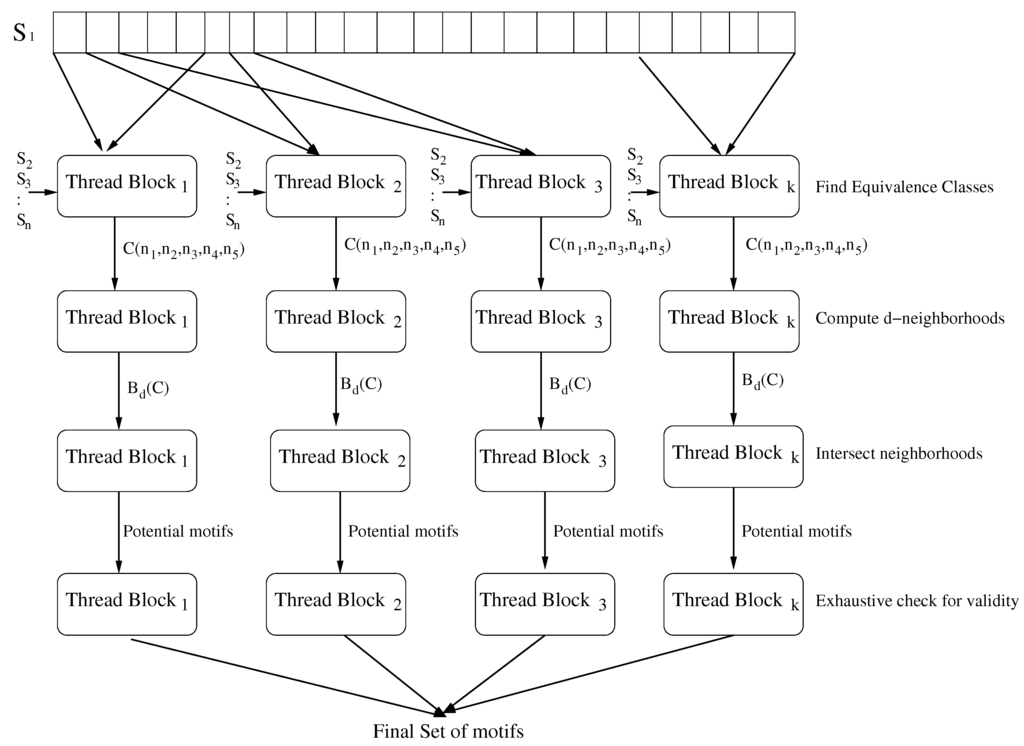
Figure 1.
PMS6MC flow diagram.
3.2. Outer-Level Parallelism
In this, each thread block processes a different x from and calls the function (Algorithm 3). Once a thread block is done with its assigned x it moves on to the next x from which is not processed yet. Threads in a thread block execute the function to find if there is any motif in the d-neighborhood of x.
| Algorithm 3: PMS6MC outer level loop. |
PMS6MC()
for each idle thread block T[i] in parallel do
{
select an that hasn’t yet been selected;
if there is no such x the thread block stops;
findMotifAtThisX(x, i);
}
|
3.3. Inner-Level Parallelization
Finding motifs in the d-neighborhood of a particular x from is done by finding the motifs of x and the strings and for . As described in Algorithm 1, this is a 4 step process. These steps are done cooperatively by all threads in a thread block. First, we find the equivalence classes for x and l-mers from and . For any triple from an equivalence class we know the number of l-mers w which are at a distance d from x, y and z from pre-computed tables. Hence, by multiplying the number of triples with the number of possible w’s we determine the total number of w’s for each equivalence class. We denote this number by . Next, we compute for these equivalence classes in decreasing order of in parallel by the threads in the thread block. This order helps in load balancing between different threads as each will be computing in parallel. This is akin to using the LPT scheduling rule to minimize finish time. store s in Q if ; i.e., when finding motifs between x, and . This can be done during the previous step while computing . For , we need to intersect the set of all s with Q. When the size of Q falls below a certain threshold, we need to execute the function to find out which l-mers in Q are valid motifs. The different steps for are given in Algorithm 4.
The data structure used in PMS6MC for Q is very similar to that used in PMS6. However, we use two character arrays and instead of one. This helps us to perform many operations on Q in parallel by multiple threads. We now describe the different steps used to finding motifs employing this modified structure for Q.
| Algorithm 4: Finding motifs in parallel. |
findMotifAtThisX(String x, Thread block i)
for to
{
findEquivalenceClasses(x, T[i], );
Sort in decreasing order of ;
for each class C in order from in parallel by threads T[i][j];
{
ComputeProcess
}
syncthreads(T[i]);
ProcessQ(Q, k, T[i]);
syncthreads(T[i]);
if break;
}
outputMotifs(Q) in parallel by threads T[i][j];
|
3.3.1. Finding Equivalence Classes in Parallel:
Each thread works on a segment of the string in parallel. For all y that belong to the thread’s assigned segment of and for all z from , the thread computes the number of type 1 through type 5 positions for the triple . Based on the number of type 1 through type 5 positions (), the triple is put into the corresponding equivalence class. Once all the threads finish, the equivalence classes formed by different threads need to be merged. As s for can only vary from 0 to l, the whole range of is divided among the threads in the thread block. Each thread then finds the equivalence classes present in its assigned range and gathers all the triples of these equivalences classes in parallel. The pseudocode for this step is given in Algorithm 5.
| Algorithm 5: Finding equivalence classes in parallel. |
findEquivalenceClasses(x, i, ) for each y and z in parallel by threads T[i][j] { Compute for ; if { Create the class with ; Add to ; } else add to class ; } syncthreads(T[i]); Merge equivalence classes in by threads T[i][j] in parallel; syncthreads(T[i]); |
3.3.2. Computing in Parallel:
Once equivalence classes are formed, we determine by multiplying the number of triples with the number of solutions for equivalence classes using pre-computed tables. Once the number of l-mers is known, the offset in to store l-mers during the first iteration is also known. Hence, each thread can store l-mers from the designated offset without conflict with other threads. To ensure that each thread in a thread block is roughly doing the same amount of work, we first order the equivalence classes in terms of decreasing . This sorting can be done by a single thread as the number of equivalence classes is typically less than 1000 even for large instances. Thread j of the thread block selects the jth equivalence class to work on; when a thread completes, it selects the next available equivalence class to work on. This strategy is akin to the LPT scheduling strategy and is known to provide good load balance in practice. Each thread computes for the class C it is working on using the same strategy as used by PMS6 (see Section 2.3).
For , we store the l-mers in from the designated offset. We also do some additional work which facilitates sorting Q in parallel during the next step. For each thread, we keep track of the number of l-mers having the same first character. This is done by maintaing a 2-D counter array indexed by thread number and the first character of the l-mer.
For , the l-mer is searched for and marked in the when found (see Section 2.4). Although there might be a write conflict while setting the bit in the , all threads can carry this step in parallel as threads that write to the same mark bit write the same value. Algorithm 6 gives the steps used to compute and process .
| Algorithm 6: Compute and process . |
ProcessBd(, Q, k, i, j)
if
{
for each l-mer
Copy l-mers in to from the offset for this class;
}
if k ≥ 2
{
For all l-mer w ∈ , set if w is present in Q;
}
|
3.3.3. Processing Q in Parallel
The processing of Q depends on the iteration number. When , we sort , then remove the duplicates and set the bucket pointers. For the remaining iterations, we need to remove all unmarked l-mers from and update the bucket pointers.
The sort is done by first computing the prefix sum of so that the counter for a particular thread and a particular character equals the total number of l-mers processed that have either smaller first character or equal first character but processed by threads with a smaller index. Since the number of counters is small (256 different counters for 8-bit characters) we compute the prefix sums using a single thread. The pseudocode is given in Algorithm 7. Next, each thread in the thread block scans through the l-mers in that it had stored while generating . Depending on the first character of the l-mer, the l-mer is moved to starting from the offset indicated by prefix sum counter. This movement of l-mers is done by the threads in a thread block in parallel. Once the movement is complete, is divided into segments such that the first characters of all l-mers within a segment are the same. Following this segmenting, the threads sort the segments of in parallel using radix sort. Each thread works on a different segment. Since the first character of the l-mers in a segment are the same, the radix sort starts from the second character. Once the segments are sorted, we proceed to eliminate duplicates and set the bucket pointers. First the threads count the number of unique l-mers in each segment in parallel by checking adjacent l-mers. Again, each thread works on a different segment. The determined counts of unique l-mers are prefixed summed by a single thread to get the offsets required for moving the unique l-mers to their final positions. Using these offsets, the threads move unique l-mers with each thread moving the unique l-mers of a different segment from to in parallel. While moving an l-mer, the threads also check to see if first p characters of the current l-mer are the same as those of the previous l-mer; if not, the appropriate pointer in is set.
| Algorithm 7: Prefix sum of counters. |
PrefixCounters()
sum = 0;
for i = 0 to 255 // There are 256 possibilities for the first character
{
for j = 1 to threads
{
}
sum = counters[threads - 1][i];
}
|
When , we need to remove from Q all the l-mers that are not marked in . This is done in two steps. First, the is divided into segments and each thread does a prefix sum on different segments in parallel. This gives the number of marked l-mers in each segment. Next, we move the marked l-mers in each segment from to . For this, a prefix sum is performed by a single thread on the counters having the number of marked l-mers in different segments to get the offset in for moving the l-mers. With these offsets, the threads then move the marked l-mers from different segments in parallel. As before, when moving an l-mer, the thread checks to see if the first p characters of the current l-mer differs from the previous one and update the appropriate pointer in . There might be a problem in updating the bucket pointers in the boundary region of the segments as one bucket can extend across the boundary of two segments and hence two threads might update that bucket pointer. These boundary bucket pointers are fixed by a single thread after all l-mers are moved. Note that there can only be as many boundary buckets as there are segments which are very few in number. The pseudocode for the processing Q for different values of k is given in Algorithm 8.
| Algorithm 8:Processing Q. |
ProcessQ((Q, k, T[i]) if { prefixCounters(counters); Move l-mers from to by threads T[i][j] in parallel; syncthreads(T[i]); Sort segments in in parallel by threads T[i][j]; syncthreads(T[i]); Count unique l-mers in each segment in parallel by threads T[i][j]; syncthreads(T[i]); Move unique l-mers to and update bucket pointers in parallel by T[i]j[j]; } if { Divide into segments; Prefix sum by threads T[i][j] in parallel; syncthreads(T[i]); Move marked l-mers from segments in to in parallel by Threads T[i][j]; Update the bucket pointers while moving l-mers; syncthreads(T[i]); Fix the boundary buckets if necessary; } |
3.3.4.
Once the size of Q drops below a certain threshold, we break out of the loop and call to determine the set of valid motifs in Q. This step can be done in parallel as checking the validity of l-mers to be motifs can be done independent of one another. So, each thread examines a disjoint set of l-mers from Q exhaustively checking if it is a motif as is done in PMS6; the threads operate in parallel.
4. Experimental Section
We evaluated the performance of PMS6MC on the challenging instances described in [22] as they are representatives of harder to solve instances and provide a uniform way to compare results from previous algorithms. For each that characterizes a challenging instance, we generated 20 random strings of length 600 each. Next, a random motif of length l was generated and planted at random positions in each of the 20 strings. The planted motif was then randomly mutated in exactly d randomly chosen positions. For each value up to (19,7), we generated 20 instances and for larger values, we generated 5 instances. The average run times for each value are reported in this section. Since the variation in run times across instances was rather small, we do not report the standard deviation. Even though we test our algorithm using only synthetic data sets, several authors (e.g., [22]) have shown that PMS codes that work well on the kind of synthetic data used by us also work well on real data.
4.1. PMS6MC Implementation
PMS6MC is implemented using the pthreads (POSIX Threads) library under Linux on an Intel 6-core system with each core running at 3.3 GHz. We experimented with different degrees of outer-level (number of thread blocks) and inner-level (number of threads in a thread block) parallelism for different challenging instances. For smaller instances (e.g., (13,4) and (15,5)), the performance is limited by the memory bandwidth of the system. Hence, increasing the degree of inner or outer level parallelism does not have much effect on the run time as most of the threads stall for memory access. For larger instances, the number of thread blocks is limited by the available memory of the system. Table 1 gives the number of thread blocks and the number of threads in a thread block for different challenging instances which produces the optimum performance.

Table 1.
Degree of inner and outer level parallelism for PMS6MC.
| Challenging instances | Outer-level blocks | Threads per block | Total threads |
|---|---|---|---|
| (13,4) | 2 | 6 | 12 |
| (15,5) | 2 | 6 | 12 |
| (17,6) | 8 | 6 | 48 |
| (19,7) | 4 | 12 | 48 |
| (21,8) | 2 | 12 | 24 |
| (23,9) | 2 | 12 | 24 |
5. Results and Discussion
5.1. PMS6 and PMS6MC
We compare the run times of PMS6 and PMS6MC on an Intel 6-core system with each core running at 3.3 GHz. PMS6 takes 22 s on an average to solve (15,5) instances and 19 h on an average to solve (23,9) instances. PMS6MC, on the other hand, takes 8 s on an average to solve (15,5) instances and 3.5 h on an average to solve (23,9) instances. The speedup achieved by PMS6MC over PMS6 varies from a low of 2.75 for (13,4) instances to a high of 6.62 for (17,6) instances. For (17,6) instance we can use many threads while staying within memory constraints and hence we get a larger speedup. For (19,7) and larger instances PMS6MC achieves a speedup of over 5 as we can’t go beyond a certain number of threads due to memory limitations. The run times for various challenging instances are given in Table 2.

Table 2.
Run times for PMS6 and PMS6MC.
| Algorithm | (13,4) | (15,5) | (17,6) | (19,7) | (21,8) | (23,9) |
|---|---|---|---|---|---|---|
| PMS6 | 22 s | 74 s | 6.82 min | 22.75 min | 2.25 h | 19.19 h |
| PMS6MC | 8 s | 21 s | 1.03 min | 4.45 min | 25.5 min | 3.57 h |
| PMS6/PMS6MC | 2.75 | 3.52 | 6.62 | 5.11 | 5.29 | 5.38 |
5.2. PMS6MC and Other Parallel Algorithms
Dasari, Desh and Zubair proposed a voting based parallel algorithm for multi-core architectures using bit arrays [24]. They followed up with an improved algorithm based on suffix trees for GPUs and multi-core CPUs from intel [25]. We estimate the relative performance of PMS6MC and these parallel algorithms using published run times and performance ratios. Table 3 and the first 4 rows of Table 4 give the performance of PMS5 and PMSPrune as reported in [22] and that of PMS6 and PMS5 as reported in [23], respectively.

Table 3.
Run times for PMS5 and PMSPrune [22].
| Algorithm | (13,4) | (15,5) | (17,6) | (19,7) |
|---|---|---|---|---|
| PMS5 | 117 s | 4.8 min | 21.7 min | 1.7 h |
| PMSPrune | 45 s | 10.2 min | 78.7 min | 15.2 h |
| PMS5/PMSPrune | 2.6 | 0.47 | 0.28 | 0.11 |

Table 4.
Total run time of different PMS algorithms.
| Algorithm | (13,4) | (15,5) | (17,6) | (19,7) | (21,8) | (23,9) |
|---|---|---|---|---|---|---|
| PMS5 | 39 s | 130 s | 11.35 min | 40.38 min | 4.96 h | 40.99 h |
| PMS6 | 22 s | 75 s | 6.72 min | 22.75 min | 2.25 h | 19.19 h |
| PMS5/PMS6 | 1.77 | 1.73 | 1.69 | 1.77 | 2.20 | 2.14 |
| PMS6/PMSPrune | 1.46 | 0.27 | 0.17 | 0.06 | - | - |
| PMSPrune/PMS6MC | 1.88 | 13.04 | 38.94 | 85.17 | - | - |
We divide the ratio by to estimate the ratio (5th row of Table 4). Next, we divide the ratio (row 4 of Table 2) by our etimate of to get an estimate of (6th row of Table 4).
The first 4 rows of Table 5 give the run times of gSPELLER-x, mSPELLER-x, and PMSPrune as reported in [25]. The "x" indicates the number of CPU cores for mSPELLER and the number of GPU devices in the case of gSPELLER. We report the times for mSPELLER-16 and gSPELLER-4 as these were the fastest reported in [25]. From this data and that of Table 4 we can estimate the speedups shown in rows 5 through 8 of Table 4. We estimate that the speed up of PMS6MC using 6 cores compared to mSPELLER-16 using 16 cores varies from a low of 0.07 for (13,4) instances to 3.58 for (19,7) instances while the speed up for PMS6MC using only one CPU with respect to gSPELLER-4 using 4 GPUs varies from a low of 0.03 for (13,4) instances to a high of 1.97 for (19, 7) instances.

Table 5.
Comparing mSPELLER and gSPELLER with PMS6MC.
| Algorithm | (13,4) | (15,5) | (17,6) | (19,7) | (21,8) |
|---|---|---|---|---|---|
| PMSPrune | 53 s | 9 min | 69 min | 9.2 h | - |
| mSPELLER-16 | 2 s | 16.5 s | 2.5 min | 23.6 min | 3.7 h |
| gSPELLER-4 | 0.8 s | 7.2 s | 1.2 min | 13 min | 2.2 h |
| PMSPrune/mSPELLER-16 | 26.5 | 32.73 | 27.6 | 23.38 | - |
| PMSPrune/gSPELLER-4 | 66.25 | 75 | 57.5 | 42.46 | - |
| mSPELLER-16/PMS6MC | 0.07 | 0.40 | 1.41 | 3.64 | - |
| gSPELLER-4/PMS6MC | 0.03 | 0.17 | 0.68 | 2 | - |
6. Conclusions
We have developed a multicore version of PMS6 that achieves a speedup that ranges from a low of 2.75 for (13,4) challenging instances to a high of 6.62 for (17,6) challenging instances on a 6-core CPU. Our multicore algorithm is able to solve (23,9) challenging instances in 3.5 h, while the single core PMS6 algorithm takes 19 h. We estimate that our multicore algorithm is faster than other parallel algorithms for the motif search problem on large challenging instances. For example, we estimate that PMS6MC can solve (19,7) instances 3.6 times faster than using our 6-core CPU mSPELLER-16 using the 16-core CPU of [25] and about two times faster than gSPELLER-4 can using four GPU devices.
Acknowledgments
This research was supported, in part, by the National Science Foundation under grant 0829916 and the National Institutes of Health under grant R01-LM010101. This paper is an extended version of [1] and this research was supported, in part, by the National Science Foundation under grant 0829916 and the National Institutes of Health under grant R01-LM010101.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bandyopadhyay, S.; Sahni, S.; Rajasekaran, S. PSM6MC: A Multicore Algorithm for Motif Discovery. In Proceedings of the Third IEEE International Conference on Computational Advances in Bio and Medical Sciences (ICCABS), New Orleans, LA, USA, 12–14 June 2013.
- Evans, P.A.; Smith, A.; Warenham, H.T. On the complexity of finding common approximate substrings. Theor. Comput. Sci. 2003, 306, 407–430. [Google Scholar] [CrossRef]
- Bailey, T.L.; Williams, N.; Misleh, C.; Li., W.W. MEME: Discovering and analyzing DNA. Nucleic Acids Res. 2006, 34, 369–373. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, C.E.; Altschul, S.F.; Boguski, M.; Liu, J.S.; Neuwald, A.F.; Wootton, J.C. Detecting subtle sequence signals: A Gibbs sampling strategy for multiple alignment. Science 2003, 262, 208–214. [Google Scholar] [CrossRef]
- Hertz, G.; Stormo, G. Identifying DNA and protein patterns with statistically significant alignments of multiple sequences. Bioinformatics 1999, 15, 563–577. [Google Scholar] [CrossRef] [PubMed]
- Buhler, J.; Tompa, M. Finding Motifs Using Random Projections. In Proceedings of the Fifth Annual International Conference on Computational Molecular Biology(RECOMB), Montreal, QC, Canada, 22–25 April 2001.
- Price, A.; Ramabhadran, S.; Pevzner, P. Finding Subtle Motifs by Branching from the Sample Strings. Bioinformatics Supplementary Edition. In Proceedings of the Second European Conference on Computational Biology (ECCB), Paris, France, 27–30 September 2003.
- Keich, U.; Pevzner, P. Finding motifs in the twilight zone. Bioinformatics 2002, 18, 1374–1381. [Google Scholar] [CrossRef] [PubMed]
- Pevzner, P.; Sze, S.H. Combinatorial Approaches to Finding Subtle Signals in DNA Sequences. In Proceedings of the English International Conference on Intelligent Systems for Molecular Biology, San Diego, CA, USA, 19–23 August 2000; Volume 8, pp. 269–278.
- Eskin, E.; Pevzner, P. Finding composite regulatory patterns in DNA sequences. Bioinformatics 2002, 18, 354–363. [Google Scholar] [CrossRef]
- Sagot, M. Spelling Approximate Repeated or Common Motifs Using a Suffix Tree. In Proceedings of the Third Latin American Theoretical Informatics Symposium (LATIN), Campinas, Brazil, 20–24 April 1998; pp. 111–127.
- Marsan, L.; Sagot, M.F. Extracting Structured Motifs Using a Suffix Tree–Algorithms And Application to Promoter Consensus Identification. In Proceedings of the Fourth Annual International Conference on Computational Molecular Biology(RECOMB), Tokyo, Japan, 8–11 April 2000.
- Carvalho, A.M.; Freitas, A.T.; Oliveira, A.L.; Sagot, M.F. A Highly Scalable Algorithm for the Extraction of Cis-Regulatory Regions. In Proceedings of the Third Asia Pacfic Bioinformatics Conference (APBC), Singapore, Singapore, 17–21 January 2005.
- Pisanti, N.; Carvalho, A.M.; Marsan, L.; Sagot, M. Finding Subtle Motifs by Branching from the Sample Strings. Bioinformatics Supplementary Edition. In Proceedings of the Second European Conference on Computational Biology (ECCB), Paris, France, 27–30 September 2003.
- Evans, P.; Smith, A. Toward Optimal Motif Enumeration. In Proceedings of Algorithms and Data Structures, 8th International Workshop (WADS), Ontario, ON, Canada, 30 July–1 August 2003; pp. 47–58.
- Chin, F.Y.L.; Leung, H.C.M. Voting Algorithms for Discovering Long Motifs. In Proceedings of the Third Asia-Pacific Bioinformatics Conference (APBC), Singapore, Singapore, 17–21 January 2005; pp. 261–271.
- Kuksa, P.P.; Pavlovic, V. Efficient motif finding algorithms for large-alphabet inputs. BMC Bioinf. 2010, 11. [Google Scholar] [CrossRef] [PubMed]
- Rajasekaran, S.; Balla, S.; Huang, C.H. Exact algorithms for planted motif challenge problems. J. Comput. Biol. 2005, 12, 1177–1128. [Google Scholar] [CrossRef] [PubMed]
- Rajasekaran, S.; Dinh, H. A speedup technique for (l, d) motif finding algorithms. BMC Res. Notes 2011, 4, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Davila, J.; Balla, S.; Rajasekaran, S. Fast and practical algorithms for planted (l, d) motif search. IEEE/ACM Trans. Comput. Biol. Bioinf. 2007, 4, 544–552. [Google Scholar] [CrossRef] [PubMed]
- Davila, J.; Balla, S.; Rajasekaran, S. Fast and Practical Algorithms for Planted (l, d) Motif Search; Technical Report; University of Connecticut: Storrs, Mansfield, CT, USA, 2007. [Google Scholar]
- Dinh, H.; Rajasekaran, S.; Kundeti, V. PMS5: An efficient exact algorithm for the (l,d) motif finding problem. BMC Bioinf. 2011, 12, 410–420. [Google Scholar] [CrossRef] [PubMed]
- Bandyopadhyay, S.; Sahni, S. PSM6: A Fast Algorithm for Motif Discovery. In Proceedings of the Second IEEE International Conference on Computational Advances in Bio and Medical Sciences (ICCABS), Las Vegas, NV, USA, 23–25 Feburary 2012.
- Dasai, N.S.; Desh, R.; Zubair, M. An Efficient Multicore Implementation of Planted Motif Problem. In Proceedings of the International Conference on High Performance Computing and Simulation (HPCS), Caen, France, 28 June–2 July 2010.
- Dasai, N.S.; Desh, R.; Zubair, M. High Performance Implementation of Planted Motif Problem using Suffix trees. In Proceedings of the International Conference on High Performance Computing and Simulation (HPCS), Istanbul, Turkey, 4–8 July 2011.
- Horowitz, E.; Sahni, S.; Mehta, D. Fundamentals of Data Structures in C++; Silicon Press: Summit, NJ, USA, 2007. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).