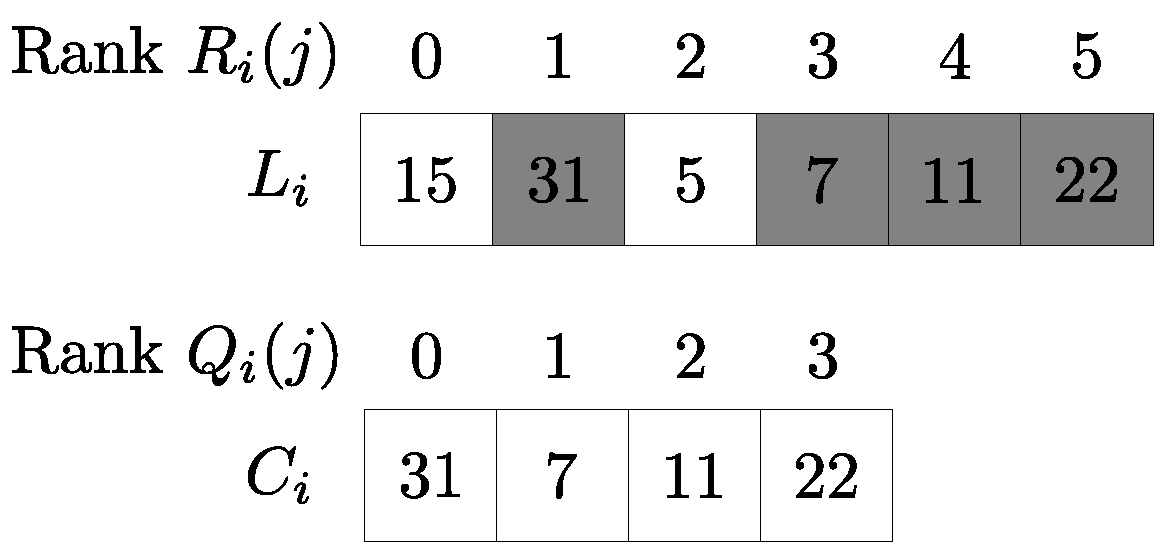1. Introduction
Overlays represent a significant puzzle piece in contemporary and future networking infrastructure, whether they are intended to support resource sharing or other collaborative applications, such as searching, ad hoc connectivity and persistent services. The common scenario is that peers are able to know part of the overlay network (in terms of potential neighbors), but want to connect only to a small number of other peers in order to conserve resources. Connection decisions are not to be taken blindly, but should rather be based on some suitability metric related to, e.g., the peer’s distance, interests, recommendations, transaction history or available resources. In the fully distributed scenario, every peer may follow an individually chosen metric (that it may even not want to disclose to other peers), but still wants to be able to coordinate with others in order to improve the quality of its connections. We present algorithms that enable peers that follow them to achieve a guaranteed level of collective quality in their connections. They achieve that by disclosing a limited amount of metric information to their immediate neighbors, but not the metric itself and are, in fact, independent of any individual metric choices. At the same time, the algorithms proposed here are able to adapt and tolerate the high dynamicity commonly found in these resource sharing overlays, with peers leaving, joining or changing the metrics about their neighbors at any time.
Observe that finding good methods to help peers establish connections and accommodate such needs or preferences relates to some form of
matching problem in a graph. Moreover, in the context of overlay networks, an important goal is to enable peers to satisfy their preferences during overlay construction: note that these “preference lists” point towards a form of stable marriage/roommates problem [
1,
2,
3]. The first to observe the relation between overlay construction and stable marriage problems were Gai
et al. [
4], followed by Mathieu [
5], in which overlay construction is regarded as a
generalized stable roommates matching problem [
6] (also referred to as a
b-matching problem [
5,
7]). In such a problem, the agents under consideration have more than one opportunity to connect to each other, in a similar way to, e.g., attendees in a conference exchanging the limited amount of calling cards they brought with them. The goal for each agent in this setting is to be able to form the desired amount of connections with the highest quality (most preferred) neighbors. However, the existence of cycles among the preference lists of the peers may turn overlay construction into a challenging task: matchings between peers on a cycle always create opportunities for improvement at other sites in the network, leading to infinite loops and unstable configurations. Gai
et al. in [
4] proved that, in the case of an acyclic preference system, there is always a stable configuration and also supplied examples of preference systems based on global or symmetric metrics. Furthermore, in order to give a qualitative measure of the stabilization process, Mathieu in [
5] defined the notion of
satisfaction gleaned by a peer out of its current matching choices.
With the research focused on preference systems that are known to have a stable configuration, such as acyclic ones, there is a relative scarcity of results concerning arbitrary preference systems and practical algorithms for achieving stable configurations (if existing) or good approximations thereof. Can we look at this problem from a different perspective? How can a solution be measured? What are the characteristics of a practical algorithm in a fully distributed scenario? Can we adapt to and tolerate changes in the overlay, such as preference change or peer joining/leaving?
To propose answers to these questions, we focus on the distributed b-matching problem: we suggest a novel modeling, present algorithms for both its adaptive and non-adaptive forms, show convergence and guaranteed approximation bounds and complement our results with an extensive experimental study.
Novel modeling:We start by reflecting further on the evaluation of different matching choices of peers (as proposed in [
5]). By considering satisfaction about the peer’s connection choices (compared to the optimal choices) as an optimization metric, we focus on distributed algorithms that try to maximize the satisfaction of peers that follow them (either a group or the whole overlay). We then proceed to propose a method of constructing an acyclic preference system from any arbitrary one, and we use this helper acyclic system to reduce the initial problem to a many-to-many maximum weighted matching problem.
Algorithmic solutions:Generalizing the approximation algorithm for the one-to-one matching problem found in [
8,
9], we present a simple, fully distributed,
-approximation algorithm for the many-to-many maximum weighted matching problem using only communication among immediate neighbors. In addition, we complement our distributed algorithm with a variant that can adapt to and tolerate changes in the overlay, such as peer joining/leaving and preference changes. We prove that both algorithms converge and that their computed solution is at least
of the maximum total satisfaction of the initial system, where
bmax is the maximum connection quota in the graph and
is the ratio of the maximum and minimum neighbor list sizes in the graph,
Lmax and
Lmin, respectively, resulting in a
-approximation algorithm in total.
Experimental study: We also provide an extensive experimental study of the behavior of the algorithm under a variety of scenarios, including normal operation, but also operation under high stress. Under normal operation, we focus on the levels of achieved satisfaction, as well as convergence time (in the case of our non-adaptive algorithm) and reconvergence time (in the case of our adaptive algorithm). Specifically, we show that the resulting satisfaction is always significantly higher than the worst-case theoretical bound after convergence, but also remains at high levels during and after reconvergence, while reconvergence is achieved in an efficient way under a variety of changes. Besides, motivated by [
10,
11], we conducted experiments that focus on the stability of the network under join/leave attacks, by exposing it to high churn rates, and observed that the algorithm withstands the attacks while maintaining graceful satisfaction values throughout them.
The rest of the paper is organized as follows. In
Section 2, we introduce the necessary notation and define our problem, while in
Section 3, we present, separately, the notion of node satisfaction, along with an extensive commentary, due to its importance in our modeling. In
Section 4, we show how our original b-matching problem can be reduced into a many-to-many maximum weighted matching problem that is guaranteed to have a stable solution, and we prove that this can be done with constant factor approximation. We present our distributed algorithm for the many-to-many maximum weighted matching problem in two variations, adaptive and non-adaptive, in
Section 5, along with analytical proofs of their approximation ratio for our original problem. Our extensive experimental study can be found in
Section 6, while discussion on the presented, as well as related work can be found in
Section 7. Finally,
Section 8 concludes the paper.
2. Problem Model
We represent a connectivity network as an undirected graph
G(
V,
E), with |
V| =
n, |
E| =
m, where
V is the set of overlay peers and
E the set of potential connections. Each node
i has degree
di and keeps a preference list
Li of all nodes in its neighborhood Γ
i (in the rest of the paper and when it is clear from the context, we will use notation
Li to denote both the list and its length). Let
Ri(
j) denote the rank of node
j in node
i’s preference list, with
Ri(·) ∈ {0, 1, …, |
Li| − 1}, attributing zero to its most desirable neighbor. Each node
i wants to maintain at most
bi connections (in order to form the overlay) to the best possible nodes according to its preference list and rank function, and at no point can it exceed this number. Clearly, it must be
bi ≤ |
Li|. In the following sections, we will refer to two nodes as
neighboring nodes when they are connected by an edge in graph
G and
connected nodes when they are matched by a matching algorithm. The problem of trying to find a many-to-many matching that respects the individual preferences and connection quotas
bi is a form of a generalized stable roommates problem called the
stable fixtures problem [
6] or
b-matching [
5]. We call
adaptive b-matching the dynamic form of b-matching, where nodes can join, leave or change preferences at any time. In the remainder of this paper, we will refer to these events simply as
changes. We will also consider an asynchronous model for messages and will not consider link or node failures,
i.e., messages arrive asynchronously, but do not get lost, and nodes depart gracefully or their absence can be detected by other means (for example, special periodic “alive” messages).
In order to measure the success of node
i’s efforts in establishing its
bi connections, we make use of the notion of
satisfaction,
Si, which is defined in [
5] by the following formula:
where
Ci (with |
Ci| =
ci ≤
bi) is an
ordered list of node i’s connections in decreasing preference. Satisfaction, due to its significance in the context of this paper, is discussed and analyzed separately in
Section 3.
We define an optimization variation of the b-matching problem, which we call the
maximizing satisfaction b-matching problem, where the objective is to find a b-matching that maximizes the total sum of the nodes’ satisfaction. Later on, we also define a
truncatedSmaximizing satisfaction b-matching problem, which is based on the same basic b-matching problem, but tries to maximize a different (truncated) satisfaction function (see
Section 4) (although we may refer to them simply as the b-matching problem and the truncatedS b-matching problem, respectively, it will be clear from the context that we are referring to the optimization versions).
Consider that edges e = (i, j) ∈ E in the previously defined graph G(V, E) have assigned weights w(i, j) = wij. A weighted matching problem on this graph is the problem of finding a set of edges, such that their weight sum is maximized and there are no common endpoints between them. The many-to-many variant that we will use replaces the last constraint on no common endpoints with node capacities that need to be respected, which, in this case, are the connection quotas bi per node i.
During the analysis of the distributed algorithm, we will use the notion of a
locally heaviest edge [
9]: if we define the set
Eij as the set of edges that have either node
i or node
j as an endpoint (but not both):
an edge (
i,
j) is called locally heaviest if it has the greatest weight among all edges
e ∈
Eij:
In the following sections, we will assume that the nodes following the algorithms proposed here, whether a group or the whole network, cooperate willfully, and we will provide guarantees about the maximization of the total satisfaction in this group or network.
4. Approximating B-Matchings with Weighted Matchings
In this section, we show how a simple modification connects the maximizing satisfaction b-matching problem with well known optimization problems, such as the maximum weighted matching.
4.1. Discarding the A Posteriori Term
As the first step to approximate the maximizing satisfaction b-matching problem, we define a modified problem based on the same basic b-matching problem, but computing satisfaction using a modified version of Equation (4) (and subsequently Equation (1)):
Using the above definition, we effectively disregard the dynamic part of Equation (4), making the prospective satisfaction increase of node i independent of the number of connections. We refer to the node satisfaction defined by Equation (7) as truncated satisfaction and the corresponding maximizing satisfaction b-matching problem as a truncatedS maximizing satisfaction b-matching problem. In the following lemma, we prove that by solving the truncatedS maximizing satisfaction b-matching problem, we get an approximation of the original problem.
Lemma 1 The truncatedS maximizing satisfaction b-matching problem is a -approximation of the maximizing satisfaction b-matching problem, where bmax is the maximum connection quota in the graph and is the ratio of the maximum and minimum neighbor list sizes in the graph, Lmax and Lmin, respectively.
Proof: Since only
is used in the modified maximizing satisfaction b-matching problem, we are interested in studying the ratio:
and, specifically, its minimum value,
rmin. Knowing this minimum value, we can conclude that the total satisfaction of the modified problem,
Smod, is a
rmin-approximation of the total satisfaction of original b-matching problem
Sorig, since:
where
n = |
V| is the number of nodes in the graph. Note that we are looking for the minimum value
rmin, and therefore, we can assume that a given node
i has connected with the desired amount of neighbors
bi since then the difference between
and
is maximized, as we show below.
Initially, consider the scenario in which every node
i is connected with its bottom-most
bi neighbors. It is easy to see that
gets its maximum value when the length of the list is maximized (|
Ci| =
bi), since the dynamic part of the satisfaction increase
is due to the connection list
Ci of node
i. In this case of |
Ci| =
bi connections,
achieves its minimum value when the connections
j ∈
Ci are drawn from the bottom of the preference list
Li. Since both of these conditions are met in the scenario considered here, the relative value of
is maximized or, equivalently, the relative value of
is minimized and the sums of dynamic and static parts,
and
, acquire the values of
and
, respectively. For these values
and
, we have:
meaning that the relative ratio of the sum of the static parts
is at least:
This is clearly the worst possible case for all nodes and a lower bound for the
ratio, since:
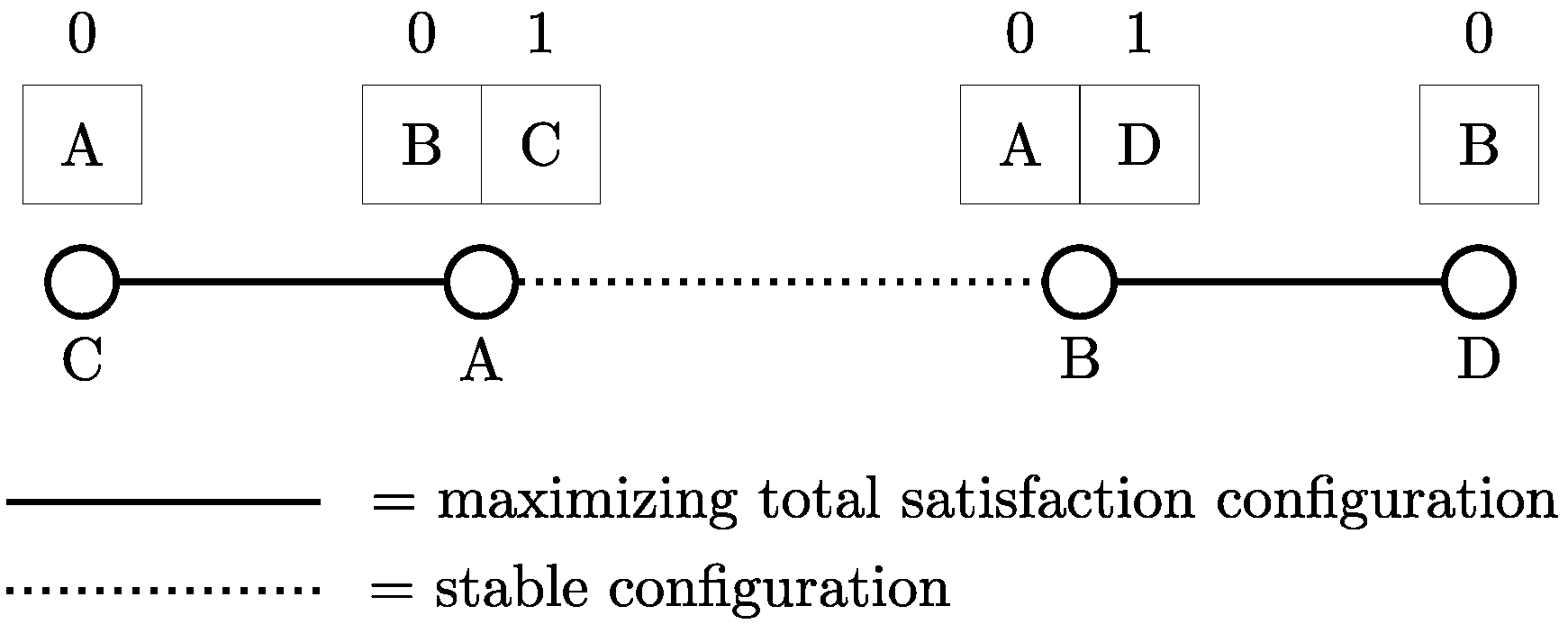
However, note that each node i that connects with its bi bottom-most neighbors must have been rejected by its Li − bi > 0 top-most ones. This means that these neighbors j cannot connect to their bj bottom-most neighbors, since in the worst case the last place must be occupied by node i. In this case, the worst possible scenario connects them to bj neighbors starting at the previous to last position and moving without gaps towards more preferable neighbors. We write B for the set of nodes that connect to their bottom-most neighbors, and we call these nodes bottom-choosers. Note here that we discuss a worst case scenario and therefore we do not include nodes with Li − bi = 0 in set B; in such a case the bi bottom-most neighbors are the same as the bi top-most ones, which is the best possible outcome for node i.
Since both bottom-choosers and non-bottom-choosers are connected to their desirable number of neighbors, but the former are connected to their bottom-most neighbors, while the later are connected to their bottom-most-but-one neighbors, for each node
bci ∈
B we have:
while for each node
nbi ∈
V/
B we have:
Using Equations (11) to (17) we get:
For reasons of clarity, in the remaining proof we are going to refer to quantities
and
with
Q and
q, respectively, as well as
qmin for the minimum value of the latter. Using the above notation and Equations (13) and (18), we get:
In order to calculate
qmin, we bound the sum
as follows:
where
Lmax is the maximum neighbor list size in the graph. For |
B|, we observe that each bottom-chooser corresponds to
Li −
bi non-bottom-choosers (its
Li −
bi top-most neighbors), and summing up for the whole graph, we have:
since
.
For every node
i we define
Li −
bi =
ciLi, where
ci is the percentage of list
Li that is covered by
Li −
bi. By the same definition, we have
. By Equations (20) and (21) and the above definition, we get:
From Equations (19) and (22) and using the observation that
, we get:
where
is the ratio of the maximum and minimum neighbor list sizes in the graph,
Lmax and
Lmin respectively, which proves the desired approximation ratio. □
4.2. Converting to a Maximum Weighted Matching
The truncatedS b-matching problem, as defined above, assumes privately kept preference lists and cannot be considered a maximum weighted matching problem, which needs the weights associated with edges to be known and common to both endpoints. In order to convert it, we will create edge weights by adding the satisfaction gleaned by the two endpoints for the specific link. For an edge
e = (
i,
j) ∈
E, the weight should be:
By using these weights to construct and solve a many-to-many weighted matching problem, we also get a solution for the truncatedS b-matching problem, as the following lemma suggests.
Lemma 2 We consider the truncatedS b-matching problem that uses Equation (6) for satisfaction calculations. A solution derived from a many-to-many maximum weighted matching on the same graph, with edge weights given by Equation (24), is also a solution for the truncatedS b-matching problem, and vice versa.
Proof: Let
A ⊆
E be the edge set that is the solution of a many-to-many maximum weighted matching on a graph
G(
V,
E) with edge weights defined by Equation (24). This set
A corresponds to a collection
C of connection lists
Ci ∀
i ∈
V, and maximizes the expression
to a value
w(
A):
Let also
A′ ⊆
E be the corresponding edge set for the truncatedS b-matching problem (using Equation (6)) on the same graph. This set corresponds to a collection
C′ of connection lists
∀
i ∈
V, and maximizes the expression,
, to a value
w(
A′) where
is the satisfaction gleaned by node
i for the connections of list
:
We will prove that these solutions
w(
A) and
w(
A′) are equal. Assume that
w(
A) >
w(
A′). If we group the satisfaction increases
in Equation (25) for a node
i, we can write:
By the assumption and Equation (27), we have:
implying that the collection
C achieves a greater value than
C′ for the maximizing expression of the truncatedS b-matching problem. However, this contradicts the definition of
C′.
Symmetrically, assuming that w(A) < w(A′) also leads to a contradiction, meaning that any solution for the many-to-many maximum weighted matching we are considering is also a solution for the corresponding truncatedS b-matching problem, and vice versa. □
The following theorem follows directly from Lemmas 1 and 2.
Theorem 1 We consider the maximizing satisfaction b-matching problem that uses Equation (4) to maximize the total satisfaction. A solution derived from a many-to-many maximum weighted matching on the same graph, with edge weights given by Equation (24), is a -approximation of the b-matching problem, where bmax is the maximum connection quota in the graph and is the ratio of the maximum and minimum neighbor list sizes in the graph, Lmax and Lmin, respectively.
Having approximated the original b-matching problem by a many-to-many maximum weighted matching, we need only a distributed algorithm for that problem. The rest of this paper presents a simple, distributed algorithm in two variations, an adaptive and a non-adaptive, that solve the many-to-many maximum weighted matching problem using a -approximation guarantee. We also present and utilize a centralized helper algorithm that we employ in order to prove the approximation ratio of the distributed algorithm.
5. Distributed Algorithms for the Many-to-Many Maximum Weighted Matching Problem
In this section, we present a distributed algorithm, in adaptive and non-adaptive forms, that solves the many-to-many maximum weighted matching problem with an approximation ratio of
. The non-adaptive version of the algorithm is presented in
Section 5.1, followed by the analysis of its correctness and convergence properties in
Section 5.2.
Section 5.3 and
Section 5.4 present the adaptive version and its analytical properties, respectively. Finally,
Section 5.5 shows that the solutions of both variations are a
-approximation for the many-to-many maximum weighted matching problem.
5.1. LID Algorithm
The simple greedy algorithm we are proposing is fully distributed and operates by choosing the locally heaviest edges in every node’s neighborhood, generalizing the one-to-one matching algorithm by Hoepman [
8].
In the beginning, each node i reports to each neighboring node, j, only j’s relative rank in i’s preference list, in the form of , exchange between i and j, and they both compute the weight w(i, j) of their connecting edge. This ensures the flexibility of the ranking metric each node uses (it does not need to reveal the metric) at the cost of only local communication between nodes. Every node keeps these newly formed weights of its adjacent edges in a weight list, which is then used during the algorithm’s execution to determine the desirability of a neighboring node. Note that these weight lists do not replace the individual preference lists of the nodes: they are auxiliary lists that are used in a similar way (to determine desirability), but only during the algorithm’s execution, i.e., not for measuring the final satisfaction.
The
Local Information-based Distributed (LID) algorithm (
cf. Algorithm 1 for pseudocode) uses, at each node
i, four sets (
Ui,
Pi,
Ai,
Ki) and a function (
topRanked(·)) and sends two kinds of messages (PROP and REJ):
A node i sends PROP messages to propose to its heaviest-weight neighbors the establishment of a connection with them. If an asked node also sends a PROP message to node i, then the connection is established (locked or selected); note that this will happen at both endpoints. Set Pi keeps the neighbors to which node i proposed with a PROP message; Ai keeps the neighbors which approached node i with a PROP message; Ki keeps the locked neighbors, and Ui the neighbors that did not send any message to node i or were not contacted yet. The algorithm terminates when Ui = ∅.
A node sends a REJ message when it has locked as many neighbors as it could. When a node receives a REJ message, it sends a new PROP message to the next unproposed neighbor.
The topRanked(·) function returns the top ranked node of its set argument, according to the weight list of the calling node. In Algorithm 1, this means that PROP messages are sent to neighbors in decreasing ranking order and there are at most bi such unanswered messages originating from i at any time. A new PROP message is sent only if a previously asked node has explicitly declined.
When the algorithm finishes in a node i the connected neighbors can be found in set Ki.
| Algorithm 1 LID: Local Information-based Distributed algorithm for many-to-many maximum weighted matchings, run on node i |
| Ki = ∅; Ai = ∅; Pi = ∅; Ui = Γi |
![Algorithms 06 00824 i001]() |
5.2. Analysis of the LID Algorithm
At the center of the algorithm above is the notion of the locally heaviest edge [
8,
9], since the nodes send PROP and REJ messages in order to compare their heaviest edges and find the locally heaviest ones. Note here that we assume unique edge weights, since it is important for the greedy algorithms described here to be able to recognize the locally heaviest edges in an unambiguous way (ties can be broken using node identities). However, globally unique edge weights are not necessary: it is sufficient for edge weights to be unique in the local neighborhoods of their endpoint nodes.
By the definition in
Section 2, at most, one locally heaviest edge can be attached to a node
i at any specific point during the execution of the algorithm. However, once an edge is selected by node
i, another one can possibly become locally heaviest in node
i’s neighborhood, and so on, until the algorithm selects enough of them. On the other hand, when nearby nodes fill in their quotas of possible connections, any unselected edges they might have with node
i become unavailable. In order to express this recursive property of locally heaviest edges, we continue to use condition Equation (3):
but we adapt the definition of the set
Eij to include only edges of nodes
i and
j with unlocked neighbors
k (
) that have not filled their connection quotas yet (
):
Note that for the initial conditions
, the definition above coincides with the one of Equation (2).
The following two lemmas address the dynamics arising from the aforementioned recursive definition by showing two important properties: the algorithm’s execution at node i: (i) chooses only locally heaviest edges (although not in any particular order); and (ii) chooses edges in a way, such that any unselected locally heaviest edge adjacent to node i at the end of the algorithm’s execution has lower absolute edge weight than the selected ones adjacent to the same node.
Lemma 3 Every locked edge is locally heaviest at some point during the execution of the algorithm.
Proof: As edge
is eventually locked, we assume without loss of generality that node
i sent to node
j a PROP message, inserted it in
, later on received a confirmation from node
j and eventually locked the edge. It is easy to see that sets
and
contain the heaviest available edges in the neighborhoods of node
i and
j, respectively; heaviest because Algorithm LID sends PROP messages to neighbors in decreasing edge weight order and available, since PROP messages were sent, but no reply came back yet, either positive or negative (a positive answer will move the answering node to
K, and a negative answer will remove it from
P). Since we only need to search for locally heaviest edges in sets
and
, we can replace sets
with
respectively in Equation (28) and prove that the new condition holds at some point during the algorithm’s execution:
Assume that condition Equation (29) does not hold at time , but edge is selected (at that time ), and suppose a node k exists, such that . We know that node i proposed to node k before proposing to node j, since PROP messages are being sent in decreasing ranking order. Node k will answer back at some point during the execution of the algorithm, either positively or negatively, by which time it will be removed from set . At that point, condition Equation (29) will hold and edge will be locally heaviest. The same is also true if a node l exists, such that or if both nodes k and l exist. □
Lemma 4 For every node i Algorithm LID chooses all locally heaviest edges that are adjacent to it, if there is enough quota bi available, or otherwise chooses the bi of those that are heavier than any unchosen one.
Proof: Based on Lemma 3, by the end of the algorithm, all chosen edges of node i have been locally heaviest. Furthermore, if there is enough quota available, any unselected locally heaviest edges will be eventually selected. The only way some locally heaviest edge has been left unchosen is for node i to fill in its connection quota with other locally heaviest edges. We just need to prove that in this case the unchosen edge is of lower weight than the chosen ones.
Note that the LID algorithm proposes to nodes of heavier edges first and proceeds only if it receives an explicit decline (meaning it was not a locally heaviest edge or the other node filled its quota), so the chosen edges are always heavier than any unchosen one. □
Calculating edge weights in the way previously described enables the conversion of the original maximizing satisfaction b-matching problem of
Section 2 to a many-to-many maximum weighted matching problem, but as an added benefit it enables us to use the weight lists to make preference-based decisions, in a way similar to a b-matching problem. This new b-matching problem does not replace the original maximizing satisfaction b-matching: the nodes keep their original preference lists, but a new b-matching problem arises when they try to cooperate in order to collectively achieve a guaranteed level of connection quality. However, this new b-matching problem always converges regardless of the original problem, due to the symmetric nature of the edge weights [
4]. The following lemma expresses exactly this property by showing that the algorithm terminates for all nodes.
Lemma 5 Algorithm LID terminates for every node .
Proof: From the code of Algorithm LID we can see that it terminates for node i when or , that is, when every neighbor replies (and node i gets less than positive replies) or enough neighbors reply (for node i to get positive replies), respectively. The only case where the algorithm would not terminate is if some node would wait indefinitely for a neighbor’s answer, i.e., if a communication cycle exists: each node in a group of nodes, , sends a PROP message to node and awaits for an answer in order to reply back to node . In order to prove that the algorithm terminates, we only need to prove that communication cycles cannot exist.
Assume there is a communication cycle
. Since node
sent a PROP message to node
and not to node
, we know that
. If we add up the respective inequalities for all
, we get:
Using properties of the modulo operator to change the sum limits and since edge weights are symmetric to their respective endpoints (see Equation (24)), we get the following:
which is a contradiction of Equation (32) and of the assumption on the existence of a communication cycle. □
5.3. AdaptiveLID Algorithm
In a dynamic setting, where nodes join/leave the network or change preferences about their neighbors at any time, there is a partial or full solution that is disturbed by a specific operation. In this case, it is desirable to “repair” the solution locally instead of recomputing it globally. It would also be advantageous to limit the repairs to the neighborhood of the operation, so that far enough nodes would remain unaffected. Note that the locally-heaviest-edge property that we are using here seems ideal for this purpose: it only makes sense to preserve and use it further to support dynamicity.
In the adaptive algorithm, AdaptiveLID presented here, all three cases of dynamicity mentioned above (join/leave/change) are supported. In the case of a joining (respectively departing) node, neighboring nodes add (respectively delete) it to (respectively from) their preference lists. On the other hand, when a node changes preferences, no change occurs to the neighboring nodes’ preference lists, but edge weights may change radically. A common thread between these cases is that the nodes directly involved in the operations must recalculate their marginal satisfactions for their neighbors and exchange them so that their adjacent edges have the correct weights. Afterwards, they must re-evaluate their connections: if they are not locally heaviest any more, the nodes abandon the least weighted ones and try to get matched with the locally heaviest ones. Note here that this method avoids the recalculation of the solution over the whole network, instead limiting it to a neighborhood around the network area where the dynamic operation took place. An additional benefit is that the involved nodes maintain their current connections unless proven to be non-optimal, i.e., they change them only if necessary.
The A
daptiveLID algorithm uses at each node
i five sets (
) and an incoming message queue,
, and sends three kinds of messages (PROP, REJ and WAKE):
A node i sends PROP messages to propose to its heaviest-weight neighbors the establishment of a connection. If an asked node also sends a PROP message to node i, then the connection is established (locked): note that this will happen at both endpoints. Set stores the neighbors to which node i proposed with a PROP message; stores the neighbors that approached node i with a PROP message; stores the locked neighbors; stores the neighbors that rejected node i, and the neighbors that node i rejected. Sets and are copies of sets and , respectively, that do not contain neighbors of edges heavier than the edge of the worst connected neighbor.
A node sends a REJ message when it has locked as many neighbors as it could. Nodes can send additional PROP messages to available neighbors if they receive a REJ message. PROP messages are sent to neighbors in decreasing ranking order, and there are at most such unanswered messages originating from i at any time.
Node i is constantly checking if its PROP messages are addressed to heaviest-weight neighbors, as ranking can change due to a change in the network. If it detects a better available node than the currently proposed ones, it sends a REJ message to the worst connected neighbor and a PROP to the better candidate. However, if the better candidate has simultaneously rejected and been rejected by node i, node i sends only a WAKE message.
![Algorithms 06 00824 i002]() |
5.4. Analysis of the AdaptiveLID Algorithm
The following lemmas prove that the algorithm always converges after a finite amount of steps or, in the case of changes in the network, in a finite amount of steps after the changes stop. Although implied by the distributed nature of the algorithm, it is useful to note that the algorithm continues to run at all nodes regardless of any changes that are happening in the network. In fact, as we show in the experimental section, it manages to maintain a reduced but steady level of service while under extremely heavy stress or possibly a network attack. However, convergence can be guaranteed after all changes complete, since any changes that might occur require appropriate readjustment by the distributed algorithm.
Lemma 6 In a failure-free execution, edge weight updates that are caused by node or preference changes complete in a finite amount of time.
Proof: When a node joins (leaves) the network, it gets inserted to (deleted from) neighboring nodes’ preference lists, causing changes that need to be communicated to their own neighbors. The same happens to the node itself when it changes its own preference list. Therefore, every change causes a weight update that propagates at a maximum distance of two and to a bounded amount of nodes (bounded by the size of a distance of two neighborhood from the originating node). Note that the neighbor’s neighbors (or the immediate neighbors in the case of simple preference change) accept the weight update passively and do not propagate it further. Since we assumed that nodes do not fail and messages do not get lost, it is evident that all nodes are fully updated in a finite amount of time after the change. □
We define as available, with respect to node i, a node j in the neighborhood of node i that has neither been proposed by node i nor rejected node i.
A node j is the locally heaviest node in the neighborhood of node i at some point in time if there are no available nodes adjacent to node i that are endpoints of heavier edges. Note that edges with such a node as an endpoint are candidates for being locally heaviest edges (hence, the name “locally heaviest node”). In fact, when the endpoints of an edge consider simultaneously each other locally heaviest, the edge between them is the locally heaviest edge.
Lemma 7 In a finite amount of time after a node or preference change, every node cancels all proposals towards neighbors that are no longer locally heaviest and issues an equal amount towards available neighbors that are locally heaviest.
Proof: Every change triggers weight updates at a distance of one (nodes that the joining/leaving node connect to/disconnect from or direct neighbors of a node that changes preferences) and possibly at a distance of two (neighbor’s neighbors of a joining/leaving node). By Lemma 6, the weight updates complete in a finite amount of time. When procedure 3 executes next in any node i at a distance of one or two from the change, it will repeatedly examine nodes that are either available or have simultaneously rejected and been rejected by node i, as long as they are heavier than the proposed node of the lowest weight. Every time it encounters a node of the latter category, it sends a WAKE message, prompting the node to revoke its rejection, whereas every time it encounters a node of the former category, it sends a PROP message, preceded by a REJ to the proposed node of the lowest weight (note that whether a node is considered locally heaviest or not may change during a single execution of procedure 3.). In any case, at the end of procedure 3’s execution, all proposals from node i to its neighbors that are no longer locally heaviest are canceled, and complementary proposals are sent to available neighbors that are locally heaviest; the same is true for every node in the network. □
Lemma 8 The AdaptiveLID algorithm terminates for every node after changes complete.
Proof: For the static case, Lemma 5 applies, and the algorithm terminates. For the dynamic case, a change may cause some proposals to be canceled and reissued on nodes at a distance of one or two (Lemma 7). The only cases in which the algorithm may not terminate on these nodes is when they wait indefinitely for a neighbor’s answer or their preference list “oscillates”, with proposals being canceled and reissued on the same neighbors in an alternating way over time. By Lemma 6, we can ignore weight updates, since they complete in a finite amount of time.
For the first case, a node can wait indefinitely only if a communication cycle exists: each node
in a group of nodes,
, sends a PROP message to node
and awaits for an answer in order to reply back to node
, that is
. By adding all such equations on the cycle and using properties of the modulo operator, we get:
which is a contradiction.
For the second case, by Lemma 7 and since we assumed that the changes are completed, we have that any potential canceling and reissuing of proposals finishes in a finite amount of time and therefore no oscillations occur. □
Lemma 9 For every node i Algorithm AdaptiveLID chooses all locally heaviest edges that are adjacent to it, if there is enough quota available, or otherwise chooses the of those that are heavier than any unchosen one.
Proof: For a static network, Lemma 4 is applicable. For a dynamic network, by Lemma 7, after a finite amount of time, every node i cancels all proposals to neighbors that are no longer locally heaviest after a change and proposes to the locally heaviest ones. Some of these proposals will result in a match if the receiving node also considers the originating node locally heaviest. The same will happen to all proposed nodes, as long as the originating and receiving nodes have available quotas. If some node lacks in available quota, we know that its matched incident edges are heavier than its unmatched locally heaviest, since by Lemma 7, it would have to cancel the appropriate proposals and issue new ones towards locally heaviest neighbors. □
Lemma 10 The AdaptiveLID algorithm, when run on a network with changes, produces the same matching with the LID algorithm that is run on the same network after the changes complete.
Proof: By Lemma 8, we get that the AdaptiveLID algorithm terminates for every node, and by Lemma 9, we know that at termination, it has chosen only the locally heaviest edges of maximum weight. Since by Lemma 4 the static algorithm also selects the locally heaviest edges of maximum weight at termination, it follows that the two algorithms make the same choices for the same networks. □
5.5. Approximation Ratio for the Distributed Algorithms
Following the methodology in [
8], in order to further analyze the distributed algorithm in both variations, we present a centralized algorithm for many-to-many maximum weighted matchings, for which we show that it behaves in the same way with the distributed algorithm and both have the same approximation ratio of
.
| Algorithm 3 LIC: Local Information-based Centralized algorithm for many-to-many maximum weighted matchings |
| M ← ∅; P ← E |
![Algorithms 06 00824 i003]() |
Algorithm LIC is a simple greedy algorithm with the distinctive feature of using only locally available information, by selecting locally heaviest edges in a centralized way. Note that the comment of
Section 5 about the recursive nature of the locally heaviest edges is still valid here: by systematically removing from the edge pool
P the edges we select (line 6, Algorithm 3), along with any unselected edges of nodes with filled quotas (lines 8 and 9, Algorithm 3), we get the same dynamics as in the distributed case (
cf. Lemma 11). In the following theorem, using a similar proof strategy to the one used by Preis [
9] for his centralized one-to-one weighted matching algorithm, we prove that it achieves a
-approximation compared to the optimum algorithm (OPT) that selects edges with maximum weights over the whole graph.
Theorem 2 The LIC algorithm produces a many-to-many maximum weighted matching that is a -approximation of the matching produced by the optimal algorithm, OPT.
Proof: Let
be the set of nodes matched at least once by the LIC algorithm. We will show that the condition:
holds for every step of the LIC algorithm, that is, the weight of matching
,
, is at least
of the weight
of the optimal matching
when including only edges adjacent to nodes matched by LIC. Note that the algorithm can leave two or more nodes (completely) unmatched, but only if they are not connected in
(if they are connected, they will be matched, since the possibility exists and they have available connection quotas, leaving possibly one odd node unmatched). By the time LIC terminates, for every
, it would be either
or
, and Equation (33) will become
.
For the initial condition
Equation (33) holds. Let us assume that at some step of LIC, edge
is included in the matching
and the left-hand side of Equation (33) increases by
. For the right-hand side, there are only two options: either
is part of the optimal matching,
, or two other edges,
and
, occupy the respective slots of nodes
a and
b in the optimal matching. For these cases, we have the following:
□
The following lemma mirrors Lemma 4 and is the key lemma in proving the equivalence of both centralized and distributed algorithms in the subsequent theorem.
Lemma 11 For every node i Algorithm LIC chooses all locally heaviest edges that are adjacent to it, if there is enough quota available, or otherwise chooses the of those that are heavier than any unchosen one.
Proof: If there are less than locally heaviest edges, algorithm LIC will choose all of them, since, by construction, it will continue to select them until there are no quota slots available at either endpoint. Otherwise, again by construction, it will choose the heaviest of them for node i. □
Theorem 3 The LID algorithm is a -approximation algorithm for the maximizing satisfaction b-matching problem, where is the maximum connection quota in the graph and is the ratio of the maximum and minimum neighbor list sizes in the graph, and , respectively.
Proof: By Lemmas 11 and 4, we know that algorithms LIC and LID choose the same edges for each node and therefore produce the same solution. This means that the LID algorithm is also a -approximation algorithm for the many-to-many maximum weighted matching (as Theorem 2 suggests for the LIC algorithm). Furthermore, the many-to-many maximum weighted matching we solve, by theorem 1, is a -approximation of the corresponding b-matching problem. These two approximations combined give a -approximation for the original maximizing satisfaction b-matching, where is the maximum connection quota in the graph. □
From the above theorem and Lemma 10, we also get the following theorem about the approximation ratio of AdaptiveLID:
Theorem 4 The AdaptiveLID algorithm solves the adaptive b-matching with preferences problem with -approximation.
6. Experimental Study
The following extensive experimental study complements the preceding analytical part with useful observations and conclusions about the behavior of the LID and A
daptiveLID algorithms in a variety of scenarios. Focus was given on the performance of the algorithms in regard to the following points:
Convergence and reconvergence times
Satisfaction levels, both in normal operation and under heavy stress (i.e., during a network-level attack)
Fairness properties of satisfaction-based optimization
Behavior on different types of networks
Behavior during different operations (joins, leaves, preference changes and churn)
6.1. Network Types
The networks used during the experiments were power-law and random networks, created with the Barabási–Albert (
BA) [
14] and Erdős–Rényi (
ER) [
15] procedures, respectively, having mean degree and initial (joining) degree of 0.05
n and 0.05
n, respectively (where
n is the network size). These networks were selected for their different node degree distributions: in power-law networks, the vast majority of nodes has a very low degree, and few nodes have a very high degree (power-law distribution), while in ER random networks, all nodes have comparable degrees (binomial distribution). In fact, high degree nodes in BA networks are connected mostly with many low degree ones, which leads to the creation of very different neighborhoods around individual nodes for these two network types. This difference, coupled with the A
daptiveLID algorithm’s ability to perform local repairing operations, leads to the varying behaviors that can be seen in the experiments below.
On the other hand, nodes of both network types had full preference lists (consisting of all their neighbors), but ranked uniformly at random and with a desired number of connections equal to half their own degree. Focus was given on random preference lists, since previous research [
4,
5] showed that: (a) a strict matching solution cannot always be found when they are used; and (b) the measured satisfaction of unconverged instances can be relatively low. These characteristics make random preferences a challenging test case to evaluate the performance of the algorithms.
6.2. Experimental Procedure
The following experiments were conducted using the PeerSim [
16] platform in a synchronous way,
i.e., execution proceeded in rounds, where each node in each round made a receive-respond-process step, unless it had nothing to execute. This synchronous execution mode is not necessary for the algorithm, but it is used here to measure the time needed by both algorithms to converge. For each of the following experiments, networks of size
n = 100, 250, 500, 750 and 1, 000 nodes were used, considering 30 network instances for each size, and the results presented here are the mean values over these instances. For every network instance, a matching was calculated and, in the case of the A
daptiveLID algorithm, the following operations were performed on a varying amount of nodes (1% to 50% of the network size, in increments of 1%):
join/leave, where nodes enter/exit the network simultaneously;
preference change, where existing nodes change the ranking of their neighbors in their preference lists simultaneously; and
churn, where existing nodes exit and an equal amount of new nodes enter the network simultaneously. For the first three cases, the network was left to reconverge after one operation, while in the case of churn, the operation was repeated for several rounds before the network was left to reconverge.
6.3. Convergence and Reconvergence
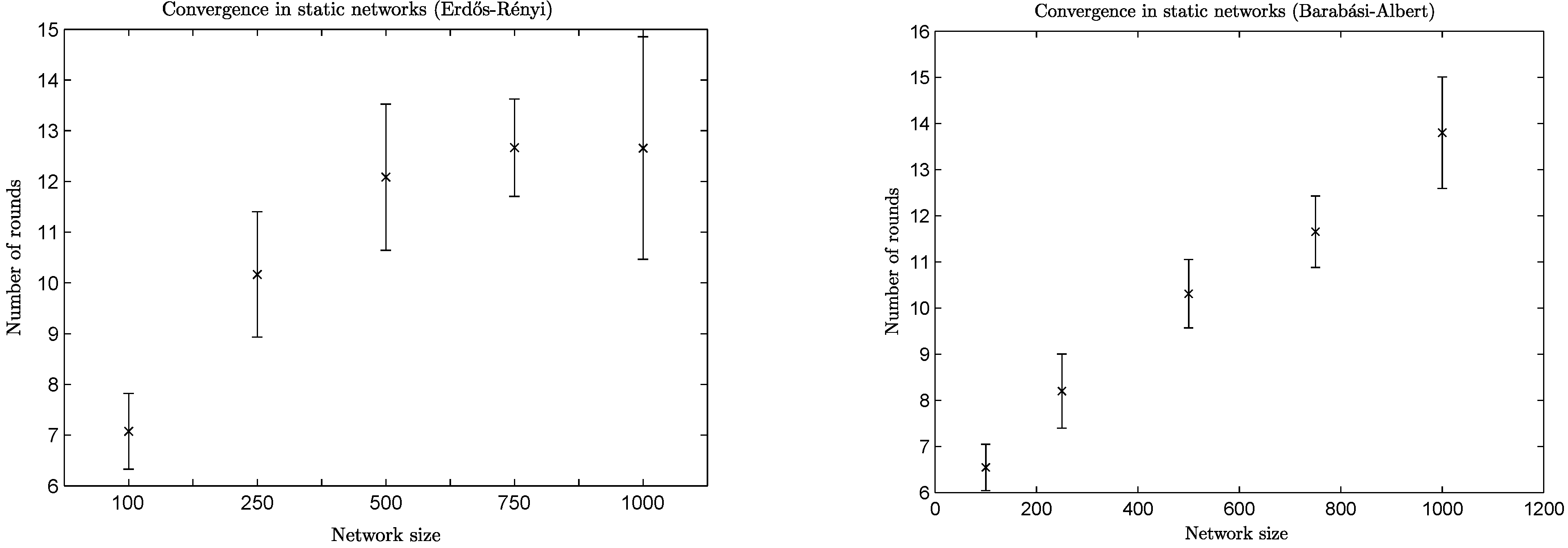
The mean value and standard deviation of convergence speed for a variety of network sizes can be found in
Figure 3. It is easy to see that the convergence speed depends on the type of the network. For example, BA networks of a size of 1,000 take almost twice the amount of time to converge than networks of a size of 100, while ER networks of a size of 1,000 need less than twice the amount of time needed by networks of a size of 100 and only a slightly higher amount of time than the networks of a size of 500 and 750.
Figure 3.
Convergence speed per network size.
Figure 3.
Convergence speed per network size.
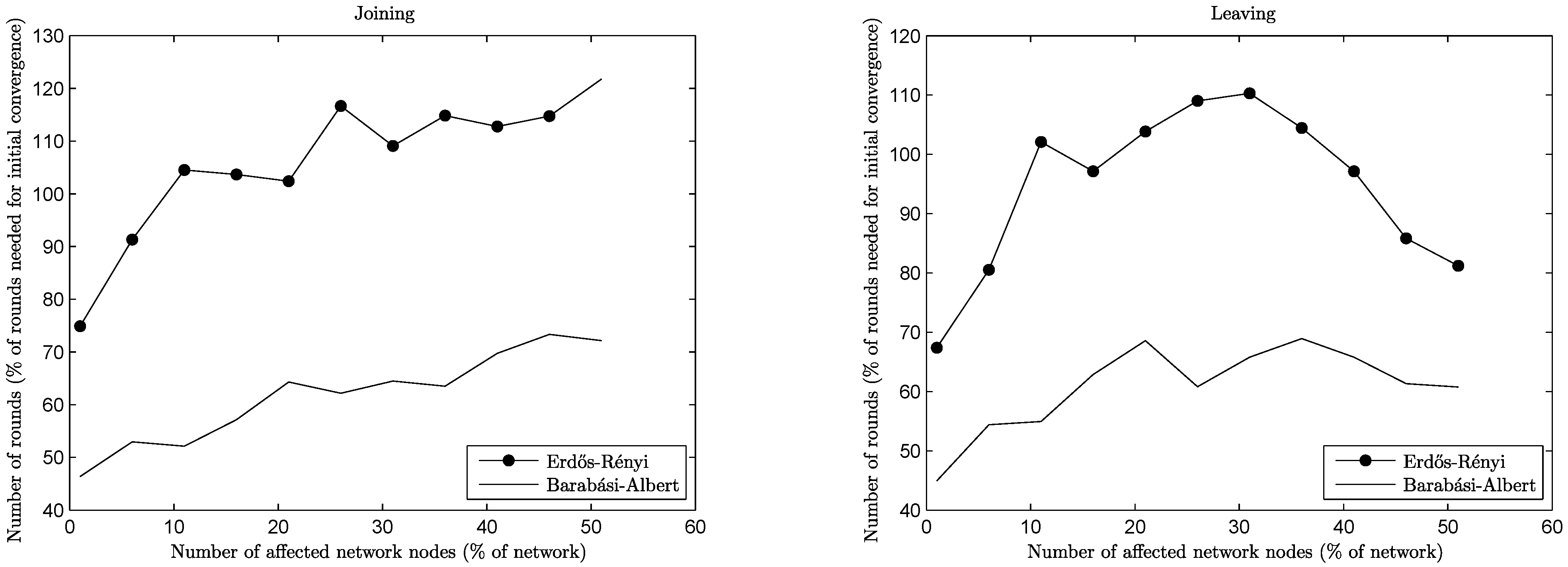
Likewise, the time needed for reconvergence can be seen in
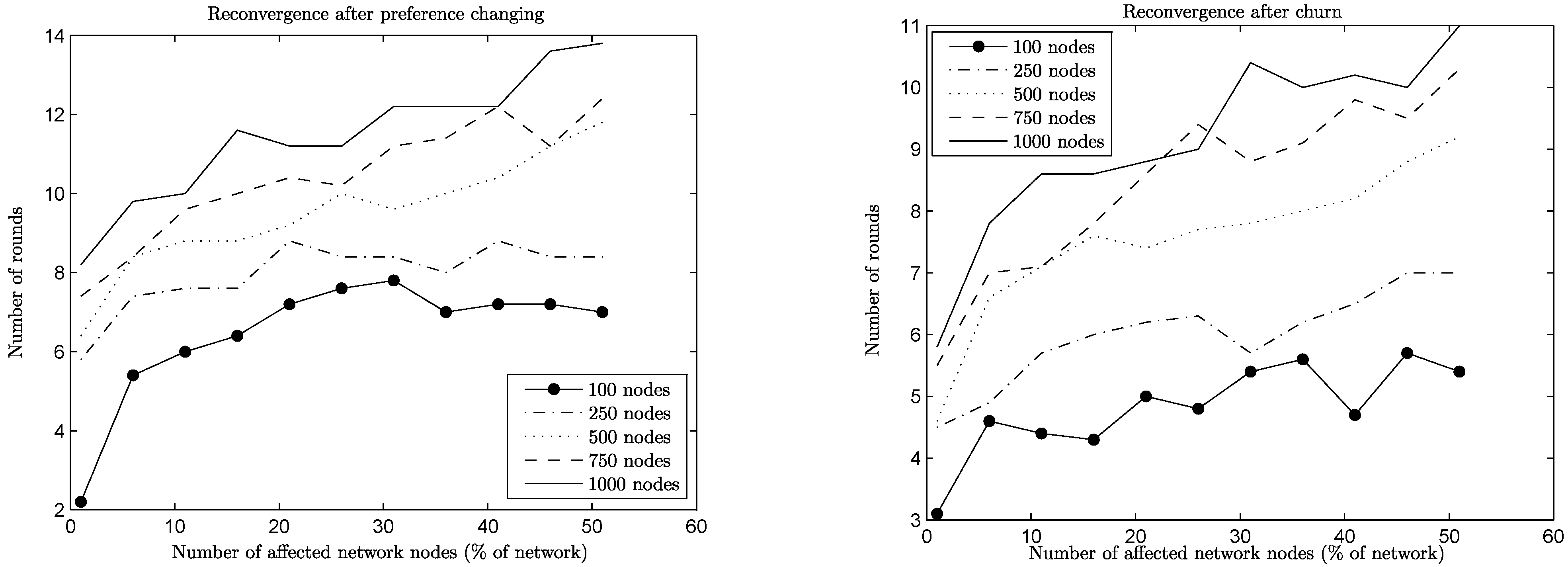
Figure 4 and
Figure 5, for networks of a size of 1,000 of both types and for the four types of operations under consideration. By focusing on low percentages of affected nodes (
i.e., up to 20% of the network size, which is a high volume of change), it is easy to see that reconvergence is obtained in most cases for a
fraction of the rounds needed for initial convergence. For join and leave operations, reconvergence is expressed not in rounds, but in relation to the convergence time, since network sizes change significantly. Note here that this extreme change in network sizes leads in some cases to percentages greater than 100%,
i.e., more rounds are needed for the reconvergence than for the initial convergence. For the preference change and churn operations, this is not the case: the network size remains the same, either because no node joins or leaves (preference change case) or the amount of nodes joining and leaving is the same (churn case), and the reconvergence time is expressed in rounds.
Figure 4.
Reconvergence speed per operation, joins/leaves, n = 1, 000.
Figure 4.
Reconvergence speed per operation, joins/leaves, n = 1, 000.
In the case of join operations, nodes arrive at the network and want to join the already established equilibrium of connections by being more attractive choices for some of the nodes with whom they are neighbors. This creates cascade effects of nodes rejecting old connections in favor of the newcomers, the rejected nodes trying to repair their lost connections, and so on. Naturally, the more nodes wanting to join the network, the bigger upheaval is created. A similar effect is generated during leave operations, where previously rejected nodes suddenly become attractive choices for nodes that were left behind by departing nodes. Note here that the BA networks reconverge much faster than the corresponding ER networks in the case of join operations. This happens because new nodes (being of a low degree) connect preferentially to relatively few high degree nodes, limiting the extension of the upheaval in the network. In the case of leave operations, the same behavior poses a challenge, since departing nodes may happen to be of a high degree themselves, leaving behind a lot of low degree nodes to repair their connections. Notice though that in both cases (ER or BA networks), when a substantial percentage of the network departs (i.e., above 35%), the remaining nodes repair their connections much more easily, since they have more unformed connections than established ones.
Preference change affects both network types in the same way: a node that changes preferences destroys some connections, creating waves of changes in its neighborhood. For the case of BA networks, it may happen that a node changing preferences is a high degree one, causing a lot of nodes to repair their connections. However, this effect dies off quickly, since most of its neighbors are of a low degree, leading to an overall performance similar to the ER case.
The two network types show their differences more prominently under churn (
Figure 5). For the ER networks, a joining node under churn can be seen as a “reincarnation” of a leaving node with all its previous connections dropped and its preferences changed, since both of them have comparable node degrees. However, the churn operation is detrimental for the BA network, since the joining nodes are of a low degree and the departing ones of a potentially much higher degree. As a result, the degree distribution itself is changing, leading to higher reconvergence times (
cf. join operation). This phenomenon can be seen more clearly when looking at networks of different sizes (
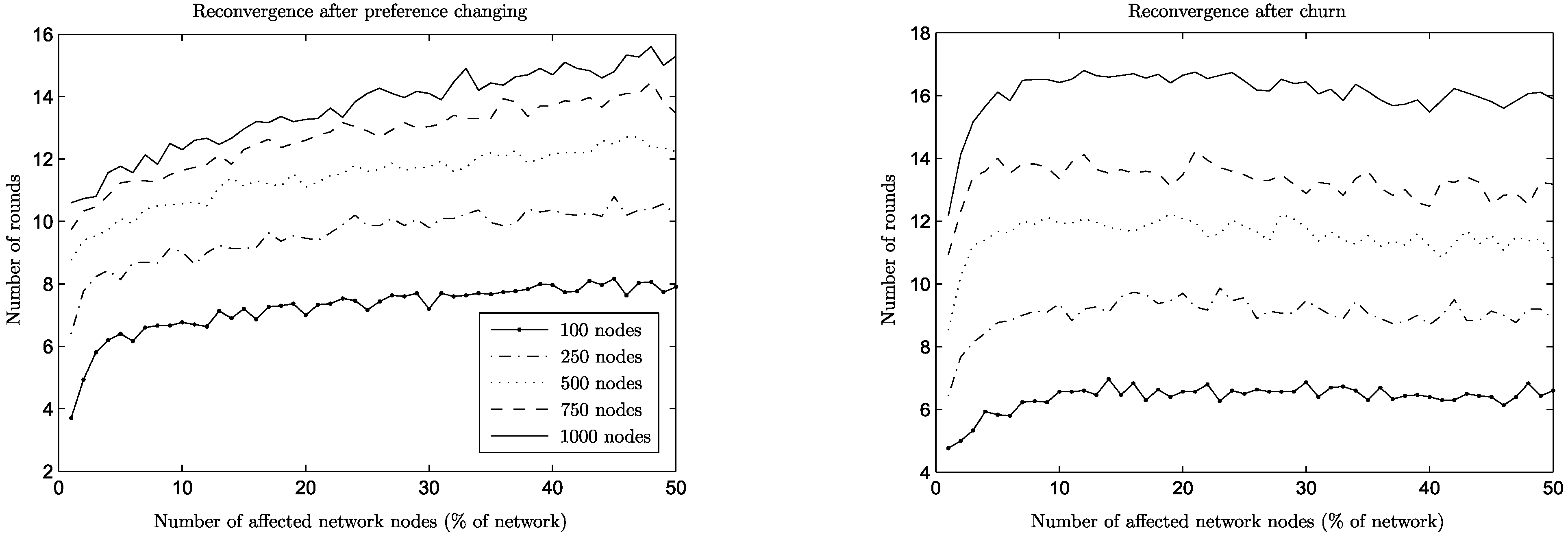
Figure 6): high churn for small networks is not particularly problematic (small slope on the graph for 100 nodes), since degree variation is limited, but for networks of a size of 1,000 it is quite detrimental, leading to higher reconvergence times (high slope on the graph for 1,000 nodes).
Figure 5.
Reconvergence speed per operation, preference change/churn, n = 1, 000.
Figure 5.
Reconvergence speed per operation, preference change/churn, n = 1, 000.
Figure 6.
Reconvergence speed for preference change and churn (Barabási–Albert).
Figure 6.
Reconvergence speed for preference change and churn (Barabási–Albert).
In both cases, though, by comparing the churn and preference change graphs in
Figure 5, it is easy to see that, somewhat counterintuitively, it takes progressively more time for the A
daptiveLID algorithm to reconverge when more nodes change preferences, but the reconvergence time stays more or less the same even for high values of churn, or it is consistently lower than preference change, as is the case in BA networks.
Figure 6 and
Figure 7 show this phenomenon in more detail for all network sizes.
Figure 7.
Reconvergence speed for preference change and churn (Erdős–Rényi).
Figure 7.
Reconvergence speed for preference change and churn (Erdős–Rényi).
The reason behind this behavior is that in churn situations, there are more parallel events taking place: a new, joining node that replaces a leaving one starts as an empty slate and sends an amount of PROP messages equal to the desired number of connections. On the other hand, a node that changes preferences might need to repair only some of its connections (which are now suboptimal) by sending appropriate PROP messages. However, in both cases, some responding nodes might decline, which will lead to additional PROP messages to be sent, and so on, until the issuing nodes are satisfied or no available nodes are left.
One may even wish to compare the two situations from the point of view of what is a desirable action by a node who changes preferences: to improve existing connections or to perform a leave and come back (thus contributing to churn). This is especially meaningful in the case of ER networks, since for BA networks churn is consistently cheaper in any case, due to their special structure and the parallelism mentioned above. In the case of ER networks, comparing the reconvergence times of the two situations, churn has the advantage over preference change in high values. This is only natural, since in that case more nodes start with no connections and all possibilities are explored in parallel. In contrast, having high values of preference change means that more nodes want to repair their connections, but other nodes have already connections that they want to maintain, leading to longer times of reconvergence. It could be useful in practical terms if there were a mechanism able to detect a high volume of preference changes in the network and to enforce a policy of pseudo-churn, with nodes dropping all connections when changing preferences. However, as is shown below, the amount of satisfaction under churn is far less than the satisfaction under preference change before reconvergence, which is a significant argument in favor of improving connections instead of dropping them and starting again.
6.4. Satisfaction
The mean satisfaction in the network achieved by both algorithms for a variety of network sizes can be found in
Figure 8, along with the values of minimum and maximum satisfaction in the network. Note that satisfaction is slightly lower in the case of BA networks, due to differences in topology (
i.e., minimum satisfaction is lower, due to the large amount of low degree nodes), but it follows the same behavior as in the ER case. It is easy to see that the algorithms achieve consistently high satisfaction values, which are also increasing as network sizes increase. Of particular interest is that: (a) the minimum satisfaction in the network is being increased, also, meaning that individual nodes enjoy high levels of satisfaction, too, implying asymptotically improved
fairness properties, as well; and (b) the minimum satisfaction does not significantly affect the mean satisfaction, which implies that the number of nodes having low satisfaction is consistently very low compared to the size of the network.
Figure 8.
Satisfaction per network size.
Figure 8.
Satisfaction per network size.
Even though the reconvergence results showed that the A
daptiveLID algorithm can efficiently repair its solution once churn stops, it is interesting to see the levels of achieved satisfaction while churn is in progress. The relative satisfaction for ER networks under churn (to the one achieved before churn starts) can be found in
Figure 9: the different graphs from top to bottom correspond to the relative satisfaction when churn affects 5% to 50% of the network’s nodes (in steps of 5%), for a network of 100 nodes. It is obvious that the amount of satisfaction achieved remains fairly constant during churn and depends greatly on the amount of churn. However, even though churn is an intense operation, it is possible to retain a significant percentage of the original satisfaction, even for churn as high as 50% (
i.e., when half of the network is changing at every round).
Figure 9.
Satisfaction while churn is in progress, affecting 5% to 50% of the network’s nodes (in steps of 5%, top to bottom).
Figure 9.
Satisfaction while churn is in progress, affecting 5% to 50% of the network’s nodes (in steps of 5%, top to bottom).
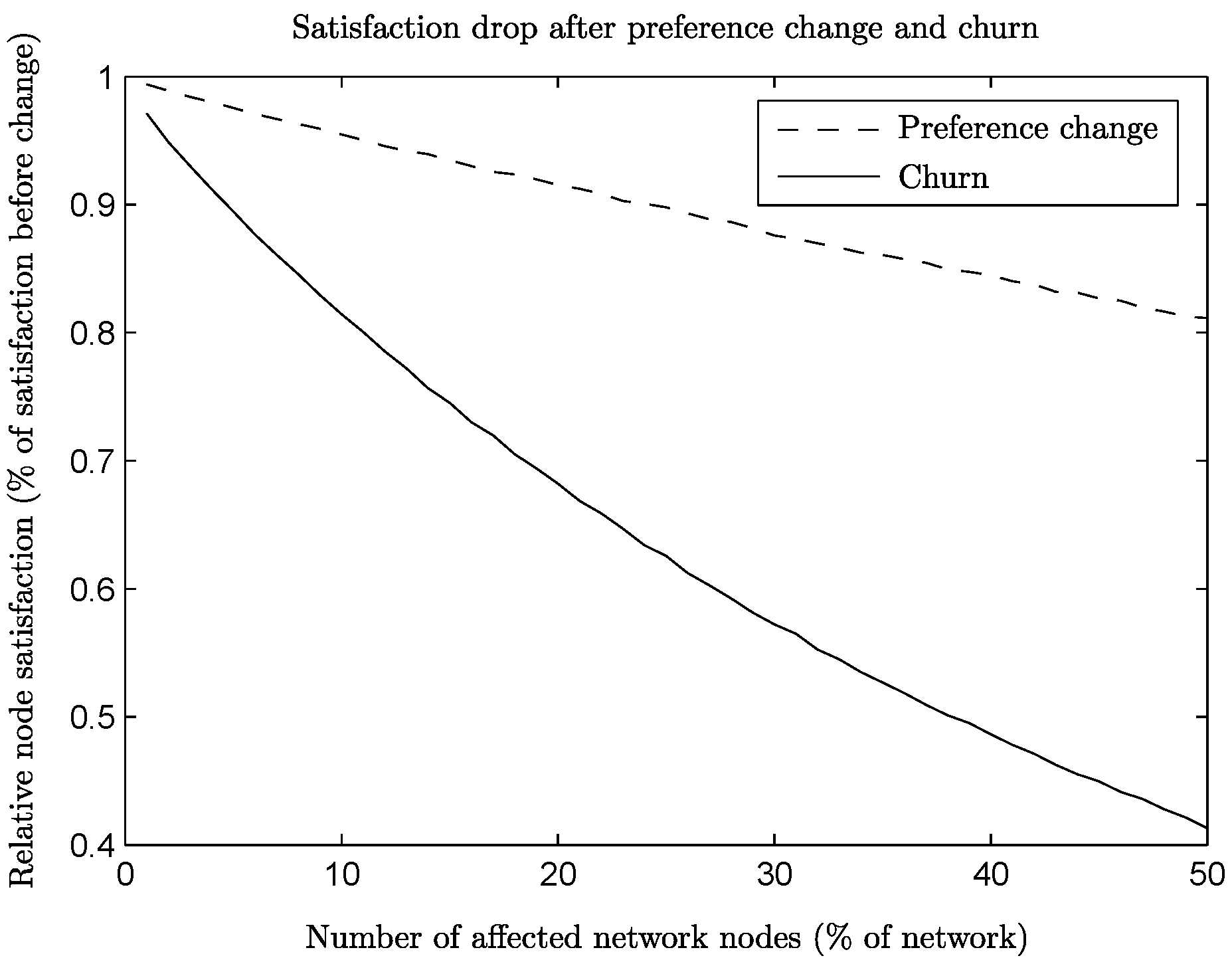
On the other hand, the satisfaction drop is significant compared to the one caused by preference change.
Figure 10 shows the relative satisfaction for both preference change and churn on ER networks, right after the change happens, for various amounts of affected nodes, supporting our argument in favor of improving connections instead of rebuilding them from the beginning.
Figure 10.
Satisfaction right after preference change or churn per amount of affected nodes.
Figure 10.
Satisfaction right after preference change or churn per amount of affected nodes.
7. Discussion
Locality Regarding the convergence complexity of the proposed algorithms, note that they achieve guaranteed approximation using only local information, and there is a well-known trade-off (as shown in [
13]) between the amount of local information and the quality of the global solution for matching problems. In addition, by arguing as in the classic Chandy and Misra [
17] Drinking Philosophers algorithm, we have the following:
Observation 2 Following the main argument of the classic Chandy and Misra [17] Drinking Philosophers algorithm, the convergence complexity is bounded by the longest increasing edge weight path in the network. Symmetry Breaking The locally unique edge weights are assumed as a means to make sure that there are no cyclic dependencies. There may be other ways to break symmetry and perhaps achieve higher parallelism; we expect that it can be possible to build further on this paper’s results, e.g., also via working with other, more elaborate algorithms for standard weighted matching as a starting point.
Other Related Work In general, matching is a quite well-studied problem in various contexts (e.g., [
18]). In the simplest forms of matching, the maximum cardinality matching and the maximum weighted matching problems, the aim is to find a subset of edges in which no pair of them shares a common endpoint and which includes as many edges as possible or exhibits the maximum sum of edge weights (if they exist), respectively. Other popular variations, such as the stable marriages/roommates problems, assume that nodes have preference lists regarding their potential partner nodes and prefer to be matched to the ones of higher ranking in their preference list. In all of the above cases, the literature usually assumes a one-to-one matching of nodes, but even less studied variations of many-to-many connections appear to be solvable in polynomial time by centralized algorithms [
6,
12,
19,
20], with the exception of particularly difficult subcategories of the stable marriages and roommates problems [
1,
2,
3].
Of particular interest in distributed and overlay applications, it has been shown [
13] that exact solutions of even simple matching problems cannot be derived locally in a distributed manner, and there is significant research interest for distributed approximation algorithms [
8,
21,
22]. Prominent examples of this research area are the one-to-one weighted matching algorithms of Manne
et al. [
23] and Lotker
et al. [
21,
24], with the former having proven self-stabilization properties and the latter having variants that can handle joins and leavings of nodes. However, whether it is possible to extend these techniques to many-to-many matchings remains an open research question. On the other hand, Koufogiannakis
et al. [
25] proposed a randomized
δ-approximation distributed algorithm for maximum weighted b-matching in hypergraphs (with
δ = 2 for simple graphs); but it addresses only static graphs, and its elaborate nature makes its extension to support a dynamic setting non-trivial.
Additionally to the approaches above, there is an extensive research focus on many-to-many matchings with preferences [
4,
5,
7,
26]. First, Gai
et al. in [
4] proved that in the case of an acyclic preference system, there is always a stable configuration and also supplied examples of preference systems based on global or symmetric metrics. Mathieu in [
5] introduced the measure of node satisfaction as a metric aimed to describe the quality of the proposed solutions. Previously, Lee [
26] had used a similar
credit metric in order to optimize the proposed solutions from their heuristic algorithms. Other approaches regarding the treatment of preferences include the notion of popular matchings, which is a relaxation of a maximum cardinality matching and where the aim is to maximize the amount of nodes that prefer a given matching over any other [
27]. While particularly suitable for game theoretic studies, this approach does not offer a way to quantify the potential of possible connections and evaluate potential matchings. The algorithms proposed here are, to our knowledge, the first to address the b-matching with the preferences problem from an optimization-oriented perspective, suitable for overlay networks. Furthermore, they are the first to support dynamic operations for the same problem and offer convergence and approximation guarantees.
Proposal-Refusal Schemes In the literature, many of the algorithms for matching with preferences are inspired by the proposal-refusal algorithm of Gale and Shapley [
20]. Here, we also utilize the proposal-refusal scheme, but in order to address a different problem with unique characteristics: while the Gale–Shapley algorithm is focused on absolute stability, we aim at solving an optimization problem with the maximum possible satisfaction. For example, in the case of the Gale-Shapley algorithm, it is important to guarantee that no cycles exist, since, given the distributed nature of the algorithm, a reply may not be possible to be given immediately by a node to another node’s proposal. This is not necessary here, since any cycles in preference lists are broken by reducing the original problem to an acyclic weighted many-to-many matching, upon which the algorithm operates (cf. also Lemma 8). On the other hand, by focusing on optimization, we are able to develop both non-adaptive and adaptive variations of our algorithm in order to tolerate and work under changes in the underlying network (
cf. Lemma 10).
The best mate initiative described in [
5] has certain similarities to the way nodes propose connections to their neighbors according to the A
daptiveLID algorithm. In particular, according to the best mate initiative, a node knows at every moment which of its edges is the best blocking edge and chooses to propose to that neighbor. By contrast, according to the A
daptiveLID algorithm, a node proposes to its neighbors by descending order of ranking (related to their truncated satisfaction), but these edges might not be the best blocking edges at that point in time (
i.e., the neighbors might not reciprocate with a proposal of their own). However, by the termination of the A
daptiveLID algorithm, it is indeed the case that every node would be connected to the endpoints of the best blocking edges related to the truncated satisfaction metric. Finally, the A
daptiveLID algorithm needs only local information, does not utilize the notion of blocking pairs and can operate in a fully distributed setting.
Approximation In Theorem 3, we proved that the proposed distributed algorithm in both variations is a
-approximation algorithm for the maximizing satisfaction b-matching problem. This approximation breaks down into: (a)
-approximation between the original maximizing satisfaction b-matching problem and the modified version we are using (Theorem1); and (b)
-approximation of a distributed many-to-many weighted matching using the LID or A
daptiveLID algorithms (see proof of Theorem 3). The first of these approximations is due to the satisfaction estimation in Lemma 1, and there is no indication whether it is a tight bound or not. The second term is due to the specific approximation algorithm used to compute a many-to-many weighted matching, in this case, the simple distributed algorithm, LID of
Section 5, which is based on the one-to-one weighted matching algorithm found in [
8]. Although there is a rather limited choice of algorithms for distributed many-to-many weighted matchings, it may be possible to convert some algorithms, such as the ones in [
21,
24] mentioned above for the simple (one-to-one) weighted matching. However, even the conversion of state-of-the-art algorithms, such as these, may give an approximation factor of
; so, further improvement of this term is the subject of future research. At the same time, this conversion, depending on whether the instances of the one-to-one matching algorithms can be executed in parallel or have to be synchronized in rounds, may hold potential implications for the computational complexity, and this, too, is the subject of future research.
8. Conclusion
In this paper, we studied the distributed b-matching problem and suggested a novel modeling that focuses on optimization of connections instead of strict matching stability (as defined in [
12]). Following this modeling, we presented a distributed algorithm in two variants, an adaptive and a non-adaptive, which enables peers with preference lists to form an overlay network while collectively achieving a guaranteed level of quality for their requested connections. Each peer is free to form its preference list according to any suitability metric it chooses, based on, e.g., the peer’s distance, interests, recommendations, transaction history or available resources. We showed that both variations of the algorithm provably terminate and succeed in maximizing the total satisfaction in the overlay with guaranteed approximation using only local information. In addition, the A
daptiveLID variation is able to handle dynamicity,
i.e., joins/leaves of peers or changing preference lists.
Besides, an extensive experimental study of the proposed algorithms encompasses a variety of scenarios, including ones that put the adaptive algorithm under heavy stress and that have been previously used in the literature to simulate network attacks. In these scenarios, the adaptive algorithm succeeds in maintaining a reduced but steady level of network service while under attack and resumes to normal service levels after the attack stops. Furthermore, both algorithms show attractive properties with respect to the satisfaction they can achieve and the convergence time (and hence overhead) needed. Regarding changes in particular, the experiments clearly strengthen the argument that it is preferable to improve connections and adapt to changes instead of rebuilding all the connections from the ground up.
To the best of our knowledge, the distributed algorithm presented here in both its adaptive and non-adaptive variations is the first method able to solve the b-matching with preferences problem with satisfaction and convergence guarantees. We expect that this contribution will be helpful for future work in the area, since the method can facilitate overlay construction with guarantees in a wide range of applications, from peer-to-peer resource sharing, to overlays in intelligent transportation systems and adaptive power grid environments. Finally, interesting paths of future research would be to develop variations of the proposed algorithm that can give minimum satisfaction guarantees individually to each collaborating peer or that can take into account scenarios in which malicious nodes actively try to disrupt the algorithm’s execution.