Sublinear Time Motif Discovery from Multiple Sequences
Abstract
:1. Introduction
2. Notations and the Model of Sequence Generation
3. Brief Introduction to the Algorithm
3.1. Algorithm
3.2. An Example
3.2.1.. Input Sequences
3.2.2.. Select Sample Points
3.2.3.. Collision Detection
3.2.4.. Improving the Boundaries
3.2.5.. Select Sample Points for the Sequences in
3.2.6.. Collision Detection Between with the Sequences in
3.2.7.. Improving the Motif Boundaries for the Sequences in
3.2.8.. Motif Boundaries for the Sequences in
3.2.9.. Extracting the Motif Regions
3.2.10.. Recovering Motif via Voting
3.3. Our Results
4. Algorithm Recover-Motif
4.1. Some Parameters
- i.
- Parameter x is selected to be 10. This parameter controls the failure probability of our algorithms to be at most .
- ii.
- The size of the alphabet is .
- iii.
- Select a constant to have inequality (1):
- iv.
- The constant is selected to satisfy:The existence of ϵ follows from inequality (1). The constant ϵ is used to control the mutation in the motif area. It is a part of parameter β defined in item (xiv) of this definition.
- v.
- Let . The constant, c, is used to simplify probabilistic bounds, which are derived from the applications of Chernoff bounds (see Corollary 18).
- vi.
- Define .
- vii.
- Define to be a large constant that, for all :
- viii.
- Select constant , such that:The existence of follows from , which is implied by inequality (2).
- ix.
- Select constant and constant positive integer v that are large enough, such that:
- x.
- Define , and:
- xi.
- Select constant , such that:
- xii.
- The maximal mutation rate, α, for the second algorithm (Theorem 4) and the third algorithm (Theorem 6) are selected as . Since the mutation rate of our sublinear time algorithm is bounded by , the maximal mutation rate α for the first algorithm (Theorem 2) is less than when n is large enough. We always assume that all mutation rates α in our three algorithms are in the range .
- xiii.
- Define . By inequality (10), the definition of and the fact that , we have:Inequality (11) implies . By inequality (6), we have that:
- xiv.
- Let . The parameter, β, controls the similarity of and the original motif, G (see Lemma 27).
- xv.
- Define .
- xvi.
- We define the following .The parameter, , used in Lemma 27 gives an upper bound of the probability that a -sequence, S, whose will not be similar enough to the original motif, G, according to the conditions in Lemma 27.
- xvii.
- Select constant , such that:
- xviii.
- Select constant , such that .
- xix.
- Select number , such that:Since only n is variable, we can make .
- xx.
- For a fixed , define .
4.2. Description of Algorithm Recover-Motif
- Two sequences, and , are weakly left matched if: (1) both and are at least ; and (2) for all integers i, , where v is defined in item (ix) in Definition 8.
- Two sequences, and , are left matched if: (1) ; (2) for ; and (3) for all integers i, .
- Two sequences, and , are weakly right matched if and are weakly left matched, where is the inverse sequence of .
- Two sequences, and , are right matched if and are left matched, where is the inverse sequence of .
- Two sequences, and , are matched if and are both left and right matched.
4.2.1.. Boundary-Phase of Algorithm Recover-Motif
4.2.2.. Extract-Phase of Algorithm Recover-Motif
4.2.3.. Voting-Phase
4.2.4.. Entire Algorithm Recover-Motif
5. Deterministic Algorithm
6. Analysis of the Algorithm
6.1. Review of Some Classical Results in Probability
- For a list of events, , .
- For two independent events, A and B, .
- For a random variable, Y, for all positive real numbers, t. This is called Markov inequality.
- i.
- and
- ii.
- .
6.2. Analysis of Boundary-Phase of Algorithm Recover-Motif
- i.
- if , then the probability that and are matched is (); and
- ii.
- the probability for is at most .
- i.
- With a probability of at most , a sequence, S, changes more than characters in its motif region, , with , where c is defined in item (v) in Definition 8.
- ii.
- With a probability of at most , a sequence, S, changes more than characters in its left motif region, , for some t with , where c is defined in item (v) in Definition 8.
- i.
- with a probability of at most ; is not in for .
- ii.
- with a probability of at most , is not in for .
- iii.
- Improve-Boundaries runs in time.
- A -sequence, S, misses its left boundary if .
- A -sequence, S, misses its right boundary if .
- i.
- A -sequence, S, contains a left half stable motif region, , if for all , where , and , as defined in Definition 8 and Section 2, respectively.
- ii.
- A -sequence, S, contains a right half stable motif region, , if for , where and .
- iii.
- A -sequence, S, contains a stable motif region, , satisfying the following conditions: (1) for ; (2) for ; and (3) the S motif region is both left and right half stable, where and .
- ;
- Scontains both a left half and a right half stable motif region and and (see Definition 8 for and v); and
- for each L with , if has and , then with a probability of at most , for , where Collision-Detection(, Point-Selection Point-Selection and Point-Selection.
- The rough boundaries for all sequences, , are computed via Collision-Detection and = Improve-Boundaries .
6.3. Analysis of Extract-Phase and Voting-Phase of Algorithm Recover-Motif
- Define to be the left part of the motif region, .
- Define to be the right part of the motif region, .
- i.
- Assume that and are fixed sequences of length . Let S be a -sequence with , and let be the number of characters of M that are not in the region of . Then, the probability is at most R that , where R is defined in (xv) of Definition 8.
- ii.
- The probability is at most that given a -sequence S, .

- i.
- If , and there are no more than () sequences, , with or , then the probability is at most that there are more than sequences, , with .
- ii.
- For arbitrary and , with a probability of at most , , where R is defined in Definition 8.
- Given two sequences, and , define:Match.
- For a sequence, S, define to be the , which is the leftmost subsequence of a length of in the motif region of S.
- For a sequence, S, define to be the , which is the rightmost subsequence of a length of in the motif region of S, where ;
- i.
- For each L with , with a probability of at most , or for , where Collision-Detection(, Point-Selection and Point-Selection.
- ii.
- For each L with , if has and , then with a probability of at most , for or , where Collision-Detection(, Point-Selection Point-Selection and Point-Selection .
- iii.
- The inequality holds for some constant , where is defined in Equation (13) and .
- iv.
- The inequality holds, where .
6.4. Deterministic Algorithm for an Mutation Rate
- i.
- with a probability of at most , the left rough boundary, , has at most distance from and the left rough boundary has at most distance from .
- ii.
- with a probability of at most , the right rough boundary, , has at most distance from and the right boundary of has at most distance from .
- i.
- Collision-Detection() takes time.
- ii.
- Point-Selection() selects positions in time.
- iii.
- in the algorithm Recover-Motif is no more than .
- iv.
- With a probability of at most , the algorithm Recover-Motif does not run in computational complexity .
6.5. Randomized Algorithms for Motif Detection
6.5.1.. Randomized Algorithm for an Mutation Rate
- i.
- with a probability of at most , the left rough boundary, , has at most distance from and the left rough boundary, , has at most distance from ;
- ii.
- with a probability of at most , the right rough boundary, , has at most distance from and the right boundary of has at most distance from .
- i.
- with a probability of at most , the left rough boundary, , has at most a distance from and the left rough boundary has at most a distance from ;
- ii.
- with a probability of at most , the right rough boundary, , has at most a distance from and the right boundary of has at most a distance from .
- i.
- With a probability of at most , there are no intervals, from and from , such that: (1) is at least ; (2) the left boundary of has at most a distance from ; (3) the left boundary of has at most a distance from ; and (4) there is a collision between the sampled positions in and .
- ii.
- With a probability pf at most , there are no intervals, from and from , such that: (1) is at least ; (2) the right boundary of has at most a distance from ; (3) the right boundary of has at most a distance from ; and (4) there is a collision between the sampled positions in and .
- i.
- Collision-Detection() takes time.
- ii.
- Point-Selection() selects positions in time if .
- iii.
- Point-Selection() selects positions in time if .
- iv.
- in the algorithm Recover-Motif is no more than .
- v.
- With a probability of at most , the algorithm Recover-Motif does not stop in time.
6.5.2.. Sublinear Time Algorithm for a Mutation Rate
- i.
- with a probability of at most , the left rough boundary, , has at most a distance from and the left rough boundary, , has at most a distance from .
- ii.
- with a probability of at most , the right rough boundary, , has at most a distance from and the right boundary of has at most a distance from .
- i.
- with a probability of at most , the left rough boundary, , has at most a distance from and the left rough boundary, , has at most a distance from .
- ii.
- With a probability of at most , the right rough boundary, , has at most a distance from and the right boundary of has at most a distance from .
- i.
- With a probability of at most , there are no intervals, from and from , such that: (1) is at least ; (2) the left boundary of has at most a distance from ; (3) the left boundary of has at most a distance from ; and (4) there is a collision between the sampled positions in and .
- ii.
- with a probability of at most , there are no intervals, from and from , such that: (1) is at least ; (2) the right boundary of has at most a distance from ; (3) the right boundary of has at most a distance from ; and (4) there is a collision between the sampled positions in and .
- i.
- Collision-Detection() takes time.
- ii.
- Point-Selection() selects positions in time if .
- iii.
- Point-Selection() selects positions in time if .
- iv.
- in the algorithm Recover-Motif is no more than .
- v.
- With a probability of at most , the algorithm Recover-Motif does not stop in time.
6.6. Experiments on Simulated Datasets
6.7. Experiments
| Set 1 | 20 | 600 | 15 | 60 | 100 | 98 |
| Set 2 | 15 | 600 | 15 | 10 | 100 | 18 |
| Set 3 | 20 | 600 | 12 | 15 | 100 | 22 |
| N | 6 | 9 | 6 | 15 | 5 |
| Our Algorithm | 10 | 8 | 4 | 45 | 5 |
| Gibbs | 8 | 51 | 5 | 202 | 7 |
| MEME | 8 | 15 | 10 | 32 | 3 |
| InfoGibbs | 9 | 21 | 5 | 46 | 9 |
| Our Algorithm | 1.67 | 0.89 | 0.67 | 3 | 1 |
| Gibbs | 1.33 | 5.6 | 0.83 | 13.46 | 1.4 |
| MEME | 1.33 | 1.67 | 1.67 | 2.13 | 0.6 |
| InfoGibbs | 1.5 | 2.33 | 0.83 | 3.06 | 1.8 |
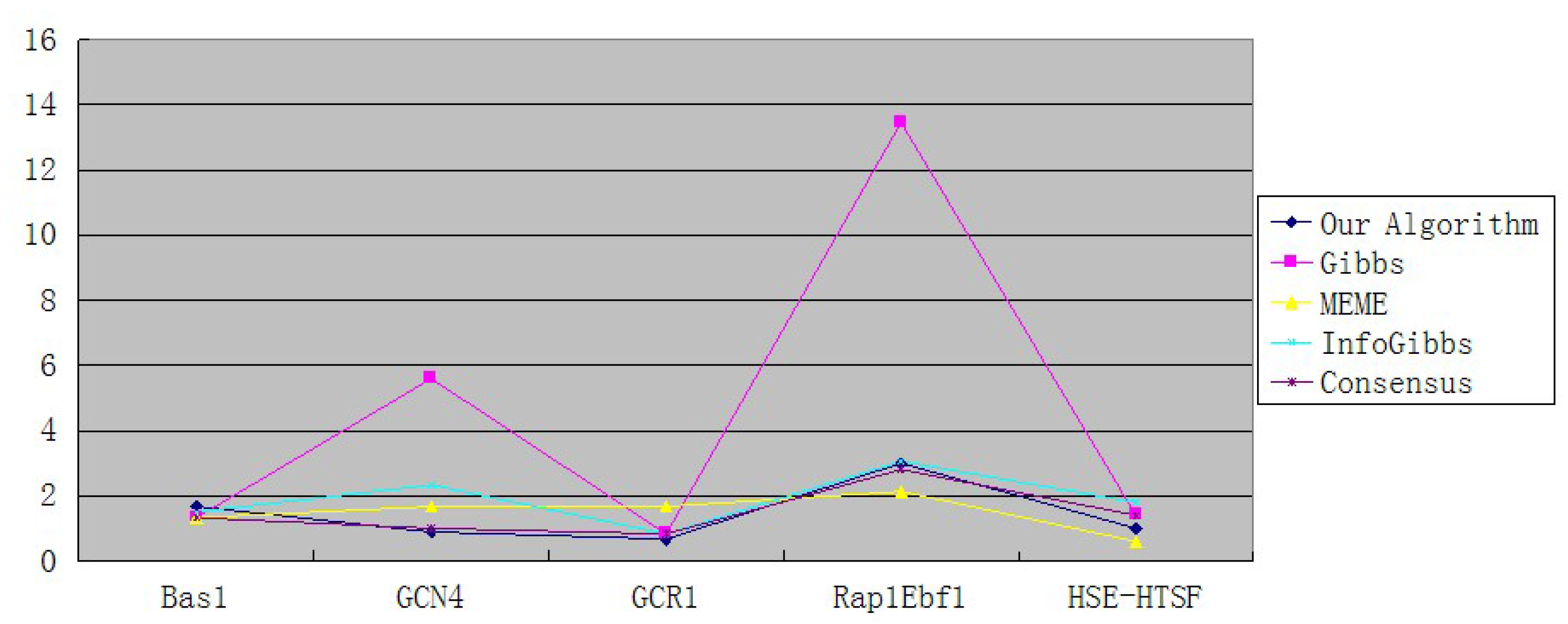
6.8. Conclusions
6.9. Future Works
Acknowledgments
Conflicts of Interest
References
- Frances, M.; Litman, A. On covering problems of codes. Theor. Comput. Sci. 1997, 30, 113–119. [Google Scholar] [CrossRef]
- Ga̧sieniec, L.; Jansson, J.; Lingas, A. Efficient Approximation Algorithms for the Hamming Center Problem. In Proceedings of the 10th Annual ACM-SIAM Symposium on Discrete Algorithms, Baltimore, MD, USA, 17–19 January 1999; pp. S905–S906.
- Stormo, G.; Hartzell, G., III. Identifying protein-binding sites from unaligned DNA fragments. Proc. Natl. Acad. Sci. USA 1991, 88, 5699–5703. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, C.; Reilly, A. An expectation maximization (EM) algorithm for the identification and characterization of common sites in unaligned biopolymer sequences. Proteins 1990, 7, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Hertz, G.; Stormo, G. Identification of Consensus Patterns in Unaligned DNA and Protein Sequences: A Large-Deviation Statistical Basis for Penalizing Gaps. In Proceedings of the 3rd International Conference on Bioinformatics and Genome Research, Tallahassee, USA, 1–4 June 1994; pp. 201–216.
- Stormo, G. Consensus patterns in DNA. In Molecular Evolution: Computer Analysis of Protein and Nucleic Acid Sequences; Doolitle, R.F., Ed.. Methods Enzymol. 1990, 183, 211–221. [Google Scholar]
- Lanctot, J.K.; Li, M.; Ma, B.; Wang, L.; Zhang, L. Distinguishing string selection problems. Inf. Comput. 2003, 185, 41–55. [Google Scholar] [CrossRef]
- Lucas, K.; Busch, M.; Mossinger, S.; Thompson, J. An improved microcomputer program for finding gene- or gene family-specific oligonucleotides suitable as primers for polymerase chain reactions or as probes. Comput. Appl. Biosci. 1991, 7, 525–529. [Google Scholar] [CrossRef] [PubMed]
- Dopazo, J.; Rodríguez, A.; Sáiz, J.C.; Sobrino, F. Design of primers for PCR amplification of highly variable genomes. Comput. Appl. Biosci. 1993, 9, 123–125. [Google Scholar] [PubMed]
- Proutski, V.; Holme, E.C. Primer master: A new program for the design and analysis of PCR primers. Comput. Appl. Biosci. 1996, 12, 253–255. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Ma, B.; Wang, L. On The Closest String and Substring Problems. J. ACM 2002, 49, 157–171. [Google Scholar] [CrossRef]
- Li, M.; Ma, B.; Wang, L. Finding Similar Regions in Many Strings. In Proceedings of the 31st Annual ACM Symposium on Theory of Computing, Atlanta, GA, USA, 1–4 May 1999; pp. 473–482.
- Pevzner, P.; Sze, S. Combinatorial Approaches to Finding Subtle Signals in DNA Sequences. In Proceedings of the 8th International Conference on Intelligent Systems for Molecular Biology, Toronto, ON, Canada, 19–23 July 2000; pp. 269–278.
- Keich, U.; Pevzner, P. Finding motifs in the twilight zone. Bioinformatics 2002, 18, 1374–1381. [Google Scholar] [CrossRef] [PubMed]
- Keich, U.; Pevzner, P. Subtle motifs: Defining the limits of motif finding algorithms. Bioinformatics 2002, 18, 1382–1390. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Dong, L. Randomized algorithms for motif detection. J. Bioinform. Comput. Biol. 2005, 3, 1039–1052. [Google Scholar] [CrossRef] [PubMed]
- Chin, F.; Leung, H. Voting Algorithms for Discovering Long Motifs. In Proceedings of the 3rd Asia-Pacific Bioinformatics Conference, Singapore, 17–21 January 2005; pp. 261–272.
- Gusfield, D. Algorithms on Strings, Trees, and Sequences; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Fu, B.; Kao, M.Y.; Wang, L. Probabilistic analysis of a motif discovery algorithm for multiple sequences. SIAM J. Discret. Math. 2009, 23, 1715–173. [Google Scholar] [CrossRef]
- Fu, B.; Kao, M.Y.; Wang, L. Discovering almost any hidden motif from multiple sequences. ACM Transactions on Algorithms 2011, 7(2), 26. [Google Scholar] [CrossRef]
- Liu, X.; Ma, B.; Wang, L. Voting Algorithms for the Motif Problem. In Proceedings of Computational Systems Bioinformatics Conference, (CSB’08), Stanford, CA, USA, 26–29 August 2008; pp. 37–47.
- Motwani, R.; Raghavan, P. Randomized Algorithms; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from complete data vis the EM algorithm. J. R. Stat. Soc. 1977, 39, 1–38. [Google Scholar]
- D’haesler, P. How does DNA sequence motif discovery work? Nat. Biotechnol. 2006, 24, 959–961. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, C.; Altschul, S.; Boguski, M.; Liu, J.; Neuwald, A.; Wootton, J. Detecting subtle sequence signals: A gibbs sampling strategy for multiple alignment. Science 1993, 262, 262–5131. [Google Scholar] [CrossRef]
- Sandve, G.K.K.; Abul, O.; Drabløs, F. Compo: Composite motif discovery using discrete models. BMC Bioinform. 2008, 9. [Google Scholar] [CrossRef] [PubMed]
- Homann, O.; Johnson, A. MochiView: Versatile software for genome browsing and DNA motif analysis. BMC Biol. 2010, 8. [Google Scholar] [CrossRef] [PubMed]
- Sinha, S.; Blanchette, M.; Tompa, M. PhyME: A probabilistic algorithm for finding motifs in sets of orthologous sequences. BMC Bioinform. 2004, 5. [Google Scholar] [CrossRef]
- Larsson, E.; Lindahl, P.; Mostad, P. HeliCis: A DNA motif discovery tool for colocalized motif pairs with periodic spacing. BMC Bioinform. 2007, 8. [Google Scholar] [CrossRef] [PubMed]
- Romer, K.; Kayombya, G.R.; Fraenkel, E. WebMOTIFS: Automated discovery, filtering and scoring of DNA sequence motifs using multiple programs and Bayesian approaches. Nucleic Acids Res. 2007, 35, W217–W220. [Google Scholar] [CrossRef] [PubMed]
- Baker, H. GCR1 of Saccharomyces cerevisiae encodes a DNA binding protein whose binding is abolished by mutations in the CTTCC sequence motif. Proc. Natl. Acad. Sci. USA 1991, 88, 9443–9447. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fu, B.; Fu, Y.; Xue, Y. Sublinear Time Motif Discovery from Multiple Sequences. Algorithms 2013, 6, 636-677. https://doi.org/10.3390/a6040636
Fu B, Fu Y, Xue Y. Sublinear Time Motif Discovery from Multiple Sequences. Algorithms. 2013; 6(4):636-677. https://doi.org/10.3390/a6040636
Chicago/Turabian StyleFu, Bin, Yunhui Fu, and Yuan Xue. 2013. "Sublinear Time Motif Discovery from Multiple Sequences" Algorithms 6, no. 4: 636-677. https://doi.org/10.3390/a6040636
APA StyleFu, B., Fu, Y., & Xue, Y. (2013). Sublinear Time Motif Discovery from Multiple Sequences. Algorithms, 6(4), 636-677. https://doi.org/10.3390/a6040636




