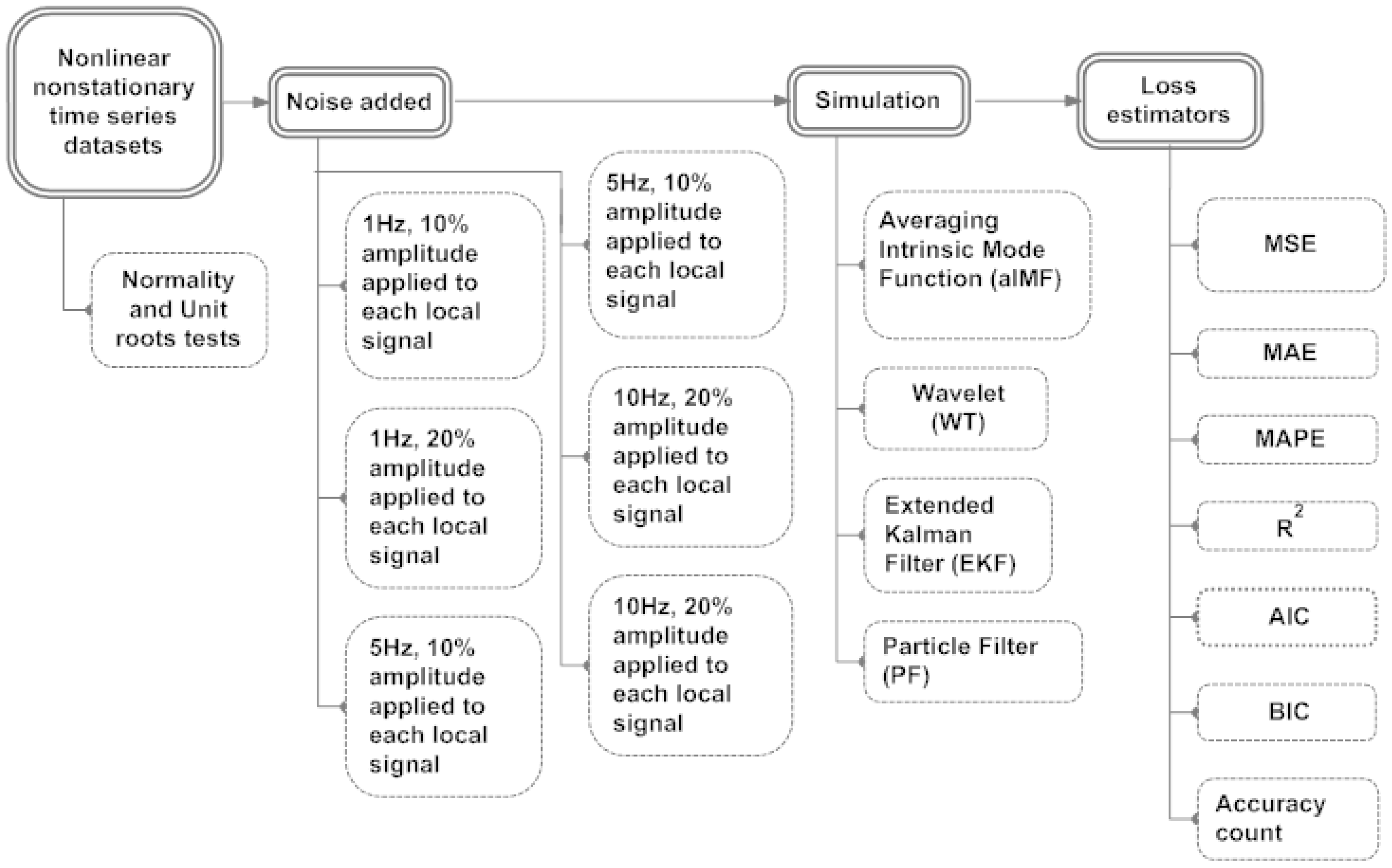
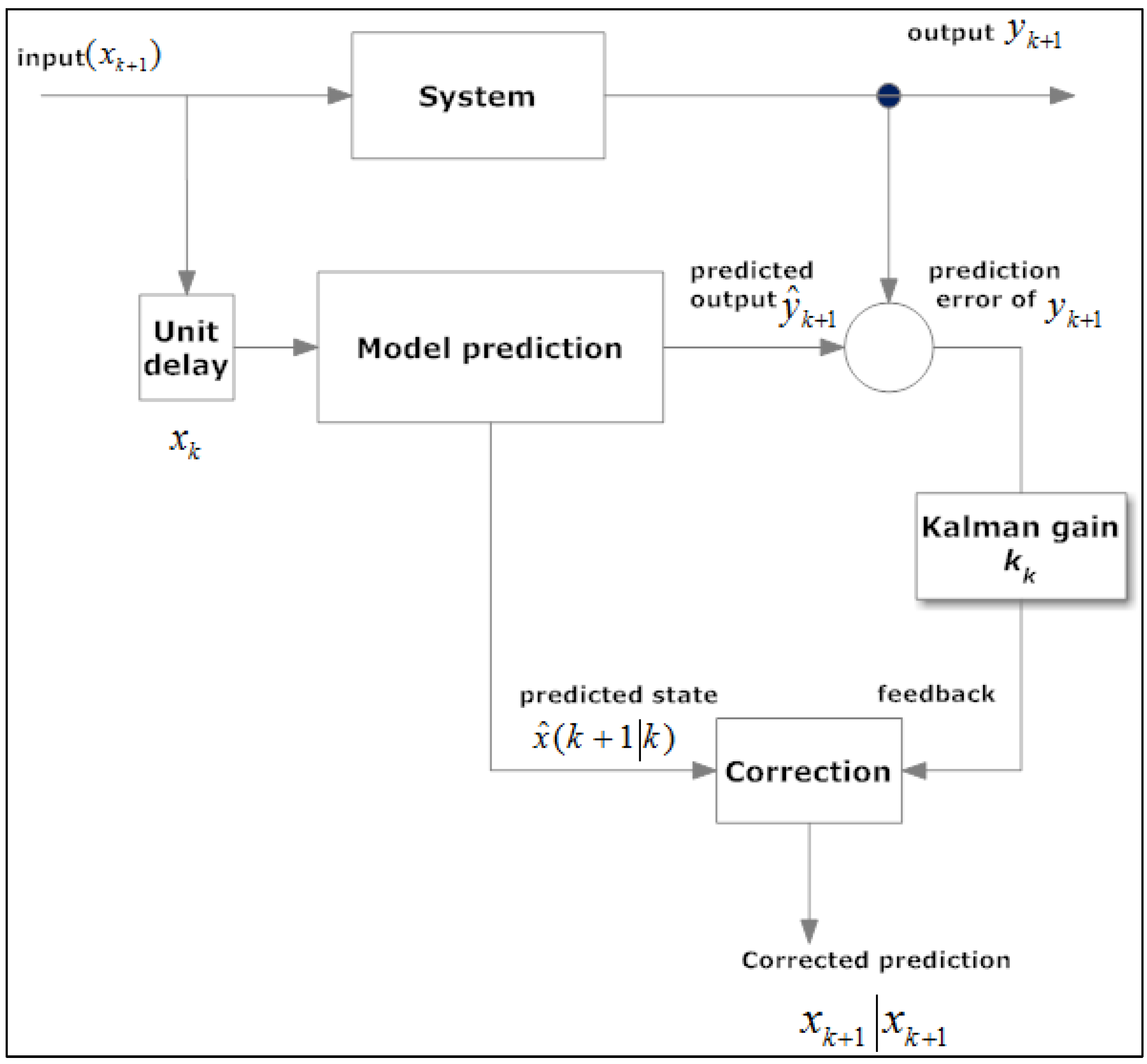
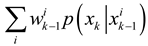The aim of this section is to compare the performances of all the proposed digital filters and recommend the best fit filter. We use R Programming to simulate the original datasets that has a suite of noise added to it. After completing the simulations, we applied a variety of loss estimations,
i.e., Mean Square Error (MSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), R
2, AIC, BIC and Accuracy count which is a sum of the upward and downward movements of all the underlying local signals after they had transited the reversion points. See flowchart of simulation and results in
Figure 5.
Figure 5.
Flowchart shows simulation and results of aIMF, WT, EKF and PF.
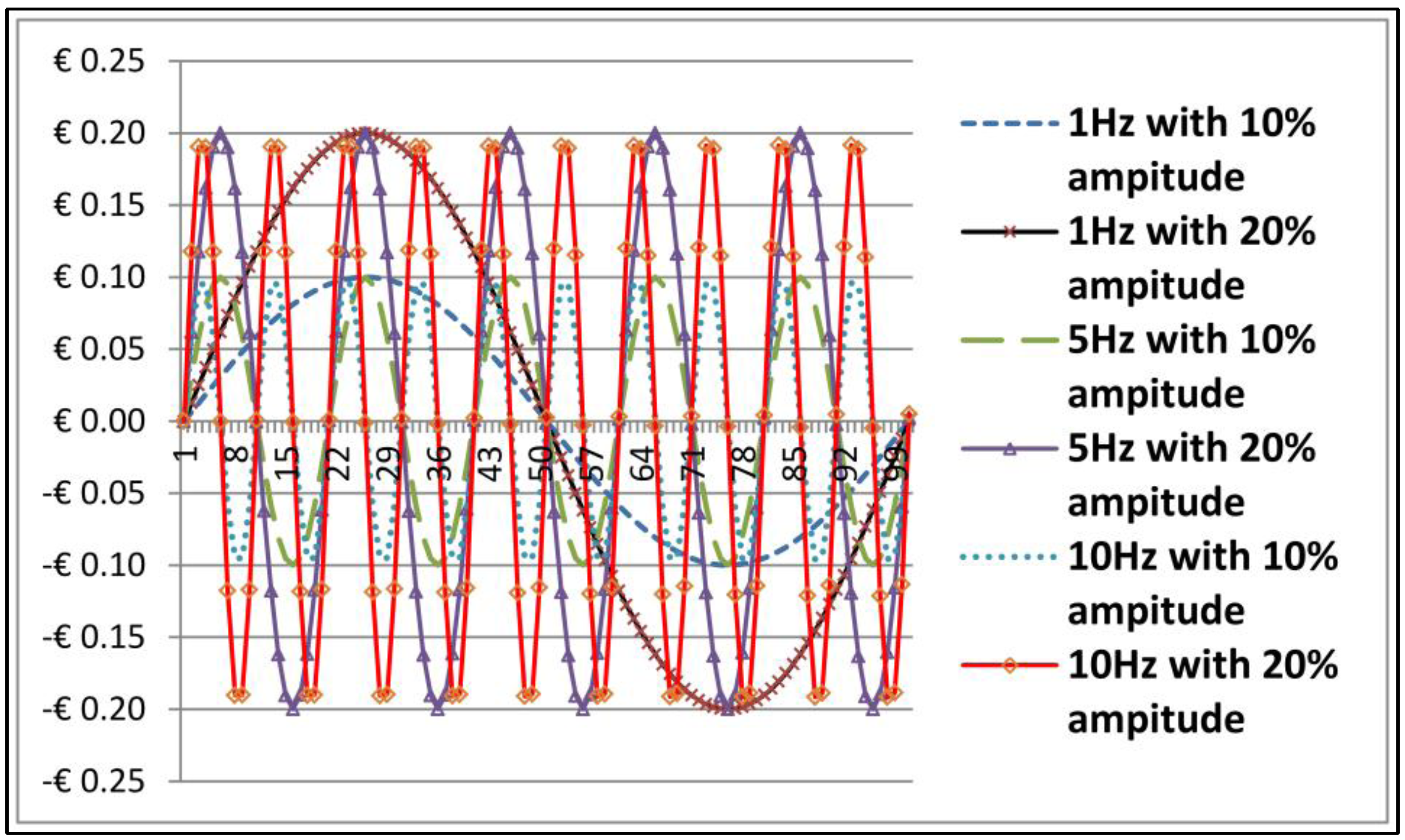
3.1. Adding White-Gaussian Noise
We created six sets of sine wave which is
i.i.d. N(0,
) for the frequencies in Hz of 1, 5 and 10 with the amplitude of 10% and 20% of the original datasets, at 100% random distribution. Those parameters were applied to the exchange rates data points
xk(
t) in time series. The distribution of these added noise are similar to white-Gaussian noise as shown in
Figure 6.
Figure 6.
Six sets of sine wave as frequencies in Hz of 1, 5 and 10 with the amplitude of 10% and 20% of exchange rates.
Figure 6.
Six sets of sine wave as frequencies in Hz of 1, 5 and 10 with the amplitude of 10% and 20% of exchange rates.
For ease of presentation,
Figure 6 shows the
x-axis representing just 100 data points out of the total 2322 data points in the time series, whereas the
y-axis is representing the amplitude. We introduced a variety of testing methods, namely; (a) Anderson-Darling, Lilliefors (Kolmogorov-Smirnov) and Pearson chi-square for nonlinear test; and (b) Augmented Dickey-Fuller and Elliott-Rothenberg-Stock for nonstationary test. Referring to Equation (23)
xk represented datasets, EUR-USD, exchange rates, in which their nonlinear and nonstationary characteristics were verified by all the testing methods; and
wk represented the six sets of sine wave created in
Section 3.1. The equation which used to add white Gaussian noise to the original datasets can be rearranged as follows
where
xkg(
t) is the original signal with the noise,
xk(
t) is the original datasets and
is the added noise with
i.i.d. N(0,1) at section of various frequencies in Hz of 1, 5 and 10 with 100% of random distribution of
xk(
t). To verify that the Equation (43) is nonlinear equation, we tested the
xkg(
t) with the different parameters of the noise added. As per the results, all of the
p-value generated by all the testing methods mentioned earlier were less than 0.05. This served to imply that the characteristics of
xkg(
t) was nonlinear and nonstationary. Later,
xkg(
t) was used as input signal to estimate the performance of the following algorithms: (i) aIMF, (ii) WT, (iii) EKF and (iv) PF.
3.2. Simulation and Performance Measurements of the aIMF Algorithm
The objective of this section is to measure the performance of the aIMF algorithm compared with the original datasets, i.e., the EUR-USD exchange rates. To test the performance of the proposed aIMF algorithm when filtering the original signals with white Gaussian noise, we applied a variety of loss estimators, i.e., MSE, MAE, MAPE, R2 and Accuracy count.
At the beginning, we tested the five exchange rates
i.e., EUR-USD with Normality and Unit Root tests and found that they are nonlinear and nonstationary time series. Next, we simulated the aIMF algorithm using an R Programming that comprised C++ scripts, which followed the logic in
Section 2.2.
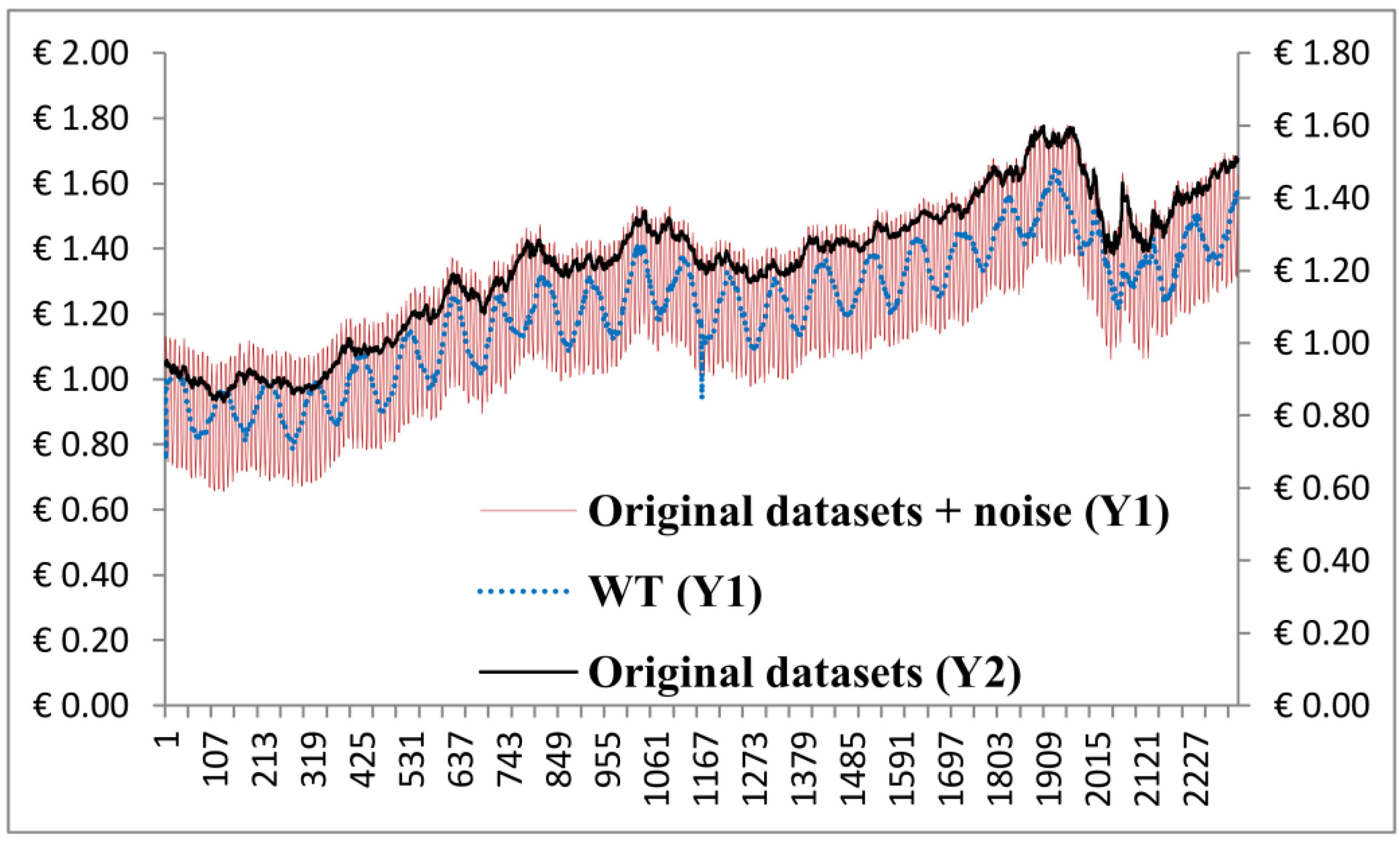
Figure 7 shows that we produced a new signal, which was filtered by the aIMF algorithm.
Figure 7.
Plots of the original datasets, original datasets + noise, and the aIMF algorithm.
Figure 7.
Plots of the original datasets, original datasets + noise, and the aIMF algorithm.
Having simulated the aIMF algorithm with all noise parameters mentioned in the early of
Section 3.1, the results are in the same magnitude and directions. To simplify the graph presentation, we selected the
x-axis representing the data points in the time series of overall data range, and two sets of
y-axis representing the original datasets, EUR-USD exchange rates (Y2) and the original datasets + noise (Y1) of which shows only the noise’s plot of 1 Hz at 10% amplitude (Y1) with 100% random distribution. We analysed the plots and found that the aIMF curve resided within the curve of “the original datasets + noise”. The trend of those three plots was in the same direction. In terms of estimation,
Table 1,
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6 indicate that all loss estimators, namely; MSE, MAE, and MAPE are relatively low ranging from 0.00296–0.00596, 0.04838–0.06618 and 4.08815–5.59678, respectively.
The R2 is in the high ranging, from 0.8533–0.9228, whereas, AIC and BIC are high, up to −6305.47 and −6974.09, respectively. The Accuracy count showed 57.69%–79.66%. As a result, the performance of the aIMF is acceptable.
We continued the simulations using 5% of random distribution of the added noise instead of 100%. The results showed that the less numbers of the random noise distributed the better performance of the aIMF algorithm. For example, at 5% random distribution of the added noise at 1 Hz with 10% amplitude, the loss estimators, namely; MSE, MAE, MAPE, R2, AIC, BIC and Accuracy count were 0.00014, 0.01019, 0.88981, 0.99820, −15723.93, −15706.68, and 95.86%, respectively; and it outperformed those of simulations with 100% random distribution.
Table 1.
Performance measurements of original datasets using noise distribution at 100% with 1 Hz and 10% amplitude of the original signals.
Table 1.
Performance measurements of original datasets using noise distribution at 100% with 1 Hz and 10% amplitude of the original signals.
| EUR-USD | MSE | MAE | MAPE | R2 | AIC | BIC | Accuracy count (%) |
|---|
| aIMF | 0.00399 | 0.05636 | 4.77093 | 0.8962 | −6305.47 | −6288.22 | 77.34 |
| WT | 0.00506 | 0.05402 | 5.54677 | 0.7231 | −6877.81 | −7857.63 | 53.82 |
| EKF | 0.00548 | 0.06432 | 5.44475 | 0.8701 | −5783.21 | −5765.96 | 47.13 |
| PF | 4.52658 | 1.65756 | 140.015 | 0.0062 | −1060.50 | −1043.25 | 50.32 |
Table 2.
Performance measurements of original datasets using noise distribution at 100% with 1 Hz and 20% amplitude of the original signals.
Table 2.
Performance measurements of original datasets using noise distribution at 100% with 1 Hz and 20% amplitude of the original signals.
| EUR-USD | MSE | MAE | MAPE | R2 | AIC | BIC | Accuracy count (%) |
|---|
| aIMF | 0.00296 | 0.04838 | 4.08815 | 0.9228 | −6991.34 | −6974.09 | 79.66 |
| WT | 0.05439 | 0.05311 | 5.79178 | 0.6759 | −6397.83 | −6804.50 | 54.23 |
| EKF | 0.02043 | 0.12765 | 10.7989 | 0.6385 | −3407.66 | −3390.41 | 48.51 |
| PF | 4.43079 | 1.64779 | 139.747 | 0.0067 | −1061.73 | −1044.48 | 49.76 |
Table 3.
Performance measurements of original datasets using noise distribution at 100% with 5 Hz and 10% amplitude of the original signals.
Table 3.
Performance measurements of original datasets using noise distribution at 100% with 5 Hz and 10% amplitude of the original signals.
| EUR-USD | MSE | MAE | MAPE | R2 | AIC | BIC | Accuracy count (%) |
|---|
| aIMF | 0.00522 | 0.06303 | 5.32770 | 0.8760 | −5891.33 | −5874.08 | 74.92 |
| WT | 0.00599 | 0.05636 | 4.77151 | 0.8962 | −6303.39 | −6286.15 | 55.51 |
| EKF | 0.00503 | 0.06159 | 5.22073 | 0.8807 | −5980.49 | −5963.24 | 47.65 |
| PF | 4.47322 | 1.64897 | 139.488 | 0.0096 | −1067.39 | −1050.14 | 50.24 |
Table 4.
Performance measurements of original datasets using noise distribution at 100% with 5 Hz and 20% amplitude of the original signals.
Table 4.
Performance measurements of original datasets using noise distribution at 100% with 5 Hz and 20% amplitude of the original signals.
| EUR-USD | MSE | MAE | MAPE | R2 | AIC | BIC | Accuracy count (%) |
|---|
| aIMF | 0.00596 | 0.06415 | 5.42792 | 0.8534 | −5501.99 | −5484.74 | 64.41 |
| WT | 0.00571 | 0.07660 | 4.78754 | 0.8761 | −6890.19 | −6897.21 | 56.13 |
| EKF | 0.01870 | 0.12247 | 10.3683 | 0.6637 | −3575.62 | −3558.38 | 48.00 |
| PF | 4.50770 | 1.64377 | 138.983 | 0.0074 | −1063.27 | −1046.02 | 50.58 |
Table 5.
Performance measurements of original datasets using noise distribution at 100% with 10 Hz and 10% amplitude of the original signals.
Table 5.
Performance measurements of original datasets using noise distribution at 100% with 10 Hz and 10% amplitude of the original signals.
| EUR-USD | MSE | MAE | MAPE | R2 | AIC | BIC | Accuracy count (%) |
|---|
| aIMF | 0.00527 | 0.06444 | 5.44396 | 0.8710 | −5799.61 | −5782.36 | 67.26 |
| WT | 0.00508 | 0.06890 | 5.79883 | 0.8948 | −6273.51 | −6745.29 | 56.82 |
| EKF | 0.00406 | 0.05546 | 4.69540 | 0.9017 | −6429.89 | −6412.64 | 51.66 |
| PF | 4.47322 | 1.64897 | 139.487 | 0.0096 | −1067.39 | −1050.14 | 50.24 |
Table 6.
Performance measurements of original datasets using noise distribution at 100% with 10 Hz and 20% amplitude of the original signals.
Table 6.
Performance measurements of original datasets using noise distribution at 100% with 10 Hz and 20% amplitude of the original signals.
| EUR-USD | MSE | MAE | MAPE | R2 | AIC | BIC | Accuracy count (%) |
|---|
| aIMF | 0.00580 | 0.06618 | 5.59678 | 0.8533 | −5501.09 | −5483.84 | 57.69 |
| WT | 0.00521 | 0.06003 | 4.57416 | 0.6941 | −6843.56 | −6899.78 | 53.34 |
| EKF | 0.01490 | 0.11046 | 9.34639 | 0.7140 | −3951.51 | −3934.26 | 51.62 |
| PF | 4.61609 | 1.67868 | 141.868 | 0.0049 | −1057.44 | −1040.19 | 50.45 |
3.6. Discussion
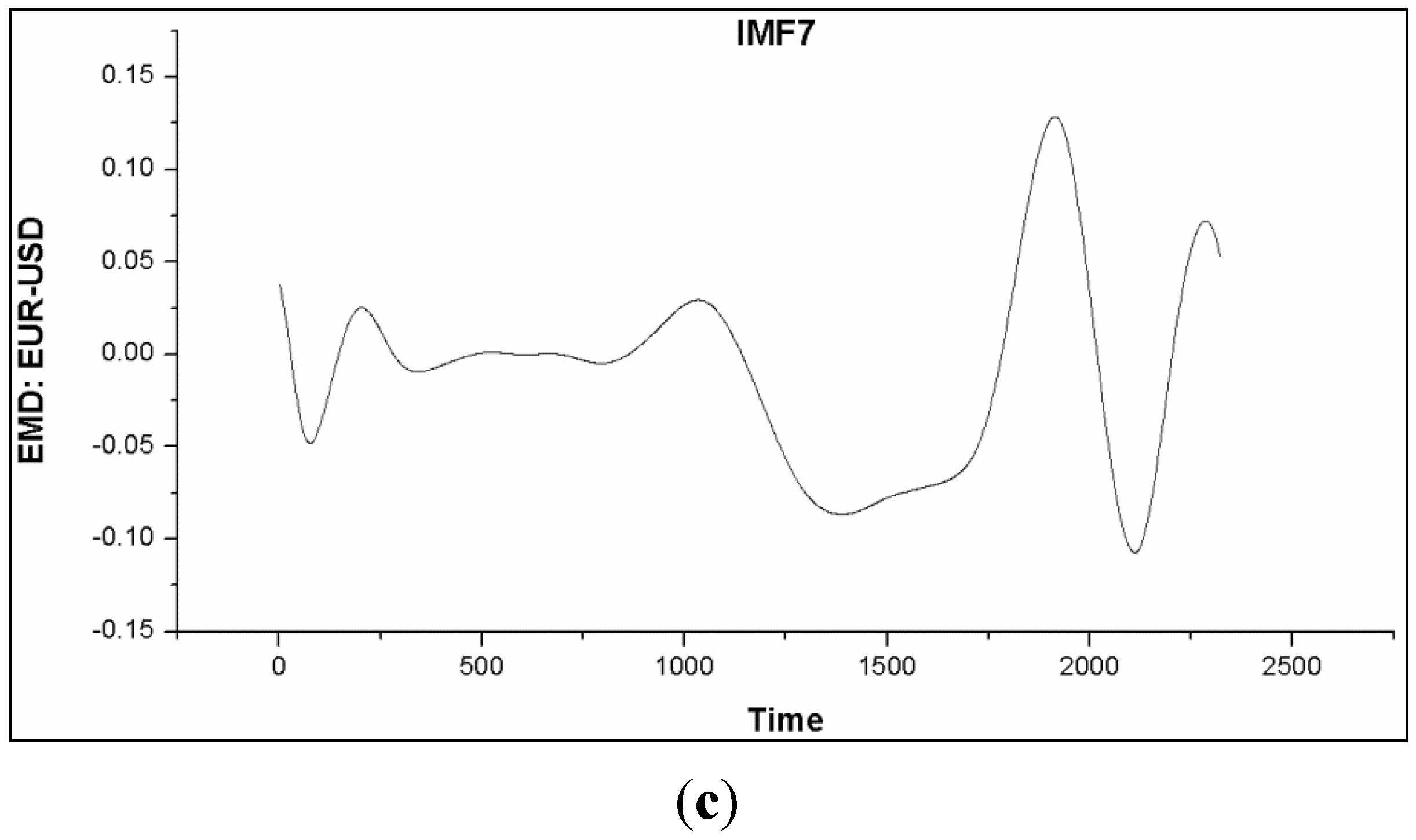
Based on the simulations of the algorithms namely; aIMF, WT, EKF and PF, we have found that the aIMF performed the best, following in the order to WT, EKF and PF. Theoretically, the successful application of EMD resides on the fact that the noise is not biased. Therefore, there is not so much of a restrictive constraint, comparing to the scenario of encountering with non-zero mean noise. As mentioned, the characteristics of IMF after several iterations move towards the normal distribution; see
Figure 11. Thus, subtracting the averaged IMF with the original signals, given aIMF, can reduce the noise inevitably. However, the proposed aIMF algorithm using cubic spline interpolation does not intend to preserve edges of the datasets/signals. This is because of our target to reduce noise that may associate with the upper and lower boundaries of the curves, which are in time series domain. In this particular case, preserving the edges/curves can unavoidably keep the noise mixing within the signals. Unlike the images whose distribution is random walk, the noise reduction can be achieved while the edges are preserved [
27]. Referring to
Section 3.1, we manually added a variety of noises into the datasets with separate simulations; and later proved that the noises have been removed significantly, displayed in
Figure 7 and
Table 1,
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6. To continue to prove the aIMF algorithm’s performance, we simulated the aIMF algorithm with the original datasets—without adding extra noise. The results measured by MSE, MAE, MAPE, R
2 and Accuracy count were 8.20211E−05, 0.00719, 0.57085, 0.9980 and 99.95%, respectively. It is noted that the original datasets, EUR-USD exchange rates, contained a certain level of noise, not pure signal only. In the real application, data of exchange rates are normally fluctuated before closing hours of trading by retailers and speculators who want to manipulate the price. The manipulations are always executed with low volumes of trade, but enable the price changes at the end of trading hours. In the financial community, we deem these trades as noise. Finally, the figures from the last loss estimators shown were similar to the results in
Table 1,
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6. Hence, it is safe to assume that the proposed aIMF algorithm can remove the unwanted signals.
Figure 11.
Graphs (a)–(c) show plots of IMF1, IMF5 and IMF7, of which their local extrema of higher order IMF moved toward the normal distribution.
Figure 11.
Graphs (a)–(c) show plots of IMF1, IMF5 and IMF7, of which their local extrema of higher order IMF moved toward the normal distribution.
On another front, the simulation results from the WT algorithm seemed to be unacceptable under the rationale that Fourier spectral analysis and its derivatives such as WT encountered with a limited time window width by sliding a predetermined window(s) along the time axis [
28]. Moreover, there is a trade-off between the time consumed in the window width and the frequency resolution, and this phenomenon has been considered by the uncertainty principle Heisenberg [
21]. In this particular case, the WT’s window width must be preselected and it is known as the primary or mother wavelet which is a prototype that provides less flexibility when handling datasets were the mean and variances are highly volatile. In case of EKF simulation, the advantage of SIS is that it does not guarantee to fail as time increases and it becomes more and more skewed, especially when sampling high-dimensional spaces [
26]. For the PF algorithm, we have found that the number of particles (data-points) was not adequate for Monte Carlo simulation. However, the drawback of the aIMF algorithm is that it requires long time to spline the local extrema.
3.7. Robustness Test
Robustness testing is any quality assurance methodology focused on testing the consistent accuracy of software. In this section, we test the algorithms of aIMF, WT, EKF and PF which function as noise reduction models. The testing strategies used different inputs other than the EUR-USD exchange rates with the added noise, which are created from 1 Hz sine wave at 10% amplitude of the original datasets with the 10% random distribution. Those different inputs are EUR-JPY with the added noise, EUR-CHF with the added noise, finally, EUR-GBP with the added noise. Later, we used loss estimators to measure the prediction performances of the proposed aIMF, WT, EKF and PF,
i.e., MSE, MAE, MAPE, R
2, AIC, BIC and Accuracy count. Having simulated with all the loss estimators indicated in
Table 7,
Table 8 and
Table 9 under the same conditions used to test for EUR-USD as input, the results shared the same trend with few deviations from each other. This served to confirm that the aIMF algorithm performed significantly better when filtering a nonlinear nonstationary time series,
i.e., EUR-JPY, EUR-CHF and EUR-GBP exchange rates, followed by WT and EKF algorithms. Moreover, we rejected using the PF algorithm to reduce the noise for the nonlinear nonstationary time series data. Additionally, we have discovered that the EKF and WT algorithm must be optimised in the areas of resampling and building up mother wavelet, respectively.
Table 7.
Performance measurements of original dataset, EUR-JPY, using noise distribution at 10% with 10 Hz and 20% amplitude of the original signals’.
Table 7.
Performance measurements of original dataset, EUR-JPY, using noise distribution at 10% with 10 Hz and 20% amplitude of the original signals’.
| EUR-JPY | MSE | MAE | MAPE | R2 | AIC | BIC | Accuracy count (%) |
|---|
| aIMF | 0.00424 | 0.057854 | 8.29746 | 0.5219 | −6782.23 | −6764.98 | 63.85 |
| WT | 0.00626 | 0.05676 | 8.67169 | 0.5514 | −6839.68 | −682.42 | 53.46 |
| EKF | 0.00516 | 0.063797 | 9.15559 | 0.4046 | −6272.94 | −6255.69 | 49.50 |
| PF | 3.37133 | 1.42611 | 204.696 | 0.0020 | −5074.33 | −5057.08 | 50.19 |
Table 8.
Performance measurements of original dataset, EUR-CHF, using noise distribution at 10% with 10 Hz and 20% amplitude of the original signals’.
Table 8.
Performance measurements of original dataset, EUR-CHF, using noise distribution at 10% with 10 Hz and 20% amplitude of the original signals’.
| EUR-CHF | MSE | MAE | MAPE | R2 | AIC | BIC | Accuracy count (%) |
|---|
| aIMF | 0.03772 | 0.145457 | 0.420782 | 0.9983 | −1086.41 | −1069.16 | 88.96 |
| WT | 0.08124 | 0.1745481 | 0.53478 | 0.5905 | −6852.24 | −6699.54 | 53.20 |
| EKF | 0.37038 | 0.176222 | 0.519026 | 0.5588 | −11843.6 | −11860.9 | 45.71 |
| PF | 1218.50 | 34.52886 | 101.8893 | 0.4421 | −12388.2 | −12405.5 | 50.84 |
Table 9.
Performance measurements of original dataset, EUR-GBP, using noise distribution at 10% with 10 Hz and 20% amplitude the original signals’.
Table 9.
Performance measurements of original dataset, EUR-GBP, using noise distribution at 10% with 10 Hz and 20% amplitude the original signals’.
| EUR-CHF | MSE | MAE | MAPE | R2 | AIC | BIC | Accuracy count (%) |
|---|
| aIMF | 0.00424 | 0.057854 | 8.306478 | 0.5191 | −6802.20 | −6784.98 | 64.92 |
| WT | 0.00826 | 0.065946 | 9.319482 | 0.6435 | −6699.65 | −6382.98 | 51.08 |
| EKF | 0.00517 | 0.063851 | 9.171988 | 0.4055 | −6309.97 | −6292.68 | 49.20 |
| PF | 3.33789 | 1.435658 | 206.7395 | 0.0006 | −5104.53 | −5087.27 | 48.68 |
The following configurations were used to perform all the simulations:
- (i)
Intel(R) Xeon(R) server with 2 × 2.4 GHz E5620 CPUs, 3.99 GB RAM and a 64-bit Microsoft Windows Operating System is configured as the main processor.
- (ii)
Sony Visio, Sony L2412M1EB Desktop with an Intel Core i5, 2.5 GHz, 8 GB RAM, and a 64-bit Microsoft Windows Operating System is used as the front-end connection to the data terminal from Bloomberg via web access using a Citrix client.
- (iii)
Application programs written using R programming scripts and some amendments to suit the requirements.
The simulation results showed that there were no bugs in the software scripts, and an average execution time of 3 s for all the Ordinary Least Square (OLS) models.

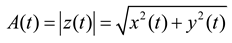










to estimate the particle at k − 1 and obtain .