Computational Study on a PTAS for Planar Dominating Set Problem

Abstract

The dominating set problem is a core NP-hard problem in combinatorial optimization and graph theory, and has many important applications. Baker [JACM 41,1994] introduces a k-outer planar graph decomposition-based framework for designing polynomial time approximation scheme (PTAS) for a class of NP-hard problems in planar graphs. It is mentioned that the framework can be applied to obtain an $O\left(2^{ck}n\right)$ time, c is a constant, $(1+1/k)$-approximation algorithm for the planar dominating set problem. We show that the approximation ratio achieved by the mentioned application of the framework is not bounded by any constant for the planar dominating set problem. We modify the application of the framework to give a PTAS for the planar dominating set problem. With k-outer planar graph decompositions, the modified PTAS has an approximation ratio $(1+2/k)$. Using $2k$-outer planar graph decompositions, the modified PTAS achieves the approximation ratio $(1+1/k)$ in $O\left(2^{2ck}n\right)$ time. We report a computational study on the modified PTAS. Our results show that the modified PTAS is practical.

1. Introduction

An important research area in graph theory and networks is domination; it has been energetically investigated for many years due to its large number of real-world applications, such as resource allocation [1,2] and voting [3]. Haynes et al. In their books, [4,5] provide a good survey on domination problems. Let G be a simple undirected graph with the set of vertices $V\left(G\right)$ and the set of edges $E\left(G\right)$. We denote $\left|V\right(G\left)\right|$ by n. The r-dominating set D of G is a subset of $V\left(G\right)$ containing r vertices, such that for every vertex v in $V\left(G\right)$, either $v\in D$ or v is adjacent to a vertex in D. The minimum integer r for which G has a r-dominating set is called the domination number of G and is denoted by $\gamma \left(G\right)$. The dominating set problem is to decide that given a graph G and an integer r, whether $\gamma \left(G\right)\le r$. The optimization version of this problem is to find a minimum dominating set.

The dominating set problem is a core NP-hard problem in combinatorial optimization and graph theory [6]. There is a long history of research on the approximation and exact algorithms to tackle the intractability of the problem. A minimization problem P is α−approximable $(\alpha \ge 1)$ if there is an algorithm which gives a solution for any instance of P in polynomial time in the instance size with solution value at most $\alpha OPT$, where $OPT$ is the value of an optimal solution for the instance of P. If P is $(1+ϵ)-$approximable for any fixed $ϵ>0$ then P has a polynomial time approximation scheme (PTAS). The dominating set problem for general graphs is $(1+logn)-$approximable [7], however, it is not approximable within a factor $(1-ϵ)lnn$ for any $ϵ>0$ unless $NP\subseteq DTIME\left(n^{loglogn}\right)$ [8]. The dominating set problem has been widely studied on an important class of graphs, the planar graphs. A graph is planar if it can be drawn on the sphere with no crossing edges. The dominating set problem in planar graphs (planar dominating set problem) remains NP-hard [6] but admits a PTAS [9].

The fixed parameter algorithms have played a central role in exact algorithms for the planar dominating set problem. A minimization problem P is fixed-parameter tractable if given a parameter r, whether $OPT$ of P is at most r can be decided in $f\left(r\right)n^{O\left(1\right)}$ time, where $f\left(r\right)$ is a computable function depending only on r [10]. Such an algorithm is called a fixed parameter tractable (FPT) algorithm. Readers may refer to [11] for a survey on new techniques for developing exact algorithms for NP-hard problems. It is shown in [10] that for general graphs, the dominating set problem is not fixed-parameter tractable unless some collapses occur between parametrized complexity classes. However, the planar dominating set problem is fixed-parameter tractable [10]. The planar dominating set problem also admits a linear size kernel [12].

Recent progresses in FPT algorithms result in subexponential time exact algorithms for the planar dominating set problem [13,14,15]. These algorithms use the tree-/branch-decomposition based approach and have running time $O(2^{c\sqrt{\gamma \left(G\right)}}n+n^{O\left(1\right)})$, c is a constant. The branch-decomposition based algorithm by Fomin and Thilikos (called FT algorithm in what follows) [14] achieves a smallest constant c in the exponent of the running time. The notion of branch-decomposition of graphs is introduced by Robertson and Seymour [16]. Informally, a branch-decomposition of a graph G is a collection of vertex cut sets of G that decomposes G into subgraphs with each edge of G a minimal subgraph. The width of a branch-decomposition is the maximum size of the vertex cuts in the collection. The branchwidth of G, denoted by $\text{bw}\left(G\right)$, is the minimum width of all possible branch-decompositions of G. Given a graph G and a branch-decomposition of G with width β, FT algorithm finds an optimal solution in $O\left(2^{\left(3{log}_{4}3\right)\beta }n\right)$ time for the dominating set problem.

For a planar graph G, it is known that a branch-decomposition of minimum width $\text{bw}\left(G\right)$ can be computed in $O\left(n^3\right)$ time [17,18] and $\text{bw}\left(G\right)\le 3\sqrt{4.5\gamma \left(G\right)}$ [14,19]. Alber et al. [12] give an $O\left(n^3\right)$ time algorithm which computes a subgraph H (kernel) of G such that H has $O\left(\gamma \right(G\left)\right)$ vertices, $\gamma \left(H\right)\le \gamma \left(G\right)$, and a minimum dominating set of G can be constructed from a minimum dominating set of H in linear time. Notice that for a subgraph H of G, $\text{bw}\left(H\right)\le \text{bw}\left(G\right)$. From the above, the FT algorithm solves the planar dominating set problem in $O(2^{\left(3{log}_{4}3\right)\text{bw}\left(G\right)}\gamma \left(G\right)+n^3)$ and $O(2^{15.13\sqrt{\gamma \left(G\right)}}\gamma \left(G\right)+n^3)$ time (The running time of FT algorithm can be further improved to $O(2^{11.98\sqrt{\gamma \left(G\right)}}\gamma \left(G\right)+n^3)$ using fast matrix multiplication in the dynamic programming step of the algorithm [20]. However, this improvement is only of theoretical interest because the fast matrix multiplication is not practical [21]).

For graphs with small treewidth/branchwidth, an FPT algorithm may be efficient to find an optimal solution, however, for graphs with large treewidth/branchwidth, one may have to rely on approximation algorithms for the planar dominating set problem. A PTAS is highly desired if the solution values are required to be close to optimal with a guaranteed approximation ratio. Baker introduces a framework to obtain PTAS for a class of NP-hard problems [9]. This framework is based on decomposing a planar graph into k-outer planar subgraphs.

A graph G is called outer planar or 1-outer planar if it has a planar embedding such that all vertices of G are incident to a same face (called outer face). For $k>1$, G is a k-outer planar graph, if it has a planar embedding such that removing the vertices of G incident to the outer face will result in a $(k-1)$-outer planar graph. A k-outer planar graph G has a branchwidth of at most $2k$. Baker’s PTAS framework for a problem P in a planar graph G is to decompose G into a collection of k-outer planar subgraphs, find an optimal partial solution of P in each subgraph by an exact algorithm, and take the union of the optimal partial solutions as a solution of P in G. When the framework is used for a minimization problem, G is decomposed in such a way that every two “neighbor" k-outer planar subgraphs share “one-level" vertices. Baker shows that the framework gives a $2^{O\left(k\right)}n$ time $(1+1/k)$-approximation algorithm for the vertex cover problem in planar graphs and mentions that the framework can be applied to obtain $2^{O\left(k\right)}n$ time $(1+1/k)$-approximation algorithms for many other minimization problems, including the planar dominating set problem [9]. For a maximization problem like the independent set problem in planar graphs, Baker’s framework gives a $2^{O\left(k\right)}n$ time $k/(k+1)$-approximation algorithm.

We show that the approximation ratio of Baker’s framework is not bounded by any constant for the planar dominating set problem when two “neighbor" k-outer planar subgraphs share only “one-level" of vertices. To get a PTAS for the planar dominating set problem, the application of the framework has to be modified. We modify the application of the framework by decomposing G into k-outer planar subgraphs such that every two “neighbor" subgraphs share “two-levels" of vertices. Let $O\left(2^{ck}n\right)$, c is a constant, be the running time of Baker’s framework with “one-level" of overlapping vertices for the planar dominating set problem. We show that the modified application of the framework gives a PTAS with approximation ratio $(1+2/k)$ for the planar dominating set problem. By decomposing G into $2k$-outer planar subgraphs with “two-level" overlapping vertices, the modified PTAS achieves the approximation ratio $(1+1/k)$ in $O\left(2^{2ck}n\right)$ time.

In addition to the theoretical progresses in the algorithms for the dominating set problem, the practical performance of algorithms for the problem has received much attention. A computational study of an exact algorithm (FT algorithm) for the planar dominating set problem is reported in [21]. The study shows that the FT algorithm is practically efficient for graphs with small branchwidth. Heuristic algorithms for the dominating set problem have also been well investigated and a computational study of heuristic algorithms is reported in [22]. However, the practical performance of a PTAS is not known for the planar dominating set problem. One hurdle in evaluating the practical performance of a PTAS is the implementation of the algorithm. We conduct a computational study to evaluate the practical performance of the modified PTAS for the planar dominating set problem. In our implementation, the FT algorithm is used to compute an optimal partial solution in each k-outer planar subgraph. Our results show that the PTAS finds solutions with values very close to optimal in a practical time and much better than those given by well used heuristic algorithms. The computational study gives a concrete example on using a PTAS for solving important NP-hard problems in planar graphs and shows that the PTAS is practical for the planar dominating set problem. This work provides a tool for computing solutions close to optimal for the planar dominating set problem.

The next section gives preliminaries of the paper. In Section 3, we review Baker’s framework, show that the approximation ratio of the framework is not bounded by a constant with “one-level" of overlapping vertices for the planar dominating set problem, and modify the application of the framework to give a PTAS for the problem. In Section 4, we report the computational study results. The final section concludes the paper.

2. Preliminaries

A graph G consists of a set $V\left(G\right)$ of vertices and a set $E\left(G\right)$ of edges, where each edge e of $E\left(G\right)$ is a subset of two elements from $V\left(G\right)$. For edge $e=\{u,v\}\in E\left(G\right)$, we say that vertices u and v are adjacent. The node degree of a vertex u is the number of vertices adjacent to u. Vertex u is dominated by vertex v if u and v are adjacent or $u=v$. Vertex u is dominated by a set D if u is dominated by a vertex of D. Edge e is covered by a vertex u if $u\in e$. For a subset $U\subseteq V\left(G\right)$ and a subset $A\subseteq E\left(G\right)$, we denote by $G\left[U\right]$ and $G\left[A\right]$ the subgraphs of G induced by U and A, respectively. For a subset $A\subseteq E\left(G\right)$, we denote by $E\left(G\right)\setminus A$ by $\overline{A}$ when G is clear from the context. A separation of graph G is a pair $(A,\overline{A})$ of subsets of $E\left(G\right)$. For each $A\subseteq E\left(G\right)$, we denote by $\partial \left(A\right)$ the vertex set $V\left(A\right)\cap V\left(\overline{A}\right)$. The order of separation $(A,\overline{A})$ is $\left|\partial \left(A\right)\right|=|\partial \left(\overline{A}\right)|$.

A graph G is planar if G has a planar embedding (a draw on a sphere without edge crossing). We call a planar embedding of G a plane graph. A face of a plane graph G is a connected region of the sphere bounded by edges and vertices of G and containing no edge or vertex of G in its interior. For a plane graph G and a face f of G, let $V_G\left(f\right)$ be the set of vertices in $V\left(G\right)$ incident to f. Given a plane graph G and a face $f_o$ (called outer face) of G, let $V_1=V_G\left(f_o\right)$. For $i\ge 1$, let $U_i={\mathrm{\cup }}_{j=1}^i{V}_j$, $G_i=G[V\left(G\right)\setminus U_i]$, $f_i$ be the face of $G_i$ such that $f_o\subseteq f_i$, and $V_{i+1}=V_{G_i}\left(f_i\right)$. We call the vertices of $V_i$level i vertices of G. Intuitively, $G_i$ is the plane graph obtained from removing vertices of levels $1,2,\dots ,i$ from G. $V_{i+1}$ is the vertices of $G_i$ incident to the outer face of $G_i$.

Branch-decomposition based algorithms play a central role in the PTAS studied in this paper. The notion of branch-decomposition is introduced by Robertson and Seymour [16]. A branch-decomposition of graph G is a pair $(\varphi ,T)$ where T is a tree each internal node of which has degree 3 and ϕ is a bijection from the set of leaves of T to $E\left(G\right)$. Consider a link e of T and let $L_1$ and $L_2$ denote the sets of leaves of T in the two respective subtrees of T obtained by removing e. We say that the separation $(\varphi \left(L_1\right),\varphi \left(L_2\right))$ is induced by this link e of T. We define the width of the branch-decomposition $(\varphi ,T)$ to be the largest order of the separations induced by links of T. The branchwidth of G, denoted by $\text{bw}\left(G\right)$, is the minimum width of all branch-decompositions of G. In the rest of this paper, we identify a branch-decomposition $(\varphi ,T)$ with the tree T, regarding each leaf of T as an edge of G.

Given a branch-decomposition T of G, an optimization problem P in G may be solved by the dynamic programming method as follows: convert T into a rooted binary tree by replacing a link $\{x,y\}$ of T with three links $\{x,z\},\{y,z\},\{z,r\}$, where z and r are new nodes to T, and r is the root of T. For a link $e=\{u,v\}$ of T, assume u is the end node reachable from root r by passing through e. Let $A_e$ be the set of leaves of T reachable from r by passing through e. Link $e=\{u,v\}$ is called a leaf link if u is a leaf node, otherwise an internal link. An internal link e has two child links $e_1$ and $e_2$ covered by u. Notice that $A_e=A_{e_1}\mathrm{\cup }{A}_{e_2}$. For a leaf link e, all partial solutions of P in the subgraph $G\left[A_e\right]$ can be computed by enumeration. For an internal link e, assume that all partial solutions of P in the subgraph $G\left[A_{e_1}\right]$ and those in $G\left[A_{e_2}\right]$ have been computed. Then all partial solutions of P in the subgraph $G\left[A_e\right]$ are computed by merging the partial solutions in $G\left[A_{e_1}\right]$ and those in $G\left[A_{e_2}\right]$. The merging process is performed in a bottom-up way, from each leaf link to the link $\{z,r\}$, to find an optimal solution of P in G.

The FT algorithm is a branch-decomposition-based algorithm for the planar dominating set problem. In FT Algorithm, the number of partial solutions in $G\left[A_e\right]$ is $3^{\left|\partial \right(A_e\left)\right|}$. To compute a partial solution in $G\left[A_e\right]$, every pair $(s_1,s_2)$ is checked, where $s_1$ and $s_2$ are partial solutions in $G\left[A_{e_1}\right]$ and $G\left[A_{e_2}\right]$, respectively. Notice that each of $|\partial \left(A_e\right)|,|\partial \left(A_{e_1}\right)|,|\partial \left(A_{e_2}\right)|$ is at most the width of the given branch-decomposition T. When an optimal branch-decomposition T (of width $\text{bw}\left(G\right)$) is given, the FT algorithm takes $O\left(2^{\left(3{log}_{4}3\right)\text{bw}\left(G\right)}\right)$ time and $O\left(3^{\text{bw}\left(G\right)}\gamma \left(G\right)\right)$ memory space to compute the partial solutions in $G\left[A_e\right]$. A planar graph G can be reduced to a kernel of size $O\left(\gamma \right(G\left)\right)$ in $O\left(n^3\right)$ time and there are $O\left(\gamma \right(G\left)\right)$ merging steps for the kernel. An optimal branch-decomposition of the kernel can be computed in $O\left({\left(\gamma \left(G\right)\right)}^3\right)$ time. The FT algorithm solves the planar dominating set problem in $O(2^{\left(3{log}_{4}3\right)\text{bw}\left(G\right)}\gamma \left(G\right)+n^3)$ time [14]. For many other NP-hard problems, branch-decomposition-based algorithms usually have exponential time and memory space in the width of a given branch-decomposition. The exponential time and memory space are often a bottle-neck in applying branch-decomposition-based algorithms in practice.

3. PTAS for Planar Dominating Set Problem

3.1. Baker’s Framework for Minimization Problem

We review Baker’s PTAS framework for minimization problems. We define the terminology for describing the framework. Given a plane graph G with m levels of vertices, for integers $2\le k<m$ and $2\le s\le k+1$, let $r=\lceil (m-s)/k\rceil$. We define $U(0,s)={\mathrm{\cup }}_{j=1}^s{V}_j$; $U(i,s)={\mathrm{\cup }}_{j=0}^k{V}_{(i-1)\times k+s+j}$ for $1\le i<r$; and $U(r,s)={\mathrm{\cup }}_{j=(r-1)\times k+s}^m{V}_j$. Then $G\left[U\right(0,s\left)\right]$ is the plane subgraph of G induced by the vertices of G with levels $1,\dots ,s$ and is s-outer planar; each $G\left[U\right(i,s\left)\right]$ is the subgraph of G induced by the vertices of G with levels $(i-1)\times k+s,\dots ,i\times k+s$ and is $(k+1)$-outer planar for $1\le i<r$; and $G\left[U\right(r,s\left)\right]$ is the subgraph of G induced by the vertices of G with levels $(r-1)\times k+s,\dots ,m$ and is t-outer planar, where $t=m-\left[\right(r-1)\times k+s]+1\le k+1$. Below is Baker’s PTAS framework for minimization problems.

• Let G be a plane graph with m levels of vertices for an outer face and $k\ge 2$ be an integer. Compute the vertex sets $V_1,\dots ,V_m$.
• for $s=2,\dots ,k+1$

  (a)

  Compute subgraphs $G\left[U\right(i,s\left)\right]$ for $i=0,1,\dots ,r$.

  (b)

  For every subgraph $G\left[U\right(i,s\left)\right]$, find an optimal solution $S(i,s)$ by an exact algorithm.

  (c)

  Let $S_s={\mathrm{\cup }}_{i=0}^{r}S(i,s)$.

• Let S be a set of $S_2,\dots ,S_{k+1}$ with the minimum cardinality.

Baker [9] gives a proof that the above framework achieves a $(1+1/k)$-approximation ratio for the minimum vertex cover problem in plane graph G: find a minimum subset C of $V\left(G\right)$ such that every edge of G is covered by a vertex in C. We review Baker’s proof of the approximation ratio for the vertex cover problem. This proof gives a base on our later argument for the planar dominating set problem.

Given a plane graph G, let C be a minimum vertex cover of G. Given integer k, let $S(i,s)$ be a minimum vertex cover of $G\left[U\right(i,s\left)\right]$ and let $C(i,s)=C\cap U(i,s)$, $s=2,\dots ,k+1$ and $0\le i\le r$. Since no vertex of G in $V\left(G\right)\setminus U(i,s)$ covers any edge of $G\left[U\right(i,s\left)\right]$, $C(i,s)$ is a vertex cover of subgraph $G\left[U\right(i,s\left)\right]$. From this and the fact that $S(i,s)$ is a minimum vertex cover of $G\left[U\right(i,s\left)\right]$, $\left|S\right(i,s\left)\right|\le \left|C\right(i,s\left)\right|$. Therefore, $S_s={\mathrm{\cup }}_{i=0}^{r}S(i,s)$ is a vertex cover of G and

$$\begin{array}{c}\hfill |S_s|\le {\displaystyle \mathrm{\sum }_{i=0}^r}\left|S(i,s)\right|\le {\displaystyle \mathrm{\sum }_{i=0}^r}\left|C(i,s)\right|\end{array}$$

(1)

Since the vertices of $V_{i\times k+s}$ appear in both subgraphs $G\left[U\right(i,s\left)\right]$ and $G\left[U\right(i+1,s\left)\right]$, $0\le i<r$,

$$\begin{array}{c}\hfill {\displaystyle \mathrm{\sum }_{i=0}^r}\left|C(i,s)\right|=\left|C\right|+{\displaystyle \mathrm{\sum }_{i=0}^{r-1}}|C\cap V_{i\times k+s}|\end{array}$$

(2)

Notice that

$$\begin{array}{c}\hfill {\displaystyle \underset{s=2}{\overset{k+1}{min}}}\{{\displaystyle \mathrm{\sum }_{i=0}^{r-1}}|C\cap V_{i\times k+s}\left|\right\}\le \frac{\left|C\right|}{k}\end{array}$$

(3)

Let S be a $S_s$ with a minimum cardinality. Then from Inequalities (1), (2), and (3), we have $\left|S\right|\le \left|C\right|+\frac{\left|C\right|}{k}$, that is, the solution produced by Baker’s framework has the approximation ratio $(1+1/k)$ for the minimum vertex cover problem in planar graphs.

3.2. Modified Framework for Planar Dominating Set Problem

In [9], it is mentioned that the framework in the previous section can be applied to obtain a $(1+1/k)$-approximation algorithm for the planar dominating set problem. We show that this is not true. Recall that for the vertex cover problem, no vertex of G in $V\left(G\right)\setminus U(i,s)$ can cover any edge of $G\left[U\right(i,s\left)\right]$. This implies that for a minimum vertex cover C, $C(i,s)=C\cap U(i,s)$ is a vertex cover of subgraph $G\left[U\right(s,i\left)\right]$ and a minimum vertex cover $S(i,s)$ of $G\left[U\right(i,s\left)\right]$ has the property $\left|S\right(i,s\left)\right|\le \left|C\right(i,s\left)\right|$. However, for the planar dominating set problem, the intersection of a minimum dominating set of G and $U(i,s)$ may not be a dominating set of $G\left[U\right(i,s\left)\right]$ because a vertex of G in $V\left(G\right)\setminus U(i,s)$ can dominate a vertex of $G\left[U\right(i,s\left)\right]$. More specifically, let D be a minimum dominating set of G, $D(i,s)=D\cap U(i,s)$ and $S(i,s)$ be a minimum dominating set of $G\left[U\right(i,s\left)\right]$. Then $D(i,s)$ may not be a dominating set of $G\left[U\right(i,s\left)\right]$ and $\left|S\right(i,s\left)\right|\le \left|D\right(i,s\left)\right|$ may not hold. Below we show by an example that the approximation ratio of the mentioned application of Baker’s framework is not bounded by any constant for the planar dominating set problem.

Let G be a plane graph with 4 levels of vertices shown in Figure 1. Let $X_i$ be the set of vertices of G with labels $(i,1),\dots ,(i,x)$, $1\le i\le 6$. The subgraph $G\left[X_i\right]$ is a chain and there is a unique vertex in G dominating all vertices of $X_i$. For a large x, G has a unique minimum dominating set D with its six vertices shown as black squares in the figure. Let $k=2$. For $s=2$, the subgraphs $G\left[U\right(0,2\left)\right]$ and $G\left[U\right(1,2\left)\right]$ are shown in Figure 2 (a) and (b), respectively. Let $D(0,2)=D\cap U(0,2)$. Then $D(0,2)$ (the set of vertices denoted by black squares) is not a dominating set of $G\left[U\right(0,2\left)\right]$. On the other hand, a minimum dominating set $S(0,2)$ of $G\left[U\right(0,2\left)\right]$ contains a fraction of vertices in $X_3$ and $\left|S\right(0,2\left)\right|>\left|D\right(0,2\left)\right|$ for large $x=|X_3|$. Similarly, a minimum dominating set $S(1,2)$ of $G\left[U\right(1,2\left)\right]$ contains a fraction of vertices in $X_2$ and $\left|S\right(1,2\left)\right|>\left|D\right(1,2\left)\right|$. Let $S_2=S(0,2)\mathrm{\cup }S(1,2)$. Then $|S_2|/|D|$ is not bounded by any constant for non-constant x.

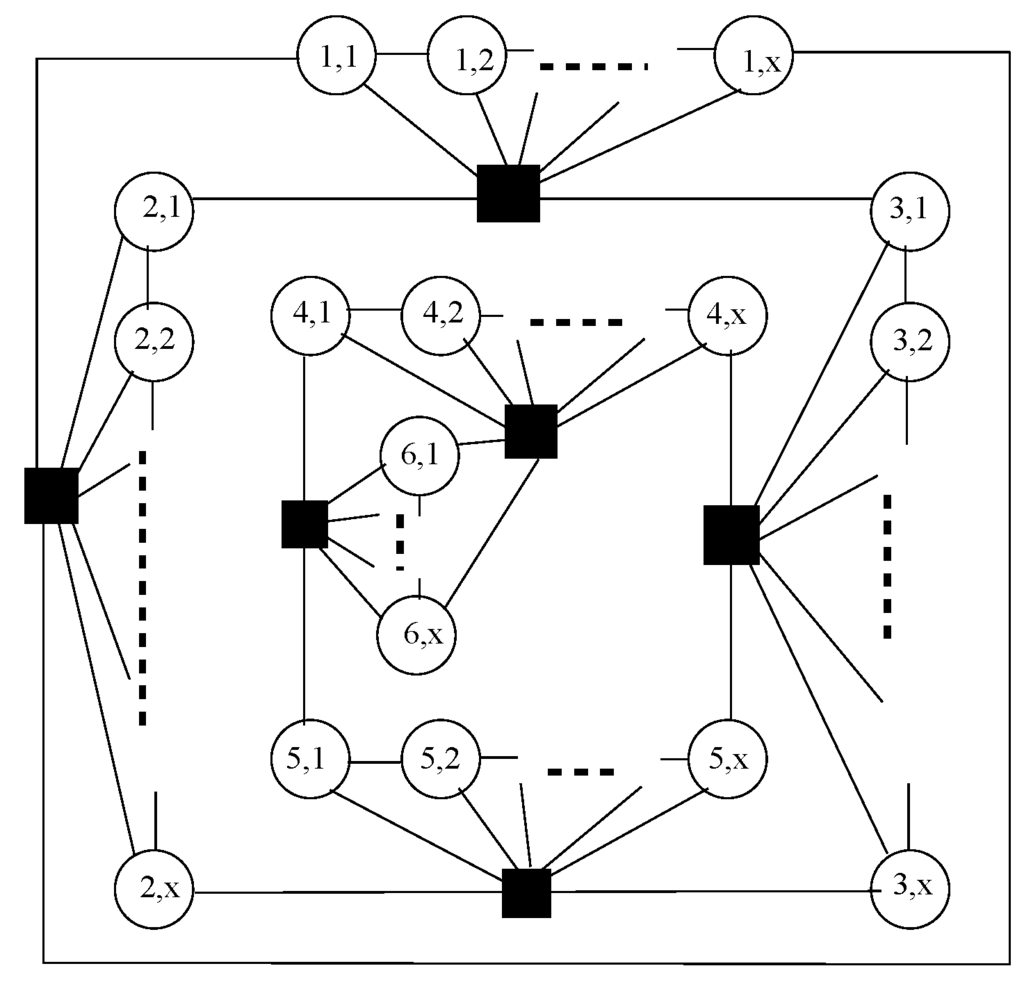
Figure 1. A plane graph G with four levels of vertices.

Figure 1. A plane graph G with four levels of vertices.

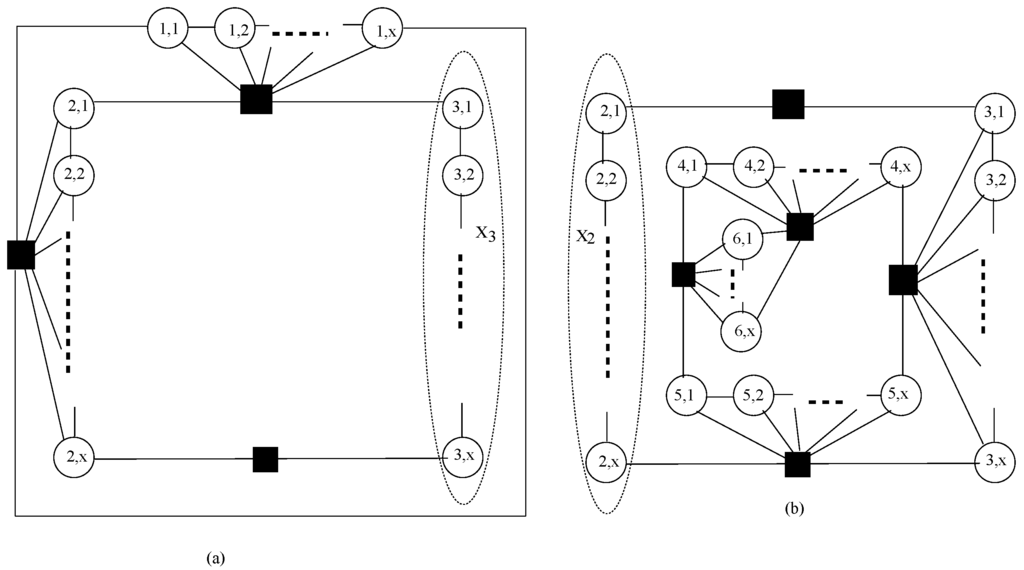
Figure 2. (a) Subgraph $G\left[U\right(0,2\left)\right]$ and (b) Subgraph $G\left[U\right(1,2\left)\right]$ of G.

Figure 2. (a) Subgraph $G\left[U\right(0,2\left)\right]$ and (b) Subgraph $G\left[U\right(1,2\left)\right]$ of G.

For $s=3$, the subgraphs $G\left[U\right(0,3\left)\right]$ and $G\left[U\right(1,3\left)\right]$ are shown in Figure 3 (a) and (b), respectively. Then a minimum dominating set $S(0,3)$ of $G\left[U\right(0,3\left)\right]$ contains a fraction of vertices in $X_4$ and a minimum dominating set $S(1,3)$ of $G\left[U\right(1,3\left)\right]$ contains a fraction of vertices in $X_5$. Let $S_3=S(0,3)\mathrm{\cup }S(1,3)$. Then $|S_3|/|D|$ is not bounded by any constant for non-constant $x=|X_4|$. Therefore, for a set S of $S_2$ and $S_3$ with the minimum cardinality, $\left|S\right|/\left|D\right|$ is not bounded by any constant for non-constant x.

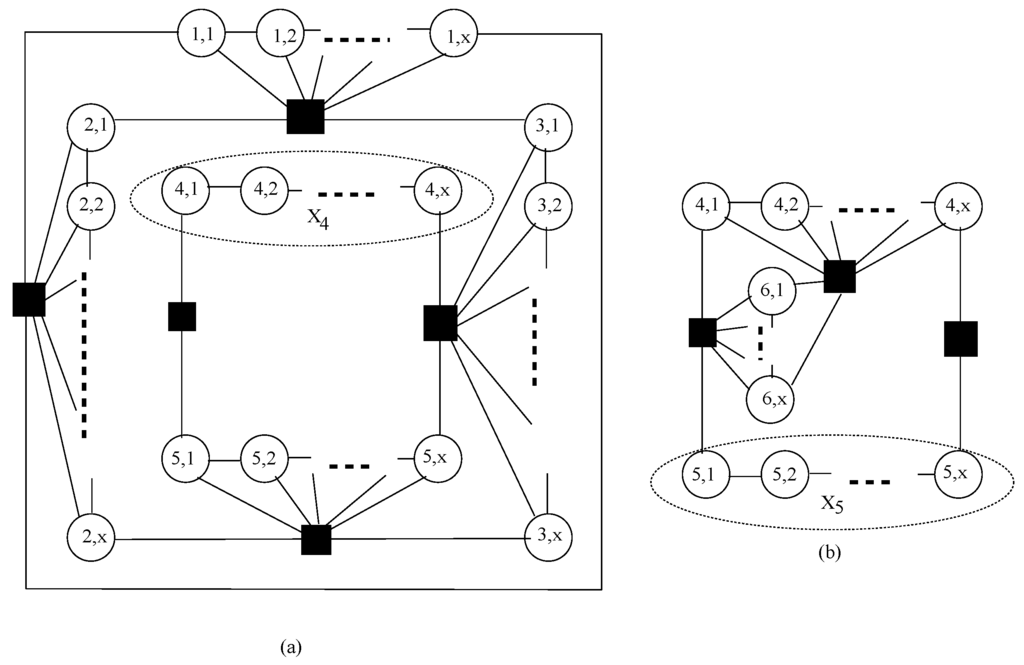
Figure 3. (a) Subgraph $G\left[U\right(0,3\left)\right]$ and (b) Subgraph $G\left[U\right(1,3\left)\right]$ of G.

Figure 3. (a) Subgraph $G\left[U\right(0,3\left)\right]$ and (b) Subgraph $G\left[U\right(1,3\left)\right]$ of G.

We modify the application of Baker’s framework to get a PTAS for the planar dominating set problem. The idea for the modification is that instead of decomposing G into $(k+1)$-outer planar subgraphs with two neighbor subgraphs $G\left[U\right(i,s\left)\right]$ and $G\left[U\right(i+1,s\left)\right]$ overlapping on one level of vertices, we decompose G into $(k+2)$-outer planar subgraphs with two neighbor subgraphs overlapping on two levels of vertices. For each subgraph, we find a minimum set which dominates only k levels of vertices in the subgraph. The formal modification is described below.

Let G be a plane graph with m levels of vertices. For integers $2\le k<m$ and $2\le s\le k+1$, let $r=\lceil (m-s)/k\rceil$. We define $W(0,s)={\mathrm{\cup }}_{j=1}^s{V}_j$; $W(i,s)={\mathrm{\cup }}_{j=-1}^k{V}_{(i-1)\times k+s+j}$ for $1\le i<r$; and $W(r,s)={\mathrm{\cup }}_{j=(r-1)\times k+s-1}^m{V}_j$. $G\left[W\right(0,s\left)\right]$ is the subgraph of G induced by the vertices of G with levels $1,\dots ,s$ and is s-outer planar; each $G\left[W\right(i,s\left)\right]$ is the subgraph of G induced by the vertices of G with levels $(i-1)\times k+s-1,\dots ,i\times k+s$ and is $(k+2)$-outer planar for $1\le i<r$; and $G\left[W\right(r,s\left)\right]$ is the subgraph of G induced by the vertices of G with levels $(r-1)\times k+s-1,\dots ,m$ and is t-outer planar, where $t=m-\left[\right(r-1)\times k+s]+2\le k+2$. We call the vertices of $G\left[W\right(0,s\left)\right]$ with level s, the vertices of each subgraph $G\left[W\right(i,s\left)\right]$ ($1\le i<r$) with levels $(i-1)\times k+s-1$ and $i\times k+s$, and the vertices of $G\left[W\right(r,s\left)\right]$ with level $(r-1)\times k+s-1$ the vertices on boundary; and call the other vertices the interior vertices.

• Let G be a plane graph with m levels of vertices for an outer face and $k\ge 2$ be an integer. Compute the vertex sets $V_1,\dots ,V_m$.
• for $s=2,\dots ,k+1$

  (a)

  Compute subgraphs $G\left[W\right(i,s\left)\right]$ for $i=0,1,\dots ,r$.

  (b)

  For subgraph $G\left[W\right(0,s\left)\right]$, find a minimum subset $S(0,s)$ of $W(0,s)$ that dominates every vertex of ${\mathrm{\cup }}_{j=1}^{s-1}{V}_j$ (every interior vertex).

  For every subgraph $G\left[W\right(i,s\left)\right]$, $i=1,\dots ,r-1$, find a minimum subset $S(i,s)$ of $W(i,s)$ that dominates every vertex of ${\mathrm{\cup }}_{j=(i-1)\times k+s}^{i\times k+s-1}{V}_j$ (every interior vertex).

  For subgraph $G\left[W\right(r,s\left)\right]$, find a minimum subset $S(r,s)$ of $W(r,s)$ that dominates every vertex of ${\mathrm{\cup }}_{j=(r-1)\times k+s}^m{V}_j$ (every interior vertex).

  (c)

  Let $S_s={\mathrm{\cup }}_{i=0}^{r}S(i,s)$.

• Let S be a set of $S_2,\dots ,S_{k+1}$ with the minimum cardinality.

Theorem 3.1 The modified application of Baker’s framework gives an $O\left(2^{\left(6{log}_{4}3\right)(k+2))}kn\right)$ time $(1+2/k)$-approximation algorithm for the planar dominating set problem.

Proof: We first show the approximation ratio of the framework. Notice that $S_s={\mathrm{\cup }}_{i=0}^{r}S(i,s)$ dominates every vertex of

$$\left({\mathrm{\cup }}_{j=1}^{s-1}{V}_j\right)\mathrm{\cup }\left[{\mathrm{\cup }}_{i=1}^{r-1}\left({\mathrm{\cup }}_{j=(i-1)\times k+s}^{i\times k+s-1}{V}_j\right)\right]\mathrm{\cup }\left({\mathrm{\cup }}_{j=(r-1)\times k+s}^m{V}_j\right)={\mathrm{\cup }}_{j=1}^m{V}_j=V\left(G\right)$$

that is, $S_s$ is a dominating set of G. Let D be a minimum dominating set of G and let $D(i,s)=D\cap W(i,s)$, $s=2,\dots ,k+1$ and $0\le i\le r$. Since no vertex of G in $V\left(G\right)\setminus W(i,s)$ can dominate any interior vertex of $G\left[W\right(i,s\left)\right]$ and D dominates every vertex of G, $D(i,s)$ dominates every interior vertex of $G\left[W\right(i,s\left)\right]$. From this and the fact that $S(i,s)$ is a minimum subset of $W(i,s)$ dominating every interior vertex of $G\left[W\right(i,s\left)\right]$, $\left|S\right(i,s\left)\right|\le \left|D\right(i,s\left)\right|$. From this, we have

$$\begin{array}{c}\hfill |S_s|\le {\displaystyle \mathrm{\sum }_{i=0}^r}\left|S(i,s)\right|\le {\displaystyle \mathrm{\sum }_{i=0}^r}\left|D(i,s)\right|\end{array}$$

(4)

Since the vertices of $V_{i\times k+s-1}$ and $V_{i\times k+s}$ appear in subgraphs $G\left[W\right(i,s\left)\right]$ and $G\left[W\right(i+1,s\left)\right]$, $0\le i<r$,

$$\begin{array}{c}\hfill {\displaystyle \mathrm{\sum }_{i=0}^r}\left|D(i,s)\right|\le \left|D\right|+{\displaystyle \mathrm{\sum }_{i=0}^{r-1}}|D\cap V_{i\times k+s-1}|+|D\cap V_{i\times k+s}|\end{array}$$

(5)

Notice that

$$\begin{array}{c}\hfill \underset{s=2}{\overset{k+1}{min}}\{{\displaystyle \mathrm{\sum }_{i=0}^{r-1}}|D\cap V_{i\times k+s-1}|+|D\cap V_{i\times k+s}\left|\right\}\le \frac{2\left|D\right|}{k}\end{array}$$

(6)

Let S be an $S_s$ with a minimum cardinality. Then from Inequalities (4), (5), and (6), we have $\left|S\right|\le \left|D\right|+\frac{2\left|D\right|}{k}$. that is, the solution produced by the modified algorithm has the approximation ratio $(1+2/k)$ for the planar dominating set problem.

Given a planar graph G, a planar embedding of G can be computed in linear time [23]. It is obvious that Step 1 and Step 3 can be computed in linear time. Step 2 (a) and (c) can be computed in $O\left(kn\right)$ time. Recall that FT Algorithm (by Fomin and Thilikos [14]) is the most efficient known exact algorithm for the planar dominaing set problem. We use FT Algorithm for Step 2 (b). Given a graph G and a branch-decomposition of G with width β, FT Algorithm finds an optimal solution for the dominating set problem in $O\left(2^{\left(3{log}_{4}3\right)\beta }n\right)$ time. Each subgraph $G\left[W\right(i,s\left)\right]$ is $(k+2)$-outer planar and has branchwidth at most $2(k+2)$. A branch-decomposition of $G\left[W\right(i,s\left)\right]$ with width at most $2(k+2)$ can be computed in linear time [24]. Each vertex of G appears in at most two subgraphs for a specific value s. Therefore, Step 2 (b) takes

$${\displaystyle \mathrm{\sum }_{s=2}^{k+1}}{\displaystyle \mathrm{\sum }_{i=0}^r}O(2^{\left(6{log}_{4}3\right)(k+2)}\left|W(i,s)\right|)={\displaystyle \mathrm{\sum }_{s=2}^{k+1}}O\left(2^{\left(6{log}_{4}3\right)(k+2)}n\right)=O\left(2^{\left(6{log}_{4}3\right)(k+2)}kn\right)$$

time which is the dominating part of the modified application’s running time. []

Notice that if G is decomposed into $(2k+2)$-outer planar subgraphs, the modified PTAS achieves the approximation ratio $(1+1/k)$ and has running time $O\left(2^{\left(12{log}_{4}3\right)(k+1)}kn\right)$.

We conclude this section by comparing the running time of the modified PTAS with that of the application of Baker’s framework in Section 3.1 for the planar dominating set problem. We assume that the most efficient FT Algorithm is used in Step 2 (b) of both algorithms. Assume that G is decomposed into $(k+1)$-outer planar subgraphs in Baker’s framework in Section 3.1. Then a branch-decomposition of $G\left[U\right(i,s\left)\right]$ with width at most $2(k+1)$ can be computed in linear time and Step 2 (b) takes

$${\displaystyle \mathrm{\sum }_{s=2}^{k+1}}{\displaystyle \mathrm{\sum }_{i=0}^r}O(2^{\left(6{log}_{4}3\right)(k+1)}\left|U(i,s)\right|)=O\left(2^{\left(6{log}_{4}3\right)(k+1)}kn\right)$$

time which is the dominating part of the framework’s running time. The constant in the exponent of the running time of the modified PTAS for the approximation ratio $(1+1/k)$ is as twice as that of Baker’s framework in Section 3.1.

4. Computational Study of PTAS

We study the practical performance of the PTAS for the planar dominating set problem. The PTAS is implemented in C++ and its performance is tested for four different classes of graphs including the Delaunay triangulations of point sets taken from TSPLIB [25] (Class (1)), triangulations (Class (2)) and intersection graphs (Class (3)) generated by LEDA [26] and Gabriel graphs (Class (4)) generated using the points uniformly distributed in a two-dimensional plane. Those classes of graphs are well used in previous computational studies and the branchwidth of the graphs increases in the size of graphs (for classes of graphs with small branchwidth such as the maximal random planar graphs from LEDA [26], the FT algorithm can find optimal solutions efficiently [21] and thus they are not interesting in this study). The computer used for testing has an AMD Athlon(tm) 64 X2 Dual Core Processor 4600+ (2.4 GHz) and 3 GByte of internal memory. The operating system is SUSE Linux 10.2.

We use the FT algorithm to compute an optimal solution for each $(k+2)$-outer planar subgraph. There are three major steps of FT Algorithm:

• Compute a linear size kernel H of the subgraph using the $O\left(n^3\right)$ time kernelization algorithm by Alber et al. [12].
• Compute an optimal branch-decomposition of H by the $O\left(n^3\right)$ time algorithm [17,18].
• Find an optimal solution for H by dynamic programming based on the branch-decomposition of H and compute an optimal solution for the subgraph from the optimal solution for H.

Step 3 has exponential time complexity and memory complexity in the width of the branch-decomposition used, and is the dominating part in the running time and used memory of the FT algorithm. Thus we include the kernelization in the FT algorithm because, for a kernel H of a graph G, $\text{bw}\left(H\right)\le \text{bw}\left(G\right)$ and it often happens that $\text{bw}\left(H\right)<\text{bw}\left(G\right)$ for a kernel computed. Also, the effort for computing an optimal branch-decomposition reduces the running time and used memory in practice. For a planar graph G, the FT algorithm implemented runs in $O(2^{\left(3{log}_{4}3\right)\text{bw}\left(H\right)}\gamma \left(G\right)+n^3)$ time and uses $O\left(3^{\text{bw}\left(H\right)}\gamma \left(G\right)\right)$ memory space. Readers may refer to [21] for more details on the practical performance of the FT algorithm.

Table Table 1 shows the computational results of the PTAS for the planar dominating set problem. For every instance, we calculate the approximated solutions for two different values of k, 3 and 4, and, for every value of k, we calculate the $(k+2)$-outer planar decomposition for every face of the instance. We choose the best value for an approximated solution. For some instances with small branchwidth, we also include the optimal solutions computed by the FT algorithm and reported in [21] in the column of ”Exact Alg.”. The size of a minimum dominating set of graph G, computed by the FT algorithm, is indicated by $\gamma \left(G\right)$ in Table 1, and for every value of k, $D_{PTAS}$ is the size of dominating set computed by the PTAS. In the table, $bw$ is the branchwidth of G, β is the branchwidth of a kernel H of G in the FT algorithm and the largest branchwidth of a kernel H of a $(k+2)$-outer planar subgraph in PTAS. The running time is in seconds. For two large instances rand16000 and rand20000, we only compute $\gamma \left(G\right)$ but not the minimum dominating sets by the FT algorithm due to the memory constraint. These values of $\gamma \left(G\right)$ are identified by “*”.

In order to compare the size of dominating sets obtained from the PTAS with the optimal solutions, we include some instances with small branchwidth for every class of graphs, such that a minimum dominating set can be computed by FT Algorithm. The Exact Alg. column shows the results of FT Algorithm reported in [21]. We use two values for k to decompose the instances into $(k+2)$-outer planar component. Notice that the branchwidth of every $(k+2)$-outer planar graph is at most $2(k+2)$. Hence, by increasing k the size of subgraphs and their branchwidth will increase. Theoretical results suggest that increasing k gives smaller approximated solutions for minimization problems. Our computing results confirm the theoretical analysis of the k-outer planar decomposition method. For example, for $k=4$, every instance can be decomposed into subgraphs with a branchwidth of at most 12. This is the largest value of branchwidth that can be processed on our computational platform in a practical time.

Since the theory of NP-completeness has reduced hopes that NP-hard problems can be solved in polynomial time, heuristic and approximation algorithms have attracted more attentions. These algorithms compute near optimal solutions within a reasonable time for problems of practical size. We compare the performance of the PTAS with the performance of three different heuristic algorithms introduced in [22] for the planar dominating set problem. In what follows we briefly explain these heuristic algorithms (for more details please refer to [22]).

In [22], six heuristic algorithms for the dominating set problem are studied. We test the performance of these six methods, but only report three of them with better performances. The three reported heuristics are described below. Let D be a dominating set computed by these heuristics.

Table 1. Computational results (time in seconds) of PTAS for the planar dominating set problem.

	Graph G	|E(G)|	bw	Exact Alg.			k = 3			k = 4
				γ (G)	β	time	DPTAS	β	time	DPTAS	β	time
(1)	kroB150	436	10	23	10	10	28	8	2.07	-	-	-
	pr299	864	11	47	11	37	56	10	11.42	-	-	-
	tsp225	622	12	37	12	110	46	9	5.21	-	-	-
	a280	788	13	43	13	337	53	10	8.40	51	12	12.09
	rd400	1183	17	-	-	-	75	10	35.30	74	12	351.93
	pcb442	1286	17	-	-	-	79	10	10.46	78	10	10.86
	d657	1958	22	-	-	-	123	10	64.89	120	12	604.10
	pr1002	2972	21	-	-	-	190	10	115.65	182	12	1253.9
(2)	tri2000	5977	8	321	7	198	361	7	175.59	-	-	-
	tri4000	11969	9	653	7	1903	724	7	733.06	-	-	-
	tri6000	17979	9	975	8	3576	1136	8	1994.53	-	-	-
	tri8000	23975	9	1283	7	7750	1430	7	2858.63	-	-	-
	tri10000	29976	9	1606	7	16495	1804	7	4977.06	-	-	-
	tri11000	32972	14	-	-	-	1987	8	5910.8	1958	8	12341.1
	tri12000	35974	14	-	-	-	2164	7	5370.18	2132	7	6865.08
	tri14000	41974	15	-	-	-	2514	7	8220.49	2434	7	9208.72
	tri16000	47969	16	-	-	-	2920	7	10060.1	2885	7	12794.4
(3)	rand6000	10293	11	1563	9	150	1658	8	104.85	-	-	-
	rand10000	17578	13	2535	10	869	2850	8	535.87	2692	9	432.23
	rand15000	26717	14	3758	12	2769	4144	10	1313.14	-	-	-
	rand16000	28624	13	4002*	13	5917	4379	10	2443.27	4295	11	2027.7
	rand20000	35975	14	4963*	14	13993	5465	10	4241.65	5368	12	5017.02
	rand25000	40378	16	-	-	-	7101	8	6407.91	6632	12	9470
(4)	Gab500	949	13	115	12	238	136	10	18.02	129	10	18.95
	Gab600	1174	14	135	14	3074	164	10	26.05	156	10	22.10
	Gab700	1302	14	162	14	5710	187	10	22.81	183	10	24.30
	Gab800	1533	17	-	-	-	225	10	51.82	205	12	24.30
	Gab900	1758	17	-	-	-	243	10	48.39	231	12	344.50
	Gab1000	1901	18	-	-	-	260	10	49.69	259	12	781.89
	Gab1500	2870	21	-	-	-	402	10	116.37	385	12	960.71

Table 1. Computational results (time in seconds) of PTAS for the planar dominating set problem.

	Graph G	|E(G)|	bw	Exact Alg.			k = 3			k = 4
				γ (G)	β	time	DPTAS	β	time	DPTAS	β	time
(1)	kroB150	436	10	23	10	10	28	8	2.07	-	-	-
	pr299	864	11	47	11	37	56	10	11.42	-	-	-
	tsp225	622	12	37	12	110	46	9	5.21	-	-	-
	a280	788	13	43	13	337	53	10	8.40	51	12	12.09
	rd400	1183	17	-	-	-	75	10	35.30	74	12	351.93
	pcb442	1286	17	-	-	-	79	10	10.46	78	10	10.86
	d657	1958	22	-	-	-	123	10	64.89	120	12	604.10
	pr1002	2972	21	-	-	-	190	10	115.65	182	12	1253.9
(2)	tri2000	5977	8	321	7	198	361	7	175.59	-	-	-
	tri4000	11969	9	653	7	1903	724	7	733.06	-	-	-
	tri6000	17979	9	975	8	3576	1136	8	1994.53	-	-	-
	tri8000	23975	9	1283	7	7750	1430	7	2858.63	-	-	-
	tri10000	29976	9	1606	7	16495	1804	7	4977.06	-	-	-
	tri11000	32972	14	-	-	-	1987	8	5910.8	1958	8	12341.1
	tri12000	35974	14	-	-	-	2164	7	5370.18	2132	7	6865.08
	tri14000	41974	15	-	-	-	2514	7	8220.49	2434	7	9208.72
	tri16000	47969	16	-	-	-	2920	7	10060.1	2885	7	12794.4
(3)	rand6000	10293	11	1563	9	150	1658	8	104.85	-	-	-
	rand10000	17578	13	2535	10	869	2850	8	535.87	2692	9	432.23
	rand15000	26717	14	3758	12	2769	4144	10	1313.14	-	-	-
	rand16000	28624	13	4002*	13	5917	4379	10	2443.27	4295	11	2027.7
	rand20000	35975	14	4963*	14	13993	5465	10	4241.65	5368	12	5017.02
	rand25000	40378	16	-	-	-	7101	8	6407.91	6632	12	9470
(4)	Gab500	949	13	115	12	238	136	10	18.02	129	10	18.95
	Gab600	1174	14	135	14	3074	164	10	26.05	156	10	22.10
	Gab700	1302	14	162	14	5710	187	10	22.81	183	10	24.30
	Gab800	1533	17	-	-	-	225	10	51.82	205	12	24.30
	Gab900	1758	17	-	-	-	243	10	48.39	231	12	344.50
	Gab1000	1901	18	-	-	-	260	10	49.69	259	12	781.89
	Gab1500	2870	21	-	-	-	402	10	116.37	385	12	960.71

Greedy: Initially, D is empty. In each iteration, a vertex which dominates a maximum number of vertices in $V\left(G\right)\setminus D$ is added to D.

Greedy-Rev: Initially $D=V\left(G\right)$. In each iteration, a vertex is removed from D, such that the resulting set remains a dominating set of G. A vertex is chosen to be removed, by ordering the vertices of D in increasing node degree, and removing the first vertex that does not dominate any vertex uniquely.

Greedy-Vote: Initially, D is empty. This algorithm does not include a vertex u in D only based on the number of vertices which are dominated by u. It uses a more complex voting scheme to select a vertex to be included. We omit the details of the selection scheme and readers may refer to [22] for details.

Table 2. Computational results for heuristic algorithms and PTAS for the planar dominating set problem (time in seconds).

	Graph G	|E(G)|	γ(G)	Greedy Alg.		Greedy-Rev Alg.		Greedy-Vote Alg.		PTAS
				DGr	time	DRev	time	DVote	time	DPTAS	time
(1)	kroB150	436	23	27	0.002	31	0.01	31	0.002	28	2.08
	pr299	864	47	54	0.003	63	0.032	62	0.005	56	11.42
	tsp225	622	37	49	0.153	54	0.02	50	0.003	46	5.21
	a280	788	43	51	0.004	62	0.025	62	0.006	51	12.09
	rd400	1183	-	78	0.007	92	0.032	90	0.009	74	351.93
	pcb442	1286	-	76	0.908	90	0.063	87	0.01	78	10.86
	d657	1958	-	126	0.016	146	0.128	143	0.021	120	604.10
	pr1002	2972	-	190	0.032	236	0.328	194	0.04	182	1253.9
(2)	tri2000	5977	321	365	0.116	379	1.119	464	0.168	361	175.59
	tri4000	11969	653	729	0.183	765	1.792	787	0.544	724	733.06
	tri6000	17979	975	1118	0.418	1166	4.14	1306	0.541	1136	1994.53
	tri8000	23975	1283	1449	0.715	1522	7.003	1653	0.918	1430	2858.63
	tri10000	29976	1606	1819	1.117	1906	11.524	2302	1.572	1804	4977.06
	tri11000	32972	-	2040	1.375	2116	14.092	3431	2.561	1958	12341.1
	tri12000	35974	-	2186	1.607	2278	16.538	2741	2.243	2132	6865.08
	tri14000	41974		2576	2.462	2664	22.976	3317	3.163	2434	9208.72
	tri16000	47969	-	2917	2.839	3033	30.694	3684	4.005	2885	12794.4
(3)	rand6000	10293	1563	1932	0.748	2166	4.517	2908	1.206	1658	104.85
	rand10000	17578	2535	3197	2.06	3618	13.33	4164	2.878	2692	432.23
	rand15000	26717	3758	4698	4.861	5402	29.487	7277	7.641	4144	1313.14
	rand16000	28624	4002*	5039	5.176	5744	35.589	7552	10.327	4295	2027.7
	rand20000	35975	4963*	6273	8.053	7168	55.948	8571	11.903	5398	5017.02
	rand25000	45327	-	7772	12.467	8942	91.039	11865	20.615	6632	9470
(4)	Gab500	949	115	146	0.006	173	0.039	160	0.007	129	18.95
	Gab600	1174	135	168	0.007	199	0.051	171	0.009	156	22.10
	Gab700	1302	162	200	0.01	242	0.072	238	0.012	183	24.30
	Gab800	1533	-	227	0.012	270	0.097	307	0.019	205	24.30
	Gab900	1758	-	254	0.016	303	0.103	323	0.022	231	344.50
	Gab1000	1901	-	280	0.019	344	0.146	423	0.03	259	781.89
	Gab1500	2870	-	426	0.042	507	0.335	496	0.051	385	960.71

Table 2. Computational results for heuristic algorithms and PTAS for the planar dominating set problem (time in seconds).

	Graph G	|E(G)|	γ(G)	Greedy Alg.		Greedy-Rev Alg.		Greedy-Vote Alg.		PTAS
				DGr	time	DRev	time	DVote	time	DPTAS	time
(1)	kroB150	436	23	27	0.002	31	0.01	31	0.002	28	2.08
	pr299	864	47	54	0.003	63	0.032	62	0.005	56	11.42
	tsp225	622	37	49	0.153	54	0.02	50	0.003	46	5.21
	a280	788	43	51	0.004	62	0.025	62	0.006	51	12.09
	rd400	1183	-	78	0.007	92	0.032	90	0.009	74	351.93
	pcb442	1286	-	76	0.908	90	0.063	87	0.01	78	10.86
	d657	1958	-	126	0.016	146	0.128	143	0.021	120	604.10
	pr1002	2972	-	190	0.032	236	0.328	194	0.04	182	1253.9
(2)	tri2000	5977	321	365	0.116	379	1.119	464	0.168	361	175.59
	tri4000	11969	653	729	0.183	765	1.792	787	0.544	724	733.06
	tri6000	17979	975	1118	0.418	1166	4.14	1306	0.541	1136	1994.53
	tri8000	23975	1283	1449	0.715	1522	7.003	1653	0.918	1430	2858.63
	tri10000	29976	1606	1819	1.117	1906	11.524	2302	1.572	1804	4977.06
	tri11000	32972	-	2040	1.375	2116	14.092	3431	2.561	1958	12341.1
	tri12000	35974	-	2186	1.607	2278	16.538	2741	2.243	2132	6865.08
	tri14000	41974		2576	2.462	2664	22.976	3317	3.163	2434	9208.72
	tri16000	47969	-	2917	2.839	3033	30.694	3684	4.005	2885	12794.4
(3)	rand6000	10293	1563	1932	0.748	2166	4.517	2908	1.206	1658	104.85
	rand10000	17578	2535	3197	2.06	3618	13.33	4164	2.878	2692	432.23
	rand15000	26717	3758	4698	4.861	5402	29.487	7277	7.641	4144	1313.14
	rand16000	28624	4002*	5039	5.176	5744	35.589	7552	10.327	4295	2027.7
	rand20000	35975	4963*	6273	8.053	7168	55.948	8571	11.903	5398	5017.02
	rand25000	45327	-	7772	12.467	8942	91.039	11865	20.615	6632	9470
(4)	Gab500	949	115	146	0.006	173	0.039	160	0.007	129	18.95
	Gab600	1174	135	168	0.007	199	0.051	171	0.009	156	22.10
	Gab700	1302	162	200	0.01	242	0.072	238	0.012	183	24.30
	Gab800	1533	-	227	0.012	270	0.097	307	0.019	205	24.30
	Gab900	1758	-	254	0.016	303	0.103	323	0.022	231	344.50
	Gab1000	1901	-	280	0.019	344	0.146	423	0.03	259	781.89
	Gab1500	2870	-	426	0.042	507	0.335	496	0.051	385	960.71

We study the performances of the above heuristic algorithms for the four classes of planar graphs that are used in the study of the PTAS. These heuristic algorithms are implemented in C++. Table 2 shows the computational results of these heuristic algorithms and the PTAS. In Table 2, $D_{Gr},D_{Rev}$, and $D_{Vote}$ are the sizes of dominating sets computed by the heuristic algorithm Greedy, Greedy-Rev, and Greedy-Vote, respectively. For every graph instance, if the size of the instance allows the application of the FT algorithm, we include the size of the minimum dominating set of the instance, as well. For the PTAS, we include the best result $D_{PTAS}$ for every instance from Table 1. Time in the table is in seconds. The results in the table show that the heuristic algorithms are always faster than the PTAS. However, the size of dominating sets computed by the heuristics are larger than those by the PTAS for most of instances.

Based on our computational results, the Greedy algorithm gives the smallest dominating sets compared to other heuristic algorithms. Table 3 shows the results of our computational study for the FT algorithm, Greedy (the best heuristic method) and PTAS for graph instances whose branchwidths are small enough to run the FT algorithm.

Table 3. Computational results for Exact, Greedy and PTAS algorithms for small instances (time in seconds).

	Graph G	|E(G)|	Exact Alg.		Greedy Alg.		PTAS
			γ(G)	time	DG	time	DPTAS	time
(1)	kroB150	436	23	10	27	0.002	28	2.08
	pr299	864	47	37	54	0.032	56	11.42
	tsp225	622	37	110	49	0.153	46	5.21
	a280	788	43	337	51	0.004	51	12.09
(2)	tri2000	5977	321	198	365	0.116	361	175.59
	tri4000	11969	653	1903	729	0.183	724	733.06
	tri6000	17979	975	3576	1118	0.418	1136	1994.53
	tri8000	23975	1283	7750	1449	0.715	1430	2858.63
	tri10000	29976	1606	16495	1819	1.117	1804	4977.06
(3)	rand6000	10293	1563	150	1932	0.748	1658	104.85
	rand10000	17578	2535	869	3197	2.06	2692	432.23
	rand15000	26727	3758	2769	4698	4.861	4144	1313.14
	rand16000	28624	4002*	5917	5039	5.176	4295	2027.7
	rand20000	35975	4963*	13993	6273	8.053	5398	5017.02
(4)	Gab500	949	115	238	146	0.006	129	18.95
	Gab600	1174	135*	3074	168	0.007	156	22.10
	Gab700	1302	162*	5710	200	0.01	183	24.30

Table 3. Computational results for Exact, Greedy and PTAS algorithms for small instances (time in seconds).

	Graph G	|E(G)|	Exact Alg.		Greedy Alg.		PTAS
			γ(G)	time	DG	time	DPTAS	time
(1)	kroB150	436	23	10	27	0.002	28	2.08
	pr299	864	47	37	54	0.032	56	11.42
	tsp225	622	37	110	49	0.153	46	5.21
	a280	788	43	337	51	0.004	51	12.09
(2)	tri2000	5977	321	198	365	0.116	361	175.59
	tri4000	11969	653	1903	729	0.183	724	733.06
	tri6000	17979	975	3576	1118	0.418	1136	1994.53
	tri8000	23975	1283	7750	1449	0.715	1430	2858.63
	tri10000	29976	1606	16495	1819	1.117	1804	4977.06
(3)	rand6000	10293	1563	150	1932	0.748	1658	104.85
	rand10000	17578	2535	869	3197	2.06	2692	432.23
	rand15000	26727	3758	2769	4698	4.861	4144	1313.14
	rand16000	28624	4002*	5917	5039	5.176	4295	2027.7
	rand20000	35975	4963*	13993	6273	8.053	5398	5017.02
(4)	Gab500	949	115	238	146	0.006	129	18.95
	Gab600	1174	135*	3074	168	0.007	156	22.10
	Gab700	1302	162*	5710	200	0.01	183	24.30

Since the branchwidth of graphs in Class(1) grow quickly in the size of graphs, we have only included small instances of this class in Table 3. From the results of the table, we recommend the FT algorithm for optimal solutions if the branchwidth of a graph in Class (1) is smaller than 14. For the instances of Class (2), FT Algorithm is time consuming. If the running time is the driving factor, we suggest the Greedy algorithm for this class of graphs. For the instances of Classes (3) and (4), as the results in Table 3 suggest, the sizes of dominating sets computed by Greedy are considerably bigger than those computed by the PTAS. Moreover, the FT algorithm is time consuming, rendering the PTAS a better choice. For instance, for graph instance rand20000 with 35,975 edges, the FT algorithm takes almost four hours to compute the size of an optimal dominating set (not the set itself), while the PTAS computes a dominating set of a slightly larger size than the optimal value in less than two hours.

Table 4 shows the computational results for the instances that the FT algorithm is not able to find an optimal solution in practical time and memory space. The computational results show that for all of these instances, except one, the $D_{PTAS}$ is smaller than $D_{Gr}$. In summary, for applications with running-time priority, Greedy is a better choice to compute an approximated dominating set, and if the running-time is not a big concern, the PTAS is a better option for instances whose optimal dominating set cannot be computed by the FT algorithm in a practical time.

Table 4. Computational results for Greedy and PTAS for large instances (time in seconds).

	Graph G	|E(G)|	Greedy Alg.		PTAS
			DGr	time	DPTAS	time
(1)	rd400	1183	78	0.007	74	351.93
	pcb442	1286	76	0.908	78	10.86
	d657	1958	126	0.016	120	604.10
	pr1002	2972	190	0.032	182	1253.9
(2)	tri11000	32972	2040	1.375	1958	12341.1
	tri12000	35974	2186	1.607	2132	6865.08
	tri14000	41974	2576	2.462	2434	9208.72
	tri16000	47969	2917	2.839	2885	12794.4
(3)	rand25000	45327	7772	12.467	6632	9470
(4)	Gab800	1533	227	0.012	205	24.30
	Gab900	1758	254	0.016	231	344.50
	Gab1000	1901	280	0.019	259	781.89
	Gab1500	2870	426	0.042	385	960.71

Table 4. Computational results for Greedy and PTAS for large instances (time in seconds).

	Graph G	|E(G)|	Greedy Alg.		PTAS
			DGr	time	DPTAS	time
(1)	rd400	1183	78	0.007	74	351.93
	pcb442	1286	76	0.908	78	10.86
	d657	1958	126	0.016	120	604.10
	pr1002	2972	190	0.032	182	1253.9
(2)	tri11000	32972	2040	1.375	1958	12341.1
	tri12000	35974	2186	1.607	2132	6865.08
	tri14000	41974	2576	2.462	2434	9208.72
	tri16000	47969	2917	2.839	2885	12794.4
(3)	rand25000	45327	7772	12.467	6632	9470
(4)	Gab800	1533	227	0.012	205	24.30
	Gab900	1758	254	0.016	231	344.50
	Gab1000	1901	280	0.019	259	781.89
	Gab1500	2870	426	0.042	385	960.71

5. Concluding Remarks

It is mentioned that Baker’s k-outer planar graph decomposition framework can be applied to obtain a PTAS for the planar dominating set problem. We show that, in order to get a PTAS for the planar dominating set problem, the mentioned application needs some modification. We modify the application and give a PTAS for the planar dominating set problem. We also report a computational study on the modified PTAS. Computational studies on exact algorithms and heuristic algorithms for the planar dominating set problem have already been conducted, but no report on PTAS has yet been given. Our study on the PTAS makes the computational study of planar dominating set problem more comprehensive. For larger k, the PTAS gives better solutions, but is more time/memory consuming. Due to the computation platform limitation, we only evaluated the PTAS for small k. It would be interesting to test the practical performances of the PTAS for larger k on more powerful computation platforms. The practical performances of PTASes for other optimization problems in planar graphs are worth investigation.

The authors thank the anonymous reviewers for their constructive comments.