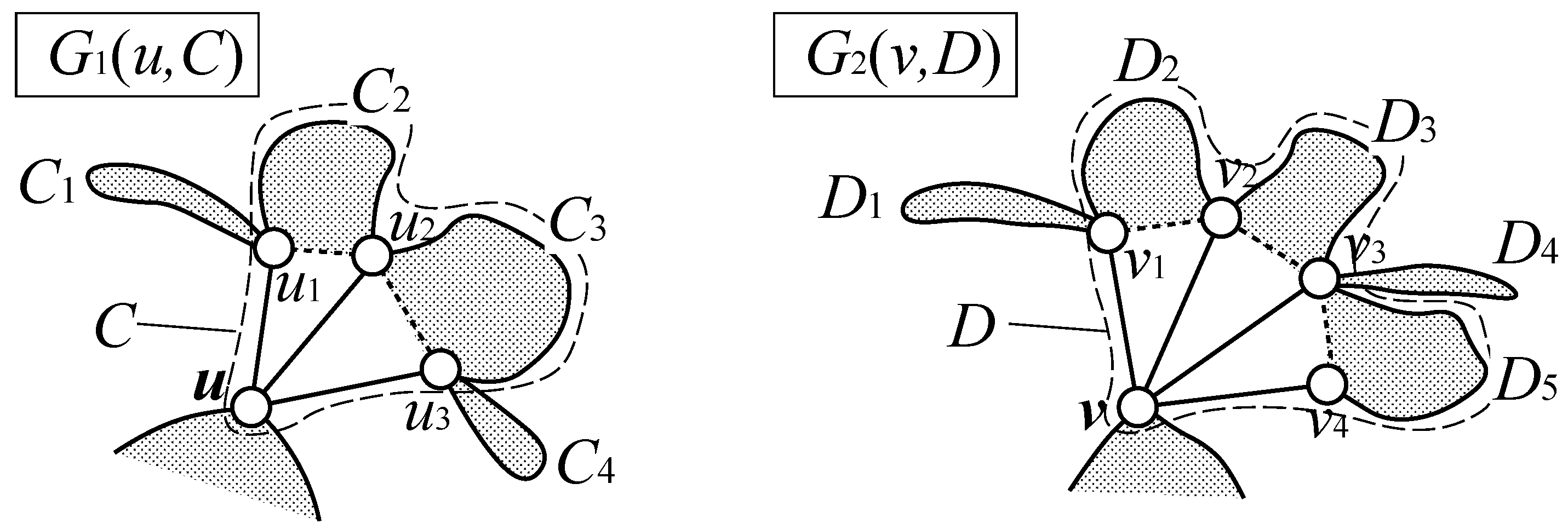A Polynomial-Time Algorithm for Computing the Maximum Common Connected Edge Subgraph of Outerplanar Graphs of Bounded Degree

Abstract

The maximum common connected edge subgraph problem is to find a connected graph with the maximum number of edges that is isomorphic to a subgraph of each of the two input graphs, where it has applications in pattern recognition and chemistry. This paper presents a dynamic programming algorithm for the problem when the two input graphs are outerplanar graphs of a bounded vertex degree, where it is known that the problem is NP-hard, even for outerplanar graphs of an unbounded degree. Although the algorithm repeatedly modifies input graphs, it is shown that the number of relevant subproblems is polynomially bounded, and thus, the algorithm works in polynomial time.

1. Introduction

Finding common parts of graph-structured data is an important and fundamental task in computer science. Among many such problems, the maximum common subgraph problem has applications in various areas, which include pattern recognition [1,2] and chemistry [3,4]. Although there are several variants, the maximum common subgraph problem (MCS) usually means the problem of finding a connected graph with the maximum number of edges that is isomorphic to a subgraph of each of the two input undirected graphs (i.e., the maximum common connected edge subgraph problem).

Because of its importance in pattern recognition and chemistry, many practical algorithms have been developed for MCS and its variants [1,2,3,4]. Some exponential-time algorithms that are better than naive ones have also been developed [5,6]. Kann studied the approximability of MCS and related problems [7].

It is also important for MCS to study a polynomially solvable subclasses of graphs, because graph structures are restricted in many application areas. It is well-known that if input graphs are trees, MCS can be solved in polynomial time using maximum weight bipartite matching [8]. Akutsu showed that MCS can be solved in polynomial time if input graphs are almost trees of bounded degree, whereas MCS remains NP-hard for almost trees of unbounded degree [9], where a graph is called an almost tree if it is connected and the number of edges in each biconnected component is bounded by the number of vertices plus some constant. Yamaguchi et al. developed a polynomial-time algorithm for MCS and the maximum common induced connected subgraph problem for a degree bounded partial k-tree and a graph with a polynomially bounded number of spanning trees, where k is a constant [10]. However, the latter condition seems rather artificial. Schietgat et al. developed a polynomial-time algorithm for outerplanar graphs under the block-and-bridge preserving subgraph isomorphism [11]. However, they modified the definition of MCS by this restriction. Although it was announced that MCS can be solved in polynomial time if input graphs are partial k-trees and MCS must be k-connected (for example, see [12]), the restriction that subgraphs are k-connected is too strict from a practical viewpoint. As for the subgraph isomorphism problem, which is closely related to MCS, polynomial-time algorithms have been developed for biconnected outerplanar graphs [13,14] and for partial k-trees with some constraints, as well as their extensions [15,16].

In this paper, we present a polynomial-time algorithm for outerplanar graphs of a bounded degree (a preliminary version has appeared in [17]). Although this graph class is not a superset of the classes in previous studies [9,10], it covers a wide range of chemical compounds (it was reported that 94.4% of chemical compounds in the NCI database have outerplanar graph structures [18]). Furthermore, the algorithm and its analysis in this paper are not simple extensions or variants of those for the subgraph isomorphism problem for outerplanar graphs [13,14] or partial k-trees [15,16]. These algorithms heavily depend on the property that each connected component in a subgraph is not decomposed. However, to be discussed in Section 4, connected components from both input graphs can be decomposed in MCS, and considering all decompositions easily leads to exponential-time algorithms. In order to cope with this difficulty, we introduce the concept of a blade. The blade and its analysis play a key role in this paper.

It is to be noted that the number of MCS can be exponential even for trees [19]. Therefore, our proposed algorithm and all polynomial-time algorithms mentioned above are focusing on finding the one of MCS’s. It should also be noted that the proposed algorithm is not practical, because the polynomial degree is very high, although it gives a non-trivial theoretical result on the computation of MCS.

2. Preliminaries

A graph is called outerplanar if it can be drawn on a plane such that all vertices lie on the outer face (i.e., the unbounded exterior region) without crossing of edges. Although there exist many embeddings (i.e., drawings on a plane) of an outerplanar graph, it is known that one embedding can be computed in linear time. Therefore, in this paper, we assume that each graph is given with its planar embedding. A path is called simple if it does not pass the same vertex multiple times. In this paper, a path always means a simple path that is not a cycle.

A cut vertex of a connected graph is a vertex whose removal disconnects the graph. A graph is biconnected if it is connected and does not have a cut vertex. A maximal biconnected subgraph is called a biconnected component. A biconnected component is called a block if it consists of at least three vertices; otherwise, it is an edge and called a bridge. An edge in a block is called an outer edge if it lies on the boundary of the outer face; otherwise, it is called an inner edge. It is well-known that any block of an outerplanar graph has a unique Hamiltonian cycle, which consists of outer edges only [20]. For the details of the terminology used in graphs and outerplanar graphs, refer to an appropriate textbook on graph theory (e.g., [21]).

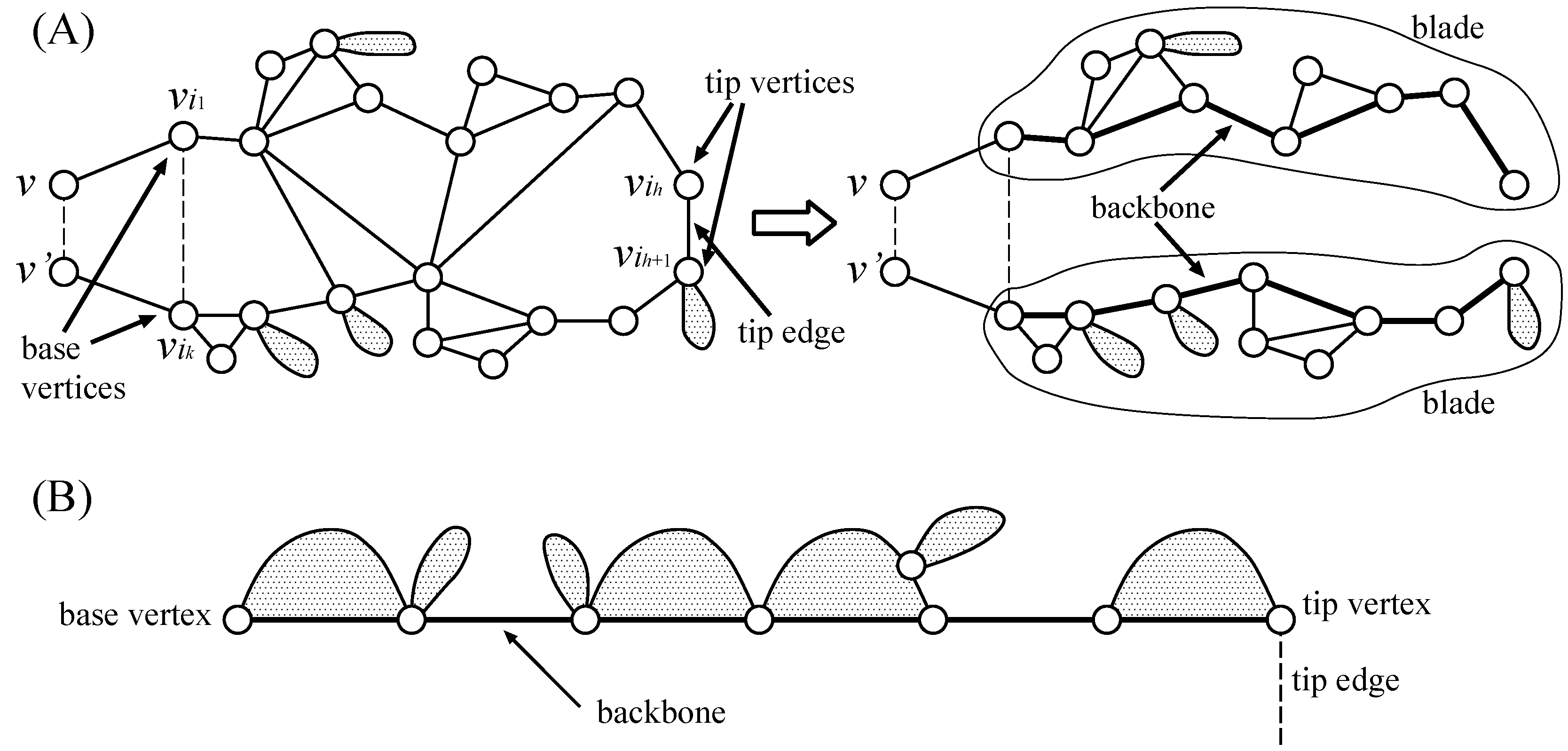
If we fix an arbitrary vertex of a graph G as the root r, we can define the parent-child relationship on biconnected components. For two vertices, u and v, u is called further than v if every simple path from u to r contains v. A biconnected component, C, is called a parent of a biconnected component $C^{\prime }$ if C and $C^{\prime }$ share a vertex v, where v is uniquely determined, and every path from any vertex in $C^{\prime }$ to the root contains v. In such a case, $C^{\prime }$ is called a child of C. A cut vertex v is also called a parent of C if v is contained in both C and its parent component ( both of a cut vertex and a biconnected component can be parents of the same component). Furthermore, the root, r, is a parent of C if r is contained in C.

For each cut vertex v, $G\left(v\right)$ denotes the subgraph of G induced by v and the vertices further than v. For a pair of a cut vertex v and a biconnected component, C, containing v, $G(v,C)$ denotes the subgraph of G induced by vertices in C and its descendant components. For a biconnected component, B, with its parent cut vertex, w, a pair of vertices, v and $v^{\prime }$, in B is called a cut pair if $v\ne v^{\prime }$, $v\ne w$ and $v^{\prime }\ne w$ hold. For a cut pair $(v,v^{\prime })$ in B, $VB(v,v^{\prime })$ denotes the set of the vertices lying on the one of the two paths connecting v and $v^{\prime }$ in the Hamiltonian cycle that does not contain the parent cut vertex, except its endpoints. $B(v,v^{\prime })$ is the subgraph of B induced by $VB(v,v^{\prime })$ and is called a half block. It is to be noted that $B(v,v^{\prime })$ contains both v and $v^{\prime }$. Then, $G(v,v^{\prime })$ denotes the subgraph of G induced by $VB(v,v^{\prime })$ and the vertices in the biconnected components, each of which is a descendant of some vertex in $VB(v,v^{\prime })-\{v,v^{\prime }\}$, and $\overline{G}(v,v^{\prime })$ denotes the subgraph of G induced by the vertices in $G(v,v^{\prime })$ and descendant components of v and $v^{\prime }$, where descendants are defined via the parent-child relationship.

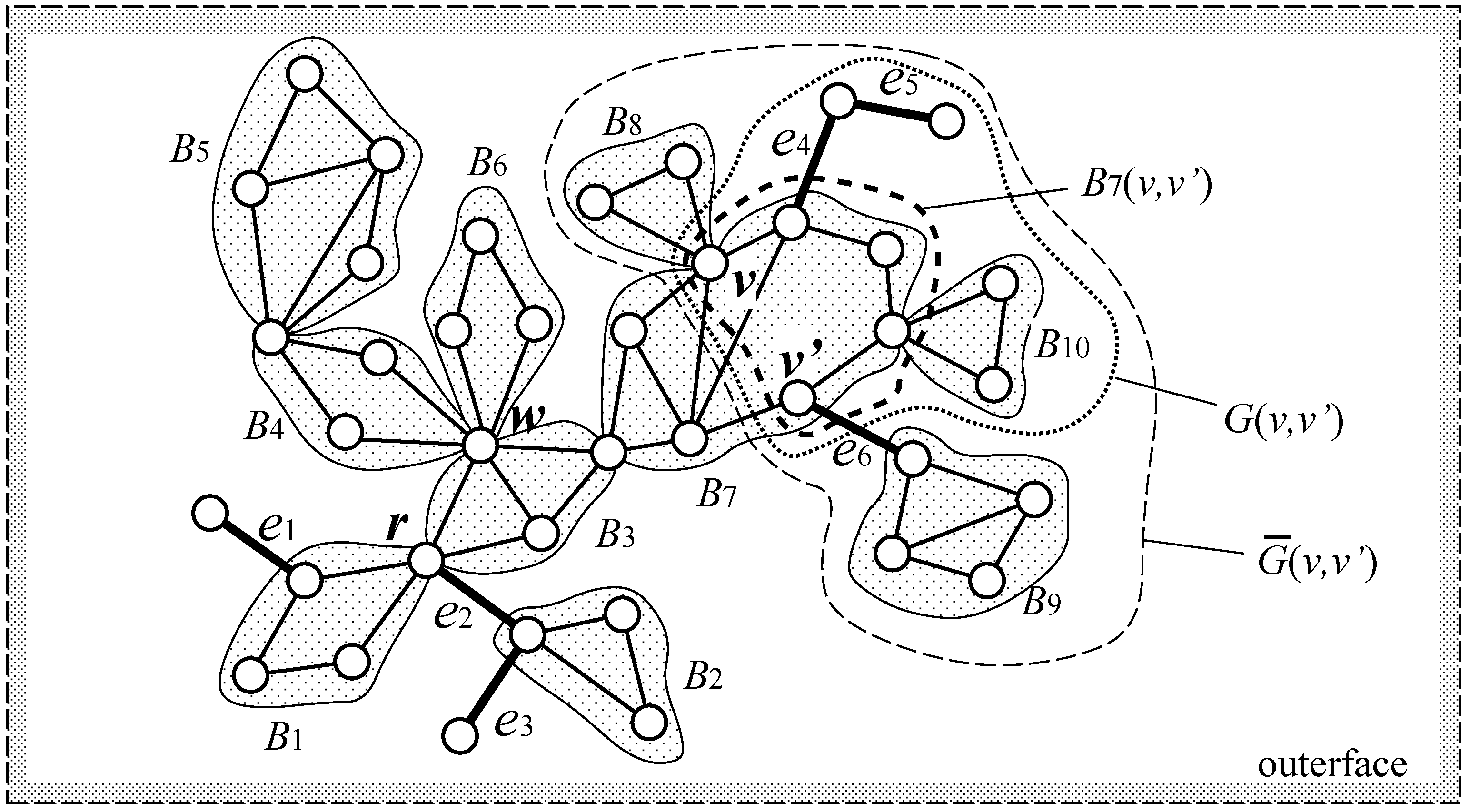
Example Figure 1 shows an example of an outerplanar graph $G(V,E)$. Blocks and bridges are shown by gray regions and bold lines, respectively. $B_1$, $B_3$ and $e_2$ are the children of the root r. $B_4$, $B_6$ and $B_7$ are the children of $B_3$, whereas $B_4$ and $B_6$ are the children of w. Both w and $B_3$ are the parents of $B_4$ and $B_6$. $G\left(w\right)$ consists of $B_4$, $B_5$ and $B_6$, whereas $G(w,B_4)$ consists of $B_4$ and $B_5$. $(v,v^{\prime })$ is a cut pair of $B_7$, and $B_7(v,v^{\prime })$ is a region surrounded by a dashed bold curve. $\overline{G}(v,v^{\prime })$ consists of $B_7(v,v^{\prime })$, $B_8$, $B_9$, $B_{10}$, $e_4$, $e_5$ and $e_6$, whereas $G(v,v^{\prime })$ consists of $B_7(v,v^{\prime })$, $B_{10}$, $e_4$ and $e_5$.

If a connected graph, $G_c(V_c,E_c)$, is isomorphic to a subgraph of $G_1$ and a subgraph of $G_2$, we call $G_c$ a common subgraph of $G_1$ and $G_2$. A common subgraph $G_c$ is called a maximum common connected edge subgraph of $G_1$ and $G_2$ if its size is the maximum among all common subgraphs (we use MCS to denote both the problem and the maximum common subgraph), where the size means the number of edges. In what follows, for the sake of simplicity, a maximum common subgraph (MCS) always means a maximum common connected edge subgraph. In this paper, we consider the following problem.

Figure 1. Example of an outerplanar graph.

Figure 1. Example of an outerplanar graph.

Maximum Common Subgraph of Outerplanar Graphs of Bounded Degree (OUTER-MCS)

Given two undirected connected outerplanar graphs, $G_1$ and $G_2$, whose maximum vertex degree is bounded by a constant, D, find a maximum common subgraph of $G_1$ and $G_2$.

Note that the degree bound is essential, because MCS is NP-hard for outerplanar graphs of unbounded degree, even if each biconnected component consists of at most three vertices [9]. Although we do not consider labels on vertices or edges, our results can be extended to vertex-labeled and/or edge-labeled cases in which label information must be preserved in isomorphic mapping. In the following, n denotes the maximum number of vertices of two input graphs ( it should be noted that the number of vertices and the number of edges are in the same order, since we only consider connected outerplanar graphs).

In this paper, we implicitly make extensive use of the following well-known fact [13], along with outerplanarity of the input graphs.

Fact 1 Let $G_1$ and $G_2$ be biconnected outerplanar graphs. Let $(u_1,u_2,\dots ,u_m)$ (resp. $(v_1,v_2,\dots ,v_n)$) be the vertices of $G_1$ (resp. $G_2$) arranged in clockwise order in a planar embedding of $G_1$ (resp. $G_2$). If there is an isomorphic mapping $\{(u_1,v_{i_1}),(u_2,v_{i_2}),\dots ,(u_m,v_{i_m})\}$ from $G_1$ to a subgraph of $G_2$, then $v_{i_1},v_{i_2},\dots ,v_{i_m}$ appear in $G_2$ in either clockwise or counterclockwise order.

3. Algorithm for a Restricted Case

In this section, we consider the following restricted variant of OUTER-MCS, which is called SIMPLE-OUTER-MCS, and present a polynomial-time algorithm for it: (i) any two vertices in different biconnected components in a maximum common subgraph, $G_c$, must not be mapped to vertices in the same biconnected component in $G_1$ (resp. $G_2$); (ii) each bridge in $G_c$ must be mapped to a bridge in $G_1$ (resp. $G_2$); (iii) the maximum degree need not be bounded.

It is to be noted from the definition of a common subgraph (regardless of the above restrictions) that no two vertices in different biconnected components in $G_1$ (resp. $G_2)$ are mapped to vertices in the same biconnected component in any common subgraph, and no bridge in $G_1$ (resp. $G_2$) is mapped to an edge in a block in any common subgraph (otherwise there would exist a cycle containing the edge in a common subgraph, which would mean that the edge in $G_1$ (resp., $G_2$) is not a bridge).

SIMPLE-OUTER-MCS is intrinsically the same as the one studied by Schietgat et al. [11]. Although our algorithm is more complex and less efficient than their algorithm, we present it here, because the algorithm for a general (but bounded degree) case is rather involved and is based on our algorithm for SIMPLE-OUTER-MCS.

Here, we present a recursive algorithm to compute the size of MCS in SIMPLE-OUTER-MCS, which can be easily transformed into a dynamic programming algorithm to compute an MCS, as is true for many other dynamic programming algorithms. The following is the main procedure of the recursive algorithm.

Procedure $SimpleOuterMCS(G_1,G_2)$

 $s_{max}\leftarrow 0$;

 for all pairs of vertices $(u,v)\in V_1\times V_2$ do

  Let $(u,v)$ be the root pair $(r_1,r_2)$ of $(G_1,G_2)$;

  $s_{max}\leftarrow max(s_{max},MC{S}_c(G_1\left(r_1\right),G_2\left(r_2\right)))$;

 return $s_{max}$.

The algorithm consists of a recursive computation of the following three scores:

$MC{S}_c(G_1\left(u\right),G_2\left(v\right))$:

the size of an MCS $G_c$ between $G_1\left(u\right)$ and $G_2\left(v\right)$, where $(u,v)$ is a pair of the roots or a pair of cut vertices, and $G_c$ must contain a vertex corresponding to both u and v.

$MC{S}_b(G_1(u,C),G_2(v,D))$:

the size of an MCS $G_c$ between $G_1(u,C)$ and $G_2(v,D)$, where $(C,D)$ is either a pair of blocks or a pair of bridges, u (resp. v) is the cut vertex belonging to both C (resp. D) and its parent, $G_c$ must contain a vertex corresponding to both u and v and $G_c$ must contain a biconnected component (which can be empty) corresponding to a subgraph of C and a subgraph D.

$MC{S}_p(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$:

the size of an MCS $G_c$ between $G_1(u,u^{\prime })$ and $G_2(v,v^{\prime })$, where $(u,u^{\prime })$ (resp. $(v,v^{\prime })$) is a cut pair, and $G_c$ must contain a cut pair $(w,w^{\prime })$ corresponding to both $(u,u^{\prime })$ and $(v,v^{\prime })$. If there does not exist such $G_c$ (which must be connected), its score is $-\infty$.

In the following, we describe how to compute these scores.

Computation of $MC{S}_c(G_1\left(u\right),G_2\left(v\right))$

As in the dynamic programming algorithm for MCS for trees or almost trees [9], we construct a bipartite graph and compute a maximum weight matching.

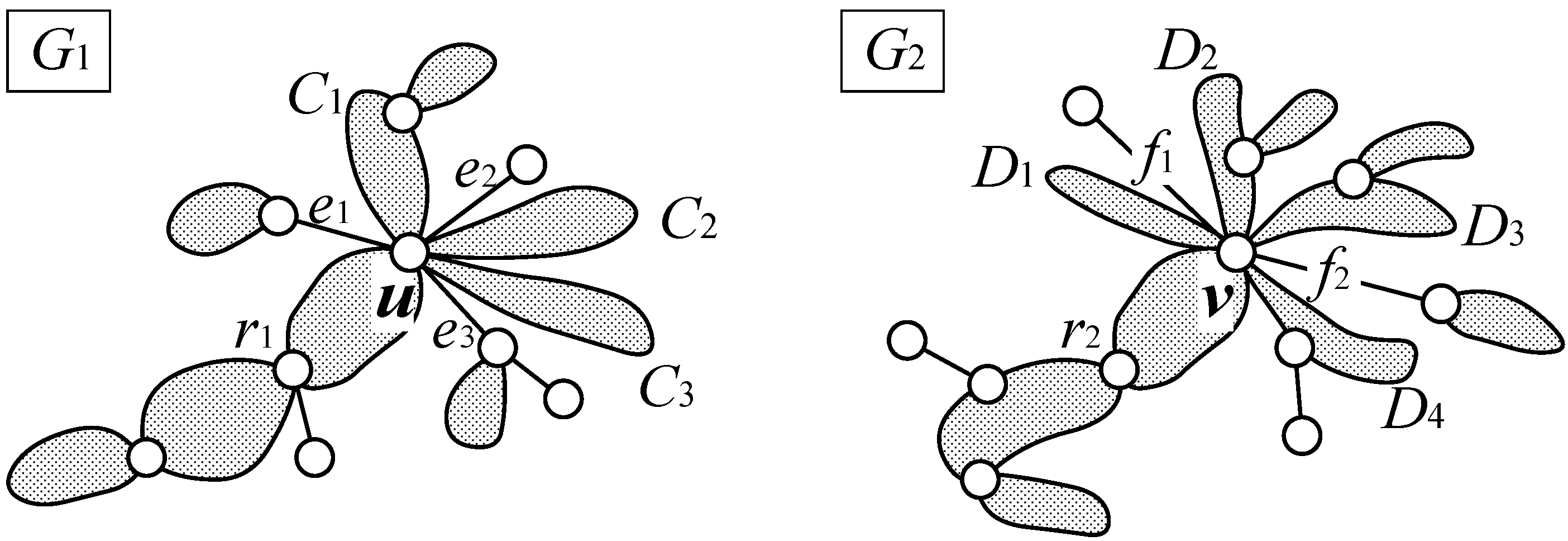
Let $C_1,\dots ,C_{h_1},e_1,\dots ,e_{h_2}$ and $D_1,\dots ,D_{k_1},f_1,\dots ,f_{k_2}$ be children of u and v respectively, where $C_i$’s and $D_j$’s are blocks and $e_i$’s and $f_j$’s are bridges (see Figure 2). We construct an edge-weighted bipartite graph $BG(X,Y;E)$ by

$$\begin{array}{ccc}\hfill X& =& \{C_1,\dots ,C_{h_1},e_1,\dots ,e_{h_2}\}\hfill \\ \hfill Y& =& \{D_1,\dots ,D_{k_1},f_1,\dots ,f_{k_2}\}\hfill \\ \hfill E& =& \left\{\right(x,y\left)\right|x\in X,y\in Y\}\hfill \\ \hfill w(C_i,f_j)& =& 0\hfill \\ \hfill w(C_i,D_j)& =& MC{S}_b(G_1(u,C_i),G_2(v,D_j))\hfill \\ \hfill w(e_i,D_j)& =& 0\hfill \\ \hfill w(e_i,f_j)& =& MC{S}_b(G_1(u,e_i),G_2(v,f_j))\hfill \end{array}$$

Then, we let $MC{S}_c(G_1\left(u\right),G_2\left(v\right))$ be the weight of the maximum weight bipartite matching of $BG(X,Y;E)$. It is to be noted that $w(C_i,f_j)=0$ (resp., $w(e_i,D_j)=0$) comes from the fact that $f_j$ must be mapped to a bridge in $G_c$, but a bridge in $G_c$ must not be mapped to an edge in any block (e.g., $C_i$), because of the condition (ii) of SIMPLE-OUTER-MCS.

Figure 2. Computation of $MC{S}_c(G_1\left(u\right),G_2\left(v\right))$.

Figure 2. Computation of $MC{S}_c(G_1\left(u\right),G_2\left(v\right))$.

Computation of $MC{S}_b(G_1(u,C),G_2(v,D))$

Let $(u_1,u_2,\dots ,u_h)$ be the sequence of vertices in $G_1(u,C)$, such that there exists an edge, $\{u_i,u\}$, for each $u_i$, where $u_1,u_2,\dots ,u_h$ are arranged in clockwise order. $(v_1,v_2,\dots ,v_k)$ is defined for $G_2(v,D)$ in the same way. It is to be noted that $(C,D)$ is either a pair of blocks or a pair of bridges. A pair of subsequences $((u_{i_1},u_{i_2},\dots ,u_{i_g}),(v_{j_1},v_{j_2},\dots ,v_{j_g}))$ is called an alignment if $i_1<i_2<\cdots <i_g$ and $j_1<j_2<\cdots <j_g$ or $j_g<j_{g-1}<\cdots <j_1$ hold ( the latter ordering is required for handling mirror images.), where $g=0$ is allowed. We compute $MC{S}_b(G_1(u,C),G_2(v,D))$ by the following (see Figure 3):

Procedure $SimpleOuterMC{S}_b(G_1(u,C),G_2(v,D))$

 $s_{max}\leftarrow 0$;

 for all alignments $((u_{i_1},u_{i_2},\dots ,u_{i_g}),(v_{j_1},v_{j_2},\dots ,v_{j_g}))$ do;

  if C is a block and $g=1$ then continue; /* blocks must be preserved */

  $s\leftarrow 0$;

  for $t=1$ to g do $s\leftarrow s+1+MC{S}_c(G_1(u_{i_t}),G_2(v_{j_t}))$;

  for $t=2$ to g do $s\leftarrow s+MC{S}_p(G_1(u_{i_{t-1}},u_{i_t}),G_2(v_{j_{t-1}},v_{j_t}))$;

  $s_{max}\leftarrow max(s,s_{max})$;

 return $s_{max}$.

In the above procedure, the first inner for loop takes care of blocks, such as $C_1$, $C_4$, $D_1$ and $D_4$ in Figure 3, whereas the second inner for loop takes care of half blocks, such as $C_2$, $C_3$, $D_2$, $D_3$ and $D_5$ in Figure 3.

For example, consider an alignment, $((u_1,u_2,u_3),(v_1,v_2,v_4))$, in Figure 3, where all alignments are to be examined in the algorithm. Then, the score of this alignment is given by $3+MC{S}_b(G_1(u_1,C_1),G_2(v_1,D_1))+MC{S}_p(G_1(u_1,u_2),G_2(v_1,v_2))$ $+MC{S}_p(G_1(u_2,u_3),G_2(v_2,v_4))$. $MC{S}_b(G_1(u_1,C_1),G_2(v_1,D_1))$ comes via the computation of $MC{S}_c(G_1\left(u_1\right),G_2\left(v_1\right))$, in which $BG(X,Y;E)$ is given by $X=\left\{C_1\right\}$, $Y=\left\{D_1\right\}$, $E=\left\{(C_1,D_1)\right\}$, and thus, the maximum weight matching is given by $w(C_1,D_1)=MC{S}_b(G_1(u_1,C_1),G_2(v_1,D_1))$. In this case, an edge, $\{v,v_3\}$, is removed and then $v_3$ is treated as a vertex on the path connecting $v_2$ and $v_4$ in the outer face. For another example, consider an alignment $(\left(u_1\right),\left(v_1\right))$ in the same figure. Then, this alignment is ignored by the “if ... then ...” line of the procedure, because a bridge in $G_c$, which would correspond to $\{u,u_1\}$ in $G_1$ and $\{v,v_1\}$ in $G_2$, must not be mapped to an edge in C or D. However, if both $\{u,u_1\}$ and $\{v,v_1\}$ are bridges, the resulting score would be $1+MC{S}_c(G_1\left(u_1\right),G_2\left(v_1\right))$.

Figure 3. Computation of $MC{S}_b(G_1(u,C),G_2(v,D))$.

Figure 3. Computation of $MC{S}_b(G_1(u,C),G_2(v,D))$.

Since the above procedure examines all possible alignments, it may take exponential time. However, we can modify it into a dynamic programming procedure, as shown below, where we omit a subprocedure for handling mirror images, because it is trivial. In this procedure, $u_1,u_2,\dots ,u_h$ and $v_1,v_2,\dots ,v_k$ are processed from left to right. In the first for loop, $M[s,t]$ stores the size of MCS between $G_1\left(u_s\right)$ and $G_2\left(v_t\right)$ plus one (corresponding to a common edge between $\{u,u_s\}$ and $\{v,v_t\}$). The double for loop computes an optimal alignment. $M[s,t]$ stores the size of MCS between $G_1(u,C)$ and $G_2(v,D)$ up to $u_s$ and $v_t$, respectively. $flag$ is introduced to ensure the connectedness of a common subgraph. For example, $flag=0$ if $G_1\left(u\right)$ is a triangle, but $G_2\left(v\right)$ is a rectangle. If C (and also D) is an edge, $flag=0$, but the procedure returns $M[1,1]$.

for all $(s,t)\in \{1,\dots ,h\}\times \{1,\dots ,k\}$ do

  $M[s,t]\leftarrow 1+MC{S}_c(G_1\left(u_s\right),G_2\left(v_t\right))$;

 $flag\leftarrow 0$;

 for $s=2$ to h do

  for $t=2$ to k do

   $M[s,t]\leftarrow M[s,t]+{max}_{s^{\prime }<s,t^{\prime }<t}\{M[s^{\prime },t^{\prime }]+MC{S}_p(G_1(u_{s^{\prime }},u_s),G_2(u_{t^{\prime }},u_t))\}$;

   if $M[s,t]>-\infty$ then $flag\leftarrow 1$;

if C is a block and $flag=0$ then return 0 else return ${max}_{s,t}M[s,t]$.

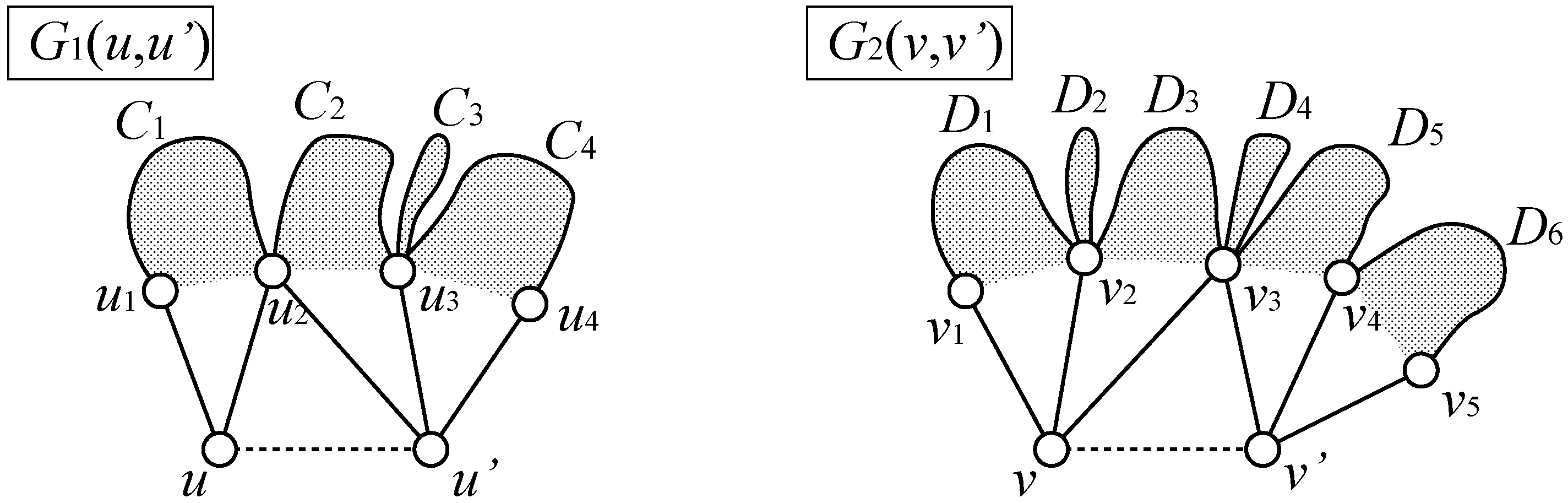
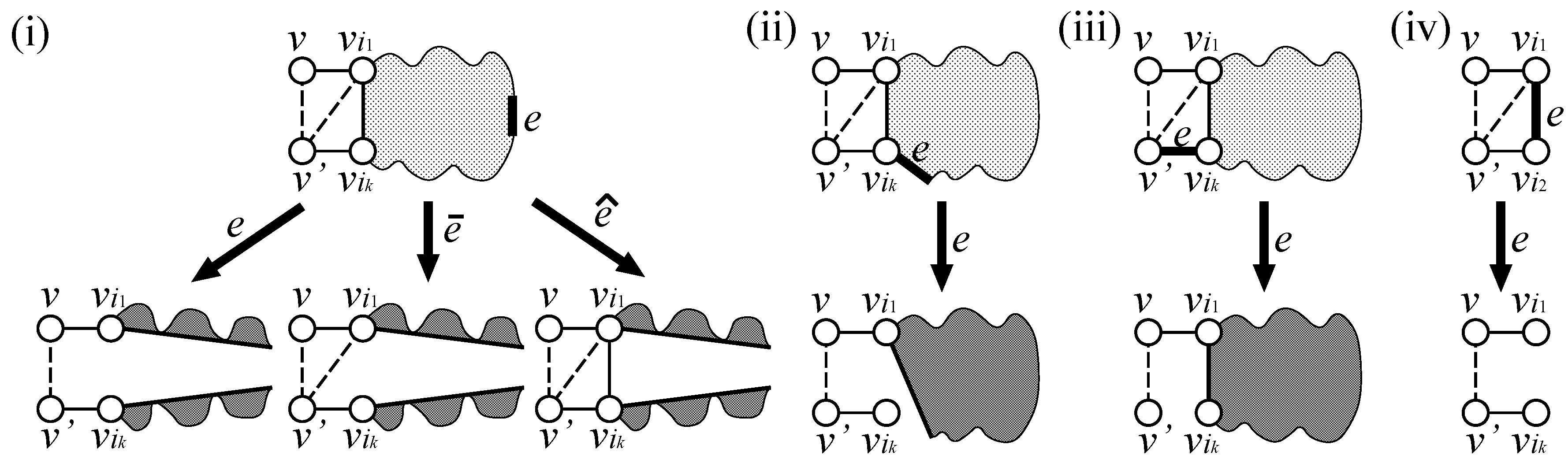
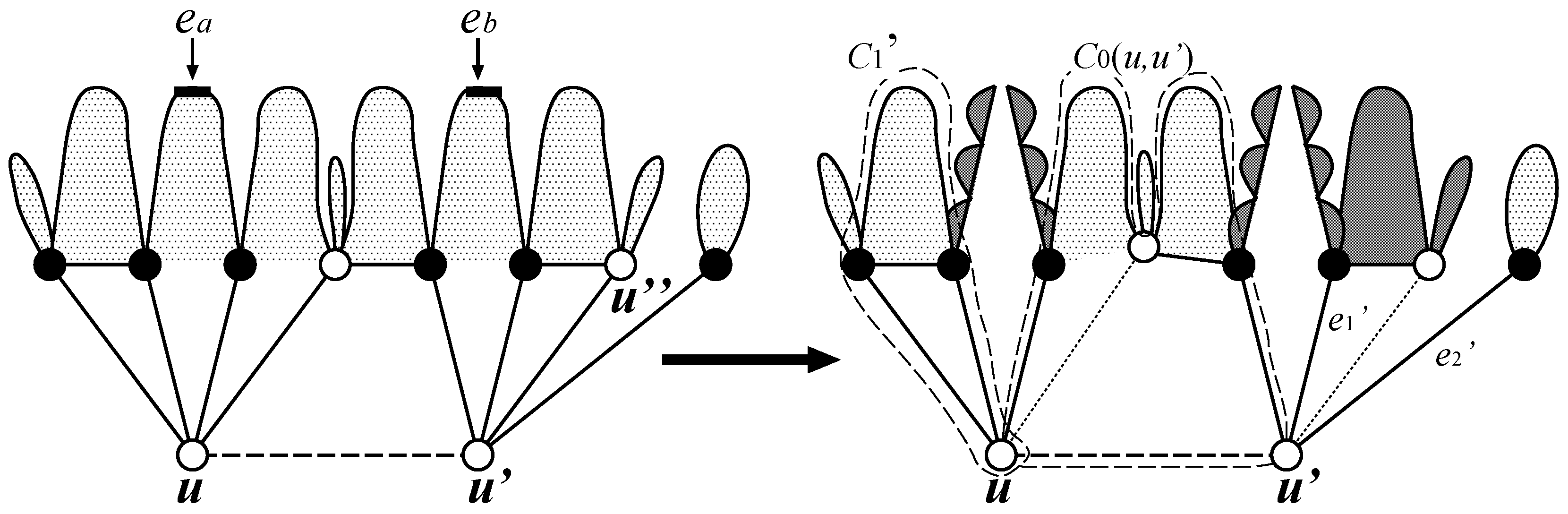
Computation of $MC{S}_p(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$

Let $(u_1,u_2,\dots ,u_h)$ be the sequence of vertices in $G_1(u,u^{\prime })$, such that there exists an edge $\{u_i,u\}$ or $\{u_i,u^{\prime }\}$ for each $u_i$, where $u_1,u_2,\dots ,u_h$ are arranged in clockwise order. $(v_1,v_2,\dots ,v_k)$ is defined for $G_2(v,v^{\prime })$ in the same way. For a pair, $(u_i,v_j)$, $l(u_i,v_j)=1$ if $\{u_i,u\}\in E_1$ and $\{v_j,v\}\in E_2$ hold, otherwise, $l(u_i,v_j)=0$. Similarly, for a pair, $(u_i,v_j)$, $r(u_i,v_j)=1$ if $\{u_i,u^{\prime }\}\in E_1$ and $\{v_j,v^{\prime }\}\in E_2$ hold, otherwise, $r(u_i,v_j)=0$. We compute $MC{S}_p(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$ by the following procedure, where it does not examine alignments with $j_g<j_{g-1}<\cdots <j_1$:

Procedure $SimpleOuterMC{S}_p(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$

 if $\{u,u^{\prime }\}\in E_1$ and $\{v,v^{\prime }\}\in E_2$ then $s_{max}\leftarrow 1$ else $s_{max}\leftarrow -\infty$;

 for all alignments $((u_{i_1},u_{i_2},\dots ,u_{i_g}),(v_{j_1},v_{j_2},\dots ,v_{j_g}))$ do

  if $l(u_{i_t},v_{j_t})=0$ and $r(u_{i_t},v_{j_t})=0$ hold for some t then continue;

  if $l(u_{i_1},v_{j_1})=0$ or $r(u_{i_g},v_{j_g})=0$ holds then continue;

  if $\{u,u^{\prime }\}\in E_1$ and $\{v,v^{\prime }\}\in E_2$ then $s\leftarrow 1$ else $s\leftarrow 0$;

  for $t=1$ to g do$s\leftarrow s+l(u_{i_t},v_{j_t})+r(u_{i_t},v_{j_t})+MC{S}_c(G_1\left(u_{i_t}\right),G_2\left(v_{j_t}\right))$;

  for $t=2$ to g do $s\leftarrow s+MC{S}_p(G_1(u_{i_{t-1}},u_{i_t}),G_2(v_{j_{t-1}},v_{j_t}))$;

  $s_{max}\leftarrow max(s,s_{max})$;

 return $s_{max}$.

This procedure returns $-\infty$ if there is no connected common subgraph between $G_1(u,u^{\prime })$ and $G_2(v,v^{\prime })$ that contains $(w,w^{\prime })$ corresponding to both $(u,u^{\prime })$ and $(v,v^{\prime })$. It should be noted that the first line in the body of the main loop puts the constraint that all corresponding pairs, $(u_{i_t},v_{j_t})$, in an alignment must be connected to either $(u,v)$ or $(u^{\prime },v^{\prime })$, and the second line puts the constraint that $(u_{i_1},v_{j_1})$ must be connected to $(u,v)$ and $(u_{i_g},v_{j_g})$ must be connected to $(u^{\prime },v^{\prime })$.

As an example, consider an alignment, $((u_1,u_2,u_3,u_4),(v_1,v_2,v_3,v_5))$, in Figure 4. Then, the score is given by $4+MC{S}_p(G_1(u_1,u_2),G_2(v_1,v_2))+MC{S}_p(G_1(u_2,u_3),$ $G_2(v_2,v_3))+MC{S}_b(G_1(u_3,C_3),G_2(v_3,D_4))+MC{S}_p(G_1(u_3,u_4),G_2(v_3.v_5))$, where $MC{S}_b(G_1(u_3,C_3),G_2(v_3,D_4))$ is given via the computation of $MC{S}_c(G_1\left(u_3\right),G_2\left(v_3\right))$.

Figure 4. Computation of $MC{S}_p(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$.

Figure 4. Computation of $MC{S}_p(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$.

For another example, the score is $-\infty$ for each of alignments, $((u_1,u_3),(v_4,v_5))$, $((u_1,u_2),(v_1,v_2))$ and $(\left(u_3\right),\left(v_3\right))$, whereas the score of $(\left(u_2\right),\left(v_3\right))$ is 2, since $\{u,u^{\prime }\}\notin E$, $\{v,v^{\prime }\}\notin E$, $l(u_2,v_3)=1$, $r(u_2,v_3)=1$ and $MC{S}_c(G_1\left(u_2\right),G_2\left(v_3\right))=0$. It is to be noted that vertices not appearing in an alignment can match in a later dynamic programming process; for example, $u_2$ can match with $v_2$ under an alignment of $((u_1,u_3),(v_1,v_4))$, although edges $\{u,u_2\}$ and $\{v,v_2\}$ are ignored.

As in the case of $SimpleOuterMC{S}_b(G_1(u,C),G_2(v,D))$, $SimpleOuterMC{S}_p$ $(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$ can be modified into a dynamic programming version.

Then, we have the following theorem:

Theorem 1 SIMPLE-OUTER-MCS can be solved in polynomial time.

Proof. First we consider the correctness of the algorithm $SimpleOuterMCS(G_1,G_2)$. The crucial points of the algorithm are that it examines all possible combinations of the neighbors via alignments examined in $SimpleOuterMC{S}_b(G_1(u,C),G_2(v,D))$ for each pair of cut vertices $(u,v)$ and via alignments examined in $SimpleOuterMC{S}_p(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$ for each pair of cut pairs $((u,u^{\prime }),(v,v^{\prime }))$, where the connectedness in the latter case is taken care of by the use of $l(u_i,v_j)$ and $r(u_i,v_j)$. It should be noted that non-neighbors of u cannot be neighbors of a node corresponding to u in MCS, and the ordering of neighbors must be preserved by Fact 1. Therefore, examination of all alignments covers all valid combinations of neighbors. Based on these facts, it is straightforward to see that $SimpleOuterMCS(G_1,G_2)$ correctly computes the size of MCS.

Next, we consider the time complexity. Since we examine $O\left(n^2\right)$ possible root pairs, we focus on the case where the roots are fixed, where n is the maximum number of vertices in $G_1$ and $G_2$.

Although $SimpleOuterMCS(G_1,G_2)$ is described as a recursive algorithm, the numbers of required scores of $MCS(G_1\left(u\right),G_2\left(v\right))$, $MCS(G_1(u,C),G_2(v,D))$ and $MCS(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$ are $O\left(n^2\right)$, $O\left(n^2\right)$ and $O\left(n^4\right)$, respectively. Therefore, by storing these values in some tables, we can transform $SimpleOuterMCS$ $(G_1,G_2)$ into a dynamic programming algorithm.

Computation of $MCS(G_1\left(u\right),G_2\left(v\right))$ can be done in $O\left(n^3\right)$ time per call, because a maximum weight bipartite matching can be computed in $O\left(n^3\right)$ time [22]. Using the dynamic programming version, the computation of each of $MCS(G_1(u,C),$ $G_2(v,D))$ and $MCS(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$ can be done in $O\left(h^2{k}^2\right)\le O\left(n^4\right)$ time per call.

Therefore, the total time complexity is $O\left(n^2\right)\times (O\left(n^2\right)\times O\left(n^3\right)+O\left(n^2\right)\times O\left(n^4\right)+O\left(n^4\right)\times O\left(n^4\right))=O\left(n^{10}\right)$.  ☐

Though it might be possible to substantially reduce the degree of polynomial by some simplification, as done in [11], we do not go further, because our main purpose is to present a polynomial-time algorithm for the non-restricted (but bounded degree) case.

4. Algorithm for Outerplanar Graphs of Bounded Degree

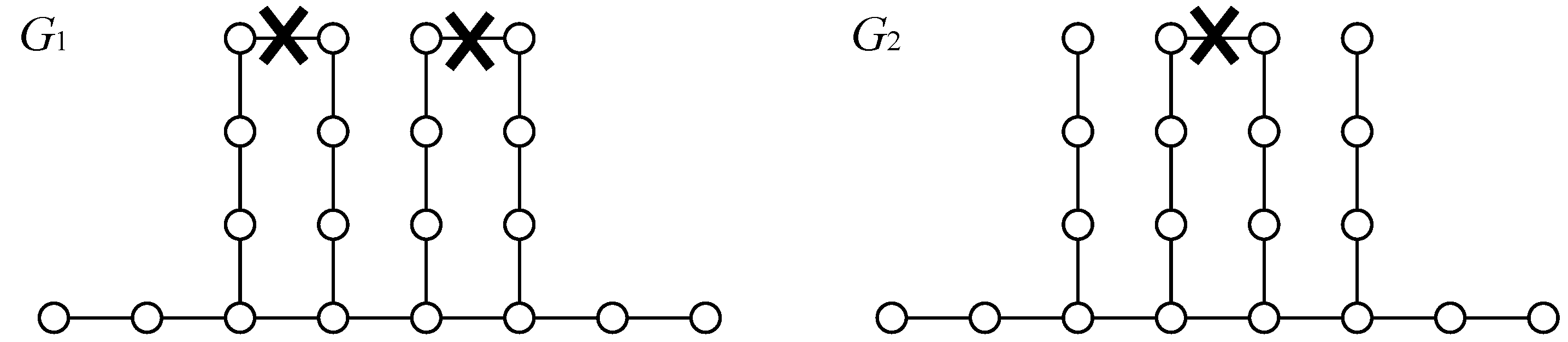
In order to extend the algorithm in Section 3 for a general (but bounded degree) case, we need to consider the decomposition of biconnected components. For example, consider graphs $G_1$ and $G_2$ in Figure 5. We can see that in order to obtain a maximum common subgraph, biconnected components in $G_1$ and $G_2$ should be decomposed, as shown in Figure 5, where there can be multiple ways of optimal decompositions in general. This is the crucial point, because considering all possible decompositions easily leads to exponential-time algorithms. In order to characterize decomposed components, we introduce the concept of a blade, as shown below (see also Figure 6).

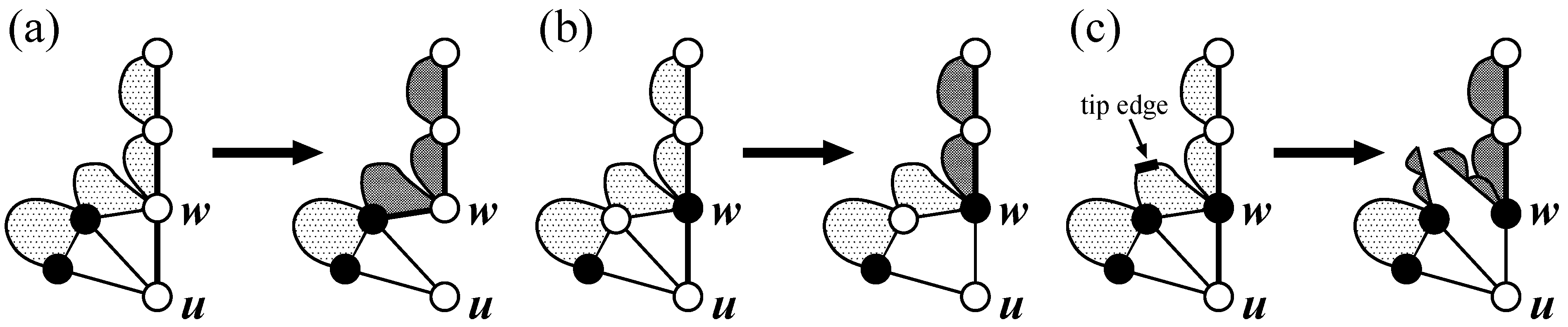
Suppose that $v_{i_1},\dots ,v_{i_k}$ are the vertices of a half block arranged in this order, and $v_{i_1}$ and $v_{i_k}$ are respectively connected to v and $v^{\prime }$, where v and $v^{\prime }$ can be the same vertex. If we cut one edge, $\{v_{i_h},v_{i_{h+1}}\}$ for $i_h\in \{2,3,...,k-2\}$, we obtain two half blocks, one induced by $v_{i_1},v_{i_2},\dots ,v_{i_h}$ and the other induced by $v_{i_k},v_{i_{k-1}},\dots ,v_{i_{h+1}}$. However, only one half block is obtained in the case of $i_1=i_h$ or $i_k=i_{h+1}$, and no half block is obtained in the case of $k=2$ (see Figure 7). Each of these half blocks is a chain of biconnected components called a blade body, and a subgraph consisting of a blade body and its descendants is called a blade. Vertices $v_{i_1}$ and $v_{i_k}$, an edge $\{v_{i_h},v_{i_{h+1}}\}$ and vertices $v_{i_h},v_{i_{h+1}}$ are called base vertices, a tip edge and tip vertices, respectively. The sequence of edges in the shortest path from $v_{i_1}$ to $v_{i_h}$ (resp. from $v_{i_k}$ to $v_{i_{h+1}}$) is called the backbone of a blade. As a result, the edges between two blades are deleted (it does not cause a problem, because all possible configurations are examined, as discussed later). In addition, there exists three subcases, depending on the existence of edges $\{v_{i_1},v_{i_k}\}$ and $\{v^{\prime },v_{i_1}\}$ (cases with $\{v,v_{i_k}\}$ can be handled in an analogous way). We need not consider the case where $\{v^{\prime },v_{i_1}\}$ is deleted, but $\{v_{i_1},v_{i_k}\}$ remains, because deletion of $\{v^{\prime },v_{i_1}\}$ can be handled in the computation of $MC{S}_p(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$):

• both $\{v_{i_1},v_{i_k}\}$ and $\{v^{\prime },v_{i_1}\}$ are deleted
• $\{v_{i_1},v_{i_k}\}$ is deleted, but $\{v^{\prime },v_{i_1}\}$ remains
• both $\{v_{i_1},v_{i_k}\}$ and $\{v^{\prime },v_{i_1}\}$ remain

where these three cases are respectively denoted by “deletion of e”, “deletion of $\overline{e}$” and “deletion of $\widehat{e}$” (see Figure 7). It is to be noted that, in any case, we cannot have multiple tip edges simultaneously for the same pair, $(v,v^{\prime })$, because disconnected component(s) would appear if multiple tip edges exist.

Figure 5. Example of a difficult case.

Figure 5. Example of a difficult case.

Figure 6. (A) Construction of blades where subgraphs, excluding gray regions (descendant components), are blade bodies; and (B) schematic illustration of a blade.

Figure 6. (A) Construction of blades where subgraphs, excluding gray regions (descendant components), are blade bodies; and (B) schematic illustration of a blade.

Figure 7. Types and subcases of blades, where two other subcases for (ii) and another subcase (i.e., $\{v^{\prime },v_{i_1}\}$ remains) for (iii) and (iv) are omitted.

Figure 7. Types and subcases of blades, where two other subcases for (ii) and another subcase (i.e., $\{v^{\prime },v_{i_1}\}$ remains) for (iii) and (iv) are omitted.

In addition, we allow $\{v,v_{i_1}\}$ (resp. $\{v^{\prime },v_{i_k}\}$) to be a tip edge. In this case, after removing this tip edge, the resulting half block induced by $v_{i_k},\dots ,v_{i_2},v_{i_1}$ (resp. $(v_{i_1},v_{i_2},\dots ,v_{i_k})$) is a blade body, where $v_{i_k}$ (resp. $v_{i_1}$) becomes the base vertex. For example, the rightmost blade in Figure 8 is created by removing a tip edge $\{u,u_5\}$ and $u_4$ becomes the base vertex.

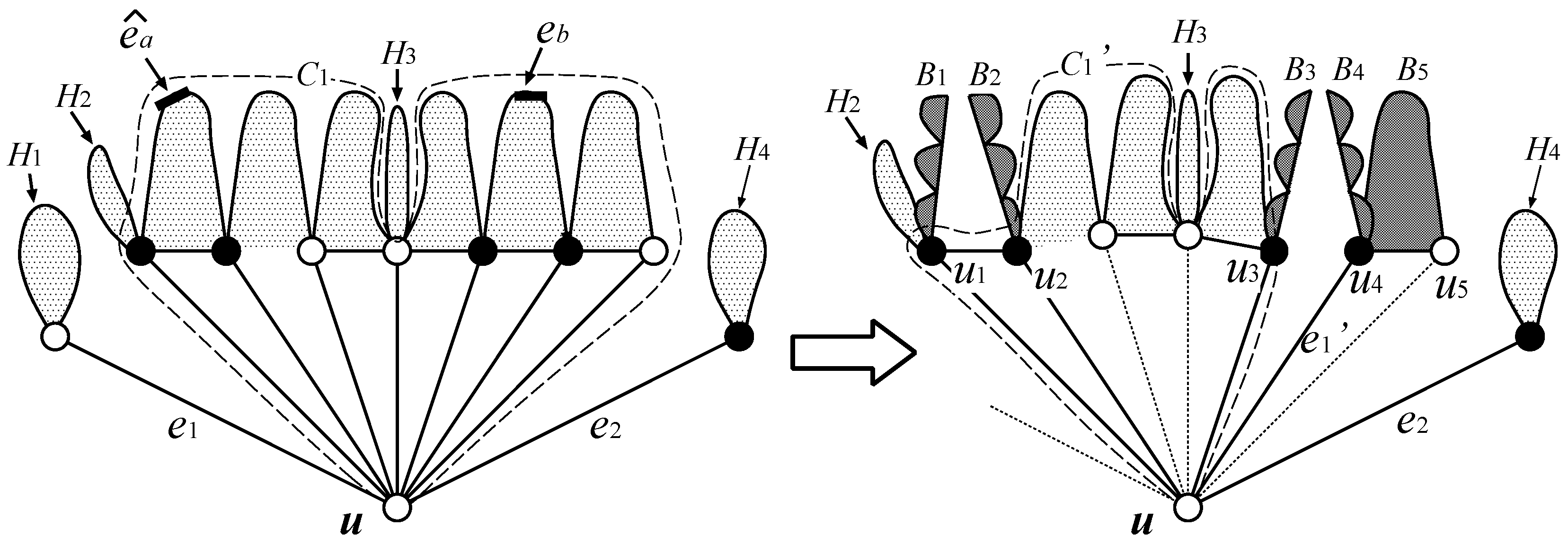
Figure 8. Example of configuration and its resulting subgraph of $G_1\left(u\right)$. Black circles, dark gray regions and thin dotted lines denote selected vertices, blades and removed edges, respectively. Block $C_1$ and edges $e_1,e_2$ are the children of u in $G_1\left(u\right)$, where block $H_1$ is a child of $e_1$, blocks $H_2,H_3$ are children of $C_1$ and block $H_4$ is a child of $e_2$. Edges, $e_a,e_b$, are tip edges, where $\{u,u_5\}$ is also regarded as a tip edge. Then, edge $e_1$ is deleted along with block $H_1$, whereas edge $e_2$ remains as it is. Block $C_1$ is divided into block $C_1^{\prime }$, blades $B_1,\dots ,B_5$ and edge $e_1^{\prime }$, where blocks, $H_2,H_3$, and blades, $B_1,B_2,B_3$, are children of $C_1^{\prime }$ and blades, $B_4,B_5$, are children of $e_1^{\prime }$. In the resulting subgraph, block, $C_1^{\prime }$, and edges, $e_1^{\prime },e_2^{\prime }$, are the children of u.

Figure 8. Example of configuration and its resulting subgraph of $G_1\left(u\right)$. Black circles, dark gray regions and thin dotted lines denote selected vertices, blades and removed edges, respectively. Block $C_1$ and edges $e_1,e_2$ are the children of u in $G_1\left(u\right)$, where block $H_1$ is a child of $e_1$, blocks $H_2,H_3$ are children of $C_1$ and block $H_4$ is a child of $e_2$. Edges, $e_a,e_b$, are tip edges, where $\{u,u_5\}$ is also regarded as a tip edge. Then, edge $e_1$ is deleted along with block $H_1$, whereas edge $e_2$ remains as it is. Block $C_1$ is divided into block $C_1^{\prime }$, blades $B_1,\dots ,B_5$ and edge $e_1^{\prime }$, where blocks, $H_2,H_3$, and blades, $B_1,B_2,B_3$, are children of $C_1^{\prime }$ and blades, $B_4,B_5$, are children of $e_1^{\prime }$. In the resulting subgraph, block, $C_1^{\prime }$, and edges, $e_1^{\prime },e_2^{\prime }$, are the children of u.

Since a blade can be specified by a pair of base and tip vertices and an orientation (clockwise or counterclockwise), there exist $O\left(n^2\right)$ blades in $G_1$ and $G_2$. Of course, we need to consider the possibility that during the execution of the algorithm, other subgraphs may appear from which new blades are created. However, we will show later that blades appearing in the algorithm are restricted to be those in $G_1$ and $G_2$.

4.1. Description of Algorithm

In this subsection, we describe the algorithm as a recursive procedure, which can be transformed into a dynamic programming one, as stated in Section 3.

The main procedure, $OuterMCS(G_1,G_2)$ is the same as that mentioned in Section 3, and we recursively compute three kinds of scores: $MC{S}_c(G_1\left(u\right),G_2\left(v\right))$, $MC{S}_b(G_1(u,C),$ $G_2(v,D))$ and $MC{S}_p(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$, where cut vertices, cut pairs, blocks and bridges do not necessarily mean those in the original graphs, but may mean those in subgraphs generated by the algorithm.

Computation of $MC{S}_c(G_1\left(u\right),G_2\left(v\right))$

Let $C_1,\dots ,C_{h_1}$ and $e_1,\dots ,e_{h_2}$ be children of u, where $C_i$’s and $e_j$’s are blocks and bridges, respectively. Let $u_{i_1},\dots ,u_{i_h}$ be the neighboring vertices of u that are contained in the children of u. We define a configuration as a tuple of the following (see Figure 8).

$s\left(u_{i_j}\right)\in \{0,1\}$ for $j=1,\dots ,k$:

$s\left(u_{i_j}\right)=1$ means that $u_{i_j}$ is selected as a neighbor of u in a common subgraph, otherwise $s\left(u_{i_j}\right)=0$. $u_{i_j}$ is called a selected vertex if $s\left(u_{i_j}\right)=1$.

$tip(u_{i_j},u_{i_k})$:

$e=tip(u_{i_j},u_{i_k})$ is an edge in $B(u_{i_j},u_{i_k})$, where B is the block containing $u_{i_j}$, $u_{i_k}$ and u. This edge is defined only for a consecutive selected vertex pair, $u_{i_j}$ and $u_{i_k}$, in the same block (i.e., $B(u_{i_j},u_{i_k})$ does not contain any other selected vertex). e is used as a tip edge, where e can be empty, which means that we do not cut any edge in $B(u_{i_j},u_{i_k})$. It is to be noted that, at most, one edge in $B(u_{i_j},u_{i_k})$ can be a tip edge, and thus, each $B(u_{i_j},u_{i_k})$ is divided into, at most, two blade bodies; further decomposition will be done in later steps. We also consider $\overline{e}$ and $\widehat{e}$ for $e=tip(u_{i_j},u_{i_k})$ whenever available.

Each configuration defines a subgraph of $G_1\left(u\right)$ as follows:

• $e_i=\{u_{i_j},u\}$ ($i\in \{1,\dots ,h_2\}$) remains if $s\left(u_{i_j}\right)=1$. Otherwise, $e_i$ is removed along with its descendants.
• If no vertex in $C_i$ is selected, it is removed along with its descendants. Otherwise, $C_i$ is divided into blocks, blade bodies (according to $s(\dots )$’s and $tip(\dots )$’s) and bridges, where edges, $\{u_{i_j},u\}$ with $s\left(u_{i_j}\right)=0$, are removed.

Let $C_1^{\prime },\dots ,C_{p_1}^{\prime }$ and $e_1^{\prime },\dots ,e_{p_2}^{\prime }$ be the resulting blocks and bridges containing u, which are new `children’ of u, for a configuration, $F_1$. Configurations are defined for $G_2\left(v\right)$ in an analogous way. Let $D_1^{\prime },\dots ,D_{q_1}^{\prime }$ and $f_1^{\prime },\dots ,f_{q_2}^{\prime }$ be the resulting new children of v for a configuration $F_2$ of $G_2$. As stated in Section 3, we construct a bipartite graph $B{G}_{F_1,F_2}$ by

$$\begin{array}{ccc}\hfill w(C_i^{\prime },f_j^{\prime })& =& 0\hfill \\ \hfill w(C_i^{\prime },D_j^{\prime })& =& MC{S}_b(G_1(u,C_i^{\prime }),G_2(v,D_j^{\prime }))\hfill \\ \hfill w(e_i^{\prime },D_j^{\prime })& =& 0\hfill \\ \hfill w(e_i^{\prime },f_j^{\prime })& =& MC{S}_b(G_1(u,e_i^{\prime }),G_2(v,f_j^{\prime }))\hfill \end{array}$$

and we compute the weight of the maximum weight matching for each configuration pair $(F_1,F_2)$ ( although a bridge cannot be mapped on a block here, a bridge can be mapped to an edge in a block of an input graph by converting the block into smaller blocks and bridges using tip edge(s)). The following is a procedure for computing $MC{S}_c(G_1\left(u\right),G_2\left(v\right))$:

Procedure $OuterMC{S}_c(G_1\left(u\right),G_2\left(v\right))$

 $s_{max}\leftarrow 0$;

 for all configurations $F_1$ for $G_1\left(u\right)$ do

  for all configurations $F_2$ for $G_2\left(v\right)$ do

   $s\leftarrow$ weight of the maximum weight matching of $B{G}_{F_1,F_2}$;

   if $s>s_{max}$ then $s_{max}\leftarrow s$;

 return $s_{max}$.

Computation of $MC{S}_b(G_1(u,C^{\prime }),G_2(v,D^{\prime }))$

This score can be computed, as stated in Section 3, although we should take blades into account. In this case, we can directly examine all possible alignments, because the number of neighbors of u or v is bounded by a constant, and we need to examine a constant number of alignments.

Computation of $MC{S}_p(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$

As in $OuterMC{S}_c(G_1\left(u\right),G_2\left(v\right))$, we examine all possible configurations by specifying selected vertices and tip edges (see Figure 9). Each configuration defines a subgraph of $G_1(u,u^{\prime })$ (resp. $G_2(v,v^{\prime })$). This subgraph contains three kinds of biconnected components:

(i)

components connecting only to u (resp. v)

(ii)

components connecting only to $u^{\prime }$ (resp. $v^{\prime }$) and

(iii)

component connecting to both u and $u^{\prime }$ (resp. v and $v^{\prime }$), where this type (iii) component is uniquely determined.

Figure 9. Example of configuration and its resulting subgraph for $G_1(u,u^{\prime })$. Black circles, dark gray regions and thin dotted lines denote selected vertices, blade, and removed edges, respectively. Edges, $e_a,e_b$, are tip edges, where $\{u^{\prime },u^{\prime \prime }\}$ is also regarded as a tip edge. In the resulting subgraph, $C_1^{\prime }$ is a type (i) component, $e_1^{\prime }$ and $e_2^{\prime }$ are type (ii) components and $C_0(u,u^{\prime })$ is a type (iii) component.

Figure 9. Example of configuration and its resulting subgraph for $G_1(u,u^{\prime })$. Black circles, dark gray regions and thin dotted lines denote selected vertices, blade, and removed edges, respectively. Edges, $e_a,e_b$, are tip edges, where $\{u^{\prime },u^{\prime \prime }\}$ is also regarded as a tip edge. In the resulting subgraph, $C_1^{\prime }$ is a type (i) component, $e_1^{\prime }$ and $e_2^{\prime }$ are type (ii) components and $C_0(u,u^{\prime })$ is a type (iii) component.

For each of type (i) and type (ii) components, we construct a bipartite graph, as in $OuterMCS(G_1\left(u\right),G_2\left(v\right))$, although blades might appear in the recursive process. Let the resulting bipartite graphs be $B{G}_{F_1,F_2}^l$ and $B{G}_{F_1,F_2}^r$, respectively. Let $C_0(u,u^{\prime })$ and $D_0(v,v^{\prime })$ be type (iii) components (i.e., half blocks) for $G_1(u,u^{\prime })$ and $G_2(v,v^{\prime })$, respectively. For this pair of components, we compute a maximum common subgraph, as in $SimpleOuterMCS(G_1(u,u^{\prime }),$ $G_2(v,v^{\prime }))$. The following is a pseudocode of $OuterMCS(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$:

Procedure $OuterMCS(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$

 $s_{max}\leftarrow 0$;

 for all configurations $F_1$ for $G_1(u,u^{\prime })$ do

  for all configurations $F_2$ for $G_2(v,v^{\prime })$ do

   $s\leftarrow$ score of the maximum common subgraph between $C_0(u,u^{\prime })$ and $D_0(v,v^{\prime })$;

   $s\leftarrow s+$ weight of the maximum weight matching of $B{G}_{F_1,F_2}^l$;

   $s\leftarrow s+$ weight of the maximum weight matching of $B{G}_{F_1,F_2}^r$;

   if $s>s_{max}$ then $s_{max}\leftarrow s$;

 return $s_{max}$.

4.2. Analysis

As mentioned before, each blade is specified by base and tip vertices in $G_1$ or $G_2$ and an orientation. Each half block is also specified by two vertices in a block in $G_1$ or $G_2$. We show that this property is maintained throughout the execution of the algorithm and bound to the number of half blocks and blades, as below.

Lemma 1 The number of different half blocks and blades appearing in $OuterMCS(G_1,G_2)$ is $O\left(n^2\right)$.

Proof. We prove it by mathematical induction on the number of steps in the execution of the algorithm. At the beginning of the algorithm, this property is trivially maintained, because we only have $G_1$ and $G_2$. A new half block (along with its descendants) or a new blade is created only when graphs are modified according to a configuration or alignment. In the alignment case, it is straightforward to see that new half blocks are half blocks of the current block or current half block. It can also be seen that whenever a blade is newly created, it is a half block (along with descendants) of the current block or current half block. The crucial cases lie when an existing blade is modified according to a configuration. Let u and $\{u,w\}$ be the base vertex and a backbone edge in a blade $BD$, respectively. Let $C_0$ be the block in $G_1$ (resp. $G_2$) from which $BD$ was created. Then, we need to consider the following three cases (Figure 10) ( new blades may also be created by a tip edge in a half block specified by a pair of selected vertices):

(a)

w is not selected.

The base vertex of a new blade is the selected vertex nearest to w in the first block (i.e., block containing u) of $BD$. Since the original blade body was a half block of a block $C_0$, the resulting blade body is also a half block of $C_0$.

(b)

w is selected, and there is no tip edge between w and its nearest selected vertex.

The resulting blade body begins from w (in the next step), which is a half block of $C_0$.

(c)

w is selected, and there is a tip edge between w and its nearest selected vertex.

The resulting blade body begins from w, which is a half block of $C_0$. Furthermore, two (or less) new blade bodies are created, both of which are half blocks of $C_0$.

Therefore, we can see that every half block or blade appearing in the algorithm is specified by two vertices in a block of $G_1$ or $G_2$, from which the lemma follows.  ☐

Figure 10. Three cases considered in the proof of Lemma 1. Bold lines and dark gray regions denote backbone edges and new blade bodies, respectively.

Figure 10. Three cases considered in the proof of Lemma 1. Bold lines and dark gray regions denote backbone edges and new blade bodies, respectively.

Finally, we obtain the following theorem.

Theorem 2 A maximum common connected edge subgraph of two outerplanar graphs of bounded degree can be computed in polynomial-time.

Proof. It is straightforward to check the correctness of the algorithm, because it implicitly examines all possible common subgraphs via alignment, decomposition by configurations and bipartite matching, where Fact 1 enables us to use alignment and dynamic programming. Therefore, we focus on the time complexity.

Since the number of half blocks and blades is $O\left(n^2\right)$ and the maximum degree is bounded, the number of different $G_1\left(u\right)$’s and $G_1(u,u^{\prime })$’s (resp. $G_2\left(v\right)$’s and $G_2(v,v^{\prime })$’s) appearing in the algorithm, some of which can be obtained from subgraphs of $G_1$ (resp. $G_2$), is $O\left(n^3\right)$, where an additional $O\left(n\right)$ factor comes from the fact that $O\left(n\right)$ new blocks and bridges may be created per blade. Therefore, we can transform the recursive algorithm into a dynamic programming algorithm using $O\left(n^3\right)\times O\left(n^3\right)=O\left(n^6\right)$ size tables.

For each subgraph appearing in $OuterMCS(G_1\left(u\right),G_2\left(v\right))$ or $OuterMCS(G_1(u,u^{\prime }),G_2(v,v^{\prime }))$ as an argument, the number of configurations is $O\left(n^{2D-3}\right)$, because there exists at most $2D-2$ neighboring vertices (excluding those nearer to the root) of u and $u^{\prime }$ (resp. v and $v^{\prime }$) for a constant, D, ($D>2$) and a tip edge lies between a path connecting two neighboring vertices. For some block pair, we need to examine all possible alignments. Since the maximum degree is bounded by constant, D, we need to examine a constant number of alignments, and thus, this calculation can be done in constant time. By the same reason, a maximum matching can be computed in constant time. All other miscellaneous operations, which include modification of edges and summation of scores, can be performed in $O\left(n^2\right)$ time per pair of configurations, pair of biconnected components and pair of half blocks. Since we need to examine $O\left(n^2\right)$ pairs of the roots, the total computation time is:

$$O\left(n^2\right)\times O\left(n^6\right)\times O\left(n^{2D-3}\right)\times O\left(n^{2D-3}\right)\times O\left(n^2\right)=O\left(n^{4D+4}\right)$$

for a constant, D (a constant factor depending only on D is ignored here, because we assume that D is a constant).  ☐

5. Concluding Remarks

We have presented a polynomial-time algorithm for the maximum common connected edge subgraph problem for outerplanar graphs of bounded degree. However, it is not practically efficient. Therefore, development of a much faster algorithm is left as an open problem. Although the proposed algorithm might be modified for outputting all maximum common subgraphs, it would not be an output-polynomial-time algorithm. Therefore, such an algorithm should also be developed.

Recently, it has been shown that the maximum common connected edge subgraph problem is NP-hard, even for partial k-trees of a bounded degree, where $k=11$ [23]. Since outerplanar graphs have treewidth 2 and most chemical compounds have a treewidth of at most 3 [10,18], to decide whether the problem for partial k-trees is NP-hard for $k=3$ is left as an interesting open problem.