1. Introduction
Social networks are usually represented and studied as graphs. Vertices represent the elements analyzed (e.g., individuals), while edges represent a binary relation between the considered elements. Among the different properties considered to study such graphs, one of the most relevant is the vertex connectivity of two given vertices. Vertex connectivity is a measure of the information flowing from one vertex to the other, and it has many applications. For example, it is used for the identifications of important structural properties of a social network, like group cohesiveness and centrality [
1,
2]. A classical result of graph theory, known as Menger’s theorem, states that vertex connectivity is equivalent to the maximum number of disjoint paths between two given vertices.
While a lot of interest has been put in the study of networks that represent a single type of relation, a natural extension that has been recently introduced in literature [
3] is to consider multi-relational social networks, that is social networks where more than one kind of relation between elements of the network is considered. In order to investigate vertex connectivity in multi-relational social networks, the combinatorial problem known as
Maximum Colored Disjoint Paths (M
AX CDP) has been introduced in [
3]. M
AX CDP asks for the maximum number of vertex-disjoint uni-color paths in an edge-colored graph, where the different edge-colors represent different kinds of relation.
The computational and approximation complexity of M
AX CDP has been investigated in [
3]. When the input graph contains exactly one color, M
AX CDP is polynomial time solvable (it can be reduced to the maximum flow problem), while it has been shown to be NP-hard when the edges of the graph are colored. Moreover, M
AX CDP is shown to be approximable within factor
c, where
c is the number of colors of the edges of the input graph, but not approximable within factor
, for any
, even when
c is a fixed constant.
In [
3], it is also investigated a variant of the problem, denoted as
ℓ-LCDP, where the length of the paths in the solution are (upper) bounded by an integer
. The
ℓ-LCDP problem is NP-hard, for
, while it admits a polynomial time algorithm when
. This variant of the problem can be approximated in polynomial time within factor
.
In this paper we investigate the approximation and parameterized complexity of M
AX CDP and
ℓ-LCDP. First, we show in
Section 3 that M
AX CDP is not approximable within factor
, for any constant
, and that the corresponding decision problem (CDP) is W[1]-hard when parametrized by the number
p of disjoint uni-color paths. Then, in
Section 4, we give a fixed-parameter algorithm for
ℓ-LCDP, when
ℓ and the number of disjoint uni-color paths are considered as parameters.
Table 1 summarizes the results known about the complexities of these problems along with the new results presented in this work.
Table 1.
Complexity status of MAX CDP.
Table 1.
Complexity status of MAX CDP.
| Problem | Parameter | Status | Ref. |
|---|
| MAX CDP | c | NP-hard for any , | [3] |
| | | c-approximable |
| | | Inapprox. within | new |
| CDP | p | W[1]-hard | new |
| ℓ-LCDP
| ℓ | NP-hard for | [3] |
| | | Poly-time for | [3] |
| ℓ-LCDPp | | FPT | new |
2. Definitions
In this section we give some preliminary definitions that will be useful in the rest of the paper. First, in this paper, we will consider only undirected graphs. Consider a set of colors . In the paper we denote by c the cardinality of C. A C-edge-colored graph (or simply an edge-colored graph when the set of colors is clear from the context) is defined as , where V denotes the set of vertices of G and denotes a collection of edge sets, where the set , with , represents the set of edges colored with color i. Notice that, for a given pair of vertices , , there may exist more than one edge between and (each of these edges is associated with a distinct color of C).
A path π in G is called a uni-color path if all the edges of π have the same color, that is they belong to the same set (for some ). Given two vertices , an -path is a path between vertices x and y. Two paths and are internally disjoint (or, simply, disjoint) if they do not share any internal vertex, while a set of paths are internally disjoint if they are pairwise internally disjoint.
Next, we introduce the formal definitions of the problems we deal with in this paper, namely the optimization problem MAX CDP, the decision problem (CDP) naturally associated with MAX CDP, and the corresponding length-bounded variants ℓ-LCDP and ℓ-LCDPp.
Problem 1. MAXIMUM COLORED DISJOINT PATHS (MAX CDP).
Input: a set C of colors, a C-edge-colored graph , and two vertices .
Output: the maximum number of disjoint uni-color -paths.
Problem 2. COLORED DISJOINT PATHS (CDP).
Input: a set C of colors, a C-edge-colored graph , a non-negative integer p, and two vertices .
Output: Do there exist at least p disjoint uni-color -paths in G?
The ℓ-LENGTH COLORED DISJOINT PATHS (ℓ-LCDP) problem is a variant of MAX CDP where the length of the paths in the solution is bounded by an integer . The ℓ-LCDP problem is the decision version of ℓ-LCDP which asks if there exists a solution of ℓ-LCDP with cardinality at least p.
3. Approximation and Parameterized Complexity of
In this section, we present a reduction from MAXIMUM INDEPENDENT SET to MAX CDP. Since the reduction preserves the solution cost, it implies that MAX CDP is not approximable within factor , for any , and that CDP is W[1]-hard when the parameter is the size p of the solution.
Given an undirected graph , the MAXIMUM INDEPENDENT SET (MAX INDSET) problem asks for an independent set of maximum cardinality, i.e., a maximum-cardinality set I such that if then . In the following, starting from a graph , we construct a gadget (an edge-colored graph) , such that finding an independent set I of cardinality k in is equivalent to finding k disjoint uni-color -paths in . First, we describe the edge-colored graph associated with a generic graph , then we prove some properties of the computed gadget.
Description of the gadget. Let
be an undirected graph, with
and
. Without loss of generality, we assume that
is connected, since a maximum independent set of a non-connected graph is the union of the maximum independent sets of its connected components. Let
be an ordered list of the edges of
, based on some ordering. We construct an edge-colored graph
associated with
as follows. Informally, the vertex set
is composed by two distinguished vertices
s and
t and a vertex for each edge of
, while each set
,
, is composed connecting the vertices associated with edges of
incident to
in the same order as they appear in
. Formally, the set of colors is:
Now, we define the vertex set
:
Finally, we define the edge set
,
:
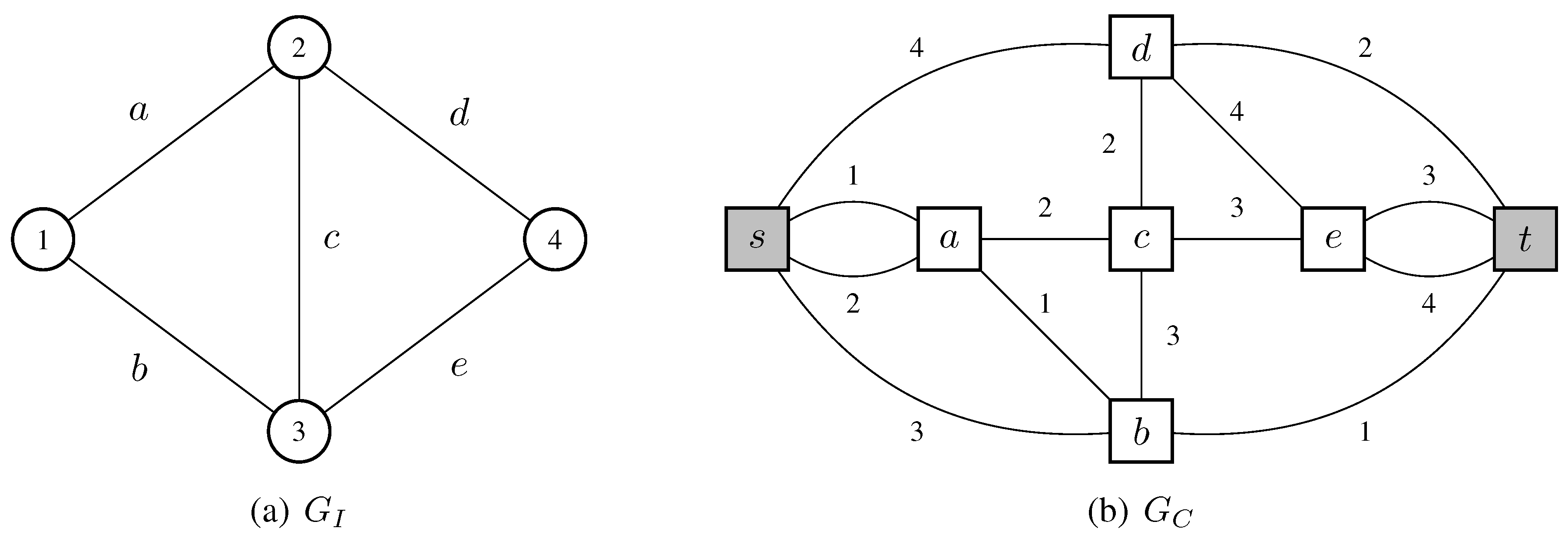
Figure 1 represents an example of an undirected graph
and of the edge-colored graph
associated with it.
Figure 1.
An example of a graph and the edge-colored graph associated with it. For convenience, we labelled the edges of such as they correspond to the vertices in . The colors of the edges in are indicated by numbers placed near the edges, while the two distinguished vertices s and t are highlighted in grey. The order of the edges of is simply the lexicographic order of their labels.
Figure 1.
An example of a graph and the edge-colored graph associated with it. For convenience, we labelled the edges of such as they correspond to the vertices in . The colors of the edges in are indicated by numbers placed near the edges, while the two distinguished vertices s and t are highlighted in grey. The order of the edges of is simply the lexicographic order of their labels.
Given a graph with n vertices and m edges, the associated edge-colored graph has vertices, edges, and n colors, i.e., .
Properties of the gadget. First, we introduce the following properties of the gadget.
Remark 1. A uni-color -path of color i, with , contains each vertex of associated with an edge incident in .
Proof.
The proof follows by construction, since the edges of color i, with , induce a -path that contains each vertex of associated with an edge incident in ordered as in list .
Next, we prove the two main results of the reduction from to MAX INDSET to MAX CDP.
Lemma 2.
Let be an undirected graph and be an independent (vertex) set for . Then, we can compute in polynomial time (at least) |I| disjoint uni-color -paths in the edge-colored graph associated with .
Lemma 3.
Let be an undirected graph and be the edge-colored graph associated with . If there exist k disjoint uni-color -paths in , then we can compute in polynomial time an independent set for , with .
The first lemma is easily proved by showing that the uni-color -paths associated with the vertices of the independent set I are pairwise disjoint. Conversely, the second lemma can be proved by showing that the vertices of associated with the k uni-color -paths of form an independent set for .
Proof of Lemma 2.
By construction, in there exists a uni-color -path associated with each vertex v of the original graph . We will show that the set P of paths of associated with each vertex are internally disjoint. Let and be two paths of P associated with vertices and , respectively, of I. Notice that the two paths and connect the vertices which represent the edges of incident to and , respectively. Since I is an independent set in , no edge is incident to both and (), thus and are (internally) disjoint.
Proof of Lemma 3.
Let P be the set of k disjoint uni-color -paths of . Since each color is (bi-univocally) associated with a single path in which, in turn, is (bi-univocally) associated with a single vertex of , we can define a set that consists of the vertices of associated with a path of P. Clearly, . We claim that I is an independent vertex set for . Suppose that I is not an independent set, thus there exist two vertices such that . Let be the vertex of representing edge . Since , then there exist two paths in P associated with and . By Remark 1, both paths must contain vertex as an internal vertex, since edge is incident to both and . Hence paths and are not internally disjoint, which contradicts our assumption and thus I is an independent set for .
Consequences. Lemmas 2 and 3 prove the existence of an L-reduction [
4] from M
AX I
NDSET to M
AX CDP with constants
. Hence, considering that, unless
, M
AX I
NDSET cannot be approximated in polynomial time within factor
for any constant
[
5], and that
, the following theorem holds.
Theorem 4.
For any constant , MAX CDP cannot be approximated within factor in polynomial time unless .
This result greatly improves the previous inapproximability factor
for M
AX CDP [
3] and, given the
c-approximation algorithm presented in [
3], it is the asymptotically optimal inapproximability ratio for M
AX CDP. However, notice that the inapproximability factor
for M
AX CDP given in [
3] holds even if
c is a fixed constant, while in our reduction
c is not fixed.
From the parameterized complexity point of view, the reduction also implies the W[1]-hardness of the decision problem CDP, as stated in the following theorem.
Theorem 5.
CDP is W[1]-hard when parameterized by the number p of disjoint uni-color -paths.
Proof.
The reduction presented by Lemmas 2 and 3 is also a parameterized reduction [
6] from I
NDEPENDENT S
ET (the decision problem naturally associated with M
AX I
NDSET) to CDP (indeed the size of an independent set of
is identical to the number of disjoint uni-color
-path in
). Since I
NDEPENDENT S
ET is W[1]-hard when the parameter is the size of the required independent set [
7], then also CDP is W[1]-hard when parametrized by number
p of disjoint uni-color
-paths. ☐
4. A Fixed-Parameter Algorithm for
In this section, we study
ℓ-LCDP
p, the length-bounded (decision) version of M
AX CDP, which asks if there exist
p uni-color disjoint
-paths of length at most
ℓ. We show that
ℓ-LCDP
p is fixed-parameter tractable when the parameters are
ℓ and
p by presenting a parameterized algorithm based on the
color coding technique [
8]. For an introduction to parameterized complexity see [
6]. Notice that
ℓ-LCDP
p is unlikely to admit fixed-parameter tractable algorithms when parameterized only by
p or only by
ℓ. Indeed in the latter case,
ℓ-LCDP
p is already -hard when
[
3]. In the former case, we have proved in the previous section that CDP (hence
ℓ-LCDP
p, when
) is W[1]-hard when parameterized by
p.
Color coding is a technique initially introduced to design fixed-parameter algorithms for various restrictions of the subgraph isomorphism problem. It then gained popularity and it has been successfully applied to tackle the computational hardness of various problems on networks and graphs [
9,
10,
11], on strings [
12,
13], and problems of subset selection [
14,
15]. The basic idea of the color coding technique applied on graph problems is, first, to “color” the vertices of the graph from a set of
k colors (for an appropriate choice of the number
k of colors), and, then, to find a solution of the given problem with the additional constraint that the vertices of the solution are colored with distinct colors (called a “colorful” or “color coded” solution), if such a solution exists. The process is re-iterated with a different coloring if a colorful solution is not found.
The key theoretical result, which allows to obtain deterministic algorithms based on the color coding technique, is the deterministic construction of
k-perfect families of hash functions. A family
F of hash functions from a set
U (the vertex set in the traditional applications of color coding) to the set
of colors is
k-perfect if, for each subset
of
U such that
, there exists a hash function
f in
F such that
is colorful w.r.t.
f,
i.e.,
f assigns a distinct label to each element of
. In fact, if the given problem has a solution
S of size
k, then there exists a hash function in
F such that solution
S is colorful. Hence, it suffices to test if there exists a colorful solution for one of the colorings given by the hash functions of the
k-perfect family in order to guarantee the existence of a solution of the original problem, if such a solution exists. Crucial to the overall running time is the size of a
k-perfect family and the time required to enumerate and evaluate the hash functions of the family. Currently, the best bounds (such as [
8,
16,
17]) are, in general, explicit constructions of families of size
in time proportional to their size.
The description of the parameterized algorithm for the ℓ-LCDPp problem is divided into two parts. First, we present a procedure that, given an edge-colored graph and a vertex-coloring function λ, verifies if in there exist p disjoint uni-color -paths long at most ℓ and with the additional constraint that the inner vertices of the p paths are colored with distinct colors. Then, we show that, by exploiting well-known properties of families of perfect hash functions, the previous procedure can be used to solve the ℓ-LCDPp problem in polynomial time (if p and ℓ are parameters). In the following, to avoid ambiguities between vertex’s and edge’s colors, function λ will be called vertex-labelling function (or, simply, a labelling function) instead of the traditional term of coloring function.
A dynamic-programming procedure for the -labelled problem. Let be a C-edge-colored graphs with two distinguished vertices s and t, and let λ be a labelling function which maps each vertex v of to a label belonging to a set (we assume that λ assigns a distinct label to each vertex of a solution of ℓ-LCDPp). Let be a fixed set of labels. A simple path π in is L-labelled if and only if the labels of its vertices (with the exclusion of s and t) are contained in L and are pairwise distinct. A set of simple paths is L-labelled if and only if there exists a partition of L such that each is -labelled. We say that a path π is g-colored, with , if all of its edges belong to set . The -labelled ℓ-LCDPp problem, given and with , asks if there exists an -labelled solution for the ℓ-LCDPp problem on . We solve the -labelled ℓ-LCDPp problem by combining two dynamic-programming recurrences. The first one, , tests if, for a set of labels , there exists an L-labelled g-colored path from vertex s to a vertex v different from t. The second one, , tests if, for a set of labels such that for some integer , there exists a partition of L in q subsets such that each set labels a -colored -path of length .
Recurrence for
is defined as follows (where ⊎ represents the disjoint union operator):
Correctness of the previous recurrence is proved by the following lemma.
Lemma 6.
is true if and only if there exists an L-labelled g-colored path from s to v.
proof.
The proof is by induction on the cardinality of L. If , the base cases apply and a path which does not use any label exits if and only if . Now, assume that is correct for any L such that (for some k) and we will prove the correctness of for all such that . Moreover, assume that , since, otherwise, the first base case applies which is clearly correct. Then, an -labelled g-colored path from s to exists if and only if and (ii) there exists an -labelled g-colored path π from s to a vertex u such that and . Since , path π exists if and only if is true. The inductive case of Equation 4.1 tests the above mentioned conditions, hence is correct also for sets of labels L such that , concluding the proof.
Clearly, M can be used to test if there exists an -labelled g-colored -path, as illustrated by the following corollary.
Corollary 7.
The existence of an -labelled g-colored -path can be tested in time .
Proof.
By Lemma 6, to test the existence of an -labelled g-colored -path, it suffices to test the existence of a vertex v such that and is true. For a fixed color g and a fixed set L of labels, the time needed to evaluate for all is since each edge is considered only a constant number of times (twice, indeed). Since there exist distinct subsets of , the overall time is .
The second recurrence,
, which, given an integer
and a subset
such that
, solves the
L-labelled
ℓ-LCDP
p problem, is defined as follows:
Notice that we implicitly assume that the solution of the
∅-labelled
ℓ-LCDP
0 problem is always Yes (
i.e.,
).
Correctness of Equation 4.2, as proved in the following lemma, derives from Corollary 7, from the bound on the cardinality of , and from the disjointness of and .
Lemma 8.
Given an edge-colored graph and a vertex-labelling function with , then there exists an -labelled set S of p disjoint uni-color -paths of length at most ℓ if and only if is true.
To prove this lemma, we first prove some intermediate results.
Property 9.
Let and be two disjoint subsets of , let and be two distinct vertices, and and be two (possibly equal) colors. Then and are both true if and only if there exist two disjoint uni-color paths and from s to and , respectively.
Proof.
By Lemma 6, since both and are true, paths and exist labelled with set and , respectively. Since and are disjoint, there could not exist a common vertex v (different from s), otherwise would belong to both and . Hence, and are disjoint.
Property 10.
The length of an L-labelled path π from s to a vertex is, at most, |L|.
Proof.
All the vertices (but s, which is not labelled) of π are labelled with distinct labels in L, hence there could be at most vertices in π.
Proof of Lemma 8.
We prove the correctness of P by induction on the number of paths p. If , then . Thus, the base case applies and, since we assume that 0 paths always exist, it is also correct. Let us assume that P is correct for any and let us prove its correctness for . First, we prove that if is true, then a solution S for ℓ-LCDPp can be built. Notice that the second case of Equation 4.2 tries every possible bi-partition of set in two sets and of cardinality and , respectively. If function is true, then at least one of the bi-partitions verifies the given conditions. Notice that . Hence, by induction hypothesis, since is true, there exists an -labelled set of k disjoint uni-color -paths. The other conditions, as shown in the proof of Corollary 7, test the existence of an -labelled g-colored -path π for some color . Thus, if there exists a bi-partition which satisfies all the conditions, then there exits an L-labelled set of uni-color -paths. Moreover, since and are disjoint, by Property 9, path π and any path of S are disjoint. Furthermore, since , by Property 10, the length of π is, at most, ℓ (in particular, from s to vertex v, plus 1 from v to t). As a consequence, S is an -labelled set of disjoint uni-color -paths of length, at most, ℓ.
Now, we prove that if there exists an -labelled set S of disjoint uni-color -paths, then is true. For each path , let be the set of labels labelling . Since the paths in S are disjoint, also the sets are disjoint. Moreover, since the length of each path is at most ℓ, we have that . Notice that || is , thus it is possible to find a partition of in p sets of cardinality such that each is a subset of . Let us consider a generic path . Since is a uni-color -path (of length at most ℓ), then there exists a vertex v and a color g such that is true and (Corollary 7). Finally, since is a set of labels of cardinality and is an -labelled set of k disjoint uni-color -paths of length at most ℓ, by induction hypothesis we have that is true. Therefore, the bi-partition satisfies all the condition of Equation 4.2 and is true.
An immediate consequence is that the -labelled ℓ-LCDPp problem can be solved in polynomial time when ℓ and p are parameters.
Corollary 11.
The -labelled problem can be solved in time , where .
Proof.
The evaluation of M needs time. For a fixed , the evaluation of requires and, since there are possible subsets of , the time needed to evaluate P is . ☐
The algorithm for ℓ-LCDPp. As explained before, it is possible to explicitly construct a
k-perfect family
F of hash functions, that is a set
F of hash functions from a universal set
U to the set of integers
such that for each
of cardinality
k there exists a hash function
which assigns distinct integers to the elements of
. It has been shown (see, for example, [
8,
16,
17]) that a
k-perfect family of hash functions of size
can be explicitly constructed in time proportional to its size. As a consequence, the
ℓ-LCDP
p problem can be solved by solving the
-labelled
ℓ-LCDP
p problem for all the labelling functions given by the hash functions of a
-perfect family (where
) in time
. We remark that this algorithm is mainly of theoretical interest, since the running times are impractical even with modest choices of the parameters
ℓ and
p. However, as formalized by the following theorem, it settles the parameterized complexity of the
ℓ-LCDP
p problem for the parameters
ℓ and
p.
Theorem 12.
The problem parameterized by the bound on the path length ℓ and the number p of disjoint uni-color -paths is in FPT.