Compression-Based Tools for Navigation with an Image Database
Abstract
:1. Introduction
2. Color Analysis
- Preprocess the database by sub-sampling each image in the database to create a thumbnail, and by constructing a small VQ codebook for feature vectors derived from each thumbnail.
- Given a query image, compress it with each codebook in the database and rank the images of the database in order of the achieved distortion (using mean squared error).

- a = Number of relevant images (same class as the query) retrieved.
- b = The number of irrelevant items that are retrieved
- c = The number of relevant items that were not retrieved.
- precision = fraction of the images retrieved that are relevant = a/(a + b)
- recall = fraction of the relevant images that are retrieved = a/(a + c)
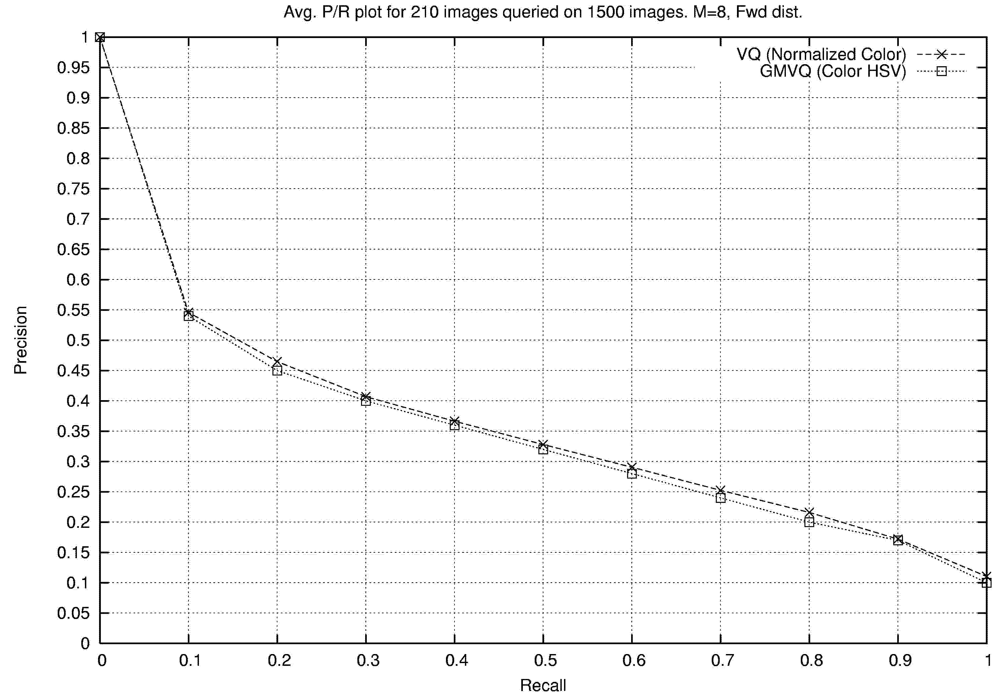
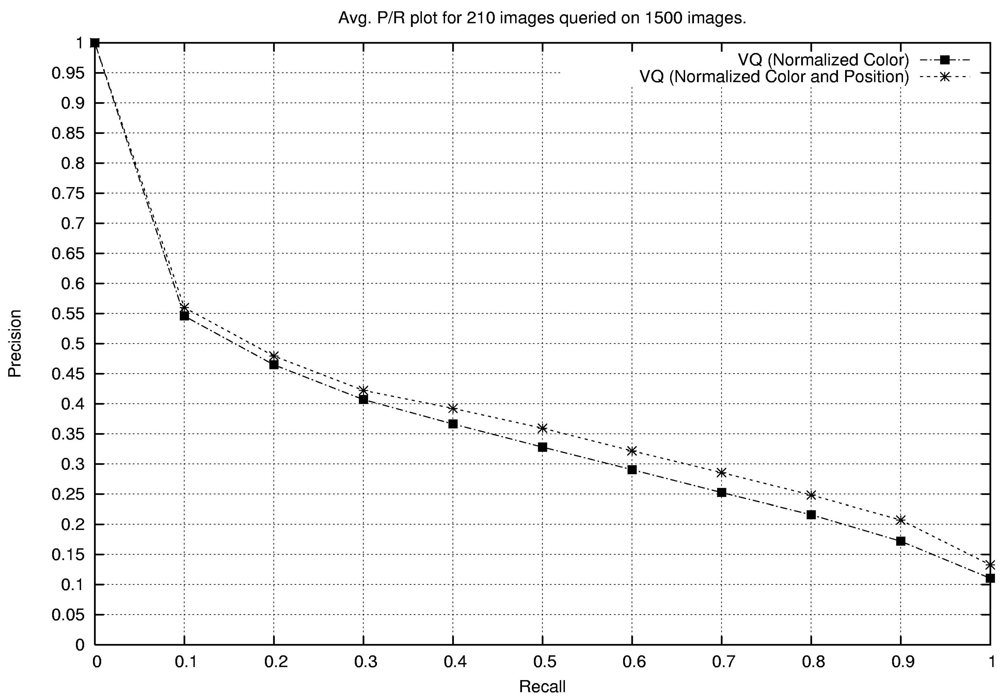
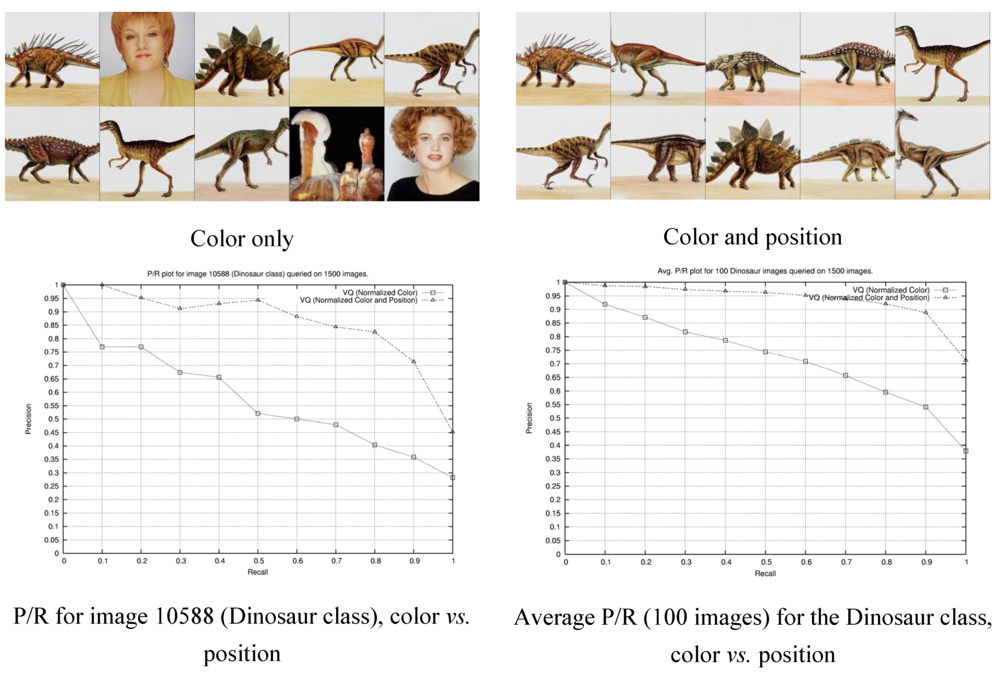
2.1. Explicit Incorporation of Position Information


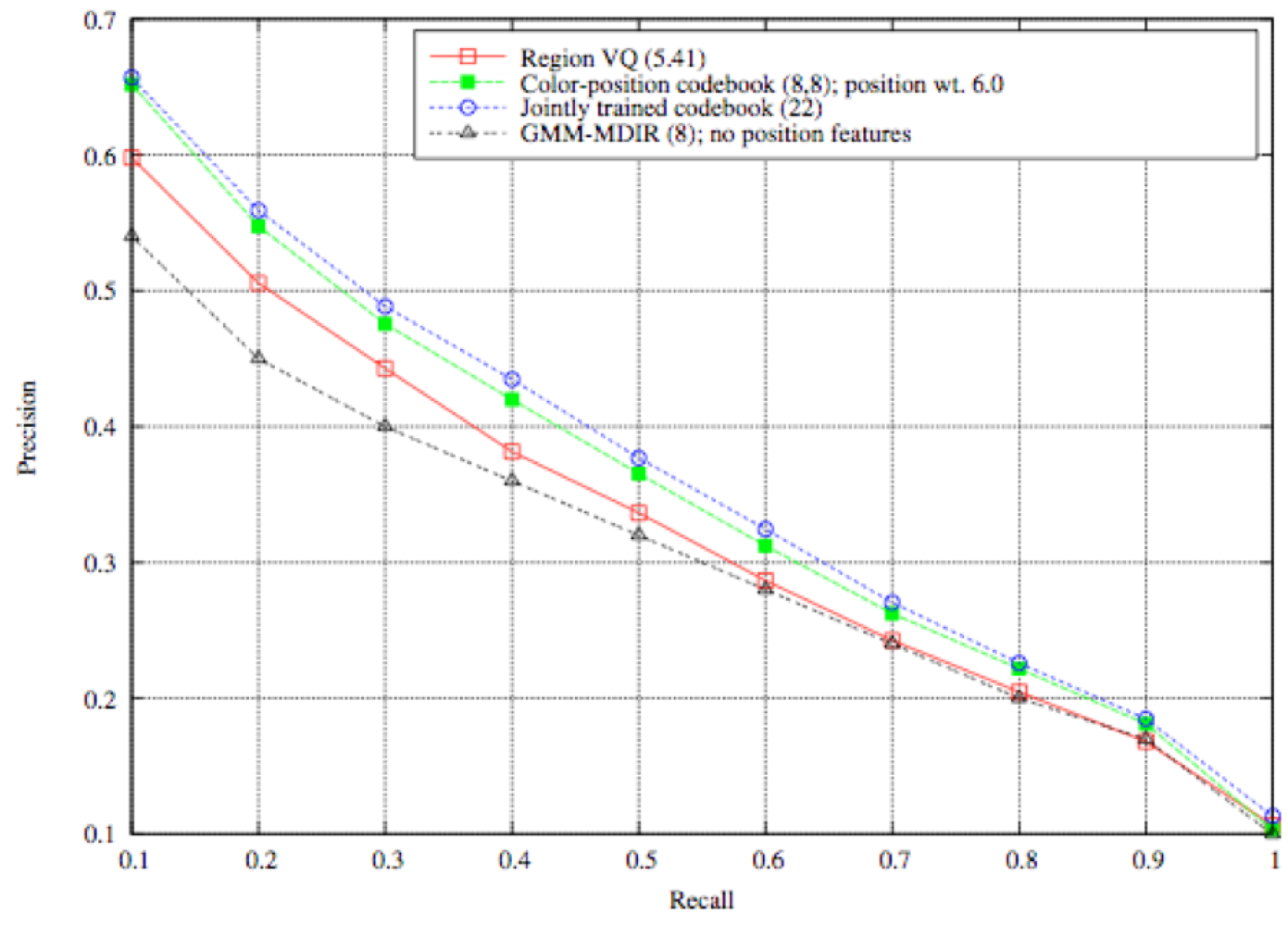
2.2. Region Based Retrieval

3. Texture
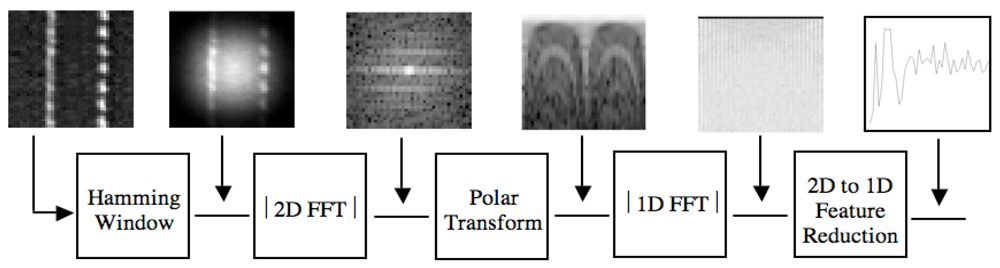
4. Object Recognition
- Curvature Scale Space (CSS) shape descriptors (Mokhtarian, Abbasi, and Kittler [12]) reduce the contours of a shape into sections of convex and concave curvature by determining the position of points at which the curvature is zero. To achieve this, the shape boundary is analyzed at different scales, i.e., filtering the contour using low-pass Gaussian filters of variable widths.
- Visual parts (Latecki and Lakämper [13]) is an algorithm based on the idea that a unique sub-assembly of an object can often provide strong cues in recognizing the larger object of which they are a distinct part.
- Shape contexts (SC) (Belongie, Malik, and Puzicha [14]) is a correspondence-based shape matching technique where the shape’s contour is sampled using a subset of points.
- Inner-distance (ID) (Ling and Jacobs [15]) is a skeleton-based approach that starting with two chosen landmark points calculates the shortest path between those points that also remains within the shape boundary.
4.1. The RBRC Algorithm


4.2. Retrieval
| Method | Score |
|---|---|
| CSS (Mokhtarian, Abbasi, and Kittler [12]) | 75.44% |
| Visual Parts (Latecki, Lakamper, and Eckhardt [17]) | 76.45% |
| SC + TPS (Belongie, Malik, and Puzicha [14]) | 76.51% |
| Curve Edit (Sebastian, Klein, and Kimia [18]) | 78.71% |
| Distance Set (Grigorescu and Petkov [19]) | 78.38% |
| MCSS (Jalba, Wilkinson, and Roerdink [20]) | 78.80% |
| Generative Models (Tu and Yuille [21]) | 80.03% |
| MDS + SC + DP (Ling and Jacobs [15]) | 84.35% |
| IDSC + DP (Ling and Jacobs [15]) | 85.40% |
| RBRC, c = 6 | 93.06% |
| 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
|---|---|---|---|---|---|---|---|---|
| 88.2 | 90.5 | 88.7 | 90.3 | 93.1 | 93.5 | 93.9 | 94.3 | 94.4 |
4.3. Separation of Training from Testing
| Train | 1st half | 1st half | 2nd half | 2nd half |
|---|---|---|---|---|
| Test | 1st half | 2nd half | 1st half | 2nd half |
| Score | 94.47% | 94.30% | 92.06% | 91.09% |
4.4. Robustness to Rotation and Scaling
| Method | Rotation | Scaling | Average |
|---|---|---|---|
| Visual Parts (Latecki, Lakamper, and Eckhardt [17]) | 100% | 88.65% | 94.33% |
| CSS (Mokhtarian, Abbasi, and Kittler [12]) | 99.37% | 89.76% | 94.57% |
| Wavelets (Chuang and Kuo [23]) | 97.46% | 88.04% | 92.75% |
| Zernike Moments (Khotanzan and Hong [24]) | 99.60% | 92.54% | 96.07% |
| Multilayer Eigenvectors | 100% | 92.42% | 96.21% |
| (Latecki, Lakamper, and Eckhardt [17], Hyundai [25]) | |||
| RBRC | 99.52% | 93.02% | 96.27% |
5. Location


6. Conclusions and Current Research
References
- Daptardar, A.; Storer, J.A. VQ Based Image Retrieval Using Color and Position Features. In Proceedings of the Data Compression Conference, Snowbird, UT, USA, 25-27 March 2008; pp. 432–441.
- Shapira, D.; Storer, J.A. In-Place Differential File Compression of Non-Aligned Files With Applications to File Distribution, Backups, String Similarity. In Proceedings of the Data Compression Conference, Snowbird, UT, USA, 23-25 March 2004; pp. 82–91.
- Shapira, D.; Storer, J.A. In-place differential file compression. Comput. J. 2005, 48, 677–691. [Google Scholar] [CrossRef]
- Jeong, S.; Gray, R.M. Minimum Distortion Color Image Retrieval Based on Lloyd-Clustered Gauss Mixtures. In Proceedings of the IEEE Data Compression Conference, Snowbird, UT, USA, 29-31 March 2005; pp. 279–288.
- Wyszecki, G.; Stiles, W.S. Color Science: Concepts and Methods, Quantitative Data and Formulae, 2nd ed; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Gersho, A.; Gray, R.M. Vector Quantization and Signal Compression; Springer: Berlin, Germany, 1992. [Google Scholar]
- Jeong, S.; Won, C.S.; Gray, R.M. Histogram-Based Image Retrieval using Gauss Mixture Vector Quantization. In Proceedings of the 2003 International Conference on Multimedia and Expo, (ICME’03), Baltimore, MD, USA, 6-9 July 2003; 94, pp. 44–66.
- Wang, J. Semantics-sensitive Integrated Matching for Picture Libraries. Available online: http://wang.ist.psu.edu/cgi-bin/zwang/regionsearch_show.cgi (accessed on 9 January 2012).
- DiLillo, A.; Motta, G.; Storer, J.A. Texture Classification Based on Discriminative Features Extracted in the Frequency Domain. In Proceedings of the IEEE International Conference on Image Processing (ICIP), San Antonio, Texas, USA, 16-19 September 2007; pp. 53–56.
- Ojala, T.T.; Mäenpää, T.; Pietikäinen, M.; Viertola, J.; Kyllönen, J.; Huovinen, S. Outex-New Framework for Empirical Evaluation of Texture Analysis Algorithms. In Proceedings of the 16th International Conference on Pattern Recognition, Quebec, Canada, 11-15 August 2002; 1, pp. 701–706.
- Bober, M. MPEG-7 visual shape descriptors. IEEE Trans. Circuits Syst. Video Technol. 2001, 11, 716–719. [Google Scholar] [CrossRef]
- Mokhtarian, F.; Abbasi, S.; Kittler, J. Efficient and Robust Retrieval by Shape Content through Curvature Scale Space. In Image Databases and Multi-Media Search; Smeulders, A.W.M., Jain, R., Eds.; World Scientific: Singapore, 1997; pp. 51–58. [Google Scholar]
- Latecki, L.J.; Lakämper, R. Shape similarity measure based on correspondence of visual parts. IEEE Trans. Pattern Anal. Mach. 2000, 22, 1185–1190. [Google Scholar] [CrossRef]
- Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape context. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef]
- Ling, H.; Jacobs, D.W. Shape classification using the inner-distance. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 286–299. [Google Scholar] [CrossRef]
- Di Lillo, A.; Motta, G.; Storer, J.A. Multiresolution Rotation-Invariant Texture Classification Using Feature Extraction in the Frequency Domain and Vector Quantization. In Proceedings of the Data Compression Conference, Snowbird, UT, USA, 25-27 March 2008; pp. 452–461.
- Latecki, L.J.; Lakamper, R.; Eckhardt, U. Shape Descriptors for Non-Rigid Shapes with a Single Closed Contour. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head Island, SC, USA, 13-15 June 2000; I, pp. 424–429.
- Sebastian, T.; Klein, P.; Kimia, B. On aligning curves. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 116–125. [Google Scholar] [CrossRef]
- Grigorescu, C.; Petkov, N. Distance sets for shape filters and shape recognition. IEEE Trans. Image Process. 2003, 12, 1274–1286. [Google Scholar] [CrossRef]
- Jalba, C.; Wilkinson, M.H.F.; Roerdink, J.B.T.M. Shape representation and recognition through morphological curvature scale spaces. IEEE Trans. Image Process. 2006, 15, 331–341. [Google Scholar] [CrossRef]
- Tu, Z.; Yuille, A.L. Shape Matching and Recognition-Using Generative Models and Informative Features. In Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 11-14 May 2004; 3, pp. 195–209.
- Jeannin, S.; Bober, M. Shape Matching and Recognition-Using Generative Models and Informative Features. In Description of core experiments for MPEG-7 motion/shape; ISO/IEC JTC1/SC29/WG11 /MPEG99/N2690; MPEG-7: Seoul, Korea, 03 1999. [Google Scholar]
- Chuang, C.; Kuo, C.-C. Wavelet descriptor of planar curves: Theory and applications. IEEE Trans. Image Process. 1996, 5, 56–70. [Google Scholar] [CrossRef]
- Khotanzan, A.; Hong, Y.H. Invariant image recognition by zernike moments. IEEE Trans. PAMI 1990, 12, 489–497. [Google Scholar] [CrossRef]
- Hyundai Electronics Industries Co., Ltd. Available online: http://www.wtec.org/loyola/satcom2/d_03.htm (accessed on 10 January 2012).
- Zamir, A.R.; Shah, M. Shah, M. Accurate Image Localization Based on Google Maps Street View. In Proceedings of the European Conference on Computer Vision (ECCV’10), Hersonissos, Heraklion, Crete, Greece, 5–11 September 2010.
- Zhang, W.; Kosecka, J. Image Based Localization in Urban Environments. In Proceedings of the 3rd International Symposium on 3D Data Visualization, and Transmission, Chapel Hill, NC, USA, 14–16 June 2006.
- Teller, S.; Antone, M.; Bodnar, Z.; Bosse, M.; Coorg, S.; Jethwa, M.; Master, N. Calibrated, registered images of an extended urban area. Int. J. Comput. Vis. 2003, 53, 93–107. [Google Scholar] [CrossRef]
- Lowe, D.G. Object Recognition from Local Scale-Invariant Features. In Proceedings of the 7th IEEE International Conference on Computer Vision, Kerkyra, Greece, 20-27 September 1999; pp. 1–8.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lillo, A.D.; Daptardar, A.; Thomas, K.; Storer, J.A.; Motta, G. Compression-Based Tools for Navigation with an Image Database. Algorithms 2012, 5, 1-17. https://doi.org/10.3390/a5010001
Lillo AD, Daptardar A, Thomas K, Storer JA, Motta G. Compression-Based Tools for Navigation with an Image Database. Algorithms. 2012; 5(1):1-17. https://doi.org/10.3390/a5010001
Chicago/Turabian StyleLillo, Antonella Di, Ajay Daptardar, Kevin Thomas, James A. Storer, and Giovanni Motta. 2012. "Compression-Based Tools for Navigation with an Image Database" Algorithms 5, no. 1: 1-17. https://doi.org/10.3390/a5010001




