2.1. Mammogram Preprocessing
The goal of preprocessing is to prepare for next two steps, segmentation and classification. Down-sampling, quantization, ROI (region of interest) extraction, denoising and enhancement are done in the preprocessing step.
To reduce computation load without losing much sensitivity, original mammograms are down-sampled by factor of 4 (i.e., the new image size is reduced to 1/16 of its original size) and quantized down to 8 bits per pixel (256 gray level). The digitized mammograms in the DDSM database are of high resolution and of high fidelity. For example, the mammograms scanned by LumiSys in the DDSM database are of 12 bits per pixel and 50 microns per pixel, a typical mammogram of which has the resolution of 6,000 by 4,000 pixels.
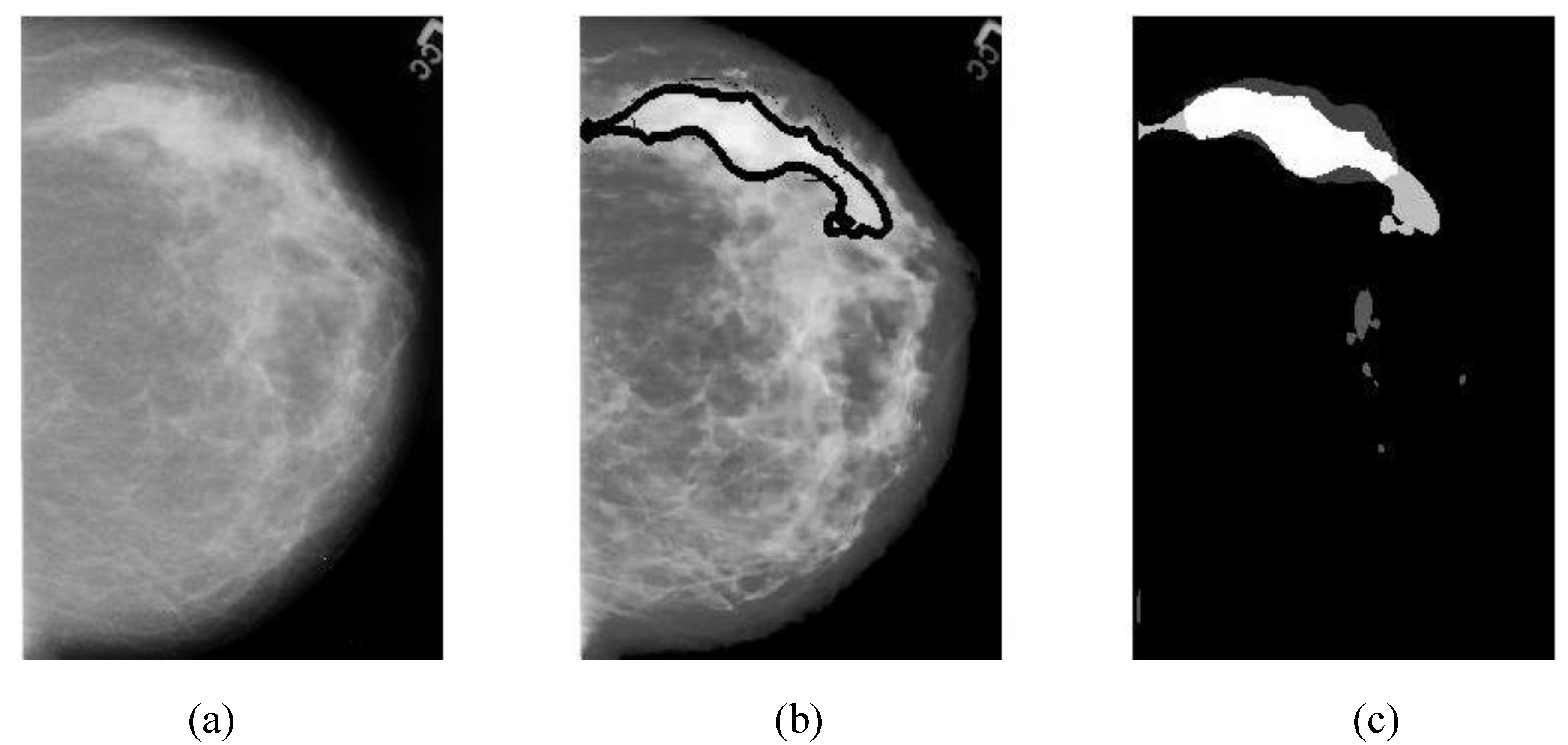
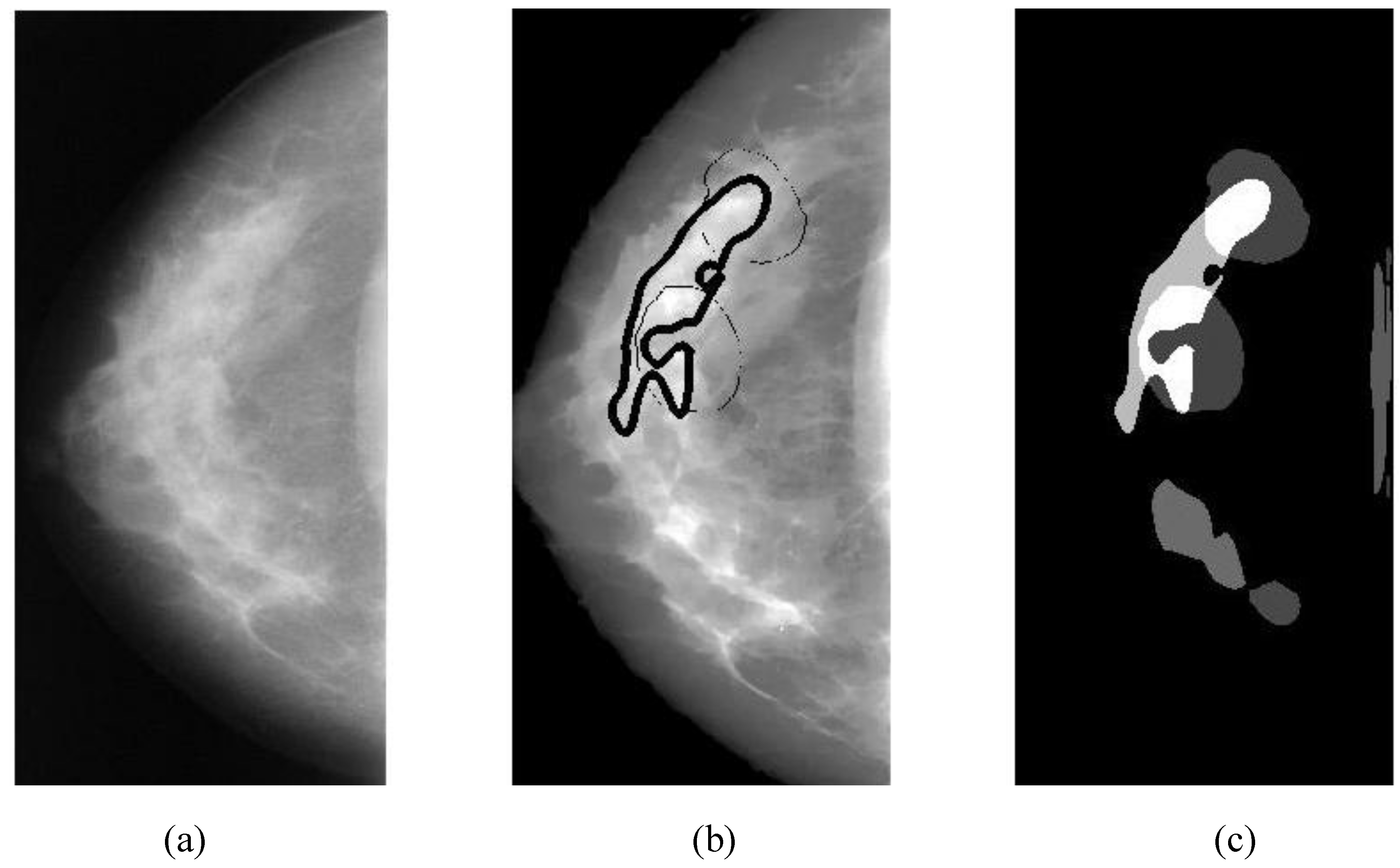
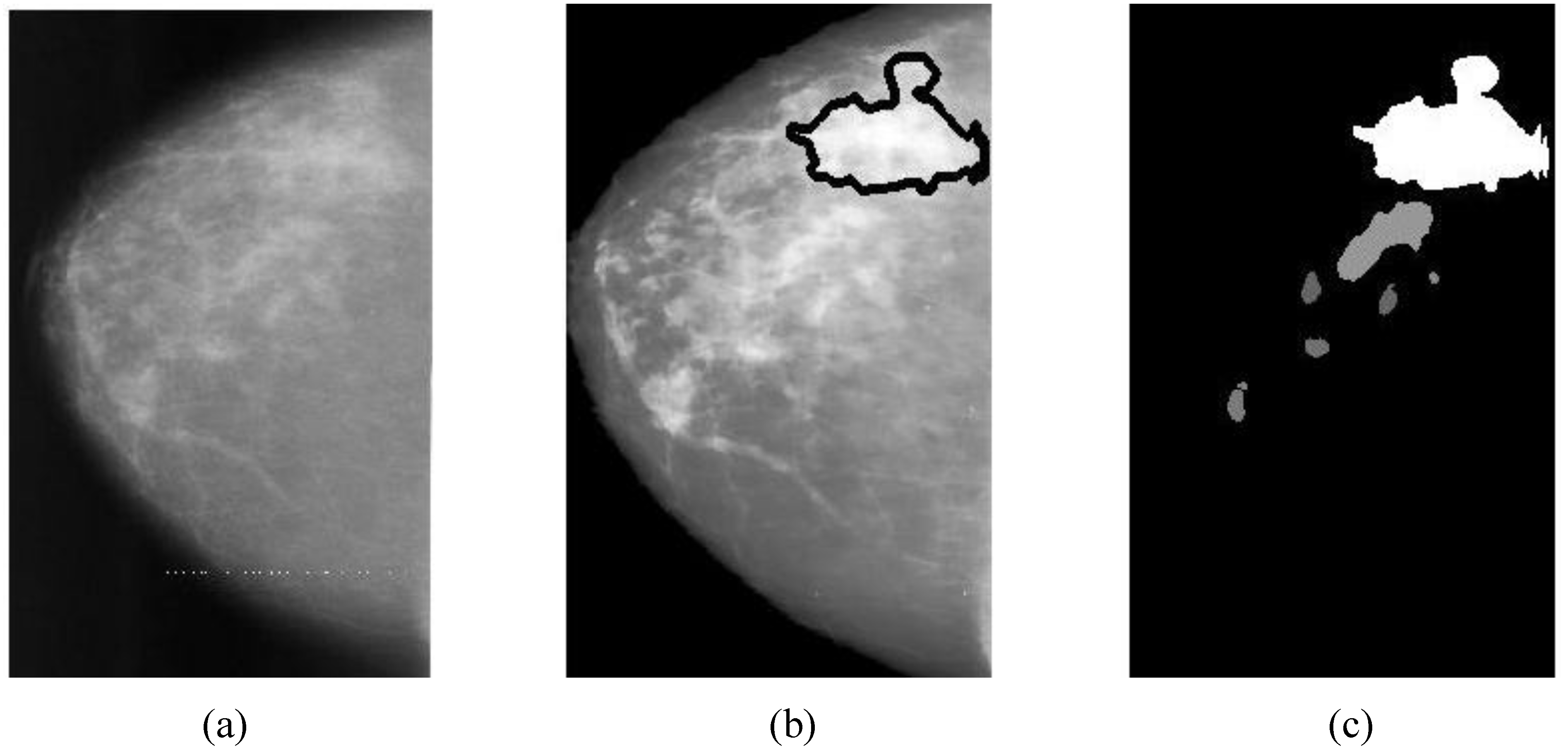
The region of interest on a mammographic image (breast ROI) is extracted to reduce the processing time (by ignoring the dark areas). First, a mammogram (
IS) is mapped onto a special target image (
IM) with Equation (1) by specifying (
μT,
σT) = (128, 0.75). Then the mapped image (
IM) is binarized with a threshold (
μT). Next, the largest 8-connected object is considered as the binary mask of breast ROI. Finally, morphological
closing operations can fill holes inside the ROI:
where
IM is the mapped (target) image,
IS is the source (original) mammographic image;
μ and
σ denote mean and standard deviation, respectively; the subscripts ‘S’ and ‘T’ refer to the source (original) and target (mapped) images.
Figure 1.
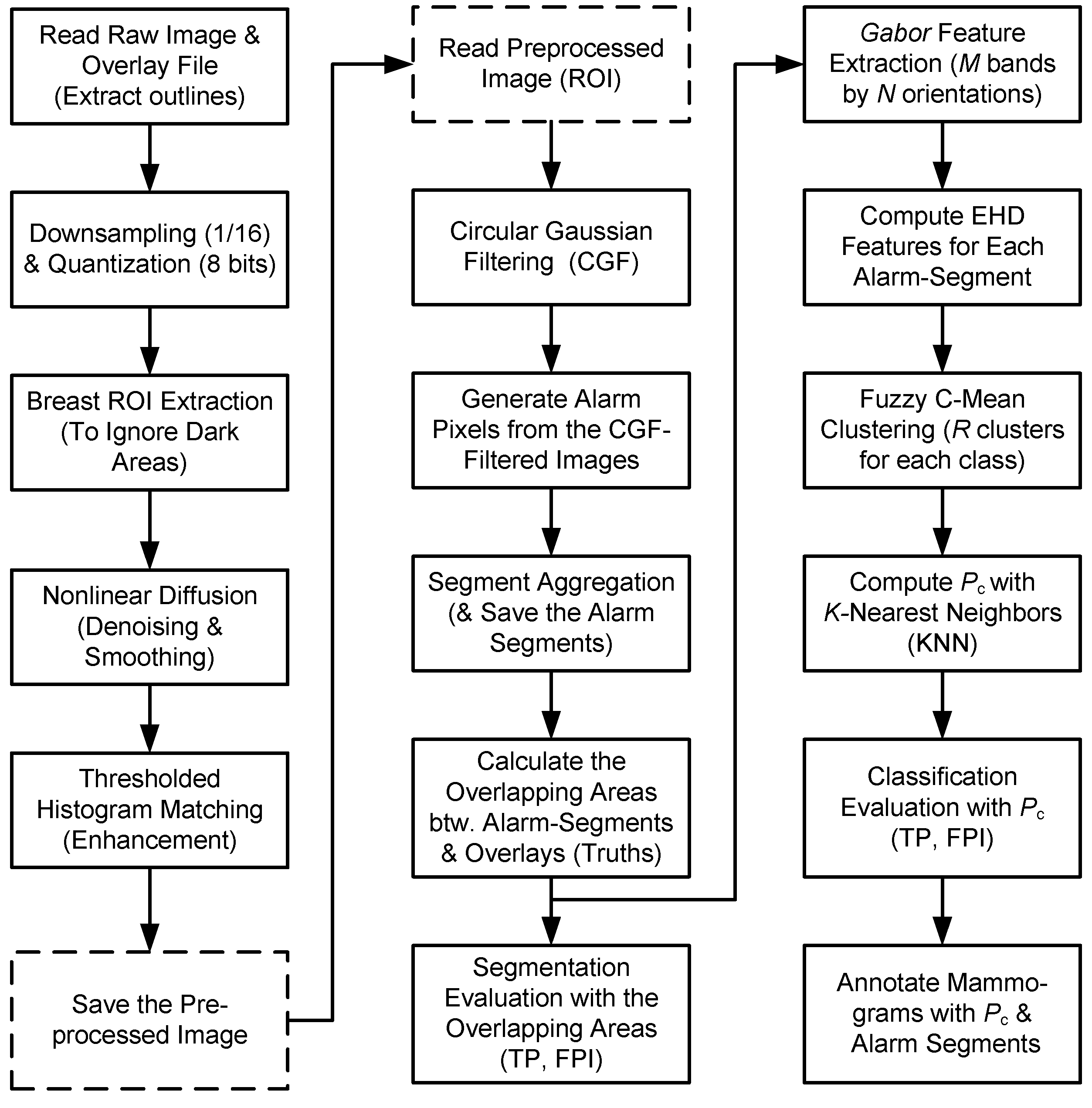
The flow chart of GCD algorithm: Three steps, preprocessing, segmentation and classification, are shown in three columns, respectively. “Save/Read the Preprocessed image” (within dashed rectangles) may be omitted in a continuous process. PC is the cancerous probability of analyzing alarm segment.
Figure 1.
The flow chart of GCD algorithm: Three steps, preprocessing, segmentation and classification, are shown in three columns, respectively. “Save/Read the Preprocessed image” (within dashed rectangles) may be omitted in a continuous process. PC is the cancerous probability of analyzing alarm segment.
Nonlinear diffusion is performed to suppress noise while retaining edges. Nonlinear diffusion methods have been proven as powerful methods in the denoising and smoothing of image intensities while retaining and enhancing edges. Such an image smoothing process can be summarized as a successive coarsening of any given image while certain structures in that image are retained on a fine scale. Nonlinear diffusion is closely connected to a specific kind of multiscale analysis referred to as scale-space [
14,
15], and was first used for image smoothing with simultaneous edge enhancement [
16]. In addition, Barash
et al. [
17] have proven that nonlinear diffusion is equivalent to adaptive smoothing. Basically, diffusion is a PDE (partial differential equation) method that involves two operators, smoothing and gradient, in 2D image space. The diffusion process smoothes the regions with lower gradients whereas stops smoothing at region boundaries with higher gradients. In other words, the diffused result is a nonlinear function of local gradients. Weickert
et al. [
18] presented a semi-implicit scheme with an “additive operator splitting” (AOS) implementation for nonlinear diffusion filtering, which is stable for all time steps (
t >> 0.25) and guarantees equal treatment of all coordinate axes. The AOS scheme is at least ten times more efficient than the widely used explicit schemes (with limited time step,
t ≤ 0.25). In our experiments, the AOS scheme is implemented for mammogram diffusion by empirically specifying parameters to achieve a good balance between noise removal and detail retaining.
Image enhancement is intended to benefit the CAD algorithm but not necessarily to favorite visual inspection, which is achieved with a “thresholded histogram matching”.
Histogram matching (also referred as histogram specification) is usually used to enhance an image when
histogram equalization fails [
19]. Given the shape of the histogram that we want the enhanced image to have, histogram matching can generate a processed image that has the specified histogram. In particular, by specifying the histogram of
Gaussian distribution and by designating a threshold (
THM), histogram matching is employed to enhance mammograms. During histogram matching, any pixel whose intensity value is less than
THM will always be kept unchanged as if it were protected from intensity (gray level) changes. Such a thresholded histogram matching can retain black background of medical images, which is useful for the following alarm generation.
2.2. Segmentation by Circular Gaussian Filter
Segmentation is one of the key steps to empower a breast CAD algorithm to be successful. Without the segmentation, it is inefficient to extract the features over the entire mammogram, which will cause too extensive computations and usually result in a poor classification. The goal of segmentation is to find all suspicious regions that should contain as many cancers (masses or calcifications) as possible; whereas the
false positives will be excluded with a trained classifier using the additional features extracted from the suspicious segments. We propose to detect mass or calcification regions using a set of band-pass filters formed by rotating a 1-D Gaussian filter (off center) in frequency space, termed as “
Circular Gaussian Filter” (CGF; refer to Equation (2) and
Figure 2). A CGF can be uniquely characterized by specifying a central frequency (
f) and a frequency band (
σ). A mass or calcification is a space-occupying lesion and usually appears as a bright region on a mammogram. On the filtered mammograms with a set of CGFs, the highlighted regions correspond to mass or calcification segments. Consequently, the suspicious mass or calcification segments can be extracted out using a threshold adaptively decided upon histogram analysis. Typically, the CGF parameters of (
f = [12 24 48],
σ = [6 12 24]) produce promising segmentation results.
In Fourier frequency domain, a
Circular Gaussian Filter (CGF) is defined as follows:
where:
where
f specifies a central frequency and
σ defines a frequency band.
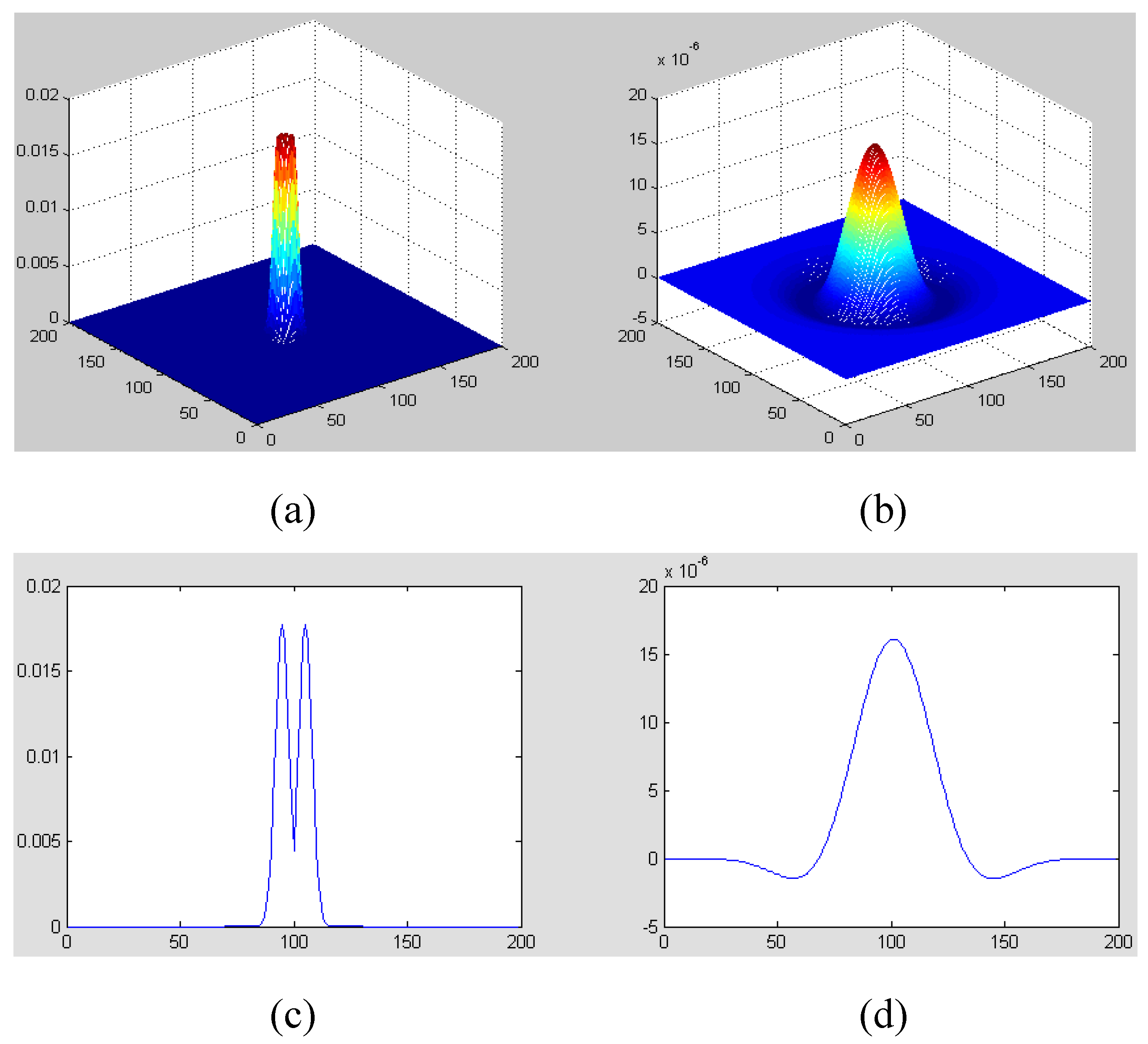
Figure 2.
Figure illustration of CGF with f = 12 and σ = 6 (Only the central part of CGF is presented): (a) CGF in frequency domain; (b) CGF in spatial domain; (c) A central slice of (a); (d) A central slice of (b).
Figure 2.
Figure illustration of CGF with f = 12 and σ = 6 (Only the central part of CGF is presented): (a) CGF in frequency domain; (b) CGF in spatial domain; (c) A central slice of (a); (d) A central slice of (b).
Alarm pixels and alarm segments are generated with the following procedures:
(1)
Alarm pixels are produced by thresholding three CGF-filtered images (
IFm) pixel-by-pixel. The
alarm threshold (
TAm) is determined by histogram analyses. For each of three CGF-filtered images (
IFm,
m = 1, 2, 3), initialize a corresponding alarm image,
IAm, with zero pixel values, and then:
- (a)
Compute the histogram and accumulated histogram: HFm and AHFm.
- (b)
Find the locations of peaks in HFm by using histogram gradient changes (of sign pattern [+ + -]): {LP1, LP2, … LPq}; and assumed this set is in the order from the lowest (LP1) to the highest (LPq) gray level.
- (c)
Choose the candidates of alarm threshold: Tk = {LPi | when (the selected alarm area) < (10% entire breast ROI area); i = 1 ~ q}, k = p, p+1, …, q (2 ≤ p ≤ q). Use AHFm to calculate the selected alarm area.
- (d)
Let the alarm threshold be one of {Tk; k = p ~ q}, i.e., TAm = Tl, p ≤ l ≤ q, such that is the maximum among {; k = p ~ q}.
- (e)
Mark a pixel at (x, y) as a candidate of alarm pixel if IFm (x, y) > TAm by assigning IAm(x, y) = 4 – m, where m = 1, 2, 3.
- (f)
A pixel at (x, y) is considered as an alarm pixel if .
(2)
Alarm segments are aggregated from
alarm pixels with morphological and geometric process as follows:
- (a)
Use morphological opening or filling to break segments or fill holes.
- (b)
Enumerate all 4-connection segments.
- (c)
Remove small alarm segments whose area is less than 9 pixels.
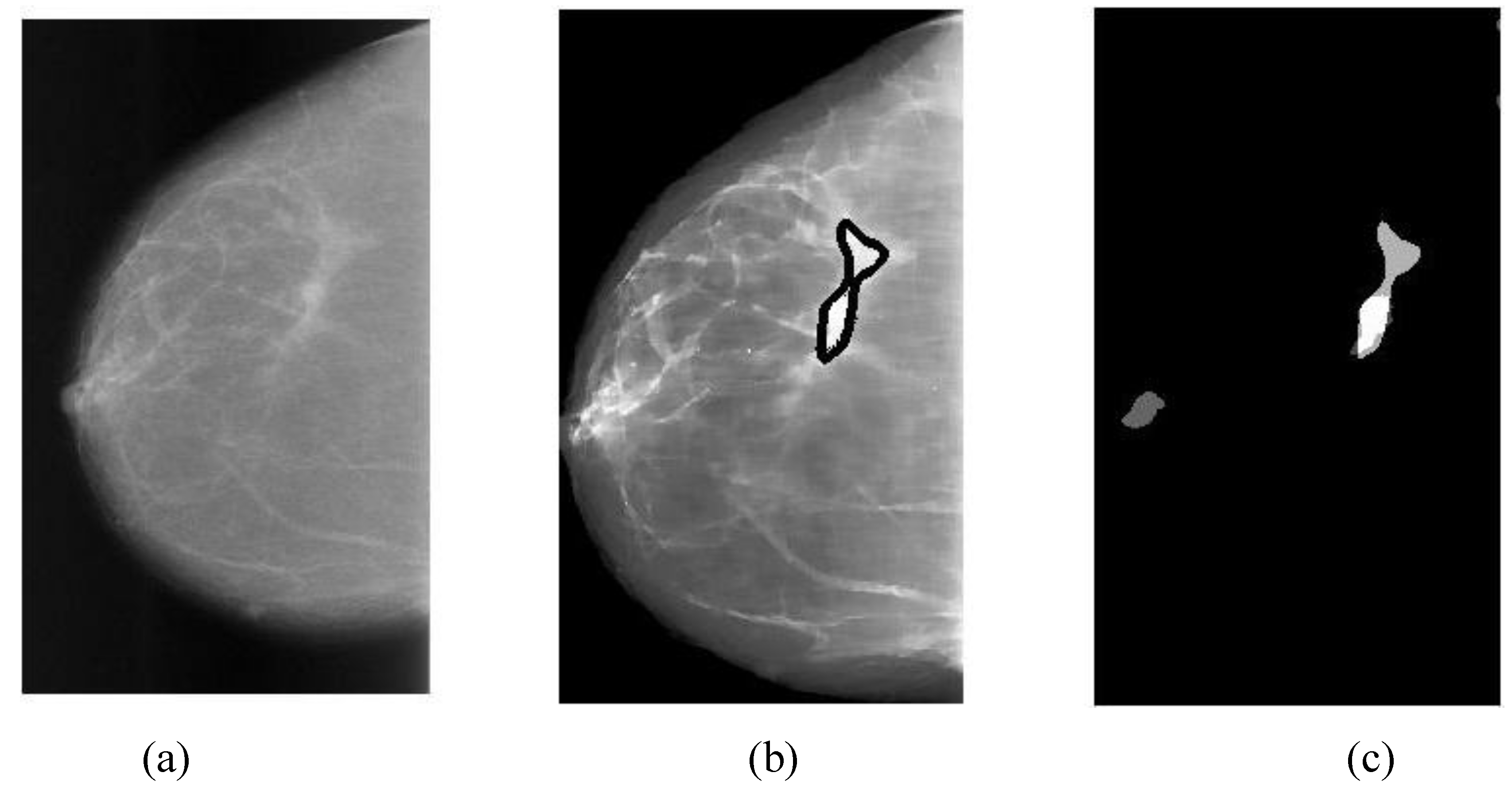
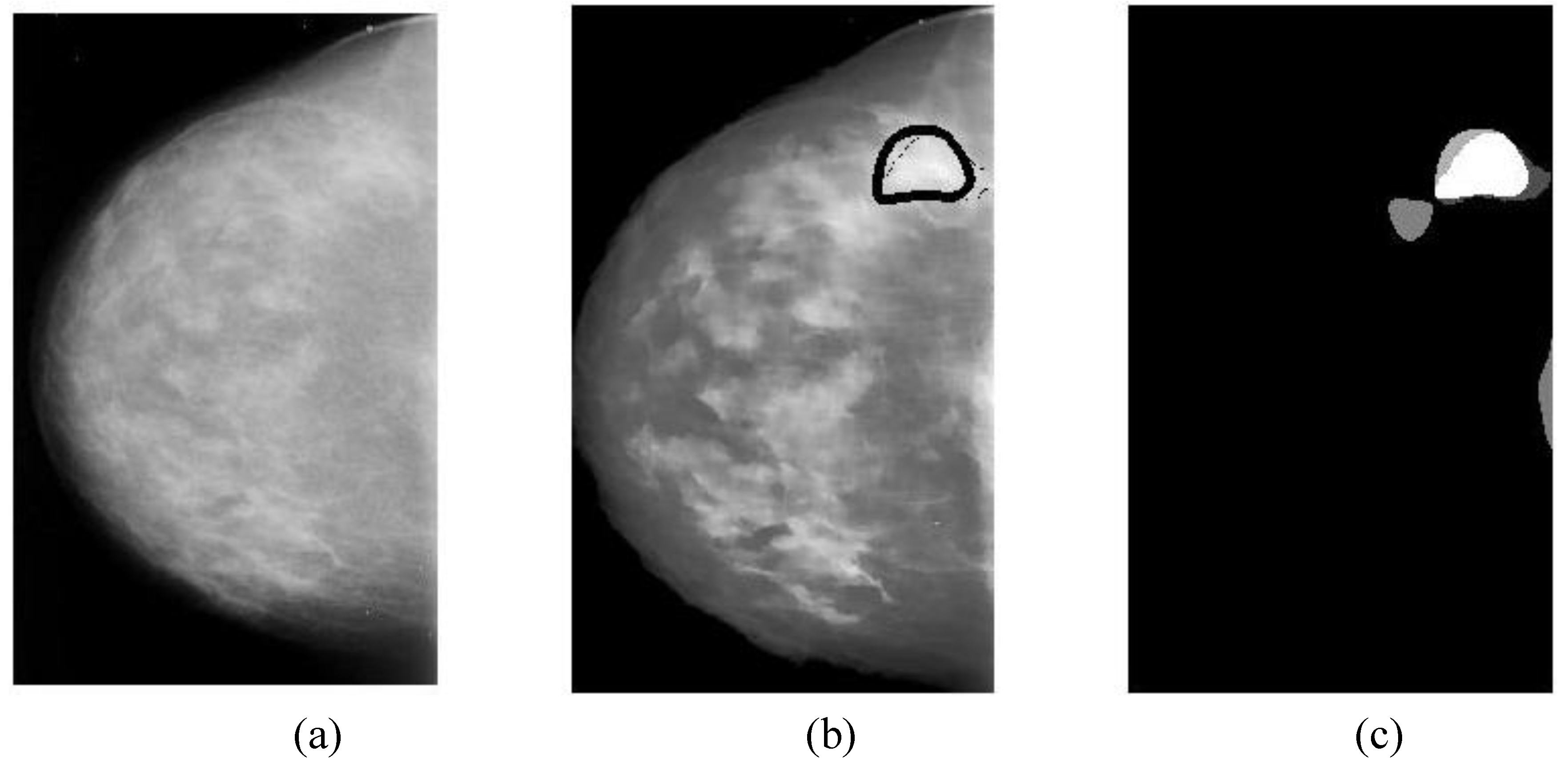
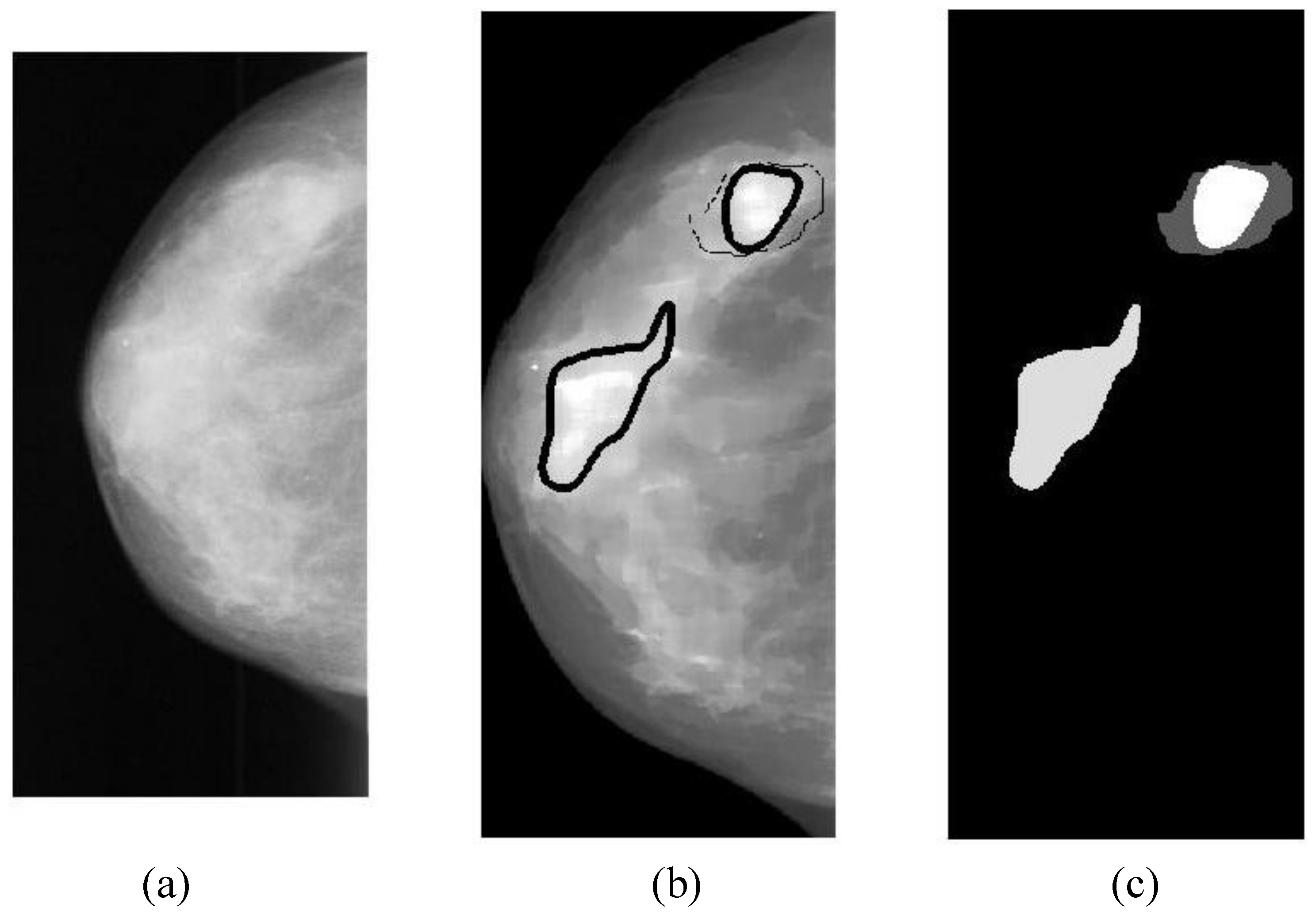
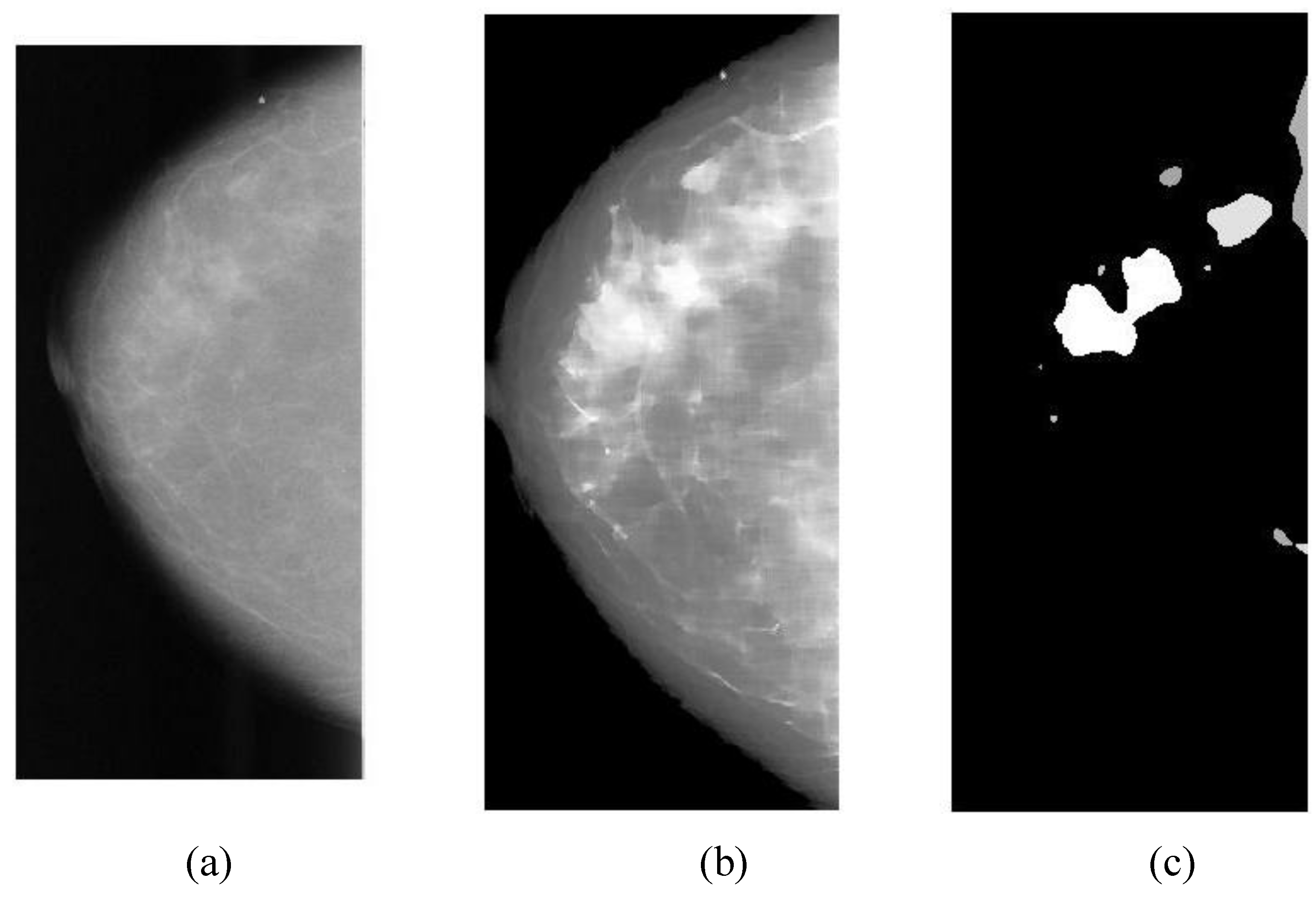
The overlapping area between alarm segments and overlays (ground truths) can be easily calculated (refer to Equation (9c)), which is an important measure of segmentation performance.
2.3. Classification with Gabor Features
Gabor filters have been used in many applications, such as texture segmentation, target detection, edge detection, retina identification, image coding and image representation [
20]. The Gabor filters have received considerable attention because the characteristics of certain cells in the visual cortex of some mammals can be approximated by these filters. Further, biological research suggests that the primary visual cortex performs a similar orientational and Fourier space decomposition [
21], so they seem to be sensible for a technical vision system. In addition these 2D band-pass filters, have been shown to posses optimal localization properties in both spatial and frequency domain and thus are well suited for extracting edges or features of an image lying in a specific frequency range and orientation.
A
Gabor filter can be viewed as a
sinusoidal plane of particular frequency and orientation, modulated by a
Gaussian envelope. It can be written as:
In Fourier frequency domain, the filter’s response consists of two 2D Gaussian functions (due to the conjugate symmetry on the spectrum) that are:
where
σu = 1/(2π
σx) and
σv = 1/(2π
σy) are the standard deviation along two orthogonal directions (which determines the width of the Gaussian envelope along the
x- and
y-axes in spatial domain), and assume that the origin of the Fourier transform has been centered. The intermediate variables are defined as following:
where
f determines the central frequency of the pass band in orientation
θ. Of course, we have
and
, where (
u0,
v0) is the center of one Gaussian function in Equation (5).
From each mammogram, a total of 20 Gabor filtered images (
IGmn,
m = 1~5,
n = 1~4, in spatial domain) are produced with 20 Gabor filters distributed along five bands (located from low to high frequencies) by four orientations (vertical, 45°, horizontal, and 135°). Four Gabor filters along four orientations at Band 2 are illustrated in
Figure 3, where only the central parts of four filters are displayed. The full size of a Gabor filter actually matches the image size being processed. Keep in mind that there is 90° directional difference between spatial domain and frequency domain. One sample of Gabor filtered images (of Case “3039_Left”, refer to
Figure 10) with the Gabor filter bank at 5 bands and 4 orientations is demonstrated in
Figure 4.
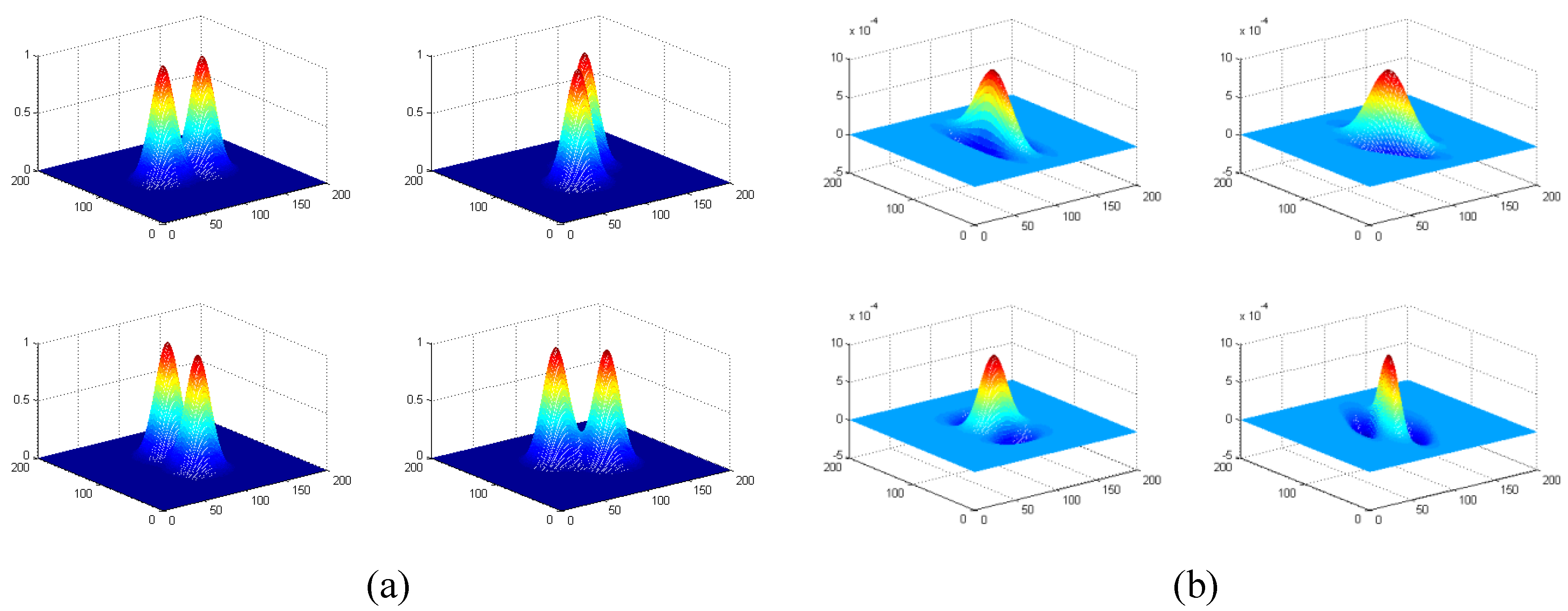
Figure 3.
Four Gabor filters along four orientations at Band 2. (a) Gabor filters in frequency domain, where f = 12, σu = σv = 6, θ = 0°, 45°, 90°, 135°. Only the central parts of four filters are displayed here. (b) Gabor filters in spatial domain. Note that there is 90° directional difference between spatial domain and frequency domain.
Figure 3.
Four Gabor filters along four orientations at Band 2. (a) Gabor filters in frequency domain, where f = 12, σu = σv = 6, θ = 0°, 45°, 90°, 135°. Only the central parts of four filters are displayed here. (b) Gabor filters in spatial domain. Note that there is 90° directional difference between spatial domain and frequency domain.
For each alarm segment found in
Section 2.2, a set of edge histogram descriptors are computed with its 20 counterparts lying in 20 Gabor filtered images (
IGmn,
m = 1~5,
n = 1~4), which will be used as features for classification. After clustering the EHD features with fuzzy C-means clustering method, a
k-nearest neighbor (KNN) classifier is used to reduce the number of false alarms.
The
edge histogram descriptor (EHD) [
22,
23] was initially proposed for MPEG-7 to express the local edge distribution in an image. The histogram generated in EHD denotes the local (within the alarm segment) frequency of four different types of edges namely vertical (90°), horizontal (0°), 45° diagonal, 135° diagonal edges at each band (refer to
Figure 3 and
Figure 4). Specifically, for a particular alarm segment at each band (each row in
Figure 4), the vertical histogram frequency (within the alarm segment) is the number of pixels of maximal intensity values in the vertical edge-extracted image (left-most column in
Figure 4) compared with the pixel values in other three directional (horizontal, 45° diagonal and 135° diagonal) edge-extracted images (columns 2, 3, 4 in
Figure 4). The other three directional frequencies can be calculated in the same way and a four-dimensional EHD signature can be formed by combining four directional frequencies together. The EHD features representing an alarm segment are obtained by joining 5-band EHD signatures together, which can be formulated as follows:
The EHD calculation is equivalent to count the numbers of maximal intensity pixels at each orientation along all bands. For example, suppose the vertical frequency of an EHD signature at band 1 is the largest (i.e., the highest bar in a histogram plot), that means vertical edges dominate band 1. Such an EHD feature (of an alarm segment) reflects both directional edge information and also frequency scale information (form low to high frequency). The EHD features are statistical features that are stable and reliable regardless of the absolute intensity values.
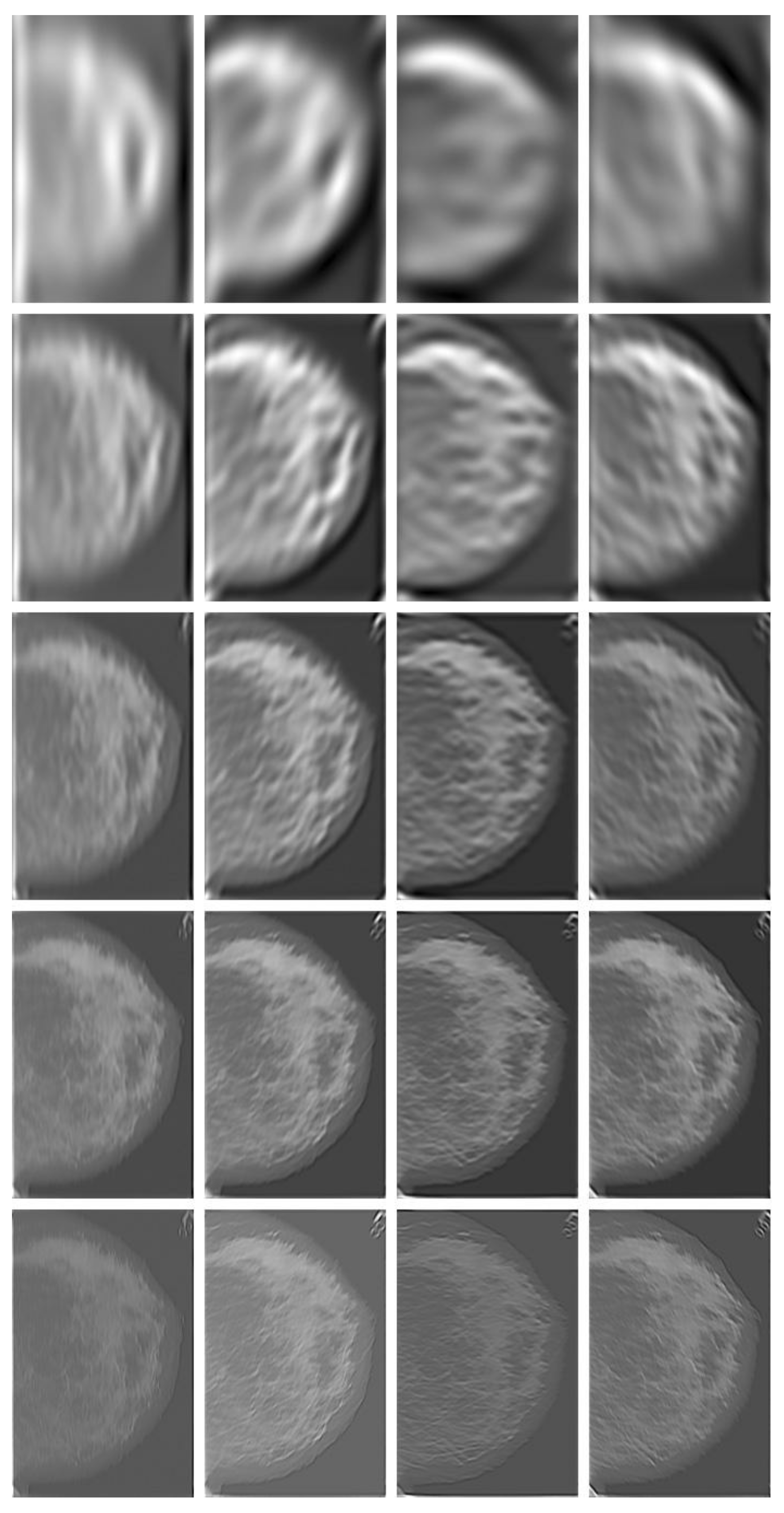
Figure 4.
Gabor-filtered images (
IGmn, Case “3039_Left” in
Figure 10, calcification present) with Gabor filter bank at five bands (along five rows) and four orientations (across four columns) for calcification detection. The four columns were Gabor filtered images corresponding to four orientations (vertical, 45°, horizontal and 135°).
Figure 4.
Gabor-filtered images (
IGmn, Case “3039_Left” in
Figure 10, calcification present) with Gabor filter bank at five bands (along five rows) and four orientations (across four columns) for calcification detection. The four columns were Gabor filtered images corresponding to four orientations (vertical, 45°, horizontal and 135°).
The most representative EHD features are mainly selected by using the
overlapping ratio (see Equation (9c)) and clustered with a
Fuzzy C-means (FCM) [
24] clustering method. The FCM is a data clustering technique wherein each data point belongs to a cluster to some degree that is specified by a membership grade. FCM starts with an initial guess (most likely incorrect) for the cluster centers, which are intended to mark the mean location of each cluster. FCM assigns every data point a membership grade for each cluster. By iteratively updating the cluster centers and the membership grades for each data point, FCM iteratively moves the cluster centers to the right location within a data set. This iteration is based on minimizing an objective function that represents the distance from any given data point to a cluster center weighted by that data point’s membership grade.
Once a certain number of clusters (say
R clusters for each of two classes, cancerous
vs. healthy) are formed by the FCM algorithm, the
k-nearest neighbors (KNN) can be found from
R × 2 clusters by using
Euclidean distance (between the analyzing feature and the clustered features). The probability,
PC, of a given alarm segment to be a malignant cancer is calculated by:
where
kC and
kH are the numbers of nearest clusters (to the analyzing features) that belong to cancerous class and healthy class, respectively. By specifying a threshold,
TP, a given alarm segment is classified as “cancer” (mass or calcification) when
PC >
TP; otherwise “Healthy” (Normal).
In general, classification performance can be evaluated using sensitivity, specificity and ROC (receiver operating characteristic) area. The performance of a CAD system for breast cancer detection is usually reported with true positive rate (TP), false positives per image (FPI), which are described as follows:
where the
Overlapping ratio defined in Equation (9c) is used to select typical patterns (for training purpose in classification) and to evaluate the annotation accuracy. Note that “positive” means cancerous whereas “negative” means healthy in the context. A “mark” is usually imposed on the mammography image when an alarm segment is classified as positive (cancerous), which is also referred as
annotation in this paper. If a positive mark matches the ground truth (referred as “overlay” herein, predefined by a radiologist) very well, then it is so-called “true positive”; otherwise “false positive”.