Bayesian Maximum Entropy Based Algorithm for Digital X-ray Mammogram Processing
Abstract
:1. Introduction
2. Methods
2.1. Inverse problems
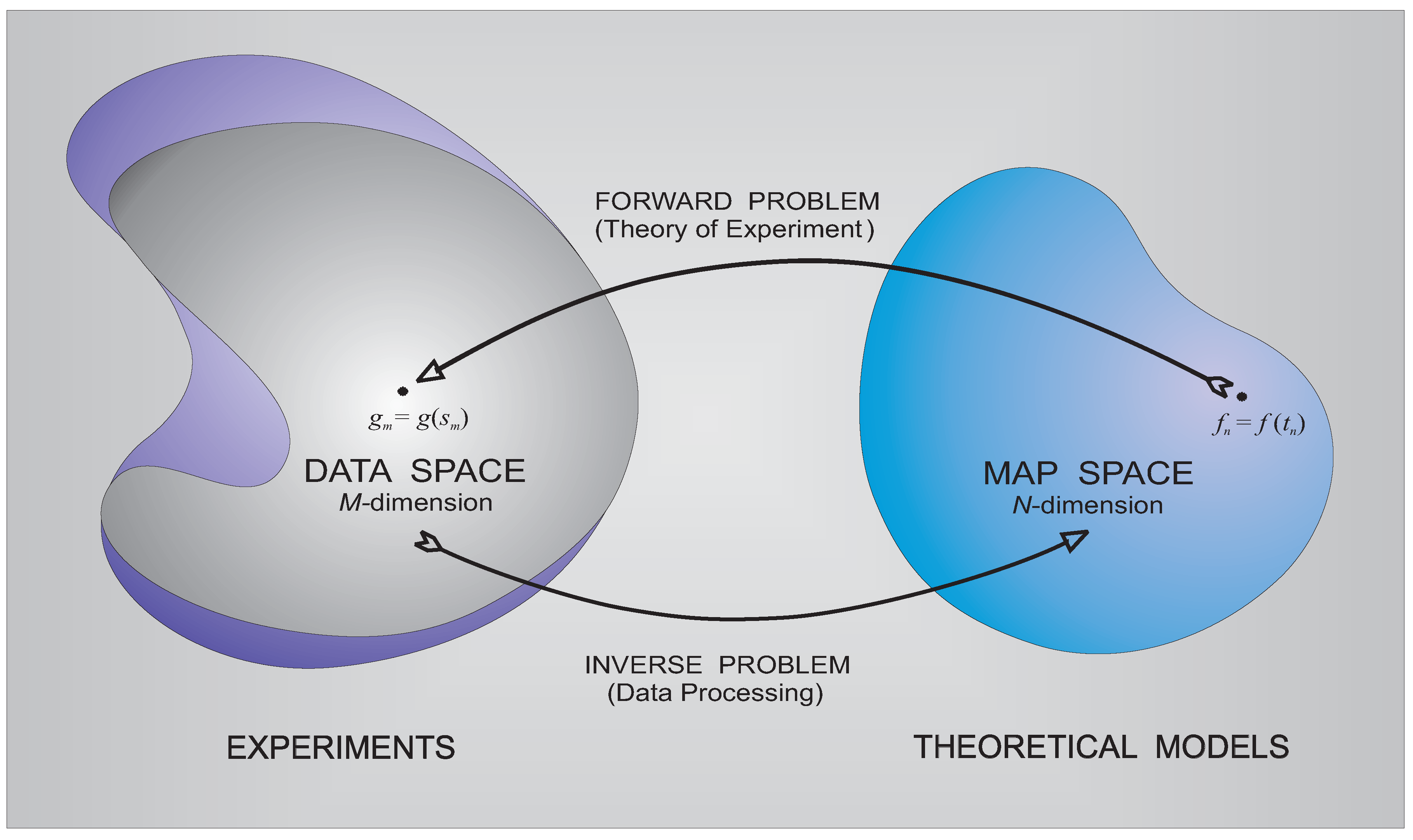
2.2. Bayesian image modeling
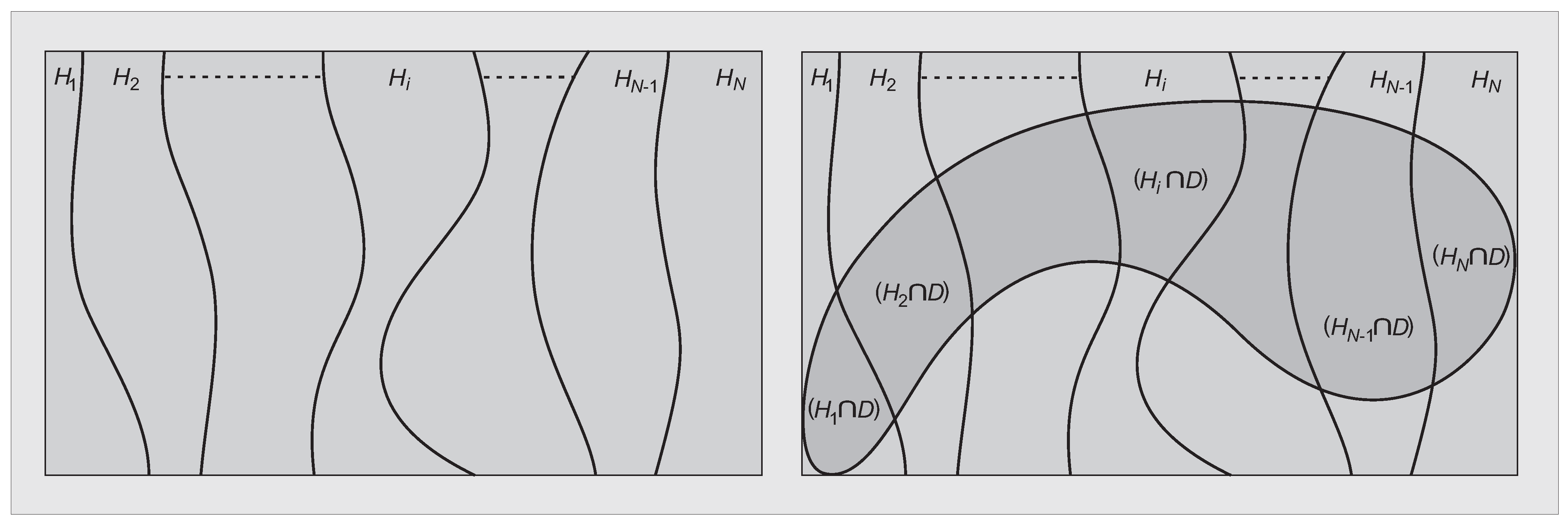


2.3. Image entropy
2.4. Bayesian image restoration
Likelihood
Prior probability
Posterior probability
2.5. Regularization of the inverse problem

2.6. Derivation of the potential function
- Conservation of the total number of photons in the measured image, g, and the model image f:
- Linear transform between the model space and the data space:
- The errors , are normally distributed with zero mean, , and variances :where Ω denotes the expected value of the statistical goodness-of-fit .
2.7. Multidimensional optimization
3. Results and Discussion
3.1. Physics of X-ray imaging
| X-ray beam energy (keV) | Central recorded photons | Total recorded photons |
| 18 | 15,660 ± 125 | 18,390 ± 135 |
| 20 | 59,130 ± 240 | 70,900 ± 270 |
| 22 | 184,070 ± 430 | 226,290 ± 475 |
| 24 | 337,400 ± 580 | 424,340 ± 650 |
| 26 | 531,130 ± 730 | 683,330 ± 825 |
| 28 | 738,230 ± 860 | 976,540 ± 990 |
| 30 | 890,710 ± 940 | 1,204,780 ± 1100 |
| Columns | (0) | (1) | ..... | (xsize-2) | (xsize-1) |
| Rows | |||||
| (0) | 0 | 1 | ..... | xsize-2 | xsize-1 |
| (1) | xsize | xsize+1 | ..... | 2*xsize-2 | 2*xsize-1 |
| (2) | 2*xsize | 2*xsize+1 | ..... | 3*xsize-2 | 3*xsize-1 |
| : | ..... | ..... | ..... | ..... | ...... |
| (ysize-2) | (ysize-2)*xsize | (ysize-2)*xsize+1 | ..... | (ysize-1)*xsize-2 | (ysize-1)*xsize-1 |
| (ysize-1) | (ysize-1)*xsize | (ysize-1)*xsize+1 | ..... | ysize*xsize-2 | ysize*xsize-1 |
| 0.0030 | 0.0050 | 0.0070 | 0.0050 | 0.0030 |
| (k-2*xsize-2) | (k-2*xsize-1) | (k-2*xsize) | (k-2*xsize+1) | (k-2*xsize+2) |
| 0.0050 | 0.0120 | 0.0160 | 0.0120 | 0.0050 |
| (k-xsize-2) | (k-xsize-1) | (k-xsize) | (k-xsize+1) | (k-xsize+2) |
| 0.0070 | 0.0160 | 0.7950 | 0.0160 | 0.0070 |
| (k-2) | (k-1) | (k) | (k+1) | (k+2) |
| 0.0050 | 0.0120 | 0.0160 | 0.0120 | 0.0050 |
| (k+xsize-2) | (k+xsize-1) | (k+xsize) | (k+xsize+1) | (k+xsize+2) |
| 0.0030 | 0.0050 | 0.0070 | 0.0050 | 0.0030 |
| (k+2*xsize-2) | (k+2*xsize-1) | (k+2*xsize) | (k+2*xsize+1) | (k+2*xsize+2) |


3.2. X-ray image quality assessment
3.3. Improvement of digital and digitized mammograms
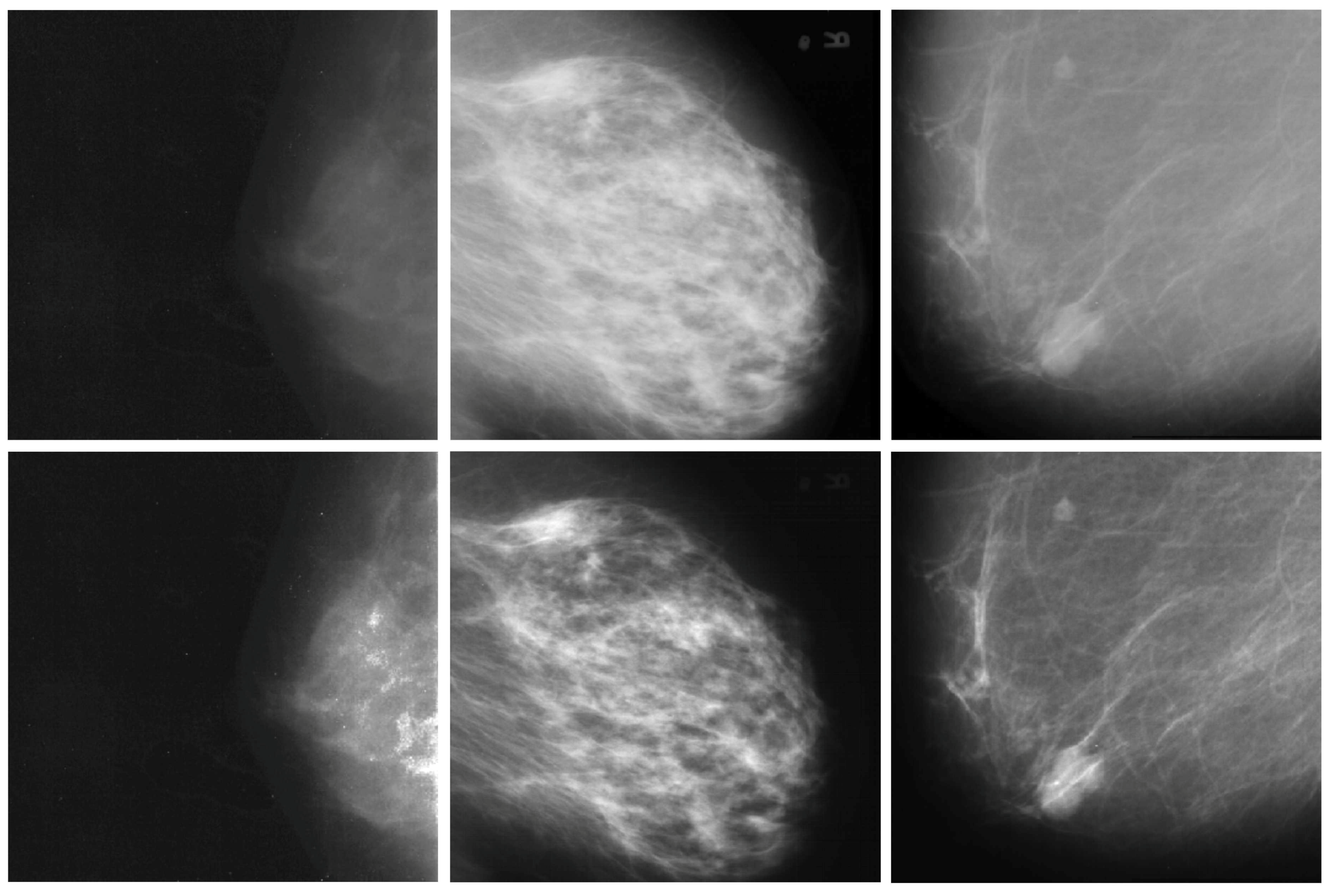

4. Conclusion
Acknowledgements
References and Notes
- Claridge, E.; Richter, J.H. Characterisation of mammographic lesions. In Digital Mammography; Gale, A.G., Astley, S.M., Dance, D.R., Alistair, A.Y., Eds.; Elsevier: Amsterdam, Netherlands, 1994. [Google Scholar]
- Meyer, Y. An introduction to wavelets and ten lectures on wavelets. Bull. Amer. Math. Soc. 1993, 28, 350–359. [Google Scholar] [CrossRef]
- Mallat, S. Une Exploration des Signaux en Ondelettes; Les Editions de l’Ecole Polytechnique, 2000. [Google Scholar]
- Donoho, D.L. Unconditional bases and bit-level compression. Applied and Computational Harmonic Analysis 1996, 1, 100–105. [Google Scholar] [CrossRef]
- Candes, E.J. Ridgelets: Theory and applications. PhD Thesis, Department of Statistics, Standford University, CA, USA, 1998. [Google Scholar]
- Mutihac, R.; Cicuttin; Jansen, K.; Mutihac, R.C. An essay on Bayesian inference and maximum entropy. Roumanian Biotechnological Letters 2000, 5, 83–114. [Google Scholar]
- Shore, J.E.; Johnson, R.W. Axiomatic derivation of the principle of maximum entropy and the principle of minimum cross-entropy. IEEE Trans. Inform. Theory 1980, IT-26, 26-39 and IT-29. 942–943. [Google Scholar] [CrossRef]
- Skilling, J. The axioms of maximum entropy. In Maximum Entropy and Bayesian Methods in Science and Engineering; Erickson, G.J., Smith, C.R., Eds.; Kluwer Academic Publishers: Dordrecht, Netherlands, 1988; Vol. I, pp. 173–187. [Google Scholar]
- Bayes, T. An essay towards solving a problem in the doctrine of chances. Phil. Trans. R. Soc. London 1763, 53, 330–418. [Google Scholar] [CrossRef]
- Jaynes, E.T. Papers on Probability, Statistics and Statistical Physics; Rosenkrantz, R.D., Ed.; Kluwer Academic Press: Dordrecht, Netherlands, 1983. [Google Scholar]
- Skilling, J. Fundamentals of MaxEnt in data analysis. In Maximum Entropy in Action; Buck, B., Macaulay, V.A., Eds.; Clarendon Press: Oxford, UK, 1994; pp. 19–39. [Google Scholar]
- MacKay, D.J.K. Information Theory, Inference, and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Berger, J. Statistical Decision Theory and Bayesian Analysis; Springer-Verlag: New York, NY, USA, 1985. [Google Scholar]
- Hadamard, J. Lectures on the Cauchy Problem in Linear Partial Differential Equations; Yale University Press: Yale, CT, USA, 1923. [Google Scholar]
- Engle, H.; Hanke, M.; Neubauer, A. Regularization of inverse problems. In Series - Mathematics And Its Applications; 375; Springer-Verlag: New York, NY, USA, 1996. [Google Scholar]
- Cox, R. Probability, frequency, and reasonable expectation. Am. J. Phys. 1946, 14, 1–13. [Google Scholar] [CrossRef]
- Djafari, A.M. Maximum entropy and linear inverse problems. In Maximum entropy and Bayesian methods; Djafari, A.M., Demoments, G., Eds.; Kluwer Academic Publishers: Dordrecht, Netherlands, 1993; pp. 253–264. [Google Scholar]
- Gull, S.F.; Daniell, G.J. Image reconstruction from incomplete and noisy data. Nature 1978, 272, 686–690. [Google Scholar] [CrossRef]
- Weiss, N.A. Introductory Statistics; Addison-Wesley: Boston, MA, USA, 2002. [Google Scholar]
- MacKay, D.J.K. A practical Bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Balasubramanian, V. Occam’s razor for parametric families and priors on the space of distributions. In Maximum Entropy and Bayesian Methods, Proceedings of the 15th International Workshop, Santa Fe, 1995; Hanson, K.M., Silver, R.N., Eds.; Kluwer Academic Publishers: Dordrecht, Netherlands, 1996; pp. 277–284. [Google Scholar]
- Balasubramanian, V. Statistical inference, Occam’s razor, and statistical mechanics on the space of probability distributions. Neural Comput. 1997, 9, 2. 349–368. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell. Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Pal, N.R.; Pal, S.K. Entropy: A new definition and its applications. IEEE Trans. Syst., Man, Cybern. 1991, 21, 1260–1270. [Google Scholar] [CrossRef]
- Skilling, J. Classic maximum entropy. In Maximum Entropy and Bayesian Methods; Skilling, J., Ed.; Kluwer Academic: Norwell, MA, USA, 1989; pp. 45–52. [Google Scholar]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in C: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Djafari, A.M. A full Bayesian approach for inverse problems. In Maximum Entropy and Bayesian Methods; Hanson, K.M., Silver, R.N., Eds.; Kluwer Academic Publishers: Dordrecht, Netherlands, 1995; pp. 135–144. [Google Scholar]
- Hanson, M.K. Making binary decisions based on the posterior probability distribution associated with tomographic reconstructions. In Maximum Entropy and Bayesian Methods; Smith, C.R., Erickson, G.J., Neudorfer, P.O., Eds.; Kluwer Academic Publishers: Dordrecht, Netherlands, 1992; pp. 313–326. [Google Scholar]
- MacKay, D.J.C. (1992), Bayesian interpolation. In Maximum Entropy and Bayesian Methods; Smith, C.R., Erickson, G.J., Neudorfer, P.O., Eds.; Kluwer Academic Publishers: Dordrecht, Netherlands, 1992. [Google Scholar]
- Myrheim, J.; Rue, H. New algorithms for maximum entropy image restoration. Graphical Models and Image Processing Archive 1992, 54, 223–238. [Google Scholar] [CrossRef]
- Agmon, N.; Alhassid, Y.; Levine, R.D. An algorithm for finding the distribution of maximal entropy. J. Comput. Phys. 1979, 30, 250–258. [Google Scholar] [CrossRef]
- Wilczek, R.; Drapatz, S. A high accuracy algorithm for maximum entropy image restoration in the case of small data sets. Astron. Astrophys. 1985, 142, 9–12. [Google Scholar]
- Ortega, J.M.; Rheinboldt, W.B. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Brodlie, K.W. Unconstrained minimization. In The State of the Art in Numerical Analysis; Jacobs, D.A.H., Ed.; Academic Press: London, UK, 1977; pp. 229–268. [Google Scholar]
- Cornwell, T.J.; Evans, K.J. A simple maximum entropy deconvolution algorithm. Astron. Astrophys. 1985, 143, 77–83. [Google Scholar]
- Evans, A.L. The evaluation of medical images. In Medical Physics Handbooks; Adam Hilger: Bristol, UK, 1981; Volume 10, pp. 45–46. [Google Scholar]
- Benini, L.; et al. Synchrotron radiation application to digital mammography. A proposal for the Trieste Project ”Elettra”. Phys. Med. 1990, VI, 293. [Google Scholar]
- Mutihac, R.; Colavita, A.A.; Cicuttin, A.; Cerdeira, A.E. Maximum entropy improvement of X-ray digital mammograms. In Digital Mammography; Karssemeijer, N., Thijssen, M., Hendriks, J., van Erning, L., Eds.; Kluwer Academic Publishers: Dordrecht, Netherlands, 1998; pp. 329–337. [Google Scholar]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H. Geant4 developments and applications. IEEE T. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Mutihac, R.; Colavita, A.A.; Cicuttin, A.; Cerdeira, A.E. X-Ray image improvement by maximum entropy. In Proceedings of the 13th IEEE & EURASIP International Conference on Digital Signal Processing, Santorini, Greece, 1997; Vol. II, pp. 1149–1152.
- Jannetta, A.; Jackson, J.C.; Kotre, C.J.; Birch, I.P.; Robson, K.J.; Padgett, R. Mammographic image restoration using maximum entropy deconvolution. Phys. Med. Biol. 2004, 49, 4997–5010. [Google Scholar] [CrossRef] [PubMed]
- Arfelli, F. Silicon detectors for synchrotron radiation digital mammography. Nucl. Instrum. Meth. 1995, A 360, 283–286. [Google Scholar] [CrossRef]
- Di Michiel, M. Un rivelatore di silicio a pixel per immagini in radiologia diagnostica. PhD Thesis (unpublished), Universita di Trieste, June 1994. [Google Scholar]
- Thijssen, M.A.O.; Bijkerk, K.R.; van der Burght, R.J.M. Manual CDRAD-phantom type 2.0; Department of Radiology, University Hospital Nijmegen: The Netherlands, 1988-1992. [Google Scholar]
- Banham, M.R.; Katsaggelos, A.K. Digital image restoration. IEEE Signal Proc. Mag. 1997, 3, 24–41. [Google Scholar] [CrossRef]
- Sprawls, P., Jr. Physical Principles of Medical ImagingMedical Physics Publishing: Madison, Wisconsin, USA, 1995, 2nd ed.; Ch. 12; pp. 171–172. [Google Scholar]
- Zadeh, H.S-.; Windham, J.P.; Yagle, A.E. A multidimensional nonlinear edge-preserving for magnetic resonance image restoration. IEEE T. Image Process. 1995, 4, 141–161. [Google Scholar]
- Goyette, J.A.; Lapin, G.D.; Kang, M.G.; Katsaggelos, A.K. Improving autoradiograph resolution using image restoration techniques. IEEE Eng. Med. Biol. 1994, 8-9, 571–574. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mutihac, R. Bayesian Maximum Entropy Based Algorithm for Digital X-ray Mammogram Processing. Algorithms 2009, 2, 850-878. https://doi.org/10.3390/a2020850
Mutihac R. Bayesian Maximum Entropy Based Algorithm for Digital X-ray Mammogram Processing. Algorithms. 2009; 2(2):850-878. https://doi.org/10.3390/a2020850
Chicago/Turabian StyleMutihac, Radu. 2009. "Bayesian Maximum Entropy Based Algorithm for Digital X-ray Mammogram Processing" Algorithms 2, no. 2: 850-878. https://doi.org/10.3390/a2020850
APA StyleMutihac, R. (2009). Bayesian Maximum Entropy Based Algorithm for Digital X-ray Mammogram Processing. Algorithms, 2(2), 850-878. https://doi.org/10.3390/a2020850




