Open Problems in Universal Induction & Intelligence

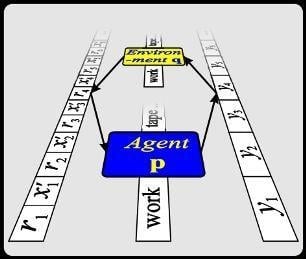
Abstract: Specialized intelligent systems can be found everywhere: finger print, handwriting, speech, and face recognition, spam filtering, chess and other game programs, robots, et al. This decade the first presumably complete mathematical theory of artificial intelligence based on universal induction-prediction-decision-action has been proposed. This informationtheoretic approach solidifies the foundations of inductive inference and artificial intelligence. Getting the foundations right usually marks a significant progress and maturing of a field. The theory provides a gold standard and guidance for researchers working on intelligent algorithms. The roots of universal induction have been laid exactly half-a-century ago and the roots of universal intelligence exactly one decade ago. So it is timely to take stock of what has been achieved and what remains to be done. Since there are already good recent surveys, I describe the state-of-the-art only in passing and refer the reader to the literature. This article concentrates on the open problems in universal induction and its extension to universal intelligence.