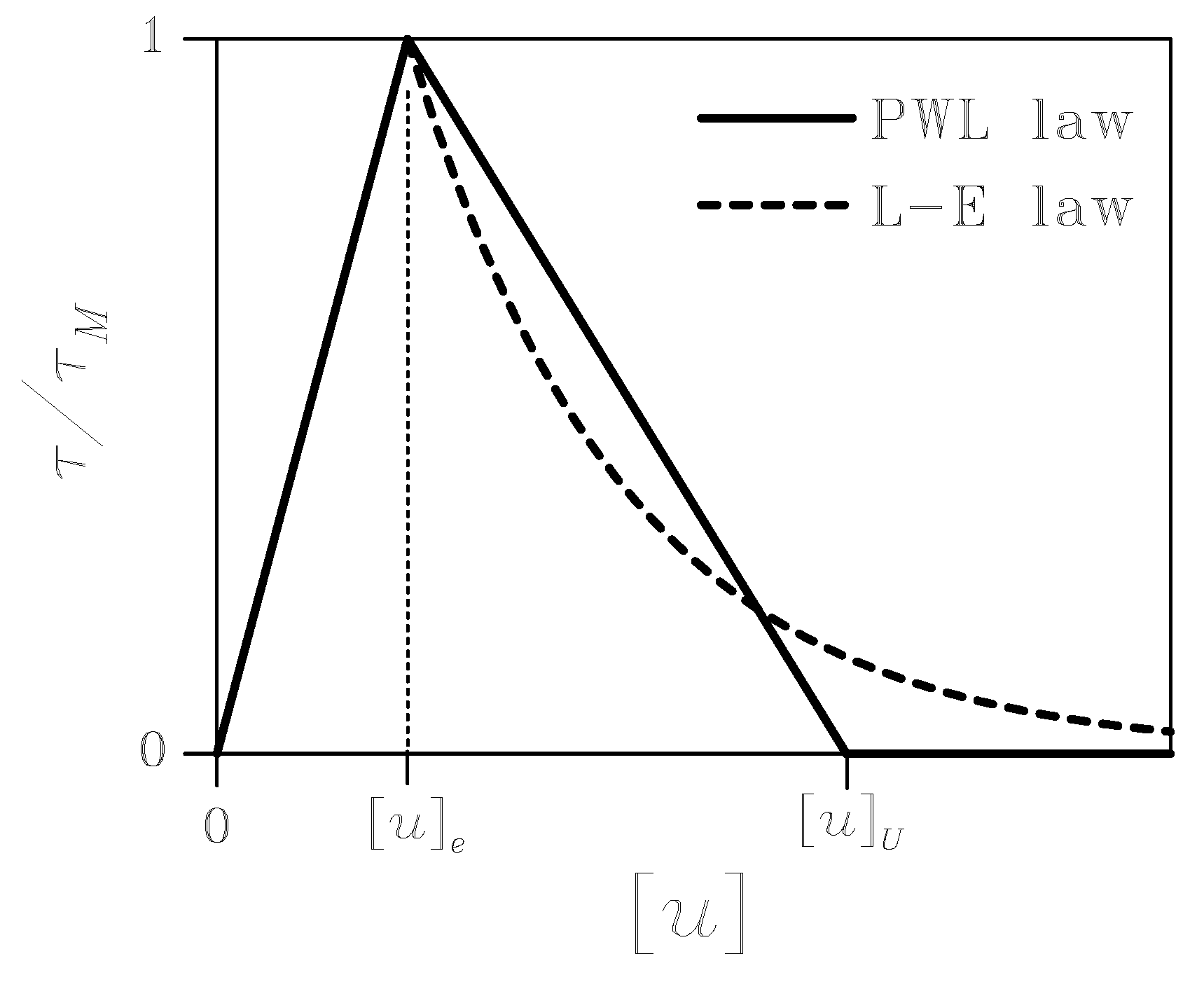1. Introduction
Composite structures are often exposed to impact loadings during their life cycle [
1]; this kind of loading conditions may become a serious issue, since composites can be very sensitive to imperfections beyond a critical threshold load. Depending on the impact energy, i.e. on the momentum of the impactor when it strikes the structural component, two different failure scenarios can be expected: (
i) in case of so-called low velocity (and, therefore, low energy) impacts, stress waves propagate inside the composite leading to diffused damage processes that progressively decrease or even annihilate the residual strength and stiffness of the structure; (
ii) in case of high velocity (and, therefore, high energy) impacts, local perforation of the laminate occurs, giving rise to very localized failure mechanisms. In the former case the response of a laminated plate to the impact is characterized by forced vibrations of the whole structure; in the latter case, the response of a plate and the damaging processes are very localized around the impact location, and deformation modes of the structure as a whole are only marginally excited.
Having as a target the development of a real-time health monitoring (and, hopefully, control) strategy for composite structures, in this work we focus on low velocity impact conditions. In such cases, the aforementioned diffused degradation processes consist in inter-laminar debonding (i.e. delamination) and intra-laminar damage, the latter being related to fibers failure, matrix cracking and fiber/matrix decoherence. Typically, a major role is played by delamination; therefore, throughout the whole paper we shall assume the laminae of the composite to behave elastically, while reduction of the structural load-carrying capacity may occur only because of inter-laminar damage.
To simplify modeling, the small ratio between the thickness of each inter-laminar phase and the thickness of the whole laminate is exploited by numerically treating inter-laminar phases as lumped interfaces. The relevant constitutive laws locally link the tractions acting upon the surfaces of the two adjacent layers to the displacement jump occurring across the interface, allowing for both opening and sliding (or shear) deformation modes. This lumped interface formulation has to be considered as a coarse grained description of the actual inter-phase behavior, as obtained via homogenization along the thickness direction (i.e. in the direction perpendicular to the stacking plane); the displacement jump thus accounts for both the elastic response of the inter-phase material and the possible discontinuity in the displacement field due to micro-cracking. To model micro-cracking processes and the relevant reduction of the inter-laminar strength, nonlinear constitutive laws are adopted; beyond the attainment of peak tractions, delamination inception is modeled through a softening regime. Since inter-phase materials are usually quasi-brittle, dissipative phenomena due to yielding can be disregarded. Moreover, viscous and rate-dependent properties of the composite phases are not considered here; therefore, only rate-independent constitutive laws will be adopted.
Within this framework, laminated plates are treated as a stacking sequence of laminae and interfaces. This scheme, sometimes referred to as meso-scale modeling (see, e.g. [
2]), was proved to furnish accurate outcomes at the length scale of the whole laminate (also in terms of delamination prediction), provided the interface constitutive laws are appropriately calibrated. Since they are typically formulated on a pure phenomenological basis and contain several parameters to be tuned, this calibration task turns out to be difficult, also because of the lower dimensionality of interfaces (two-dimensional loci in a three-dimensional setting) and because of shadowing effects due to the global laminate response, see e.g. [
3].
To accurately predict the failure mode of layered composites subject to low velocity impacts and simultaneously calibrate interface constitutive laws, a coupled finite element (FE) Kalman filter approach is here proposed. Upon space discretization (through displacement-based finite elements) and time integration (through the explicit
method, in order to damp spurious high frequency oscillations in the fully discretized solution), Kalman filtering is adopted to fully track the structural state in a stochastic frame [
4,
5,
6], exploiting system evolution to continuously improve estimates. Because of the nonlinearities induced by inter-laminar softening, the customarily adopted extended Kalman filter (EKF) is not able to provide robust state tracking and accurate estimations of inter-laminar properties like e.g. strength and toughness [
7]. We therefore attack the problem with the newly proposed sigma-point Kalman filter (SPKF) [
8,
9,
10], which avoids the occurrence of unstable evolution of the estimates (see also [
11]). While the EKF linearizes the system evolution equations (through a Taylor series expansion of the relevant mapping, thought to be analytic everywhere, arrested at first order) and accordingly updates the statistics of the structural state, the SPKF samples the probability distribution of the state via an appropriately chosen set of sigma-points, which are then evolved according to the actual nonlinear system dynamics to obtain the updated statistics of the state itself. Among alternative approaches to system identification and, specifically, to model calibration, it is worth quoting here [
12].
In this work the capability of the proposed FE-SPKF approach is assessed through comparison with experimental data available in the literature and concerning failure of laminated plates subject to plane impacts [
13,
14]; in such tests, the composites are mainly stressed in the region surrounding the impact location by dilatational waves propagating in the through-the-thickness direction and causing mode I delamination. Outcomes show that the failure mode is always correctly captured, and estimated values of inter-laminar strength and toughness well agree with available data.
Plane impact tests do not allow a complete calibration of the interface constitutive law, since only model parameters relevant to mode I failure can be estimated. Anyway, forthcoming results show that under very adverse conditions, as due to fast completion of the whole debonding process, the SPKF proves to be robust and accurate; on the contrary, under similar conditions the EKF was shown in [
7,
15] to either diverge or provide biased estimates. An extensive assessment of the SPKF performance in the presence of diffused damage/delamination patterns is beyond the scope of this paper and will be presented in future works.
As far as notation is concerned, a matrix one will be adopted throughout, with uppercase and lowercase bold symbols respectively denoting matrices and vectors. A superscript will stand for transpose, will denote the norm of vector □, and a superposed dot will represent time rates.
2. Forward problem: layered composite dynamics
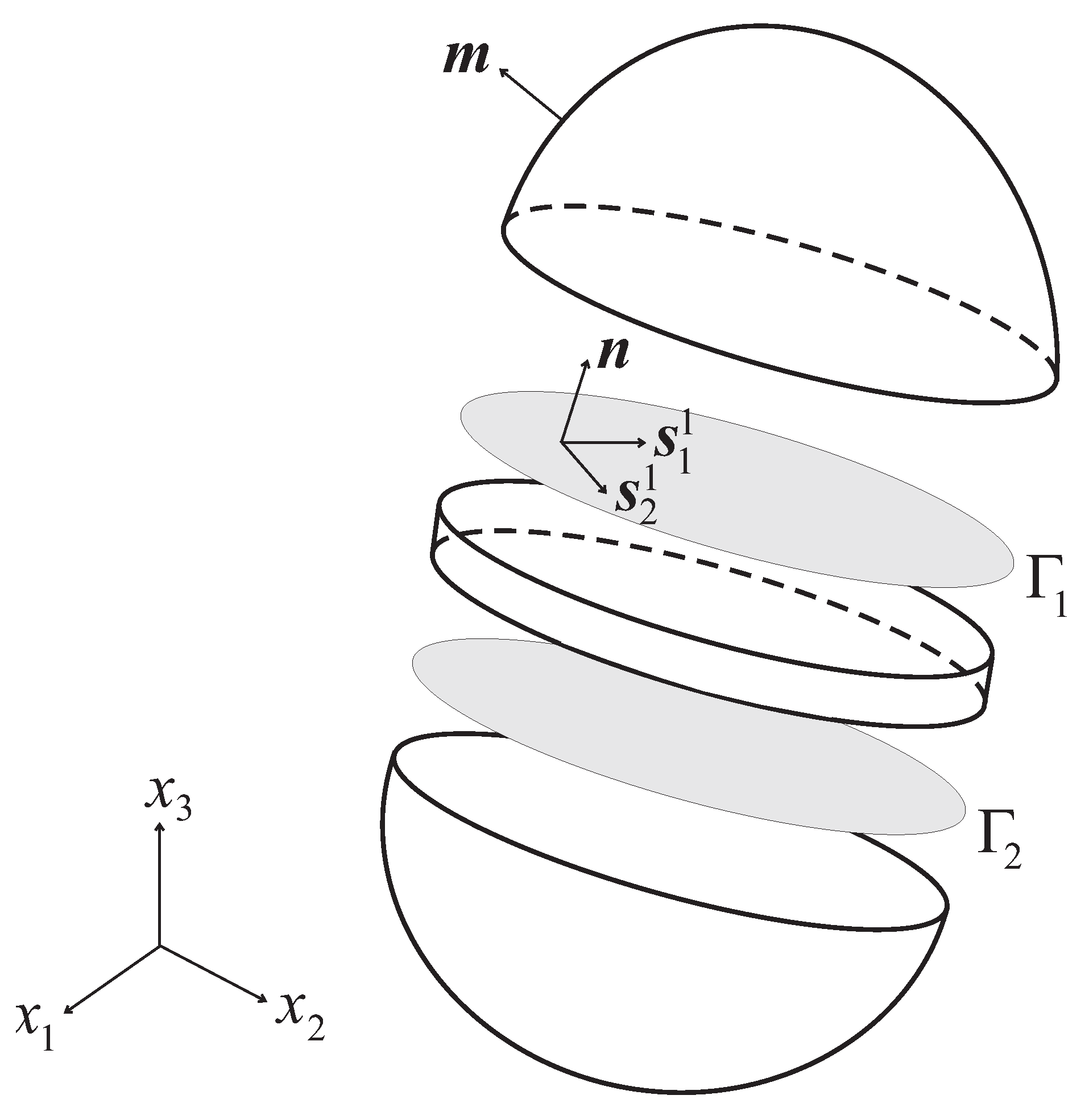
Let us consider a layered body Ω, possessing a smooth outer boundary with unit outward normal
(see
Figure 1). Ω be crossed by
non-intersecting surfaces, or interfaces
,
. Even though the local orientation
of these interfaces may vary in Ω, for ease of notation we shall assume it to be constant and equal to
along every
: interfaces are thus flat and parallel to each other.
Figure 1.
Notation adopted for layered bodies (here ).
Figure 1.
Notation adopted for layered bodies (here ).
The equilibrium of Ω at time
t is governed by:
where:
;
is the portion of the outer boundary of Ω where tractions
are assigned. Treating each
as a locus where the displacement field
may suffer jumps (alike a crack),
and
are the two sides of
; these two sides can not be distinguished in the initial configuration (at
) but, as soon as delamination occurs, they experience a relative movement. In the above equations, according to Voigt notation:
σ is the stress vector;
is the traction vector acting along surface
;
is the assigned bulk load in
;
ϱ is the bulk mass density;
is the acceleration field in
;
is the differential compatibility operator;
and
are the matrices collecting the components of unit vectors
and
, respectively.
Assuming linearized kinematics, compatibility reads:
Figure 2.
Piecewise linear (PWL) and linear-exponential (L-E) effective traction-displacement discontinuity relationships.
Figure 2.
Piecewise linear (PWL) and linear-exponential (L-E) effective traction-displacement discontinuity relationships.
where:
ε is the strain vector;
is the assigned displacement along portion
of the outer boundary of Ω;
is the displacement discontinuity along surface
.
The body is assumed to be initially at rest, in an undeformed and unstressed state:
In case of low velocity impacts, dissipation due to intra-laminar damage is assumed to be negligible when compared to that due to delamination. Hence, laminae are thought to behave elastically according to:
where
is the elasticity matrix of the bulk.
As for inter-laminar phases, to be treated as lumped surfaces along which debonding is the result of complex micro-scale damaging processes, a phenomenological coarse-grained modeling is adopted. Strength reduction preceding delamination is governed by softening constitutive laws [
3,
16,
17,
18,
19,
20,
21], which locally link tractions
(see Eq. (
2) to the displacement jump
(see Eq. (
5). Since both opening/closing (along
) and sliding (in the
plane) discontinuities are expected to take place under general loading conditions, interface kinematics is effectively represented by the displacement discontinuity
(in what follows, for ease of notation, we shall drop subscript
j), defined as [
22,
23,
24]:
where:
and
are the opening and sliding displacement discontinuities, respectively;
κ is a coupling coefficient, which phenomenologically accounts for the local ongoing mixed-mode damaging in the inter-laminar phase. The effective traction
τ, work-conjugate to
, reads (see [
22,
23]):
where
and
are the normal and shear traction components.
Since quasi-brittle materials (like inter-phase resins) show a high ratio between compressive and tensile strengths, inter-laminar damage in compression due to low velocity impacts can be disregarded. On the other hand, under tensile stress pulses the response of inter-phase materials is characterized by softening beyond the attainment of a peak traction. Two simple effective descriptions of this behavior are here envisaged: a piecewise linear (PWL) law
and a linear-exponential (L-E) law
In these cohesive-like envelopes:
is the effective displacement discontinuity at the attainment of the peak traction
(elastic limit);
K is the stiffness in the elastic regime;
Q is the (negative) slope of the softening branch in the PWL case;
is the effective displacement discontinuity beyond which the interaction of opened crack faces is annihilated in the PWL case;
ς defines the slope of the softening branch in the L-E case. The two effective models (
11) and (
12) are compared, for
, in
Figure 2 at assigned effective fracture toughness, or work of separation
. It is worth noting that, since the L-E law assumes the interaction between crack faces to continue up to
, delamination growth is modeled via a breakdown threshold; according to [
25,
26], we assume this interaction to suddenly vanish as soon as the current traction
τ becomes smaller than a pre-defined fraction (say 5-10 %) of the peak value
.
To allow for irreversibility of the micro-mechanical damage processes, unloading from the tensile envelope follows a radial path to the origin of the
plane. In rate form, constitutive modeling for interface
can thus be written:
where
is the interface tangent stiffness matrix. For additional details, readers are referred to [
23,
24].
Upon space discretization via displacement-based finite elements, the weak form of the equilibrium equations for the layered body reads:
where
is the vector of nodal displacements. In (
14) the mass matrix
, the bulk stiffness matrix
, the internal force vectors
,
, and the external load vector
are respectively given by:
Here: Φ is the matrix of nodal shape functions;
and
are, respectively, the compatibility matrices for the bulk
and surface
[
7,
27].
In the space-discretized formulation here above we have implicitly assumed that the displacement field
may be discontinuous only along inter-element boundaries. Smarter formulations [
23,
28,
29,
30,
31] allow also for intra-element discontinuities by exploiting the partition of unity property of standard nodal shape functions [
32]; since delamination in layered continua occurs along the a-priori known inter-laminar surfaces, the description of the discontinuity topology is simple and the aforementioned feature of the smart (usually termed extended) finite element formulation is of no help.
We now need to adopt a time stepping scheme for (
14), able to reduce to a minimum or even avoid spurious high frequency oscillations of the velocity field in the fully-discretized solution. In [
33] it was shown that local corrective flux terms can be adopted to accurately track discontinuities in the velocity field due to the propagation of stress wave fronts. Since this time stepping scheme is computationally expensive while our target is a low-cost scheme, a less expensive (and, indeed, less accurate) explicit
method is adopted [
34,
35]. Having partitioned the time interval of interest according to
, the solution of (
14) at time
in terms of nodal displacements, velocities and accelerations is obtained according to:
prediction:
where
is the time step size;
integration:
where:
;
and
are respectively computed (see Equation 15
) adopting
and
;
To get oscillations of small amplitude in the velocity field, the following values of the algorithmic parameters
α,
β and
γ have been adopted:
;
β and
γ finely tuned around values allowing second-order accuracy in linear elastodynamics [
36].
The time step size
has been set so as to fulfill the Courant condition in the bulk. In case of growing delamination, interface elements in the process zone (where damage is locally reducing the inter-laminar strength and stiffness) need to be sized so as to accurately resolve the traction field; this requirement is satisfied if the characteristic size of interface elements is a fraction (say
) of the process zone length, estimated e.g. through Irwin’s law [
37]. Since the surrounding FEs in the bulk are associated to interface elements via matching grids, it turns out that inter-laminar strength and toughness, which affect the process zone length, actually affect the time step size
too; for details, readers are referred to [
38,
39].
3. Inverse problem: constrained sigma-point Kalman filter
In our study the inverse problem has to provide real-time forecasts of the delamination processes, along with estimates of uncertain model parameters. Allowing for the above described explicit time integration scheme, a state vector
gathering all the information on the evolving system is obtained by joining the nodal displacement, velocity and acceleration vectors to a vector
ϑ gathering model parameters in need of calibration:
Since laminate failure due to delamination is represented by displacement discontinuities arising along the inter-laminar surfaces, vector
in (
21) also provides the requested details of the failure mode. State vectors shaped in this way, with model parameters explicitly accounted for, are typically adopted in extended Kalman filtering [
5,
40]. While the current structural state (here
,
and
) is always at least partially observed, model parameters to be calibrated can not be directly measured; by joining structural and parameter vectors in
, state tracking can consistently enhance model calibration.
Allowing for modeling and measurement errors in a stochastic framework, the discretized state-space model of the system within the time interval
reads:
where:
is the observation vector, which collects measurables;
and
are the process and measurement noises. These noises are assumed to be additive, uncorrelated white and Gaussian processes, with zero mean and time-invariant covariance matrices
and
[
6,
40]. Because of inter-laminar strength degradation, mapping
turns out to be highly nonlinear; on the other hand, since either surface displacements or velocities are measured during testing, the observation equation (22
) shows up as a linear relation between
and
(see Eq. (
21).
Table 1.
Sigma-point Kalman filter.
Table 1.
Sigma-point Kalman filter.
At , for
|
The mentioned nonlinearities of mapping
cause estimates obtained through a standard EKF to be affected by biases [
41,
42]; to get accurate results, the recently proposed SPKF [
8,
9,
43,
44] is instead here adopted. While the EKF linearizes the mapping
, the SPKF deterministically samples the probability distribution of
at time
(i.e. at the beginning of the time step) through a set of properly chosen sigma-points
,
. These sigma-points are allowed to evolve according to the nonlinear mapping
; the statistics of
at time
(i.e. at the end of the time step) are then obtained through a weighted averaging procedure performed on the evolved sigma-points [
8]. The filtering procedure is detailed in
Table 1, where
represents the expected value of □. In this scheme, the number
of sigma-points, terms
, and weights
and
need to be set so as to achieve maximum accuracy; such issue is treated in Appendix A, where fundamental results are summarized.
In Kalman filtering it is usually assumed that all the state vector components are Gaussian variables; hence, the relevant probability distributions cannot be compliant with physical side constraints (like, e.g. positiveness of inter-laminar strength and toughness). In this work we do not aim to modify this filtering frame with the adoption of alternative probability distributions; instead, we define terms
so that all the sigma-points be compliant with the aforementioned side constraints (see Appendix A). Through this procedure, which was proposed in [
27], we can assure that all the sigma-points do not follow unphysical paths in the state vector space. It is worth noting that this procedure plays a role only when the sigma-points are well scattered around the mean
(see the prediction phase in
Table 1), i.e. mainly at the beginning of filtering.
4. Failure assessment of laminates exposed to impacts
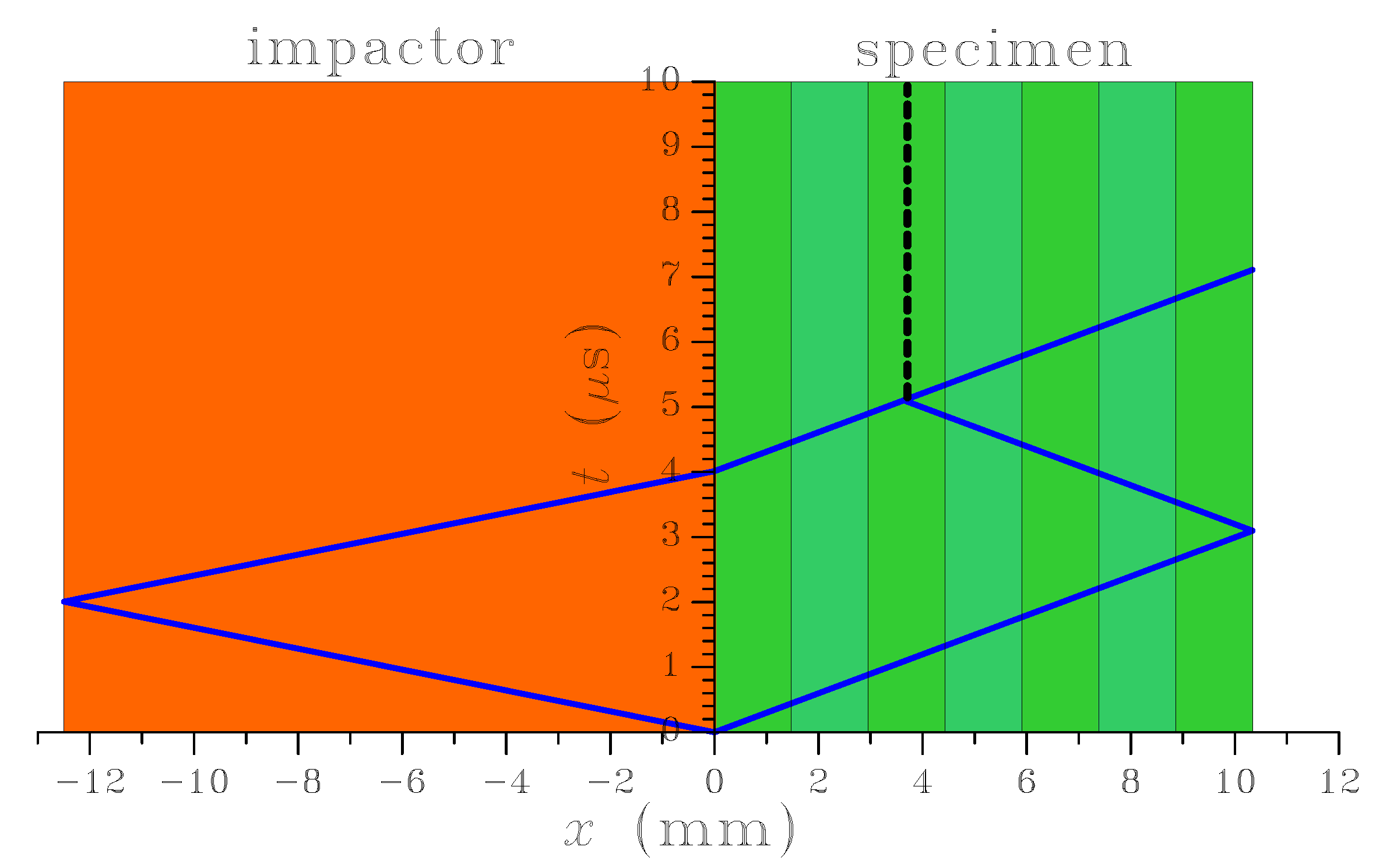
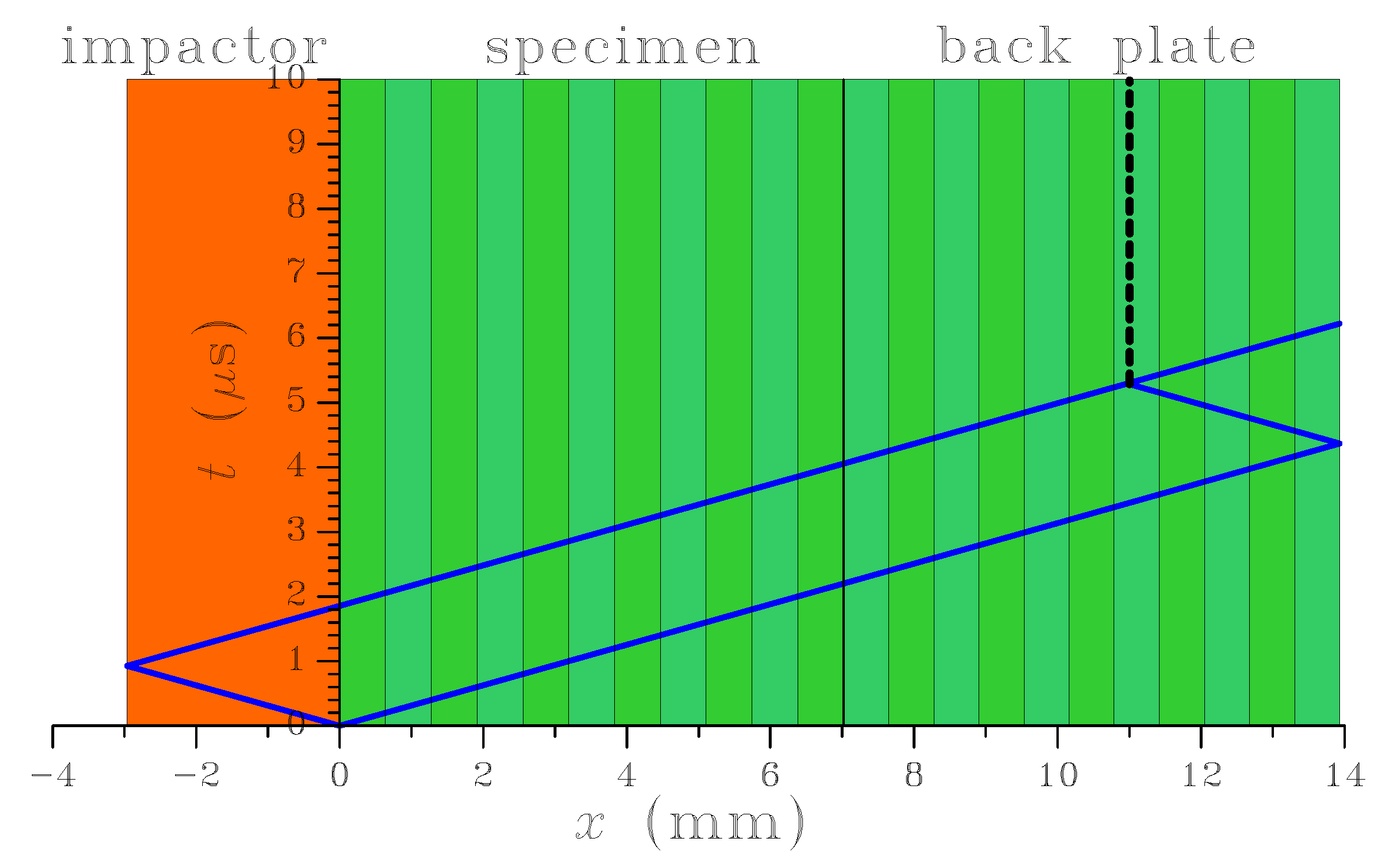
Figure 3.
Impact on a 7-layer composite [
13]: space-time diagram (the vertical dashed line here represents the possibly debonding surface of a brittle, homogeneous material).
Figure 3.
Impact on a 7-layer composite [
13]: space-time diagram (the vertical dashed line here represents the possibly debonding surface of a brittle, homogeneous material).
To assess the capability of the proposed FE-SPKF approach to provide accurate failure forecasts for layered composites subject to low velocity impacts and to simultaneously calibrate the inter-laminar constitutive laws, two experiments reported in the literature have been considered: an impact test on a 7-layer composite plate (experiment FY06001 in [
13]), and an impact test on a 11-layer composite plate backed by another 11-layer composite plate (experiment 1 in [
14]). In both cases, plane impacts caused the propagation of compressive waves behind the impact location; upon reflection at the rear surface of the plates, a spall-like failure governed by tensile tractions perpendicular to the inter-laminar surfaces took place. Because of the experimental set-up, shear tractions do not play any role in the failure events; in what follows, for ease of notation we therefore avoid using subscript
n to denote (mode I) opening/closing displacement discontinuities along interfaces.
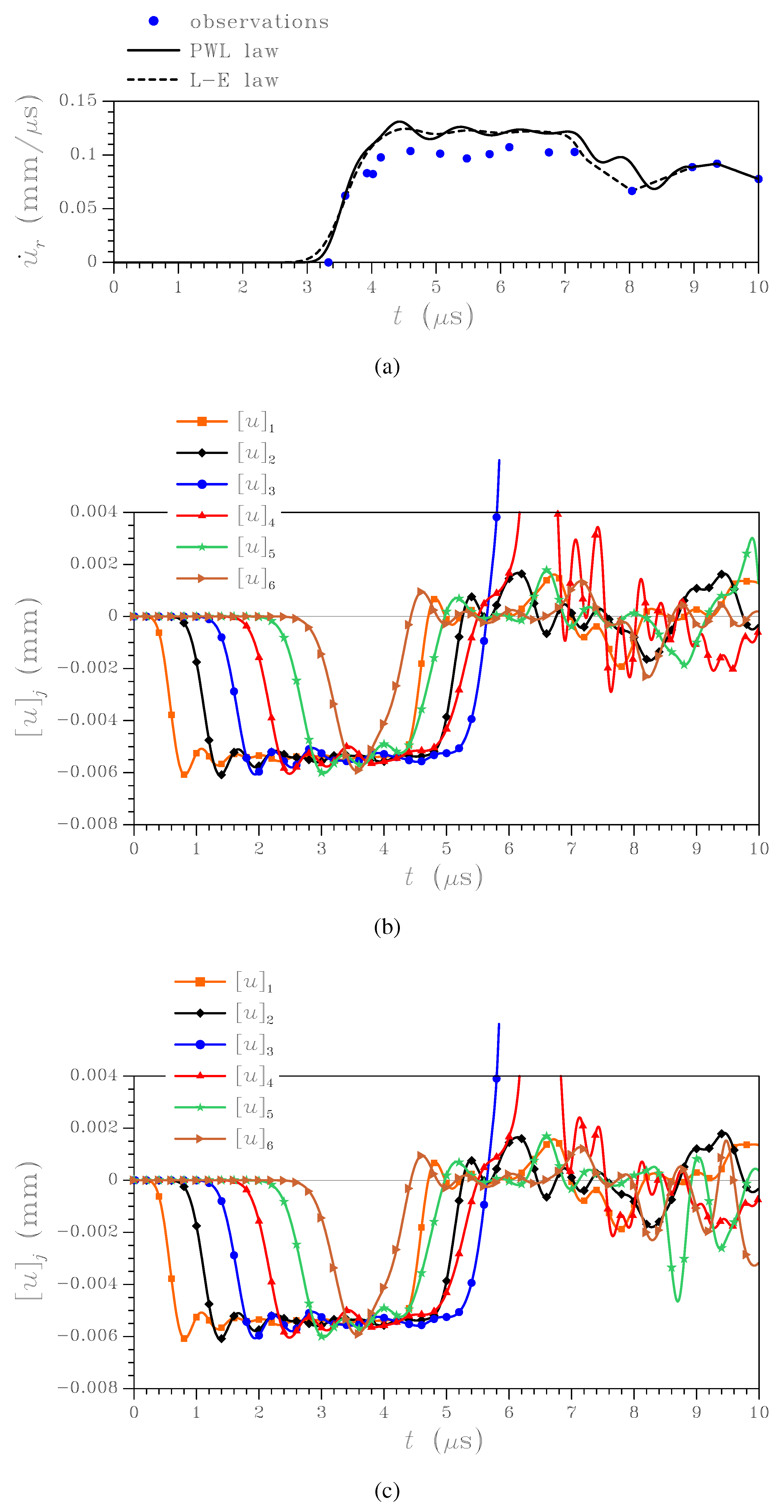
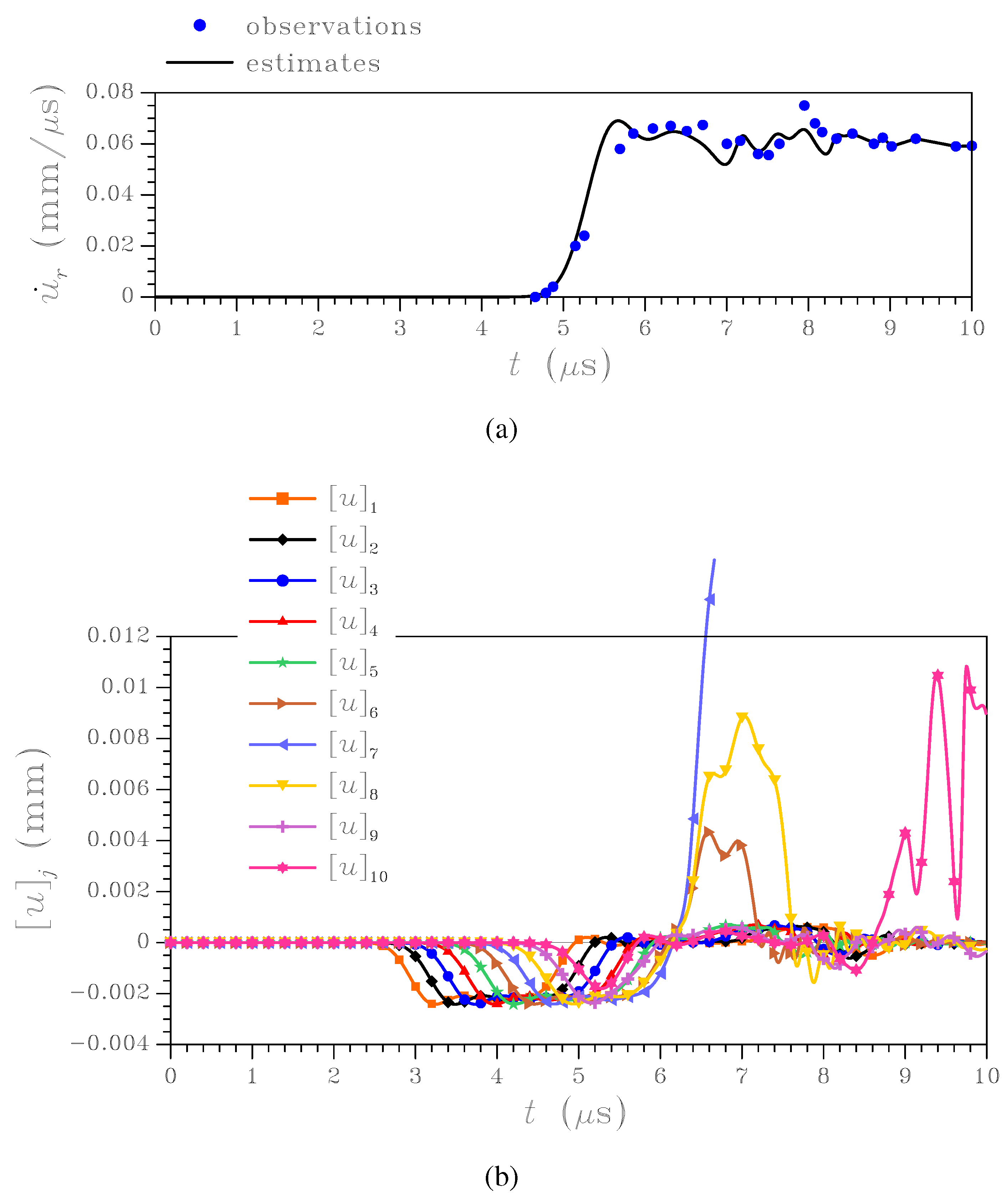
Figure 4.
Impact on a 7-layer composite [
13]: (a) comparison between experimental and tracked free surface velocity records; (b-c) estimated values of inter-laminar openings
,
(b: PWL law; c: L-E law).
Figure 4.
Impact on a 7-layer composite [
13]: (a) comparison between experimental and tracked free surface velocity records; (b-c) estimated values of inter-laminar openings
,
(b: PWL law; c: L-E law).
Figure 5.
Impact on a 7-layer composite [
13]: evolution in time of estimated inter-laminar (a) strength
and (b) toughness
G.
Figure 5.
Impact on a 7-layer composite [
13]: evolution in time of estimated inter-laminar (a) strength
and (b) toughness
G.
As far as space discretization is concerned, owing to the major role played by dilatational waves the full three-dimensional problem can be approached as a one-dimensional one featuring constrained deformation in the plane perpendicular to the wave propagation direction. Accordingly, one-dimensional meshes of constant strain elements have been adopted for the bulk; the characteristic size (length) of FEs in the through-the-thickness direction was determined by a trade-off between accuracy requirements and computational economy (leading to around 10 elements to discretize each lamina).
In the first experiment, each lamina was 1.37 mm in thickness, and was made of a balanced 5-harness satin weave E-glass and LY564 epoxy. The overall wave speed in the through-the-thickness direction was measured as 3.34 km/s, while the mass density was
kg/m
; additional details and a thorough discussion of the results from an experimental perspective can be found in [
13]. The specimen was stricken by a 12.5 mm thick aluminum impactor, flying at velocity
m/s, which led to dynamic delamination. The free surface velocity profile
was measured during the test with a velocity interferometer for any reflector (VISAR).
Figure 6.
Impact on a 7-layer composite [
13]: evolution in time of estimated inter-laminar strength
and toughness
G, and of the relevant covariances (a: PWL law; b: L-E law). In the plots the squares denote the common initial guess
, whereas the circles denote the final estimates at time
μs.
Figure 6.
Impact on a 7-layer composite [
13]: evolution in time of estimated inter-laminar strength
and toughness
G, and of the relevant covariances (a: PWL law; b: L-E law). In the plots the squares denote the common initial guess
, whereas the circles denote the final estimates at time
μs.
The space-time diagram of this test is shown in
Figure 3: in this diagram, wave reflection and dispersion due to the inter-laminar phases [
45] have been neglected. Moreover, since failure is actually caused by delamination, the possibly debonding surface highlighted in the diagram is here to be considered as a reference one: even in the presence of wave dispersion, the actual failure of the laminate is expected to occur close to this reference surface.
Figure 4 shows a comparison between the estimated and the experimentally observed free surface velocity
, and the time evolution of the tracked inter-laminar openings
,
; filter results are shown for both linear and exponential softening models. Before
μs information on the mechanical properties of the failing inter-laminar surface are not filtered, since they are not yet available through measurables in
(see
Figure 3), and some discrepancies between experimental and numerical graphs of
are shown (see
Figure 4(a)). Delamination is foreseen to occur along the third inter-laminar surface away from the impact location; in fact, only
is diverging in
Figure 4(b) and
Figure 4(c), while all the other interface openings remain bounded. This latter outcome, which is independent of the shape of the softening envelope, well agrees with the state-space diagram of
Figure 3 once wave dispersion caused by inter-laminar phases and other inner composite inhomogeneities is allowed for.
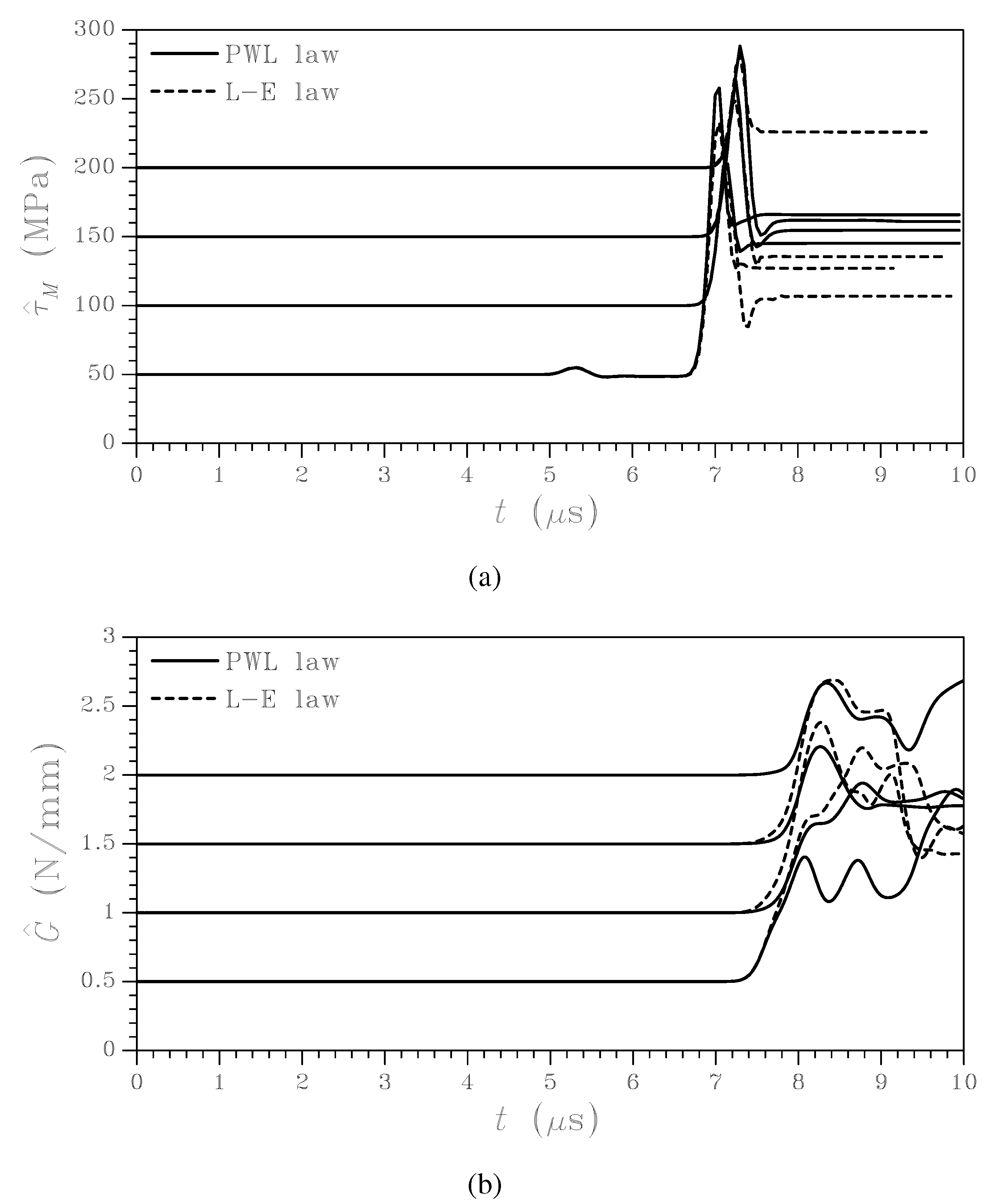
Previous results are accompanied by model calibration; in
Figure 5 the time evolution of estimated inter-laminar strength
and toughness
G are reported at varying initialization of
ϑ within the domain:
These estimates are not modified by the filter (apart from small fluctuations due to the stochastic environment) till the so-called pull back signal is processed at
μs. Since
is already diverging at that time (see
Figure 4), the SPKF cannot obtain much information on the inter-laminar properties; hence, depending on the initialization in
, it sometimes happens that parameter estimates are eventually affected by biases. Anyway, it is worth noting that, under the same conditions, the standard EKF is not able to provide results featuring the same degree of accuracy [
7]. In fact, the average converged estimates of
are in good agreement with the tensile strength of 119.5 MPa reported in [
13], while final estimates of
G well represent the behavior of this kind of composites. On the basis of the similar accuracy in the calibration of the softening envelopes here considered, it can be said that the shape of the softening regime does not play a major role in this kind of laminate failure.
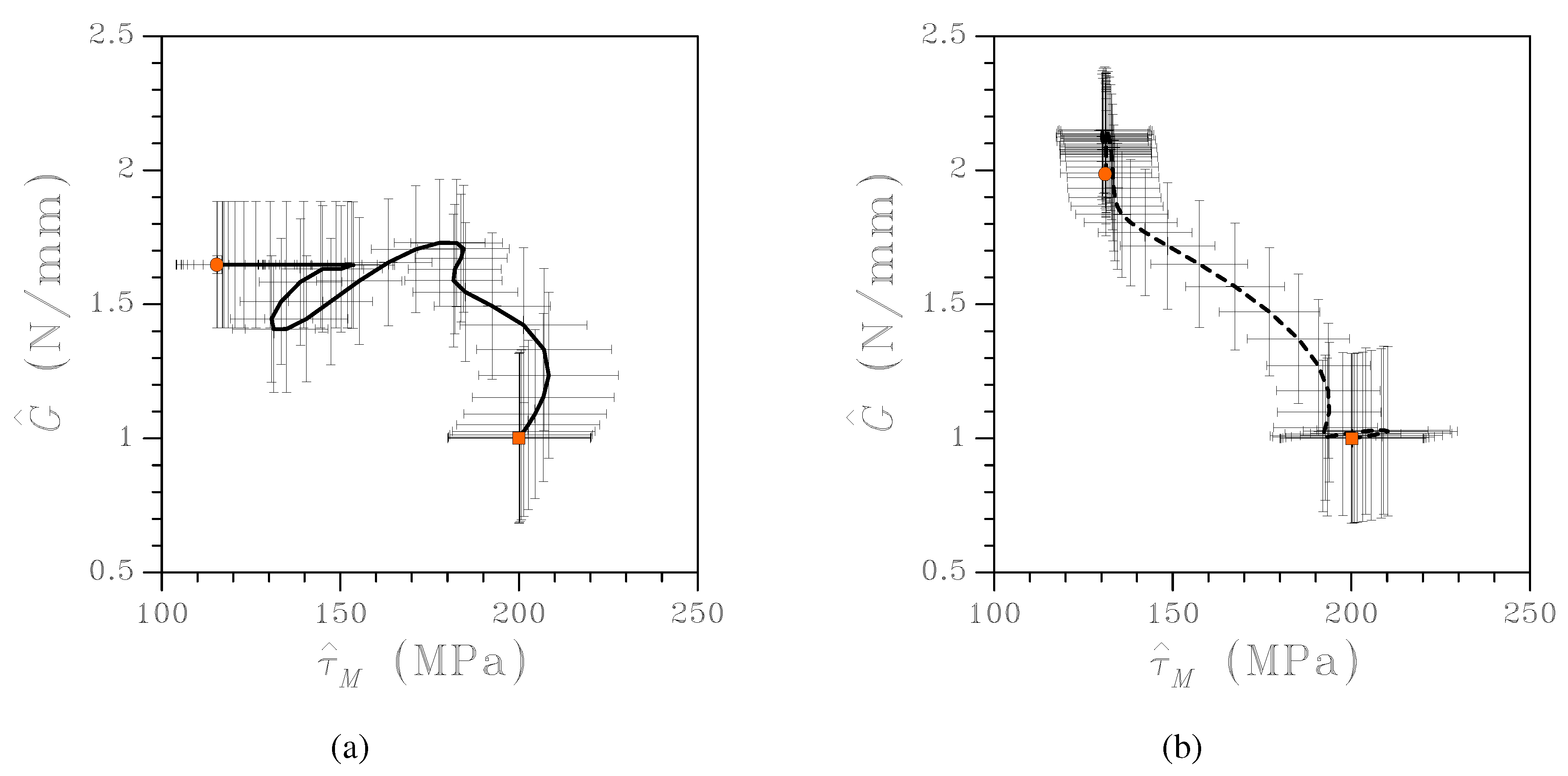
To provide further insights into the performance of the FE-SPKF approach,
Figure 6 shows an example of the time evolution of estimated model parameters along with the relevant statistical dispersion (here represented through error bars) around the expected values. Because of the aforementioned fast opening of the only decohering inter-laminar surface, entries in the covariance matrix
are not enhanced much by the SPKF.
Figure 7.
Impact on a 11+11-layer composite [
14]: space-time diagram (the vertical dashed line here represents the possibly debonding surface of a brittle, homogeneous material).
Figure 7.
Impact on a 11+11-layer composite [
14]: space-time diagram (the vertical dashed line here represents the possibly debonding surface of a brittle, homogeneous material).
In the second experiment a glass fiber reinforced plastic (GRP) specimen,
mm thick, was backed by a 6.91 mm thick GRP plate. The overall wave speed in the through-the-thickness direction of the plates amounted to 3.19 km/s, and the mass density was
kg/m
[
14]. The specimen was stricken by a 5-layer GRP flyer,
mm in thickness and flying at velocity
m/s, which caused dynamic delamination. During the test the free surface velocity profile was again measured via a VISAR. The reference space-time diagram is depicted in
Figure 7; it is here shown that, because of the test set-up, release waves interact causing delamination inside the back plate.
Results of the FE-SPKF approach are reported in
Figure 8 in terms of comparison between experimental and tracked free surface velocity
, and in terms of estimated displacement jumps along all the inter-laminar surfaces of the back plate (sequence starting at the specimen/back plate contact surface).
Figure 8.
Impact on a 11+11-layer composite [
14]: (a) comparison between experimental and tracked free surface velocity records; (b) estimated values of inter-laminar openings
,
.
Figure 8.
Impact on a 11+11-layer composite [
14]: (a) comparison between experimental and tracked free surface velocity records; (b) estimated values of inter-laminar openings
,
.
Tracking capabilities turn out again to be independent of the interface law: in
Figure 8 discrepancies due to the shape of the softening regime cannot be detected. Such results have been obtained for any initialization values of
and
G inside the domain:
Delamination is foreseen to take place along the 7-th inter-laminar surface, in good agreement with the space-time diagram of
Figure 7 and with the results of [
7,
14]. As for model calibration, outcomes are qualitatively similar to those reported for the previous test in terms of accuracy and convergence of the estimates.
5. Concluding remarks
In this paper we have proposed a finite element, sigma-point Kalman filter approach to the failure assessment of layered composites subject to low velocity impacts. Since under such loading conditions the damage and energy dissipation are mainly linked to the propagation of inter-laminar cracks (delamination), softening interface constitutive laws have been adopted to locally link the tractions transmitted between adjacent laminae to the opening/sliding displacement discontinuities occurring across the debonding surfaces.
To track in real time the whole state of the laminate and predict failure, a Kalman filter has been adopted. The filter has also allowed to calibrate the interface constitutive laws, whose parameters can be difficult to estimate due to the lower dimensionality of the inter-laminar surfaces. To properly deal with the nonlinearities induced by strength degradation phenomena, the sigma-point version of the Kalman filter has been implemented: this filter was already proved to be robust in highly nonlinear regimes, and to furnish more accurate outcomes than the customarily used extended Kalman filter (see [
27,
35]).
Through analysis of failures induced by plane waves propagating in the through-the-thickness direction of stricken laminates, it has been shown that debonding events are accurately tracked by the offered procedure. Furthermore, inter-laminar strength and toughness, which have been assumed unknown in the simulations, turned out to be accurately estimated.
In future works, to track and monitor diffused damage/delamination events, even featuring more complicated patterns than those here investigated, order reduction techniques will be coupled to the present methodology; this coupling will allow to get closer to the design of health monitoring systems for complex heterogeneous structures, able to detect in real time possible strength degradation phenomena induced by loading and environment.
A. Sigma-point transformation
In this Appendix we summarize the fundamentals of sigma-point transformation, with focus on its performance in representing the probability distribution of a random variable vector undergoing a nonlinear transformation [
8,
9].
Let
be a Gaussian random vector, with mean
and covariance
at time
. If
undergoes an analytic, nonlinear transformation
within the time interval
, its expected value at time
reads:
where:
being the dimension of
. The relevant error covariance matrix is:
Through the sigma-point transformation, the probability distribution of
at time
is sampled via a set of sigma-points
scattered around
according to (see
Table 1):
where:
ψ is a scaling factor to be determined;
is the square root of the (positive definite) covariance matrix
;
is a unit vector pointing towards the
th component of the state vector in the relevant space, whose role in (
28) is to sample the
th column of matrix
;
.
Information conveyed by the evolved sigma-points are merged at time
via a weighted averaging scheme, according to:
and:
where:
Weights
in (
29) can be determined by matching the series expansions (
25) and (
29) up to third order; by assuming
for
this requirement results in:
To also set the value of the scaling factor
ψ, a further condition needs to be established. Usually, it is suggested to match the diagonal entries of the fourth order terms in (
25) and (
29): this leads to
. In [
27], partially exploiting the features of the so-called scaled sigma-point transformation [
46], we proposed to adaptively set
ψ so as to always fulfill the physical constraints:
where
and
are, respectively, the minimum and maximum (if applicable) allowed values of model parameters. These side constraints need to be fulfilled by all the sigma-points
: for
, conditions (
33) are automatically satisfied; for
, conditions (
33) are satisfied if:
where:
;
is a Boolean matrix, defined as
;
is the dimension of vector
ϑ.
Weights
in (
30) are set by first letting
for
. Value of
is then obtained by matching the fourth order terms involving
in (
27) and (
30), thus getting
[
27].