Probabilistic Upscaling of Material Failure Using Random Field Models – A Preliminary Investigation
Abstract
:1. Introduction
2. Micro-to-Meso Upscaling
2.1 Micro-cracking in a random field
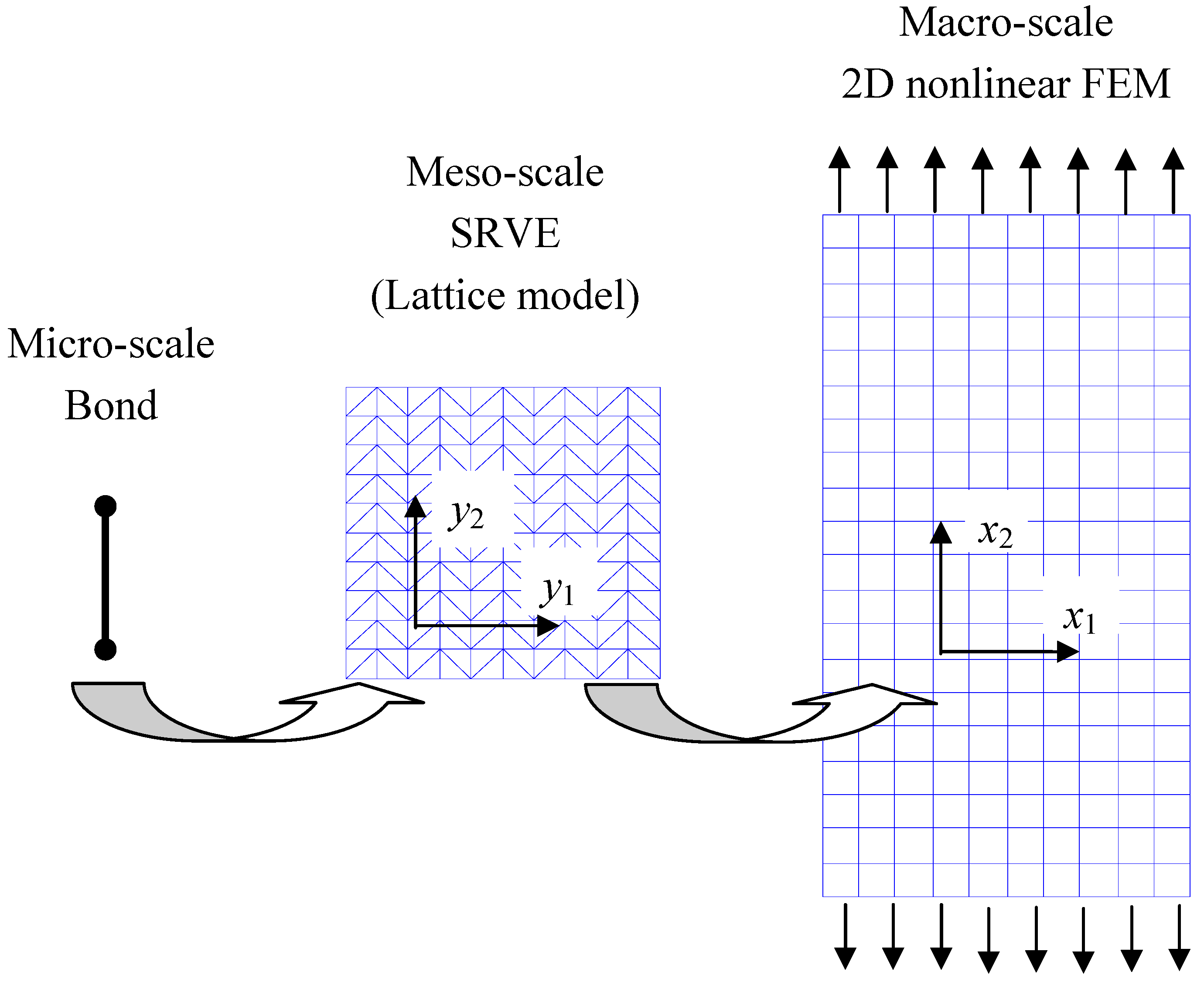
2.2 Numerical simulation
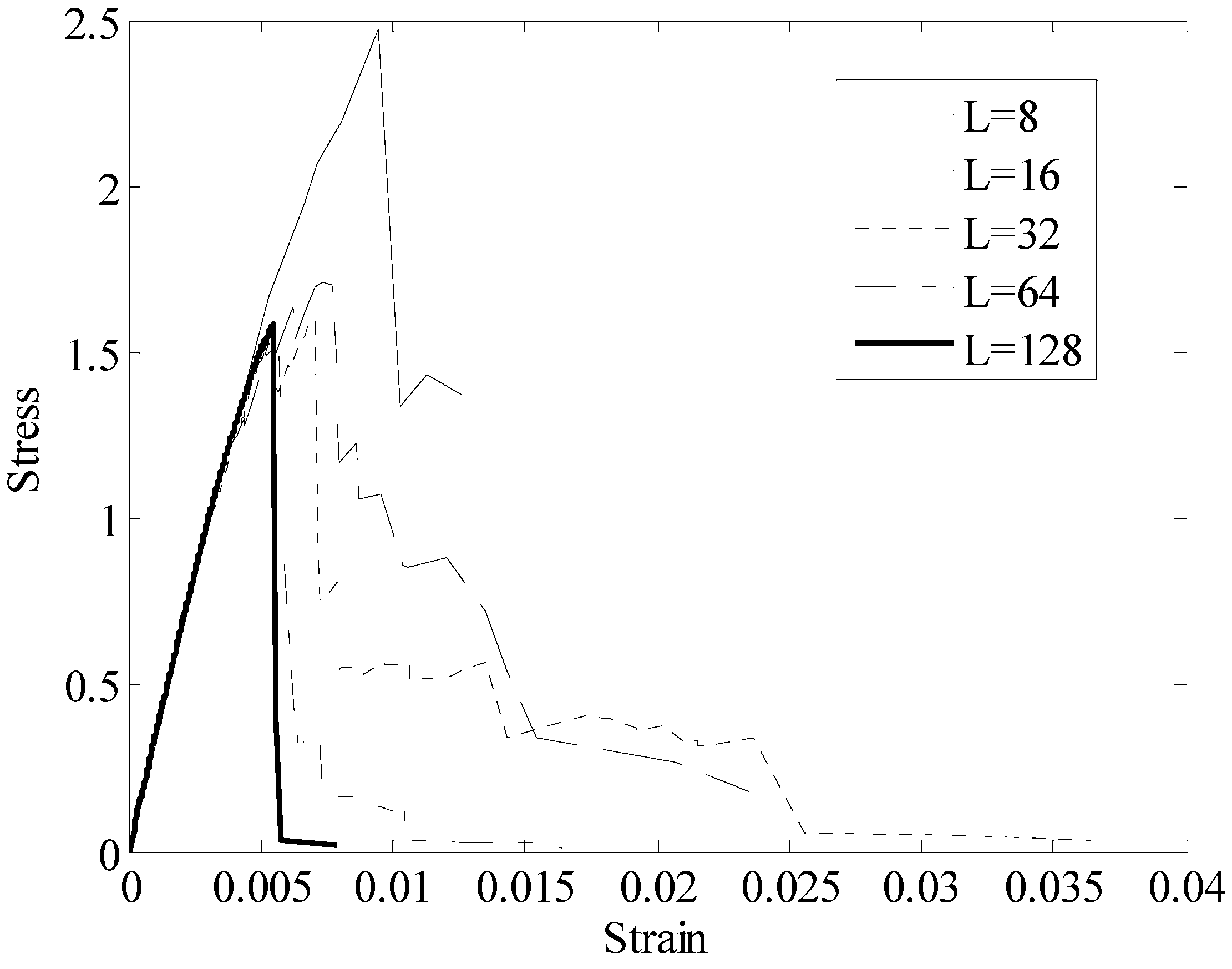
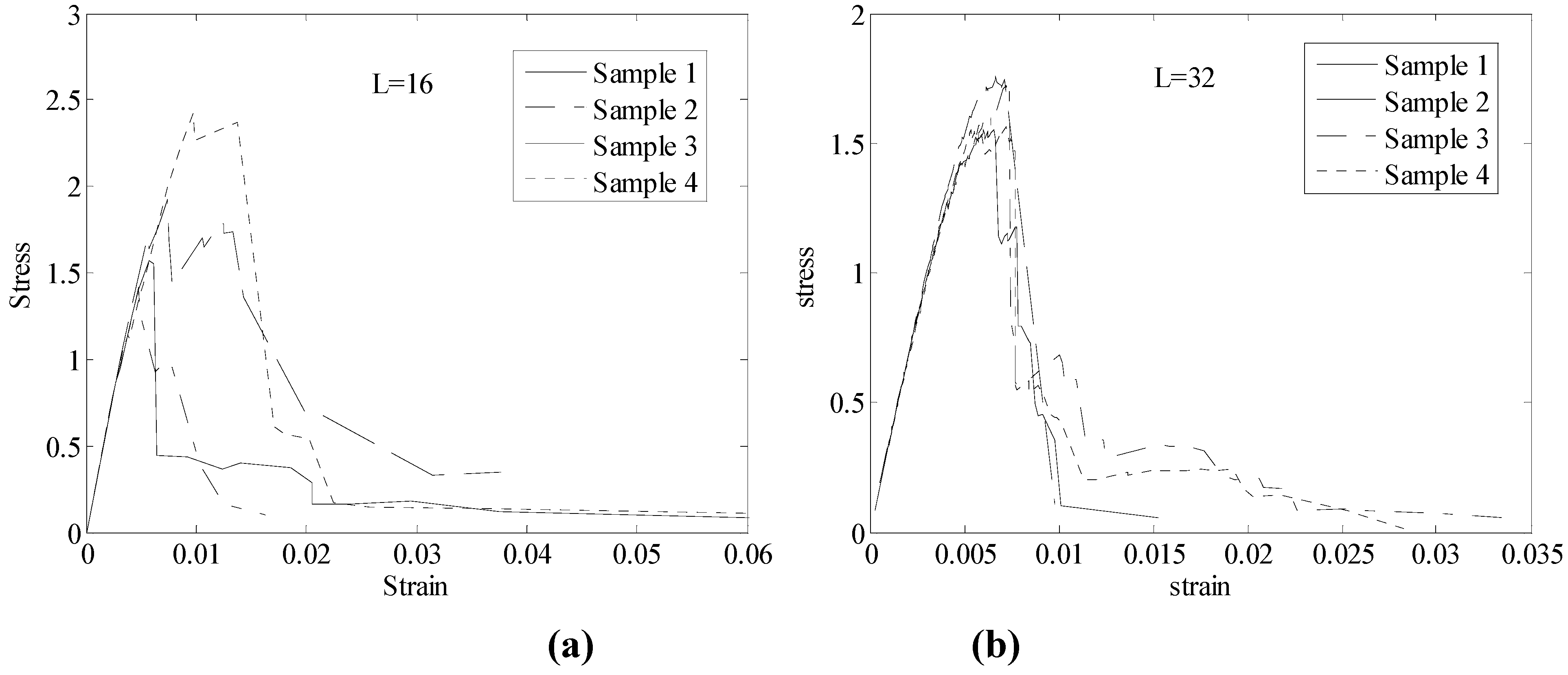
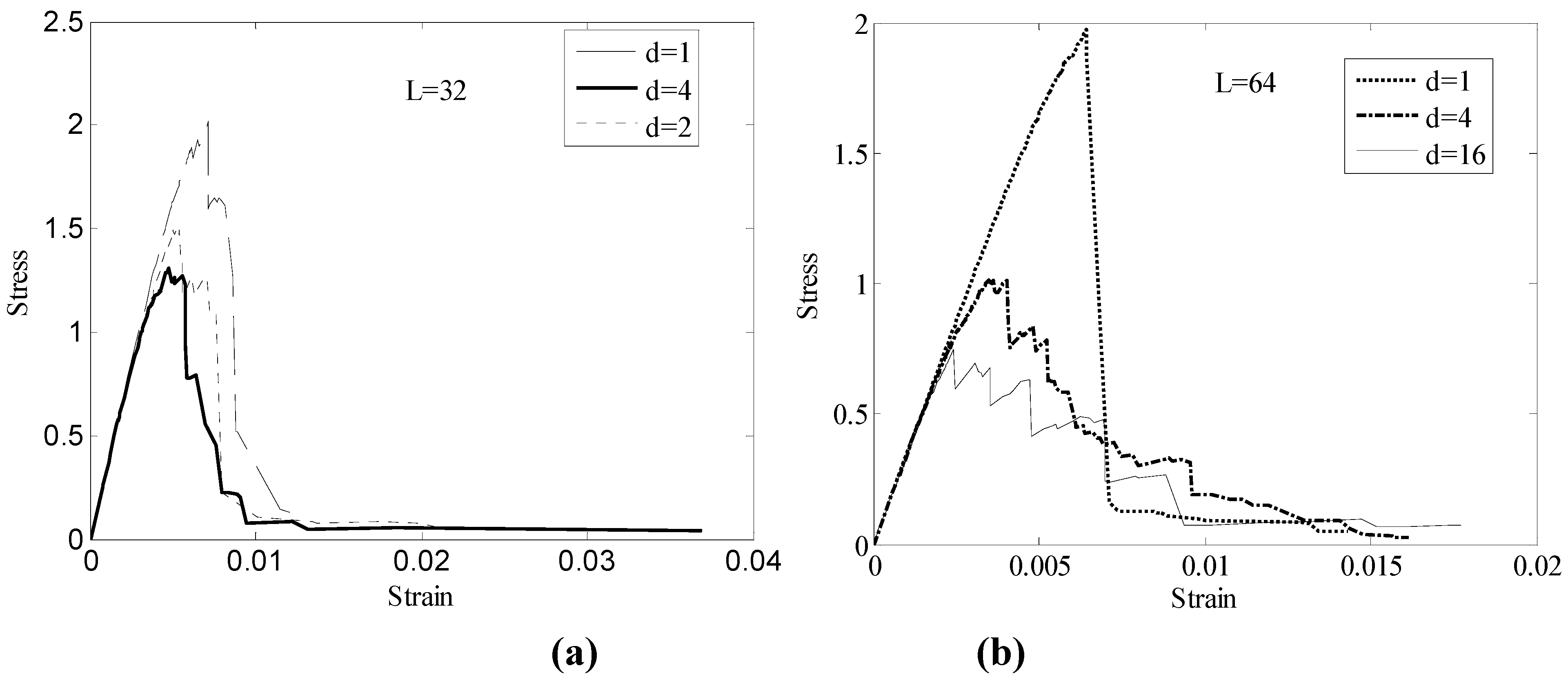
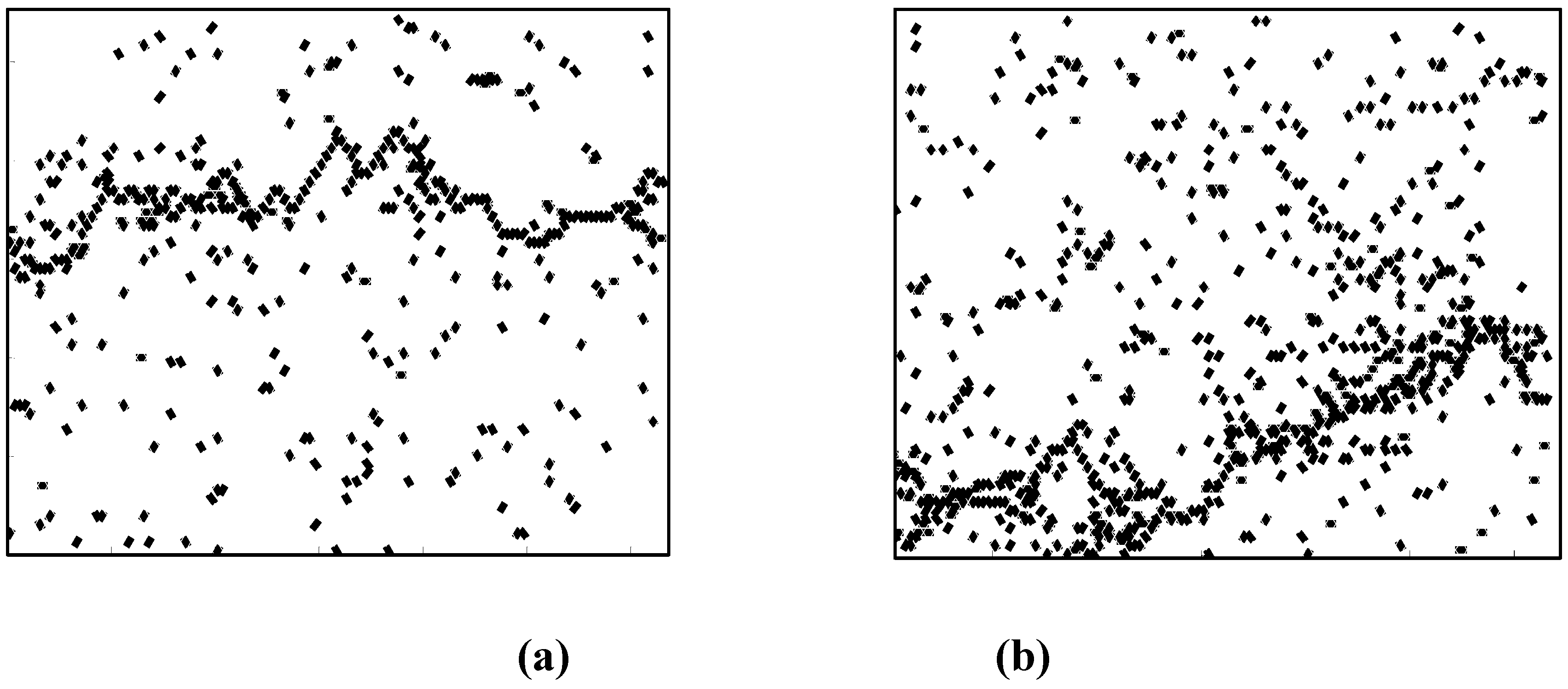
2.3 Probabilistic characterization of SRVE strength
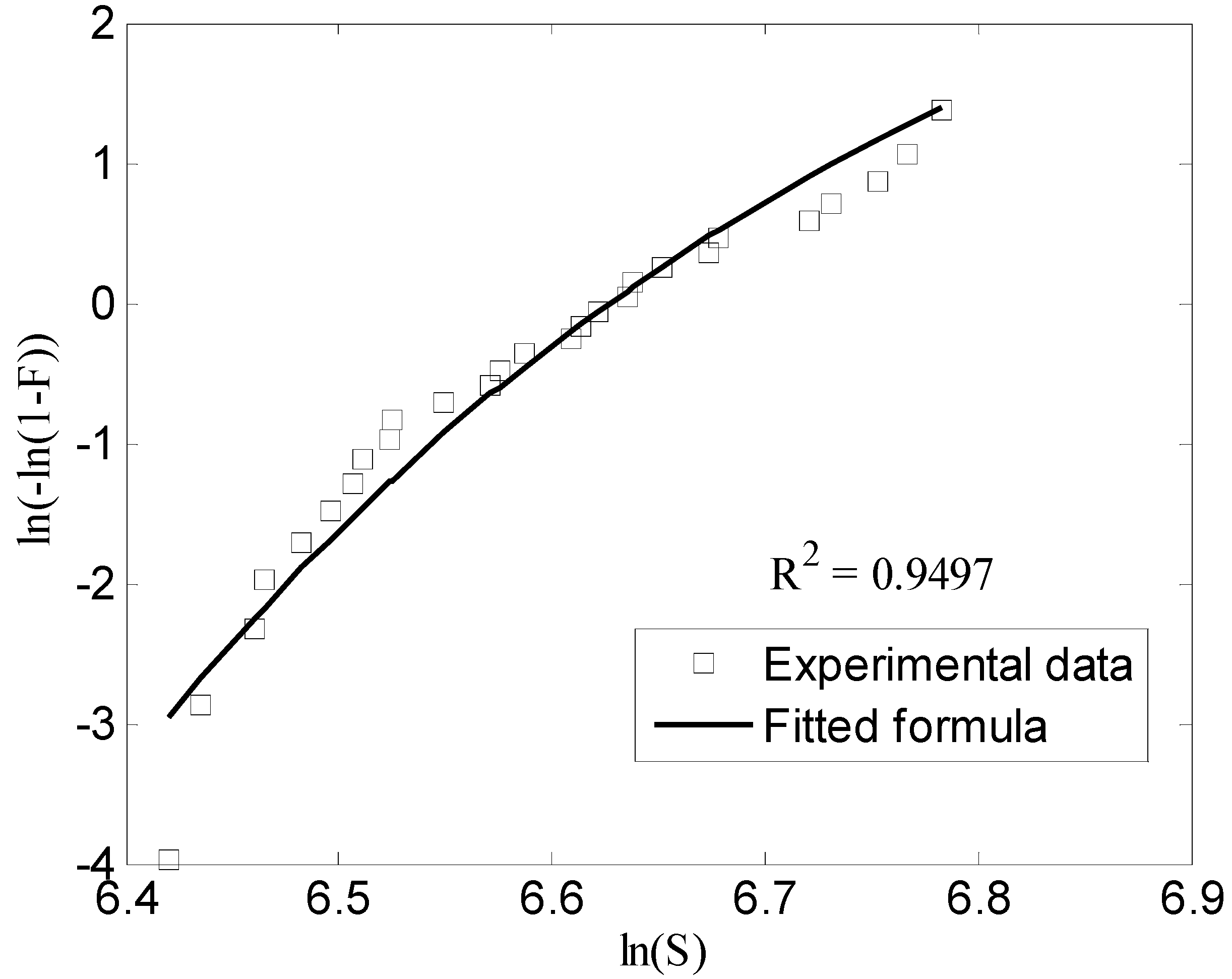
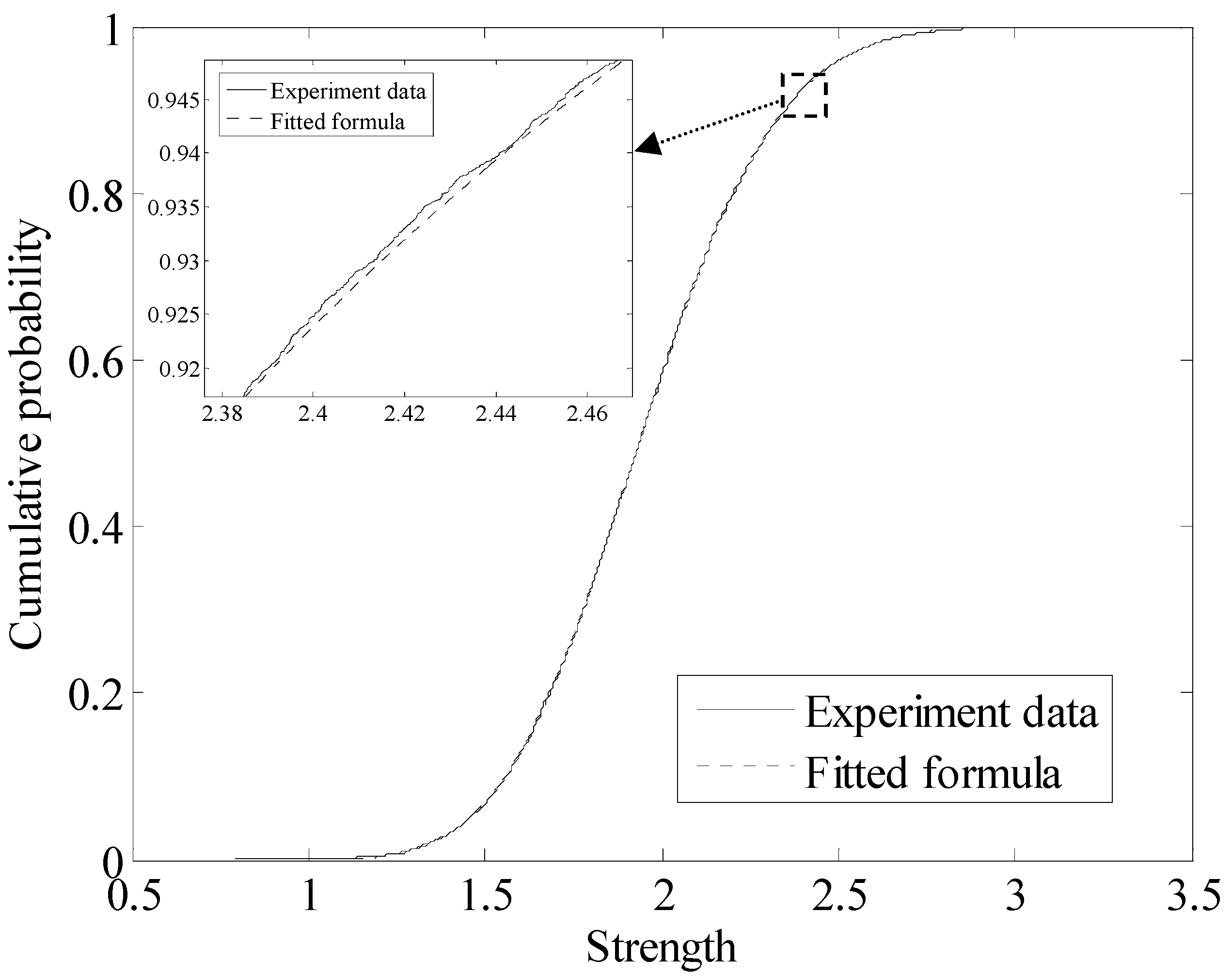
3. Meso-to-Macro Upscaling
3.1 Mesoscale damage model
3.2 Numerical example
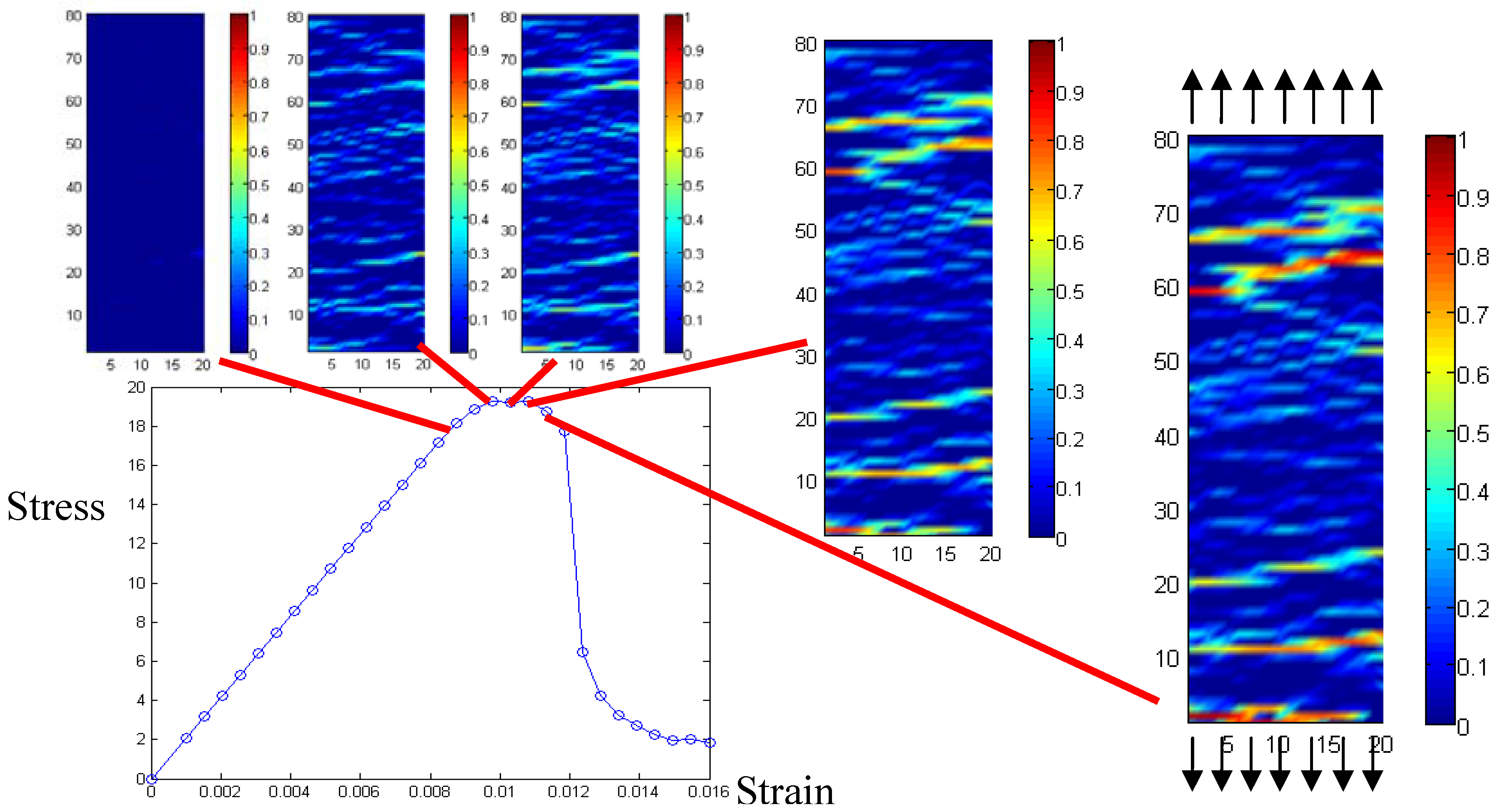
4. Conclusion
Acknowledgements
References
- Xu, X.F. A multiscale stochastic finite element method on elliptic problems involving uncertainties. Computer Methods in Applied Mechanics and Engineering 2007, 196, 2723–2736. [Google Scholar] [CrossRef]
- de Borst, R.; Gutiérrez, M.A.; Wells, G.N.; Remmers, J.J.C.; Askes, H. Cohesive-zone models, higher-order continuum theories and reliability methods for computational failure analysis. International Journal for Numerical Methods in Engineering 2004, 60, 289–315. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Lee, Y.H.; Willam, K. J. Nonlinear finite element reliability analysis of concrete. Journal of Engineering Mechanics 1996, 122, 1174–1182. [Google Scholar] [CrossRef]
- Anders, M.; Hori, M. Three-dimensional stochastic finite element method for elasto-plastic bodies. International Journal for Numerical Methods in Engineering 2001, 51, 449–478. [Google Scholar] [CrossRef]
- Herrmann, H. J.; Roux, S. Statistical Models for the Fracture of Disordered Media; Elsevier North-Holland: Amsterdam, 1990. [Google Scholar]
- Graham-Brady, L.; Xu, X.F. Stochastic morphological modeling of random multiphase materials. Journal of Applied Mechanics 2008, 75, 061001. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Pang, S.D. Activation energy based extreme value statistics and size effect in brittle and quasibrittle fracture. Journal of the Mechanics and Physics of Solids 2007, 55, 91–131. [Google Scholar] [CrossRef]
- Lemaitre, J.A. Continuous damage mechanics model for ductile fracture. Journal of Engineering Materials and Technology, Transactions of the ASME 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, X.F. A Heterogeneous cohesive model for quasi-brittle materials considering spatially varying random fracture properties. Computer Methods in Applied Mechanics and Engineering 2008, 197, 4027–4039. [Google Scholar] [CrossRef]
- Belytschko, T.; Mish, K. Computability in non-linear solid mechanics. International Journal for Numerical Methods in Engineering 2001, 52, 3–21. [Google Scholar] [CrossRef]
- Ruelle, D. Chance and Chaos; Princeton University Press, 1990. [Google Scholar]
- Francfort, G.A.; Marigo, J.J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Asokana, B.V.; Zabaras, N. A stochastic variational multiscale method for diffusion in heterogeneous random media. Journal of Computational Physics 2006, 218, 654–676. [Google Scholar] [CrossRef]
- Koutsourelakis, P. S. Stochastic upscaling in solid mechanics: An excercise in machine learning. Journal of Computational Physics 2007, 226, 301–325. [Google Scholar] [CrossRef]
- Chakraborty, A.; Rahman, S. Stochastic multiscale models for fracture analysis of functionally graded materials. Engineering Fracture Mechanics 2008, 75, 2062–2086. [Google Scholar] [CrossRef]
- Pugno, N.M.; Bosia, F.; Carpinteri, A. Multiscale stochastic simulations for tensile testing of nanotube-based macroscopic cables. Small 2008, 4(8), 1044–1052. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.F.; Chen, X. Stochastic homogenization of random multi-phase composites and size quantification of representative volume element. Mechanics of Materials 2009, 41, 174–186. [Google Scholar] [CrossRef]
- Xu, X.F. Generalized variational principles for uncertainty quantification of boundary value problems of random heterogeneous materials. ASCE Journal of Engineering Mechanics. In Press. [CrossRef]
- Xu, X.F.; Graham-Brady, L. Computational stochastic homogenization of random media elliptic problems using Fourier Galerkin method. Finite Elements in Analysis and Design (Special issue on 17th Melosh Competition) 2006, 42(7), 613–622. [Google Scholar] [CrossRef]
- Xu, X.F.; Graham-Brady, L. A stochastic computational method for evaluation of global and local behavior of random elastic media. Comput. Methods Appl. Mech. Engrg. 2005, 194(42-44), 4362–4385. [Google Scholar] [CrossRef]
- Xu, X.F.; Chen, X.; Shen, L. A Green-function-based multiscale formulation for uncertainty quantification of finite body random heterogeneous materials. Submitted.
- Alava, M; Nukala, P. K.V.; Zapperi, S. Statistical models of fracture. Advances in Physics 2006, 55, 349. [Google Scholar]
- Mariano, P.M. Premises to a multifield approach to stochastic damage evolution. In Damage and Fracture in Disordered Materials; Krajcinovic, D., van Mier, J., Eds.; Springer-Verlag: Berlin, 2000; pp. 217–263. [Google Scholar]
- Gross, B. Least squares best fit method for the three parameter Weibull distribution: Analysis of tensile and bend specimens with volume or surface flaw failure. NASA Technical Memorandum 1996, 4721. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hu, K.; Xu, X.F. Probabilistic Upscaling of Material Failure Using Random Field Models – A Preliminary Investigation. Algorithms 2009, 2, 750-763. https://doi.org/10.3390/a2020750
Hu K, Xu XF. Probabilistic Upscaling of Material Failure Using Random Field Models – A Preliminary Investigation. Algorithms. 2009; 2(2):750-763. https://doi.org/10.3390/a2020750
Chicago/Turabian StyleHu, Keqiang, and X. Frank Xu. 2009. "Probabilistic Upscaling of Material Failure Using Random Field Models – A Preliminary Investigation" Algorithms 2, no. 2: 750-763. https://doi.org/10.3390/a2020750



