Mixed Variational Formulations for Micro-cracked Continua in the Multifield Framework
Abstract
:1. Introduction and modeling
1.1. Introductory remarks
1.2. The constitutive model
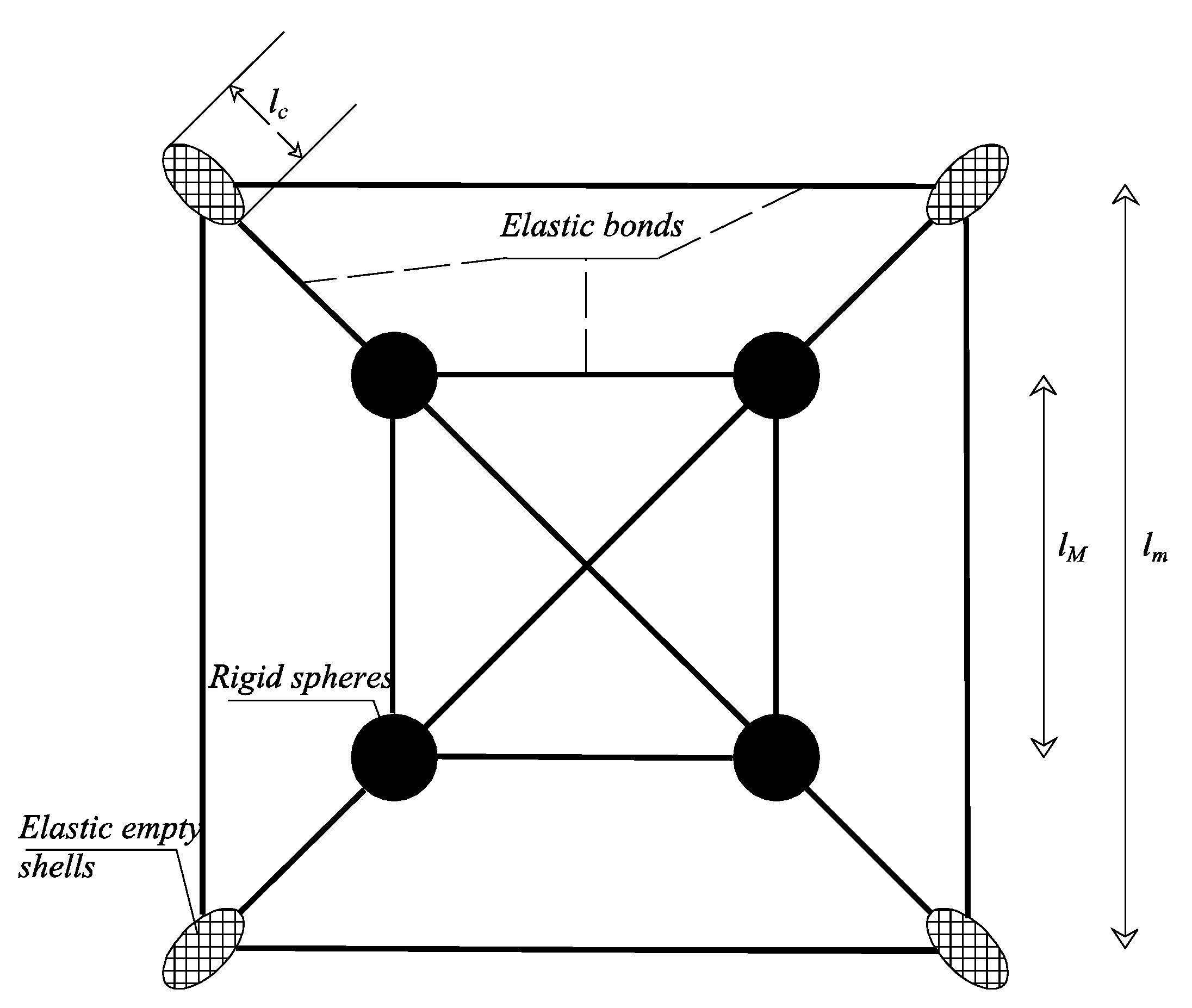
| t | = | specimen thickness |
| = | material reference volume element = | |
| = | micro-fracture reference volume element = | |
| E | = | Young modulus of the bonds between macro-spheres |
| = | Young modulus of the bonds between macro-spheres and micro-holes | |
| = | = macro-lattice stiffness | |
| = | = mean stiffness of the ellipsoidal micro-holes | |
| = | = stiffness of the bonds between macro and meso lattices | |
| = | cross section of rods between adjacent micro-cracks. |
2. Mixed variational formulations
2.1. Primal Hellinger–Reissner formulation
2.2. Dual Hellinger–Reissner formulation
2.3. Implementation
3. Numerical studies
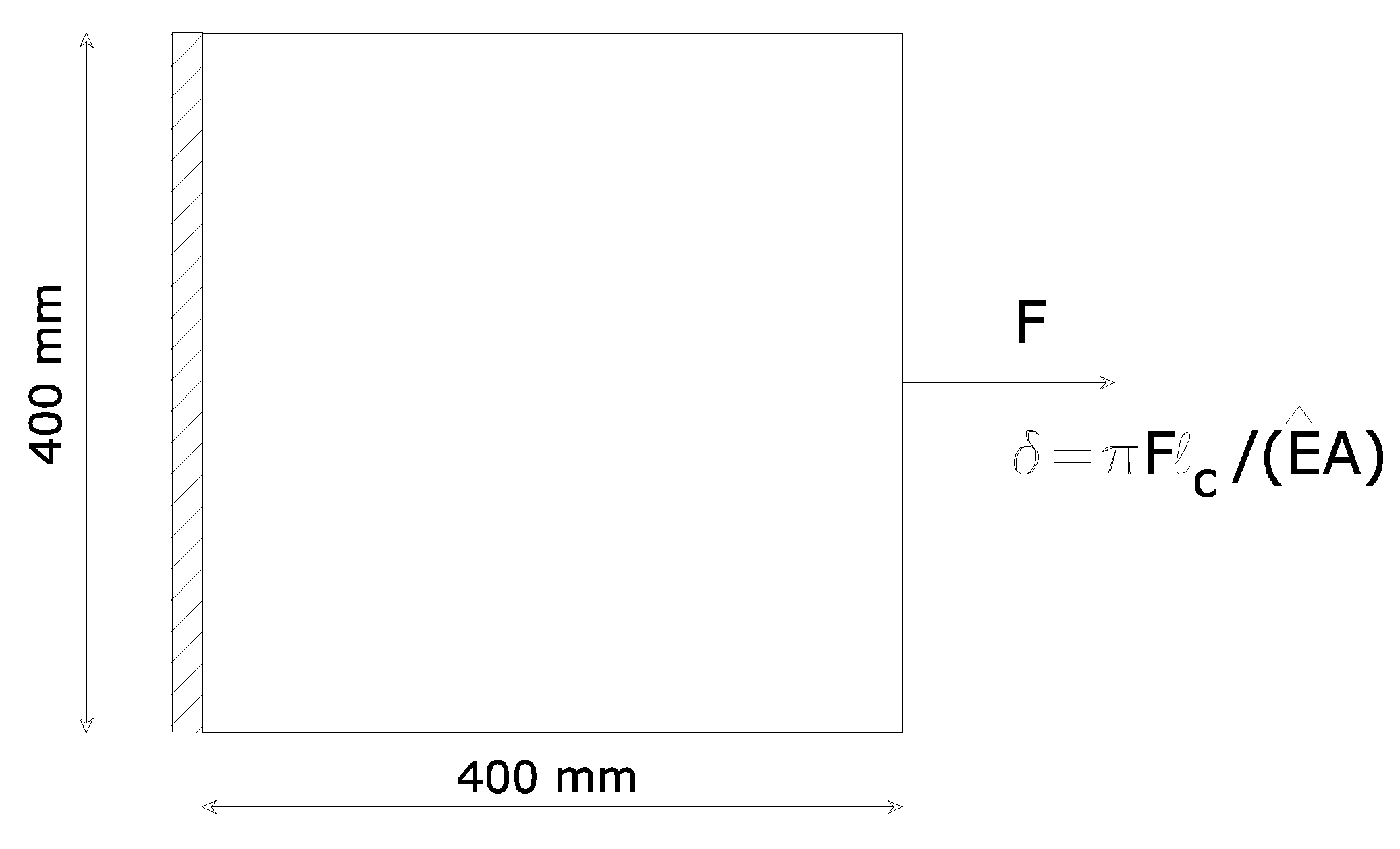
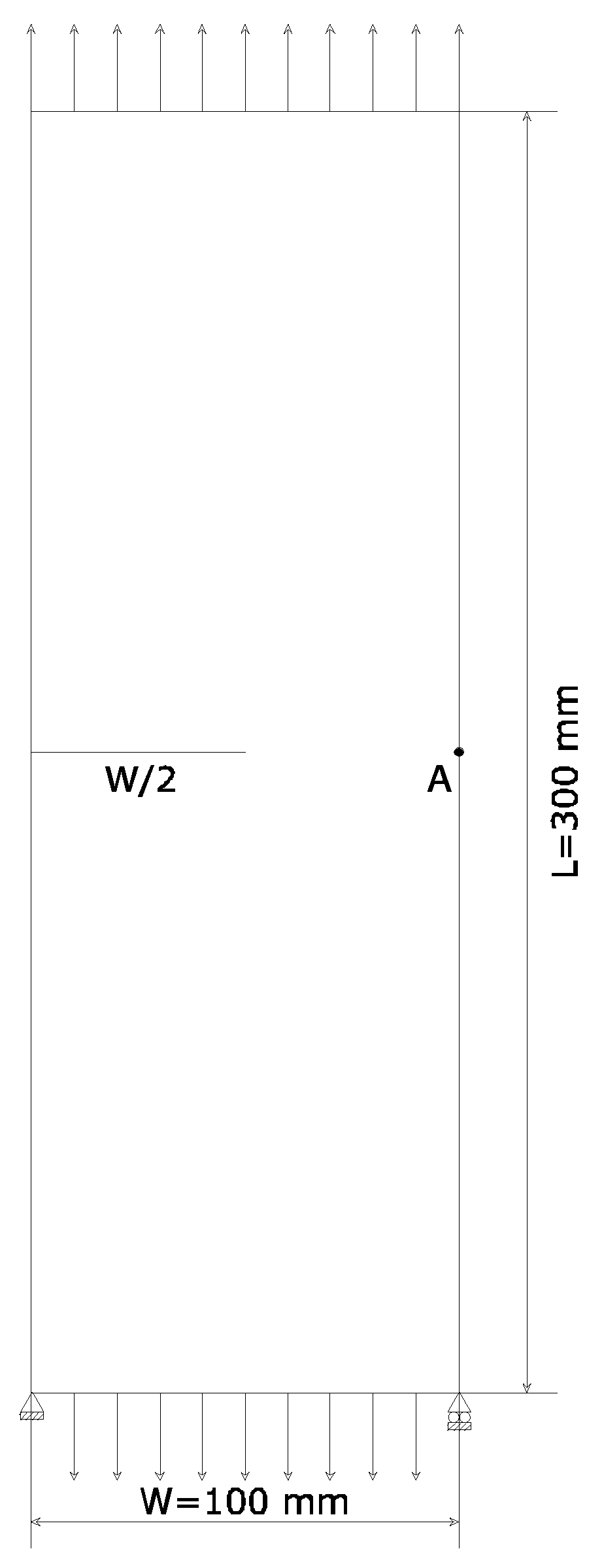
3.1. A clamped square lamina
| δ | E | A | |||||
| 200 | 1 | 0.1 | 1 | 0.314 | 1 | 50 |
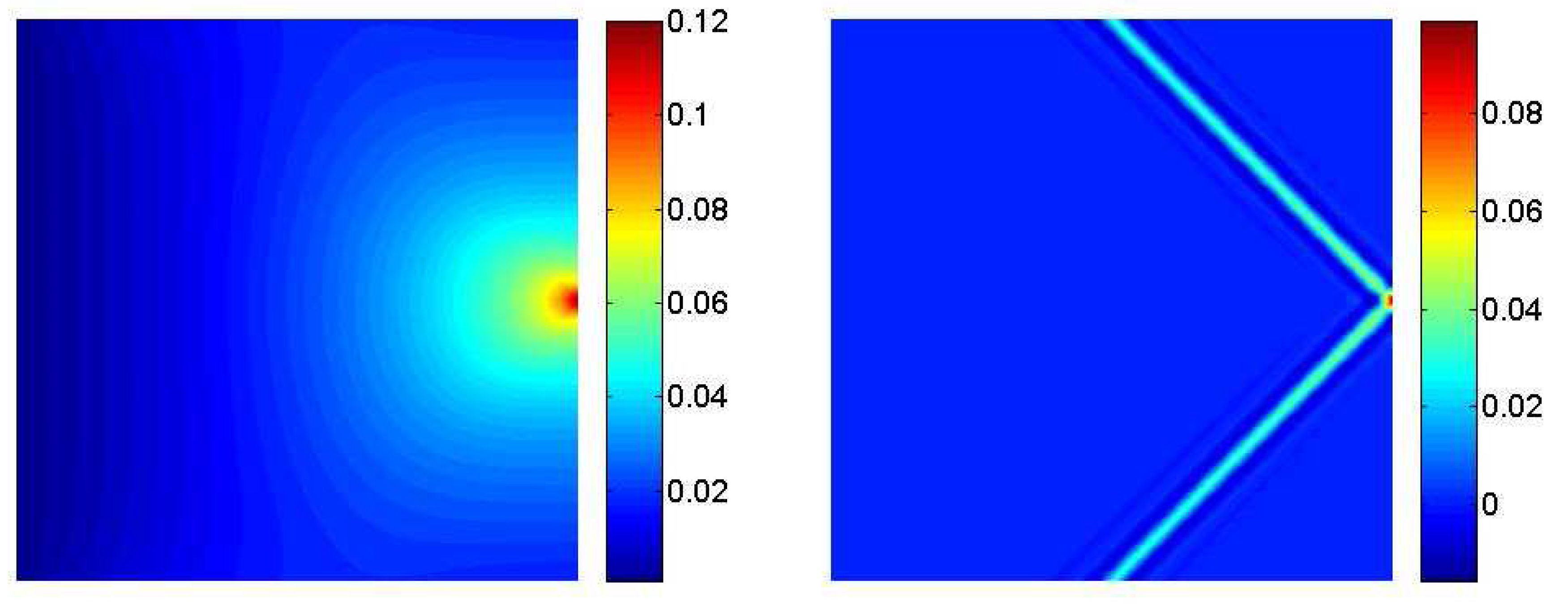
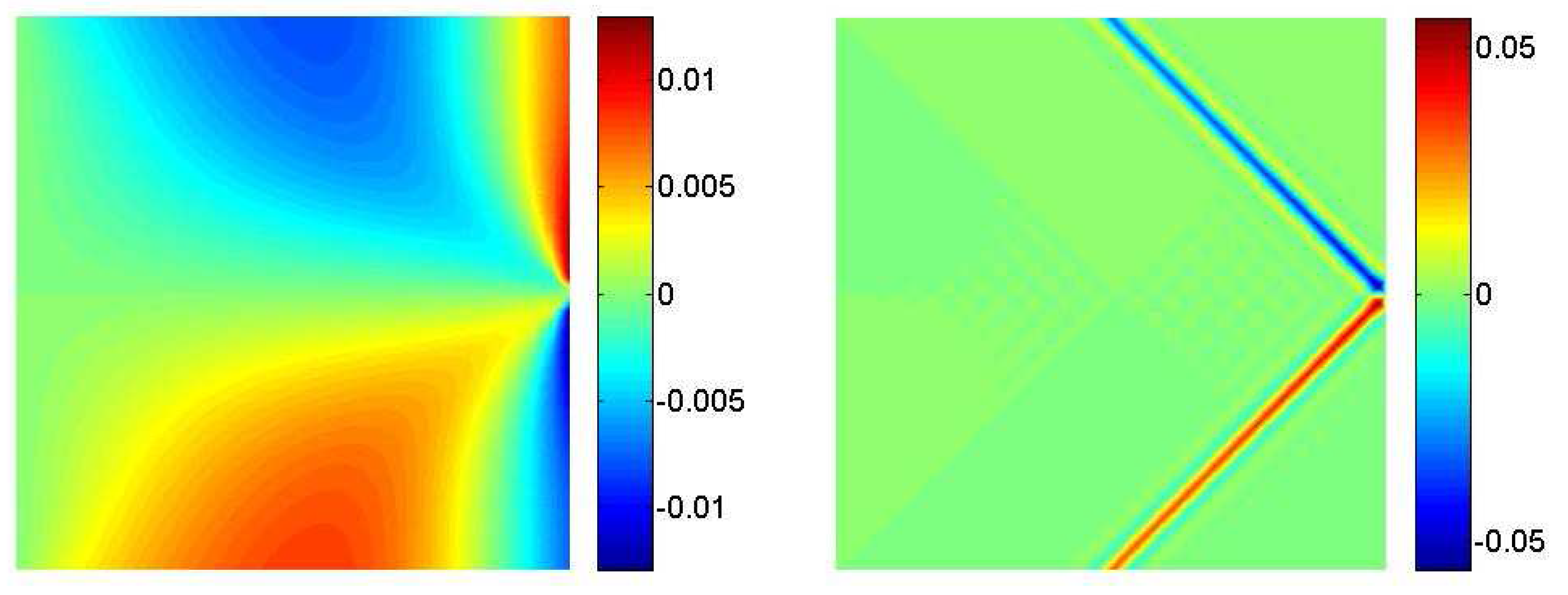
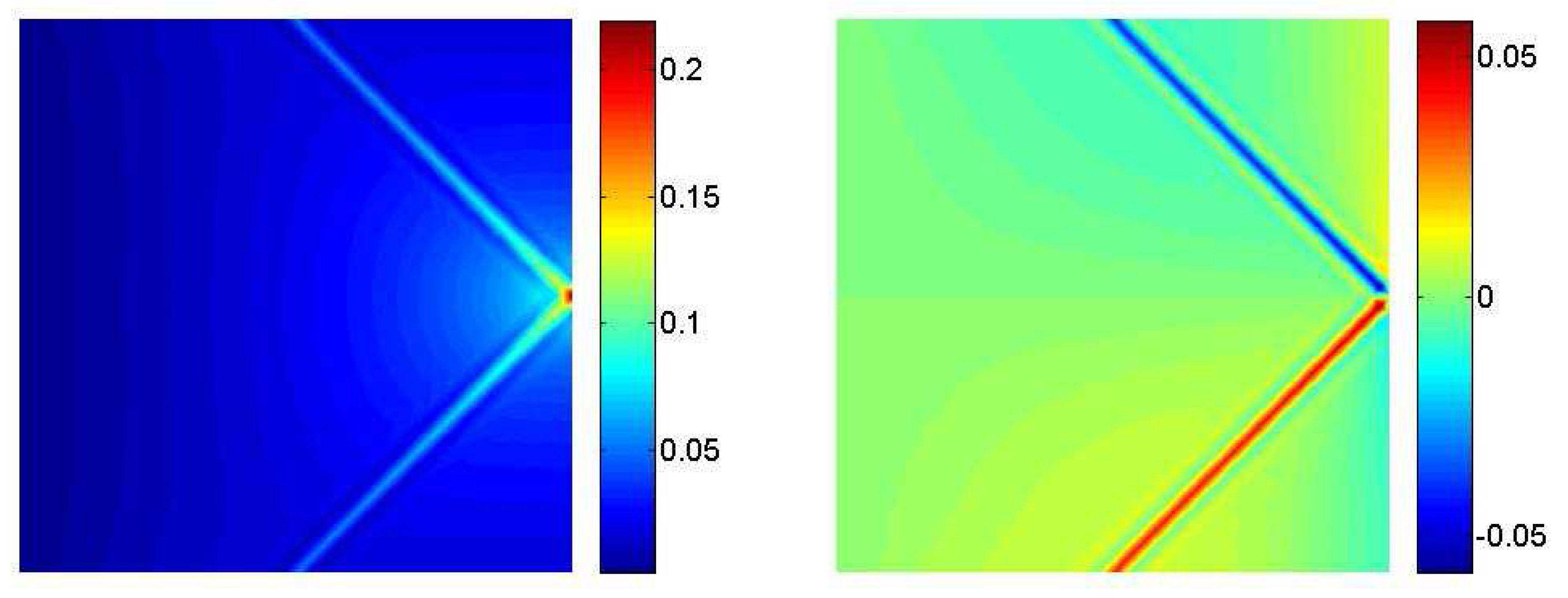
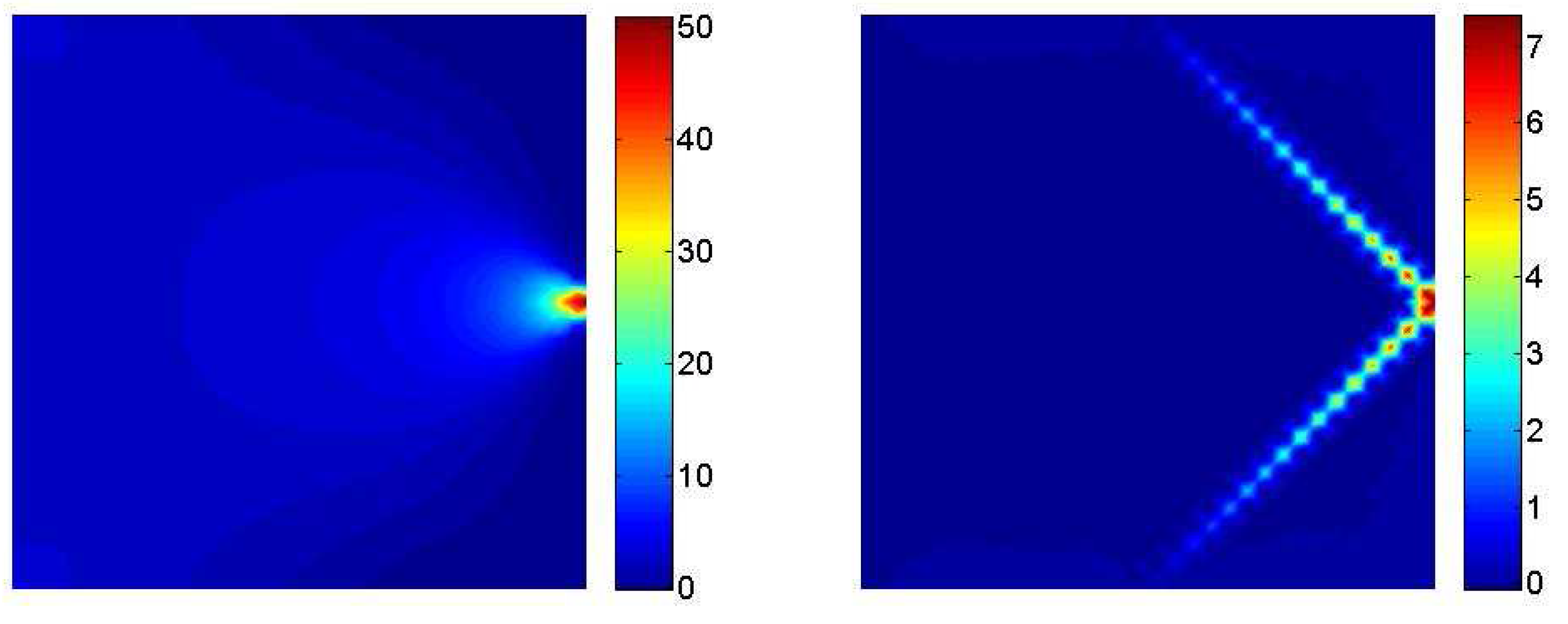
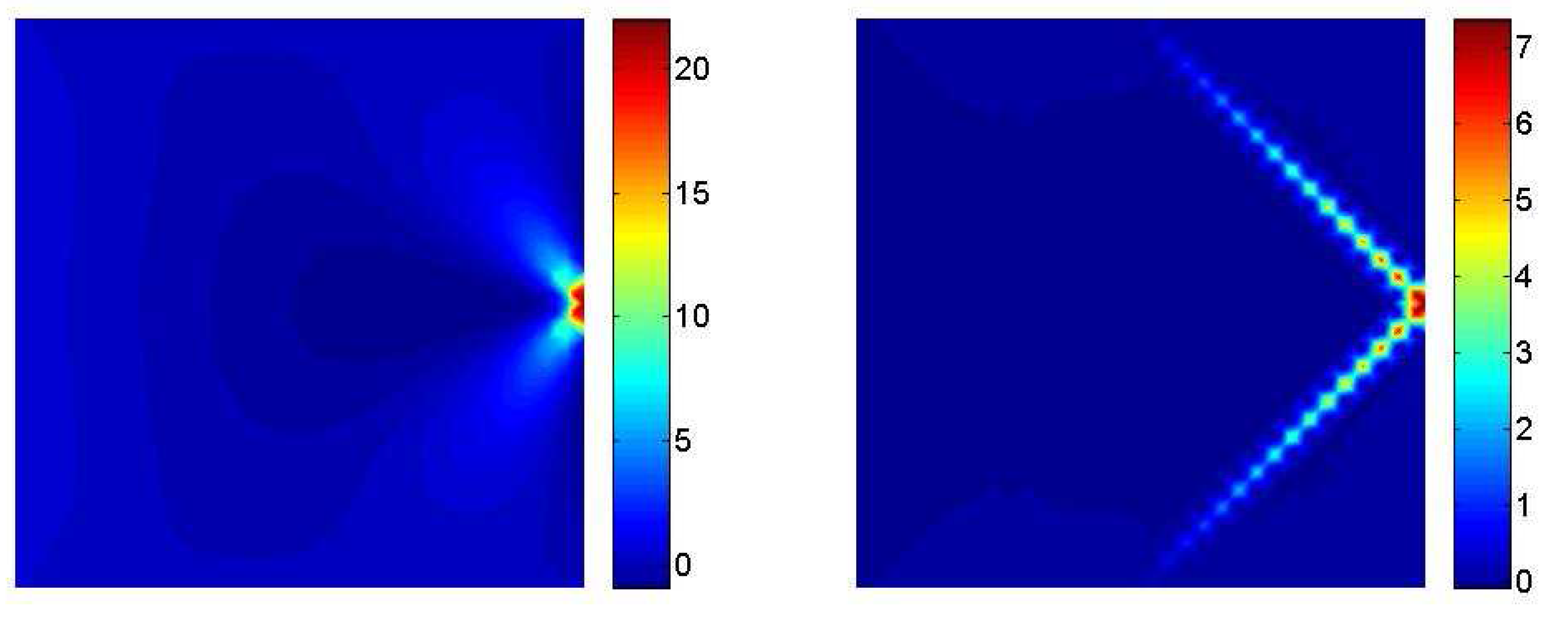

3.2. Interaction between a macrocrack and diffuse microcracks
| E | A | χ | ||||
| 75 | 5 | 1 | 0.0314 | 1 | 50 |
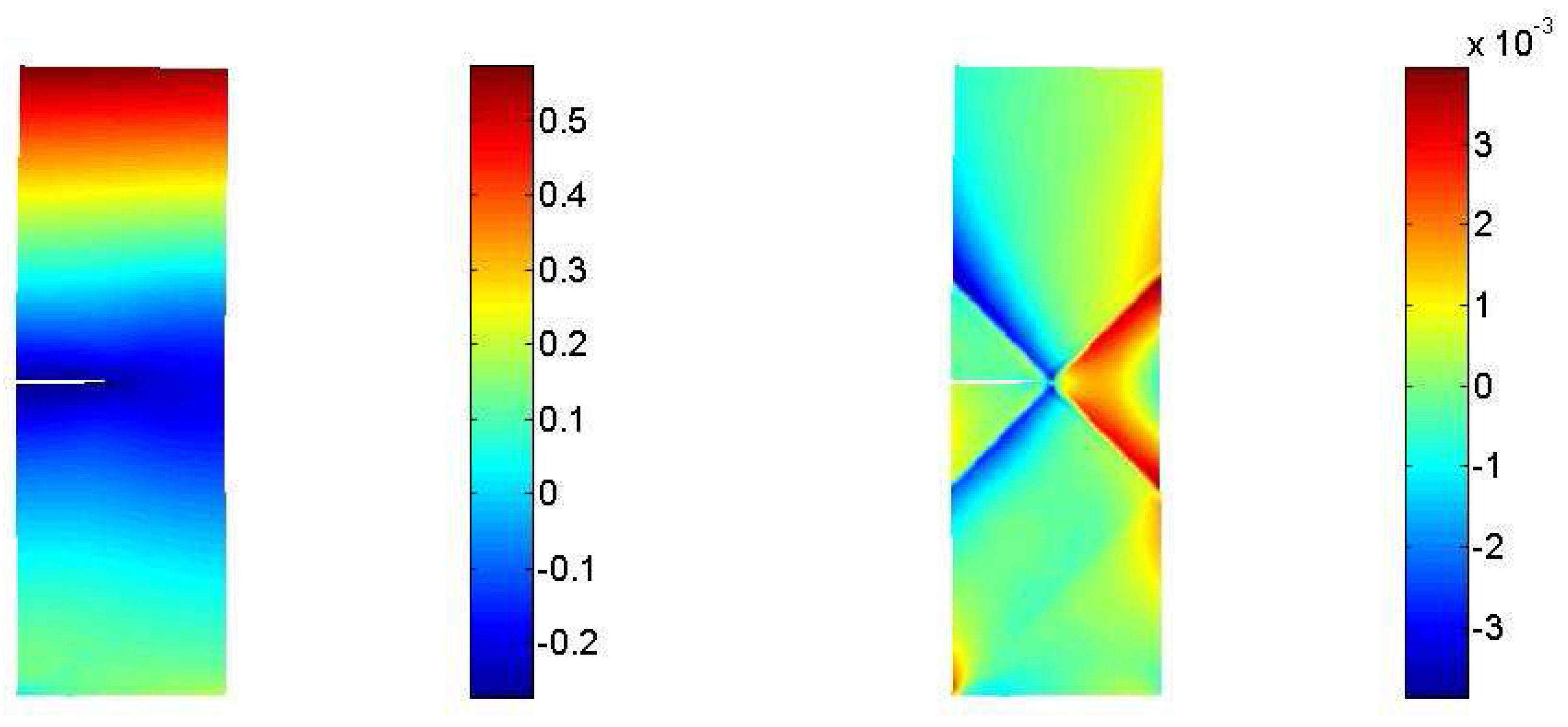
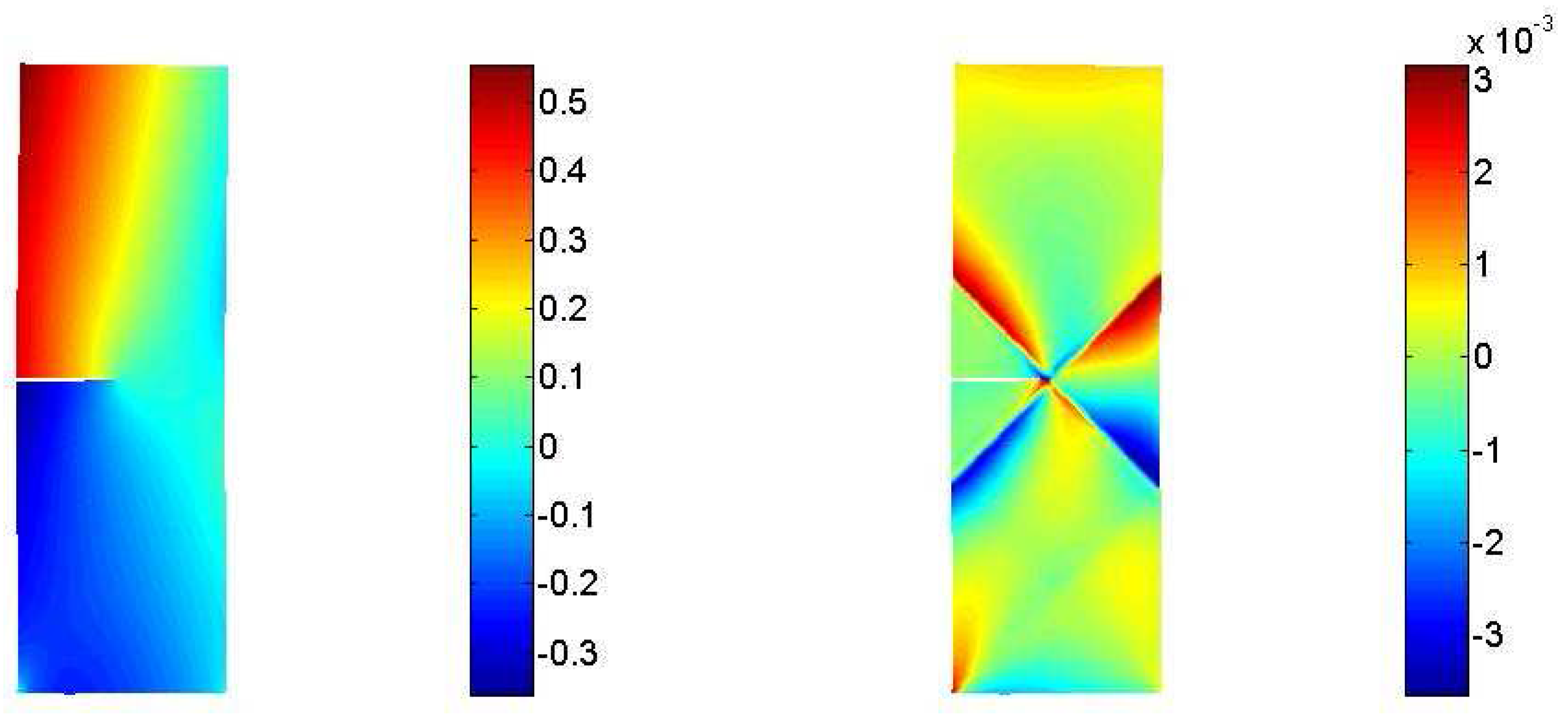
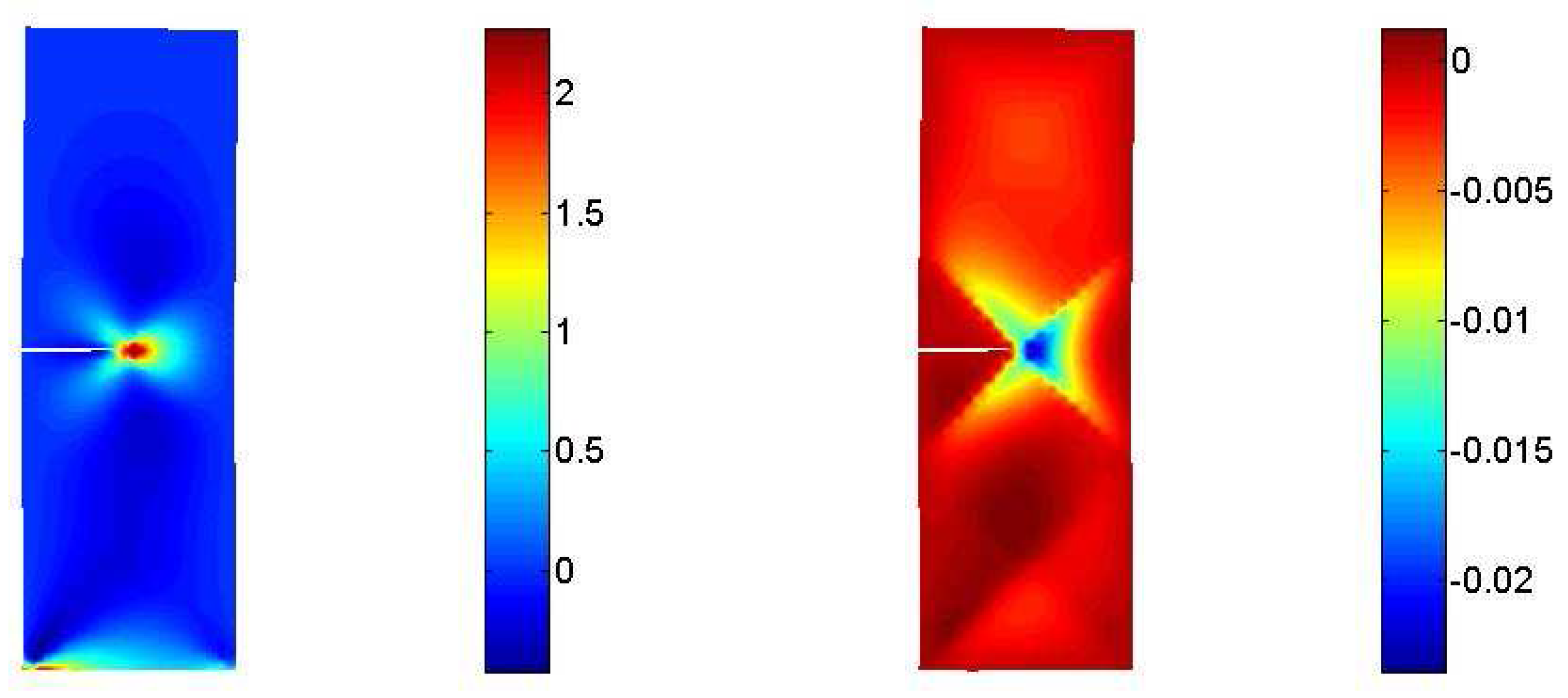
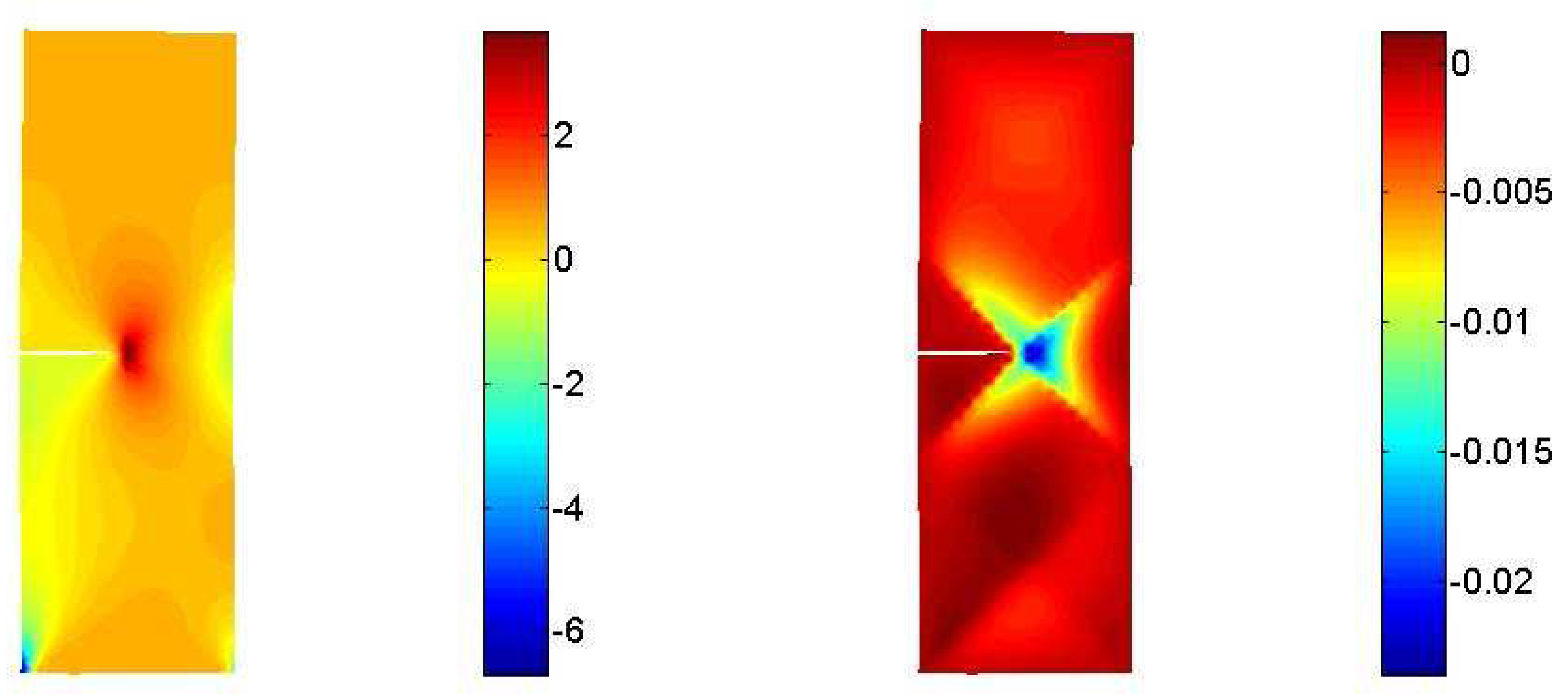
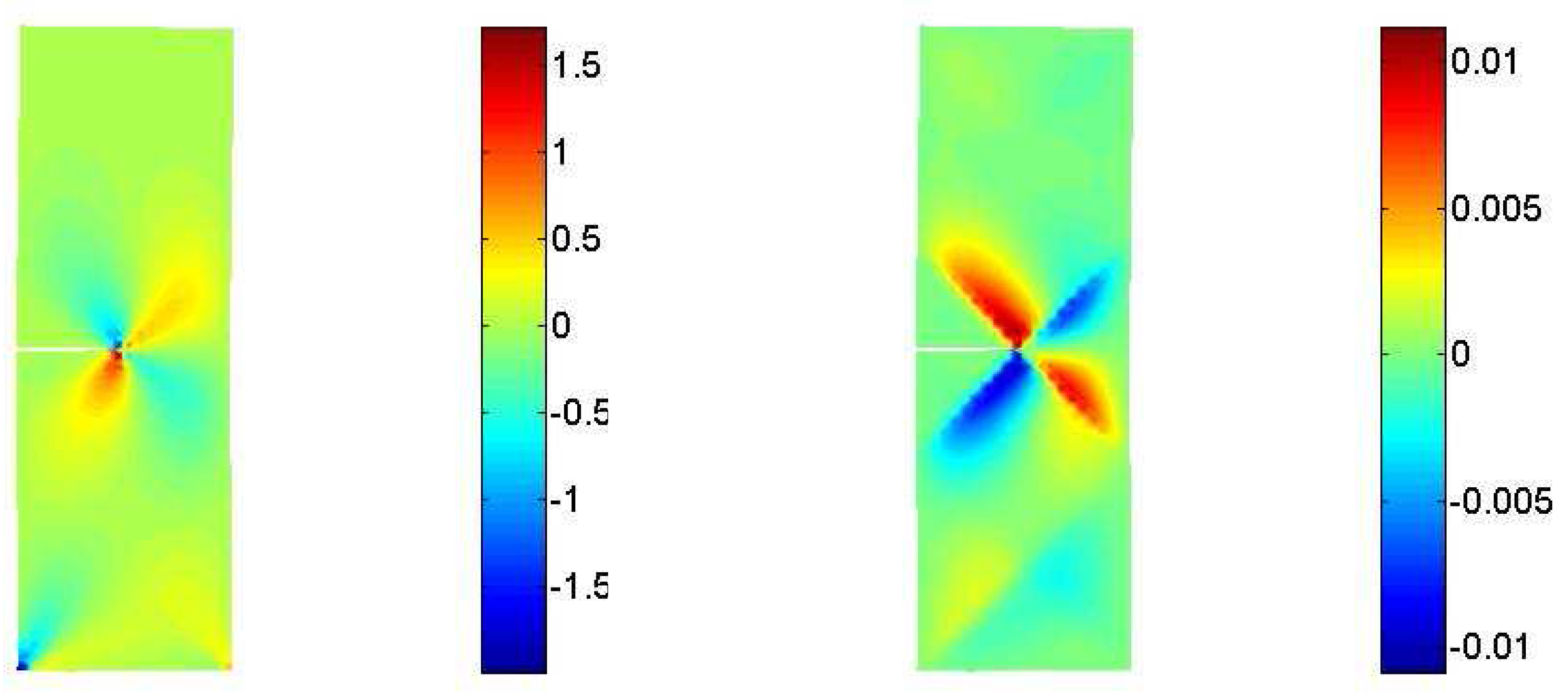
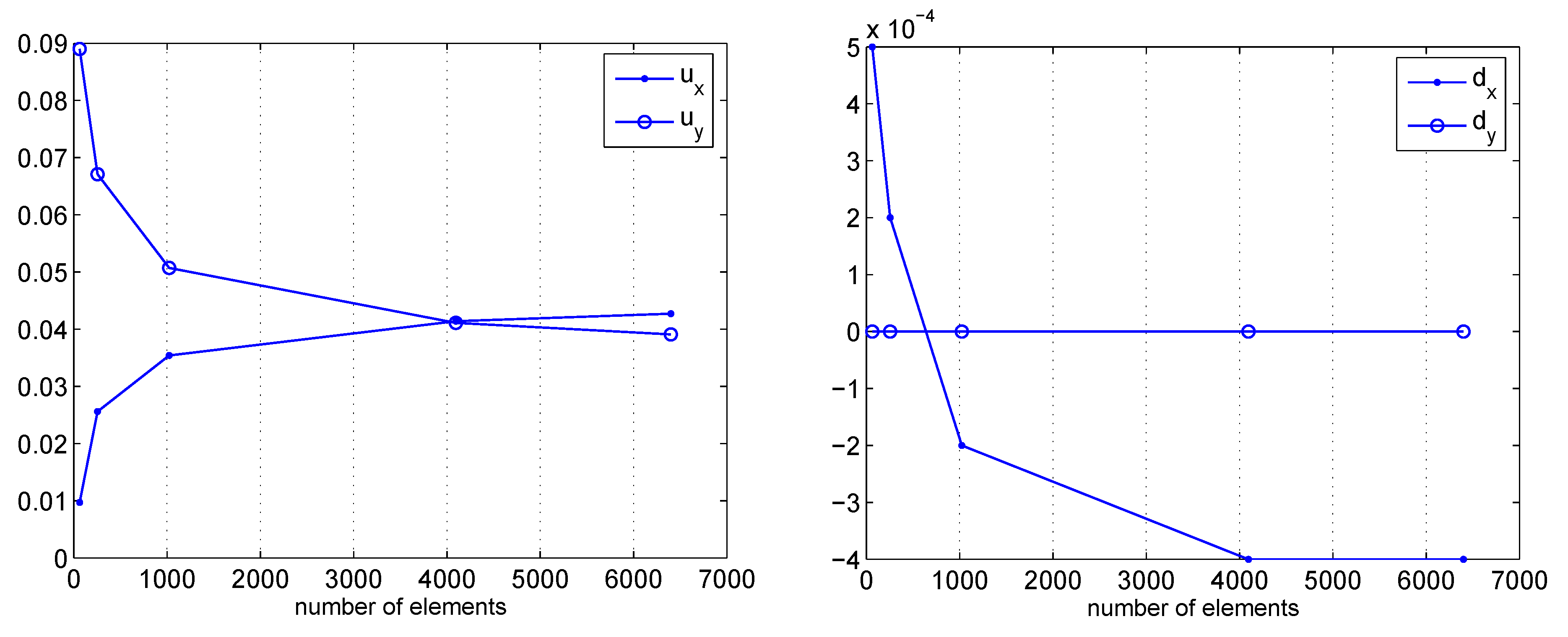
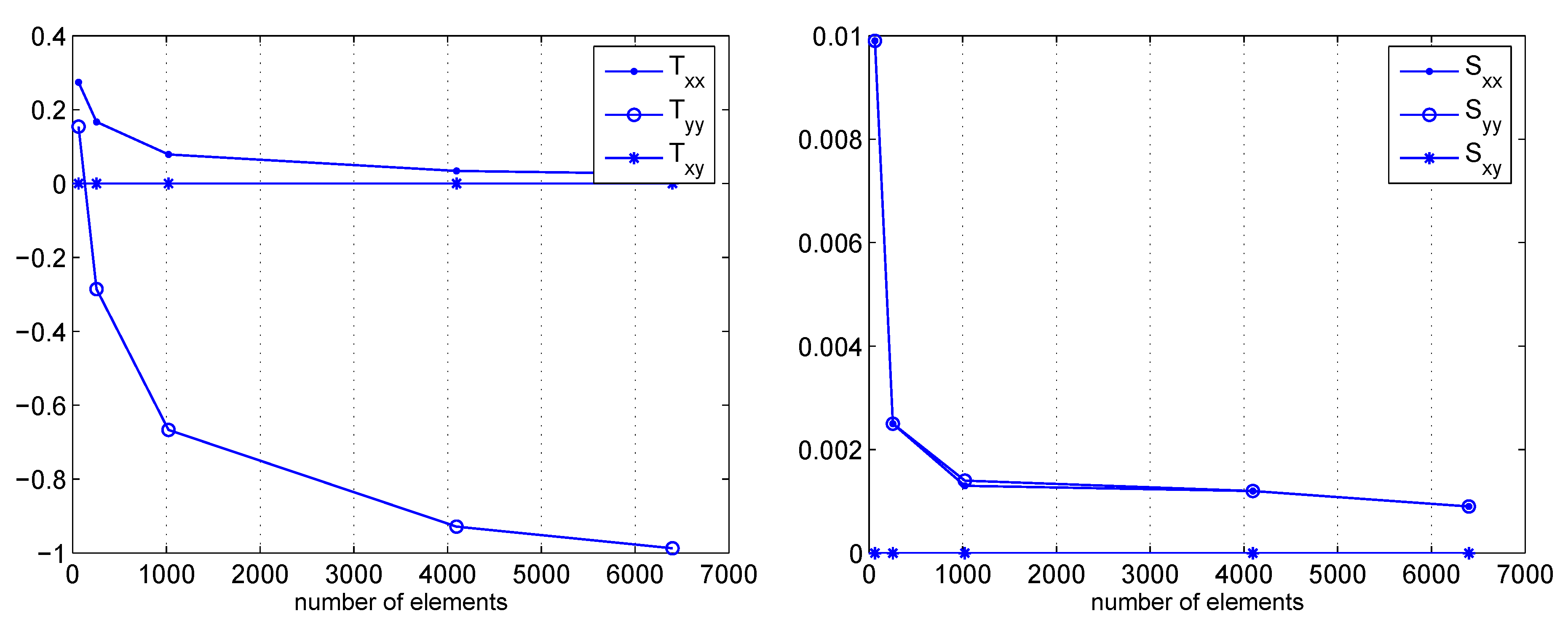

4. Conclusions and future work
Acknowledgements
References and Notes
- Arnold, D.N.; Brezzi, F.; Douglas, J.D. PEERS: a new mixed finite element for plane elasticity. Japan Journal of Applied Mathematics 1984, 1, 347–367. [Google Scholar]
- Brezzi, F.; Fortin, M. Hybrid and Mixed Finite Element Methods; Springer: New york, 1991. [Google Scholar]
- Bruggi, M.; Venini, P. A Truly Mixed Approach for Cohesive–Crack Propagation in Functionally Graded Materials. Mechanics of Advanced Materials and Structures 2007, 14, 643–654. [Google Scholar]
- Bruggi, M.; Venini, P. A mixed FEM approach to stress-constrained topology optimization. International Journal for Numerical Methods in Engineering 2008, 73, 1693–1714. [Google Scholar]
- Capriz, G. Continua with microstructures; Springer Tracts in Natural Philosophy, 35; Springer: Berlin, 1989. [Google Scholar]
- Johnson., C.; Mercier, B. Some equilibrium finite elements methods for two dimensional elasticity problems. Numer: Math. 1978, 30, 103–116. [Google Scholar]
- Krajcinovic, D. Damage mechanics; North-Holland: Amsterdam, 1996. [Google Scholar]
- Mariano, P.M. Multifield Theories in mechanics of solids. Adv. Appl. Mech. 2002, 38, 1–93. [Google Scholar]
- Mariano, P.M.; Stazi, F.L. Strain localization in elastic microcracked bodies. Comp. Methods Appl. Mech. Engrg. 2001, 190, 5657–5677. [Google Scholar]
- Mariano, P.M.; Stazi, F.L. Strain localization due to crack-microcrack interactions: X-FEM for a multifield approach. Comp. Methods Appl. Mech. Engrg. 2004, 193, 5035–5062. [Google Scholar]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Engineering Fracture Mechanics 2002, 69, 813–833. [Google Scholar]
- Schenk, O.; Gärtner, K. Solving Unsymmetric Sparse Systems of Linear Equations with PARDISO. Journal of Future Generation Computer Systems 2004, 20, 475–487. [Google Scholar]
- Schenk, O.; Gärtner, K. On fast factorization pivoting methods for symmetric indefinite systems. Elec. Trans. Numer. Anal. 2006, 23, 158–179. [Google Scholar]
- Torquato, S. Random heterogeneous materials; Springer Verlag: Berlin, 2002. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bruggi, M.; Venini, P. Mixed Variational Formulations for Micro-cracked Continua in the Multifield Framework. Algorithms 2009, 2, 606-622. https://doi.org/10.3390/a2010606
Bruggi M, Venini P. Mixed Variational Formulations for Micro-cracked Continua in the Multifield Framework. Algorithms. 2009; 2(1):606-622. https://doi.org/10.3390/a2010606
Chicago/Turabian StyleBruggi, Matteo, and Paolo Venini. 2009. "Mixed Variational Formulations for Micro-cracked Continua in the Multifield Framework" Algorithms 2, no. 1: 606-622. https://doi.org/10.3390/a2010606
APA StyleBruggi, M., & Venini, P. (2009). Mixed Variational Formulations for Micro-cracked Continua in the Multifield Framework. Algorithms, 2(1), 606-622. https://doi.org/10.3390/a2010606




