Genetic Algorithms in Application to the Geometry Optimization of Nanoparticles

Abstract

Applications of genetic algorithms to the global geometry optimization problem of nanoparticles are reviewed. Genetic operations are investigated and importance of phenotype genetic operations, considering the geometry of nanoparticles, are mentioned. Other efficiency improving developments such as floating point representation and local relaxation are described broadly. Parallelization issues are also considered and a recent parallel working single parent Lamarckian genetic algorithm is reviewed with applications on carbon clusters and SiGe core-shell structures.

1. Introduction

Many hard problems of today’s science and engineering can be represented as optimization problems [1] of some sort of parameters to achieve a desired solution which is most of the time an extremum in the configuration space spanned by the parameters. The correspondence of desired solution being an extremum is actually related to the least action principle [2] that we know from the Lagrangian formulation of classical mechanics. We can explain many things such as the reason that light rays prefer the path which minimizes the needed time by using this fundamental principle of physics.

These optimization problems are considered as hard because of the exponentially increasing number of solution candidates as the size of the subjected system increases. Optimization problems are classified in the complexity class of non-deterministic polynomial (NP) [3] since the scaling of their solution time with increasing system size is exponential and can not be reduced to polynomial without using some sort of approximations. In terms of the configuration space, these exponentially increasing solution candidates correspond to local extrema which are similar to the desired global extremum in a topological manner and consequently there is no way to decide if an extremum is a local or a global one other than to search for better solutions. A famous example of the NP complexity problems is a combinatorial problem known as the traveling salesman problem (TSP) [4], which searches for the shortest path for a salesman whose objective is visiting a certain number of cities and eventually returning to the starting city. As the number of cities increases linearly, the number of possible paths increases exponentially and therefore, our unfortunate salesman starts having trouble in estimating the shortest path for his travel. Another well known problem of the NP complexity class is from chemical physics about finding the most stable structure of nanoparticles composed of certain number and types of atoms or molecules [5,6]. Even though this important problem of chemical physics does not resemble TSP at a first glance, a deeper analysis shows that these two problems are indeed very similar combinatorial problems if the solution space of the nanoparticle problem is constructed as being composed of stable isomers only. The number of stable isomers of the nanoparticle increases exponentially just like the possible paths in TSP as the system size increases and an exact solution becomes intractable even for moderate sized nanoparticles [7].

Because of the exponential scaling property of computation time with the system size, these kind of problems can only be solved approximately in a reasonable amount of time by the search algorithms seeking configuration space extensively to find the desired solution. Monte Carlo methods, simulated annealing, basin-hoping and genetic algorithms (GAs) are examples of such search methods used in various branches of science and engineering [8,9]. The common stochastic nature of these methods is an advantage for the optimization problems with higher dimensional configuration spaces. Monte Carlo methods use the random walk concept as the search technique and jump over local minima by thermal fluctuations. Simulated annealing tries to find the global minimum by decreasing thermal fluctuations with passing time. The main theme of basin-hoping is a potential energy surface (PES) transformation to reduce the configuration space to the space of local minima. This transformed PES is then searched by Monte Carlo methods. GAs use principles of natural evolution to make a search in the configuration space and they gained importance because of their wide applicability and success for the global optimization problems.

This article reviews application of GAs to the geometry optimization problem of nanoparticles by mentioning past and recent developments on the GAs specific for this problem of chemical physics with some illustrating examples from the literature. Methodology of GA optimization is explained in Section 2 together with some historical remarks. Information about the geometry optimization problem of nanoparticles and usage of GAs in this field is given in section 3 and two GA applications of the current authors to the geometry optimization of atomic clusters using a single parent Lamarckian GA implementation, are presented in section 4 together with some discussion about the relative power of single parent GAs for the geometry optimization problem.

2. Genetic algorithms

GA [10,11] is a generic name for the global optimization methods which facilitate principles of biological evolution. Despite the fact that biological systems with highly sensitive relations between different kinds of species have much more complexity compared to our model systems, the fundamental idea of survival of the fittest individuals and also the fittest species in general may be used as a powerful search technique in optimization problems. A suitable artificial environment in which solution candidates evolve in competition with each other should be prepared in order to make use of this idea for a certain problem.

Even though the concept of GAs has been known since the 50s, it has become famous after studies of John H. Holland in 70s [12] and now it is being used in many fields such as scheduling [13], finance [14], and telecommunication [15], in addition to the field of chemical physics which is the subject of this review.

GA’s search technique may be attributed to be intelligent in a sense since it focuses on the regions of the configuration space where the global minimum is more likely to be found by the selection mechanism and the reproduction of selected individuals while not being stuck to local minima with the help of variation generating operations of mutation and crossover. If we had the opportunity to visualize the individuals of a fine tuned GA simulation in the higher dimensional configuration space of parameters, we would observe that initial randomly distributed individuals would start being aggregated around some number of local minima and the aggregation would spread apart to nearby local minima as the time passes leaving some of the local minima as better ones are found. Eventually aggregation would be around the global minimum and around some local minima in the close neighborhood.

While GAs are applicable in general to all kinds of optimization problems, its efficiency may be debatable for some of them. Topology of the objective function [16] is the decisive factor in determining the efficiency of GAs for a specific problem. As an extremal example, if the objective function is monotonically increasing or decreasing until the point of global extremum, simple local optimization routines would obviously outperform GAs. In addition to this, for an objective function whose overall behavior is increasing or decreasing with some slight counter directional steps, finite temperature Monte Carlo methods or simulated annealing should be the preferred optimization methods. However, if the topology of the objective function is very complicated or if there is not enough information about it, GA may be a good choice to try. In the article of Mitchell at al. [17], GA is compared with traditional hill climbing for some different objective function landscapes and some comments are made about the effect of objective function landscape on the efficiency of GAs.

2.1. Representation

Solution candidates, being the individuals of a population in the prepared artificial environment, should be represented as a compact encoding of parameters whose values are adjusted to span all the relevant solutions of the system. In the history of GAs, binary representation which is a string composed of ones and zeros only, has been used solely for a long time. This representation had been preferred probably because of its resemblance to the DNA encoding in biological systems. The idea is that if a representation similar to the DNA encoding is used, then genetic operations such as mutation and crossover can also be applied similar to the cases in biological systems, mutation being an alternation of a bit from 1 to 0 or vice a versa and crossover being merging parts of the strings to form a new one. Figure 1 can be seen for an illustration of binary strings and genetic operations of mutation and crossover.

Different representation schemes may be developed considering the properties of specific problems. These special representation schemes allow more convenient application of genetic operations also developed considering the problem specifications.

Figure 1. Mutation and crossover operations are shown on binary strings of 8 bits length. Red bits show mutation operation of alternating bits and last line shows the child individual formed by crossover operation of merging parts of parent individuals

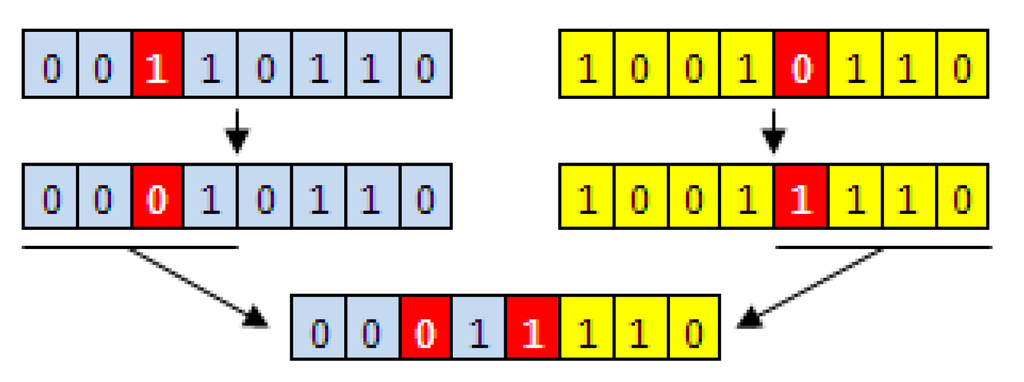
Figure 1. Mutation and crossover operations are shown on binary strings of 8 bits length. Red bits show mutation operation of alternating bits and last line shows the child individual formed by crossover operation of merging parts of parent individuals

2.2. Variation generation

Mutation and crossover mentioned above are variation generating processes that we see in biological systems and they can be included in our artificial environment for having individuals evolving with slight changes. These two processes of mutation and crossover have different roles in satisfying the variation. While mutation alters a specific property in a randomized manner supplying new alternatives to the simulation environment, crossover merges properties of the two individual solutions in order to form a new one which has the potential to utilize the good properties of the parent individuals.

Genetic operations of mutation and crossover as stated above, being applied on the genes of individuals, are generally applicable for all kinds of GAs and are called as genotype operators in the article of Pullan [18]. Phenotype genetic operators, on the other hand, are designed by considering certain properties of the studied problem and therefore they alter individuals in a more controlled manner. In the above cited article of Pullan, these two kinds of genetic operators are compared extensively on the atomic cluster problem and phenotype operators have found to be more efficient. Genotype operators as simple alternation of bits on binary strings may seem to be better representations of genetic operations of biological systems acting on DNA. However, detailed examination would show that mutation and crossover in biological systems is not so simple and therefore random alternation of bits on binary strings does not reflect all the properties of these processes happening in nature. Considering the mating in biological systems, children inherit most of the parent properties and thus they are usually very similar to their parents [19,20]. This high inheritance property can not be achieved by the genotype crossover operator of merging parts of strings in totally randomized manner for all problems. However, carefully designed phenotype crossover operators can satisfy this high inheritance property and therefore increase the efficiency of GAs as stated in the article of Pullan. Likewise, phenotype mutation operators changing certain properties of individuals may be designed for the specific problems being studied. Phenotype mutation and crossover operations for the geometry optimization problem of nanoparticles will be discussed broadly in Section 3.

Mutation and crossover are used as complementary operations in most contemporary GA applications. However, their separate effects on the optimization process are most of the time not well understood and there is controversy about the relative importance of these operations and about make a choice between two [21,22]. General belief is that, mutation alone is more efficient for simple problems but two operations should be used together for more sophisticated problems. Observation from the natural evolution also supports this belief since mutation precedes crossover in the history of evolution where the evolution process started with very simple living organisms facilitating single parent reproduction which is still being used by many kinds of single celled organisms. The necessity of crossover for the relatively simple problems such as TSP and geometry optimization problem of nanoparticles may be said to be an arguable issue considering the fact that these simple organisms, being still much more complex compared to our model systems studied by GAs, survived until our time with good adaptation capability without any need for crossover between individuals.

2.3. Selection

These two variation generating processes do not always yield individuals which are better adapted according to the fitness criteria and therefore a selection mechanism is also needed to pick up better solutions from a pool of new born individuals. Natural selection is the term used in biological systems for this selection mechanism, explaining some strange behavior observed in nature such as a bird not feeding her weakest baby in a situation of low resources. In the case of GAs, selection is made according to the fitnesses of the individuals usually in a probabilistic manner. That is, individuals having higher fitnesses do have greater chances of being selected. The probabilistic property of the selection mechanism reflects the random effects observed in nature such as the strongest tiger in the forest being killed in an unexpected fire. These random effects in fact increase the efficiency of GAs by avoiding the population being evolved rapidly to an undesired half optimized situation and stop evolving there. In more technical terms, randomness helps GAs to jump over local extrema mentioned in the previous section, allowing the algorithm to continue searching for the global extremum when a local extremum is reached without being trapped to it.

In biological systems, the definition of successful individuals and species may depend on the environment and it may also change with time. However, some general specifications such as adaptation capability, intelligent use of the resources and also, starting with Homo sapiens, the ability to change environment according to the current needs can be counted as ingredients of the fitness criteria in nature. Likewise, it is usually possible to define a fitness criterion considering the problem at hand using scientific facts or observation and experimenting. A good choice of fitness criterion should be a simple function of parameters defining the individuals and could be calculated easily for all possible solutions of the problem. For the famous problem of the traveling salesman, fitness criteria should rely on the lengths of possible paths connecting the cities and the fitness should be higher when the length is shorter.

Roulette wheel selection and tournament selection are commonly used selection mechanisms [23] both respecting the fitness criteria by different means. In the roulette wheel selection mechanism, the probability of an individual being selected is proportional to its fitness value and therefore fitness criteria should be chosen with care in this selection regime. Numerical values of fitnesses of the individuals should not be very close to each other for the roulette wheel selection to function properly. A higher order polynomial or an exponential form function may be used to arrange the fitness values to not be very close to each other. In the alternative tournament selection regime, the exact fitness value is not the decisive factor but selection is made according to the order of the fitness values. Certain number of individuals are chosen to form a tournament pool and the fittest individuals whose number is determined according to the reproduction type of GA, are picked from the pool to form a child. A privilege for some small number of fittest individuals, called as elitism, may be applied in the selection process to reduce the probability of losing fittest genes from the pool. The fittest individual may always be selected as a simple and common example of elitism.

2.4. Reproduction

A certain number of individuals are selected in each GA step according to the fitness criteria chosen for the problem while remaining eliminated individuals are being killed. These selected individuals should be subjected to some sort of reproduction in order to keep the population size constant. The ratio of selected individuals is a variable parameter which should be tuned to increase the efficiency of GA for the specific problem being studied and type of the selection together with reproduction being sexual or single parent should be decided. While two or more parents are used in sexual reproduction to form new generations by the crossover of genes, one individual is cloned in the single parent reproduction scheme [24]. All the variations are generated by mutations in single parent GAs since no crossover between individuals is made. Therefore, mutation ratio should be chosen to be very high in single parent GAs.

The reproduction process supplies new individuals to the population and hence increases the diversity. However, if there is the possibility of supplied individuals becoming very similar to the old ones accidentally, this diversity increasing property may not function properly and all individuals may become very similar as time passes. Therefore, a control mechanism may also be added to the reproduction process to eliminate those new individuals which are practically the same as one of the parent individuals. An example of this elimination can be seen in the work of Hartke [25].

2.5. Lamarckian GAs

An enhancement for GAs is the application of local optimization routines in each GA step in order to reduce the search space to the possible local minima configurations. This technique is proven to be efficiency improving in spite of the extra time needed for the local optimization. GAs using this trick have the property of Lamarckian evolution since the individuals develop properties during their lifetime and pass them to new generations.

Local optimization is a highly time consuming process and it takes almost all of the computation time in Lamarckian GAs. However, local optimizations of separate individuals are totally independent from each other and therefore Lamarckian GAs are very suitable for parallel processing. Individuals may be distributed to available computing nodes prior to the local optimization step and the optimized individuals may be gathered at the master node for the application of genetic operations for a Lamarckian GA implementation with parallel processing. Very efficient parallel algorithms may be designed in this way since the communications between computing nodes are negligible.

It is currently well known that biological individuals do not pass their developed properties to next generations and therefore direct Lamarckian evolution is not a natural phenomenon. However, an individual who developed adaptive properties especially during early lifetime would have a higher probability of being selected by nature and consequently he has a higher probability of giving offspring. Therefore, developed properties have an indirect effect on the evolution process and Lamarckian evolution is not something totally against the current view about the evolution theory. Beside this, its positive effect on efficiency of GAs is proven by many applications. Further information about Lamarckian GAs can be found in the reference [26].

2.6. GA parameters

A typical GA has some parameters to be tuned about the application of genetic operations mentioned above [27]. Representation length, population size, mutation and crossover ratios, number of elite individuals and ratio of selected individuals are the most important ones of such parameters affecting the efficiency of the method. While, insufficient number of individuals causes low variety among the population and makes it harder to search all the configuration space, an over-populated simulation would slow down the computation without further gain. Low mutation and crossover ratios again reduce the variety and very high values of these parameters distort optimized individuals a great amount causing loss of properties gained during the optimization. There would be some other parameters about the details of the selection mechanism and other genetic operations depending on the specifications of the GA whose values should be decided with care according to the problem being studied. Finding suitable values for the parameters and deciding about the kinds of the genetic operations are the most difficult part of a GA implementation and they should be decided considering the properties of the studied problem since there are no generally applicable rules about these decisions. There are also some attempts to design GA codes that optimize their own parameters during the simulation and these kinds of algorithms may be classified in the field of artificial intelligence. Parameters of the GA are also encoded in the individuals of the GA in these self adaptive GAs [27,28,29] as an addition to the normal encoding for the properties of the individuals in traditional GA formalism.

3. GAs for geometry optimization of nanoparticles

The geometry optimization problem of nanoparticles can be stated as the problem of finding the most stable structure of the physical system composed of a certain number and types of atoms or molecules. The extremum rule manifests itself for this problem as the fact that the most stable structure of the molecule corresponds to the configuration of atoms with minimum total energy. Interactions between atoms or the molecules can be modeled with a good approximation using empirical potential energy functions (PEFs) [30,31,32] ignoring their complicated inner structures. With a further assumption that stable structures of nanoparticles do not include moving atoms which is actually true for the systems that are relevant for chemical physics, we can state the extremum rule as the minimum potential energy for atomic and molecular systems. Hence, an optimization algorithm should be used in order to minimize the potential energy of the system for the solution of this problem. There are some simple optimization routines such as Newton-Raphson and conjugate gradient that can be tried for solving this problem. However, a good initial guess should be supplied for these methods since the best thing they can do is to find the closest local minimum around the initial guess. Considering the fact that even small molecules with dozens of atoms have millions of stable isomers corresponding to local minima [33], it is obvious that local optimization can not solve this problem and we need something more sophisticated. GA is suitable for the solution of this problem since its intelligent search technique focuses on the regions of the configuration space where the possibility of finding the global minimum is relatively higher.

There are a vast number of studies using GAs for the geometry optimization problem in the last decade [18,19,20,24,25,26,34,35,36,37,38,39,40,41,42,43,44,45,46,48,49,50] using some sort of enhancements developed for this problem and some recent GA applications are given in the references [51,52,53,54,55,56,57,58,59]. A single parent GA application can be seen in the reference [24]. Broader discussion about application of GAs to the geometry optimization problem can be found in the references [6,33,39,44].

GA enhancements for the geometry optimization of nanoparticles are described below in separate subsections:

3.1. Floating point array representation

The preferred representation type for the problem of molecular systems is floating point arrays of atomic positions instead of binary strings since it allows non-discrete continuous positions which increases precision especially for sharp PEF landscapes. Usage of floating point arrays as a representation for the geometry optimization problem was introduced by Zeiri in his study for predicting lowest energy structures of Ar_nH₂ clusters [34]. Some other studies facilitating this continuous representation can be seen in the references [19,35,36,37,38]. As stated in Section 2.1., floating point array representation allows applications of phenotype genetic operations (see next section) considering the nanoparticle geometry in a more convenient way and it avoids the necessity for decoding and encoding the atomic coordinates.

3.2. Phenotype genetic operations for geometry optimization problem

Some knowledge about the physical system makes it possible to design more effective phenotype mutation and crossover operations as stated in Section 2.2. Geometric mutation operations such as particle permutation, particle displacement, piece rotation, piece reflection [18,24,39] have been developed for the molecular geometry optimization problem:

• Particle permutation : Positions of two or more particles are exchanged. This mutation technique is used for heteronuclear nanoparticles.
• Particle displacement : Positions of one or more particles are modified slightly in a randomized manner.
• Piece rotation : One part of the nanoparticle is rotated a certain amount around a chosen axis. Axis and rotation amount are usually determined randomly. This mutation technique is preferred for atomic or molecular clusters having spherical shapes.
• Piece reflection : One part of the nanoparticle is exchanged with a reflection of the same part or another part of the nanoparticle.
• Shrinkage : Size of the nanoparticle is shrank by multiplying atomic coordinates with a factor less than unity.

There is also one geometric crossover operation being preferred mostly for the spherical shaped atomic clusters, called cut and splice, in which two nanoparticles are cut from their halves arbitrarily and half of an individual nanoparticle is merged with half of the other individual nanoparticle to form a child (see Figure 2) [19]. In a variant form of this crossover technique, quadrant or orthant of a nanoparticle is merged with a remaining sized part of another nanoparticle as described in the reference [18]. Efficiency of cut and splice crossover may be increased by determining the cutting plane considering lower and higher energy regions of the nanoparticle. Merging lower energy halves of two nanoparticles would increases the fitness of emerging child. 10-20% efficiency increment is observed in the study of Hartke [40] by the usage of this enhancement in the application of cut and splice crossover.

Direct application of the cut and splice crossover to the nanoparticles having two or more types of atoms would modify type ratios and would therefore not be appropriate. For this reason, cut and splice operation should be applied with extra care for heteronuclear nanoparticles as described in the article of Darby et al. [37] in order to preserve type ratios.

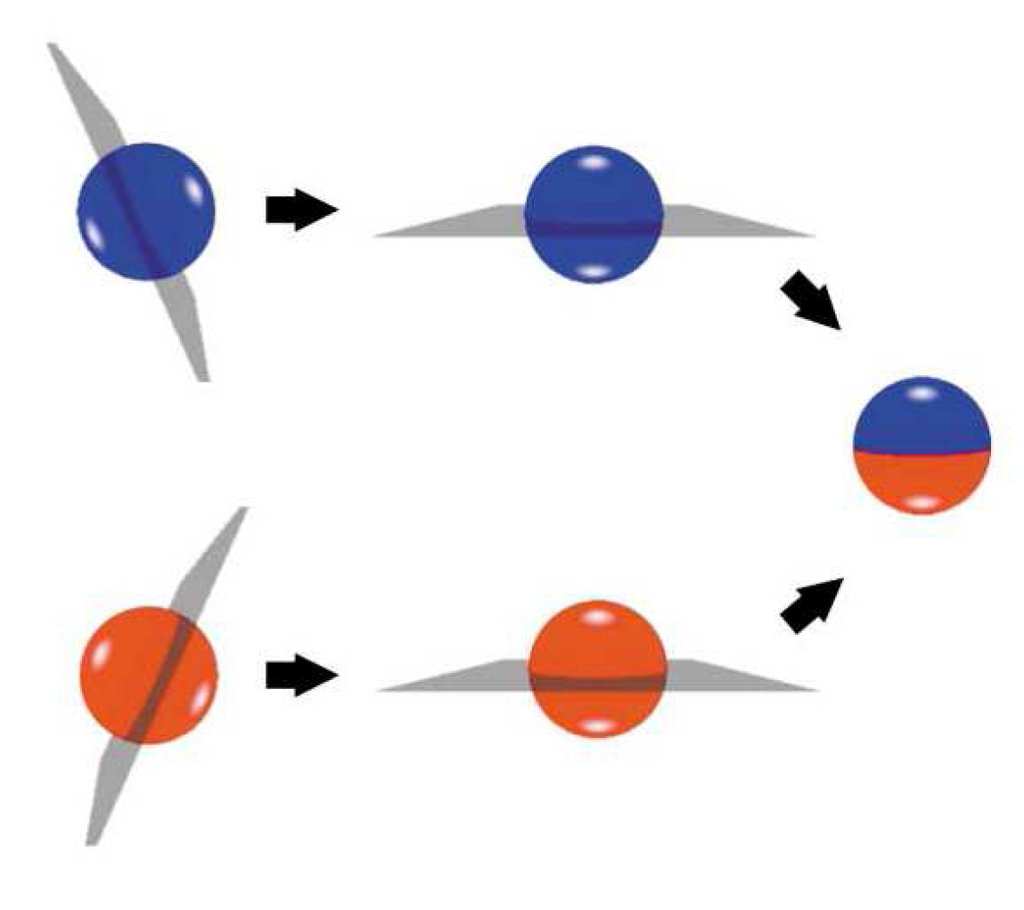
Figure 2. Illustration of phenotype cut and splice crossover operation developed by Deaven and Ho [19].

Figure 2. Illustration of phenotype cut and splice crossover operation developed by Deaven and Ho [19].

3.3. Local relaxation

Lamarckian feature is added to GAs for the nanoparticles as some sort of local relaxation of individual nanoparticles in each GA step. Application of this enhancement started with the work of Gregurick et al. in 1995 [41] in which conjugate gradient type local relaxation is used. Conjugate gradient method is used also in the works of Deaven and Ho [19] and Rata et al. [24] while an alternative local relaxation method, Nelder-Mead simplex local search, is used in the works of Iwamatsu [36] and Sastry and Xiao [42] and limited memory BFGS subroutine is used in the works of Hobday and Smith [43] and Zhao and Xie [44].

Even though these deterministic local relaxation routines are mostly preferred for the geometry optimization problem of nanoparticles, stochastic methods such as Monte Carlo and simulated annealing may also be used for local relaxation in GAs [45,46]. They may be more advantageous since some of the local minima are eliminated by these stochastic methods and therefore search space of the GA reduces even further.

4. Single parent parallel Lamarckian GA implementation

A single parent GA implementation has been developed recently by the current authors in order to study new developments on the GA methodology for atomic clusters [47] and also for possible application considerations [20]. Single parent GA is preferred in order to test the argument mentioned in Section 2.2. about the necessity of crossover for these kinds of problems. Performance of the method in the applications on the carbon clusters and SiGe core-shell structures suggests that single parent GAs can perform very well and thus crossover is not the key point of evolutionary algorithms for the problems with this much complexity.

4.1. Method overview

The preferred representation type for this implementation is floating point arrays of atomic coordinates and phenotype mutation operations designed for the cluster optimization problem are used for variation generation. 100% mutation ratio is used since all the variations are generated using mutations in this single parent GA without crossover between individuals. Half of the individuals are selected in each GA step using roulette wheel selection and selected individuals are cloned in order to keep the population size constant. A polynomial form fitness function as V¹⁰, V being the potential energy of the molecular system, is used in the roulette wheel selection mechanism since potential energies of different isomers are usually very close to each other. The fittest five individuals are selected certainly for elitism and the fittest individual obtained so far during the optimization process is not allowed to mutate in a way that reduces its fitness value. Classical Monte Carlo method is used as the local optimizer in each GA step for all individuals, causing the method to be a Lamarckian GA.

Two phenotype mutation operations considering geometries of atomic clusters are used in this implementation for variation generation. First one, called as piece rotation, is applied as a random rotation of one half of the cluster in which the rotation axis changes in sequential order between three major axes and the rotation amount is determined randomly for each individual cluster. This phenotype mutation operation facilitates the knowledge that atomic clusters usually have spherical shapes and therefore modifies optimized structures slightly. Second mutation operation is shrinkage of cluster size by multiplying all atomic coordinates with a factor less than unity. Consequently, the local optimization process becomes an inflationary motion for the atoms in the cluster, increasing the efficiency of local optimization for spherical shaped atomic clusters especially for the cage like fullerenes formed by carbon atoms. Shrinkage amount is a parameter which can be tuned according to the size of the cluster being studied.

4.2. Algorithm layout

Parallel GA implementation for atomic clusters which is written using C₊₊ object oriented programming language and MPI parallelization library, may be summarized as follows:

• Population initialization : Each computing node initializes a number of (populationSize / numberOfNodes) individual atomic clusters by generating random positions for the atoms in a cubical box of a certain size which is smaller than the expected size of the cluster.
• GA loop

  -

  Local optimization : Each individual cluster is relaxed by the MC local optimizer at the computing node initializing the cluster.

  -

  Gathering at master node : Atomic coordinates and potential energy values of locally optimized clusters are gathered at the master node by MPI communication.

  -

  Selection : Half of the individuals are selected by roulette wheel selection with elitism using the fitness function V¹⁰. The number of GA steps with no progress in the potential energy of the fittest individual is counted and when this number reaches a certain amount, an alternative selection mechanism is applied in which all the individuals are transformed to the fittest individual.

  -

  Termination check : Number of alternative selection mechanism loops with no progress in best fitness value is counted. When this number reaches a certain amount GA loop terminates.

  -

  Variation generation : Phenotype mutation operations of piece rotation and shrinkage are applied on the selected individuals.

  -

  Distribution of individuals : Individual clusters are distributed to available computing nodes by MPI communication for local optimization.

• Output : Atomic coordinates and potential energy value of the fittest individual are given as the output of GA implementation.

An illustration of the method is given in Figure 3 for the C₂₀ cluster in which three GA steps of the evolution of the fittest individual winning the competition is given ignoring some intermediate GA steps. This illustration is for the evolution of a single individual and therefore natural selection and reproduction steps are not shown.

4.3. Application on carbon clusters

The single parent parallel GA implementation summarized in previous section has been applied to moderate sized carbon clusters for benchmarking purposes [20]. Carbon clusters are suitable for testing the method since it is well known that the global energy minimum geometry of carbon clusters can not be found by local relaxation. Directional bonds between carbon atoms results in high energy barriers between different isomers of the molecule [19] making the optimization process tricky also for global optimization methods. Comparison of the single parent GA with a GA facilitating crossover between individuals suggested that single parent GAs are also promising for the geometry optimization problem of nanoparticles.

Brenner potential energy function (PEF) [60] has been used to define the two-body and three-body interactions between carbon atoms forming clusters ranging from 3 atoms to 38 atoms. Population size of the GA has been chosen to be 32 individual clusters for the reasons of both this number being close to the optimal population size for this problem and for it is being suitable for parallelization. Multiplication factors varying between 0.5 and 1.0 are used in the shrinkage mutation operation. While a multiplication factor of 0.5 shrinks the cluster to half its size, a factor 1.0 leaves it unchanged. Shrinkage operation is found to be efficiency increasing for the carbon clusters having more than 20 atoms since they form cage like structures and the optimal value of multiplication factor increases as the cluster size goes up from 20 atoms. Images of some optimized carbon clusters are given in Figure 4 as examples together with their symmetry groups if applicable. The rest of the images can be seen in the original article of the current authors cited above [20].

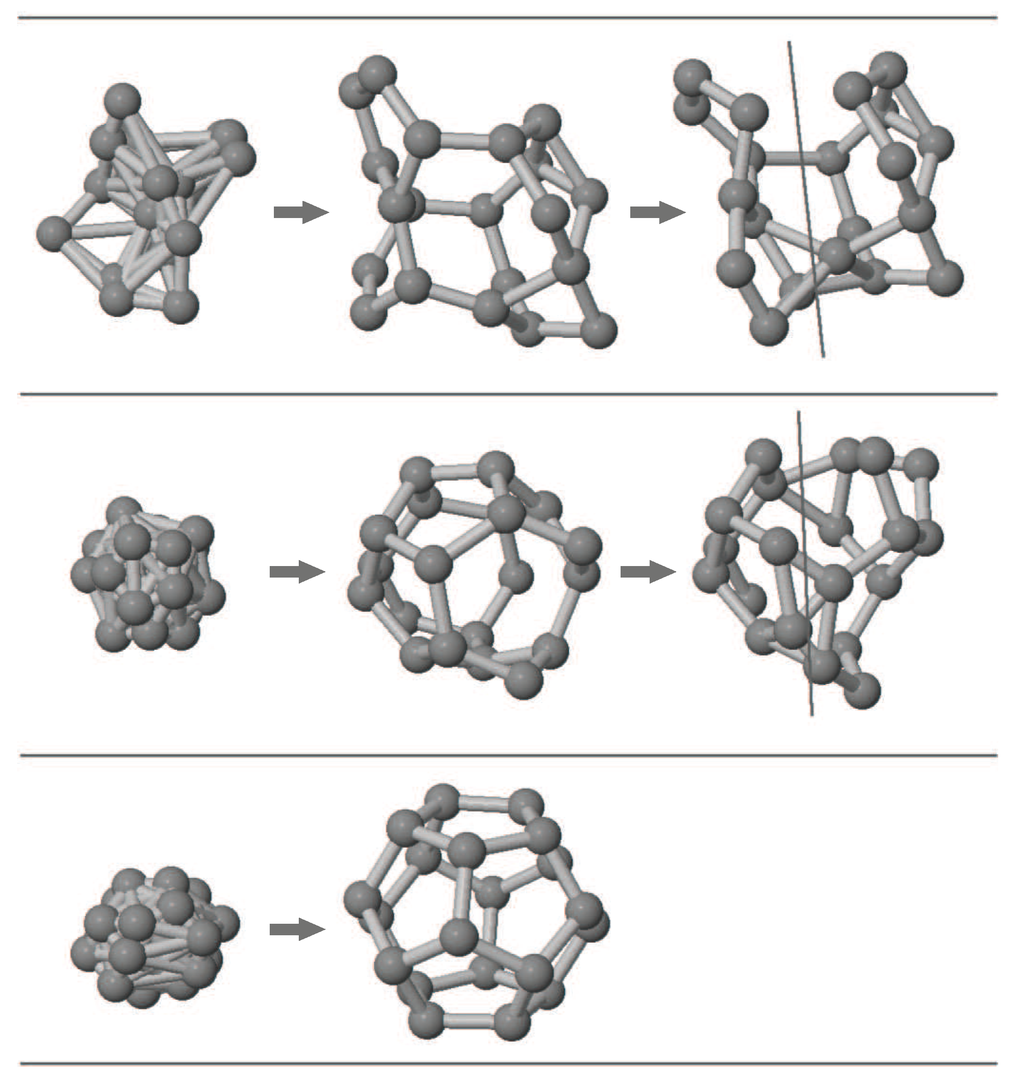
Figure 3. Illustration of the single parent GA implementation showing evolution of the fittest individual in C₂₀ optimization. Three GA step samples are shown in separate lines ignoring some intermediate GA steps. 1. Column shows the cluster just after the shrinkage mutation operation (initial geometry in top line), 2. Column shows the result of local optimization and 3. Column shows the cluster after the piece rotation mutation step together with the cutting plane.

Figure 3. Illustration of the single parent GA implementation showing evolution of the fittest individual in C₂₀ optimization. Three GA step samples are shown in separate lines ignoring some intermediate GA steps. 1. Column shows the cluster just after the shrinkage mutation operation (initial geometry in top line), 2. Column shows the result of local optimization and 3. Column shows the cluster after the piece rotation mutation step together with the cutting plane.

Optimized geometries of carbon clusters have been compared with the results of another GA study [43] and the results of these two studies agree on the fullerene geometries of the clusters with number of atoms even and larger than 20 except the case of 36 atoms for which different isomers of the corresponding fullerene structure is found by the two methods. This agreement on the fullerene structures suggests that the GA implementation described in the previous section works fine for moderate sized carbon clusters. There is some inconsistency in the results of the two methods for small carbon clusters as a consequence of the slight difference in the PEF used which was discussed in the original article.

A very small number of GA steps are observed in the application of carbon clusters for the single parent Lamarckian GA used. Lamarckian property of the GA is responsible for reduction of GA step number since it reduces the search space a great amount. Comparison of the number of GA steps for the C₂₀ cluster with the other GA method mentioned above which also has the Lamarckian property (13 in authors work and 800 in the comparison work) suggests that MC optimization used in the current GA may have some advantages compared to deterministic local optimization routines even though single MC local optimization is more time consuming.

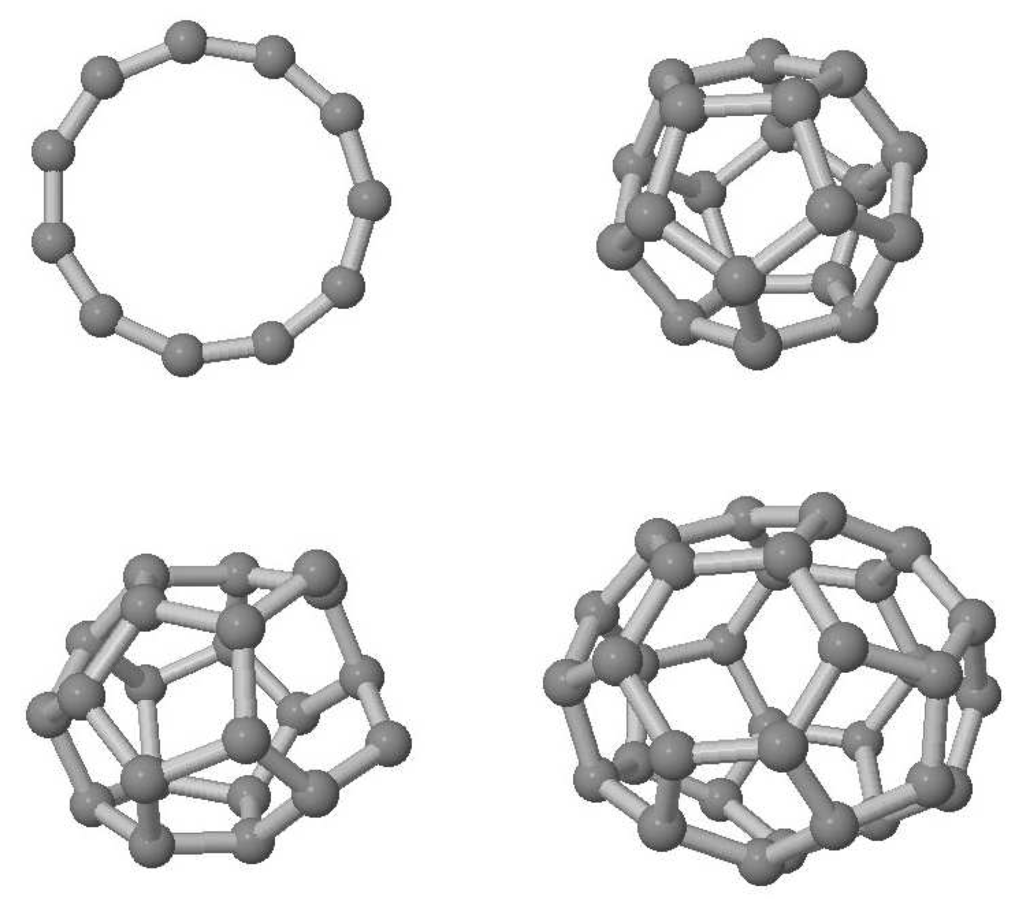
Figure 4. Optimized structures of carbon clusters. Top line: 11 atoms, 20 atoms (I_h symmetry); Bottom line: 22 atoms, 32 atoms (D₃ symmetry)

Figure 4. Optimized structures of carbon clusters. Top line: 11 atoms, 20 atoms (I_h symmetry); Bottom line: 22 atoms, 32 atoms (D₃ symmetry)

4.4. Application on silicon germanium core-shell structures

GA implementation has been applied on the core-shell structures of SiGe heteronuclear clusters when the benchmark on carbon clusters is completed [61]. The main objective of this application is comparing Si-core, Ge-core and mixed structures in order to understand the preference of SiGe clusters when these three alternatives are considered. More information about nanoalloys can be found in the reference [59].

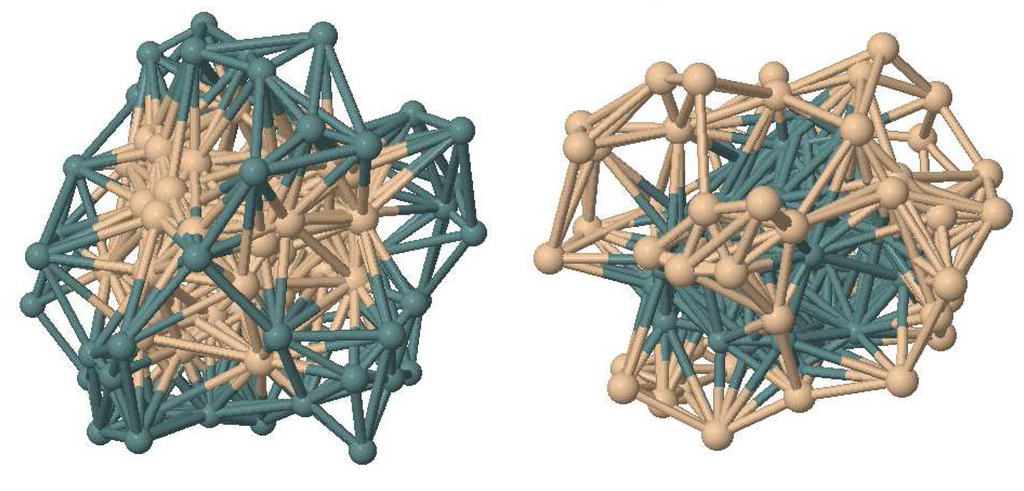
Figure 5. Initial core shell geometries of the Si₅₀Ge₅₀ cluster.

Figure 5. Initial core shell geometries of the Si₅₀Ge₅₀ cluster.

Stillinger Weber PEF [62] has been used to define Si-Si, Si-Ge and Ge-Ge interactions in the clusters. 100 atom and 150 atom clusters have been studied with three different type ratios and subjected three structures which are Si-core, Ge-core and mixed atoms have been used as initial geometries as separate run instances. Si₂₅Ge₇₅, Si₅₀Ge₅₀ and Si₇₅Ge₂₅ clusters have been studied in 100 atom case and Si₅₀Ge₁₀₀, Si₇₅Ge₇₅ and Si₁₀₀Ge₅₀ clusters have been studied for 150 atom case. Si-core and Ge-core initial geometries for Si₅₀Ge₅₀ cluster is shown in Figure 5 for exemplification. Population size has been chosen to be 16 and 24 individuals for 100 atom and 150 atom clusters respectively. Value of the shrinkage factor is not crucial for SiGe clusters and thus it has been fixed to the value of 0.7 for all separate run instances.

Finding global minimum is beyond the capabilities of the described single parent GA implementation when 100 atom and 150 atom heteronuclear clusters are considered. Nevertheless it was helpful to decide about the preference of SiGe clusters between Si-core, Ge-core and mixed geometries. When the population was initialized with Si-core geometry clusters, individual clusters conserved the Si-core geometry during the GA optimization process and final geometries are again totally in the form of Si-core Ge-shell. However, when Ge-core initial geometry was used for individual clusters, initial core-shell structures become distorted during GA optimization and some Ge atoms reach the surface at the end of the optimization process and mixed initial geometry runs concluded with Si rich cores and Ge rich shells. These results have been obtained regardless of the atom type ratios and therefore, it has been concluded that SiGe clusters prefer Si-core Ge-shell structures. Images of the final geometries may be seen in Figure 6 for Si₂₅Ge₇₅ (initial Si-core), Si₅₀Ge₅₀ (initial mixed) and Si₇₅Ge₂₅ (initial Ge-core) clusters. Tendency of Ge atoms for going up to surface can be seen clearly in these images.

Figure 6. Optimized structures of Si-core initial geometry Si₂₅Ge₇₅ (left), mixed initial geometry Si₅₀Ge₅₀ (middle) and Ge-core initial geometry Si₇₅Ge₂₅ (right) clusters .

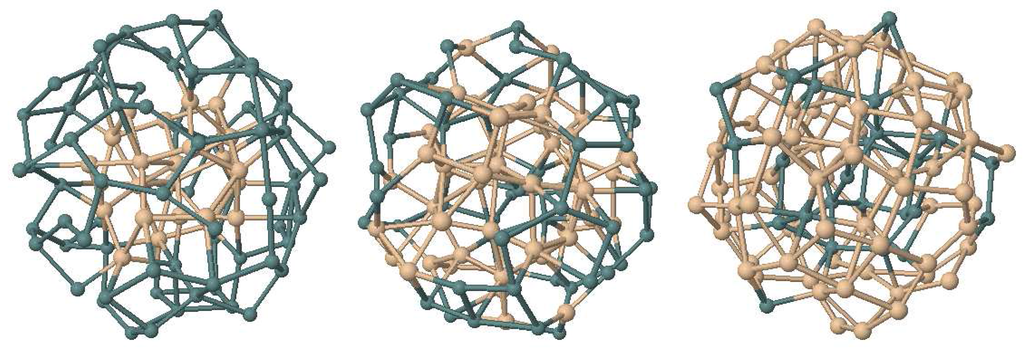
Figure 6. Optimized structures of Si-core initial geometry Si₂₅Ge₇₅ (left), mixed initial geometry Si₅₀Ge₅₀ (middle) and Ge-core initial geometry Si₇₅Ge₂₅ (right) clusters .

5. Discussion and guidelines

GAs are well suited for the geometry optimization problem of nanoparticles. However, their application is not straight forward and should be carried out with care considering the properties of the studied system. On the other hand, particularly using empirical PEFs, the method of optimization is not the only critical factor but the type of interaction PEF can also affect the result of optimization. For the same system different PEFs may give different results [49].

As stated in Section 2.6., GAs have parameters to be tuned about the representation, selection and application of variation generating genetic operations mutation and crossover. The difficult part of doing a GA application is deciding about genetic operations for specific problems and tuning related parameters. For small systems GA is most probably not a good choice but basin hoping, Monte Carlo and simulated annealing methods might be preferred. While general purpose GA optimizers included in common mathematical package programs can be tried for small and moderate sized nanoparticles, phenotype genetic operations and floating point array representation developed for the geometry optimization problem of nanoparticles should be preferred for GA applications in this field for large scale applications.

Unfortunately, there are no generally applicable guidelines for deciding about the genetic operations and parameters. However, for the geometry optimization problem of nanoparticles, common sense suggests using floating point arrays as the representation scheme and preferring variation generation operations considering expected geometries of studied nanoparticles. Importance of mutation and crossover may vary depending on the problem size and crossover may not be crucial for the nanoparticles of all ranges. Since roulette wheel selection considers exact numerical values of fitness criteria, objective function should be chosen with care for this type of selection mechanism and tournament selection should be preferred if there are doubts about the chosen objective function.

The idea of a population with social network used in particle swarm optimization [63] may be combined with GA concept. Selection of the individuals may be carried out considering fitnesses of neighbor individuals beside individuals’ own fitnesses. Efficiency of GA may be improved this way especially for large systems of nanoparticles.

A GA package with a convenient user interface towards applications for nanoparticles including all the enhancements for this specific problem is highly desirable. It would provide a working environment for GA developers for the geometry optimization of nanoparticles and would be a useful tool for the applications in nanoscience. Self adaptive property would be crucial for this GA package which may help in the difficult task of parameter tuning.