Self-organization of Dynamic Distributed Computational Systems Applying Principles of Integrative Activity of Brain Neuronal Assemblies

Abstract

This paper presents a method for self-organization of the distributed systems operating in a dynamic context. We propose the use of a simple biologically (cognitive neuroscience) inspired method for system configuration that allows allocating most of the computational load to off-line in order to improve the scalability property of the system. The method proposed has less computational burden at runtime than traditional system adaptation approaches.

1. Introduction

The adaptation of the computing systems requires execution of computationally complex algorithms at runtime. We propose to use a simple technique for system self-organization, where most of the computational burden for system adaptation is allocated to the design time.

The distinguishing features of distributed computing systems under investigation are their dynamicity and operating environment uncertainty. Therefore, the adaptation mechanism should be introduced to the system for coping with the dynamics and uncertainty [23]. Large scale personalized mobile applications and services with the evolving functional and non-functional requirements that operate in a changing context are examples of the dynamic computing systems under investigation.

We are going to design a system that will serve as a platform for the applications that adapt their behavior according to the current needs of end-users and take into account the context of the environment. By the context, we mean such parameters of the environment as the current time, the users’ location and preferences, and 3^rd party services available. A large variety of the end-user-cases and scenarios has been suggested in [20, 21, 18].

We employ a systems reconfiguration method to enable system adaptation. By reconfiguration, we mean addition of new components to the system and removing others for fulfilling functional and non-functional requirements.

Two alternative methods for system adaptation are described. The first approach is based on the centralized feedback control [3], where the dedicated decision making body collects requirements to the system, estimates current state of the system, and proposes an adaptation process for achieving the desired goal. After many attempts to find the best way for algorithm optimization, we opted for Cognitive Neuroscience field. The Fingelkurts brothers have in their experimental work provided evidence for some form of dynamic reconfiguration in neural tissue, which has been generalized within the Operational Architectonics framework of brain-mind functioning [5, 6, 7, 8, 9]. Here we intend to design a computing system that will similarly permit dynamic reconfiguration in a given domain of application – the Intelligent Services Broker.

2. Intelligent Service Broker

Authors propose the Intelligent Services Broker (ISB) as a reference example of an adaptive computing system. The goal of the ISB is to aggregate the information about available services in the information space and deliver the best quality of service (QoS) for consumers that are placed in a certain context by means of intelligent services composition.

At the initial step, the available services and consumers shall be provisioned in the ISB. Service providers have to present profile description for what they offer. These profiles contain description of the service functionality and the context required for services to operate. Consumers fill-in their static profile with demographic data, interests and preferences; in addition to that, the ISB collects dynamic data about subscribers. Users’ geographic coordinates, their services consumption behavior and other types of context information can be collected for better targeting of the services promotion.

At runtime, the ISB analyses the current context for subscribers and their requirements, and optimizes the services composition offer for delivering the best QoS in the present situation taking into account resources available for the system.

The users’ requirements can be defined explicitly, for example, expressed verbally or entered as a plain text; and implicitly – derived from the users’ preferences.

The ISB is architecturally decomposed for two layers, see Figure 1. Network infrastructure, required hardware, and available sensors are depicted at the bottom layer. On the upper abstraction layer one can see a collection of the software components that serve as a mapping of the available services, sensors, and registered end-users to the virtual space. In other words, each consumer has its digital software agent as well as every sensor, and all services offered by the service providers.

The software components organize clusters dynamically on demand for collaborative work in order to fulfill the needs of subscribers. For example, on the diagram we can see a cluster of red colored components that represent a service composition for the correspondent red-colored consumer.

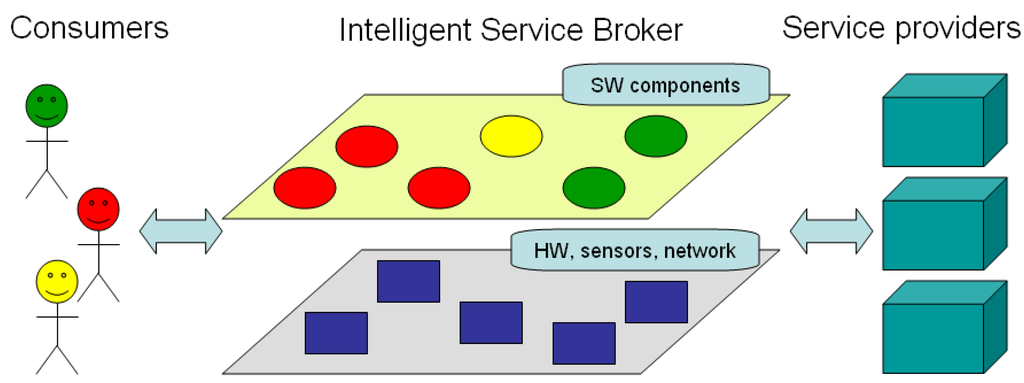
Figure 1. Concept architecture of the Intelligent Services Broker ISB. Similarly colored SW components represent clusters that serve to the equally marked consumers. SW – software, HW – hardware.

Figure 1. Concept architecture of the Intelligent Services Broker ISB. Similarly colored SW components represent clusters that serve to the equally marked consumers. SW – software, HW – hardware.

Let us consider an illustrative end-user scenario where the ISB helps subscribers with their everyday life issues. An ISB subscriber Alex is walking in a city’s downtown. He is carrying a mobile device that connects him to the virtual information space managed by ISB. Alex stated in his profile that he is interested in the topic of self-organizing systems and would be interested to meet new buddies with similar interests. Passing by the bookstore that is provisioned in the ISB, Alex receives a notification message regarding the sale in the shop and availability of the items of his interest.

After entering the bookstore Alex is able to read the virtual messages left there by other customers that also involved in the same research. The virtual messages are posted in a certain situation. The message originator defines the condition in which the message can be read. In our use-case, message has been left in the bookstore, and can be accessed at certain time by selected group of people.

With support from ISB, the software agent “alex” is forming a cluster with the “bookstore”, “positioning sensor” and the “virtual bulleting board” software components for delivering the relevant services experience for the user. After some time, Alex is leaving the store and going to a meeting with his friends. The ISB is providing a trip navigation service; therefore the cluster is to be reconfigured according to the new context and needs.

The following sections of the paper are devoted for description and comparison of alternative mechanisms for the intelligent services composition.

3. Model description

A system consists of a number of components. The components are joined together to solve a problem assigned to the system.

System S is a collection of components C_j, where j is from 1 to N. M is the number of available components, N is the number of components in the system, M >= N.

The state of the system is denoted by vector X. Input (requirements) to the system – Y. The external unexpected disturbances to the system are denoted by the vector D (Figure 2).

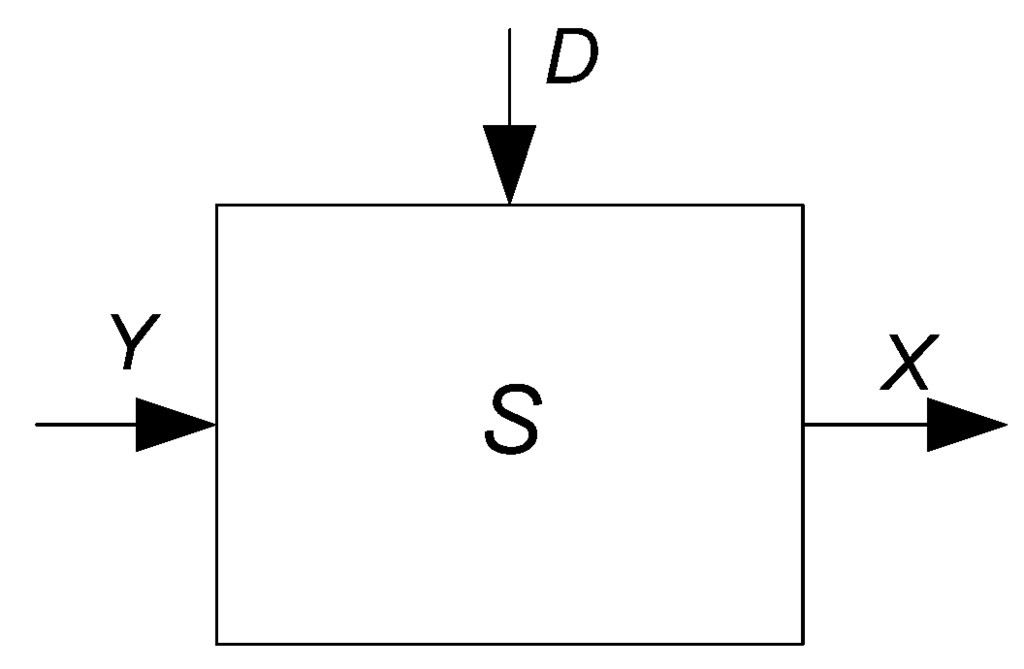
Figure 2. System is operating in a dynamic environment, where Y is the input, X is the state, D denotes the unexpected disturbances.

Figure 2. System is operating in a dynamic environment, where Y is the input, X is the state, D denotes the unexpected disturbances.

The system is dynamic – S(t), where t is time. S is an adaptive system. The adaptation is accomplished by means of structural reconfiguration where a set of the system’s constituent components is changing over time.

The following two operations are introduced over the set of components of S(t):

• Op1: “add component” to the system
• Op2: “remove component” from the system

The set of operations can be extended with two more operations such as “add connection” and “remove connection” between the components. In that case, flexibility for system reconfiguration increases significantly, but at the same time search of an optimal configuration becomes more demanding.

Available configurations of a system of three components A, B, and C, are presented in Figure 3.

Figure 3. Possible states of a system of three components A, B, C; “–“ stands for empty set with no active components.

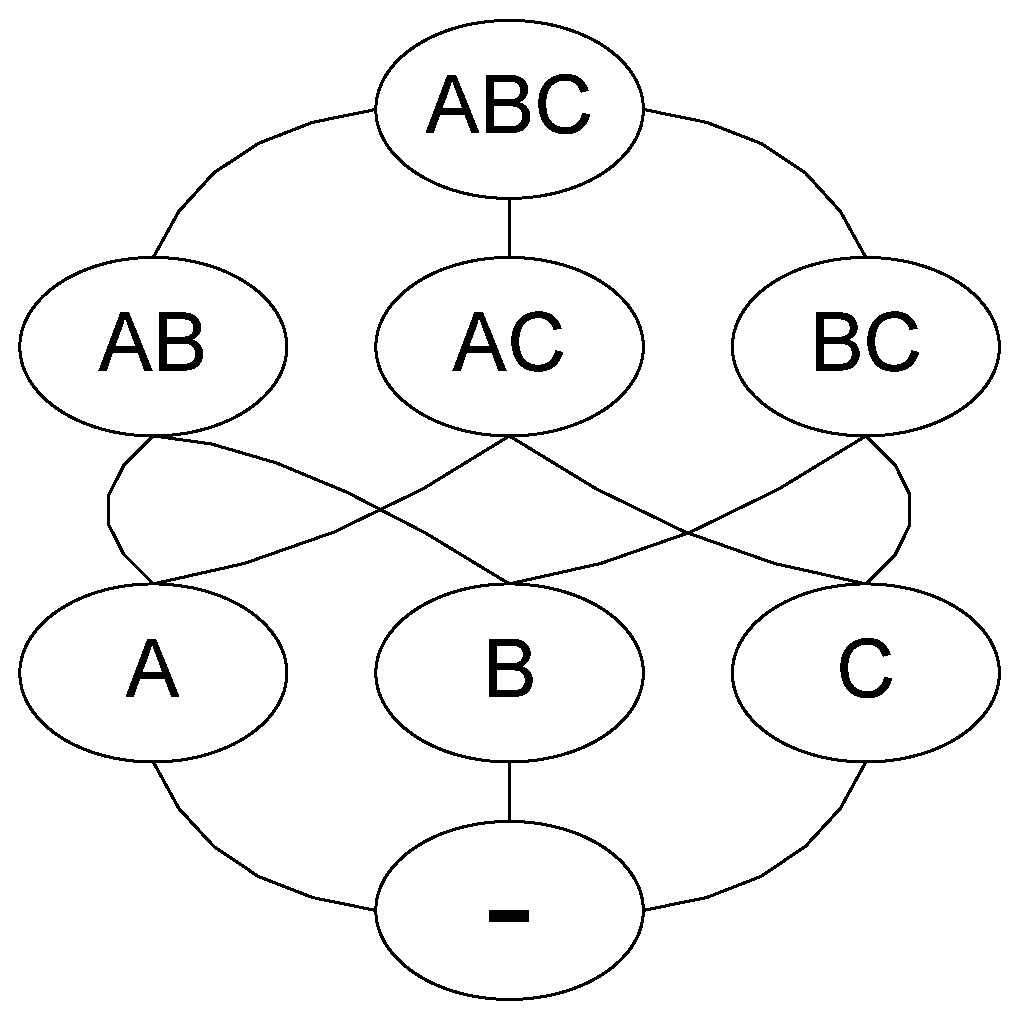
Figure 3. Possible states of a system of three components A, B, C; “–“ stands for empty set with no active components.

The system reconfiguration happens at runtime. Therefore, the algorithm employed for search of an optimal configuration will be very efficient and applicable to large scale systems with fast dynamics.

4. Centralized optimization approach for the system reconfiguration

This algorithm requires a dedicated decision making body in the system, the Reconfigurator denoted as R. This Reconfigurator will collect information about the current state of the system – X, current requirements – Y, and generate a reconfiguration request to the system – U. Thus, discrepancy between the desired and actual state of the system is acceptable (Figure 4).

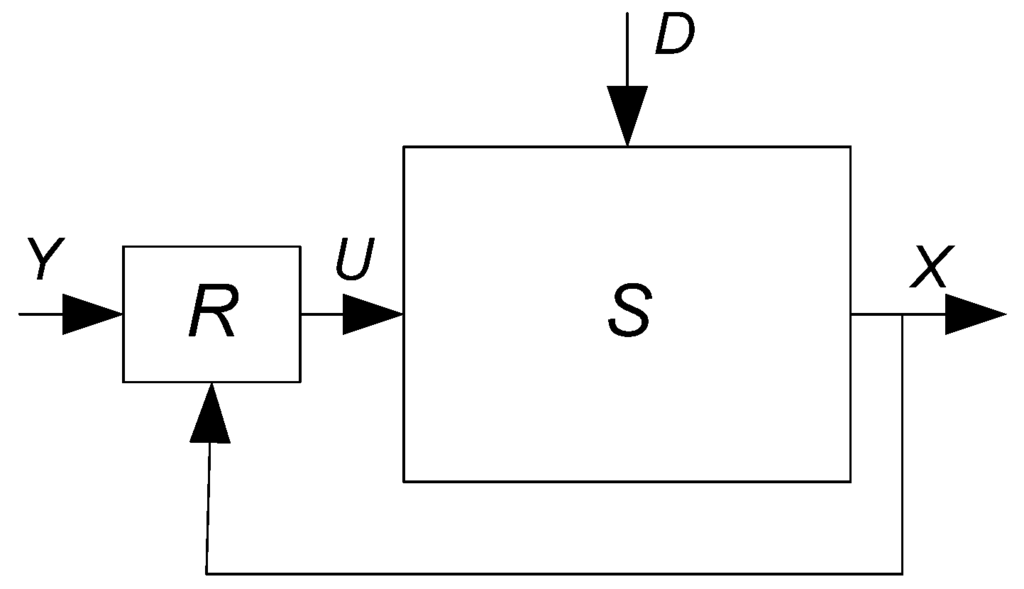
Figure 4. Feedback controlled system. R (Reconfigurator) is a decision making body or controller. U is a control signal generated by R.

Figure 4. Feedback controlled system. R (Reconfigurator) is a decision making body or controller. U is a control signal generated by R.

Q is the quality criterion that will be minimized by R during the search for an optimal configuration of system S.

Q = | ( F – Ф ) + P |, where Ф is a vector of functions provided by S in state X. F is a vector of functional requirements at moment t_j; it is derived from Y. P is the cost for the system to be in the current state X(t_j).

The detailed description of the criterion and its properties is provided in [3].

For estimation the P, part of Q, the Reconfigurator needs to have an access to the components’ profile.

The profile includes parameters such as provided functionality by the component, the required resources, and the operational requirements.

The Reconfigurator searches the configuration of system S that will provide a minimal value of the criterion Q.

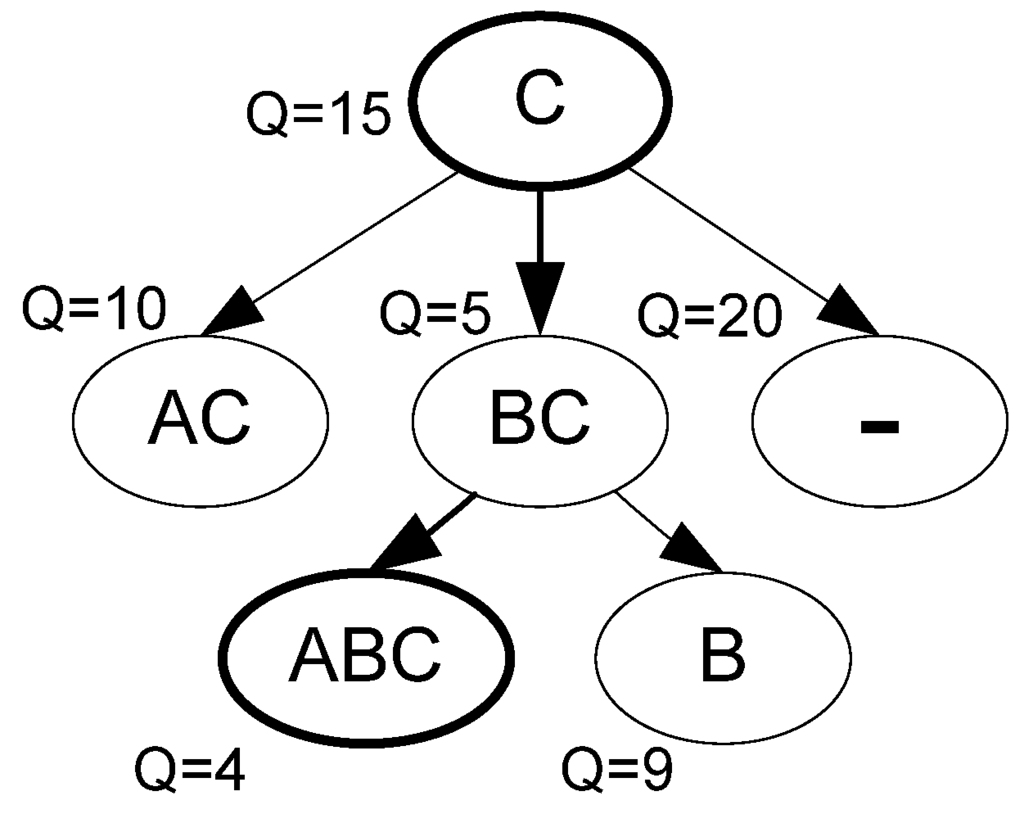
Figure 5. Search of the optimal configuration. S=(C) is the initial configuration with quality criterion Q=15 and S=(ABC) is the goal state with Q=4. Bold circles stand for current (C) and future (ABC) configurations.

Figure 5. Search of the optimal configuration. S=(C) is the initial configuration with quality criterion Q=15 and S=(ABC) is the goal state with Q=4. Bold circles stand for current (C) and future (ABC) configurations.

The search of the optimal configuration can be based on a number of search algorithms, for instance on the A* algorithm [24] with the optimality criterion Q as the heuristic function. For illustrative purposes, we provide the algorithm description (Figure 5):

Step 1. Take the current node of the configuration search graph, calculate Q and move the node to the list “Open”.

Step 2. If “Open” is empty, then the algorithm ends and generates an exception of no solution having been found, otherwise to Step 3.

Step 3. Select a node with the smallest value of Q from the list “Open” and move node “Current” to the list “Closed”.

Step 4. If the “Current” node is good enough, then the algorithm ends (“End”), providing the solution as a set of pointers from “Current” node to “Initial” node, otherwise go to Step 5.

Step 5. Take the node “Current” and build all child nodes. If no child nodes can be built, then go to Step 2. otherwise go to Step 6 (the reconfiguration graph is building dynamically).

Step 6. Estimate Q for all of child nodes of “Current”, move them to the list “Open”, and build the pointers from them to the parent node “Current”. Go to Step 2.

As a result of the algorithm execution at the time t_j, we acquire:

• optimal (with minimal Q) configuration of S at the moment t_j
• set of reconfiguration steps that will be taken for reaching optimal configuration.

The described approach employs system adaptation with architectural support [25]. The key idea is to have a dedicated decision making unit that manages the system configuration, which consists of a few fairly simple components. However, the solution based on this idea lacks scalability. The Reconfigurator becomes a performance bottleneck when there is a large number of system components and high level of system dynamics.

In the worst case scenario, the computational complexity of the presented search algorithm increases exponentially [24]. Obviously, executing such an algorithm at runtime for a system with a large number of components and with a significant number of potential states leads to degradation of the system responsiveness to a changing context and to the evolving requirements.

For a partial scalability improvement, we may split the system into a number of subsystems with their own Reconfigurators [19], or introduce a few optimization constraints to the formula of Q for reaching only a sub-optimal configuration within the defined number of reconfiguration steps [3].

According to the research done earlier [3, 17, 19], tuning of the heuristic function and the sub-optimal search restrictions might improve the performance for particular applications; however in the general case, the widely used approach looks reasonable only for systems with a limited number of components. Therefore the novel solution is needed.

The following sections address the issue and describe an alternative method that attempts to solve the bottleneck problem cased by centralization of the decision making process in the feedback controlled system at runtime based on the operational principles of brain-mind functioning.

5. Coalition of the neuronal assemblies in the human brain

According to the Operational Architectonics (OA) [5, 6, 7, 8, 9] of the brain-mind functioning, a viewed image/scene or an idea created in a human mind result in ignition and coalition formation among several areas/neuronal assemblies of the human brain. It is well established, that single neurons (highly distributed along the cortex) can quickly become associated (or dis-associated) by synchronization of their activity and giving rise to functional transient assemblies. Anatomical connections are not necessarily an important prerequisite for such synchronization; it is rather a stimulus (external – physical or internal – mental) and/or a task that is important and is the causal source of synchrony [8]. Each of these functional neuronal assemblies maintains discrete complex brain operations: they process different attributes of object or environmental scene, thus being simple cognitive operations [6]. The joint functionally connected activity of many neuronal assemblies produces complex cognitive/mental operations.

Each neuronal assembly makes a specific contribution to the performance of complex cognitive operation, and the contribution is determined by the position which a particular neural assembly occupies within the richly connected, parallel, and distributed brain system. The temporal synchronization of many operations of local neuronal assemblies together (Operational Synchrony, OS) gives rise to a new level of brain abstractness – metastable brain states [7]. It is suggested that these metastable brain states or functional Operational Modules (OM), as we name them, underlie complex brain functions and/or mind complex operations (cognitive percepts and mental states that have representational nature). Indeed, a clear correlation between the type of event and the spatial-temporal pattern of the joint assemblies (OM) has been observed [6]. It is important that no central coordination unit is presented, either in each assembly or in the OMs. The units (neuronal assemblies) are specialized for certain functions rather than used as generic purpose components.

Coordination of the integrative activity of the brain neuronal assemblies (located in different brain areas) is reached to the extent that these assemblies are able to mutually influence each other in order to reach a common functional state, concurrently stabilizing main parameters of their activity [8]. Thus, the “transition” of the same neural assembly into the new OM, in accordance with participation in the realization of another complex cognitive operation, must depend on the ability of this neural assembly to adapt to the main variables of the new OM. As a consequence, discrete parts (or assemblies) of the neural networks may gain another functional meaning when they are recruited by other OM, and therefore, take part in realization of another perceptual or cognitive act [6, 7, 8]. In this process, some local neuronal assemblies in the large-scale network become temporarily coordinated (formation of an OM), while others are temporarily excluded from participation in the coordination state. Furthermore, the spatial activity pattern within each coordinated local neural assembly, representing its contribution to the large-scale pattern (indexed as OM), becomes temporarily stabilized [8]. However, each specialized neuronal assembly performs a unique role by expressing its own form of information, and at the same time, its performance is largely constrained by interactions with other neuronal assemblies to which it is functionally connected. This regimen of brain functioning was named metastability [7, 10, 11].

Thus, the OA framework [5, 6, 7, 8, 9] describes the dynamic self-assembling process, where parts of the brain engage and disengage in time, allowing a person to perceive objects or scenes, and to separate remembered parts of an experience, and to bind them all together into a coherent whole. In this view (Figure 6), the potential multivariability of the neuronal networks appears to be far from continuous in time [9], but confined by the dynamics of short-term local and global metastable brain states [7, 10, 12, 13].

However, to avoid any possible misunderstanding, we should stress that the OA framework establishes discrete states without fundamentally violating the demand of continuity of brain/experience dynamics (for a comprehensive analysis, see Ref. 9). In short, the continuity of OMs exists as long as the set of neuronal assemblies in distant brain areas keeps synchronicity between their discrete operations.

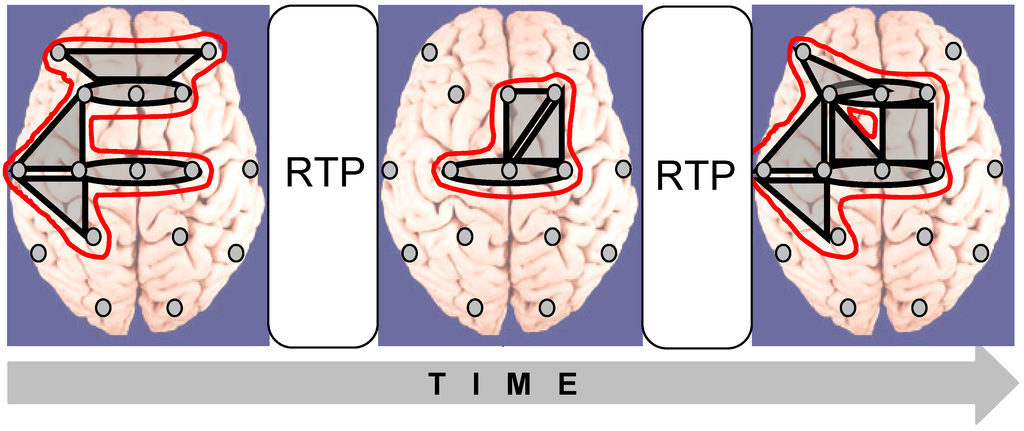
Figure 6. Brain activity dynamics. It is presented as a chain of periods of short-term metastable states (operational modules, OM) of the individual brain subsystems (grey shapes), when the numbers of degrees of freedom of the neuronal assemblies are maximally decreased. Larger shapes outlined in red illustrate complex OMs which are separated from each other by rapid transitional periods (RTPs). During such RTPs, the evaluation about the achieved (previous) state is done and the decision of what should be done and how to achieve the new adaptive state is made [5, 9]. Note, that in the transition period, cortical system (complex and simple OMs) rapidly breaks functional couplings within one set of brain areas and establishes new couplings within another set.

Figure 6. Brain activity dynamics. It is presented as a chain of periods of short-term metastable states (operational modules, OM) of the individual brain subsystems (grey shapes), when the numbers of degrees of freedom of the neuronal assemblies are maximally decreased. Larger shapes outlined in red illustrate complex OMs which are separated from each other by rapid transitional periods (RTPs). During such RTPs, the evaluation about the achieved (previous) state is done and the decision of what should be done and how to achieve the new adaptive state is made [5, 9]. Note, that in the transition period, cortical system (complex and simple OMs) rapidly breaks functional couplings within one set of brain areas and establishes new couplings within another set.

The described neuronal assemblies’ and OM’s formation process served as a starting point for designing the self-organization method for the dynamic computing systems.

6. Biologically inspired self-organization method

A self-organized system is a set of active components, and in this case, the system does not need to have a dedicated decision making unit for defining the best configuration. The intelligence required for optimal adaptation is distributed among the components.

Each component C_i (i=1..M) can be described by the set of variables C_i=C(f_in_i, f_out_i, state_i), where, f_in_i is a frequency that activates the component C_i; f_out_i – frequency of the output signal produced by the activated C_i; state_i is a boolean variable: {‘active’, ‘passive’} that represents the state of C_i; M is a number of available components.

System S is a set {C_j} j=1..N (N=<M), where for all j, state_j = ‘active’; N is the number of activated components. Therefore, only the activated components are considered to be part of the system S.

Activation of the components is done by means of the signals F=U{F_ext, F_int} that are broadcasted among all the components, where, F_ext is multimodal activation signal created by external stakeholders and F_int is a set of signals induced in the system U{f_out_j}.

State machine of the component C_i is presented in Figure 7.

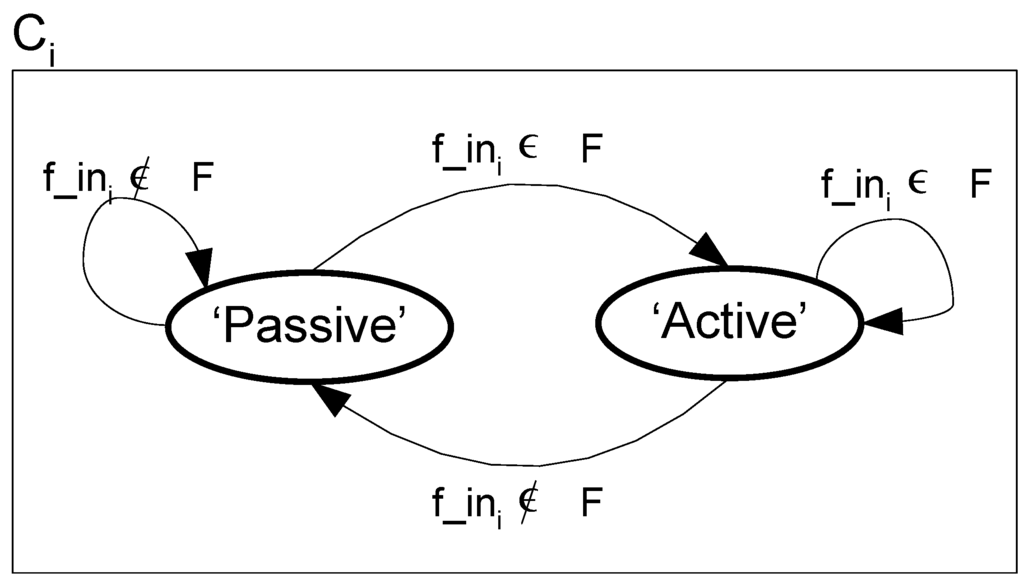
Figure 7. State machine of a component. The state can be changed from Passive to Active and back depending on the structure and content of the activation signal F.

Figure 7. State machine of a component. The state can be changed from Passive to Active and back depending on the structure and content of the activation signal F.

Signal F activates only those components that can “understand” one of the inbuilt frequencies of F, see Figure 8.

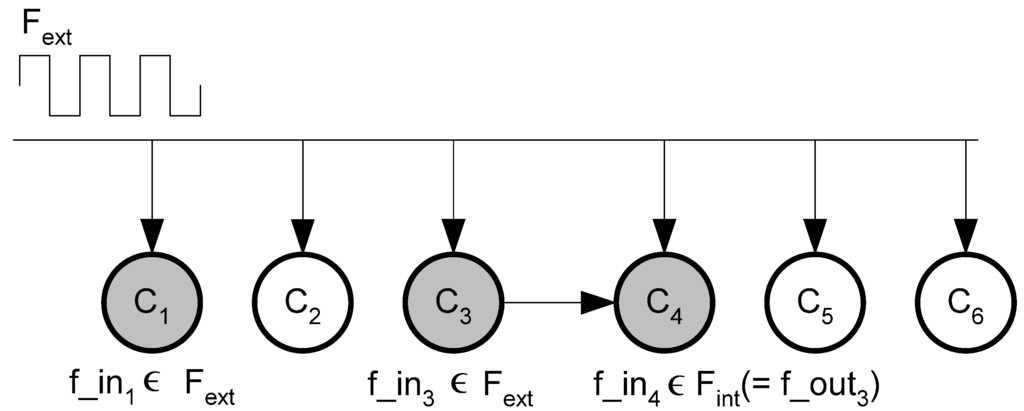
Figure 8. Activation of the system components. External activation signal F_ext activates components C₁ and C₃. f_out₃ the output signal of C₃ activates component C₄. Grey circles stand for activated components.

Figure 8. Activation of the system components. External activation signal F_ext activates components C₁ and C₃. f_out₃ the output signal of C₃ activates component C₄. Grey circles stand for activated components.

Referring to the example presented in Figure 8, all the components receive F_ext simultaneously and process it in parallel. Then, the output signal of the activated C₃ is broadcasted among all the components as F_int. It is processed in parallel, and activates C₄. Therefore, total system activation time, in this case, is equal to two signal processing operations due to the parallel nature of the data processing.

The maximal computational effort in the presented example is equal to six operations when F_ext activates only one component C₁ and all other are activated consequently, for instance, as follows C₁->C₃->C₂->C₆->C₅->C₄. This short analysis shows that computational complexity of the proposed system formation approach is proportional to M – the number of available components.

Through cross-activation and initiation by external requests, the components form a system in which they collectively solve the required tasks and head towards a defined goal.

7. Conclusions and future work

The proposed brain inspired self-organization method reduces real-time computational burden for the system’s formation and adaptation process. For the computational effort analysis, we estimated a number of computing operations needed for the system formation at runtime. The related computational effort of the proposed self-organization method is growing linearly with the increase of the number of components in the system while the real-time effort in the centralized feedback controlled systems is growing exponentially.

In this paper, we have addressed the scalability issue of adaptive distributed systems by decoupling real-time part of the adaptation method and design-time part.

Future development will concentrate on implementing an off-line algorithm to define activation signals; this algorithm will take performance criteria and the desired values (attractors) for the system evolution as the inputs and provides the settings required for optimal real-time system functioning.

8. Related work

A service broker engine that adapts the composite application structure to provide the best service for end-users (taking into account their preferences and the current status of their context data) is proposed in SPICE [20, 25]. Agha [1] and Kon et al. [2] propose architectures for adaptive and reflective middleware that can be used for development of context-sensitive applications. Kokas et al. [22] and Shi et al. [4] propose to create adaptive software systems based on control optimization framework. Costa et al. [21] in the research project RUNES are developing systems with rule-based or policy-based adaptation. This approach is feasible mostly for systems with predefined set of states.

The above-listed works represent a significant research segment of the current state of the art in the domain. However, most of them propose the use of the centralized adaptation algorithms that share similar scalability problems as the one presented in Section 3.

Valvassori [26] presents a biologically inspired implementation of the blob structures as a set of distributed processors. The blob formation method applies broadcasting of signals from a processor to the neighboring units.

The closest to the ideas presented in this paper is the CASCADAS project [28], which defines a software framework for development of the agents that can collaborate among each other for collective problem solving. The significant difference, however, is in the approach for developing the algorithm for the purposeful clusters formation. Hence, we consider the CASCADAS as a complementary project to the work presented here due to the fact that CASCADAS covers lots of implementation details that are not emphasized in the present paper.