Probabilistic Distributed Algorithms for Energy Efficient Routing and Tracking in Wireless Sensor Networks

Abstract

In this work we focus on the energy efficiency challenge in wireless sensor networks, from both an on-line perspective (related to routing), as well as a network design perspective (related to tracking). We investigate a few representative, important aspects of energy efficiency: a) the robust and fast data propagation b) the problem of balancing the energy dissipation among all sensors in the network and c) the problem of efficiently tracking moving entities in sensor networks. Our work here is a methodological survey of selected results that have already appeared in the related literature. In particular, we investigate important issues of energy optimization, like minimizing the total energy dissipation, minimizing the number of transmissions as well as balancing the energy load to prolong the system’s lifetime. We review characteristic protocols and techniques in the recent literature, including probabilistic forwarding and local optimization methods. We study the problem of localizing and tracking multiple moving targets from a network design perspective i.e. towards estimating the least possible number of sensors, their positions and operation characteristics needed to efficiently perform the tracking task. To avoid an expensive massive deployment, we try to take advantage of possible coverage overlaps over space and time, by introducing a novel combinatorial model that captures such overlaps. Under this model, we abstract the tracking network design problem by a covering combinatorial problem and then design and analyze an efficient approximate method for sensor placement and operation.

1. Introduction

1.1. A Brief Description of Wireless Sensor Networks

Recent dramatic developments in micro-electro-mechanical (MEMS) systems, wireless communications and digital electronics have already led to the development of small in size, low-power, low-cost sensor devices. Such extremely small devices integrate sensing, data processing and wireless communication capabilities. Current devices have a size at the cubic centimeter scale, a CPU running at 4 MHz, some memory and a wireless communication capability at a 4kbps rate. Also, they are equipped with a small but effective operating system and are able to switch between “sleeping” and “awake” modes to save energy. Pioneering groups (like the “Smart Dust” Project at Berkeley, the “Wireless Integrated Network Sensors” Project at UCLA and the “Ultra low Wireless Sensor” Project at MIT) pursue further important goals, like a total volume of a few cubic millimeters and extremely low energy consumption, by using alternative technologies, based on radio frequency (RF) or optical (laser) transmission.

Examining each such device individually might appear to have small utility, however the effective distributed co-ordination of large numbers of such devices may lead to the efficient accomplishment of large sensing tasks. Large numbers of sensor nodes can be deployed in areas of interest (such as inaccessible terrains or disaster places) and use self-organization and collaborative methods to form a sensor network.

We note that a single, universal and technology independent model is missing in the state of the art, so in each case we precisely state the particular modeling assumptions (weaker or stronger) needed. Also, in Section 1.3 we make an attempt to define a hierarchy of models and relations between them.

Their wide range of applications is based on the possible use of various sensor types (i.e. thermal, visual, seismic, acoustic, radar, magnetic, etc.) in order to monitor a wide variety of conditions (e.g. temperature, object presence and movement, humidity, pressure, noise levels etc.). Thus, sensor networks can be used for continuous sensing, event detection, location sensing as well as micro-sensing. Hence, sensor networks have important applications, including (a) military (like forces and equipment monitoring, battlefield surveillance, targeting, nuclear, biological and chemical attack detection), (b) environmental applications (such as fire detection, flood detection, precision agriculture), (c) health applications (like telemonitoring of human physiological data) and (d) home applications (e.g. smart environments and home automation). For an excellent survey of wireless sensor networks, see [1,15,29].

1.2. Critical Challenges

The efficient and robust realization of such large, highly-dynamic, complex, non-conventional networking environments is a challenging algorithmic and technological task. Features including the huge number of sensor devices involved, the severe power, computational and memory limitations, their dense deployment and frequent failures, pose new design, analysis and implementation aspects which are essentially different not only with respect to distributed computing and systems approaches but also to ad-hoc networking techniques.

We emphasize the following characteristic differences between sensor networks and ad-hoc networks:

• The number of sensor particles in a sensor network is extremely large compared to that in a typical ad-hoc network.
• Sensor networks are typically prone to faults.
• Because of faults as well as energy limitations, sensor nodes may (permanently or temporarily) join or leave the network. This leads to highly dynamic network topology changes.
• The density of deployed devices in sensor networks is much higher than in ad-hoc networks.
• The limitations in energy, computational power and memory are much more severe in sensor networks.

Because of the above rather unique characteristics of sensor networks, efficient and robust distributed protocols and algorithms should exhibit the following critical properties:

Scalability

Distributed protocols for sensor networks should be highly scalable, in the sense that they should operate efficiently in extremely large networks composed of huge numbers of nodes. This feature calls for an urgent need to prove by analytical means and also validate (by large scale simulations) certain efficiency and robustness (and their trade-offs) guarantees for asymptotic network sizes.

Efficiency

Because of the severe energy limitations of sensor networks and also because of their time-critical application scenaria, protocols for sensor networks should be efficient, with respect to both energy and time.

Fault-tolerance

Sensor particles are prone to several types of faults and unavailabilities, and may become inoperative (permanently or temporarily). Various reasons for such faults include physical damage during either the deployment or the operation phase, permanent (or temporary) cease of operation in the case of power exhaustion (or energy saving schemes, respectively). The sensor network should be able to continue its proper operation for as long as possible despite the fact that certain nodes in it may fail.

1.3. Models and Relations between them

We note that a single, universal, technology- and cost- independent model is missing in the state of the art, so for each protocol and problem we precisely state the particular modeling assumptions (weaker or stronger) needed. Also, we provide the following hierarchy of models and relations between them.

Basic Model M₀

A smart dust (or sensor) cloud (a set of sensors, which may be called grain particles) is spread in an area (for a graphical presentation, see Figure 1). The deployment is random uniform. Two important network parameters (crucially affecting connectivity) are the particle density d (usually measured in numbers of particles/m²), and the maximum transmission range ℜ of each grain particle. The sensors do not move. A two-dimensional framework is adopted.

There is a single point in the network, which is called the “sink” S, that represents the fixed control center where data should be reported to. The sink is very powerful, in terms of both energy and computing power. Sensors can be aware of the direction (and position) of the sink, as well as of their distance to the sink. Such information can be e.g. obtained during a set-up phase, by having the (powerful) sink broadcast control messages to the entire network region.

We assume that events, that should be reported to the control center, occur in the network region. Furthermore, we assume that these events are happening at random uniform positions.

As far as energy dissipation is concerned, we assume that the energy spent at a sensor when transmitting data is proportional to the square of the transmitting distance. Note however that the energy dissipation for receiving is not always negligible with respect to the energy when sending such as in case when transmissions are too short and/or radio electronics energy is high [23].

Figure 1. A Smart Dust Cloud.

Figure 1. A Smart Dust Cloud.

A variation of this basic model includes multiple and/or mobile sinks. The following wall notion generalizes that of the sink and may correspond to multiple (and/or moving) sinks. A receiving wall $𝒲$ is defined to be an infinite line in the smart-dust plane. Any particle transmission within range ℜ from the wall $𝒲$ is received by $𝒲$. $𝒲$ is assumed to have very strong computing power, is able to collect and analyze received data and has a constant power supply and so it has no energy constraints. The wall represents in fact the authorities (the fixed control center) which the realization of a crucial event and collected data should be reported to. Note that a wall of appropriately big (finite) length may suffice. The notion of multiple sinks which may be static or moving has also been studied in [46], where Triantafilloy, Ntarmos, Nikoletseas and Spirakis introduce “NanoPeer Worlds”, merging notions from Peer-to-Peer Computing and Smart Dust.

The M₀ model is assumed for the LTP protocol.

A stronger model M₁

This model is derived by augmenting model M₀ with additional (stronger) assumptions about the abilities of the sensors and the sensor deployment. In particular, the network topology can be a lattice (or grid) deployment of sensors. This grid placement of grain particles is motivated by certain applications, where it is possible to have a pre-deployed sensor network, where sensors are put (possibly by a human or a robot) in a way that they form a 2-dimensional lattice. Note indeed that such sensor networks, deployed in a structured way, might be useful e.g. in precise agriculture, where humans or robots may want to deploy the sensors in a lattice structure to monitor in a rather homogenous and uniform way certain conditions in the spatial area of interest. Also, exact terrain monitoring in military applications may also need some sort of a grid-like shaped sensor network. Note that Akyildiz et al. in a state of the art survey refer to the pre-deployment possibility [1]. Also, [25] explicitly refers to the lattice case. Moreover, as the authors of [25] state in an extended version of their work, they consider, for reasons of “analytic tractability”, a square grid topology [26].

We also assume that each grain particle has the following abilities:

(i) It can estimate the direction of a received transmission (e.g. via the technology of direction-sensing antennae). We note that at least a gross sense of direction may be technologically possible by smart and/or multiple antennas. Regarding the extra cost of the antennas and circuitry, we note that certainly such a cost is introduced but as technology advances this cost may lower.

(ii) It can estimate the distance from a nearby particle that did the transmission (e.g. via estimation of the attenuation of the received signal).

(iii) It knows the direction towards the sink S. This can be implemented during a set-up phase, where the (very powerful in energy) sink broadcasts the information about itself to all particles.

(iv) All particles have a common co-ordinates system.

Notice that GPS information is assumed by this model. Also, the global structure of the network is not assumed known.

This model is used in the PFR protocol.

Variations

Both models above can be augmented by assuming certain additional abilities, like the ability of sensors to vary their wireless transmission range (this is used in the EBP and the tracking protocols). Also, problem specific assumptions may apply (such as the model for the targets in the tracking problem).

1.4. The Energy Efficiency Challenge in Routing and Tracking

Since one of the most severe limitations of sensor devices is their limited energy supply, one of the most crucial goals in designing efficient protocols for wireless sensor networks is minimizing the energy consumption in the network. This goal has various aspects, including: (a) minimizing the total energy spent in the network (b) minimizing the number (or the range) of data transmissions (c) combining energy efficiency and fault-tolerance, by allowing redundant data transmissions which however should be optimized to not spend too much energy (d) maximizing the number of “alive” particles over time, thus prolonging the system’s lifetime and (e) balancing the energy dissipation among the sensors in the network, in order to avoid the early depletion of certain sensors and thus the breakdown of the network.

We note that it is very difficult to achieve all the above goals at the same time. There even exists trade-offs between some of the goals above. Furthermore, the importance and priority of each of these goals may depend on the particular application. Thus, it is important to have a variety of protocols, each of which may possibly focus at some of the energy efficiency goals above (while still performing well with respect to the rest goals as well).

In this paper, we focus on energy optimization. We investigate both on-line aspects of energy efficiency related to data propagation, as well as off-line network design issues, related to tracking, an important problem which is considered canonical in the literature. In particularly for routing we present three methodologically characteristic energy efficient protocols:

• The Local Target Protocol (LTP), that performs a local optimization trying to minimize the number of data transmissions.
• The Probabilistic Forwarding Protocol (PFR), that creates redundant data transmissions that are probabilistically optimized, to trade-off energy efficiency with fault-tolerance.
• The Energy Balanced Protocol (EBP), that focuses on guaranteeing the same per sensor energy dissipation, in order to prolong the lifetime of the network.

Because of the complex nature of a sensor network (that integrates various aspects of communication and computing), protocols, algorithmic solutions and design schemes for all layers of the networking infrastructure are needed. Far from being exhaustive, we mention the need for frequency management solutions at the physical layer, for Medium Access Control (MAC) protocols to cope with multi-hop transmissions at the data link layer. Our approach focuses on routing and does not consider other important issues like link fading and hidden station interference, i.e. we assume that other network layers are resolving these issues. Also, regarding reliability, an endemic issue to wireless sensor networks, we consider permanent physical failures i.e. we do not deal with bad values from physical sensing or transient failures. The interested reader may use the excellent survey by Akyildiz et al. [4] for a detailed discussion of design aspects of all layers of the networking infrastructure.

For tracking, we study the problem of localizing and monitoring multiple moving targets in wireless sensor networks, from a network design perspective i.e. towards estimating the least possible number of sensors to be deployed, their positions and operation characteristics needed to efficiently perform the tracking task. To avoid an expensive massive deployment, we try to take advantage of possible coverage overlaps over space and time, by introducing a novel combinatorial model that captures such overlaps.

Under this model, we abstract the tracking network design problem by a combinatorial problem of covering a universe of elements by at least three sets to ensure that each point in the network area is covered at any time by at least three sensors, and thus being localized, i.e. we assume that 3-coverage suffices for (at least gross) localization; our method can be extended to k-coverage, for constant k ≥ 4, for more accuracy. We then design and analyze an efficient approximate method for sensor placement and operation, that with high probability and in polynomial expected time achieves a Θ(log n) approximation ratio to the optimal solution. Our network design solution can be combined with alternative collaborative processing methods, to suitably fit different tracking scenaria.

Part A: On-Line Energy Optimization 

2. LTP: A Hop-by-Hop Data Propagation Protocol

The LTP Protocol was introduced in [8]. The authors assume the basic model M₀ defined in Section 1.3.

2.1. The Protocol

Let d(p_i, p_j) the distance (along the corresponding vertical lines towards $𝒲$) of particles p_i, p_j and d(p_i, $𝒲$) the (vertical) distance of p_i from $𝒲$. Let info($ℰ$) the information about the realization of the crucial event $ℰ$ to be propagated. Let p the particle sensing the event and starting the execution of the protocol. In this protocol, each particle p′ that has received info($ℰ$), does the following:

• Search Phase: It uses a periodic low energy directional broadcast in order to discover a particle nearer to $𝒲$ than itself. (i.e. a particle p″ where d(p″, $𝒲$) < d(p′, $𝒲$)).
• Direct Transmission Phase: Then, p′ sends info($ℰ$) to p″.
• Backtrack Phase: If consecutive repetitions of the search phase fail to discover a particle nearer to $𝒲$, then p″ sends info($ℰ$) to the particle that it originally received the information from.

Note that one can estimate an a-priori upper bound on the number of repetitions of the search phase needed, by calculating the probability of success of each search phase, as a function of various parameters (such as density, search angle, transmission range). This bound can be used to decide when to backtrack.

For a graphical representation see Figure 2 and Figure 3.

Figure 2. Example of the Search Phase.

Figure 2. Example of the Search Phase.

Figure 3. Example of a Transmission.

Figure 3. Example of a Transmission.

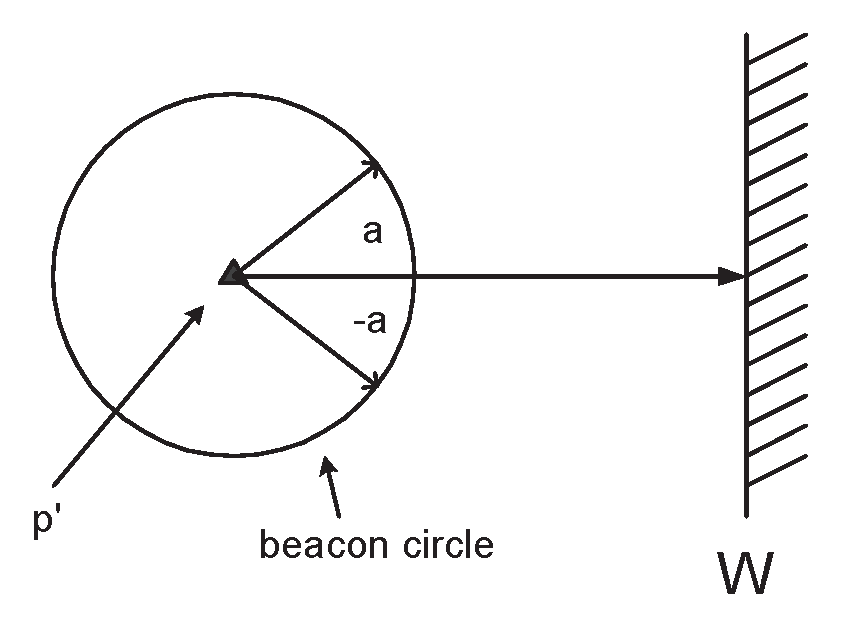
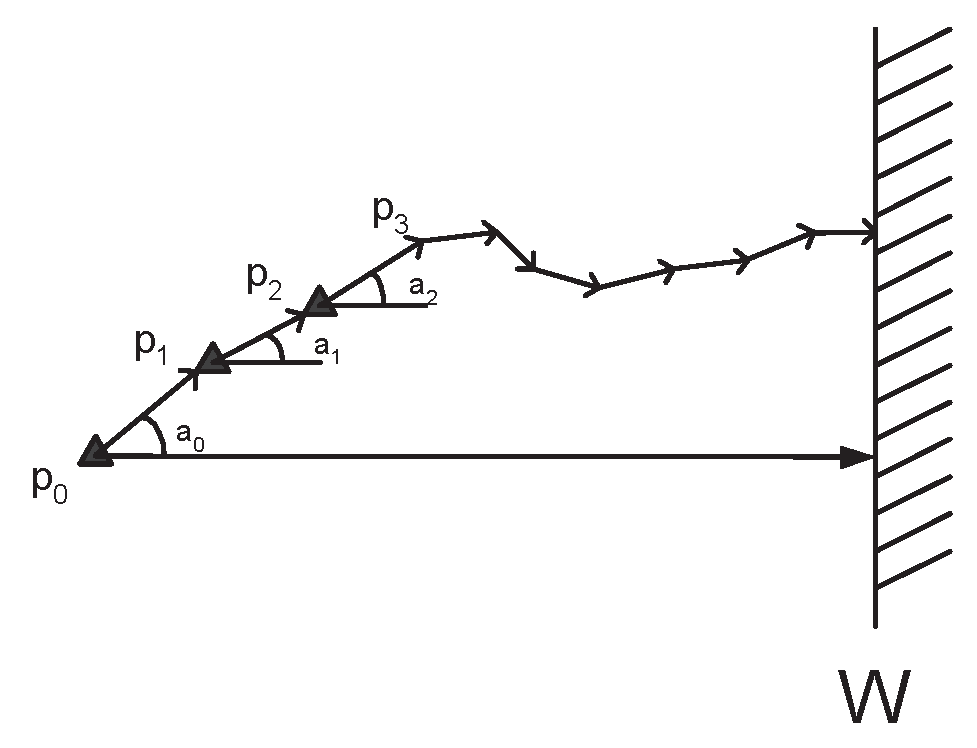
2.2. Theoretical Analysis

[8] first provides some basic definitions.

Definition 1 

Let h_opt(p, $𝒲$) be the (optimal) number of “hops” (direct, vertical to $𝒲$ transmissions) needed to reach the wall, in the ideal case in which particles always exist in pair-wise distances ℜ on the vertical line from p to $𝒲$. Let Π be a smart-dust propagation protocol, using a transmission path of length L(Π, $𝒲$) to send info about event $ℰ$ to wall $𝒲$. Let h(Π, $𝒲$) be the actual number of hops (transmissions) taken to reach $𝒲$. The “hops” efficiency of protocol Π is the ratio

$$C_h=\frac{h(\Pi ,p,\mathcal{W})}{h_{opt}(p,\mathcal{W})}$$

Clearly, the number of hops (transmissions) needed characterizes the energy consumption and the time needed to propagate the information $ℰ$ to the wall. Remark that $h_{opt}=⌈\frac{d(p,\mathcal{W})}{\mathcal{R}}⌉$, where d(p, $𝒲$) is the (vertical) distance of p from the wall $𝒲$.

In the case where the protocol Π is randomized, or in the case where the distribution of the particles in the cloud is a random distribution, the number of hops h and the efficiency ratio C_h are random variables and one wishes to study their expected values.

The reason behind these definitions is that when p (or any intermediate particle in the information propagation to $𝒲$) “looks around” for a particle as near to $𝒲$ as possible to pass its information about $ℰ$, it may not get any particle in the perfect direction of the line vertical to $𝒲$. This difficulty comes mainly from three causes: a) Due to the initial spreading of particles of the cloud in the area and because particles do not move, there might not be any particle in that direction. b) Particles of sufficient remaining battery power may not be currently available in the right direction. c) Particles may temporarily “sleep” (i.e. not listen to transmissions) in order to save battery power.

Note that any given distribution of particles in the smart dust cloud may not allow the ideal optimal number of hops to be achieved at all. In fact, the least possible number of hops depends on the input (the positions of the grain particles). [8] however, compares the efficiency of protocols to the ideal case. A comparison with the best achievable number of hops in each input case will of course give better efficiency ratios for protocols.

To enable a first step towards a rigorous analysis of smart dust protocols, [8] makes the following simplifying assumption: The search phase always finds a p″ (of sufficiently high battery) in the semicircle of center the particle p′ currently possessing the information about the event and radius R, in the direction towards $𝒲$. Note that this assumption on always finding a particle can be relaxed in the following ways: (a) by repetitions of the search phase until a particle is found. This makes sense if at least one particle exists but was sleeping during the failed searches, (b) by considering, instead of just the semicircle, a cyclic sector defined by circles of radiuses ℜ − Δℜ and also take into account the density of the smart cloud, (c) if the protocol during a search phase ultimately fails to find a particle towards the wall, it may backtrack.

[8] also assumes that the position of p″ is uniform in the arc of angle 2a around the direct line from p′ vertical to $𝒲$. Each data transmission (one hop) takes constant time t (so the “hops” and time efficiency of our protocols coincide in this case). It is also assumed that each target selection is stochastically independent of the others, in the sense that it is always drawn uniformly randomly in the arc (−α, α).

The above assumptions may not be very realistic in practice, however, they can be relaxed and in any case allow to perform a first effort towards providing some concrete analytical results.

Lemma 1 ([8]) 

The expected “hops efficiency” of the local target protocol in the a-uniform case is

$$E\left(C_h\right)\simeq \frac{\alpha }{sin\alpha }$$

for large h_opt. Also

$$1\le E\left(C_h\right)\le \frac{\pi }{2}\simeq 1.57$$

for $0\le \alpha \le \frac{\pi }{2}$.

Proof: 

Due to the protocol, a sequence of points is generated, $p_0=p,p_1,p_2,\cdots ,p_{h-1},p_h$ where $p_{h-1}$ is a particle within $\mathcal{W}$’s range and $p_h$ is part of the wall. Let ${\alpha }_i$ be the (positive or negative) angle of $p_i$ with respect to $p_{i-1}$’s vertical line to $\mathcal{W}$. It is:

$$\sum _{i=1}^{h-1}d(p_{i-1},p_i)\le d(p,\mathcal{W})\le \sum _{i=1}^{h}d(p_{i-1},p_i)$$

Since the (vertical) progress towards $\mathcal{W}$ is then ${\Delta }_i=d(p_{i-1},p_i)=\mathcal{R}cos{\alpha }_i$, we get:

$$\sum _{i=1}^{h-1}cos{\alpha }_i\le h_{opt}\le \sum _{i=1}^{h}cos{\alpha }_i$$

From Wald’s equation for the expectation of a sum of a random number of independent random variables [42], then

$$E(h-1)·E(cos{\alpha }_i)\le E\left(h_{opt}\right)=h_{opt}\le E\left(h\right)·E(cos{\alpha }_i)$$

Now, $\forall i$, $E(cos{\alpha }_i)={\int }_{-\alpha }^{\alpha }cosx\frac{1}{2\alpha }dx=\frac{sin\alpha }{\alpha }$. Thus

$$\frac{\alpha }{sin\alpha }\le \frac{E\left(h\right)}{h_{opt}}=E\left(C_h\right)\le \frac{\alpha }{sin\alpha }+\frac{1}{h_{opt}}$$

Assuming large values for h_opt (i.e. events happening far away from the wall, which is the most interesting case in practice since the detection and propagation difficulty increases with distance) we have (since for $0\le \alpha \le \frac{\pi }{2}$ it is $1\le \frac{\alpha }{sin\alpha }\le \frac{\pi }{2}$) and the result follows.

2.3. Local Optimization: The Min-two Uniform Targets Protocol (M2TP)

[8] further assumes that the search phase always returns two points p″, p‴ each uniform in (−α, α) and that a modified protocol M2TP selects the best of the two points, with respect to the local (vertical) progress. This is in fact an optimized version of the Local Target Protocol.

In a similar way as in the proof of the previous lemma, the authors prove the following result:

Lemma 2 ([8]) 

The expected “hops efficiency” of the “min two uniform targets” protocol in the a-uniform case is

$$E\left(C_h\right)\simeq \frac{{\alpha }^2}{2(1-cos\alpha )}$$

for $0\le \alpha \le \frac{\pi }{2}$ and for large h.

Now remark that

$$\underset{\alpha \to 0}{lim}E\left(C_h\right)=\underset{\alpha \to 0}{lim}\frac{2\alpha }{2sina}=1$$

and

$$\underset{\alpha \to \frac{\pi }{2}}{lim}E\left(C_h\right)=\frac{{(\pi /2)}^2}{2(1-0)}=\frac{{\pi }^2}{8}\simeq 1.24$$

Thus, [8] proves the following:

Lemma 3 ([8]) 

The expected “hops” efficiency of the min-two uniform targets protocol is

$$1\le E\left(C_h\right)\le \frac{{\pi }^2}{8}\simeq 1.24$$

for large h and for $0\le \alpha \le \frac{\pi }{2}$.

Remark that, with respect to the expected hops efficiency of the local target protocol, the min-two uniform targets protocol achieves, because of the one additional search, a relative gain which is (π/2 − π²/8)/(π/2) ≃ 21.5%. [8] also experimentally investigates the further gain of additional (i.e. m > 2) searches.

3. PFR - A Probabilistic Forwarding Protocol

The LTP protocol, as shown in the previous section manages to be very efficient by always selecting exactly one next-hop particle, with respect to some optimization criterion. Thus, it tries to minimize the number of data transmissions. LTP is indeed very successful in the case of dense and robust networks, since in such networks a next hop particle is very likely to be discovered. In sparse or faulty networks however, the LTP protocol may behave poorly, because of many backtracks due to frequent failure to find a next hop particle. To combine energy efficiency and fault-tolerance, the Probabilistic Forwarding Protocol (PFR) has been introduced. The trade-offs in the performance of the two protocols implied above are shown and discussed in great detail in [10].

The PFR protocol was introduced in [9]. Authors assume the model M₁ (defined in section 1.3).

3.1. The Protocol

The PFR protocol is inspired by the probabilistic multi-path design choice for the Directed Diffusion paradigm mentioned in [25]. Its basic idea of the protocol (introduced in [9]) lies in probabilistically favoring transmissions towards the sink within a thin zone of particles around the line connecting the particle sensing the event $ℰ$ and the sink (see Figure 4). Note that transmission along this line is energy optimal. However it is not always possible to achieve this optimality, basically because certain sensors on this direct line might be inactive, either permanently (because their energy has been exhausted) or temporarily (because these sensors might enter a sleeping mode to save energy). Further reasons include:

• physical damage of sensors,
• deliberate removal of some of them (possibly by an adversary in military applications),
• changes in the position of the sensors due to a variety of reasons (weather conditions, human interaction etc.), and
• physical obstacles blocking communication.

The protocol evolves in two phases:

• Phase 1: The “Front” Creation Phase. Initially the protocol builds (by using a limited, in terms of rounds, flooding) a sufficiently large “front” of particles, in order to guarantee the survivability of the data propagation process. During this phase, each particle having received the data to be propagated, deterministically forwards them towards the sink. In particular, and for a sufficiently large number of steps $s=180\sqrt{2}$, each particle broadcasts the information to all its neighbors, towards the sink. Remark that to implement this phase, and in particular to count the number of steps, we use a counter in each message. This counter needs at most $\lceil log180\sqrt{2}\rceil$ bits.
• Phase 2: The Probabilistic Forwarding Phase. During this phase, each particle P possessing the information under propagation, calculates an angle ϕ by calling the subprotocol “ϕ-calculation” (see description below) and broadcasts info($ℰ$) to all its neighbors with probability ${\mathrm{I}\mathrm{P}}_{fwd}$ (or it does not propagate any data with probability $1-{\mathrm{I}\mathrm{P}}_{fwd}$) defined as follows:

  $${\mathrm{I}\mathrm{P}}_{fwd}=\{\begin{array}{cc}1& \text{if}\varphi \ge {\varphi }_{threshold}\\ \frac{\varphi }{\pi }& \text{otherwise}\end{array}$$

  where ϕ is the angle defined by the line EP and the line PS and ϕ_threshold = 134^o (the selection reasons of this ϕ_threshold can be found in [9].

In both phases, if a particle has already broadcast info($ℰ$) and receives it again, it ignores it. Also the PFR protocol is presented for a single event tracing. Thus no multiple paths arise and packet sizes do not increase with time.

Remark that when ϕ = π then P lies on the line ES and vice-versa (and always transmits).

If the density of particles is appropriately large, then for a line ES there is (with high probability) a sequence of points “closely surrounding ES” whose angles ϕ are larger than ϕ_threshold and so that successive points are within transmission range. All such points broadcast and thus essentially they follow the line ES (see Figure 4).

Figure 4. Thin Zone of particles.

Figure 4. Thin Zone of particles.

Figure 5. Angle ϕ calculation example.

Figure 5. Angle ϕ calculation example.

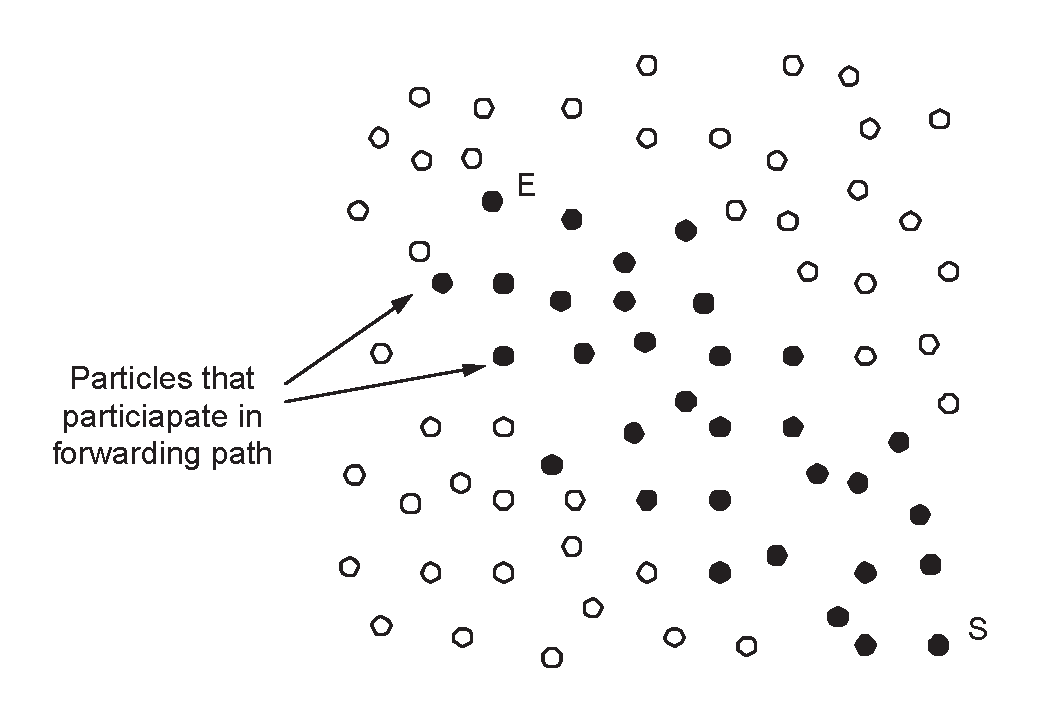
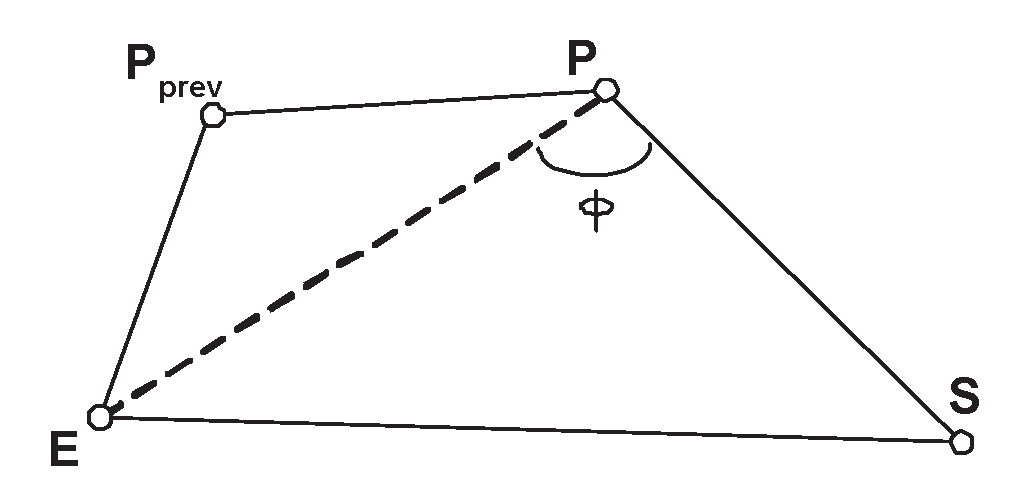
The ϕ-calculation subprotocol (see Figure 5)

Let P_prev the particle that transmitted info(E) to P.

(1) When P_prev broadcasts info(E), it also attaches the info |EP_prev| and the direction $\overrightarrow{P_{prev}E}$.

(2) P estimates the direction and length of line segment P_prevP, as described in the model.

(3) P now computes angle $(\widehat{E{P}_{prev}P})$, and computes |EP| and the direction of $\overrightarrow{PE}$ (this will be used in further transmission from P).

(4) P also computes angle $(\widehat{P_{prev}PE})$ and by subtracting it from $(\widehat{P_{prev}PS})$ it finds ϕ.

Notice the following:

(i) The direction and distance from activated sensors to E is inductively propagated (i.e. P becomes P_prev in the next phase).

(ii) The protocol needs only messages of length bounded by log A, where A is some measure of the size of the network area, since (because of (i) above) there is no cumulative effect on message lengths.

Essentially, the protocol captures the intuitive, deterministic idea “if my distance from ES is small, then send, else do not send”. [9] has chosen to enhance this idea by random decisions (above a threshold) to allow some local flooding to happen with small probability and thus to cope with local sensor failures.

3.2. Properties of PFR

Any protocol Π solving the data propagation problem must satisfy the following three properties:

• Correctness. Π must guarantee that data arrives to the position S, given that the whole network exists and is operational.
• Robustness. Π must guarantee that data arrives at enough points in a small interval around S, in cases where part of the network has become inoperative.
• Efficiency. If Π activates k particles during its operation then Π should have a small ratio of the number of activated over the total number of particles $r=\frac{k}{N}$. Thus r is an energy efficiency measure of Π.

[9] shows that this is indeed the case for PFR.

Consider a partition of the network area into small squares of a fictitious grid G (see Figure 6). Let the length of the side of each square be l. Let the number of squares be q. The area covered is bounded by ql². Assuming that we randomly throw in the area at least αq log q = N particles (where α > 0 a suitable constant), then the probability that a particular square is avoided tends to 0. So with very high probability (tending to 1) all squares get particles.

[9] conditions all the analysis on this event, call it F, of at least one particle in each square.

Figure 6. A Lattice Dissection G.

Figure 6. A Lattice Dissection G.

Figure 7. A Lattice Sensor Network.

Figure 7. A Lattice Sensor Network.

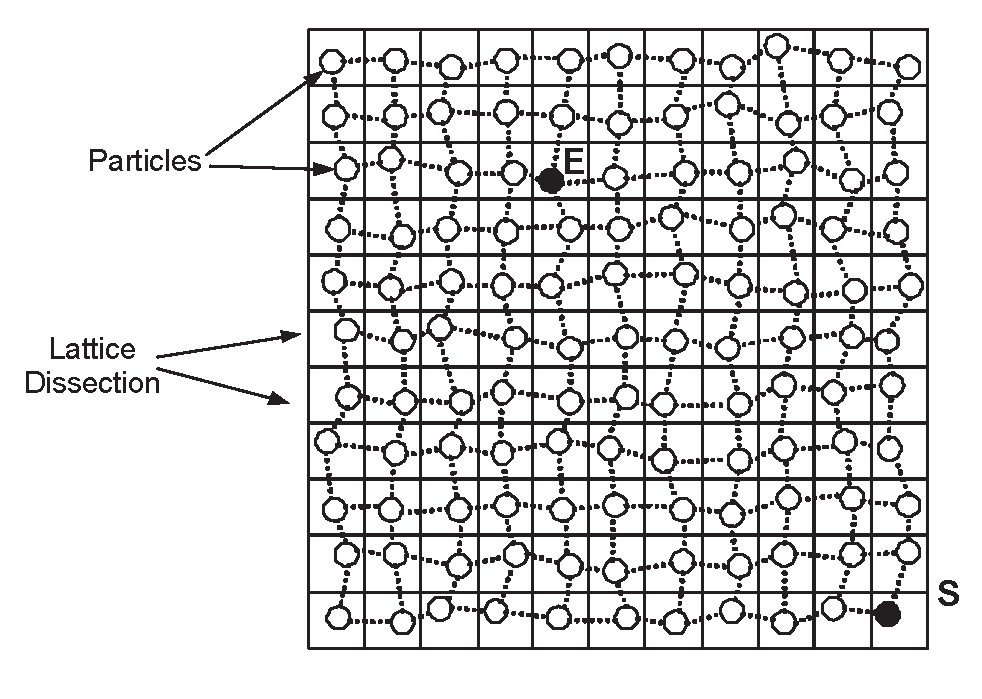
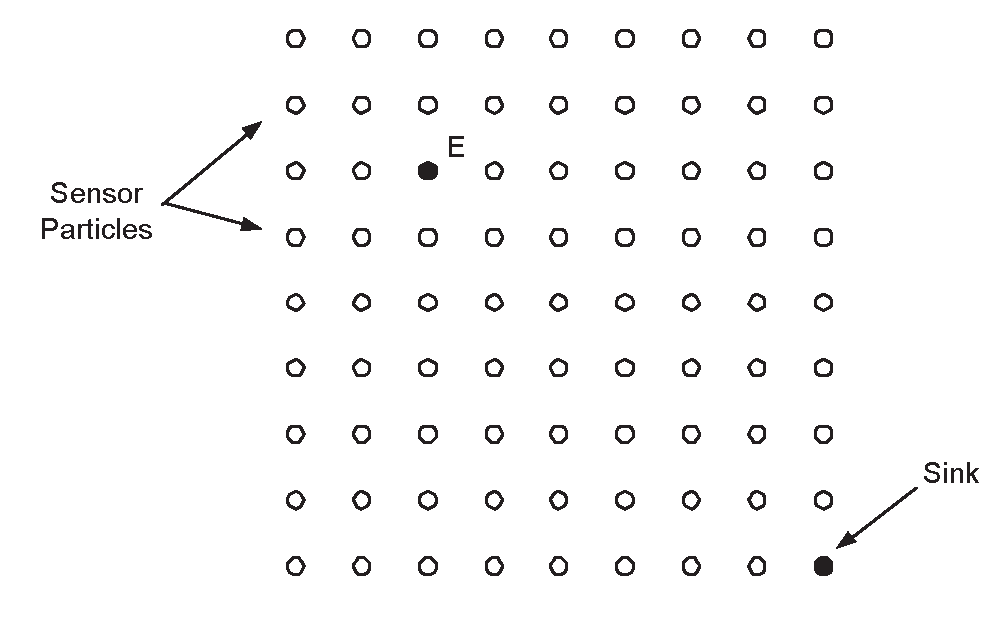
3.3. The Correctness of PFR

Without loss of generality, we assume each square of the fictitious lattice G to have side length 1.

In [9] the authors prove the correctness of the PFR protocol, by using a geometric analysis. We below sketch their proof.

Consider any square Σ intersecting the ES line. By the occupancy argument above, there is with high probability a particle in this square. Clearly, the worst case is when the particle is located in one of the corners of Σ (since the two corners located most far away from the ES line have the smallest ϕ-angle among all positions in Σ).

By some geometric calculations, [9] finally proves that the angle ϕ of this particle is ϕ > 134^o. But the initial square (i.e. that containing E) always broadcasts and any intermediate intersecting square will be notified (by induction) and thus broadcast because of the argument above. Thus the sink will be reached if the whole network is operational.

Lemma 4 ([9]) 

PFR succeeds with probability 1 in sending the information from E to S given the event F.

3.4. The Energy Efficiency of PFR

[9] considers the fictitious lattice G of the network area and let the event F hold. There is (at least) one particle inside each square. Now join all nearby particles of each particle to it, thus by forming a new graph G′ which is “lattice-shaped" but its elementary “boxes” may not be orthogonal and may have varied length. When squares of G become smaller and smaller, then G′ will look like G. Thus, for reasons of analytic tractability, in [9] the authors assume that particles form a lattice (see Figure 7). They also assume length l = 1 in each square, for normalization purposes. Notice however that when l → 0 then “G′ → G” and thus all results in this Section hold for any random deployment “in the limit”.

The analysis of the energy efficiency considers particles that are active but are as far as possible from ES. Thus the approximation is suitable for remote particles.

[9] estimates an upper bound on the number of particles in an n × n (i.e. N = n × n) lattice. If k is this number then $r=\frac{k}{n^2}$ (0 < r ≤ 1) is the “energy efficiency ratio” of PFR.

More specifically, in [9] the authors prove the (very satisfactory) result below. They consider the area around the ES line, whose particles participate in the propagation process. The number of active particles is thus, roughly speaking, captured by the size of this area, which in turn is equal to |ES| times the maximum distance from |ES| (where maximum is over all active particles).

This maximum distance is clearly a random variable. To calculate the expectation and variance of this variable, the authors in [9] basically “upper bound” the stochastic process of the distance from ES by a random walk on the line, and subsequently “upper bound” this random walk by a well-known stochastic process (i.e. the “discouraged arrivals” birth and death Markovian process, see e.g. [31]). Thus they prove the following:

Theorem 1 ([9]) 

The energy efficiency of the PFR protocol is $\Theta \left({\left(\frac{n_0}{n}\right)}^2\right)$ where n₀ = |ES| and $n=\sqrt{N}$, where N is the number of particles in the network. For n₀ = |ES| = o(n), this is o(1).

3.5. The Robustness of PFR

To prove the following robustness result, the authors in [9] consider particles “very near” to the ES line. Clearly, such particles have large ϕ-angles (i.e. ϕ > 134^o). Thus, even in the case that some of these particles are not operating, the probability that none of those operating transmits (during the probabilistic phase 2) is very small. Thus, [9] proves the following.

Lemma 5 ([9]) 

PFR manages to propagate the crucial data across lines parallel to ES, and of constant distance, with fixed nonzero probability (not depending on n, |ES|).

4. The Energy Balance Problem

In order to save energy and keep the network functional for as long as possible, various approaches, including hop-by-hop transmission techniques [8,25,26], as well as clustering techniques [23] and alternating power-saving modes [44] have been proposed.

All such techniques, in their basic form presented in section 2 and section 3, do not explicitly take care of the possible overuse of certain sensors in the network. As an example, remark that in hop-by-hop transmissions towards the sink, the sensors lying closer to the sink tend to be utilized exhaustively (since all data passes through them). Thus, these sensors may die out very early, thus resulting to network collapse although there may be still significant amounts of energy in the other sensors of the network. Similarly, in clustering techniques the cluster-heads that are located far away with respect to the sink, tend to spend a lot of energy.

In this paper, we present the EBP (Energy Balance) protocol, introduced in [16], that probabilistically chooses between either propagating data one hop towards the sink or sending directly to the sink. The first choice is more energy efficient, while the latter bypasses the critical (close to the sink) sectors. The appropriate probability for each choice in order to achieve energy balance is calculated in [16]. We also mention a related, extended protocol (VTRP: Variable Transmission Range Protocol), proposed in [3], that implicitly contributes to energy balance by appropriately adapting (increasing) the transmission range, thus bypassing critical sensors and avoiding possible obstacles.

Figure 8. Sensor Network with n ring sectors, angle ϕ and ring “width” R

Figure 8. Sensor Network with n ring sectors, angle ϕ and ring “width” R

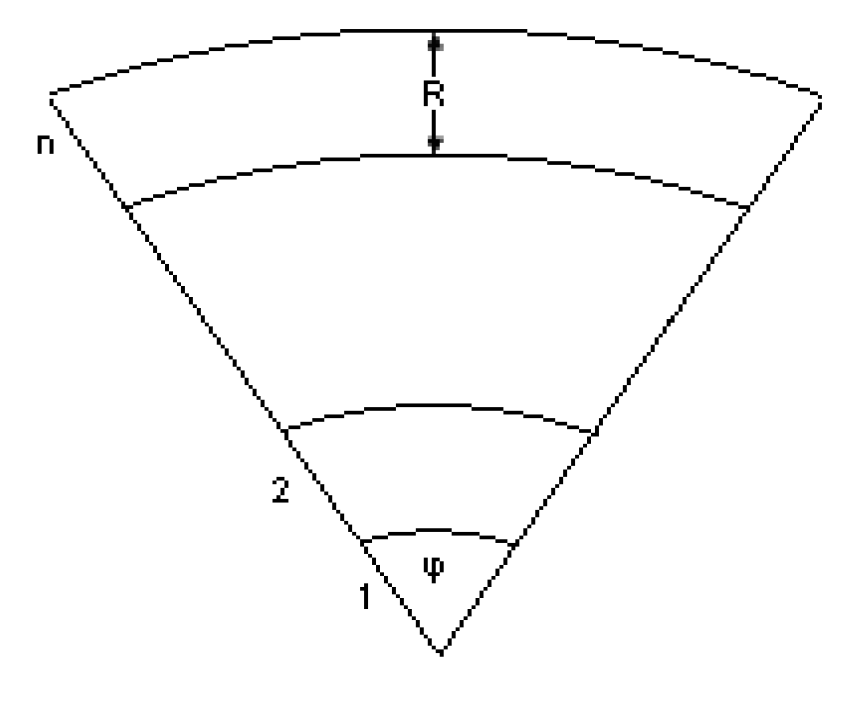
4.1. The Model and the Problem

The basic model M₀ (see section 1.3) is assumed. Additionally, we assume that the transmission range of sensors can vary with time (in fact, for each sensor our protocol may use only two different ranges: R and i · R, where i is a measure of the sensor’s distance to the sink).

We virtually “cover” the network area by a cycle sector of angle ϕ (see Figure 8). Similar ring formation by flooding of beacon messages with hop count has been proposed in [54]. The cycle sector is divided into n ring sectors or “slices”. The first slice has radius R (i.e. the sensors’ transmission range). Slice i (2 ≤ i ≤ n) is defined by two cycles sectors, one of radius i · R and the other of radius (i − 1) · R. We do not address what is the largest allowable transmission range (e.g. the largest i above); this would be limited by technology and interferences. However, taking a sufficiently large angle ϕ and/or by hierarchically taking multiple sectors, we can cover the whole area without increasing i beyond the maximum allowable limit.

In the analysis, we only count (for simplicity) energy spent during transmissions. Since however in our protocol (see next section) there is one receipt for each transmission, it is clear that even when energy during receipt is more or less the same as energy during transmissions, the analysis can be extended easily to the full case (counting both transmissions and receipts). We do not consider energy aspects due to duty-cycling, i.e. we assume that an appropriate power saving scheme is resolving this.

Definition 2 

The area between two consecutive cycle sectors is called a ring sector (or “slice”). Let T_i (1 ≤ i ≤ n) be the i-th ring sector of the network.

T₁ stands for the ring sector with center the sink and radius equal to R.

Definition 3 

Let S_i be the area size of the ring sector T_i of the network (1 ≤ i ≤ n).

We wish to solve the “energy balanced data propagation problem”, i.e. to propagate data to the sink in such a way that the “average” energy dissipation in each sensor is at each time the same. The average energy dissipation per sensor is taken to be the fraction of the total energy spent by sensors in a ring sector over the number of sensors in that sector. Because of our assumption that the number of sensors in an area is proportional to the area size, the average energy dissipation per sensor is calculated by dividing the total energy spent in a sector by the sector size.

We do not study here medium access aspects, assuming the existence of underlying MAC protocol.

4.2. EBP: The Energy Balance Protocol

We assume that each event is sensed by only one sensor. This assumption is not restrictive since we may consider multiple sensing and propagation of an event by various sensors as sensing and propagation of many different events, assuming methods to resolve symmetry (such as clustering, leader election) in cases like when sensors are acoustic and the event is a thunderclap. A sensor sensing an event generates then a data message which should be eventually delivered to the sink. On each ring sector, T_i, a number of events occur and a corresponding number of messages (one for each event) is generated.

Randomization is used to achieve some “load balancing” by evenly spreading the “load” (energy dissipation). In particular, on ring sector T_i each event is propagated to T_i−1 (i.e. the “next” sector towards the sink) with probability p_i, while with probability 1 − p_i it is propagated directly to the sink S. Each message in T_i is handled stochastically independently of the other events’ messages.

The choice of probability p_i for T_i is made so as the average energy consumption per area unit (and thus per sensor) is the same for the whole network. There is a trade-off from choosing p_i: if p_i increases then transmissions tend to happen locally, thus energy consumption is low, however sensors closer to the sink tend to be overused since all data passes through them. On the other hand, if p_i decreases, there are distant transmissions (thus a lot of energy is consumed) however closer to sink particles are bypassed. Calculating the appropriate probability p_i for each T_i and solving the problem of energy balance is very important since it combines efficient data propagation with increased network’s lifetime.

By using an underlying subprotocol [8,25] we can guarantee that only one “next hop” sensor receives the transmitted message. Note also that data messages are of fixed size i.e. no further info is added to a message on its route towards the sink.

Our protocol is (a) distributed, since each sensor chooses propagation probability independently of other sensors, (b) it uses only local information, in the sense that p_i depends only on i, i.e. a parameter related to the distance from the sink. Note that distance from the sink info for each sensor can be easily obtained i.e. during a set-up phase where the sink broadcasts control messages to the network. Several techniques (including signal attenuation evaluation) can be used to estimate each sensor’s distance for the sink. (c) The protocol is very simple, since it just uses a random choice based only on parameter i.

4.3. Basic Definitions - Preliminaries

We aim at calculating probability p_i for each i in order to ensure the energy balance property. Using simple geometry, one can easily prove the following Lemmas.

Lemma 6 

The area size, S₁, of the ring sector T₁ is $S_1=\frac{\varphi }{2}·R^2$

Lemma 7 

The relation between the area size of the ring sector T_i and that of T₁ is S_i = (2i − 1) · S₁

Definition 4 

Let λ_i the probability that an event will occur on the ring sector T_i.

There are n ring sectors in the network.

Lemma 8 

Assuming a random uniform generation of events in the network area, the probability λ_i of an event occurring on the ring sector T_i (1 ≤ i ≤ n), is:

$${\lambda }_i=\frac{(2i-1)}{n^2}$$

Let us now consider sector T_i.

Definition 5 

An area T_i “handles” an event generated in ring sector j if either the message was generated in the area T_i (i.e. j = i) or the message was propagated to T_i from the ring sector T_i+1.

Definition 6 

Let h_i be the number of the messages that are “handled” by the area T_i.

We now define energy ϵ_ij spent for message j when sector i handles it.

Definition 7 

Let ϵ_ij a random variable which measures the energy that dissipates the sector T_i so as to handle the message j. For ϵ_ij we have that:

$${ϵ}_{ij}=\left\{\begin{array}{ccc}c{R}^2\hfill & & \text{with} \text{probability} p_i\hfill \\ c{\left(iR\right)}^2\hfill & & \text{with} \text{probability} 1-p_i\hfill \end{array}\right.$$

where cR² is the energy dissipation for sending a message j from T_i to its adjacent ring sector T_i−1 and c is a constant.

Thus, the expected energy dissipation in sector i for handling a message is

$$E\left[{ϵ}_{i,j}\right]=c{R}^2·[i^2-p_i(i^2-1)]$$

(1)

Note: The expected energy above is the same for all messages; we use j just for counting purposes.

Definition 8 

Let $ℰ$_i the total energy spent by sensors in T_i. Clearly:

$${\mathcal{E}}_i=\sum _{j=1}^{h_i}{ϵ}_{ij}$$

(2)

Energy balance is defined as follows:

Definition 9 

The network is energy balanced if the average per sensor energy dissipation is the same for all sectors, i.e. when

$$\frac{E\left[{\mathcal{E}}_i\right]}{S_i}=\frac{E\left[{\mathcal{E}}_j\right]}{S_j}i,j=1,\dots ,n$$

(3)

4.4. The General Solution

We next provide a lemma useful in the estimation of the total energy dissipation in a sector.

Lemma 9 

The expected total energy dissipation in sector i is:

$$E\left[{\mathcal{E}}_i\right]=E\left[h_i\right]·E\left[{ϵ}_{ik}\right]$$

Proof: 

$$\begin{array}{ccc}\hfill E\left[{\mathcal{E}}_i\right]& =& E\left[\sum _{k=1}^{h_i}{ϵ}_{ik}\right]\hfill \\ & =& \sum _{n=0}^{N}E\left[\sum _{k=0}^{h_i}\left({ϵ}_{ik}\cap h_i=n\right)\right]\hfill \\ & =& \sum _{n=0}^{N}E\left[\sum _{k=1}^{h_i}{ϵ}_{ik}|h_i=n\right]·\mathrm{I}\mathrm{P}\{h_i=n\}\hfill \end{array}$$

Furthermore,

$$\begin{array}{ccc}E\left[\sum _{k=1}^{h_i}{ϵ}_{ik}|h_i=n\right]\hfill & =& E\left[\sum _{k=1}^n{ϵ}_{ik}\right]=\sum _{k=1}^{n}E\left[{ϵ}_{ik}\right]\hfill \\ & =& n·E\left[{ϵ}_{ik}\right]\hfill \end{array}$$

Thus, we have from the above that:

$$\begin{array}{ccc}\hfill E\left[{\mathcal{E}}_i\right]& =& \sum _{n=0}^{N}E\left[\sum _{k=1}^{h_i}{ϵ}_{ik}|h_i=n\right]·\mathrm{I}\mathrm{P}\{h_i=n\}\hfill \\ & =& E\left[{ϵ}_{ik}\right]·E\left[h_i\right]\hfill \end{array}$$

Definition 10 

Let g_i be the number of the messages that are generated in the area T_i.

Note that messages are generated in an area only when events occur in this area.

Definition 11 

Let f_i be the number of the messages that are forwarded to the area T_i.

We note that messages are forwarded to a ring sector (say i) only because of an event generation at a sector j > i and successive one-hop propagations from sector j to sector i.

We notice the following important relation:

$$h_i=g_i+f_i$$

(4)

which means that the number of messages that area T_i handles equals the number of the messages that are generated in T_i, plus the number of messages that are forwarded to it. Because of event generation according to a probability distribution and also because of the probabilistic nature of message propagation in, all three quantities above are random variables. By linearity of expectation, we get:

Lemma 10 

E[h_i] = E[g_i] + E[f_i]

We establish a relationship between E[f_i] and E[h_i+1].

Lemma 11 

E[f_i] = p_i+1 · E[h_i+1]

Proof: 

Let δ_i,j an indicator random variable that is equal to 1 if area T_i forwards the message j to the area T_i−1 and 0 otherwise. Thus:

$${\delta }_{i,j}=\left\{\begin{array}{ccc}1\hfill & & \text{with} \text{probability} p_i\hfill \\ 0\hfill & & \text{with} \text{probability} 1-p_i\hfill \end{array}\right.$$

Clearly, δ_i,j depends only on i, but we add j for counting purposes. Obviously, E[δ_i,j] = p_i. It is:

$$f_i=\sum _{j=0}^{h_{i+1}}{\delta }_{i+1,j}$$

Similarly to the proof of Lemma 9, we get:

$$E\left[f_i\right]=\sum _{n=0}^{N}E\left[\sum _{j=0}^{h_{i+1}}{\delta }_{i+1,j}|h_{i+1}=n\right]·\mathrm{I}\mathrm{P}\{h_{i+1}=n\}$$

and the proof is completed.

Recall that, according to Definition 9, to achieve the same on the average energy dissipation per area unit (and thus per sensor) in the network area, the following equality should hold:

$$E\left[\frac{{\sum }_{k=1}^{h_i}{ϵ}_{ik}}{S_i}\right]=E\left[\frac{{\sum }_{k=1}^{h_j}{ϵ}_{jk}}{S_j}\right]\forall i,j\in \{1,\dots n\}$$

(5)

i.e. the average energy consumption per sensor should be equal in any two ring sectors. By induction, it suffices to guarantee this for any two adjacent sectors. In what follows, we guarantee the above balance property, requiring a certain recurrence relation to hold. This recurrence basically relates 3 successive terms of the E[f_i] sequence (the E[g_i] terms depend only on i and on input parameters).

Theorem 2 

To achieve energy balance in the network, the following recurrency equation should hold:

$$\begin{array}{c}\hfill a_{i+1}E\left[f_{i+1}\right]-(d_i+a_i)E\left[f_i\right]+d_{i-1}E\left[f_{i-1}\right]=\\ \hfill =a_{i}E\left[g_i\right]-a_{i+1}E\left[g_{i+1}\right]\end{array}$$

where

$$\begin{array}{ccc}{a}_i=\frac{i^2}{2i-1}\hfill & & d_i=\frac{{(i+1)}^2-1}{2i+1}\hfill \end{array}$$

Proof: 

For the case j = i + 1 of the equation 5 and using the lemmata 7 and 9 we have:

$$\begin{array}{c}\frac{E\left[h_i\right]E\left[{ϵ}_{i,j}\right]}{S_i}=\frac{E\left[h_{i+1}\right]E\left[{ϵ}_{i+1,j}\right]}{S_{i+1}}\iff \hfill \\ \\ \frac{E\left[h_i\right][i^2-p_i(i^2-1)]}{(2i-1)}=\frac{E\left[h_{i+1}\right]\{{(i+1)}^2-p_{i+1}[{(i+1)}^2-1]\}}{(2i+1)}\iff \hfill \\ \\ \frac{i^2}{2i-1}E\left[h_i\right]-p_{i}E\left[h_i\right]\frac{i^2-1}{2i-1}=\hfill \\ \\ =\frac{{(i+1)}^2}{2i+1}E\left[h_{i+1}\right]-p_{i+1}E\left[h_{i+1}\right]\frac{{(i+1)}^2-1}{2i+1}\hfill \end{array}$$

Let a_i, d_i as defined in the Theorem statement above. By lemma 11 we know that p_iE[h_i] = E[f_i−1] and by lemma 10 it is E[h_i] = E[g_i] + E[f_i] thus the last equation becomes:

$$\begin{array}{c}{a}_{i+1}E\left[f_{i+1}\right]-(d_i+a_i)E\left[f_i\right]+d_{i-1}E\left[f_{i-1}\right]=\hfill \\ \\ =a_{i}E\left[g_i\right]-a_{i+1}E\left[g_{i+1}\right]\hfill \end{array}$$

To solve the above recurrency we must compute E[g_i].

Lemma 12 

If N is the total number of events that are generated in the network, the mean value of g_i is given by the following relationship:

$$E\left[g_i\right]=N·{\lambda }_i$$

Proof: 

Because the position of each event is independent of other events and because for each sector i, probability λ_i is the same, clearly g_i is binomial with parameters N, λ_i.

In order to have a simpler recurrence involving only two (successive in fact) terms of the E[f_i] sequence, we will transform the recurrency relation of Theorem 2 into the following (easier to solve) relation:

Lemma 13 

The recurrency relation:

$$\begin{array}{c}{t}_i-t_{i-1}=a_i·E\left[f_i\right]-a_{i+1}·E\left[f_{i+1}\right]\hfill \\ \text{for}i=1,\dots n-1\hfill \\ \text{and}{t}_0=a_1·E\left[f_1\right]\hfill \end{array}$$

has as a solution the function

$$t_i=\sum _{j=1}^i\left(a_{j}E\left[g_j\right]-a_{j+1}E\left[g_{j+1}\right]\right)+a_1·E\left[f_1\right]$$

Proof: 

The proof is done by induction on i. For i = 0, it is obviously true. Let it be true for i − 1. For i we have:

$$t_i=t_{i-1}+a_i·E\left[g_i\right]-a_{i+1}·E\left[g_{i+1}\right]$$

By the induction hypothesis we get the solution

$$t_i=\sum _{j=1}^i\left(a_{j}E\left[g_j\right]-a_{j+1}E\left[g_{j+1}\right]\right)+a_1·E\left[f_1\right]$$

Now the recurrency relation of Thrm 2 is simplified:

$$a_{i+1}·E\left[f_{i+1}\right]-d_i·E\left[f_i\right]=t_{i}i=1,\dots ,n-1$$

Thus, we get a recurrence for sequence E[f_i] involving only two successive terms of the sequence:

Theorem 3 

The recurrency relation

$$a_{i+1}E\left[f_{i+1}\right]-d_{i}E\left[f_i\right]=t_{i}i=1,\dots n-1$$

where t_i is defined in lemma 13, has the following solution

$$E\left[f_{n-i}\right]=-\sum _{k=1}^i\frac{{\prod }_{j=k}^{i-1}{a}_{n-j}}{{\prod }_{j=k}^i{d}_{n-j}}·t_{n-k}$$

The proof is rather complex, so we omit it here. The interested reader may find it in [16].

The full expression for E[f_i] can be expressed by substituting i with n − i, thus

$$\begin{array}{c}E\left[f_i\right]=-\sum _{k=1}^{n-i}\frac{{\prod }_{j=k}^{n-i+1}{a}_{n-j}}{{\prod }_{j=k}^{n-i}{d}_{n-j}}·\left(\sum _{j=1}^{n-k}(a_{j}E\left[g_j\right]-a_{j+1}E\left[g_{j+1}\right])+a_1·E\left[f_1\right]\right)\hfill \end{array}$$

where ${\prod }_i^{i-1}{a}_i=1$.

We note that all the parameters of the recurrency solution above are expressed as a function of E[f₁] and i. So as to compute them, we firstly compute the value of E[f₁]. Then we can compute all the other parameters by replacing the already computed E[f₁].

Now, the calculation of the probabilities p_i is quite easy.

Theorem 4 

The energy balance property is achieved if any ring sector (say T_i) propagates each message it handles with probability p_i to the next ring sector, T_i−1, and with probability 1 − p_i it propagates the message directly to the sink. The value of each p_i is given by the following relation

$$p_i=\frac{E\left[f_{i-1}\right]}{E\left[g_i\right]+E\left[f_i\right]}$$

where the values of E[f_i] and E[g_i] are obtained from lemma 3 and lemma 12, respectively.

Proof: 

From equation 11 we know that E[f_i−1] = p_iE[h_i] and also by lemma 10 we know that E[h_i] = E[g_i] + E[f_i]. ⋄

Remark. 

Note that, interestingly, p_i’s are independent of the number N of the events that occur in the network, since p_i’s depend only on i and the number of ring sectors n (which is broadcast to sectors by the sink). Thus the protocol assumes only local information.

We note that the analysis above allows the exact derivation of probabilities p_i’s as a function of i and n which (although complicated and not obviously leading to a closed form) can be easily calculated by the sensors in the network by carrying out very simple calculations.

The authors of [16] also prove the correctness of the protocol:

Theorem 5 

Given that the energy is each time on the average the same in all network sensors, each message will finally get to the sink.

4.5. A Closed Form

Under specific assumptions (that we discuss and motivate) we can make the calculation of probabilities p_i simpler. Combining lemma 10 and lemma 12 we have that

$$E\left[h_i\right]={\lambda }_{i}N+E\left[f_i\right]=\frac{2i-1}{n^2}N+E\left[f_i\right]$$

(6)

By the corresponding relation for E[h_i−1] it must be:

$$\begin{array}{c}\frac{\frac{2i-1}{n^2}N+E\left[f_i\right]}{(2i-1)\frac{\varphi }{2}{R}^2}[p_i+(1-p_i)i^2]R^2=\frac{\frac{2i-3}{n^2}N+E\left[f_{i-1}\right]}{(2i-3)\frac{\varphi }{2}{R}^2}[p_{i-1}+(1-p_{i-1}){(i-1)}^2]R^2\hfill \end{array}$$

But 2i − 1 ≃ 2i − 3 and $\frac{\varphi }{2}$, R² cancel. Dividing by N we get:

$$\begin{array}{c}\left[1+\frac{E\left[f_i\right]}{N}\right]\left[p_i+(1-p_i)i^2\right]\simeq \left[1+\frac{E\left[f_{i-1}\right]}{N}\right]\left[p_{i-1}+(1-p_{i-1}){(i-1)}^2\right]\hfill \end{array}$$

If E[f_i] ≃ E[f_i−1] then the previous relation becomes:

$$p_i+(1-p_i)i^2=p_{i-1}+(1-p_{i-1}){(i-1)}^2$$

(7)

In [16] we show how to solve the above recurrence.

Theorem 6 

If E[f_i] ≃ E[f_i−1], 3 ≤ i ≤ n, then the one-hop forwarding probability, guaranteeing energy balance, is

$$p_i=1-\frac{3x}{(i+1)(i-1)}$$

where p₂ = x ∈ (0, 1) a free parameter and p₁ = 0.

We remark that the assumption E[f_i] ≃ E[f_i−1] is quite reasonable and well motivated. We provide the following intuitive explanation of why this happens. Remark indeed that the area sizes of adjacent sectors (and thus the number of events generated in such sections) are more or less the same, especially when i increases. Furthermore, the probability p_i of forwarding to the adjacent (towards the sink) sector increases very fast with i and becomes 1 in most sectors of the network (in the middle territory).

4.6. Further research on energy balance

In [59] the authors propose a generalized data propagation algorithm, which allows to jump over bottleneck nodes. They investigate whether hops to intermediate slices help. They consider mixed propagation (i.e. only single hops and direct to sink transmissions) and interestingly show that mixed strategies beat every other possible strategy (wrt optimizing the network lifespan). Indeed, they prove that lifespan is maximized by a mixed data propagation algorithm. They then use this fact to propose am optimal distributed data propagation algorithm. Their method uses a LP maximizing the generalized flow, subject to certain constraints (detection rates, energy and flow constraints). They rigorously prove that if there exists an energy-balanced mixed flow it maximizes the mixed-flow and it also maximizes the generalized-flow. Thus, they can maximize the generalized-flow problem using a mixed-flow and a local property (energy-balance). Their algorithm produces a mixed flow and at the same time balances energy, while its stability is shown using Markov Chain methods.

In [58] the authors consider that nodes can send messages directly to the sink. They propose an algorithm to compute the optimal solution (in terms of lifetime), i.e. to compute the ejection probabilities. They interestingly show that when there exists an energy balanced solution, it is optimal. When it is not possible to balance energy, the algorithm still finds an optimal solution. They give a necessary and sufficient condition for a solution to be optimal.

Part B: Network Design for Energy Optimization 

5. Tracking Moving Entities

5.1. Problem Description

We wish to solve the problem of localizing and continuously tracking mobile objects moving in a domain described by a set of set of three-dimensional curves, S, over a period of time T i.e. we want the wireless sensor network to be able to detect the position of any moving object, at any time t in T. We allow multiple targets that arise in the network area at random locations and at random times. The movement of each target can follow an arbitrary but continuous path i.e. we disallow the target to instantaneously “jump” to another location; still, we can handle such discontinuities as multiple targets.

In our setting, the set S of 3D curves is the set of possible trajectories of objects moving for some time within the period T. Such a moving object might follow a part of a curve in S, and possibly arrive to an intersection of curves and then follow another curve.

We can assume that each such curve in S is specified (for t = 0, …, T) by an analytic equation (e.g. in x, y, z coordinates). Thus, we can compute a curve (route) piece τ_ij for the curve (route) R_i, via some criterion (e.g. to split R_i into pieces of equal length). We, then, wish to deploy some sensors (either standing or even moving for some time) in some (initial) places within S. A basic demand for such a deployment consists of the following rule:

(Rule R) For every point $\stackrel{\rightharpoonup }{p}=(x,y,z)$ in S and for every t ∈ [0, T] there are at least three sensors, active at time t, whose sensing range includes the point $\stackrel{\rightharpoonup }{p}$. Here, for a sensor σ operating at time t, its sensing range is a sphere of some radius R_σ(t) and with center the position of σ at time t.

Note that rule R guarantees localization of any moving target in S at any time t in T, via triangulation.

We follow a network design approach to this problem. Let us assume, hypothetically, that we could have an abundance of sensors, each characterized by an initial position, an operation period, and an initial available energy (battery) that allows a particular implementation of sensing ranges during the operation of the sensor. Then, the decision to actually select one sensor (with the initial position, operating period and available energy) has a certain cost. Our goal is to be able to select a subset of sensors that implement rule (R) and is of nearly minimal cost.

The problem we study is related (but different) to the problems of network coverage and tracking. In fact, we extend the well-studied coverage problems by being able to track the moving path, and by also taking time into account. On the other hand, to reduce the energy dissipation and overhead of our tracking solution, we avoid some of the collaborative information processing components (like which nodes should sense, which have useful information and should communicate, which should receive information and how often). Thus, we are not dealing directly with queries of the type “how many targets are in a certain region during a certain time interval”. Still, our solution performs the collaborative processing tasks (triangulation by at least three sensors) that allow localization of the targets as they move in the network. Also, we discuss how alternative collaborative processing methods can be combined with our approach to provide full tracking.

5.2. Our Contribution

Our approach indeed tries to avoid the expensive, massive placement of all the time functioning sensors all over the monitoring area, by exploiting possible overlaps of routes at certain places in the network area, using sensors that can simultaneously monitor pieces of several ("nearby") routes during their operation, or even exploit sensors on top of certain moving objects of our own that wander in the maze of routes. Thus, we somehow “multiplex” (both over space and time) the use of deployed sensors, since our approach identifies overlaps over space and time and thus deploys fewer sensors compared to the trivial approach.

In fact, the analysis of our method shows that it is very efficient, especially in very large domains, both with respect to computational time and the deployment cost, since it finds in polynomial expected time a deployment solution which approximates the optimal solution within a logarithmic factor. Thus, we avoid expensive dense deployment of sensors, where the information about the target is simultaneously generated by multiple sensors; we instead achieve a low cost solution (by removing unnecessary redundancy) that still keeps tracking accuracy at high levels.

To be able to handle overlaps, we propose a novel combinatorial model for possible routes in the network domain. This model, although abstract, captures several of the technical specifications of real sensor devices, such as the energy spent as a function of the transmission range, the ability to vary this range to save energy or increase connectivity, the ability of sensors to employ power saving (sleep-awake) schemes to save energy etc. This combinatorial model allows us to reduce the tracking problem to a variation of a combinatorial problem of set covering (in particular to “at least 3 cover”, i.e. having each point of the domain covered at any time by at least 3 sensors, and thus being localized). We feel that this combinatorial model is of independent interest and can (itself or its variations) be used in modeling other problems as well.

5.3. Related Work and Comparison

As discussed in the problem definition part, the problem we study is relevant to network coverage and tracking, that we discuss below.

Coverage

Sensor deployment strategies play a very important role in providing better QoS, which relates to the issue of how well each point in the sensing field is covered. However, due to severe resource constraints and hostile environmental conditions, it is nontrivial to design an efficient deployment strategy that would minimize cost, reduce computation, minimize node-to-node communication, and provide a high degree of area coverage.

Several deployment strategies have been studied for achieving an optimal sensor network architecture. Dhilon et al. propose a grid coverage algorithm that ensures that every grid point is covered with a minimum confidence level [13]. They consider a minimalistic view of a sensor network by deploying a minimum number of sensors on a grid that would transmit a minimum amount of data. Their algorithm is iterative and uses a greedy heuristic to determine the best placement of one sensor at a time. It terminates when either a preset upper limit on the number of sensors is reached or sufficient coverage of the grid points is achieved. However, the algorithm assumes line of sight of the target and the sensor. Also, since a complete knowledge of the terrain is assumed, the algorithm is not very applicable in cluttered environments, such as interior of buildings, because modeling obstacles becomes extremely difficult in those scenarios. Finally, a main difference of this approach (and in fact the other coverage methods as well) with ours, is that we explicitly take time into account.

In contrast to static sensor networks, nodes in mobile sensor networks are capable of moving in the sensing field. Such networks are capable of self-deployment starting from an initial configuration. The nodes would spread out such that coverage in the sensing field is maximized while maintaining network connectivity. A potential field-based deployment approach using mobile autonomous robots has been proposed to maximize the area coverage [40]. Clearly, the assumptions of this method (and the one described below) are different to ours, since we do not use sensor mobility as an algorithmic design element (although we handle mobility when it appears).

Similar to the potential field approach, a sensor deployment algorithm in the presence of mobility based on virtual forces has been proposed in [53] to increase the coverage after an initial random deployment. A sensor is subjected to forces, which are either attractive or repulsive in nature. In this approach, obstacles exert repulsive forces, while areas of preferential coverage (sensitive areas where a high degree of coverage is required) exert attractive forces, and other sensors exert attractive or repulsive forces. A hard threshold distance is defined between two sensors to control how close they can approach each other.

Other interesting network coverage approaches are discussed in the book chapter by A. Ghosh and S. Das in [43].

Tracking

Our method follows and extends the well-established line of research for a network architecture design for centralized placement/distributed tracking (see e.g. the book [43] for a nice overview). According to that approach, optimal (or as efficient as possible) sensor deployment strategies are proposed to ensure maximum sensing coverage with minimal number of sensors, as well as power conservation in sensor networks.

Centralized Approaches

In one of the methods, that focuses on deployment optimization, a grid manner discretization of the space is performed [7]. Their method tries to find the grid point closest to the target, instead of finding the exact coordinates of the target. In such a setting, an optimized placement of sensors will guarantee that every grid point in the area is covered by a unique subset of sensors. Thus, the sensor placement problem can be modeled as a special case of the alarm placement problem described by Rao [41]. That problem is the following: given a graph G, which models a system or a network, one must determine how to place ”alarms” on the nodes of G so that any single node fault can be diagnosed. It has been shown in [41] that the minimal placement of alarms for arbitrary graphs is an NP-complete problem. Clearly, their problem is easier than ours, since they relax the requirement to find exact coordinates of moving objects by just finding the nearest grid point. Since their problem is computationally difficult, this implies the inherently high complexity of our problem. Another indication of the hardness of the problem is the fact that, as shown in [5], the localization problem is NP-hard in sparse wireless sensor networks.

Also, our problem is related but different to the following other well known approach that focuses on power conservation: in [18] sleep−awake patterns for each sensor node are obtained during the tracking stage, to obtain power efficiency. The network operates in two stages: the surveillance stage during the absence of any event of interest, and the tracking stage, in response to the presence of moving targets. Each sensor initially works in the low-power mode when there are no targets in its proximity. However, it should exit the low-power mode and be active continuously for a certain amount of time when a target is sensed, or even better, when a target is shortly about to enter. Finally, when the target passes by and moves farther away, the node should decide to switch back to the low-power mode. Our approach is also power aware in the same sense (since we also affect the duration of sensors’ operation), but additionally we also control the transmission range (and thus the power dissipation).

Another centralized approach, is “sensor specific”, in the sense it uses some smart powerful sensors that have high processing abilities [19]. In particular, this algorithm assumes that each node is aware of its absolute location via a GPS or a relative location. The sensors must be capable of estimating the distance of the target from the sensor readings.

Distributed Approaches

As opposed to centralized processing, in a distributed model sensor networks distribute the computation among sensor nodes. Each sensor unit acquires local, partial, and relatively coarse information from its environment. The network then collaboratively determines a fairly precise estimate based on its coverage and multiplicity of sensing modalities. Several such distributed approaches have been proposed. Although we are not comparing with them, we shortly discuss some of them, for completeness.

In [32], a cluster-based distributed tracking scheme is provided. The sensor network is logically partitioned into local collaborative groups. Each group is responsible for providing information on a target and tracking it. Sensors that can jointly provide the most accurate information on a target (in this case, those that are nearest to the target) form a group. As the target moves, the local region must move with it; hence groups are dynamic with nodes dropping out and others joining in. It is clear that time synchronization is a major prerequisite for this approach to work. Furthermore, this algorithm works well for merging multiple tracks corresponding to the same target. However, if two targets come very close to each other, then the mechanism described will be unable to distinguish between them.

Another nice distributed approach is the dynamic convoy tree-based collaboration (DCTC) framework that has been proposed in [51]. The convoy tree includes sensor nodes around the detected target, and the tree progressively adapts itself to add more nodes and prune some nodes as the target moves. In particular, as the target moves, some nodes lying upstream of the moving path will drift farther away from the target and will be pruned from the convoy tree. On the other hand, some free nodes lying on the projected moving path will soon need to join the collaborative tracking. As the tree further adapts itself according to the movement of the target, the root will be too far away from the target, which introduces the need to relocate a new root and reconfigure the convoy tree accordingly. If the moving target’s trail is known a priori and each node has knowledge about the global network topology, it is possible for the tracking nodes to agree on an optimal convoy tree structure; these are at the same time the main weaknesses of the protocol, since in many real scenaria such assumptions are unrealistic.

The interested reader is encouraged to refer to [52], the nice book by F. Zhao and L. Guibas, that even presents the tracking problem as a “canonical” problem for wireless sensor networks. Also, several tracking approaches are presented in [43]. Other tracking methods, including interesting algorithmic components, have appeared in [53,55,56,57]. This work has appeared in [37].

5.4. The Model and its Combinatorial Abstraction

Sensors and Sensor Network

The basic model M₀ is used, with some additional assumptions (see section 1.3). Let n be the total number of available sensor devices for deployment. Let S be the set of possible deployment positions (i.e. the union of 3D curves as we described earlier). Let T be a period of time. For each sensor σ of the n available sensors, a placement act, A_σ, is a decision (i) either not to deploy σ or (ii) to deploy σ in an initial position $\stackrel{\rightharpoonup }{p}$ in S, for a period T_σ ⊆ T, with a pre-specified pattern of R₁(t), R₂(t) (t ∈ T_σ) and a possible trajectory of σ moving in S for all t in T_σ. All the placement acts, together, form a sensor network N. We assume here that N is capable of (somehow) reporting the sensing of local events (i.e. tracking events) to some set of sinks T_N.

A model for targets

In contrast to models that allow only a single moving target, we allow multiple targets. We assume that the initial positions of all targets are arbitrary. Also, we assume that all targets arise in arbitrary times during the network operation.

With respect to target mobility, we assume that each target follows an arbitrary path in S which is however continuous i.e. we disallow the target to instantaneously “jump” to another location. Furthermore, we do not limit the movement speed of targets; we only assume that when a target enters the sensing area of an (awake) sensor, it does not manage to leave this area before being sensed. This limit on motion speed is rather trivial, since sensing speed is very high i.e. practically the time needed for a target to be sensed is very close to zero.

The combinatorial model

Assume a given complicated 3D domain, S, with obstacles that disallow signal transmissions (e.g. a set of corridors in buildings or different shape obstacles in a mountain). By “complicated” we mean that the domain can be represented by arbitrary three-dimensional curves (see also the problem description subsection), i.e. the only modeling restriction on the curves is their continuity. We further assume that the domain can be represented by the union of λ routes R₁, …, R_λ (each can be realized by e.g. a moving robot or air-vessel). We are also given a period T of time.

We wish to equip each route with sensors (of varying capabilities e.g. varying transmission range and operation times) so that any moving object in the domain at any time t in T can be “seen” by at least three sensors (and, thus, its instantaneous position can be found by triangulation). If we can manage this, we can monitor the motion of any moving object within S during T.

A trivial, but very costly, solution is to equip each route with sensors (in various points of the route) each operating during the whole T and being able to track any motion in a part of the route. However, one could exploit overlaps of routes at certain places, sensors that can monitor pieces of several routes (“nearby”) during their operation, or even sensors on top of certain moving objects of our own that wander in the maze of routes.

In order to argue about such economic tracking methods, we view each R_i partitioned into several “route pieces” r_ij. Let n_i be the number of the pieces of R_i. We also partition the period T into suitable intervals τ₁, …, τ_k so that T = τ₁ + … + τ_k.

We call an “element” each pair (r_ij, τ_m) , for 1 ≤ i ≤ λ, 1 ≤ j ≤ n_i and 1 ≤ m ≤ k. There are $n=\left({\sum }_{i=1}^{\lambda }{n}_i\right)·k$ such elements.

We can then describe sensor placements (that work for a certain duration each) as relations (sets) between those elements. For example: (a) a sensor placed at $r_{i5}$ can also “see” $r_{j7}$, $r_{k30}$. This sensor can operate for 3 intervals. If we start it at ${\tau }_1$ then the element ($r_{i5},{\tau }_1$) “covers” the elements ($r_{i5},{\tau }_2$), ($r_{i5},{\tau }_3$) but also ($r_{j7},{\tau }_1$), ($r_{j7},{\tau }_2$), ($r_{j7},{\tau }_3$) and ($r_{k30},{\tau }_1$) ($r_{k30},{\tau }_2$) ($r_{k30},{\tau }_3$). (b) A sensor is attached to a moving object that moves from $r_{11}$ to $r_{12}$ to $r_{13}$ and then $r_{34}$, $r_{35}$, $r_{36}$. The sensor lasts 6 intervals and our moving object starts at ${\tau }_5$. Then, element ($r_{11},{\tau }_5$) “covers” elements ($r_{12},{\tau }_6$), ($r_{13},{\tau }_7$) and also ($r_{34},{\tau }_8$), ($r_{35},{\tau }_9$), ($r_{36},{\tau }_{10}$) (and itself, of course).

In general, each placement of a certain sensor activated at a certain time and operating for a certain time, corresponds to a set of “covered” elements. Each such “set” has a certain cost e.g. it is more expensive if the sensor’s battery is such that the sensor lasts for a long time. Also it is more expensive if its sensing range is large and can “see” more route pieces.

Definition 12 

A redundant monitoring design (RMD) D is a set of possible choices of $q\le n$ sensors ${\sigma }_1,\dots ,{\sigma }_q$, each with a placement act $A\left({\sigma }_i\right)$ of the form “deploy” and the associated cost of the placement act.

Each RMD results in a family of sets ${\Sigma }_1,\dots ,{\Sigma }_q$, each having a cost $c\left({\Sigma }_i\right)>0$ and each being a subset of our universal set of elements $U=\{e:e\text{ is a pair}(r_{ij},{\tau }_m)\}$.

For feasibility of the RMD we can require:

(a)

that the union of all ${\Sigma }_i$ is U.

(b)

that each e in U belongs to at least 3 ${\Sigma }_i$ sets initially.

However, this is not necessary for our method, since the method itself will discover an infeasible RMD.

Definition 13 

Given are an instance of an RMD of sets ${\Sigma }_1,\dots ,{\Sigma }_q$ on the universe U of elements related to the domain S and the period T, and also a cost $c\left({\Sigma }_i\right)\ge 0$ for each ${\Sigma }_i$. Then, an optimal final monitoring decision (Optimal FMD) is a sub-collection, F, of sets $\{{\Sigma }_{t_1},\dots ,{\Sigma }_{t_{q^{\prime }}}\}$ (where $q^{\prime }\le q$ and each $t_i\in \{1,2,\dots ,q\}$), whose total cost $c\left(F\right)={\sum }_{j=1}^{q^{\prime }}c\left({\Sigma }_{t_j}\right)$ is minimum, and such that (i) ${\cup }_i{\sum }_{t_i}^{}=U$ (ii) each e in U belongs to at least 3 sets in the sub-collection F.

We note that we can construct several RMDs for each run of our Algorithm, get a close to optimal solution (FMD) for each and select the best among them.

5.5. A way to compute near optimal FMDs

From the above formulation, the Optimal FMD problem is actually the following “AT-LEAST-3-SET-COVER” problem:

AT-LEAST-3-SET-COVER ($\ge 3SC$): Given $D=({\Sigma }_1,\dots ,{\Sigma }_q)$ where each ${\Sigma }_i\subseteq U$ (and the union of all ${\Sigma }_i$ is U) and given the costs $c\left({\Sigma }_i\right)\ge 0$, select a minimum total cost sub-collection F of D so that each element e in U belongs to (is “covered” by) at least 3 sets in F.

Important note: Note that geometry and geometric covers can not help here because the domain since S is a complicated 3D domain that can be highly irregular; also, the timing parts of the elements escape the Cartesian geometry; finally, the cost of each ${\Sigma }_i$ is a complicated function of placement decisions of sensors of various capabilities.

The problem of $\ge 3SC$ is NP-hard. This is so, since the usual min-cost SET-COVER problem can be reduced to it by adding to any instance of SET-COVER two sets of zero cost, each covering all elements.

We now describe a formulation of the problem as an integer linear program and give an approximate solution based on randomized rounding. Note that our method can be extended to low cost “SET-COVER by a at least l sets” (let us denote this problem as $\ge l$-SET-COVER) if the redundancy of $l>3$ is needed to make the redundant monitoring decision D easier to construct and fault-tolerant.

We remind the reader of the computational complexity of set covering problems: Lund and Yannakakis showed in 1994 that set cover cannot be approximated in polynomial time to within a logarithmic factor, unless NP has quasi-polynomial time algorithms [33]. Feige improved their inapproximability lower bound, under the same assumptions, giving a slightly better bound that essentially matches the approximation ratio achieved by the greedy algorithm [17]. Alon, Moshkovitz, and Safra established a larger lower bound, under the weaker assumption that P ≠ NP [2]. The k-set cover problem is a variant in which every set is of size bounded by k. While k-set cover problem can be solved in polynomial time (via matchings) for $k=2$, it is NP-complete and even MAX SNP-hard for $k\ge 3$. Greedy algorithms in that case achieve an approximation ratio of $lnk+\Theta \left(1\right)$. Hardness results show that it is not approximable within $(1-ϵ)lnn$, under strong complexity-theoretic evidence [17]. For 3-set cover, besides linear programming techniques (fractional covers), also local and “semi-local” approximation techniques have been used e.g. in [14,20,21].

The randomized rounding method

For set Σ let $x(\Sigma )$ be 1 if Σ is selected and 0 else. We want to

$$\text{minimize} \sum _{\Sigma \text{in} D}^{}x(\Sigma )·c(\Sigma )$$

subject to

(1)

$x(\Sigma )\in \{0,1\}$

(2)

Let $E\left(e\right)$ be the collection of all Σ containing element e. Then, for each element e,

$$\sum _{\Sigma \text{in} E_e}^{}x(\Sigma )\ge 3$$

Let IP1 be the above integer linear program.

We relax the above integer program to the following linear program (LP1):

$$\text{minimize} \sum _{\Sigma \text{in} D}^{}x(\Sigma )c(\Sigma )$$

given that

(1)

$\forall \Sigma ,0\le x(\Sigma )\le 1$

(2)

$\forall e,{\sum }_{\Sigma \text{in} E\left(e\right)}^{}x(\Sigma )\ge 3$

Let $\left\{p\right(\Sigma \left)\right\}$ be the optimal solution to the above (i.e. $x(\Sigma )=p(\Sigma )$ get the minimum). We can find $\left\{p\right(\Sigma \left)\right\}$ in polynomial time in the size n of the redundant monitoring decision D.

We then form a subcollection of sets as follows:

Initially $C=\varnothing$

Experiment E.

For each Σ in D, put Σ into the sub-collection C with probability $p(\Sigma )$, independently of the others.

The experiment E above outputs a sub-collection C. Clearly,

$$E\left(cost\left(C\right)\right)=\sum _{\Sigma \text{in} D}^{}c(\Sigma )\mathrm{I}\mathrm{P}\{\Sigma \text{in} \text{picked}\}=\sum _{\Sigma \text{in} D}^{}c(\Sigma )p(\Sigma )=OP{T}_f$$

where $OP{T}_f$ is the optimal value of the linear program LP1. The found collection C has a very nice expected cost (even better than what one can achieve in our original integer problem) but we have to examine feasibility.

Since we want to get a C where each e in U belongs to at least 3 sets of C, we must examine whether the (random) C obtained has this property.

Definition 14 

Let α be an element in U and C obtained by the experiment E. We denote by $p(\alpha ,C)$ the probability that α belongs to at least 3 sets of C.

Let w.l.o.g. ${\Sigma }_1,\dots ,{\Sigma }_{\lambda }$ be the sets of our RMD containing element α. Here, we must have $\lambda \ge 3$, else LP1 will report infeasibility. W.l.o.g. denote by $p_i$ the probability $p\left({\sum }_i^{}\right)$ obtained via LP1, i.e. that ${\Sigma }_i$ is chosen to be in C. Assuming that LP1 is feasible we get:

$$\gamma =p_1+\cdots +p_{\lambda }\ge 3$$

(8)

Let $A_3,N_0,N_1,N_2$ be the events:

A₃ = “α is covered by at least 3 sets in C”

N₀ = “α does not belong to any set in C”

N₁ = “α belongs to exactly one set in C”

N₂ = “α belongs to exactly two sets in C”

Now,

$$p(\alpha ,C)=\mathrm{I}\mathrm{P}\left\{A_3\right\}=1-\mathrm{I}\mathrm{P}\left\{N_0\right\}-\mathrm{I}\mathrm{P}\left\{N_1\right\}-\mathrm{I}\mathrm{P}\left\{N_2\right\}$$

(9)

We now estimate $\mathrm{I}\mathrm{P}\left\{N_i\right\}$, for $i=0,1,2$:

We will repeatedly use the following fact:

Fact (*) If the numbers $x_1,\dots ,x_{\lambda }$ are each in $[0,1]$ and $x_1+\cdots +x_{\lambda }\ge \gamma$, then $(1-x_1)\cdots (1-x_{\lambda })\le {\left(1-\frac{\gamma }{\lambda }\right)}^{\lambda }\le e^{-\gamma }$ (it is assumed that $\gamma \le \lambda$).

Fact (*) can be proved via an easy induction, or via the fact that the arithmetic mean is bigger or equal than the geometric one.

Proof of Fact (*) Let $y_i=1-x_i,i=1,\dots ,\lambda$. Then, ${\sum }_{}^{}{y}_i=\lambda -{\sum }_{}^{}{x}_i\le \lambda -\gamma$. So,

$$\frac{{\sum }_{}^{}{y}_i}{\lambda }\le 1-\frac{\gamma }{\lambda }$$

(10)

But, $\frac{{\sum }_{}^{}{y}_i}{\lambda }\ge \sqrt[\lambda ]{\pi y_i}$ (arithmetic mean vs geometric mean), so:

$$\frac{{\sum }_{}^{}{y}_i}{\lambda }\ge \sqrt[\lambda ]{(1-x_1)\cdots (1-x_{\lambda })}$$

So, by Equation (3), $\sqrt[\lambda ]{(1-x_1)\cdots (1-x_{\lambda })}\le 1-\frac{\gamma }{\lambda }$. So, $(1-x_1)\cdots (1-x_{\lambda })\le {\left(1-\frac{\gamma }{\lambda }\right)}^{\lambda }$ ⋄

We now have:

(a) $\mathrm{I}\mathrm{P}\left\{N_0\right\}=(1-p_1)\cdots (1-p_{\lambda })$. By the Fact (*), then

$$\mathrm{I}\mathrm{P}\left\{N_0\right\}\le {\left(1-\frac{\gamma }{\lambda }\right)}^{\lambda }\le \text{exp}(-\gamma )$$

Also, by inclusion-exclusion,

$$\mathrm{I}\mathrm{P}\left\{N_1\right\}=p_1·\mathrm{I}\mathrm{P}\{\text{no} \text{cover} \text{of} \alpha \text{in} \text{the} \text{trials} \text{of} {\Sigma }_2,\dots ,{\Sigma }_{\lambda }\}+$$

$$+(1-p_1)\mathrm{I}\mathrm{P}\{1 \text{cover} \text{of} \alpha \text{in} \text{the} \text{trials} \text{of} {\Sigma }_2,\dots ,{\Sigma }_{\lambda }\}\le p_1·\frac{1}{e^{\gamma -p_1}}+(1-p_1)\mathrm{I}\mathrm{P}\left\{N_1\right\}$$

(because $p_2+\cdots +p_{\lambda }=\gamma -p_1$ so $(1-p_2)\cdots (1-p_{\lambda })\le {\left(1-\frac{\gamma -p_1}{\lambda }\right)}^{\lambda }=\text{exp}(-(\gamma -p_1))$ and also because $\mathrm{I}\mathrm{P}\{1 \text{success} \text{in} \text{the} \text{trials} \text{of} {\Sigma }_2,\dots ,{\Sigma }_{\lambda }\}\le \mathrm{I}\mathrm{P}\{N_1$ } ).

So,

$$\mathrm{I}\mathrm{P}\left\{N_1\right\}\le p_1·\frac{1}{e^{\gamma -p_1}}+(1-p_1)\mathrm{I}\mathrm{P}\left\{N_1\right\}$$

so

$$\mathrm{I}\mathrm{P}\left\{N_1\right\}\le \frac{1}{e^{\gamma -p_1}}\le \frac{1}{e^{\gamma -1}}$$

Similarly,

$$\mathrm{I}\mathrm{P}\left\{N_2\right\}=p_1·\mathrm{I}\mathrm{P}\left\{1 \text{cover} \text{of} \alpha \text{in} \text{the} \text{trials} \text{of} {\Sigma }_2,\dots ,{\Sigma }_{\lambda }\right\}+$$

$$+(1-p_1)\mathrm{I}\mathrm{P}\left\{2 \text{covers} \text{of} \alpha \text{in} \text{the} \text{trials} \text{of} {\Sigma }_2,\dots ,{\Sigma }_{\lambda }\right\}\le p_1·\frac{1}{e^{\gamma -p_1}}+(1-p_1)\mathrm{I}\mathrm{P}\left\{N_2\right\}$$

also, so $\mathrm{I}\mathrm{P}\left\{N_2\right\}\le \frac{1}{e^{\gamma -1}}$.

Thus,

$$\mathrm{I}\mathrm{P}\left\{A_3\right\}=p(a,c)\ge 1-\frac{1}{e^{\gamma }}-\frac{2}{e^{\gamma -1}}$$

and $\gamma \ge 3$. So, $\mathrm{I}\mathrm{P}\left\{A_3\right\}=p(a,c)\ge 1-\frac{1}{e^3}-\frac{2}{e^2}>\frac{1}{2}$. Let $\xi =1-\frac{1}{e^3}-\frac{2}{e^2}$. Hence, we get the following:

Theorem 7 

$$\mathrm{I}\mathrm{P}\{\alpha \text{is} \text{covered} \text{by} \text{at} \text{least} 3 \text{sets} \text{in} C\}=p(\alpha ,c)\ge 1-\frac{1}{e^3}-\frac{2}{e^2}=\xi$$

We now repeat the experiment E (with the same $p\left({\Sigma }_i\right)$) to get $r=clogn$ such collections $C_1,C_2,\dots ,C_r$.

Let $V=C_1\cup C_2\cup \dots \cup C_r$. By independence of the repeated experiments, if the event $A{V}_3$ is :

$A{V}_3=$“element α is not covered by at least 3 sets in V” then

$$\mathrm{I}\mathrm{P}\left\{A{V}_3\right\}\le {(1-\xi )}^{c log n}$$

We can always choose c so that ${(1-\xi )}^c<1/4$. Then,

$$\mathrm{I}\mathrm{P}\left\{A{V}_3\right\}\le {\left(\frac{1}{4}\right)}^{log n}\le \frac{1}{n^2}$$

Thus the probability that there is an element in U not covered by at least 3 sets of V is bounded by above by $n·n^{-2}=1/n$.

So, we get the following:

Theorem 8 

The collection V obtained satisfies: (i)

$$\mathrm{I}\mathrm{P}\left\{V \text{covers} \text{each} \text{element} \text{by} \text{at} \text{least} 3 \text{sets}\right\}\le 1-\frac{1}{n}$$

and (ii)

$$E\left(cost\left(V\right)\right)\le c log nOP{T}_f\le clognOPT$$

where $OPT$ is the cost of the optimal FMD.

Let $\rho =clogn$. Note that by the Markov inequality it is

$$\mathrm{I}\mathrm{P}\{cost\left(V\right)<2\rho OP{T}_f\}\ge \frac{1}{2}$$

Thus, the probability that V is valid and has cost less than $2\rho OP{T}_f$ is at least

$$1-\left(\frac{1}{n}+\frac{1}{2}\right)=\frac{1}{2}-\frac{1}{n}$$

We can then repeat the whole process an expected number of at most 2 times and get a V which is verified to be an almost optimal and valid FMD. Note that we have also shown:

Theorem 9 

The problem $\ge 3SC$ can be approximated in polynomial expected time with an approximation ratio $\Theta (logn)$.

5.6. The triangulation issue

The solution to $\ge 3SC$ of the last section selects a close to optimal FMD. Thus, it also specifies the initial positions of the associated (selected) sensors. However, no guarantee is provided that for any element e, the 3 elements “covering” e actually form a triangle (e.g. they may be on a line). We propose to handle this via a “post-processing” step as follows:

For each $e=(r_{ij},{\tau }_m)$ let ${\sigma }_1\left(e\right),{\sigma }_2\left(e\right),{\sigma }_3\left(e\right)$ be the 3 sensors covering e (i.e. covering $r_{ij}$ at ${\tau }_m$). We now modify their placement act by perturbing the positions $p_i^{*}$ of ${\sigma }_i\left(e\right)$ at ${\tau }_m$ by a random, small perturbation of center their $p_i^{*}$ and radius $ϵ>0$, small enough so that the same sets are covered by them. We perform the perturbation act only for those e for which the ${\sigma }_i\left(e\right)$ are not forming a triangle.

At the end of the post-processing step, each e in U is covered by (at least) 3 sensors, whose positions (during ${\tau }_m$) form a triangle with high probability. We can repeat the perturbation until the triangle is indeed formed.

This post-processing step can always be done, provided that S gives an infinitesimal free space around each of its points. This is safe to assume for any application. We note that our solution works for static sensors, and moving sensors whose motion is controlled by us, while it can not be applied to the case of sensors moving on their own.

5.7. Alternative collaborative processing methods for our approach

Our method is based on an easy to get RMD which is then “cleared” via the randomized rounding technique to get a low cost final monitoring decision. Its result is a selection of sensor placement acts, guaranteed to monitor each point $\stackrel{\rightharpoonup }{p}$ in S by at least 3 sensors for any time in the period T. When our localization method is combined with ability to distinguish all observed objects (e.g. by using unique IDs) then tracking of objects can be performed.

Clearly our method must be complemented by a way to report target positions and their associated times to some central facility. If the reporting delay is comparable to the speed of the target then the central facility can reconstruct the target’s motion in real time. To this end, Delay and Disruption Tolerant Networking (DTN, see e.g. [28]) approaches can be useful, to improve network communication when connectivity is periodic, intermittent or prone to disruptions and when multiple heterogeneous underlying networks may need to be utilized to effect data transfers.

The sensor network may handle the localization reports (i.e. reports on target position at a certain time) distributedly. This reduces communication cost but the central facility must have a way to compare those reports into a consistent information about the trajectory of the target. The issues of local clocks and their synchronization is crucial for this and we do not solve it here. In fact, we view our approach as a building block for full tracking approaches.

6. Conclusions

We investigated several aspects of energy optimization in sensor networks, like minimizing the total energy spent in the network, minimizing the number (or the range) of data transmissions, combining energy efficiency and fault-tolerance (by allowing redundant data transmissions which however should be optimized to not spend too much energy), and balancing the energy dissipation among the sensors in the network, in order to avoid the early depletion of certain sensors and thus the breakdown of the network. Since it is very difficult (if possible at all) to achieve all the above goals at the same time we presented a variety of protocols, each of which may possibly focus at some of the energy efficiency goals above (while still performing well with respect to the rest goals as well). In particular, we presented three energy efficient protocols: (a) The Local Target Protocol (LTP), that performs a local optimization trying to minimize the number of data transmissions (b) The Probabilistic Forwarding Protocol (PFR), that creates redundant data transmissions that are probabilistically optimized, to trade-off energy efficiency with fault-tolerance and (c) The Energy Balanced Protocol (EBP), that focuses on guaranteeing the same per sensor energy dissipation, in order to prolong the lifetime of the network.

For the problem of how to design low cost sensor networks able to efficiently localize and track multiple moving targets, we tried to take advantage of possible coverage overlaps over space and time, by introducing an abstract, combinatorial model that captures such overlaps. Under this model, we abstracted the localization and tracking problem by a combinatorial problem of set covering (by at least three sets, to ensure localization of any point in the network area, via triangulation). We then provided an efficient approximate method for sensor placement and operation, that with high probability and in polynomial expected time achieves monitoring decisions with a $\Theta (logn)$ approximation ratio to the optimal solution.

Open issues for further research include considering the impact on protocols’ performance of other important types of faults (malicious, byzantine). Also, it is worth investigating other performance aspects like congestion (possibly using game-theoretic methods).