Exploring Kalman Filtering Applications for Enhancing Artificial Neural Network Learning
Abstract
1. Introduction
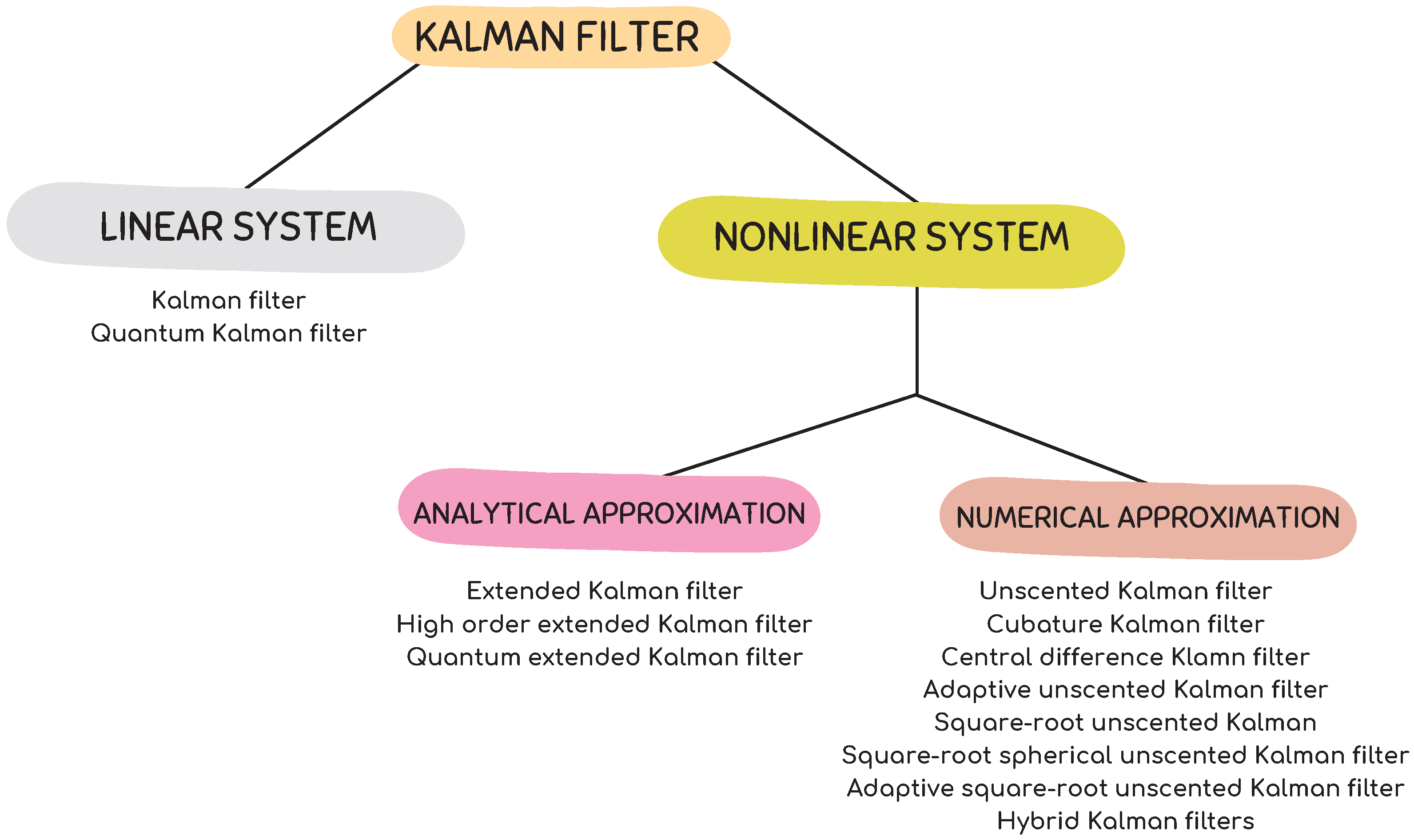
2. Main Variants of Kalman Filter
3. Neural Network Learning
| Author | Type of KF | Main Contribution | Learning | Examples |
|---|---|---|---|---|
| [52] | EKF | Real-time learning algorithm for a multilayered neural network | Online | Numerical |
| [53] | DEKF | Feedforward multilayered neural networks based on an EKF | Offline | Simulation |
| [54] | EKF | Real-time neural controller for three phase induction motors | Online | Experimental |
| [55] | EKF, UKF | Sequential growing-and-pruning learning algorithm | Offline | Simulation |
| [41] | KF, EKF, UKF, DEKF | Kalman filtering as applied to the learning and use of neural networks | Offline Online | Numerical Simulation Experimental |
| [5] | EKF, DEKF | Radial basis neural networks trained with an extended Kalman filter | Online | Simulation |
| [49] | EKF | State-space recurrent neural networks for nonlinear system identification | Offline | Simulation |
| [56] | KF | Q-learning with KF for action selection in cooperative control | Offline | Simulation |
| [57] | KF | Continuous state-space via Q-Learning for Markov decision process | Offline | Numerical |
| [58] | KF | Online Sequential Extreme Learning Machine and Kalman filter regression | Offline | Simulation |
| [59] | KF | Kalman filter with iterative learning control | Offline | Simulation |
| [60] | EKF | Induction motor control, combining EKF with a fuzzy logic controller | Offline | Simulation |
| [61] | KF | Kalman Filter and a Temporal Differencing | Offline | Simulation |
| [21] | EKF | Real-time neural controller for autonomous robotic navigation | Online | Experimental |
| [62] | KF | Kalman filter to update weights of a Single Layer Feedforward Network | Offline | Simulation |
| [63] | KF | Q-learning is represented in the framework of Kalman filter model | Offline | Simulation |
| [64] | KF | NN-based learning modules to update a Kalman filter for estimation | Offline | Simulation |
| [35] | DEKF | Estimation charge for lithium-ion batteries | Online | Experimental |
| [65] | KF | KF learning for stochastic claims reserving | Offline | Simulation |
| [66] | KF | Federated Kalman filters are proposed | Offline | Simulation |
| [67] | KF | Q-learning Approach with Kalman Filter for Self-balancing Robot | Offline | Simulation |
| [68] | EKF | State estimation algorithm combines the EKF and a Q-learning method | Offline | Simulation |
| [69] | KF | It is proposed an extreme learning Kalman filter for NN | Offline | Simulation |
| [70] | KF | Kalman filtering with a dedicated recurrent neural network | Online | Numerical |
| [71] | KF | KF filter is combined with a NN to predict the transaction throughput in a blockchain | Offline | Experimental |
| [72] | KF | Reinforcement learning adaptive KF for signal’s autoregressive modeling | Online | Experimental |
| [73] | EKF | Continuous action learning automata for tuning of Kalman filter | Offline | Experimental |
| [74] | KF | KF agents that operate sequentially to estimate optimal learning rate | Offline | Simulation |
| [75] | KF | Kalman filter-based cycle-consistent adversarial learning framework for time series | Offline | Simulation |
| [76] | EKF | Neural controller applied to an auxiliary energy system for electric vehicles | Online | Experimental |
| [77] | EKF | Real-time fault-tolerant closed-loop neural controller | Online | Experimental |
| [78] | KF | A neural network combined with a robust KF | Offline | Simulation |
| Work | Application | Processing Hardware | Processing Time |
|---|---|---|---|
| [54] | Three-phase induction motor | DSP-DS1104 | 1 ms |
| [79] | Mobile robot | FPGA Cyclone IV, DE2-115 | 14 μs |
| [21] | Mobile robot | DS1104 | 1 ms |
| [80] | Smart grid | LAUNCHXL-F28379D | 0.5 ms |
| [77] | Three-phase induction motor | DS1104 | 1 ms |
4. Kalman Filter for Neural Network Learning
4.1. Concepts Prior to KF
Optimal Estimation
- Cost function is non-negative.
- Cost function is a non-decreasing function of the estimation error, defined by:
- i.
- Stochastic processes and are Gaussian, or;
- ii.
- Optimal estimated is restricted to be a linear function of measures and mean square error cost function.
- iii.
- Then, optimal estimate , with measurements , is orthogonal to the projection of in generated space for such measurements.
4.2. Kalman Filter Realization
- State-space model:where and are Gaussian independent noises with zero means, where the covariance matrices are and , respectively.
- Initialization:
- Propagation of estimated state
- Propagation of estimation error covariance
- Kalman gain matrix
- State estimation update
- Estimation error covariance update
4.3. Extended Kalman Filter
- State-space model for discrete-time nonlinear systemswhere y Gaussian independent noises with zero mean and covariance matrices and , respectively.
- Initialization:
- Propagation of estimated state
- Propagation of estimation error covariance
- Kalman gain matrix
- State estimation update
- Estimation error covariance update
4.4. Relevant Results on KF for Neural Network Learning
4.4.1. Comparison Between Kalman Filter and Recursive Least Squares Algorithm
4.4.2. Retropropagation Versus EKF
4.5. Multilayer Perceptron Trained with EKF
4.6. Recurrent High-Order Neural Network Trained with EKF
4.7. Radial Basis Neural Network Trained with an EKF
Possible Modifications
- Just weight estimation (arbitrary centers of fixed centers).
- Global EKF.
- Decoupled EKF.
- −
- Centers decoupled from weights.
- −
- Weights decoupled from centers and other weights.
- Other combinations.
5. Challenges, Limitations, Open Problems and Future Work
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| KF | Kalman Filter |
| EKF | Extended Kalman Filter |
| UKF | Unscented Kalman Filter |
| CKF | Cubature Kalman Filter |
| QKF | Quantum Kalman Filter |
| QEKF | Quantum Extended Kalman Filter |
| MLP | Multilayer Perceptron |
| RBF | Radial Basis Function |
| RHONN | Recurrent High Order Neural Networks |
References
- Crassidis, J.L.; Junkins, J.L. Optimal Estimation of Dynamic Systems; Chapman and Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Grewal, M.S.; Andrews, A.P. Kalman Filtering Theory and Practice Using MATLAB; Wiley: Hoboken, NJ, USA, 2023. [Google Scholar]
- Jazwinski, A.H. Stochastic Processes and Filtering Theory; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Maybeck, P.S. Stochastic Models, Estimation, and Control; Academic Press: Cambridge, MA, USA, 1982; Volume 3. [Google Scholar]
- Simon, D. Optimal state Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Panomruttanarug, B.; Longman, R.W. Using Kalman filter to attenuate noise in learning and repetitive control can easily degrade performance. In Proceedings of the 2008 SICE Annual Conference, Chofu, Japan, 20–22 August 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 3453–3458. [Google Scholar]
- Khodarahmi, M.; Maihami, V. A review on Kalman filter models. Arch. Comput. Methods Eng. 2023, 30, 727–747. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. In Proceedings Volume 3068, Signal Processing, Sensor Fusion, and Target Recognition VI; SPIE: Bellingham, WA, USA, 1997; pp. 182–193. [Google Scholar]
- Urrea, C.; Agramonte, R. Kalman filter: Historical overview and review of its use in robotics 60 years after its creation. J. Sensors 2021, 2021, 9674015. [Google Scholar] [CrossRef]
- Kim, S.; Petrunin, I.; Shin, H.S. A review of Kalman filter with artificial intelligence techniques. In Proceedings of the 2022 Integrated Communication, Navigation and Surveillance Conference (ICNS), Dulles, VA, USA, 5–7 April 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–12. [Google Scholar]
- Poincaré, H. Les méThodes Nouvelles de la méCanique céLeste; Gauthier-Villars: Paris, France, 1892. [Google Scholar]
- Kalman, R.E. Contributions to the theory of optimal control. Bol. Soc. Mat. Mex. 1960, 5, 102–119. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Wiener, N. Extrapolation, Interpolation, and Smoothing of Stationary Time Series; MIT Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Belavkin, V. Measurement, filtering and control in quantum open dynamical systems. Rep. Math. Phys. 1999, 43, A405–A425. [Google Scholar] [CrossRef]
- Emzir, M.F.; Woolley, M.J.; Petersen, I.R. A quantum extended Kalman filter. J. Phys. A: Math. Theor. 2017, 50, 225301. [Google Scholar] [CrossRef]
- Iida, S.; Ohki, K.; Yamamoto, N. Robust quantum Kalman filtering under the phase uncertainty of the probe-laser. In Proceedings of the 2010 IEEE International Symposium on Computer-Aided Control System Design, Yokohama, Japan, 8–10 September 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 749–754. [Google Scholar]
- Zhang, G.; Dong, Z. Linear quantum systems: A tutorial. Annu. Rev. Control 2022, 54, 274–294. [Google Scholar]
- Ma, K.; Kong, J.; Wang, Y.; Lu, X.M. Review of the applications of Kalman filtering in quantum systems. Symmetry 2022, 14, 2478. [Google Scholar] [CrossRef]
- Zhou, X.; Qiao, D.; Li, X. Neural network-based method for orbit uncertainty propagation and estimation. IEEE Trans. Aerosp. Electron. Syst. 2023, 60, 1176–1193. [Google Scholar] [CrossRef]
- Alanis, A.Y.; Arana-Daniel, N.; Lopez-Franco, C. Artificial Neural Networks for Engineering Applications; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Gruber, M. An Approach to Target Tracking; Technical Note 1967-8, DDC 654272; MIT Lincoln Laboratory: Lexington, MA, USA, 1967. [Google Scholar]
- Larson, R.E.; Dressler, R.M.; Ratner, R.S. Application of the Extended Kalman Filter to Ballistic Trajectory Estimation; Final Report 5188-103; Stanford Research Institute: Monlo Park, CA, USA, 1967. [Google Scholar]
- Duan, P.; Duan, Z.; Lv, Y.; Chen, G. Distributed finite-horizon extended Kalman filtering for uncertain nonlinear systems. IEEE Trans. Cybern. 2019, 51, 512–520. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, S.; Wu, B.; Fernandez, C.; Xiong, X.; Coffie-Ken, J. A state-of-charge estimation method of the power lithium-ion battery in complex conditions based on adaptive square root extended Kalman filter. Energy 2021, 219, 119603. [Google Scholar] [CrossRef]
- Dai, Z.; Jing, L. Lightweight extended Kalman filter for MARG sensors attitude estimation. IEEE Sens. J. 2021, 21, 14749–14758. [Google Scholar] [CrossRef]
- Williams, R.J.; Zipser, D. A learning algorithm for continually running fully recurrent neural networks. Neural Comput. 1989, 1, 270–280. [Google Scholar] [CrossRef]
- Chang, L.; Hu, B.; Li, A.; Qin, F. Transformed unscented Kalman filter. IEEE Trans. Autom. Control 2012, 58, 252–257. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Provost, F.; Fawcett, T. Data Science for Business: What you Need to Know About Data Mining and Data-Analytic Thinking; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2013. [Google Scholar]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Härter, F.P.; de Campos Velho, H.F. New approach to applying neural network in nonlinear dynamic model. Appl. Math. Model. 2008, 32, 2621–2633. [Google Scholar] [CrossRef]
- Chen, X.; Bettens, A.; Xie, Z.; Wang, Z.; Wu, X. Kalman filter and neural network fusion for fault detection and recovery in satellite attitude estimation. Acta Astronaut. 2024, 217, 48–61. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Y. Extended and unscented Kalman filtering based feedforward neural networks for time series prediction. Appl. Math. Model. 2012, 36, 1123–1131. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, M.; Zhou, A.; Li, Y.; Li, S.; Fu, C.; Gong, C. State of charge estimation for lithium-ion batteries based on adaptive dual Kalman filter. Appl. Math. Model. 2020, 77, 1255–1272. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Cajal, S.R.Y.; Azoulay, D. Histology of the Nervous System: Of Man and Vertebrates; Oxford Academic: Oxford, UK, 1995. [Google Scholar]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef]
- Widrow, B.; Hoff, M.E. Adaptive switching circuits. In Neurocomputing: Foundations of Research; MIT Press: Cambridge, MA, USA, 1988; pp. 123–134. [Google Scholar]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Committee on Applied Mathematics, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Haykin, S. Kalman Filtering and Neural Networks; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Ljung, L. Asymptotic behavior of the extended Kalman filter as a parameter estimator for linear systems. IEEE Trans. Autom. Control 1979, 24, 36–50. [Google Scholar] [CrossRef]
- Song, Y.; Grizzle, J.W. The extended Kalman filter as a local asymptotic observer for discrete-time nonlinear systems. J. Math. Syst. Estim. Control 1995, 5, 59–78. [Google Scholar]
- De Mulder, W.; Bethard, S.; Moens, M.F. A survey on the application of recurrent neural networks to statistical language modeling. Comput. Speech Lang. 2015, 30, 61–98. [Google Scholar] [CrossRef]
- Jaeger, H. Tutorial on Training Recurrent Neural Networks, Covering BPPT, RTRL, EKF and the Echo State Network Approach; GMD-Forschungszentrum Informationstechnik: Bonn, Germany, 2002; Voluem 5. [Google Scholar]
- Ruck, D.W.; Rogers, S.K.; Kabrisky, M.; Maybeck, P.S.; Oxley, M.E. Comparative analysis of backpropagation and the extended Kalman filter for training multilayer perceptrons. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 14, 686–691. [Google Scholar] [CrossRef]
- Simon, D. Training radial basis neural networks with the extended Kalman filter. Neurocomputing 2002, 48, 455–475. [Google Scholar] [CrossRef]
- Singhal, S.; Wu, L. Training feed-forward networks with the extended Kalman algorithm. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Glasgow, UK, 23–26 May 1989; Volume 2, pp. 1187–1190. [Google Scholar] [CrossRef]
- Cordova, J.J.; Yu, W. Recurrent wavelets neural networks learning via dead zone Kalman filter. In Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–7. [Google Scholar]
- Camacho, J.; Villaseñor, C.; Alanis, A.Y.; Lopez-Franco, C.; Arana-Daniel, N. sKAdam: An improved scalar extension of KAdam for function optimization. Intell. Data Anal. 2020, 24, 87–104. [Google Scholar]
- Diederik, K. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Iiguni, Y.; Sakai, H.; Tokumaru, H. A real-time learning algorithm for a multilayered neural network based on the extended Kalman filter. IEEE Trans. Signal Process. 1992, 40, 959–966. [Google Scholar] [CrossRef]
- Jin, L.; Nikiforuk, P.N.; Gupta, M.M. Weight-Decoupled Kalman Filter Learning Algorithm of Multi-Layered Neural Networks. 1995. Available online: https://madangupta.com/pages/info/mmg/paper/RJ/RJ-088.pdf (accessed on 10 September 2025).
- Alanis, A.Y.; Sanchez, E.N.; Loukianov, A.G. Discrete-time adaptive backstepping nonlinear control via high-order neural networks. IEEE Trans. Neural Netw. 2007, 18, 1185–1195. [Google Scholar]
- Yingxin, L.; Min, W.; Jinhua, S.; Kaoru, H. Sequential growing-and-pruning learning for recurrent neural networks using unscented or extended Kalman filter. In Proceedings of the 2008 27th Chinese Control Conference, Kunming, China, 16–18 July 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 242–247. [Google Scholar]
- Liu, Q.; Jiachen, M.; Wei, X. Action selection in cooperative robot soccer using Q-learning with Kalman filter. J. Comput. Inf. Syst. 2012, 8, 10367–10374. [Google Scholar]
- Tripp, C.; Shachter, R.D. Approximate Kalman filter Q-learning for continuous state-space MDPs. arXiv 2013, arXiv:1309.6868. [Google Scholar]
- Nobrega, J.P.; Oliveira, A.L. Kalman filter-based method for online sequential extreme learning machine for regression problems. Eng. Appl. Artif. Intell. 2015, 44, 101–110. [Google Scholar] [CrossRef]
- Cao, Z.; Lu, J.; Zhang, R.; Gao, F. Iterative learning Kalman filter for repetitive processes. J. Process Control 2016, 46, 92–104. [Google Scholar] [CrossRef]
- Douiri, M.R. Extended Kalman Filter Based Learning Fuzzy for Parameters Adaptation of Induction Motor Drive. In Proceedings of the 2014 13th Mexican International Conference on Artificial Intelligence, Tuxtla Gutierrez, Mexico, 16–22 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 147–151. [Google Scholar]
- Bekhtaoui, Z.; Meche, A.; Dahmani, M.; Meraim, K.A. Maneuvering target tracking using q-learning based Kalman filter. In Proceedings of the 2017 5th International Conference on Electrical Engineering-Boumerdes (ICEE-B), Boumerdes, Algeria, 29–31 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Nobrega, J.P.; Oliveira, A.L. A sequential learning method with Kalman filter and extreme learning machine for regression and time series forecasting. Neurocomputing 2019, 337, 235–250. [Google Scholar] [CrossRef]
- Li, Z.; Shi, L.; Yang, L.; Shang, Z. An Adaptive Learning Rate Q-Learning Algorithm Based on Kalman Filter Inspired by Pigeon Pecking-Color Learning. In Proceedings of the International Conference on Bio-Inspired Computing: Theories and Applications, Zhengzhou, China, 22–25 November 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 693–706. [Google Scholar]
- Ullah, I.; Fayaz, M.; Naveed, N.; Kim, D. ANN based learning to Kalman filter algorithm for indoor environment prediction in smart greenhouse. IEEe Access 2020, 8, 159371–159388. [Google Scholar]
- Chukhrova, N.; Johannssen, A. Kalman filter learning algorithms and state space representations for stochastic claims reserving. Risks 2021, 9, 112. [Google Scholar] [CrossRef]
- Hu, K.; Wu, J.; Weng, L.; Zhang, Y.; Zheng, F.; Pang, Z.; Xia, M. A novel federated learning approach based on the confidence of federated Kalman filters. Int. J. Mach. Learn. Cybern. 2021, 12, 3607–3627. [Google Scholar] [CrossRef]
- Srichandan, A.; Dhingra, J.; Hota, M.K. An improved Q-learning approach with Kalman filter for self-balancing robot using OpenAI. J. Control. Autom. Electr. Syst. 2021, 32, 1521–1530. [Google Scholar] [CrossRef]
- Xiong, K.; Wei, C.; Zhang, H. Q-learning for noise covariance adaptation in extended KALMAN filter. Asian J. Control 2021, 23, 1803–1816. [Google Scholar] [CrossRef]
- Wang, H. Extreme learning Kalman filter for short-term wind speed prediction. Front. Energy Res. 2023, 10, 1047381. [Google Scholar] [CrossRef]
- Revach, G.; Shlezinger, N.; Ni, X.; Escoriza, A.L.; Van Sloun, R.J.; Eldar, Y.C. KalmanNet: Neural network aided Kalman filtering for partially known dynamics. IEEE Trans. Signal Process. 2022, 70, 1532–1547. [Google Scholar] [CrossRef]
- Hang, L.; Ullah, I.; Yang, J.; Chen, C. An improved Kalman filter using ANN-based learning module to predict transaction throughput of blockchain network in clinical trials. Peer-Netw. Appl. 2023, 16, 520–537. [Google Scholar] [CrossRef]
- He, P.; Wang, B.; Liu, X. Reinforcement learning adaptive Kalman filter for ae signal’s ar-mode denoise. In Proceedings of the 2023 IEEE 11th International Conference on Information, Communication and Networks (ICICN), Xi’an, China, 17–20 August 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 643–648. [Google Scholar]
- de Araujo, P.R.M.; Noureldin, A.; Givigi, S. Continuous Action Learning Automata: A Strategy for Dynamic Optimization of Invariant Kalman Filter Covariances. In Proceedings of the 2024 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Kingston, ON, Canada, 6–9 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 160–161. [Google Scholar]
- Krishnamurthy, V.; Rojas, C.R. Slow convergence of interacting Kalman filters in word-of-mouth social learning. In Proceedings of the 2024 60th Annual Allerton Conference on Communication, Control, and Computing, Urbana, IL, USA, 24–27 September 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–6. [Google Scholar]
- Liu, S.T.; Fan, J.J.; Wang, R.D.; Han, H.; Zhang, D.Y. Kalman Filter-based Cycle-Consistent Adversarial Learning for Time Series Anomaly Detection. J. Netw. Intell. 2024, 9, 790–803. [Google Scholar]
- Ruz Canul, M.A.; Ruz-Hernandez, J.A.; Alanis, A.Y.; Rullan-Lara, J.L.; Garcia-Hernandez, R.; Vior-Franco, J.R. Intelligent Robust Controllers Applied to an Auxiliary Energy System for Electric Vehicles. World Electr. Veh. J. 2024, 15, 479. [Google Scholar] [CrossRef]
- Alanis, A.Y.; Alvarez, J.G.; Sanchez, O.D.; Hernandez, H.M.; Valdivia-G, A. Fault-Tolerant Closed-Loop Controller Using Online Fault Detection by Neural Networks. Machines 2024, 12, 844. [Google Scholar]
- Hao, P.; Karakuş, O.; Achim, A. RKFNet: A novel neural network aided robust Kalman filter. Signal Process. 2025, 230, 109856. [Google Scholar] [CrossRef]
- Quintal, G.; Sanchez, E.N.; Alanis, A.Y.; Arana-Daniel, N.G. Real-time FPGA decentralized inverse optimal neural control for a Shrimp robot. In Proceedings of the 2015 10th System of Systems Engineering Conference (SoSE), San Antonio, TX, USA, 17–20 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 250–255. [Google Scholar]
- Sensor fault-tolerant control for a doubly fed induction generator in a smart grid. Eng. Appl. Artif. Intell. 2023, 117, 105527. [CrossRef]
- Kamwa, I.; Grondin, R. Fast adaptive schemes for tracking voltage phasor and local frequency in power transmission and distribution systems. IEEE Trans. Power Deliv. 2002, 7, 789–795. [Google Scholar] [CrossRef]
- Zhang, L.; Luh, P.B. Neural network-based market clearing price prediction and confidence interval estimation with an improved extended Kalman filter method. IEEE Trans. Power Syst. 2005, 20, 59–66. [Google Scholar] [CrossRef]
- Malartic, Q.; Farchi, A.; Bocquet, M. State, global, and local parameter estimation using local ensemble Kalman filters: Applications to online machine learning of chaotic dynamics. Q. J. R. Meteorol. Soc. 2022, 148, 2167–2193. [Google Scholar] [CrossRef]
- Chen, H.; Grant-Muller, S. Use of sequential learning for short-term traffic flow forecasting. Transp. Res. Part C Emerg. Technol. 2001, 9, 319–336. [Google Scholar] [CrossRef]
- Gerber, A.; Green, D.P. Rational learning and partisan attitudes. Am. J. Political Sci. 1998, 42, 794–818. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Kumpati, S.N.; Kannan, P. Identification and control of dynamical systems using neural networks. IEEE Trans. Neural Netw. 1990, 1, 4–27. [Google Scholar]
- Ghosh, J.; Shin, Y. Efficient higher-order neural networks for classification and function approximation. Int. J. Neural Syst. 1992, 3, 323–350. [Google Scholar] [CrossRef]
- Feldkamp, L.A.; Prokhorov, D.V.; Feldkamp, T.M. Simple and conditioned adaptive behavior from Kalman filter trained recurrent networks. Neural Netw. 2003, 16, 683–689. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alanis, A.Y. Exploring Kalman Filtering Applications for Enhancing Artificial Neural Network Learning. Algorithms 2025, 18, 587. https://doi.org/10.3390/a18090587
Alanis AY. Exploring Kalman Filtering Applications for Enhancing Artificial Neural Network Learning. Algorithms. 2025; 18(9):587. https://doi.org/10.3390/a18090587
Chicago/Turabian StyleAlanis, Alma Y. 2025. "Exploring Kalman Filtering Applications for Enhancing Artificial Neural Network Learning" Algorithms 18, no. 9: 587. https://doi.org/10.3390/a18090587
APA StyleAlanis, A. Y. (2025). Exploring Kalman Filtering Applications for Enhancing Artificial Neural Network Learning. Algorithms, 18(9), 587. https://doi.org/10.3390/a18090587





