Extended von Bertalanffy Equation in Solow Growth Modelling

Abstract

The aim of this work is to model the growth of an economic system and, in particular, the evolution of capital accumulation over time, analysing the feasibility of a closed-form solution to the initial value problem that governs the capital-per-capita dynamics. The latter are related to the labour-force dynamics, which are assumed to follow a von Bertalanffy model, studied in the literature in its simplest form and for which the existence of an exact solution, in terms of hypergeometric functions, is known. Here, we consider an extended form of the von Bertalanffy equation, which we make dependent on two parameters, rather than the single-parameter model known in the literature, to better capture the features that a reliable economic growth model should possess. Furthermore, we allow one of the two parameters to vary over time, making it dependent on a periodic function to account for seasonality. We prove that the two-parameter model admits an exact solution, in terms of hypergeometric functions, when both parameters are constant. In the time-varying case, although it is not possible to obtain a closed-form solution, we are able to find two exact solutions that closely bound, from below and from above, the desired one, as well as its numerical approximation. The presented models are implemented in the Mathematica environment, where simulations, parameter sensitivity analyses and comparisons with the known single-parameter model are also performed, validating our findings.

1. Introduction

Neoclassical growth theory describes the evolution of an economic system, identifying its state variables in populations and technical progress. Initial studies on this topic were performed by Domar [1], who hypothesised that the production yield $Y$ was a function of the capital $K,$ obtaining an output proportional to the capital stocks. Solow [2] hypothesised that $Y$ also depended on the labour force $L$ (workforce, manpower), as well as on the technical progress $A$ assumed positive and constant. Solow employed a Cobb–Douglas-type production function:

$$Y=A{K}^{\alpha }{L}^{1-\alpha }=AL{k}^{\alpha },0<\alpha <1,$$

(1)

where $k=K/L$ is the capital/labour ratio, $K$ is positive and $L$ follows a Malthus model, $L\left(t\right)=L_0{e}^{\nu t},$ with a positive growth rate $\nu =\dot{L}/L$ and starting from $L_0=L\left(t_0\right)$ for some initial time $t_0$ (usually $t_0=0).$ Note that, here and throughout the paper, $\dot{f}$ denotes differentiation of a function $f$ with respect to time $t.$

Swan [3] introduced in (1) the depletion of capital at a constant rate $0<\delta <1.$ Among the numerous references, we mention the economic motivation of the Solow–Swan model presented in the popular monograph [4] (chap. 1), where the details leading to Equation (2) are provided. For our purposes, it is sufficient to recall that this macroeconomic model produces an ordinary differential equation (ODE) that describes how capital-per-worker (capital-per-capita) varies over time:

$$\dot{k}+(\nu +\delta )k=A{k}^{\alpha }.$$

(2)

The Bernoulli Equation (2), in the dependent unknown $k=K/L$ and in the independent variable $t,$ can be solved with elementary methods.

This macroeconomic model has constituted—and still constitutes—a fundamental point of reference for neoclassical theory, from which modifications have been proposed to increase its representative effectiveness of capital accumulation, and to overcome the fact, known in the literature (see [5] for example), that the Solow–Swan model lacks reality with respect to the evolution of $L,$ since it uses a Malthusian labour force.

It is not our aim to enter into the theoretical economic debate: our contribution is purely modelling in nature, like that of many others [5,6,7,8,9,10]; nonetheless, modelling enriches the theoretical debate while ensuring greater accuracy in the description of the systems treated.

Donghan [7] proposed replacing the (exponential, thus unbounded) Malthusian $L$ with the logistic law, without reaching a closed-form solution, but demonstrating the existence of a steady state and a stability theorem for the capital-per-capita evolution.

An exact solution, given in terms of the Gauss hypergeometric function ${}_2\mathrm{F}_1,$ was obtained by [5], where a non-constant growth rate $\nu =\nu \left(t\right)$ is assumed in Equation (2) and the $L$-evolution is represented as a logistic equation (Verhulst model):

$$\dot{L}\left(t\right)=aL\left(t\right)-b{L}^2\left(t\right),a,b>0,$$

solved by

$${\displaystyle L\left(t\right)=\frac{a{L}_0{e}^{at}}{a+b{L}_0(e^{at}-1)},L_0=L\left(0\right),}$$

so that

$${\displaystyle \nu \left(t\right)=\frac{\dot{L}\left(t\right)}{L\left(t\right)}=\frac{a(a-b{L}_0)}{a+b{L}_0(e^{at}-1)}.}$$

(3)

The integration of (2) with $\nu$ as in (3) requires the use of ${}_2\mathrm{F}_1.$

Other authors have employed different growth laws to describe $L:$ the Richards law [11], which is a generalised logistic model, was introduced in [12,13]; the impact of adding a constant negative labour force to the classic Malthus law was studied in [9], where a closed-form solution was obtained, again in terms of ${}_2\mathrm{F}_1.$

More recent contributions have investigated the role of labour dynamics more explicitly: for instance, an intersectoral migration model with distinct population growth rates across sectors is developed in [14], while the spatial extensions in [15,16] analyse the effects of labour migration induced by capital accumulation and transport costs. Other works, although not directly modelling the labour force, are nonetheless related to the broader field of economic growth laws: examples include models of financial contagion based on epidemic analogies [17], delay logistic equations with nonlinear harvesting [18], continuous-time estimation of endogenous growth in open economies [19], and models of R&D competition generating complex dynamics [20]. The authors of [21] introduce the use of special functions, specifically Gaussian hypergeometric functions, to solve and analyse the equilibrium dynamics of the Lucas–Uzawa model of economic growth. They argue that this method provides an explicit, global representation of the dynamics of variables, avoiding the limitations of dimension reduction and offering a more complete understanding of transition dynamics in endogenous growth models. It is worth noting that this contribution does not refer to the Solow-type growth models.

In this work, we extend the model presented by Brida and Maldonado [6] by introducing new parameters, whose role enters into the $L$-dynamics. In [6], the authors propose modelling the population evolution through the Cauchy initial value problem (IVP):

$$\left\{\begin{array}{c}\dot{L}\left(t\right)=r(L_{\infty }-L\left(t\right))\hfill \\ L\left(0\right)=L_0\hfill \end{array}\right.$$

(4)

where the ODE is a von Bertalaffy equation and the parameter $r$ controls the speed at which $L$ reaches its carrying capacity $L_{\infty },$ the latter being the theoretical maximum asymptote of the population. The solution of (4) is

$$L\left(t\right)=L_{\infty }-e^{-rt}(L_{\infty }-L_0),$$

(5)

and the related growth rate is

$${\displaystyle \nu \left(t\right)=\frac{\dot{L}\left(t\right)}{L\left(t\right)}=\frac{r(L_{\infty }-L_0)}{L_0+L_{\infty }(e^{rt}-1)}.}$$

A more reliable economic growth model should take into account population dynamics that present three particular characteristics [6,22]:

• the population grows at a constant rate when it is small compared to $L_{\infty };$
• scarcity of resources slows population growth as it approaches $L_{\infty };$
• the population growth rate approaches zero over time.

To reproduce these three features, we modify Model (4) following [6,23]. In particular, we consider two different parameters $\{r_1,r_2\}$ in place of the single $r;$ as a second extension, we make $r_1$ time-varying. In both variants, once we obtain the solution $L\left(t\right)$ of the modified model, we form the related growth rate $\nu \left(t\right)$ and insert it into Equation (2), with the aim of finding its closed-form solution $k\left(t\right).$

This paper is organised as follows. Section 2 describes the model governed by our novel pair of constant parameters, while in Section 3 one of these new parameters is allowed to vary with time; each of these sections is subdivided into three parts, in which the dynamics of population and capital accumulation are discussed, the problem solution is presented and numerical simulations are included and commented on. Section 4 summarises the obtained results and outlines current and future work.

2. Constant Parameter Model

2.1. Dynamics of Population and Capital Accumulation

Here, we extend the model in [6] by making the population dynamics equation dependent on two constant parameters, so that (4) becomes

$$\left\{\begin{array}{c}\dot{L}\left(t\right)=r_1{L}_{\infty }-r_{2}L\left(t\right)\hfill \\ L\left(0\right)=L_0\hfill \end{array}\right.$$

(6)

solved by

$${\displaystyle L\left(t\right)=\frac{r_1}{r_2}{L}_{\infty }-e^{-r_{2}t}(\frac{r_1}{r_2}{L}_{\infty }-L_0).}$$

(7)

The ratio ${\displaystyle \frac{r_1}{r_2}}$ is related to the speed with which the population evolves and approaches the theoretical carrying capacity $L_{\infty }.$ To obtain an increase in population over time, we assume $r_1>r_2>0;$ the original Equation (4) clearly corresponds to $r=r_1=r_2.$ Note that the solution of (6) is such that

$${\displaystyle \underset{t\to \infty }{lim}L\left(t\right)=\frac{r_1}{r_2}{L}_{\infty },}$$

(8)

which is, therefore, the real carrying capacity of this two-parameter model. Moreover, the closer $r_1,r_2$ are to each other, the faster the population reaches the asymptote (8), as shown in Figure 1. Here and throughout the paper, the visualisations are performed in Mathematica, version 14 [24].

• In this context, adding an initial condition for $k\left(t\right)$ at time $t=0$ and including the saving propensity $s\in [0,1],$ the capital-per-capita ODE (2) becomes an IVP:

  $$\left\{\begin{array}{c}\dot{k}+(n\left(t\right)+\delta )k=sA{k}^{\alpha }\hfill \\ k\left(0\right)=k_0\hfill \end{array}\right.$$

  (9)
• The non-constant rate $n\left(t\right)$ of population growth related to (7) is

  $${\displaystyle n\left(t\right)=\frac{\dot{L}\left(t\right)}{L\left(t\right)}=\frac{r_2(L_{\infty }{r}_1-L_0{r}_2)}{L_0{r}_2+L_{\infty }{r}_1(e^{r_{2}t}-1)}.}$$

  (10)

2.2. Constant Parameter Model Solution

The change of variable $u=k^{1-\alpha }$ can be used to linearise the Bernoulli ODE (9), which becomes $\dot{u}=(1-\alpha )k^{-\alpha }\dot{k}$ and is then transformed, multiplying all terms in (9) by $(1-\alpha )k^{-\alpha },$ to yield a non-homogeneous non-autonomous variable coefficient equation:

$$\left\{\begin{array}{c}\dot{u}+(1-\alpha )(n\left(t\right)+\delta )u=(1-\alpha )sA\hfill \\ u\left(0\right)=k_0^{1-\alpha }\hfill \end{array}\right.$$

(11)

whose solution is

$$u\left(t\right)=e^{H\left(t\right)}\left(k_0^{1-\alpha }+(1-\alpha )sA{\int }_0^t{e}^{-H\left(\tau \right)}d\tau \right),$$

(12)

where, using (10):

$${\displaystyle H\left(t\right)=(\alpha -1){\int }_0^t(n\left(\tau \right)+\delta )d\tau =(\alpha -1)\left((\delta -r_2)t+ln\left(\frac{L_0{r}_2+L_{\infty }{r}_1(e^{r_{2}t}-1)}{L_0{r}_2}\right)\right).}$$

To obtain the explicit expression of $u\left(t\right),$ what is left to compute is

$$Z\left(t\right)={\int }_0^t{e}^{-H\left(\tau \right)}d\tau ,$$

(13)

where

$${\displaystyle e^{-H\left(\tau \right)}={\left({\displaystyle \frac{L_0{r}_2{e}^{(r_2-\delta )\tau }}{L_0{r}_2+L_{\infty }{r}_1(e^{r_2\tau }-1)}}\right)}^{\alpha -1}=\frac{L_0^{\alpha -1}{r}_2^{\alpha -1}{e}^{r_2\tau (\alpha -1)}{e}^{\delta \tau (1-\alpha )}}{{\left(L_0{r}_2-L_{\infty }{r}_1+L_{\infty }{r}_1{e}^{r_2\tau }\right)}^{\alpha -1}}.}$$

Here, we employ another change of variable $p=e^{r_2\tau },$ so that ${\displaystyle \tau =\frac{ln\left(p\right)}{r_2}}$ and $dp=r_2{e}^{r_2\tau }d\tau .$ Then (13) becomes

$${\displaystyle Z\left(t\right)={\int }_1^{e^{r_{2}t}}\frac{L_0^{\alpha -1}{r}_2^{\alpha -2}{p}^{\alpha -2}{p}^{\frac{\delta (1-\alpha )}{r_2}}}{{\left(L_0{r}_2-L_{\infty }{r}_1+L_{\infty }{r}_{1}p\right)}^{\alpha -1}}dp=\mathcal{B}{\int }_1^{e^{r_{2}t}}{\left(\mathcal{M}+\mathcal{N}p\right)}^{1-\alpha }{p}^{\mathcal{C}}dp,}$$

(14)

with

$$\mathcal{B}=L_0^{\alpha -1}{r}_2^{\alpha -2},\mathcal{M}=L_0{r}_2-L_{\infty }{r}_1,\mathcal{N}=L_{\infty }{r}_1,\mathcal{E}={\displaystyle \frac{\delta (1-\alpha )}{r_2}},\mathcal{C}=\mathcal{E}+\alpha -2.$$

At this point, the dependency of the sought solution on the hypergeometric ${}_2\mathrm{F}_1$ function appears, clearly, from the computation of the following integrals:

$$I_0={\int }_0^1{\left(\mathcal{M}+\mathcal{N}p\right)}^{1-\alpha }{p}^{\mathcal{C}}dp={\displaystyle \frac{{(\mathcal{M}+\mathcal{N})}^{2-\alpha }}{\mathcal{M}(\mathcal{C}+1)}}{}_2\mathrm{F}_1\left(1,\mathcal{E}+1,\mathcal{E}+\alpha ,{\displaystyle \frac{-\mathcal{N}}{\mathcal{M}}}\right),$$

(15)

$$\begin{array}{cc}\hfill I\left(t\right)& ={\int }_0^{e^{r_{2}t}}{\left(\mathcal{M}+\mathcal{N}p\right)}^{1-\alpha }{p}^{\mathcal{C}}dp\phantom{fillfillfillfillfillfillfillfillfillfillfillfillfillfillfill}\hfill \\ \hfill & ={\displaystyle \frac{e^{r_{2}t(\mathcal{C}+1)}{(\mathcal{M}+\mathcal{N}{e}^{r_{2}t})}^{2-\alpha }}{\mathcal{M}(\mathcal{C}+1)}}{}_2\mathrm{F}_1\left(1,\mathcal{E}+1,\mathcal{E}+\alpha ,{\displaystyle \frac{-\mathcal{N}{e}^{r_{2}t}}{\mathcal{M}}}\right),\hfill \end{array}$$

(16)

that allow us to redefine (14) as

$$Z\left(t\right)=\mathcal{B}\left(I\left(t\right)-I_0\right).$$

The computation of integrals (15) and (16) relates to the Euler integral representation of the Gauss hypergeometric function ${}_2\mathrm{F}_1$ (see [25,26,27]):

$${}_2\mathrm{F}_1\left(a,b,c,z\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(a\right)}_n{\left(b\right)}_n}{{\left(c\right)}_n}}{\displaystyle \frac{z^n}{n!}}={\displaystyle \frac{\mathrm{\Gamma }\left(c\right)}{\mathrm{\Gamma }(c-b)\mathrm{\Gamma }\left(b\right)}}{\int }_0^1{t}^{b-1}{(1-t)}^{c-b-1}{(1-zt)}^{-a}dt,$$

(17)

where ${(.)}_n$ is a Pochhammer symbol. The series is convergent for any $a,b,c$ if $\left|z\right|<1,$ and for $Re(a+b-c)<0$ if $\left|z\right|=1.$ For the integral representation, $Re\left(c\right)>Re\left(b\right)>0$ is required. Here, $\mathrm{\Gamma }\left(z\right)$ denotes the gamma function. A quick overview of the Gauss hypergeometric function can be found in [21]. The steps to obtain (15) and (16) via (17) are the same as those presented in [9] and are based on the decomposition of the integral as the difference between the integral from 0 to the upper limit and the integral from 0 to $1,$ followed by the normalisation of the first integral, in order to exploit the integral representation theorem of the hypergeometric function given by (17).

• Note that, while $I\left(t\right)$ changes over time, $I_0$ is a fixed number for a given scenario of the parameters. This feature is obviously inherited by (12), which becomes

  $$u\left(t\right)=e^{H\left(t\right)}\left(k_0^{1-\alpha }+(1-\alpha )sA\mathcal{B}\left(I\left(t\right)-I_0\right)\right).$$

  (18)
• To recover the solution of (9), with $n\left(t\right)$ as in (10), it suffices to take

  $$k\left(t\right)=u{\left(t\right)}^{{\displaystyle \frac{1}{1-\alpha }}},$$

  (19)

  with $u\left(t\right)$ given by (18).

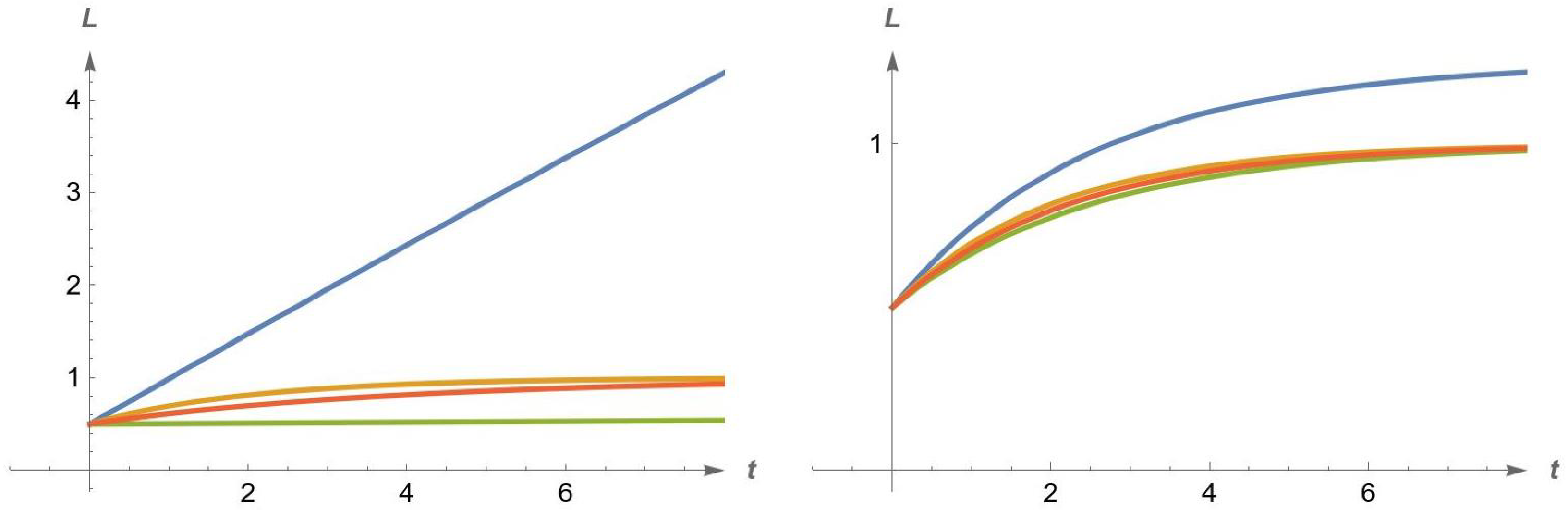
2.3. Simulations and Sensitivity Analysis

Figure 2 displays the solution (19) for different values of $r_1\ne r_2;$ the case of $r=r_1=r_2$ is also taken into account; the left plots show that the solution obtained with $r={\displaystyle \frac{1}{100}}$ is close but distinct from that correspondent to $\{r_1,r_2\}=\left\{{\displaystyle \frac{1}{50}},{\displaystyle \frac{1}{100}}\right\},$ and the same applies to the solution obtained with $r={\displaystyle \frac{1}{50}}.$ The right plots show that the solutions corresponding to the parameter values $r={\displaystyle \frac{1}{2}},$ $r={\displaystyle \frac{1}{10}}$ and $\{r_1,r_2\}=\left\{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{10}}\right\},$ after an adequate amount of time, all tend to the same asymptotic value. In all the scenarios considered, the other constant parameters are set to the values $k_0=1,$ $\alpha ={\displaystyle \frac{1}{3}},$ $s={\displaystyle \frac{1}{4}},$ $A=1,$ $\delta ={\displaystyle \frac{1}{5}},$ $L_0={\displaystyle \frac{1}{2}},$ $L_{\infty }=1.$

3. Model with a Time-Varying Parameter

3.1. Dynamics of Population and Capital Accumulation

We now improve model (6) by considering a time-varying perturbation on parameter $r_1,$ which we substitute with $r\left(t\right),$ a generic function of time $t,$ so that our Cauchy problem becomes

$$\left\{\begin{array}{c}\stackrel{.}{L}\left(t\right)=r\left(t\right)L_{\infty }-r_{2}L\left(t\right)\hfill \\ L\left(0\right)=L_0,\hfill \end{array}\right.$$

(20)

The linear ODE in (20) implies that its solution is

$$L\left(t\right)=e^{-r_{2}t}\left(L_0+L_{\infty }{\int }_0^t{e}^{r_2\tau }r\left(\tau \right)d\tau \right),$$

(21)

and its growth rate is

$${\displaystyle n\left(t\right)=\frac{\dot{L}\left(t\right)}{L\left(t\right)}=\frac{L_{\infty }{e}^{r_{2}t}r\left(t\right)}{L_0+L_{\infty }{\int }_0^t{e}^{r_2\tau }r\left(\tau \right)d\tau }-r_2.}$$

(22)

Among the possible effects that can be analysed in a population model, seasonality is one of the most interesting ones. Indeed, as pointed out in [28], there is evidence of seasonality effects of the parameter $r$ in the von Bertalanffy IVP (4); in fact, this model is used to study the evolution of populations of fish [29,30,31] characterised by seasonal effects.

A possible way to account for seasonality is to consider a periodic function in place of a constant parameter of the model: we thus extend our parametrised version (6) of the von Bertalanffy model by proposing its dynamic variant (20), in which the constant $r_1$ is replaced by

$$r\left(t\right)=r_1+bcos\left(\omega t\right).$$

(23)

With $r\left(t\right)$ as in (23), the solution of (20) is

$$L\left(t\right)={\displaystyle \frac{\mathcal{G}\left(t\right)e^{-r_{2}t}}{r_2(r_2^2+{\omega }^2)}},$$

(24)

with

$$\mathcal{G}\left(t\right)=b{L}_{\infty }{r}_{2}g\left(t\right)e^{r_{2}t}-b{L}_{\infty }{r}_2^2+\left(L_0{r}_2-L_{\infty }{r}_1+L_{\infty }{r}_1{e}^{r_{2}t}\right)(r_2^2+{\omega }^2),$$

(25)

$$g\left(t\right)=r_{2}cos\left(\omega t\right)+\omega sin\left(\omega t\right).$$

(26)

The growth rate related to (24) is

$$\begin{array}{cc}\hfill n\left(t\right)& {\displaystyle =\frac{\dot{L}\left(t\right)}{L\left(t\right)}=\frac{L_{\infty }\left(r_1+bcos\left(\omega t\right)\right)}{L\left(t\right)}-r_2}\hfill \\ \hfill & ={\displaystyle \frac{r_2}{\mathcal{G}\left(t\right)}}\left(b{L}_{\infty }\omega h\left(t\right)e^{r_{2}t}+b{L}_{\infty }{r}_2^2-(L_0{r}_2-L_{\infty }{r}_1)(r_2^2+{\omega }^2)\right)\hfill \end{array}$$

(27)

with

$$h\left(t\right)=\omega cos\left(\omega t\right)-r_{2}sin\left(\omega t\right).$$

Then, the expression (27) of $n\left(t\right)$ enters the capital/labour dynamics governed by (9) in a way similar to the approach adopted in Section 2.1.

For different choices of the parameters $r_1$ and $r_2,$ Figure 3 contains a comparison of the original one-parameter solution (5) with our two-parameter solutions (7) and (24), i.e., the constant and time-varying cases, respectively. The left and right figures differ only in the integration time interval: this is intentional, to highlight the behaviour at the beginning and after a sufficiently long period of integration. All solutions behave similarly, especially after an adequate time period and asymptotically. The wave-like behaviour of solution (24) is obviously due to the choice of $r\left(t\right)$ in (23).

3.2. Time-Varying Parameter Model Solution

To linearise (9) with $n\left(t\right)$ given by (27), we employ the change of variable $u=k^{1-\alpha },$ to obtain a Cauchy problem of the form (11) with a solution of the form (12), where, in this case:

$$H\left(t\right)=(\alpha -1){\int }_0^t(n\left(\tau \right)+\delta )d\tau =(\alpha -1)\left((\delta -r_2)t+ln\left({\displaystyle \frac{\mathcal{G}\left(t\right)}{L_0{r}_2(r^2+{\omega }^2)}}\right)\right),$$

(28)

with $\mathcal{G}\left(t\right)$ as in (25).

• We are faced, again, with solving

  $$Z\left(t\right)={\int }_0^t{e}^{-H\left(\tau \right)}d\tau \mathrm{with}{e}^{-H\left(\tau \right)}={\left({\displaystyle \frac{L_0{r}_2(r_2^2+{\omega }^2)e^{(r_2-\delta )\tau }}{\mathcal{G}\left(\tau \right)}}\right)}^{\alpha -1}.$$
• This time, though, the $Z\left(t\right)$ integral has no closed-form solution, due to the presence of the periodic perturbation. We can only compute its approximation $\widehat{Z}\left(t\right)$ using a numerical method of integration. At the same time, however, we can compute exactly an inferior bound and a superior bound for $Z\left(t\right)$ and show that the approximate $\widehat{Z}\left(t\right)$ also lies within these bounds.

To do so, we notice that $g\left(t\right)$ in (26) is surely bounded, since it is a linear combination of the sine and cosine functions; then, we look for the maximum $g_{max}$ and the minimum $g_{min}$ of $g\left(t\right)$ in the interval $[0,t]$ with $t>0:$

$$g_{min}=-\sqrt{P},g_{max}=\sqrt{P},\mathrm{where}P=r_2^2+{\omega }^2.$$

(29)

Accordingly, we define the inferior and superior solutions as

$$\begin{array}{cc}\hfill Z_{min}\left(t\right)& ={\int }_0^t{\displaystyle \frac{L_0^{\alpha -1}{r}_2^{\alpha -1}{P}^{\alpha -1}{e}^{r_2\tau (\alpha -1)}{e}^{\delta \tau (1-\alpha )}}{{\left(b{L}_{\infty }{r}_2{e}^{r_2\tau }(-\sqrt{P})-b{L}_{\infty }{r}_2^2+(L_0{r}_2-L_{\infty }{r}_1+L_{\infty }{r}_1{e}^{r_2\tau })P\right)}^{\alpha -1}}}d\tau ,\hfill \\ \hfill Z_{max}\left(t\right)& ={\int }_0^t{\displaystyle \frac{L_0^{\alpha -1}{r}_2^{\alpha -1}{P}^{\alpha -1}{e}^{r_2\tau (\alpha -1)}{e}^{\delta \tau (1-\alpha )}}{{\left(b{L}_{\infty }{r}_2{e}^{r_2\tau }\sqrt{P}-b{L}_{\infty }{r}_2^2+\left(L_0{r}_2-L_{\infty }{r}_1+L_{\infty }{r}_1{e}^{r_2\tau }\right)P\right)}^{\alpha -1}}}d\tau .\hfill \end{array}$$

(30)

At this point, we perform the change of variable $p=e^{r_2\tau },$ so that

$$\begin{array}{cc}\hfill Z_{min}\left(t\right)& ={\int }_1^{e^{r_{2}t}}{\displaystyle \frac{L_0^{\alpha -1}{r}_2^{\alpha -2}{P}^{\alpha -1}{p}^{\alpha -2}{p}^{\frac{\delta (1-\alpha )}{r_2}}}{{\left(-b{L}_{\infty }{r}_{2}p\sqrt{P}-b{L}_{\infty }{r}_2^2+\left(L_0{r}_2-L_{\infty }{r}_1+L_{\infty }{r}_{1}p\right)P\right)}^{\alpha -1}}}dp,\hfill \\ \hfill Z_{max}\left(t\right)& ={\int }_1^{e^{r_{2}t}}{\displaystyle \frac{L_0^{\alpha -1}{r}_2^{\alpha -2}{P}^{\alpha -1}{p}^{\alpha -2}{p}^{\frac{\delta (1-\alpha )}{r_2}}}{{\left(b{L}_{\infty }{r}_{2}p\sqrt{P}-b{L}_{\infty }{r}_2^2+\left(L_0{r}_2-L_{\infty }{r}_1+L_{\infty }{r}_{1}p\right)P\right)}^{\alpha -1}}}dp,\hfill \end{array}$$

that is

$$Z_{min}\left(t\right)=\mathcal{B}{\int }_1^{e^{r_{2}t}}{\left(\mathcal{M}+{\mathcal{N}}_{min}p\right)}^{1-\alpha }{p}^{\mathcal{C}}dp,Z_{max}\left(t\right)=\mathcal{B}{\int }_1^{e^{r_{2}t}}{\left(\mathcal{M}+{\mathcal{N}}_{max}p\right)}^{1-\alpha }{p}^{\mathcal{C}}dp,$$

with

$$\begin{array}{cc}\hfill \mathcal{B}& =L_0^{\alpha -1}{r}_2^{\alpha -2}{P}^{\alpha -1},\mathcal{M}=(L_0{r}_2-L_{\infty }{r}_1)P-b{L}_{\infty }{r}_2^2,\hfill \\ \hfill \mathcal{E}& ={\displaystyle \frac{\delta (1-\alpha )}{r_2}},\mathcal{C}=\mathcal{E}+\alpha -2,\hfill \end{array}$$

and

$${\mathcal{N}}_{min}=L_{\infty }{r}_{1}P-b{L}_{\infty }{r}_2\sqrt{P},{\mathcal{N}}_{max}=L_{\infty }{r}_{1}P+b{L}_{\infty }{r}_2\sqrt{P}.$$

Now, we consider the following four integrals:

$$I_{0,min}={\int }_0^1{\left(\mathcal{M}+{\mathcal{N}}_{min}p\right)}^{1-\alpha }{p}^{\mathcal{C}}dp={\displaystyle \frac{{(\mathcal{M}+{\mathcal{N}}_{min})}^{2-\alpha }}{\mathcal{M}(\mathcal{C}+1)}}{}_2\mathrm{F}_1\left(1,\mathcal{E}+1,\mathcal{E}+\alpha ,{\displaystyle \frac{-{\mathcal{N}}_{min}}{\mathcal{M}}}\right),$$

$$I_{0,max}={\int }_0^1{\left(\mathcal{M}+{\mathcal{N}}_{max}p\right)}^{1-\alpha }{p}^{\mathcal{C}}dp={\displaystyle \frac{{(\mathcal{M}+{\mathcal{N}}_{max})}^{2-\alpha }}{\mathcal{M}(\mathcal{C}+1)}}{}_2\mathrm{F}_1\left(1,\mathcal{E}+1,\mathcal{E}+\alpha ,{\displaystyle \frac{-{\mathcal{N}}_{max}}{\mathcal{M}}}\right),$$

$$\begin{array}{cc}\hfill I_{min}\left(t\right)& ={\int }_0^{e^{r_{2}t}}{(\mathcal{M}+{\mathcal{N}}_{min}p)}^{1-\alpha }{p}^{\mathcal{C}}dp\hfill \\ \hfill & ={\displaystyle \frac{{(\mathcal{M}+{\mathcal{N}}_{min}{e}^{r_{2}t})}^{2-\alpha }{e}^{r_{2}t(\mathcal{C}+1)}}{\mathcal{M}(\mathcal{C}+1)}}{}_2\mathrm{F}_1\left(1,\mathcal{E}+1,\mathcal{E}+\alpha ,{\displaystyle \frac{-{\mathcal{N}}_{min}{e}^{r_{2}t}}{\mathcal{M}}}\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_{max}\left(t\right)& ={\int }_0^{e^{r_{2}t}}{(\mathcal{M}+{\mathcal{N}}_{max}p)}^{1-\alpha }{p}^{\mathcal{C}}dp\hfill \\ \hfill & ={\displaystyle \frac{{(\mathcal{M}+{\mathcal{N}}_{max}{e}^{r_{2}t})}^{2-\alpha }{e}^{r_{2}t(\mathcal{C}+1)}}{\mathcal{M}(\mathcal{C}+1)}}{}_2\mathrm{F}_1\left(1,\mathcal{E}+1,\mathcal{E}+\alpha ,{\displaystyle \frac{-{\mathcal{N}}_{max}{e}^{r_{2}t}}{\mathcal{M}}}\right).\hfill \end{array}$$

Note that $I_{0,min},$ $I_{0,max}$ are fixed numbers for a given scenario of the parameters, while $I_{min}\left(t\right)$, $I_{max}\left(t\right)$ change over time, and they all contribute to the redefinition of (30) in terms of hypergeometric functions:

$$Z_{min}\left(t\right)=\mathcal{B}\left(I_{min}\left(t\right)-I_{0,min}\right),Z_{max}\left(t\right)=\mathcal{B}\left(I_{max}\left(t\right)-I_{0,max}\right).$$

With this construction, we have arrived at a lower solution and an upper solution:

$$u_{min}\left(t\right)=e^{H\left(t\right)}\left(k_0^{1-\alpha }+(1-\alpha )sA{Z}_{min}\left(t\right)\right),$$

(31)

$$u_{max}\left(t\right)=e^{H\left(t\right)}\left(k_0^{1-\alpha }+(1-\alpha )sA{Z}_{max}\left(t\right)\right),$$

(32)

that bound the true solution:

$$u\left(t\right)=e^{H\left(t\right)}\left(k_0^{1-\alpha }+(1-\alpha )sAZ\left(t\right)\right).$$

In the end, the sought solution $k\left(t\right)=u{\left(t\right)}^{{\displaystyle \frac{1}{1-\alpha }}}$ of the IVP (9), with $n\left(t\right)$ as in (27), is bounded below and above by

$$k_{min}\left(t\right)=u_{min}{\left(t\right)}^{{\displaystyle \frac{1}{1-\alpha }}},k_{max}\left(t\right)=u_{max}{\left(t\right)}^{{\displaystyle \frac{1}{1-\alpha }}}.$$

(33)

In the following Section 3.3, we show that $k_{min}\left(t\right)$ and $k_{max}\left(t\right)$ also bound the numerical approximation $\widehat{k}\left(t\right)$ of $k\left(t\right),$ where

$$\widehat{k}\left(t\right)=\widehat{u}{\left(t\right)}^{{\displaystyle \frac{1}{1-\alpha }}},\widehat{u}\left(t\right)=e^{H\left(t\right)}\left(k_0^{1-\alpha }+(1-\alpha )sA\widehat{Z}\left(t\right)\right),$$

(34)

and where $\widehat{Z}\left(t\right)$ represents the approximation of $Z\left(t\right)$ computed by numerical integration.

• Note that an approximate solution $\widehat{k}\left(t\right)$ can also be computed by solving (9), with $n\left(t\right)$ as in (27), with a numerical differential equation solver.

3.3. Simulations and Sensitivity Analysis

Figure 4 displays the behaviour of the symbolic solutions $k_{min}\left(t\right)$ and $k_{max}\left(t\right),$ and that of the numerical solution $\widehat{k}\left(t\right);$ the latter is computed through the generic differential equation solver provided within the Mathematica environment by the built-in routine NDSolve [32,33,34,35,36]. In our case, given the non-stiff and linear nature of the first-order IVP to be solved, the default method used belongs to the class of multistep Adams solvers [37,38]. As can be observed, $\widehat{k}\left(t\right)$ is always bounded by $k_{min}\left(t\right)$ and $k_{max}\left(t\right),$ and the three solutions behave similarly.

To evaluate the impact of the various parameters on the solutions found, an analytical sensitivity analysis can be performed. First, let us observe how the two bounding solutions in (33), and also the numerical solution, behave as the parameter $\alpha$ varies. Recalling the Cobb–Douglas-type Equation (1), the role of $\alpha$ in the considered scenarios can be interpreted as follows:

• $\alpha <1/2$ means that labour force prevails over capital, in the production function $Y;$
• $\alpha =1/2$ represents a situation of equilibrium;
• $\alpha >1/2$ means that, in $Y,$ capital prevails over labour force.

Figure 5 shows that both solutions $k_{min}\left(t\right)$ and $k_{max}\left(t\right)$ increase (in their maximum value) as $\alpha$ increases, keeping a bounded periodic pattern over time; this resembles the results presented in [5].

A similar feature also occurs when the technological coefficient $A$ is the varying parameter; in particular, in Figure 6, it can be seen how $k_{min}\left(t\right)$ and $k_{max}\left(t\right)$ increase and get closer to each other as $A$ increases, thus providing a stricter and better bound for the theoretical solution $k\left(t\right),$ although the latter remains unexpressed in closed form.

Similar results to those introduced in [5] are obtained when taking into account variations in the capital depletion $\delta$: Figure 7 illustrates how a lower $\delta$ corresponds to an increment in both $k_{min}\left(t\right)$ and $k_{max}\left(t\right);$ that is, the two bounding solutions increase rapidly as $\delta$ decreases.

Finally, as regards the sensitivity analysis on the saving propensity $s,$ Figure 8 shows that the two solutions $k_{min}\left(t\right)$ and $k_{max}\left(t\right)$ decrease as s decreases, maintaining a bounded periodic pattern; moreover, as s decreases, $k_{min}\left(t\right)$ and $k_{max}\left(t\right)$ get closer to each other in a way that is similar to what was observed in the case of varying $A.$

3.4. Final Remark

The oscillatory patterns generated by the extended model have a natural economic interpretation. In real economies, the labour force rarely follows a smooth trend, but is subject to recurrent fluctuations. These oscillations can be associated with several mechanisms: (i) cyclical effects of the business cycle, whereby recessions reduce participation rates and employment, while expansions bring additional workers into the market; (ii) migration shocks, which can produce sudden increases or decreases in the available workforce; and (iii) seasonal or sectoral dynamics, particularly relevant in industries such as agriculture and tourism, where employment follows a recurrent annual cycle. From a macroeconomic perspective, such oscillations imply that the capital–labour ratio and, consequently, output-per-worker are driven not only by long-term demographic or technological trends, but also by short-term fluctuations in the supply of labour. Capturing these dynamics within the growth model allows us to reproduce more realistic trajectories for output and factor accumulation, bridging the gap between purely theoretical dynamics and observed macroeconomic behaviour.

4. Conclusions

In this paper, we have presented a two-parameter extension of the single-parameter von Bertalanffy model, used in the literature to describe population growth and the related evolution of capital accumulation within an economic system. We considered the case of constant parameters, as well as the situation where one parameter varies over time, following a periodic trend, to account for seasonality.

In the constant case, it is possible to provide a closed-form solution, given in terms of the special Gauss hypergeometric function, to the initial value problem that governs the capital-per-capita dynamics. In the time-varying case, a closed-form solution is unattainable; however, it is possible to define two exact solutions that closely bound the one sought, from below and from above. These two solutions are, again, given in terms of the Gauss hypergeometric function and represent a bound also for the approximation to the desired solution, obtained with classical numerical integration methods.

We remark that, although the proposed two-parameter extension has exclusively theoretical purposes, several numerical experiments demonstrate the feasibility of the model itself and, above all, that the dynamics it generates are compatible with macroeconomic theory.

We have implemented the two variants (constant and time-varying cases) of our model in Mathematica, where extensive simulations were also performed, as well as comparisons with the single-parameter von Bertalanffy model in [6] and several parameter sensitivity analyses. As mentioned, all results show the validity of our extended models: they are consistent with the single-parameter form in [6], they retain the features required for realistic economic growth, and improve some of them, such as seasonality.

The Solow–Swan model, while mathematically elegant, is based on the assumption that the labour force grows at a constant Malthusian rate. Although this exponential law may serve as a reasonable short-run approximation, it does not align with long-run macroeconomic evidence. Labour supply is influenced by demographic transitions, ageing, migration, and institutional arrangements, all of which generate irregular and non-exponential trajectories. Moreover, the effective labour force displays procyclical behaviour: participation rates vary with the business cycle, and recessions, crises, or migratory shocks can cause sharp fluctuations. Consequently, the hypothesis of smooth and unbounded growth is too restrictive for a realistic macroeconomic framework.

To overcome this limitation, the von Bertalanffy growth law is adopted and enriched with a periodic component. The saturation feature inherent in the von Bertalanffy formulation provides a more credible representation of long-run labour dynamics, while the periodic extension captures recurrent oscillations driven by seasonality (e.g., agricultural or tourism employment), business cycles, or migration flows. Unlike in its traditional ecological applications, the present extension is grounded in observable macroeconomic mechanisms, yielding a formulation that more accurately reflects the behaviour of labour supply.

The literature has already explored several extensions of the Solow–Swan model, including the use of logistic and Richards-type laws for population growth and the explicit modelling of migration flows. While these approaches highlight the limitations of the purely Malthusian formulation, they too present drawbacks. Logistic and Richards laws effectively capture saturation, but they fail to account for cyclical fluctuations that are well-documented in modern economies. Migration-based models, on the other hand, often introduce exogenous shocks with a narrow scope, limiting their general applicability.

In contrast, the proposed von Bertalanffy formulation with a periodic term provides a more balanced framework. The saturation element is consistent with demographic and institutional constraints on labour supply, while the periodic component offers a parsimonious mechanism to reproduce recurrent oscillations, due to seasonality, migration shocks, or cyclical downturns, without the need for additional exogenous processes. The result is a unified analytical structure that combines long-term demographic convergence with short-term cyclical variation. In this sense, the model integrates the strengths of previous extensions while addressing their main shortcomings, offering a more flexible and economically grounded representation of labour dynamics.

At this stage, the focus is deliberately restricted to the theoretical development of the model and to its closed-form analytical solution. The objective is to establish the mathematical foundations of the extended framework and to highlight its comparative advantages over existing alternatives. Preliminary numerical simulations suggest that the formulation is robust, but a full econometric implementation would require extensive data collection and calibration, which lies beyond the scope of the present study. This is identified as a promising direction for future research, where a systematic empirical assessment of the model will be carried out. Current and future works also involve further optimisation via other types of time-dependent parametric functions.