Abstract
To address the problems of random noise interference, inadequate disturbance estimation and compensation, and the difficulty in controller parameter tuning in speed tracking control of high-speed trains, an improved Active Disturbance Rejection Control (ADRC) strategy combined with a Sobol-based Black Widow Optimization (SBWO) algorithm is proposed. An improved Tracking Differentiator (TD) is adopted by integrating a novel optimal control synthesis function with a phase compensator to suppress input noise and ensure a smooth transition process. A novel Extended State Observer (ESO) using a nonlinear saturation function is designed to improve the observation accuracy and decrease chattering. An enhanced Nonlinear State Error Feedback (NLSEF) law that incorporates an error integral and adaptive parameter update laws is developed to reduce steady-state error and achieve self-tuned proportional and derivative gains. A feedforward compensation term is added to provide real-time dynamic compensation for ESO estimation errors. Finally, an enhanced Black Widow Optimization (BWO) algorithm, which initializes its population with Sobol sequences to improve its global search capability, is employed for parameter optimization. The simulation results demonstrate that compared with the control methods based on Proportional–Integral–Derivative (PID) control and conventional ADRC, the proposed strategy achieves higher steady-state tracking accuracy, better adaptability to dynamic operating conditions, stronger anti-disturbance ability, and more precise stopping precision.
1. Introduction
Possessing notable advantages such as high efficiency, safety, and environmental friendliness, high-speed rail has become a strategic pillar in the evolution and modernization of global transportation systems. At present, the operation of high-speed trains predominantly relies on manual driving, which is increasingly revealing its limitations in enhancing operational efficiency and accommodating the complex demands of modern high-speed rail networks. Consequently, to align with the trend towards the intelligentization of modern railways, the implementation of Automatic Train Operation (ATO) technology has emerged as a pivotal research direction. Research on ATO technology primarily concentrates on two aspects: the optimization of the target speed profile and the design of the tracking controller for tracking the profile. Substantial advancements have been achieved in the domain of profile optimization [1,2,3,4]; however, the optimization of target profiles will lose its significance without the support of a highly effective tracking control strategy. Therefore, the design of an efficient and precise tracking control strategy constitutes the central challenge in the realization of ATO for high-speed trains [5].
Extensive research has been conducted on train speed tracking control strategies. Pu et al. [6] proposed a train speed control algorithm based on an adaptive Proportional–Integral–Derivative (PID), which achieved good tracking performance. However, it exhibited poor robustness and anti-disturbance capability in complex disturbance environments. Xu et al. [7] designed a model predictive control algorithm capable of accurately tracking the speed profile, but the method is highly dependent on a precise model. To address this, Wang et al. [8] and Kang et al. [9] introduced train speed tracking control methods that incorporate fuzzy logic. Although this approach does not require a precise model, the formulation of fuzzy rules relies heavily on engineering experience, resulting in poor adaptability and hindering real-time tracking. Liu et al. [10] proposed a fault-tolerant control method based on adaptive backstepping that utilizes a novel time-varying function to address unknown time-varying uncertainties, but it exhibits insufficient disturbance rejection capability. When subjected to the effects of multi-source disturbances in complex dynamic environments, the existing control strategies still suffer from issues such as strong model dependency, limited adaptability, insufficient disturbance rejection capability [11,12], and so on. Therefore, there is an urgent need to develop a train speed tracking controller that is independent of a precise model, provides high control accuracy, and exhibits strong adaptability and disturbance rejection capabilities.
To address issues such as excessive reliance on precise mathematical models, difficulty in adapting to time-varying uncertainties during train operation, and insufficient disturbance rejection capability due to a lack of real-time estimation and compensation mechanisms, Scholars have gradually shifted their focus to train speed tracking control methods that do not rely on precise models and have strong anti-disturbance capabilities. Among these, Active Disturbance Rejection Control (ADRC) has garnered significant attention for its independence from precise mathematical models, its ability to estimate and compensate for total disturbance online, and its superior dynamic performance and robustness compared to traditional methods. ADRC has been widely applied in various fields, including quadrotor UAV flight control [13], robot and manipulator control [14], electric vehicle control [15], motor drive control [16], and so on.
However, application of ADRC in the field of train speed tracking control remains relatively limited [17,18,19]. In [17], a train speed tracking controller based on ADRC was designed, and its effectiveness was validated. A cooperative ADRC method was proposed in [18] for heavy-haul trains; it employs an Extended State Observer (ESO) for the online estimation and compensation of disturbances, thereby effectively mitigating speed tracking errors and overshoot in inter-train spacing. By integrating Model Reference Adaptive Control (MRAC) with ADRC, Yang et al. [19] developed a robust control method with low model dependency for magnetic levitation (Maglev) trains, which enhanced the controller’s disturbance rejection capabilities. Although the above speed tracking control strategies based on ADRC have shown good steady-state and dynamic performance, they are still beset by several limitations: the adopted conventional ADRC exhibits an insufficient capacity for the real-time, precise compensation of time-varying external disturbances [17]; the optimal control synthesis function employed by the Tracking Differentiator (TD) is structurally complex and is susceptible to issues including overshoot, chattering, and phase delay when designing the transition profile of the input signal [17]; the conventional nonlinear saturation function utilized within the ESO is non-differentiable at the origin and exhibits poor smoothness, which leads to excessively high observer gains and subsequently provokes frequent error switching and chattering phenomena [18]; and the Nonlinear State Error Feedback (NLSEF) law has demonstrated subpar steady-state performance and speed tracking precision in train speed control [19].
Moreover, a significant challenge inherent in ADRC-based speed tracking control strategies is the difficulty in tuning the numerous controller parameters. To address this issue, swarm intelligence algorithms, such as Particle Swarm Optimization (PSO) [20], Genetic Algorithms (GAs) [21], and Ant Colony Optimization (ACO) [22], have been employed to facilitate parameter optimization. These optimization approaches, however, remain susceptible to premature convergence to local optima and exhibit slow convergence rates. Although the conventional Black Widow Optimization (BWO) algorithm [23,24] alleviates these concerns to some degree through its distinctive population update mechanism, it still exhibits limitations concerning its population diversification and global exploration capability [25]. Accordingly, Yang et al. [26] employed an improved PSO algorithm to optimize the parameters of the ADRC controller. Although this improved PSO algorithm enhances the global search capability, it remains susceptible to premature convergence to local optima and exhibits slow convergence rates. Furthermore, the controller with parameters obtained via PSO shows limited adaptability to the complex and unknown variations in the external environment.
Based on the foregoing considerations, this paper proposes a novel speed tracking control strategy for high-speed trains, which is founded upon an improved adaptive active disturbance rejection controller augmented with feedforward compensation and optimized using an improved BWO algorithm. The key contributions are structured as follows. First, the TD is enhanced by introducing a novel optimal control synthesis function in conjunction with a phase compensator. Second, an improved ESO and an NLSEF control law are designed based on the caufal function; concurrently, the NLSEF control law is further enhanced with an adaptive parameter update law, which enables the self-tuning of the proportional and derivative coefficients. In addition, a feedforward compensation mechanism is incorporated to bolster the system’s real-time disturbance compensation capability. Finally, to circumvent the problem of local convergence arising from insufficient population coverage, an improved BWO algorithm initialized with Sobol sequences is employed for controller parameter optimization. The efficacy of the proposed controller is subsequently validated through simulations conducted in MATLAB R2022a.
The remainder of this paper is organized as follows. Section 2 establishes the operational model of the high-speed train. Section 3 presents the proposed speed tracking controller, which is based on an improved adaptive ADRC framework augmented with feedforward compensation. In Section 4, an improved BWO algorithm employing Sobol sequences is designed for the optimization of the controller parameters. Section 5 provides the simulation results to validate the efficacy of the proposed control strategy. Finally, Section 6 concludes the paper.
2. High-Speed Train Dynamic Model
In comparison with multi-particle dynamic models, the single-particle model is better suited for analyzing the train’s overall operational characteristics [27]. The corresponding force analysis for the single-particle model is depicted in Figure 1.
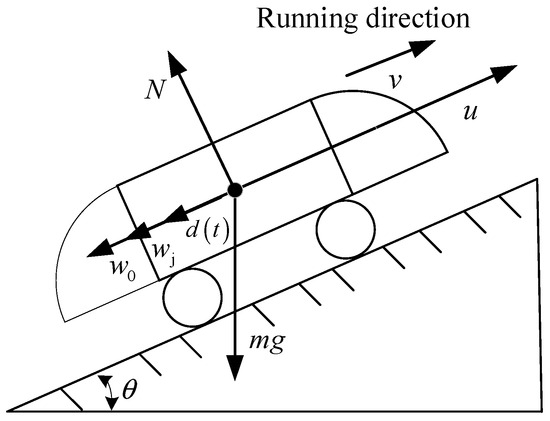
Figure 1.
Train operation force analysis diagram.
Based on Newton’s second law, the single-particle dynamic model of a train is formulated as
where x is the train displacement; v is the train speed; u represents the control input, corresponding to the traction force (traction state, the same as the running direction) or braking force (braking state, opposite to the running direction), which are mutually exclusive; m is the train mass; is the wheel rotation mass coefficient; and P denotes the total disturbance, which is expressed as
where represents the external disturbances, and and are the basic running resistance and the additional resistance, which can be expressed, respectively, as
where , , , and are the coefficients of rolling mechanical resistance, frictional resistance, and aerodynamic resistance, respectively; , , and denote the additional resistances due to the track gradient, curvature, and tunnels, respectively [26], in which is the grade angle, is the curve length, is the central angle of the curve, and is the tunnel length.
3. Speed Tracking Controller Design Based on Improved ADRC
Active Disturbance Rejection Control, which does not rely on a precise model and possesses strong disturbance rejection capabilities, has been employed to design train speed tracking controllers [17]. However, when confronted with the complex nonlinear system and significant disturbances inherent in train operations, conventional ADRC exhibits several deficiencies [28], such as an insufficient ability to manage the transient process of the input signal, inadequate performance in disturbance estimation and compensation, poor adaptability to changes in the external environment, and so on. To this end, this paper proposes an improved ADRC strategy for train speed tracking, the system architecture of which is depicted in the block diagram in Figure 2.
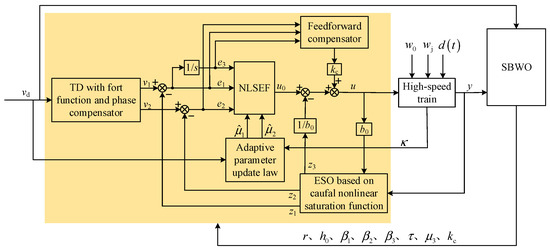
Figure 2.
The block diagram of the improved ADRC speed tracking system for a train.
3.1. Tracking Differentiator Design
When designing the transient process for the input signal, the conventional TD exhibits significant drawbacks, including overshoot, chattering, phase delay, and so on [29]. To overcome these limitations, an improved TD constructed with a composite control architecture is proposed. The architecture is developed by first determining the boundary layer of a time-optimal discrete second-order system via the isochronous region method [30] and then combining this layer with the reachable set. It employs a mechanism integrating multi-step prediction, boundary layer adjustment, and a signum-function-based decision logic. The resulting controller incorporates a novel optimal control synthesis function and a phase compensation mechanism, with its discrete expression given by
where is the desired input, is the tracking signal of , is the derivative of , is the sampling period, is the speed factor, is the filtering factor, and fort is a novel optimal control synthesis function, which is invoked as
To further address the phase-delay problem that occurs during the processing of noisy signals, a phase compensator is integrated to predict the tracking and differential signals output by the TD and to correct the phase lag [31]. The algorithm is formulated as follows:
where is the phase compensator parameter.
To validate the tracking performance of the novel TD, a comparative simulation was conducted for two cases with noisy square wave and sinusoidal wave inputs, and the simulation results for the tracking performance are shown in Figure 3. The frequency of both input signals is Hz, and the noise is Gaussian white noise with a signal-to-noise ratio of 40 dB. As can be observed, compared with the conventional TD based on the fhan function, the new TD using the improved fort function adapts more rapidly to the dynamic transients of the signal, effectively mitigating the lag effect. It compensates for the phase delay while effectively filtering out the noise, thereby exhibiting a superior dynamic response.
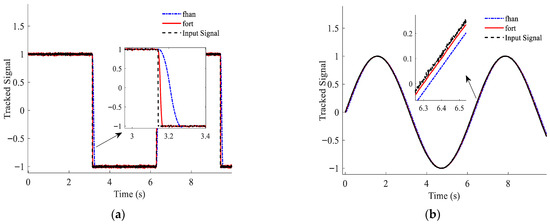
Figure 3.
Tracking performance for noisy input signals: (a) tracking performance for a noisy square wave input signal; (b) tracking performance for a noisy sinusoidal input signal.
3.2. Extended State Observer Design
An ESO can estimate the unknown disturbances and unmodeled dynamics of a system in real time [32]. However, the conventional ESO, employing the fal function, is characterized by a slow convergence speed and limited anti-disturbance performance, rendering it unable to satisfy the high-precision and real-time control requirements of high-speed trains [17]. To effectively suppress chattering near the origin, improve the global convergence speed, and ensure stability under dynamic disturbances, an ESO based on an improved caufal function is introduced in this paper.
The expression for the fal function is
where τ determines the width of the nonlinear interval in the fal function. If τ is excessively large, the fal function degenerates into a linear function, defeating the original purpose of its non-smooth feedback design. Conversely, if τ is too small, the nonlinearity becomes overly strong, leading to chattering that causes the system to oscillate around the origin. Therefore, the selection of τ requires a trade-off between the effective utilization of nonlinearity and the avoidance of adverse effects, such as chattering or linear degradation.
Given the continuous and non-smooth characteristic of the fal function, measurement noise in the feedback loop may induce chattering due to the abrupt change in the function’s derivative [33]. To address this, a Dirac function is introduced to smooth the fal function, which satisfies the following conditions:
can be considered a continuous probability density function.
Assume that there exists a smooth approximation function such that . Then
The function is chosen as
Based on the above analysis, the smooth approximation function can be expressed as
To validate the control performance of the caufal function, a simulation is conducted for the case where parameter settings are , , . Figure 4 and Figure 5 show the characteristic curves and sensitivity curves for the fal and caufal functions, respectively. It can be observed that the caufal function exhibits superior smoothness, continuity, and convergence when the error approaches zero. In the small-error region, its sensitivity is lower than that of the fal function, which mitigates the chattering problem caused by excessive sensitivity while also preventing dynamic overshoot.
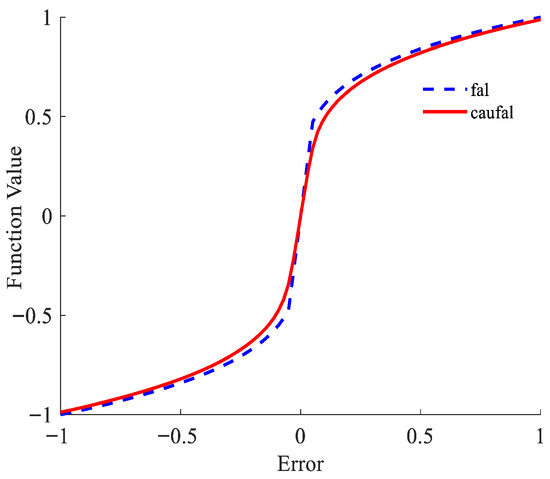
Figure 4.
Function characteristic curve.
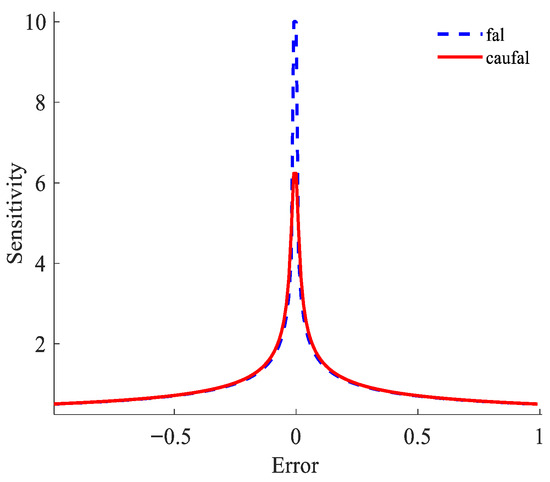
Figure 5.
Sensitivity curve.
The total disturbance of system P is expanded into a new state variable, and the following third-order nonlinear ESO is constructed:
where y is the system output; z1, z2, and z3 are the estimations of the speed, acceleration, and the total disturbance of the system, respectively; b0 is the compensation factor, given by ; and β1, β2, and β3 are the observer gains.
Assuming the system disturbance is zero, the ESO error state equation can be written as
To prove the asymptotic stability of the ESO error system at the equilibrium point, the system can be transformed into
where , and , in which , .
Let . Obviously , . When , the resulting matrix has all positive diagonal elements, making a symmetric positive-definite matrix.
where , and are infinitesimal positive constants.
To prove the stability of the improved ESO, a Lyapunov function is constructed in the following form:
Expanding Equation (19) gives
When , it follows that
The integral is bounded at the equilibrium point. Therefore, if is sufficiently large, .
Differentiating with respect to t yields
From Equations (21) and (22), when B > 0, the system is asymptotically stable at the equilibrium point, and the observer gains are positive and satisfy , thereby guaranteeing asymptotic stability of the ESO at the equilibrium point.
3.3. NLSEF Control Law Design Based on Adaptive Parameter Update Law
To address the poor steady-state performance and insufficient speed tracking accuracy in traditional nonlinear control laws for train speed tracking control, an error integral term is introduced into the conventional NLSEF control law. This modification makes μ3 analogous to the integral coefficient of a PID controller, thereby optimizing the nonlinear control. A novel NLSEF control law is then designed by incorporating the caufal function, yielding the control input as
where , , and . , , and are the proportional, differential, and integral coefficients, respectively. , , and are adjustable parameters. , , and satisfy the following constraint: .
To further improve the adaptability and the disturbance rejection capability of the control strategy, an adaptive parameter update law is introduced to dynamically adjust the key parameters ( and ) in the NLSEF control law.
The displacement and speed tracking errors of the high-speed train are defined as and , respectively, where and are the desired displacement and speed. The adaptive parameter estimation errors are defined as and .
The tracking error function for the adaptive parameter update law is defined as
where is a properly selected constant.
The adaptive parameter update laws for and are designed as
where and are designed constants, and are the initial parameter values, which are implemented to avoid potential singularity problems in the adaptive update law, ensuring that the variables and do not approach zero during the iteration process [34].
Thus, the control input can be rewritten as
3.4. Feedforward Compensation Design
The estimation errors of the ESO can introduce additional disturbance into the system’s double-integrator structure. To further improve the disturbance rejection capability and tracking performance of the control system, a feedforward compensation term is introduced, which is expressed as
where is the feedforward compensation coefficient.
The second-order dynamic model of the high-speed train can be given by
When an error exists between the disturbance estimated by the ESO and the actual disturbance, i.e., , the compensation mechanism can form a dual disturbance rejection architecture combining feedforward compensation and feedback regulation. This structure can offset a portion of the disturbance estimation error, thereby achieving effective disturbance compensation.
Combining Equations (27) and (28), the control input for the train can be designed as
4. Parameter Optimization Based on SBWO
To address the issues of swarm intelligence optimization algorithms being prone to local optima and exhibiting slow convergence during parameter tuning for the ADRC speed tracking controller, a Sobol-based Black Widow Optimization (SBWO) algorithm is proposed to enhance the population update and global search capabilities.
To effectively generate uniformly distributed sample points in a high-dimensional search space, the Sobol sequence is introduced to generate the initial positions of individuals in the population [23], which can be represented as
where denotes the generated position coordinate, is the search range, and represents the random number generated by the Sobol sequence.
To validate the influence of the population initialization strategy on algorithm performance, 500 individuals are initialized using a Sobol sequence and traditional pseudo-random numbers, respectively. These individuals are then mapped into a two-dimensional search space within the range of [−1, 1] to compare their position distributions [35]. The simulation results are shown in Figure 6. As can be observed, the SBWO algorithm based on the Sobol sequence, owing to its superior ergodicity and uniformity, accelerates the convergence of the algorithm and enhances its global exploration capability [36], thereby effectively avoiding entrapment in local optima.
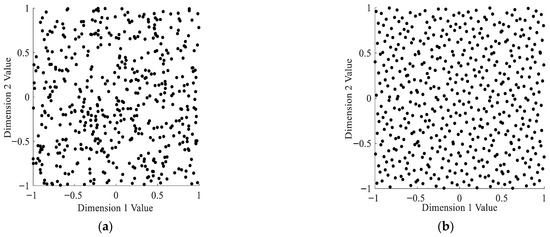
Figure 6.
Comparison of population initialization using Sobol and pseudo-random sequences: (a) pseudo-random number sequence distribution; (b) Sobol sequence distribution.
The Integral of Time-weighted Absolute Error (ITAE) criterion is adopted as the fitness function JITAE, which is formulated as follows:
where e(t) is the speed tracking error.
The schematic diagram of the ADRC controller optimization process based on the SBWO algorithm is shown in Figure 7.
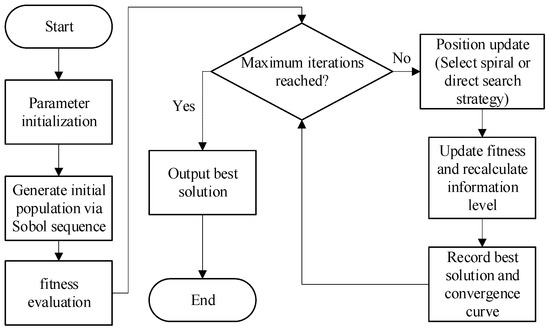
Figure 7.
Schematic of the ADRC controller optimization process using the SBWO algorithm.
To demonstrate the parameter optimization performance of SBWO, a comparative simulation was conducted against the PSO algorithm, as shown in Figure 8. It is evident from the figure that the SBWO algorithm converges to a smaller optimal fitness value within approximately ten generations. Compared to the PSO algorithm, the SBWO algorithm demonstrates a faster convergence speed, superior global search capability, and greater stability.
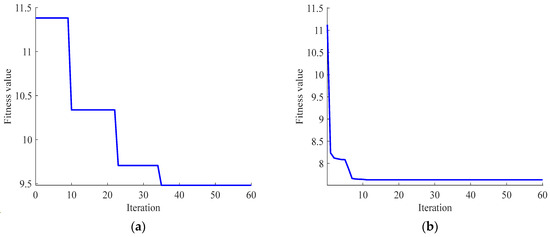
Figure 8.
Comparison of optimal fitness values between the PSO and SBWO algorithms: (a) fitness value of the PSO algorithm; (b) fitness value of the SBWO algorithm.
5. Simulation Results and Analysis
5.1. Parameter Selection
To validate the performance of the designed controller, simulations are conducted. The train parameters are as follows [13]: m = 452,300 kg, f = 0.16 + 0.0053v + 0.00018v2 (N/kN), , and (N). The key controller parameters , , , , , , , and are automatically tuned using the SBWO algorithm, whereas are adaptively adjusted based on an adaptive parameter update law.
The additional running resistance is given as
The track parameters are set as follows: , , , and .
5.2. Simulation Results and Analysis of the Control Strategy
The simulation is configured for an operating profile that includes two acceleration phases, three cruising phases, and two deceleration phases. The maximum speed is 336 km/h, with a total running time of 3000 s and a distance of 239.148 km. The desired speed and displacement curves are shown in Figure 9.
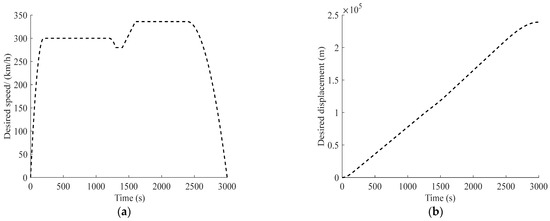
Figure 9.
Desired train operation curves: (a) desired speed; (b) desired displacement.
To validate the performance of the designed controller, the proposed speed tracking control strategy based on improved ADRC is compared with strategies using traditional ADRC [13] and PID control [37] through simulations. The results are presented in Figure 10. It can be seen that, during steady-state operation, the speed and displacement tracking errors of the improved ADRC are maintained within [−1.6 × 10−4, 1.2 × 10−4] km/h and [−0.14, −0.13] m, respectively, achieving the highest steady-state tracking accuracy; when operating conditions change, the improved ADRC responds more rapidly and ensures a smoother transition, demonstrating better adaptability to dynamic conditions; when the conditions of the line vary, the proposed strategy exhibits the minimum tracking error fluctuation, indicating strong anti-disturbance capability; and when stopping, the displacement error with the improved ADRC is −0.0006 m, which is the smallest, thus yielding the highest stopping precision. The simulation results confirm that the proposed speed tracking controller based on improved ADRC performs excellently in terms of steady-state tracking accuracy, dynamic condition adaptability, anti-disturbance performance, and stopping precision, thereby validating the feasibility and effectiveness of the designed controller.
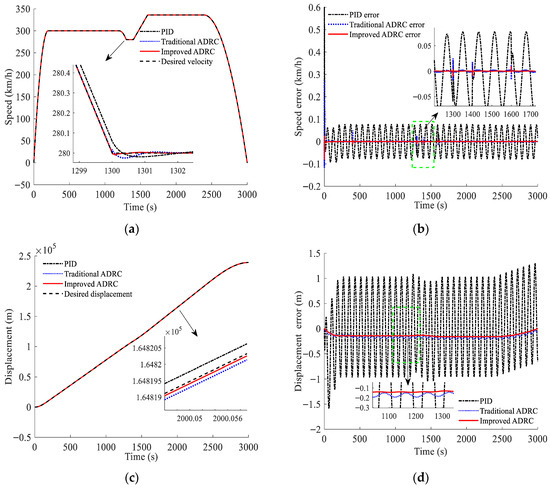
Figure 10.
Comparison of speed tracking performance among three controllers: (a) speed tracking curves; (b) speed tracking errors; (c) displacement tracking curves; (d) displacement tracking errors.
To quantitatively analyze the control performance of the improved ADRC, the root mean square error (RMSE) and the integral of absolute error (IAE) are introduced as speed error performance indexes. The definitions of RMSE and IAE are as follows:
The comparison of high-speed train speed error indexes based on the proposed improved ADRC, traditional ADRC, and PID speed tracking controllers is shown in Table 1. It is evident that the proposed improved ADRC yields the lowest RMSE and IAE values. The result demonstrates that the improved ADRC exhibits superior overall tracking accuracy and control performance compared to both the conventional ADRC and the PID controller.

Table 1.
Comparison of speed error indexes.
To further validate the robustness of the proposed control strategy against the system’s total disturbance, which comprises basic resistance, additional resistance, and external disturbances in practical train operation, a simulation experiment is conducted. In the simulation, the system’s total disturbance is increased, and the basic resistance coefficients are set as follows: , , and , where rand is a function that generates a random number uniformly from the interval [0, 1]. The additional resistance coefficient θ is adjusted to 1.2 times its original value, and the external disturbance is doubled. The results are presented in Figure 11, where it can be seen that even when the total disturbance is increased, the designed controller still enables the train to accurately track the desired trajectory throughout the entire operation. The simulation results indicate that the designed controller is highly robust against the system’s total disturbance and demonstrate the strong anti-disturbance capability of the system.
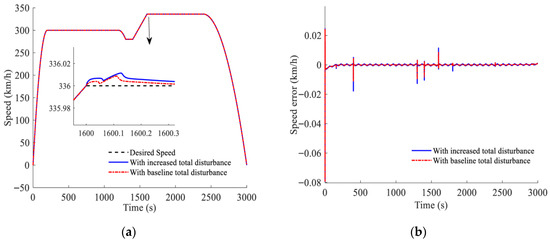
Figure 11.
Speed tracking comparison under increased total disturbance: (a) speed tracking curve under increased total disturbance; (b) speed tracking error under increased total disturbance.
The simulation results for speed and total disturbance observation based on the improved ESO are presented in Figure 12. It is evident that, during train operation, the observation errors for both speed and total disturbance are small. The designed observer achieves an accurate estimation of the train’s speed and the total disturbance, which ensures the excellent steady-state and dynamic performance of the train.
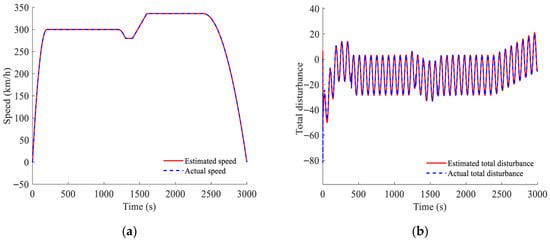
Figure 12.
Simulation results for speed and total disturbance observation with the improved ESO: (a) speed observation; (b) total disturbance observation.
To verify the impact of the improved ESO on the speed tracking performance of the train, a quantitative study was conducted. The simulation results are presented in Table 2, which shows that the control strategy incorporating the improved ESO achieves lower RMSE and IAE values. The simulation results indicate that the proposed method possesses superior speed tracking performance and disturbance rejection capability.

Table 2.
Performance comparison of control strategies with different ESOs.
6. Conclusions
This paper presents an improved feedforward-compensated adaptive ADRC strategy, with its parameters optimized by the SBWO algorithm. An improved TD based on the fort function is introduced, providing a smooth transition for the train’s speed signal while filtering noise and compensating for phase delay; an ESO designed with a caufal function achieves precise estimation and compensation of composite disturbances; the NLSEF control law is enhanced by incorporating an error integral term through nonlinear operations, which reduces the steady-state tracking error, while an adaptive parameter update law enables the self-adjustment of its proportional and differential coefficients; and a feedforward compensation mechanism is integrated to provide real-time dynamic compensation for ESO estimation errors. The core controller parameters are tuned using the proposed SBWO algorithm, which initializes its population with the Sobol sequence and employs a diversified search strategy, thereby enhancing global search capability, convergence speed, and optimization accuracy. This strategy effectively improves the system’s anti-disturbance performance, overcomes the challenges of parameter tuning, and achieves high-precision tracking of the train’s target curve under multi-source disturbances in complex dynamic environments.
Author Contributions
Conceptualization, C.X. and M.X.; methodology, C.Z.; software, C.Z. and Z.H.; validation, C.Z., J.C. and L.W.; formal analysis, C.X. and C.Z.; investigation, L.W.; resources, C.X.; data curation, L.W.; writing—original draft preparation, C.Z.; writing—review and editing, C.X. and M.X.; visualization, J.C.; supervision, C.X.; project administration, M.X.; funding acquisition, M.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Liaoning Provincial Education Department Scientific Research Project (LJ212510150031, LJ212410150040, JYTMS20230038) and the Liaoning Province Transportation Science and Technology Project (202318, 202344).
Data Availability Statement
The raw data supporting this study’s conclusions are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhou, L.; Tong, L.C.; Chen, J.; Tang, J.; Zhou, X. Joint optimization of high-speed train timetables and speed profiles: A unified modeling approach using space-time-speed grid networks. Transp. Res. Part B Methodol. 2017, 97, 157–181. [Google Scholar] [CrossRef]
- Zhou, F.R.; Zhou, K.; Zhang, D.; Peng, Q.Y. Optimization of the cruising speed for high-speed trains to reduce energy consumed by motion resistances. Appl. Energy 2024, 374, 124039. [Google Scholar] [CrossRef]
- Qin, Y.; Guo, J.; Xu, P.; Li, D.; Wang, Y. Train energy-efficient speed profile generation under various track alignments: A quantum evolutionary algorithm with cosine annealing. Swarm Evol. Comput. 2025, 97, 102027. [Google Scholar] [CrossRef]
- Bin, Z.; Shijun, Y.; Lanfang, Z.; Daming, L.; Yalan, C. Energy-efficient speed profile optimization for high-speed railway considering neutral sections. IEEE Access 2021, 9, 25090–25100. [Google Scholar] [CrossRef]
- Li, Z.; Huang, D.; Cai, L. Adaptive nonsingular terminal sliding mode tracking control for high-speed trains with input constraints and parametric uncertainties. Int. J. Control. Autom. Syst. 2024, 22, 753–764. [Google Scholar] [CrossRef]
- Pu, Q.; Zhu, X.; Zhang, R.; Liu, J.; Cai, D.; Fu, G. Speed profile tracking by an adaptive controller for subway train based on neural network and PID algorithm. IEEE Trans. Veh. Technol. 2020, 69, 10656–10667. [Google Scholar] [CrossRef]
- Xu, X.; Peng, J.; Zhang, R.; Chen, B.; Zhou, F.; Yang, Y.; Gao, K.; Huang, Z. Adaptive model predictive control for cruise control of high-speed trains with time-varying parameters. J. Adv. Transp. 2019, 2019, 7261726. [Google Scholar] [CrossRef]
- Wang, X.; Tang, T. Optimal operation of high-speed train based on fuzzy model predictive control. Adv. Mech. Eng. 2017, 9, 1687814017693192. [Google Scholar] [CrossRef]
- Kang, Z.; Jia, L.M.; Zuo, X.L.; Shen, P.J.; Qin, Y.; Chai, Y.Y. A novel controller based on fuzzy sliding mode control for train speed tracking. IEEE Trans. Veh. Technol. 2024, 73, 7653–7668. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, B.; Mao, Z.; Ding, S.X. Adaptive backstepping based fault-tolerant control for high-speed trains with actuator faults. Int. J. Control. Autom. Syst. 2019, 17, 1408–1420. [Google Scholar] [CrossRef]
- Mou, R.; Chen, C.; Chen, C.; Zhang, Y. Analysis and control of high-speed train lateral vibration on the basis of a conditionally triggered model predictive control strategy. J. Mech. Sci. Technol. 2024, 38, 1703–1717. [Google Scholar] [CrossRef]
- Tong, Y.; Ren, Z.; Tong, D.; Fan, Z.; Feng, X. Combined finite-time state feedback for high-speed train systems with time-varying delays and disturbances. Int. J. Robust Nonlinear Control 2024, 34, 2184–2205. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Zhang, X.; Sun, Q.; Sun, M. A novel control scheme for quadrotor UAV based upon active disturbance rejection control. Aerosp. Sci. Technol. 2018, 79, 601–609. [Google Scholar] [CrossRef]
- Jiang, W.; Chen, D.; Zheng, Y.; Qiu, X.; Wang, C. Active disturbance rejection control based on inertia estimation and variable gain for servomechanism of industrial robot. Meas. Control 2022, 55, 189–197. [Google Scholar] [CrossRef]
- Sun, Z.; Zheng, J.; Man, Z.; Wang, H.; Lu, R. Sliding mode-based active disturbance rejection control for vehicle steer-by-wire systems. IET Cyber-Phys. Syst. Theory Appl. 2018, 3, 1–10. [Google Scholar] [CrossRef]
- Xie, F.; Hong, W.; Qiu, C. Speed fluctuation suppression of PMSM using active disturbance rejection and feedback compensation control. IET Electr. Power Appl. 2021, 15, 1056–1067. [Google Scholar] [CrossRef]
- Lian, W.B.; Liu, B.H.; Li, W.W.; Liu, X.Q.; Gao, F.Y.; Li, M.Q. Automatic operation speed control of high-speed train based on ADRC. J. China Railw. Soc. 2020, 42, 76–81. [Google Scholar] [CrossRef]
- Song, Z.; Li, S.; Yu, X.; Yang, Y.; Wang, X. Cooperative Active Disturbance Rejection Control for Heavy-Haul Trains. J. Adv. Comput. Intell. Intell. Inform. 2025, 29, 165–174. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, C.; Dai, C.; Long, Z. An Active Resisting Disturbance Control Method for High-speed Maglev Train With Weak Model Dependence. ISA Trans. 2025, 163, 172–183. [Google Scholar] [CrossRef]
- Lin, B.; Zheng, M.; Han, B.; Chu, X.; Zhang, M.; Zhou, H.; Ding, S.; Wu, H.; Zhang, K. PSO-based predictive PID-backstepping controller design for the course-keeping of ships. J. Mar. Sci. Eng. 2024, 12, 202. [Google Scholar] [CrossRef]
- Rodríguez-Abreo, O.; Rodríguez-Reséndiz, J.; García-Cerezo, A.; García-Martínez, J.R. Fuzzy logic controller for UAV with gains optimized via genetic algorithm. Heliyon 2024, 10, e26363. [Google Scholar] [CrossRef]
- Chauhan, S.; Singh, B.; Singh, M. Modified ant colony optimization based PID controller design for coupled tank system. Eng. Res. Express 2021, 3, 045005. [Google Scholar] [CrossRef]
- Hu, G.; Du, B.; Wang, X.; Wei, G. An enhanced black widow optimization algorithm for feature selection. Knowl.-Based Syst. 2022, 235, 107638. [Google Scholar] [CrossRef]
- Mathur, N.; Meena, V.P.; Singh, V.P. Black widow optimisation-based controller design for riverol-pilipovik water treatment system. Int. J. Model. Identif. Control 2022, 40, 204–209. [Google Scholar] [CrossRef]
- Chen, Z.; Li, W.; Liu, X.; Wang, Y.; Chan, T.H. A Multistrategy Fusion–Improved Black Widow Optimization Algorithm for Structural Damage Identification. Struct. Control Health Monit. 2025, 2025, 2939779. [Google Scholar] [CrossRef]
- Yang, J.; Chen, Y.Q.; Wang, P.P. Design of active disturbance rejection controller for train speed tracking based on improved particle swarm optimization. J China Railw. Soc. 2021, 43, 40–46. [Google Scholar] [CrossRef]
- Xu, C.; Liang, T.; Wang, L.; Yang, F. Robust Adaptive Dynamic Surface Fault-tolerant Tracking Control for High-speed Trains Considering Actuator Output Magnitude and Rate Saturation Constraints. Int. J. Control Autom. Syst. 2025, 23, 55–67. [Google Scholar] [CrossRef]
- Zou, K.; Wang, Y.; Liu, B.; Zhang, Z. Load Frequency Optimal Active Disturbance Rejection Control of Hybrid Power System. Algorithms 2024, 17, 403. [Google Scholar] [CrossRef]
- Tan, S.L.; Lei, H.M.; Wang, P.F. Design of tracking differentiator based on tangent Sigmoid function. Syst. Eng. Electron. 2019, 41, 1590–1596. [Google Scholar] [CrossRef]
- Chen, P.; Shi, T.C.; Yu, M.Y.; Chen, Y.; Shi, Y. Sliding mode active disturbance rejection levitation control algorithm of the medium-and low-speed maglev vehicles. J. Railw. Sci. Eng. 2023, 20, 682–693. [Google Scholar] [CrossRef]
- Lu, L.; Wang, J.; Yuan, C.; Wu, Y. Design and application of tracking differentiator based on inverse hyperbolic tangent function. Syst. Eng. Electron. 2020, 42, 2875–2883. [Google Scholar] [CrossRef]
- Wang, P.P.; Yang, J.; Zou, J.Q.; Liu, H.E. Design maglev train speed tracking system based on improved active disturbance rejection controller. J. Railw. Sci. Eng. 2023, 20, 310–320. [Google Scholar] [CrossRef]
- Cao, H.; Deng, Y.; Zuo, Y.; Liu, X.; Wang, J.; Lee, C.H. A variable structure ADRC for enhanced disturbance rejection and improved noise suppression of PMSM speed system. IEEE Trans. Ind. Electron. 2025, 72, 4481–4495. [Google Scholar] [CrossRef]
- Wu, Z.; Fan, K.; Zhang, X.; Li, W. Based on sliding mode and adaptive linear active disturbance rejection control for a magnetic levitation system. J. Sens. 2023, 2023, 5568976. [Google Scholar] [CrossRef]
- Hayyolalam, V.; Kazem, A.A.P. Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103249. [Google Scholar] [CrossRef]
- Singh, S.P.; Pathak, D.; Kumar, A.; Padmanaban, S. An optimized fractional-order modified adaptive variable step-size LMS control approach to enhance DVR performance. IEEE Trans. Consum. Electron. 2023, 70, 471–483. [Google Scholar] [CrossRef]
- Zhang, C.; Tan, N.; Zhou, T.; Liu, M.; Shan, H. Research on optimal control of subway train based on fractional order PID controller. J. China Railw. Soc. 2018, 40, 8–14. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).