A Reinforcement Learning Hyper-Heuristic with Cumulative Rewards for Dual-Peak Time-Varying Network Optimization in Heterogeneous Multi-Trip Vehicle Routing
Abstract
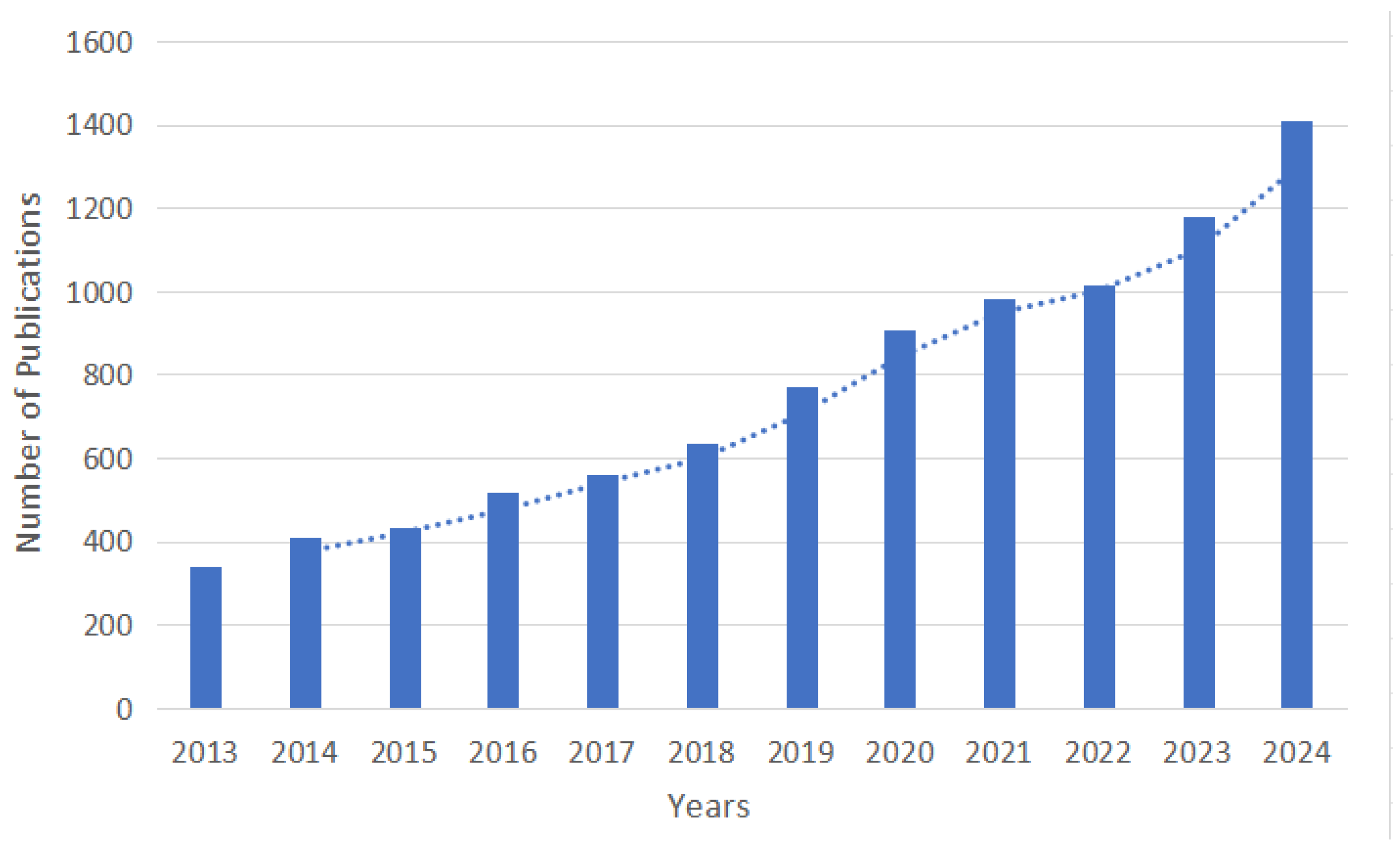
1. Introduction
1.1. Background and Motivation
1.2. Related Work
1.2.1. Research on Multi-Trip Vehicle Routing Problems (MTVRPs)
1.2.2. Reinforcement Learning Approaches for MTVRP
- In response to the warehouse transfer issues faced by the company’s B2C operations, we have simultaneously considered the balance of driver workload, time windows, heterogeneous fleet, loading capacity, and time-varying road networks (morning and evening peaks), which are significant real-world characteristics with substantial practical value for logistics enterprises. To date, we have not found any MTVRP studies that comprehensively account for all these realistic features.
- To address the problem, we define this problem as the Heterogeneous Multi-Trip Vehicle Routing Problem with Time Windows and Time-Varying Networks (HMTVRPTW-TVN) and develop a mixed-integer linear programming (MILP) formulation. A dual-peak time discretization method is proposed to efficiently model time-varying networks by segmenting continuous peak periods, alongside an exact linearization technique for handling times to enable coordinated scheduling of heterogeneous fleets.
- Based on the characteristics of this real-world problem, we propose a novel HHCRQL algorithm that incorporates reinforcement learning (RL) into MTVRP. The algorithm effectively reduces the total time required for scheduling multiple trips, with its performance advantages becoming more pronounced when handling large-scale instances.
- We established an appropriate Markov Decision Process (MDP) model and proposed a cumulative reward assignment method based on time steps, applying the concept of cumulative rewards throughout the training process. By solving the MDP model, we effectively reduced the number of iterations and improved overall computational efficiency.
2. Materials and Methods
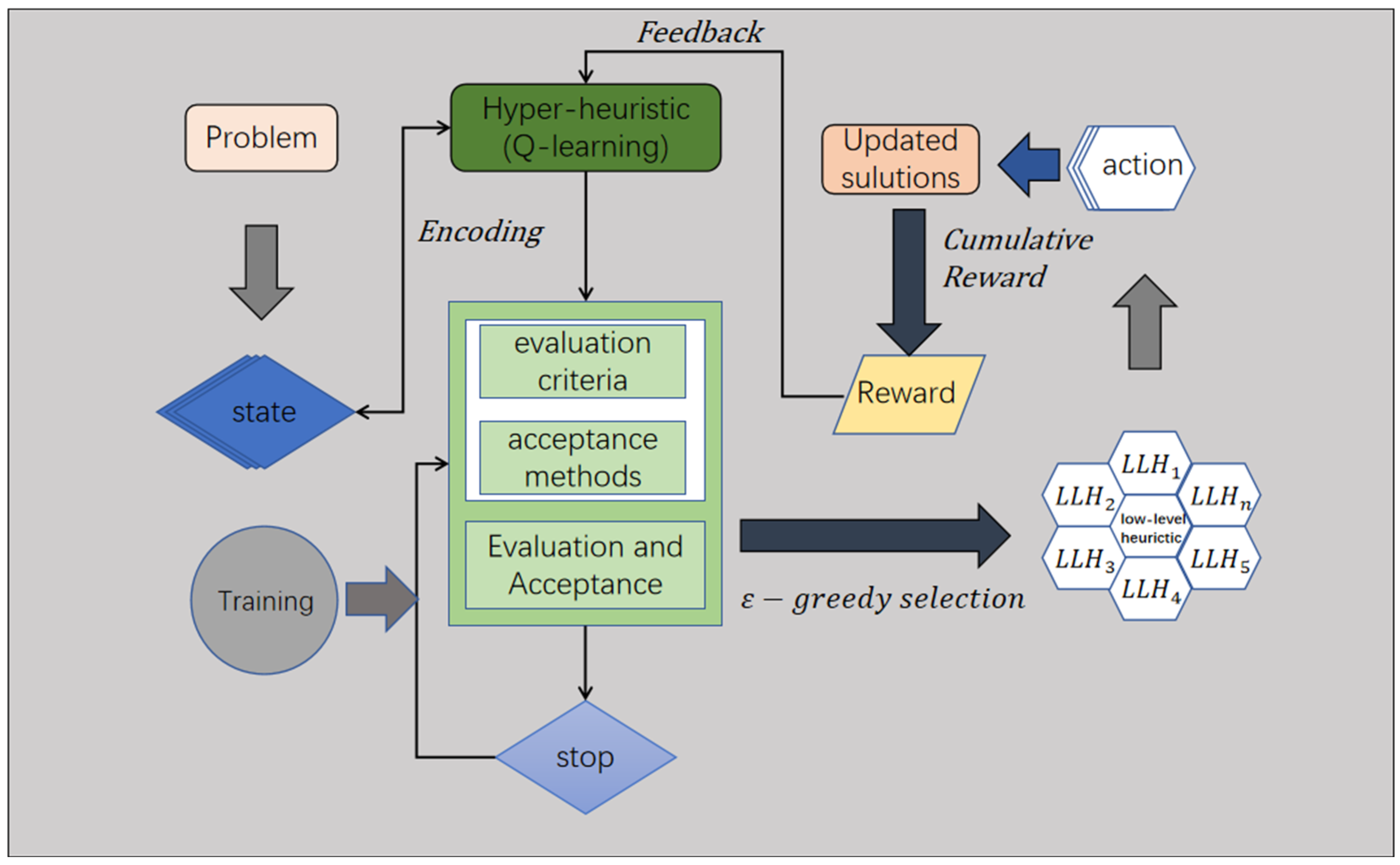
2.1. Heuristic Operators–Reinforcement Learning Framework
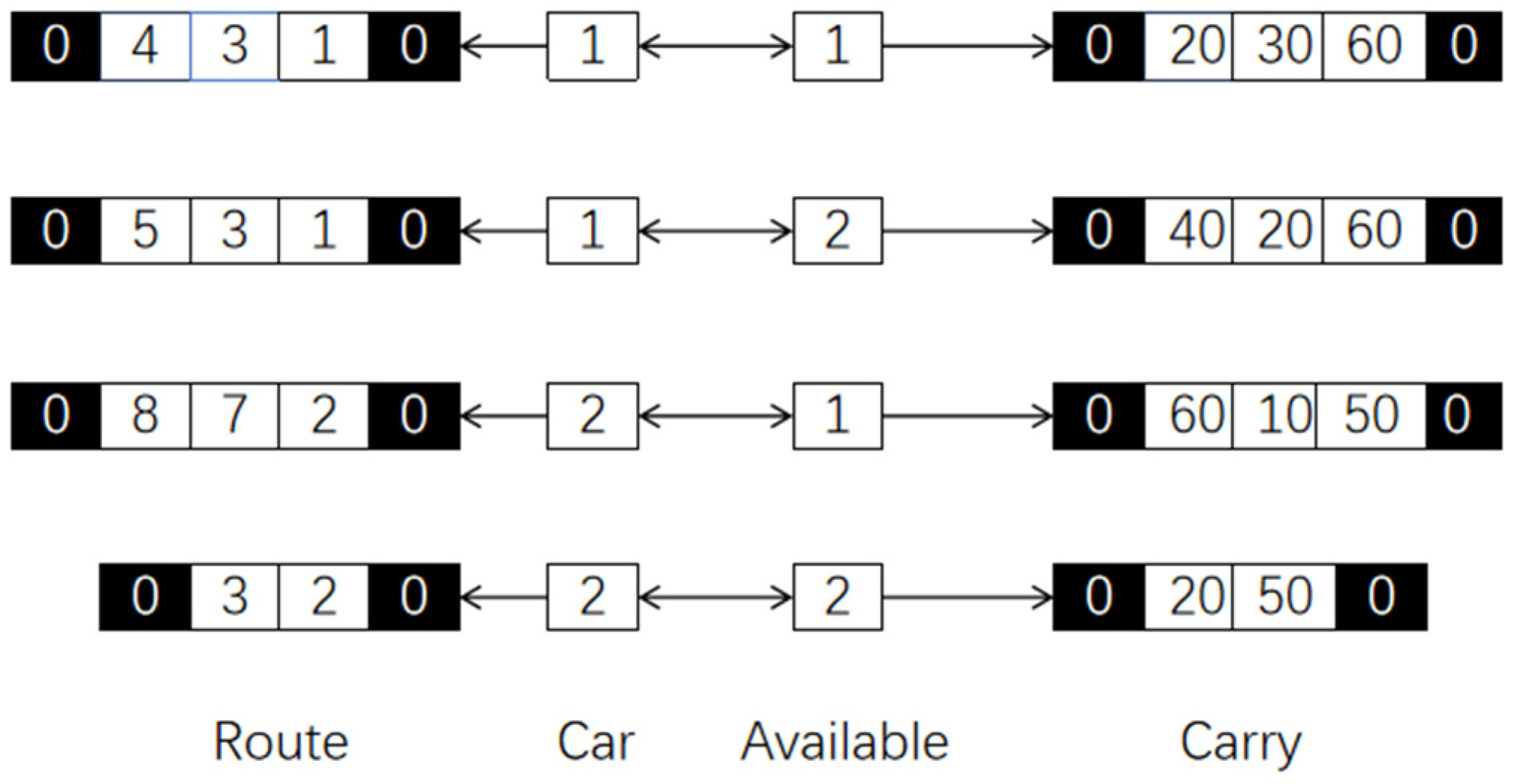
2.1.1. Initial Solution Generation
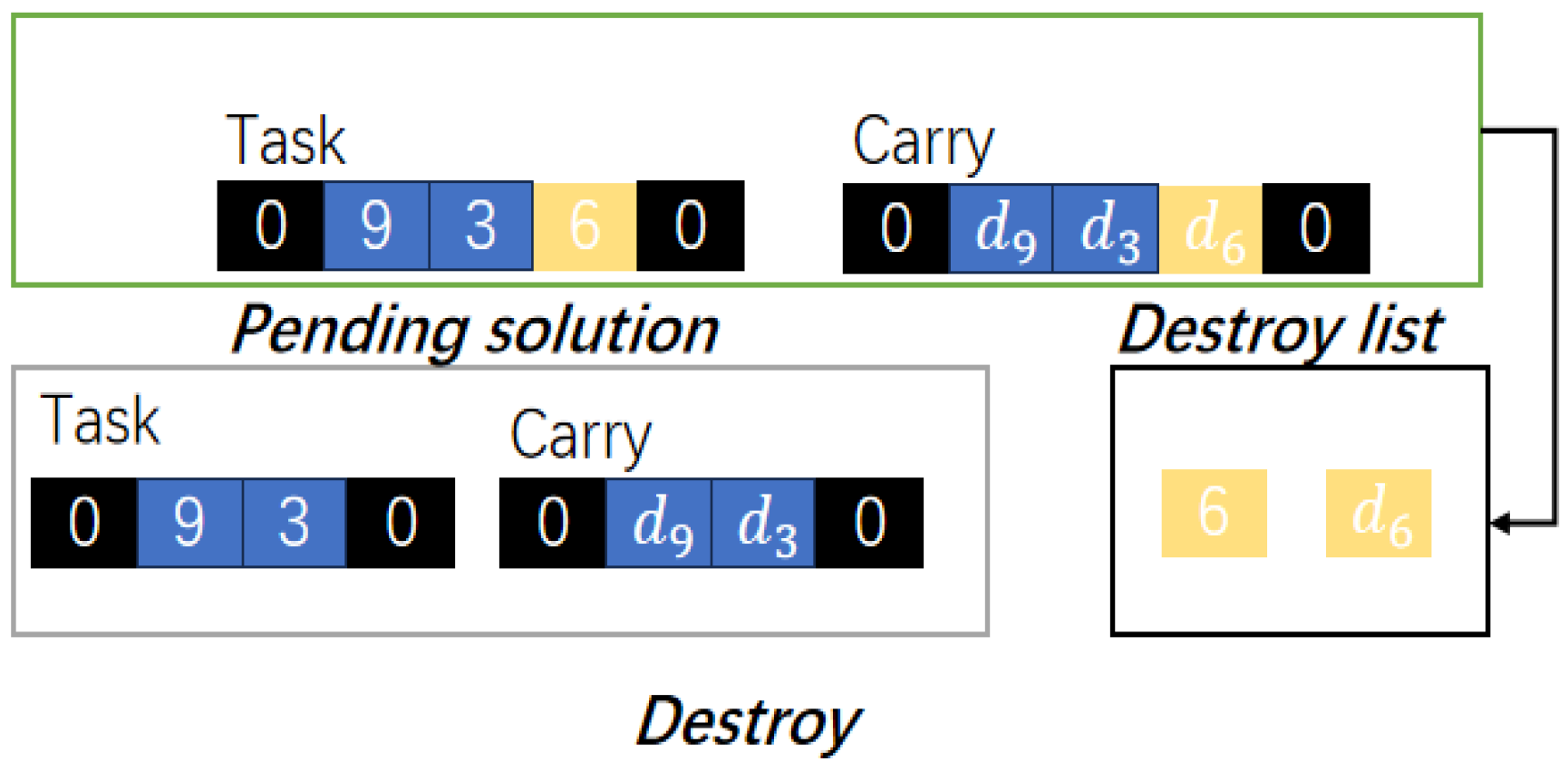
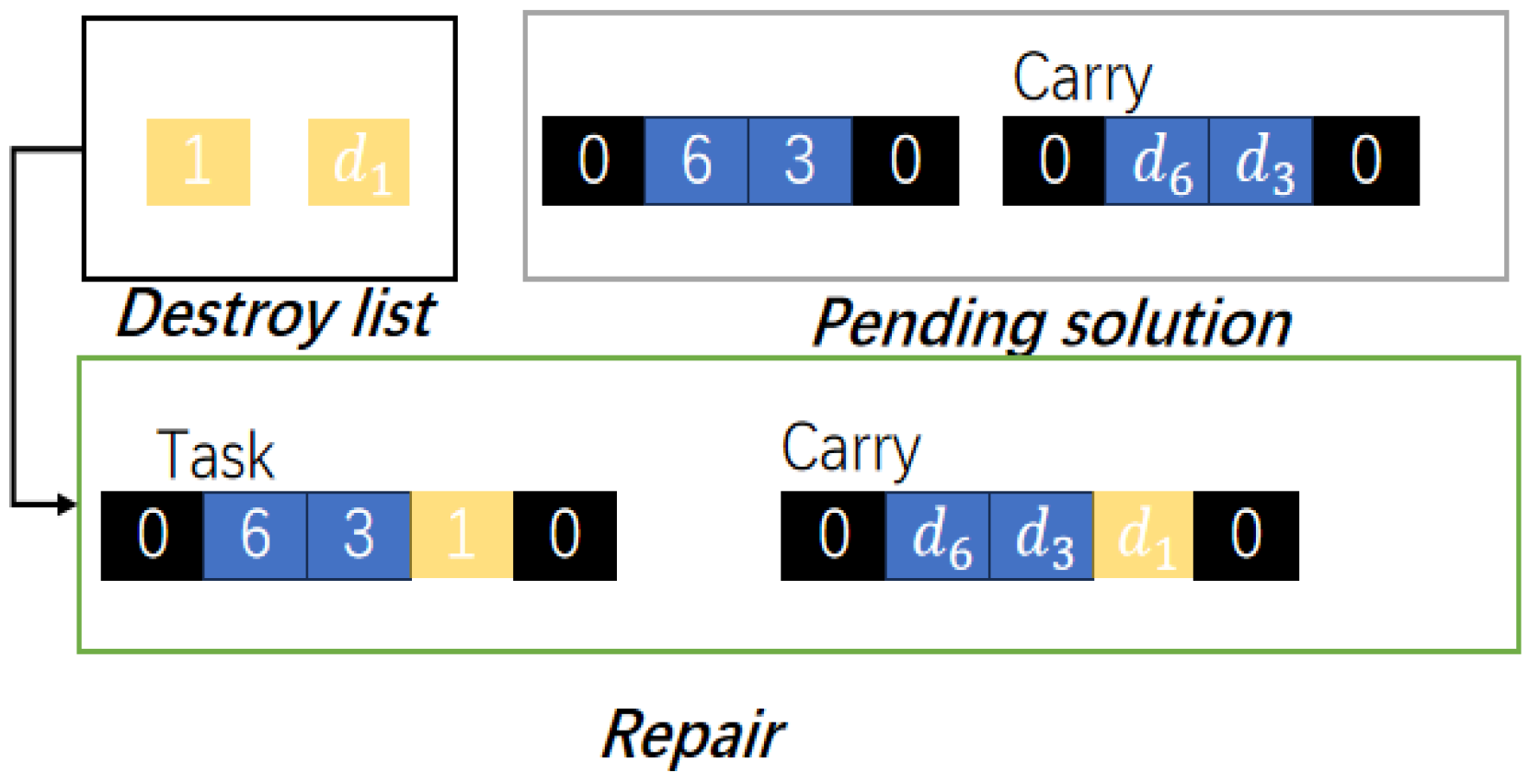
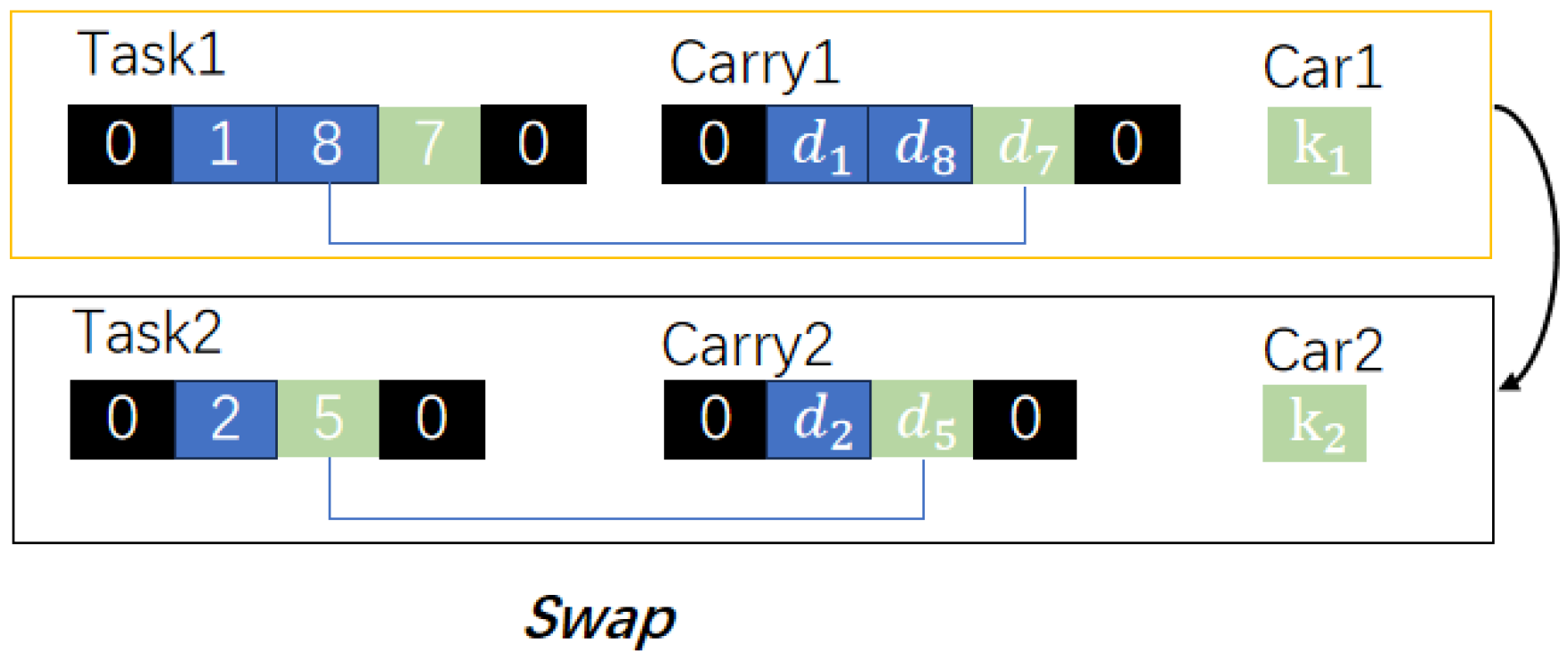
2.1.2. Low-Level Heuristic Operator Operations
2.2. MDP Model Establishment
2.2.1. Definition of the State Set
- (1)
- Feasibility Indicator:
- (2)
- Number of Vehicle Types:
- (3)
- Remaining Task Ratio Segmentation:
- (4)
- Vehicle Load Utilization Interval:
2.2.2. Design of Action Set and Reward Function
2.2.3. Policy Function
2.3. Hyper-Heuristic Based on CR-Q-Learning
2.3.1. CR-Selection Strategy
2.3.2. HHCRQL Algorithm Procedure
| Algorithm 1 HHCRQL |
| HHCRQL Algorithm parameters: number_episodes (max_e), max_step (max_s), episode (e), step (s), Q table, state set (S), action set (A), learning rate (alpha), exploration rate (epsilon), discount factor (gamma). 1. Initial solution generation 2. Initialize the Q table |
| 3. Input: algorithm parameters to HHCRQL Algorithm |
| 4. while episode (e) < max_e do |
| 5. : choose state (F, V, , U) |
| 6. for time step (t) in max_step (max_s) 7. choose action according to ε-greedy |
| 8. Execution: executes the selected action based on the |
| 9. : Determination of the feasibility of the current time step |
| 10. if feasibly: |
| 11. : calculate the reward 12. : Fitness value calculation of the current time step 13. if better 14. : accrue reward and update Q table 15. else: no accrue reward 16. else: give punishment in reward and update Q table 17. t = t + 1 18. END While: satisfy stopping criterion 19. Output: optimal solution and Q table |
3. Problem Description and Modeling
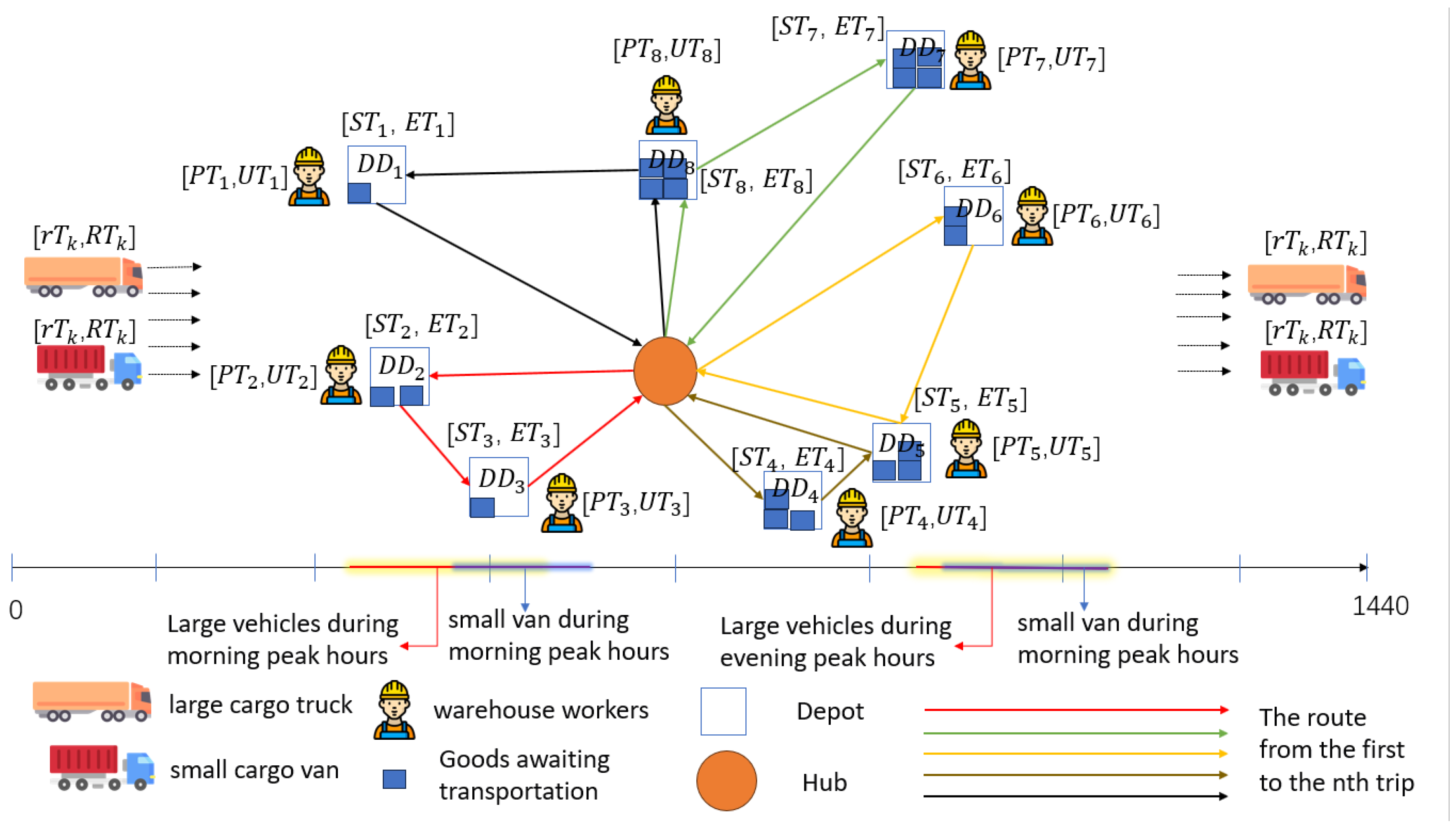
3.1. Problem Description
3.2. Parameter and Variable Definitions
3.3. Construction of HMTVRPTW-TVN
- Objective function consisting of two components, with cost calculation varying by vehicle type:Subject to the following:
- Capacity and demand constraints:
- Flow conservation constraints:
- Vehicle task execution sequence constraints:
- Peak period constraints for small vehicles:
- Peak period constraints for large vehicles:
- Warehouse worker rest time-window constraints:
- Driver working time-window constraints:
- Trip count limitations:
- Trip sequence limitations:
- Warehouse operating time-window constraints:
- Other constraints (non-zero loading, inter-trip time coupling, and binary variable declarations):
4. Numerical Experiments
4.1. Solution Results Based on Real Cases
4.1.1. Real-Case Analysis
4.1.2. Real-Case Study and Result Analysis
4.2. Algorithm and Model Validity
4.2.1. Benchmark Methods
4.2.2. Parameter Settings
4.3. Convergence and Parameter Sensitivity Analysis
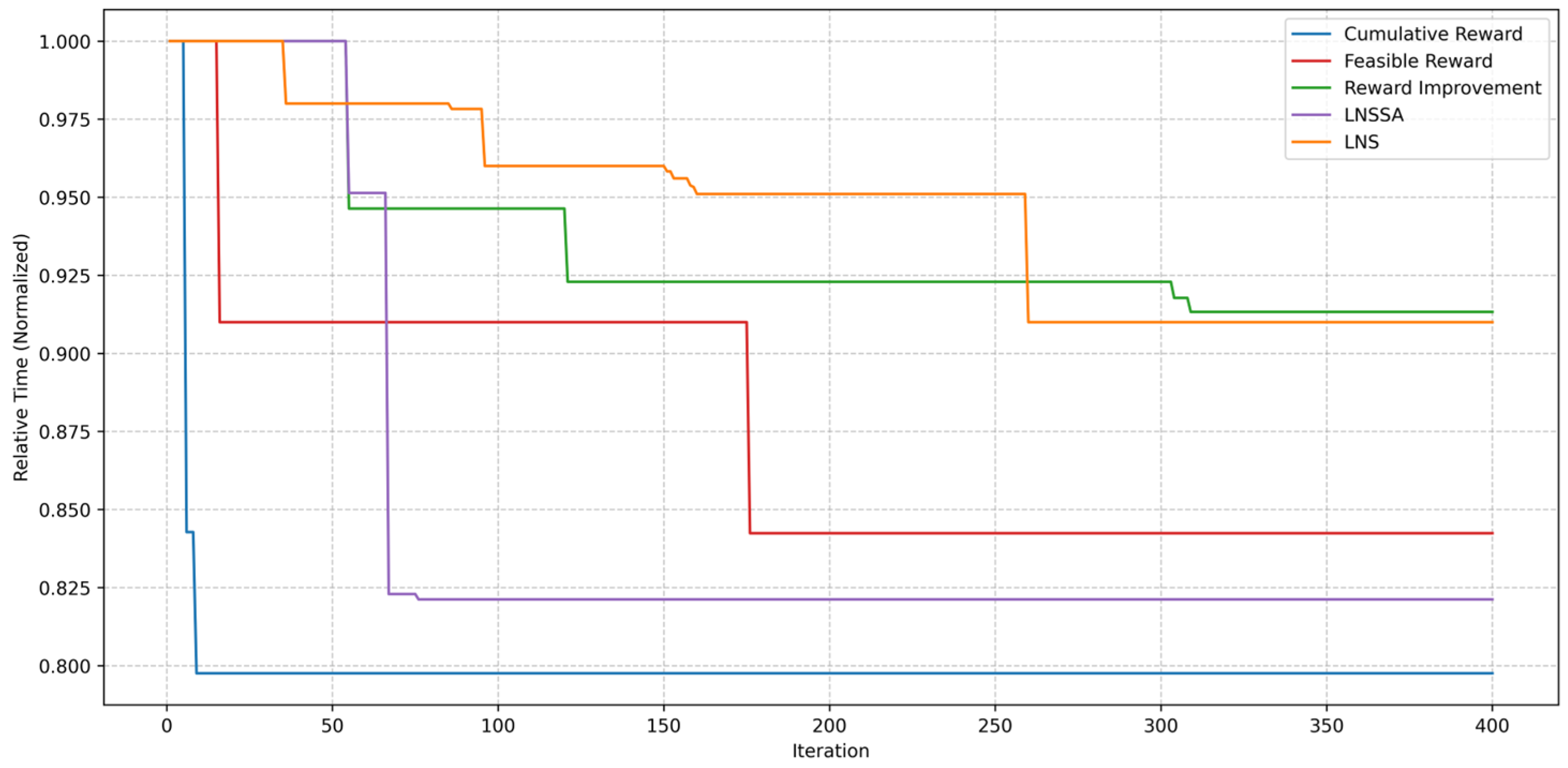
4.3.1. Convergence Analysis
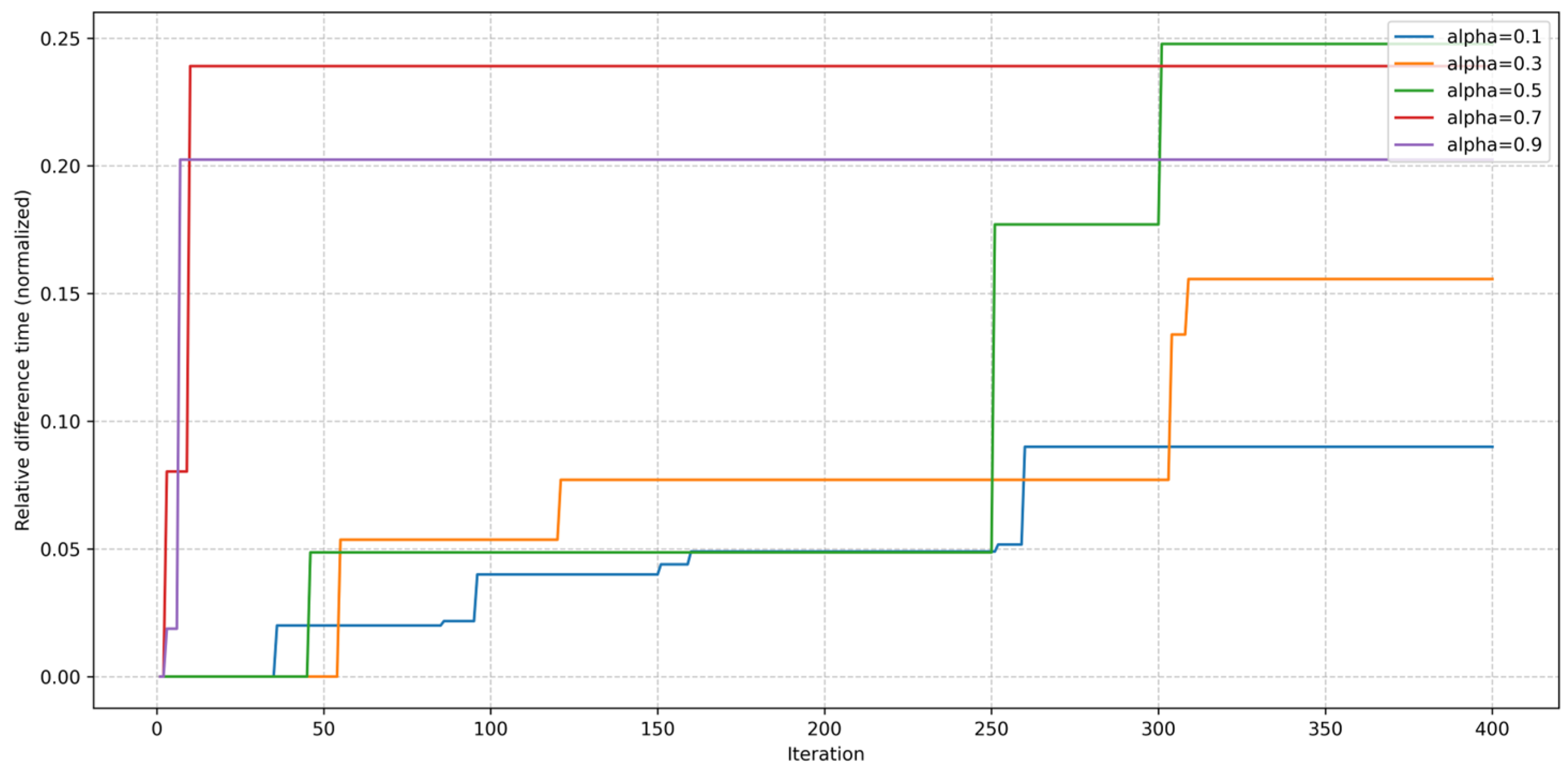
4.3.2. Learning Rate Sensitivity
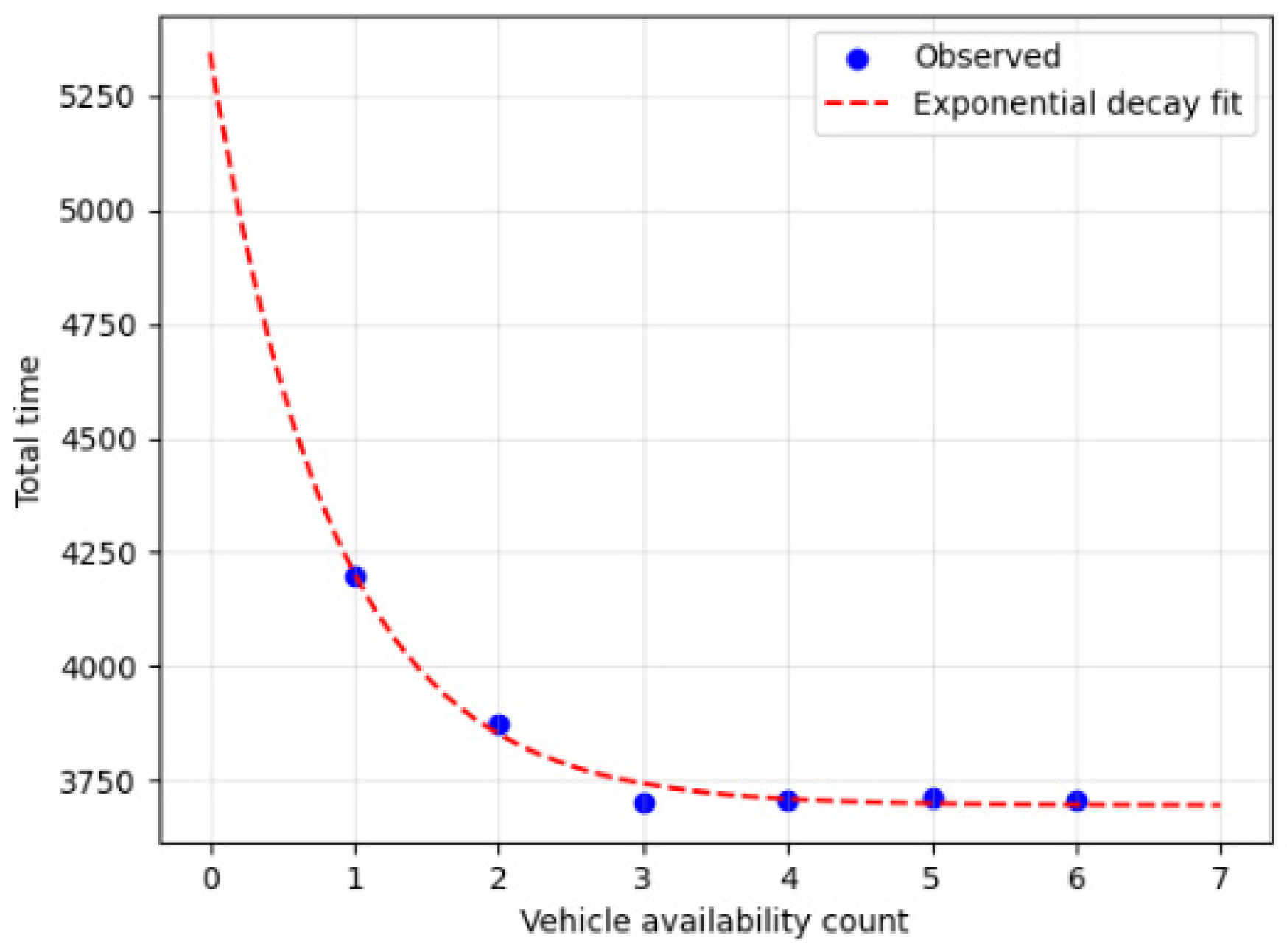
4.3.3. Theoretical Discussion
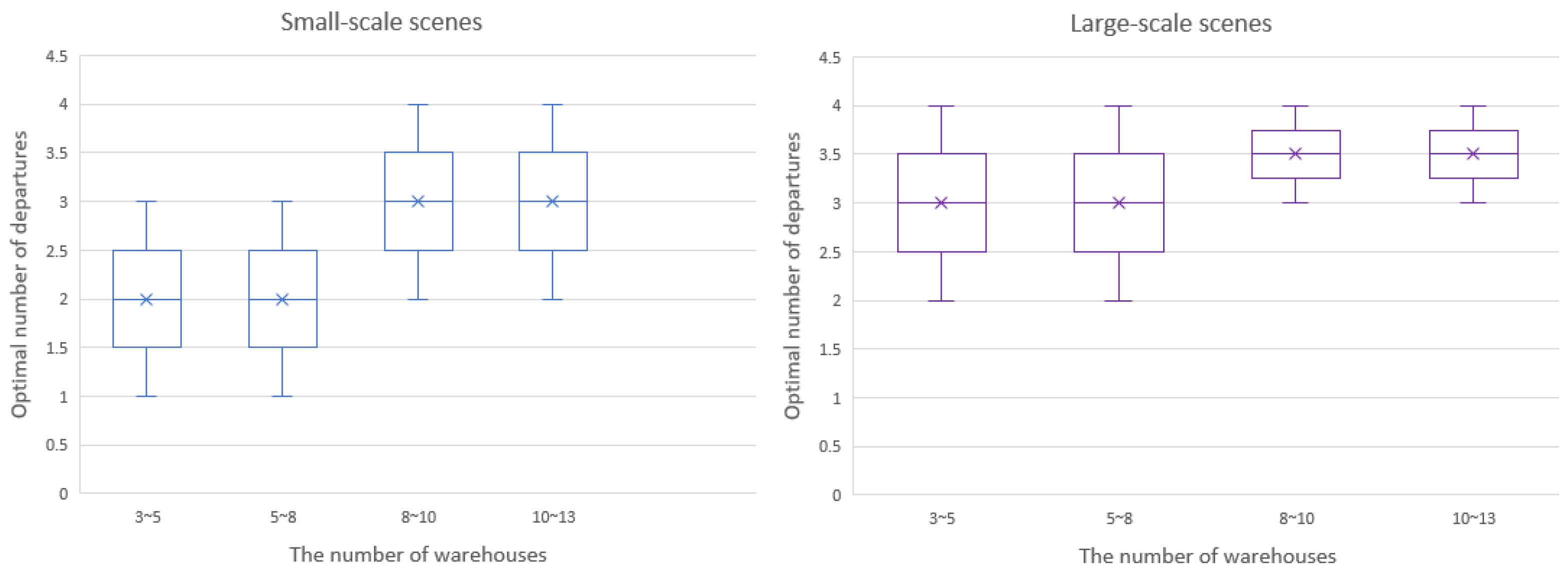
4.4. Analysis of Driver Workload Balance
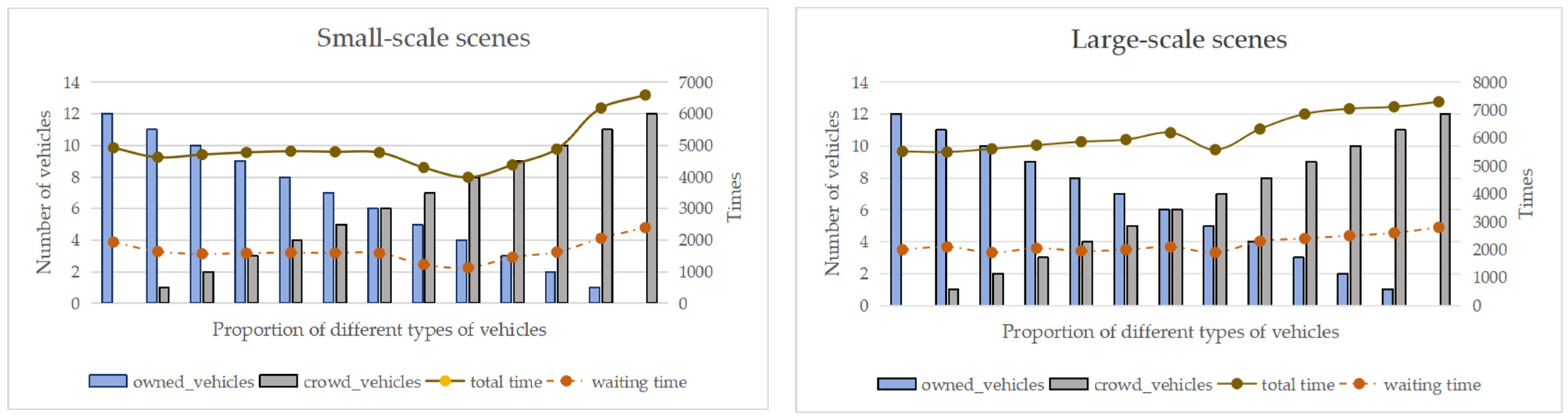
4.5. Fleet-Composition Analysis for a Heterogeneous Fleet
4.6. Managerial Implications
- 1.
- Institutionalize the Driver Trip Limit
- 2.
- Dynamic Fleet Mix Governance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Warehouse | Operation Rate | |||
|---|---|---|---|---|
| Serial Number | Large Cargo Truck | Small Cargo Van | ||
| Loading Rate (Cubic Meters/ Minute) | Fixed Time (Cubic Meters/Minute) | Loading Rate (Cubic Meters/ Minute) | Fixed Time (Cubic Meters/ Minute) | |
| 1.5 | 10 | 1.67 | 10 | |
| 1 | 1 | 15 | 1.06 | 15 |
| 2 | 1 | 15 | 1.67 | 15 |
| 3 | 1.78 | 15 | 1.67 | 15 |
| 4 | 1 | 15 | 1.06 | 15 |
| 5 | 1 | 15 | 1.06 | 15 |
| 6 | 1.78 | 15 | 1.48 | 15 |
| 7 | 1 | 15 | 1.06 | 15 |
| 8 | 1 | 15 | 1.06 | 15 |
| 9 | 1 | 15 | 1.06 | 15 |
| 10 | 1 | 15 | 1.06 | 15 |
| 11 | 1 | 15 | 1.06 | 15 |
| … | 1 | 15 | 1.06 | 15 |
| n | 1 | 15 | 1.06 | 15 |
| Round | Car | Task | Time | Carry |
|---|---|---|---|---|
| 1 | 0 | 0-1-11 | 330, 400, 777 | 110 |
| 1 | 0-1-11 | 330, 400, 777 | 110 | |
| 2 | 0-1-11 | 330.400.770 | 110 | |
| 3 | 0-1-11 | 330, 400, 777 | 110 | |
| 4 | 0-1-11 | 360, 430, 703 | 45 | |
| 5 | 0-4-11 | 360, 430, 697 | 38.65 | |
| 6 | 0-3-11 | 360, 430, 684 | 45 | |
| 7 | 0-7-11 | 360, 430, 703 | 45 | |
| 8 | 0-6-8-11 | 360, 430, 673, 807 | 21.02 | |
| 9 | 0-9-11 | 360, 430, 696 | 39.26 | |
| 2 | 0 | 0-1-11 | 861, 931, 1257 | 110 |
| 1 | 0-1-11 | 861, 931, 1257 | 110 | |
| 2 | 0-1-11 | 861, 931, 1257 | 110 | |
| 3 | 0-1-11 | 861, 931, 1257 | 110 | |
| 4 | 0-1-11 | 743, 813, 960 | 45 | |
| 5 | 0-5-11 | 733, 810, 946 | 33.37 | |
| 6 | 0-2-4-10-11 | 724, 810, 934, 1008, 1098 | 21.79 | |
| 7 | 0-3-11 | 743, 813, 936 | 36.3 | |
| 8 | 0-2-11 | 844, 914, 1032 | 26.54 |
| Algorithm A1 Large Neighborhood Search—Simulated Annealing |
| LNSSA Algorithm parameters: Initial temperature (T0), End time (Tend), Cooling rate (α), Acceptance rate (p) Input: algorithm parameters 1. initial solution: Greedy strategy 2. update feasible: get feasible solutions 3. while ture: 4. Destroy operation: choose different operation to destroy initial solution 5. Repair operation: choose different operation to repair destroyed solution 6. Swap operation: choose different operation to swap repaired solution 7. if feasible 8. break 9. end while 10. while T ≥ Tend 11. feasible solutions = update feasible (initial solution) 12. Record better solutions and Accept the worse solution with Acceptance rate (p) 13. satisfy criterion 14. END while 15. output: Optimal solution |
| Warehouse | Demand |
|---|---|
| 1 | 863.96 |
| 2 | 48.33 |
| 3 | 81.3 |
| 4 | 170.91 |
| 5 | 33.37 |
| 6 | 25.35 |
| 7 | 45.45 |
| 8 | 23.98 |
| 9 | 39.26 |
| 10 | 0.95 |
| 11 | 0 |
| 12 | 0 |
| 13 | 0 |
| Parameter | Demand |
|---|---|
| Epsilon | 0.1 |
| alpha | 0.5 |
| gamma | 0.9 |
| Max_episodes | 20 |
| Max_steps | 20 |
| T | 1000 |
| T_end | 10 |
| q | 0.8 |
| 9 | 39.26 |
| 10 | 0.95 |
| 11 | 0 |
| 12 | 0 |
| 13 | 0 |
Appendix B
Appendix B.1. ILS Pseudocode
Appendix B.2. Initial Defacilitation Code
References
- Jamrus, T.; Wang, H.; Chien, C. Dynamic coordinated scheduling for supply chain under uncertain production time to empower smart production for Industry 3.5. Comput. Ind. Eng. 2020, 142, 106375. [Google Scholar] [CrossRef]
- Zhao, Z.; Lee, C.K.M.; Ren, J.; Tsang, Y. Quality of service measurement for electric vehicle fast charging stations: A new evaluation model under uncertainties. Transp. A Transp. Sci. 2025, 21, 2232044. [Google Scholar] [CrossRef]
- Nguyen, V.S.; Pham, Q.D.; Nguyen, T.H.; Bui, Q.T. Modeling and solving a multi-trip multi-distribution center vehicle routing problem with lower-bound capacity constraints. Comput. Ind. Eng. 2022, 172, 108597. [Google Scholar] [CrossRef]
- Friggstad, Z.; Mousavi, R.; Rahgoshay, M.; Salavatipour, M.R. Improved approximations for capacitated vehicle routing with unsplittable client demands. In Integer Programming and Combinatorial Optimization, Proceedings of the 23rd International Conference, IPCO 2022, Eindhoven, The Netherlands, 27–29 June 2022; Springer: Cham, Switzerland, 2020; Volume 13265, pp. 251–261. [Google Scholar]
- Qi, R.; Li, J.; Wang, J.; Jin, H.; Han, Y. QMOEA: A Q-learning-based multiobjective evolutionary algorithm for solving time-dependent green vehicle routing problems with time windows. Inf. Sci. 2022, 608, 178–201. [Google Scholar] [CrossRef]
- Li, M.; Zhao, P.; Zhu, Y.; Cai, K. A learning and searching integration approach for same-day delivery problem with heterogeneous fleets considering uncertainty. Transp. A Transp. Sci. 2024, 44, 1–44. [Google Scholar] [CrossRef]
- Kou, S.; Golden, B.; Bertazzi, L. Estimating optimal split delivery vehicle routing problem solution values. Comput. Oper. Res. 2024, 168, 106714. [Google Scholar] [CrossRef]
- François, V.; Arda, Y.; Crama, Y.; Laporte, G. Large neighborhood search for multi-trip vehicle routing. Eur. J. Oper. Res. 2016, 255, 422–441. [Google Scholar] [CrossRef]
- Agrawal, A.K.; Yadav, S.; Gupta, A.A.; Pandey, S. A genetic algorithm model for optimizing vehicle routing problems with perishable products under time-window and quality requirements. Decis. Anal. J. 2022, 5, 100139. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Q.; Ma, L.; Zhang, Z.; Liu, Y. A hybrid ant colony optimization algorithm for a multi-objective vehicle routing problem with flexible time windows. Inf. Sci. 2019, 490, 166–190. [Google Scholar] [CrossRef]
- Ahmed, Z.H.; Yousefikhoshbakht, M. An improved tabu search algorithm for solving heterogeneous fixed fleet open vehicle routing problem with time windows. Alex. Eng. J. 2023, 64, 349–363. [Google Scholar] [CrossRef]
- Osorio-Mora, A.; Escobar, J.W.; Toth, P. An iterated local search algorithm for latency vehicle routing problems with multiple depots. Comput. Oper. Res. 2023, 158, 106293. [Google Scholar] [CrossRef]
- Kuo, R.J.; Luthfiansyah, M.F.; Masruroh, N.A.; Zulvia, F.E. Application of improved multi-objective particle swarm optimization algorithm to solve disruption for the two-stage vehicle routing problem with time windows. Expert Syst. Appl. 2023, 225, 120009. [Google Scholar] [CrossRef]
- Su, E.; Qin, H.; Li, J.; Pan, K. An exact algorithm for the pickup and delivery problem with crowdsourced bids and transshipment. Transp. Res. Part B Methodol. 2023, 177, 102831. [Google Scholar] [CrossRef]
- Zhou, H.; Qin, H.; Cheng, C.; Rousseau, L. An exact algorithm for the two-echelon vehicle routing problem with drones. Transp. Res. Part B Methodol. 2023, 168, 124–150. [Google Scholar] [CrossRef]
- Pan, B.; Zhang, Z.; Lim, A. Multi-trip time-dependent vehicle routing problem with time windows. Eur. J. Oper. Res. 2021, 291, 218–231. [Google Scholar] [CrossRef]
- Moon, I.; Salhi, S.; Feng, X. The location-routing problem with multi-compartment and multi-trip: Formulation and heuristic approaches. Transp. A Transp. Sci. 2020, 16, 501–528. [Google Scholar] [CrossRef]
- Yu, V.F.; Salsabila, N.Y.; Gunawan, A.; Handoko, A.N. An adaptive large neighborhood search for the multi-vehicle profitable tour problem with flexible compartments and mandatory customers. Appl. Soft Comput. 2024, 156, 111482. [Google Scholar] [CrossRef]
- You, J.; Wang, Y.; Xue, Z. An exact algorithm for the multi-trip container drayage problem with truck platooning. Transp. Res. Part E Logist. Transp. Rev. 2023, 175, 103138. [Google Scholar] [CrossRef]
- Sethanan, K.; Jamrus, T. Hybrid differential evolution algorithm and genetic operator for multi-trip vehicle routing problem with backhauls and heterogeneous fleet in the beverage logistics industry. Comput. Ind. Eng. 2020, 146, 106571. [Google Scholar] [CrossRef]
- Neira, D.A.; Aguayo, M.M.; De la Fuente, R.; Klapp, M.A. New compact integer programming formulations for the multi-trip vehicle routing problem with time windows. Comput. Ind. Eng. 2020, 144, 106399. [Google Scholar] [CrossRef]
- Liu, W.; Dridi, M.; Ren, J.; El Hassani, A.H.; Li, S. A double-adaptive general variable neighborhood search for an unmanned electric vehicle routing and scheduling problem in green manufacturing systems. Eng. Appl. Artif. Intell. 2023, 126, 107113. [Google Scholar] [CrossRef]
- Qin, W.; Zhuang, Z.; Huang, Z.; Huang, H. A novel reinforcement learning-based hyper-heuristic for heterogeneous vehicle routing problem. Comput. Ind. Eng. 2021, 156, 107252. [Google Scholar] [CrossRef]
- Xu, B.; Jie, D.; Li, J.; Yang, Y.; Wen, F.; Song, H. Integrated scheduling optimization of U-shaped automated container terminal under loading and unloading mode. Comput. Ind. Eng. 2021, 162, 107695. [Google Scholar] [CrossRef]
- Duan, J.; Liu, F.; Zhang, Q.; Qin, J. Tri-objective lot-streaming scheduling optimization for hybrid flow shops with uncertainties in machine breakdowns and job arrivals using an enhanced genetic programming hyper-heuristic. Comput. Oper. Res. 2024, 172, 106817. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, F.; Qian, B.; Hu, R.; Wang, L.; Jin, H. A Q-learning-based hyper-heuristic evolutionary algorithm for the distributed flexible job-shop scheduling problem with crane transportation. Expert Syst. Appl. 2023, 234, 121050. [Google Scholar] [CrossRef]
- Li, L.; Zhang, H.; Bai, S. A multi-surrogate genetic programming hyper-heuristic algorithm for the manufacturing project scheduling problem with setup times under dynamic and interference environments. Expert Syst. Appl. 2024, 250, 123854. [Google Scholar] [CrossRef]
- Li, J.; Ma, Y.; Gao, R.; Cao, Z.; Lim, A.; Song, W.; Zhang, J. Deep reinforcement learning for solving the heterogeneous capacitated vehicle routing problem. IEEE Trans. Cybern. 2022, 52, 13572–13585. [Google Scholar] [CrossRef]
- Zhang, Z.; Qi, G.; Guan, W. Coordinated multi-agent hierarchical deep reinforcement learning to solve multi-trip vehicle routing problems with soft time windows. IET Intell. Transp. Syst. 2023, 17, 2034–2051. [Google Scholar] [CrossRef]
- Shang, C.; Ma, L.; Liu, Y. Green location routing problem with flexible multi-compartment for source-separated waste: A Q-learning and multi-strategy-based hyper-heuristic algorithm. Eng. Appl. Artif. Intell. 2023, 121, 105954. [Google Scholar] [CrossRef]
- Xu, K.; Shen, L.; Liu, L. Enhancing column generation by reinforcement learning-based hyper-heuristic for vehicle routing and scheduling problems. Comput. Ind. Eng. 2025, 206, 111138. [Google Scholar] [CrossRef]
- Dastpak, M.; Errico, F.; Jabali, O. Off-line approximate dynamic programming for the vehicle routing problem with a highly variable customer basis and stochastic demands. Comput. Oper. Res. 2023, 159, 106338. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, X.; Wang, Y.; Zhao, J.; Sun, G.; Qin, B. Token-based deep reinforcement learning for Heterogeneous VRP with Service Time Constraints. Knowl. Based Syst. 2024, 300, 112173. [Google Scholar] [CrossRef]
- Huang, N.; Li, J.; Zhu, W.; Qin, H. The multi-trip vehicle routing problem with time windows and unloading queue at depot. Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102370. [Google Scholar] [CrossRef]
- Fragkogios, A.; Qiu, Y.; Saharidis, G.K.D.; Pardalos, P.M. An accelerated benders decomposition algorithm for the solution of the multi-trip time-dependent vehicle routing problem with time windows. Eur. J. Oper. Res. 2024, 317, 500–514. [Google Scholar] [CrossRef]
- Blauth, J.; Held, S.; Müller, D.; Schlomberg, N.; Traub, V.; Tröbst, T.; Vygen, J. Vehicle routing with time-dependent travel times: Theory, practice, and benchmarks. Discret. Optim. 2024, 53, 100848. [Google Scholar] [CrossRef]
- Sun, B.; Chen, S.; Meng, Q. Optimizing first-and-last-mile ridesharing services with a heterogeneous vehicle fleet and time-dependent travel times. Transp. Res. Part E Logist. Transp. Rev. 2025, 193, 103847. [Google Scholar] [CrossRef]
- Gutierrez, A.; Labadie, N.; Prins, C. A Two-echelon Vehicle Routing Problem with time-dependent travel times in the city logistics context. EURO J. Transp. Logist. 2024, 13, 100133. [Google Scholar] [CrossRef]
- Lu, J.; Nie, Q.; Mahmoudi, M.; Ou, J.; Li, C.; Zhou, X.S. Rich arc routing problem in city logistics: Models and solution algorithms using a fluid queue-based time-dependent travel time representation. Transp. Res. Part B Methodol. 2022, 166, 143–182. [Google Scholar] [CrossRef]
- Coelho, V.N.; Grasas, A.; Ramalhinho, H.; Coelho, I.M.; Souza, M.J.F.; Cruz, R.C. An ILS-based algorithm to solve a large-scale real heterogeneous fleet VRP with multi-trips and docking constraints. Eur. J. Oper. Res. 2016, 250, 367–376. [Google Scholar] [CrossRef]
- Zhao, J.; Poon, M.; Tan, V.Y.F.; Zhang, Z. A hybrid genetic search and dynamic programming-based split algorithm for the multi-trip time-dependent vehicle routing problem. Eur. J. Oper. Res. 2024, 317, 921–935. [Google Scholar] [CrossRef]
- He, D.; Ceder, A.A.; Zhang, W.; Guan, W.; Qi, G. Optimization of a rural bus service integrated with e-commerce deliveries guided by a new sustainable policy in China. Transp. Res. Part E Logist. Transp. Rev. 2023, 172, 103069. [Google Scholar] [CrossRef]
- Vieira, B.S.; Ribeiro, G.M.; Bahiense, L. Metaheuristics with variable diversity control and neighborhood search for the Heterogeneous Site-Dependent Multi-depot Multi-trip Periodic Vehicle Routing Problem. Comput. Oper. Res. 2023, 153, 106189. [Google Scholar] [CrossRef]
- Li, K.; Liu, T.; Kumar, P.N.R.; Han, X. A reinforcement learning-based hyper-heuristic for AGV task assignment and route planning in parts-to-picker warehouses. Transp. Res. Part E Logist. Transp. Rev. 2024, 185, 103518. [Google Scholar] [CrossRef]
| Author | Problem Characteristics | Method | |||
|---|---|---|---|---|---|
| HF | Multi-Trip | LC | TVN | ||
| Nguyen et al. [3] | ✔ | AHA | |||
| Pan et al. [16] | ✔ | HMA | |||
| Yu et al. [18] | ✔ | ✔ | ALNS | ||
| You et al. [19] | ✔ | BPC + PPC | |||
| Sethanan et al. [20] | ✔ | ✔ | DE + FLC | ||
| Liu et al. [22] | ✔ | ALNS | |||
| Wang et al. [33] | ✔ | TDRL | |||
| Huang et al. [34] | ✔ | ✔ | BPC + CG | ||
| Fragkogios et al. [35] | ✔ | ✔ | ✔ | BD | |
| Blauth et al. [36] | ✔ | Local Search | |||
| Sun et al. [37] | ✔ | ✔ | RHCG | ||
| Gutierrez et al. [38] | ✔ | ✔ | HH | ||
| Lu et al. [39] | ✔ | BP | |||
| Coelho et al. [40] | ✔ | ✔ | ILS | ||
| Zhao et al. [41] | ✔ | HH | |||
| He et al. [42] | ✔ | ✔ | HH | ||
| Vieira et al. [43] | ✔ | ✔ | AVNR | ||
| Our work | ✔ | ✔ | ✔ | ✔ | HHCRQL |
| State Variable | Description | Possible Values/Intervals | Notes |
|---|---|---|---|
| Feasibility Indicator | 0/1 | Indicates whether the current solution satisfies all constraints (1 = feasible, 0 = infeasible) | |
| Number of Vehicle Types | Discrete integers, e.g., 1, 2–3, ≥4 | Number of distinct vehicle types used, reflecting fleet heterogeneity and problem complexity | |
| Remaining Task Ratio | [0, 0.25), [0.25, 0.5), [0.5, 0.75), [0.75, 1.0] | Proportion of remaining demand relative to initial demand, representing progress stages | |
| Vehicle Load Utilization | <33%, 33–66%, >66% | Overall fleet load utilization intervals, reflecting resource efficiency |
| Actions | Heuristic Operators |
|---|---|
| Destroy operation 1, repair operation 1, swap 1 | |
| Destroy operation 1, repair operation 1, swap 2 | |
| Destroy operation 1, repair operation 2, swap 1 | |
| Destroy operation 1, repair operation 2, swap 2 | |
| Destroy operation 2, repair operation 1, swap 1 | |
| Destroy operation 2, repair operation 1, swap 2 | |
| Destroy operation 2, repair operation 1, swap 1 | |
| Destroy operation 2, repair operation 2, swap 1 |
| Variables | Definition |
|---|---|
| The actual travel time of small cargo van from point to point | |
| The binary variable equals 1 if vehicle travels along arc during its trip; otherwise, it equals 0. | |
| The arrival time of vehicle at node during its trip. | |
| The amount of goods picked up by vehicle at node during its trip | |
| The waiting time of vehicle at node during its trip | |
| The binary variable equals 1 if vehicle makes a departure; otherwise, it equals 0. | |
| The total load of Vehicle on trip | |
| Lunch break window auxiliary variable | |
| Lunch break window auxiliary variable. | |
| Small cargo van morning peak period indicator (auxiliary variable) | |
| Small cargo van morning peak period indicator (auxiliary variable) | |
| Linearization auxiliary variables |
| Parameters | Definition |
|---|---|
| Normal travel time from node to node . | |
| Peak period travel time from node to node . | |
| The loading and unloading capacity of warehouse . | |
| Departure time of vehicle at node during its trip. | |
| The fixed working hours of warehouse can be denoted as . | |
| The loading capacity of vehicle can be denoted as | |
| The lower bound of the working time window for warehouse . | |
| The upper bound of the working time window for warehouse . | |
| The lower bound of the worker’s rest time window for warehouse . | |
| The upper bound of the worker’s rest time window for warehouse . | |
| The lower bound of the driver’s working time window for vehicle . | |
| The upper bound of the driver’s working time window for vehicle . | |
| The demand at warehouse can be denoted as | |
| The number of times vehicle is used. | |
| C | The set of warehouses |
| D | The distribution center |
| The origin distribution center | |
| The destination distribution center | |
| M | The infinitely large constant |
| V | The set of all nodes |
| K | The set of vehicles can be denoted as K |
| E | The set of arcs defined by can be denoted as E |
| q | The number of vehicle departures can be denoted as q |
| A | The number of times a vehicle can be used |
| The set of small cargo van can be denoted as S. | |
| The set of large cargo truck can be denoted as L | |
| The morning restricted time window for small cargo van | |
| The evening restricted time window for large cargo truck | |
| The morning peak time window for small cargo van | |
| The evening peak time window for large cargo truck |
| Instance | Actual Solution (AS) | Solution Derived from HHCRQL (HS) | ||||||
|---|---|---|---|---|---|---|---|---|
| Number of Warehouses | Total Times | Waiting Times | Car Number | Total Times | Waiting Times | Car Number | ||
| 4 | 6944 | 1587 | 10 | 6024 | 1185 | 12 | 13.25% | 25.33% |
| 5 | 7481 | 1784 | 12 | 6345 | 1298 | 13 | 15.19% | 27.24% |
| 6 | 7854 | 1978 | 15 | 6587 | 1445 | 17 | 16.13% | 26.95% |
| 7 | 8120 | 2145 | 17 | 6976 | 1554 | 19 | 14.09% | 27.55% |
| 8 | 8478 | 2215 | 19 | 7359 | 1798 | 20 | 13.20% | 18.83% |
| 9 | 8752 | 2354 | 19 | 7640 | 1851 | 21 | 12.71% | 21.37% |
| 10 | 9352 | 2524 | 20 | 7640 | 1904 | 22 | 18.31% | 24.56% |
| 11 | 9531 | 2710 | 20 | 7637 | 1844 | 22 | 19.87% | 31.96% |
| 12 | 9778 | 3041 | 20 | 7534 | 2045 | 23 | 22.95% | 32.75% |
| 13 | 9965 | 3278 | 24 | 7506 | 2119 | 24 | 24.68% | 35.36% |
| Instance | The Algorithm of the Solution | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Warehouses | |||||||||||
| Obj(s) | CPU(s) | Obj(s) | CPU(s) | Obj(s) | CPU(s) | Obj(s) | CPU(s) | - | - | 1 | |
| [0–5] | 910 | 193.6 | 1009 | 0.58 | 972 | 0.85 | 932 | 0.39 | −2.36% | 8.26% | 4.29% |
| [5–10] | 1846 | 1635.5 | 2034 | 2.52 | 1938 | 0.85 | 1869 | 0.66 | −1.25% | 8.83% | 3.69% |
| [10–15] | 4291 | 2859.7 | 4542 | 16.62 | 4501 | 23.54 | 4265 | 0.82 | 0.61% | 6.49% | 5.53% |
| [15–20] | - | - | 5079 | 18.41 | 4872 | 43.20 | 4661 | 1.21 | - | 8.97% | 4.53% |
| [20–25] | - | - | 7112 | 49.02 | 6895 | 68.52 | 6589 | 1.70 | - | 7.94% | 4.64% |
| [25–30] | - | - | 7616 | 63.24 | 7469 | 79.97 | 7032 | 2.15 | - | 8.30% | 6.21% |
| [30–35] | - | - | 11,839 | 314.52 | 11,252 | 352.3 | 10,550 | 2.97 | - | 12.22% | 6.65% |
| [35–40] | - | - | 13,859 | 561.3 | 13,489 | 622.4 | 12,227 | 3.85 | - | 13.35% | 10.32% |
| [40,45] | - | - | 14,922 | 744.2 | 14,525 | 754.0 | 13,149 | 4.03 | - | 13.48% | 10.46% |
| [45,50] | 16,524 | 1454.2 | 16,245 | 1604.2 | 14,895 | 4.35 | - | 10.94% | 9.06% | ||
| Instance | The Algorithm of the Solution | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Warehouses | |||||||||||
| Obj(s) | CPU(s) | Obj(s) | CPU(s) | Obj(s) | CPU(s) | Obj(s) | CPU(s) | - | - | 1 | |
| [50,55] | 17,366 | 1595 | 17,058 | 1952 | 16,854 | 2118 | 15,908 | 4.36 | 9.17% | 6.74% | 5.95% |
| [55,60] | 18,725 | 2077 | 18,450 | 2105 | 18,275 | 2351 | 17,652 | 4.78 | 6.08% | 4.33% | 3.53% |
| [60,65] | 19,625 | 2185 | 19,300 | 2350 | 19,216 | 2745 | 18,739 | 5.41 | 4.73% | 2.91% | 2.55% |
| [65,70] | 21,482 | 2215 | 21,173 | 2451 | 21,102 | 2785 | 20,475 | 5.87 | 4.92% | 3.30% | 2.57% |
| [70,75] | 22,041 | 2237 | 21,763 | 2841 | 21,630 | 2965 | 21,037 | 5.69 | 4.77% | 3.34% | 2.82% |
| [75,80] | 23,425 | 2269 | 23,156 | 2894 | 22,931 | 3102 | 22,520 | 5.47 | 4.02% | 2.75% | 1.83% |
| [80,85] | 24,495 | 2154 | 24,207 | 2734 | 23,997 | 2941 | 23,695 | 4.91 | 3.38% | 2.12% | 1.27% |
| [85,90] | 25,954 | 2198 | 25,633 | 2965 | 25,413 | 3210 | 25,124 | 5.95 | 3.30% | 1.99% | 1.15% |
| [90,95] | 27,658 | 2184 | 27,258 | 2936 | 27,137 | 3354 | 26,710 | 5.56 | 3.55% | 2.01% | 1.60% |
| [95,100] | 28,965 | 2236 | 28,496 | 2812 | 28,386 | 3247 | 27,874 | 5.72 | 3.91% | 2.18% | 1.84% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, N.; Jin, X. A Reinforcement Learning Hyper-Heuristic with Cumulative Rewards for Dual-Peak Time-Varying Network Optimization in Heterogeneous Multi-Trip Vehicle Routing. Algorithms 2025, 18, 536. https://doi.org/10.3390/a18090536
Wang X, Li N, Jin X. A Reinforcement Learning Hyper-Heuristic with Cumulative Rewards for Dual-Peak Time-Varying Network Optimization in Heterogeneous Multi-Trip Vehicle Routing. Algorithms. 2025; 18(9):536. https://doi.org/10.3390/a18090536
Chicago/Turabian StyleWang, Xiaochuan, Na Li, and Xingchen Jin. 2025. "A Reinforcement Learning Hyper-Heuristic with Cumulative Rewards for Dual-Peak Time-Varying Network Optimization in Heterogeneous Multi-Trip Vehicle Routing" Algorithms 18, no. 9: 536. https://doi.org/10.3390/a18090536
APA StyleWang, X., Li, N., & Jin, X. (2025). A Reinforcement Learning Hyper-Heuristic with Cumulative Rewards for Dual-Peak Time-Varying Network Optimization in Heterogeneous Multi-Trip Vehicle Routing. Algorithms, 18(9), 536. https://doi.org/10.3390/a18090536






