Abstract
Secret image sharing (SIS) is an image protection technique based on cryptography. However, traditional SIS schemes have limited noise resistance, making it difficult to ensure reconstructed image quality. To address this issue, this paper proposes a robust SIS scheme based on QR codes, which enables the efficient and lossless reconstruction of the secret image without pixel expansion. Moreover, the proposed scheme maintains high reconstruction quality under noisy conditions. In the sharing phase, the scheme compresses the length of shares by optimizing polynomial computation and improving the pixel allocation strategy. Reed–Solomon coding is then incorporated to enhance the anti-noise capability during the sharing process, while achieving meaningful secret sharing using QR codes as carriers. In the reconstruction phase, the scheme further improves the quality of the reconstructed secret image by combining image inpainting algorithms with the error-correction capability of Reed–Solomon codes. The experimental results show that the scheme can achieve lossless reconstruction when the salt-and-pepper noise density is less than , and still maintains high-quality reconstruction when . Compared with the existing schemes, the proposed method significantly improves noise robustness without pixel expansion, while preserving the visual meaning of the QR code carrier, and achieves a secret sharing strategy that combines robustness and practicality.
1. Introduction
Secret sharing [1] is a cryptographic technique that aims to achieve the secure storage and sharing of secret information. (k, n)-threshold polynomial-based secret image sharing (P-SIS) [2] is the most classical secret sharing strategy. It has been widely applied in fields such as secure communication [3,4], the Internet of Things (IoT) [5], healthcare [6,7], and blockchain technology [8,9]. Figure 1 illustrates the basic framework of P-SIS: the original secret image is encoded through polynomial encoding to generate n shares, and the secret image can be accurately reconstructed using the Lagrange interpolation function only when at least k shares are collected. A primary issue that most of the existing research mainly focuses on is how to ensure the security and privacy of secret information [10,11], but this does not pay sufficient attention to noise and interference issues. However, in the actual secret sharing process, the shared shares are easily affected by factors such as electromagnetic interference, signal attenuation, and bandwidth limitations during transmission and storage, thereby introducing various kinds of random noise. These noises may damage the information in the shares, leading to errors in the reconstructed secret information, and further affecting the effectiveness and security of the scheme. To cope with this challenge, researchers have begun to incorporate noise resistance into traditional secret sharing schemes [12,13,14] in order to improve their robustness and reliability under noisy environments.
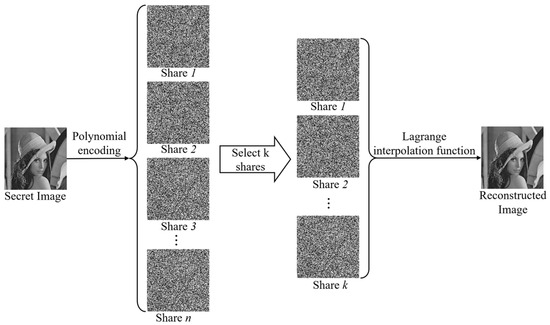
Figure 1.
Flowchart of the P-SIS algorithm.
Luo et al. [15] proposed a lossless reconstruction secret image sharing scheme. This scheme connects two 8-bit pixels into 16-bit secret data and utilizes Shamir’s scheme for sharing, ensuring that the secret information can be reconstructed losslessly without pixel expansion. The main drawback of this scheme lies in its weak noise resistance. If the shares are contaminated by noise or data corruption during transmission or storage, the reconstructed image may contain errors. Therefore, although the scheme performs well in lossless data reconstruction, it may still produce reconstruction errors in noisy environments. This further demonstrates the importance of incorporating noise resistance into secret sharing schemes.
To enhance the noise resistance of secret sharing schemes, Yan et al. [16] proposed a scheme combining the Chinese Remainder Theorem (CRT) and Bose–Chaudhuri–Hocquenghem (BCH) error-correcting codes [17]. In the share generation phase, BCH coding is introduced to improve the fault tolerance of shares through redundancy design, enabling effective resistance against data loss and noise interference during storage and transmission. Specifically, the scheme is optimized for common noise types such as the least significant bit (LSB) flipping noise, JPEG compression noise, and salt-and-pepper noise. Even if some shares are slightly corrupted, the secret image can still be successfully reconstructed. However, under moderate noise conditions, the noise resistance of this scheme remains limited, and the quality of the reconstructed image deteriorates. Therefore, although the scheme achieves significant progress in improving the noise resistance of secret sharing, further optimization is required to enhance its applicability and robustness in complex environments.
To further improve the noise resistance of secret sharing schemes, Luo et al. [18] proposed a scheme that combines secret image sharing with Reed–Solomon (RS) coding [19]. This scheme introduces RS coding within the traditional polynomial-based secret sharing (P-SIS) framework to enhance resistance against various noise types. Additionally, by compressing RS codes and optimizing pixel block construction, the scheme increases the tolerance of shares to burst noise. The experimental results show that the scheme can achieve lossless reconstruction under a salt-and-pepper noise density of and still reconstruct high-quality images when . Compared with the scheme based on Yan et al.’s work, this method demonstrates superior anti-interference performance in complex noise environments. However, the scheme does not fully exploit the capability of RS coding; its noise resistance and lossless reconstruction ability remain limited. In some cases, it can only achieve approximate reconstruction rather than guaranteeing that the reconstructed image is completely consistent with the original.
To further enhance the robustness against noise, while taking into consideration the universality and flexibility of QR codes [20], this paper proposes a robust secret image sharing algorithm based on QR codes. By optimizing the embedding strategy of secret information and fully leveraging the capabilities of RS coding, the algorithm achieves stronger noise resistance and lossless reconstruction capability. Specifically, the scheme compresses the length of share information by adjusting the polynomial modulus, so that after embedding the shares into the QR code pixel regions, the readability of the QR code is not affected, thereby improving the information storage efficiency. This scheme fully exploits both the error-correction and error-detection capabilities of RS codes. During the sharing phase, RS code error correction is used to add redundancy to the shares, while in the reconstruction phase, the error-detection function of RS codes is applied to generate error masks, which, combined with image restoration algorithms [21], further optimize the quality of the reconstructed image. This strategy significantly enhances resistance to various noise types including salt-and-pepper noise, Gaussian noise, JPEG compression noise, and LSB-flipping noise. The experimental results show that the proposed scheme can achieve the lossless reconstruction of secret images at a salt-and-pepper noise density of and still maintain high-quality reconstruction at . Compared to Luo et al.’s scheme, the proposed method effectively maintains the quality of reconstructed images under higher noise intensities and exhibits superior noise resistance.
The main contributions of this paper are as follows:
- (1)
- Improved noise resistance of the secret sharing scheme: Compared with existing algorithms, the proposed algorithm demonstrates higher noise resistance.
- (2)
- Enhanced lossless reconstruction capability of secret images: The proposed algorithm achieves the lossless reconstruction of secret images under certain noise densities, and its lossless reconstruction capability surpasses that of existing algorithms.
- (3)
- Meaningful sharing strategy: For the first time, this paper realizes a secret sharing strategy that simultaneously possesses noise resistance and the meaningful sharing of shares, without pixel expansion.
- (4)
- Improved sharing efficiency: While achieving noise resistance based on the P-SIS framework, the additional computational overhead introduced by the proposed algorithm is minimal, and thus the impact on sharing efficiency remains within an acceptable range.
The remainder of this paper is organized as follows: Section 2 briefly introduces some preliminary techniques. Section 3 presents the design concept of the sharing scheme. Section 4 describes the experimental results of the proposed scheme and provides comparisons with related works. Finally, Section 5 concludes this paper.
2. Related Works
2.1. Polynomial-Based Secret Sharing
The polynomial-based secret sharing strategy originates from the secret sharing scheme proposed by Shamir. This scheme mainly uses polynomials to divide the secret information into n shares. During reconstruction, the secret can only be correctly recovered when the number of participating shares meets a predefined threshold. To use the polynomial-based secret sharing strategy, all data must first be converted into integers over a finite field , where p is a prime number. Then, the secret information S is assigned as the first coefficient of the polynomial, and the remaining coefficients are randomly selected to obtain the polynomial, as shown in Equation (1):
According to this polynomial, n shared values can be calculated. During reconstruction, at least k shares are required to participate. By substituting these k shares into the Lagrange interpolation function, the secret information can be correctly recovered. If all the coefficients of the polynomial need to be determined, Gaussian elimination over the finite field must be used. The detailed formula of Gaussian elimination is as follows:
Based on this formula, all the coefficients including can be obtained.
2.2. RS Code
The RS code is an error-correcting code based on Galois Field operations. It divides the original information into multiple data blocks and adds redundant information to these blocks using a specific algorithm to correct errors. RS codes have a strong error-correction capability and can correct a certain amount of burst and random errors. For example, in an RS code consisting of r codewords with d data codewords, up to codeword errors can be corrected. The width of RS codewords is mainly determined by the size of the Galois Field. If the Galois Field is , then each data unit has a bit length of m. Therefore, RS encoding is characterized by three parameters: m, r, and d, where m represents the bit length of a single codeword, r denotes the total length of the RS encoded data, and d indicates the number of data codewords in the RS code. By adjusting these three parameters, RS codes can be adapted to different application scenarios. Based on the strong error-correction capability and flexibility of RS codes, this algorithm adopts RS coding as the foundation for noise-resistant sharing and uses to represent the RS code size selected in this scheme.
3. The Proposed Scheme
3.1. Design Concept
This paper proposes a secret image sharing scheme based on QR codes, which guarantees the lossless reconstruction of the secret image without pixel expansion. The sharing process ensures that the secret image can still be fully reconstructed even when the share images are subjected to a certain degree of noise contamination. To achieve these goals, the scheme addresses the following problems.
Problem 1: How to achieve the lossless reconstruction of secret information. Most of the existing research is based on Shamir’s polynomial interpolation function. To ensure the correctness of secret information reconstruction, all computations are performed in the finite field GF(251), while the data range of an image pixel is between 0 and 255. Therefore, the image pixels involved in the calculation need to be truncated during preprocessing if their values exceed 251, to ensure that the pixels meet the calculation requirements. However, this direct truncation causes pixel loss in the secret image, resulting in the inability to reconstruct the secret image losslessly. To achieve the lossless reconstruction of the secret information, this scheme makes the following modifications to the polynomial-based sharing strategy. Modification 1: Adjust the polynomial modulus. This scheme modifies the range of the finite field by adjusting the modulus, allowing the algorithm to control the amount of information carried by each coefficient of the polynomial function. Modification 2: Adjust the number of polynomial coefficients used for embedding. Traditional polynomial-based secret sharing stores secret information only in the first coefficient of the polynomial, whereas this algorithm uses the first three coefficients of the polynomial to store secret information. Modification 3: Adjust the secret image pixel grouping strategy. Traditional polynomial-based secret sharing inputs only a single secret image pixel as a coefficient into the polynomial function. This algorithm divides the secret image into multiple groups and inputs each group of information as coefficients into the polynomial function. The specific group size is related to the range of the finite field. Based on the above three modification strategies, as long as the secret information embedded into the corresponding coefficients during the modification process does not exceed the finite field’s range, the scheme can achieve the lossless reconstruction of the secret information, while also compressing the bit length of the share information.
Problem 2: How to enable the share images to have noise resistance. In the secret sharing process, the noise resistance of the secret information directly affects the quality of the reconstructed image. However, the share images generated by traditional secret sharing schemes almost lack noise resistance. If the share images are affected by noise during transmission, it is very likely to cause serious distortion in the reconstructed secret image or even reconstruction failure. To improve the noise resistance of share images, the most fundamental approach is to add redundant check information to each share pixel, and generally, the longer the redundancy, the stronger the noise resistance. However, directly adding redundancy to share pixels will bring additional overhead to the secret sharing algorithm. This scheme hopes that the share images have noise resistance while the algorithm introduces no extra overhead. To achieve this goal, this scheme first processes the share images using the method from Problem 1, which not only achieves lossless reconstruction but also greatly compresses the bit length of share image pixels. Then, redundancy is added to the compressed share images. Thanks to the high compression efficiency of the method in Problem 1, even after adding redundancy to each share pixel, no extra overhead is generated. Therefore, this scheme can enable share images to resist noise without additional overhead.
Problem 3: How to embed share image information into the QR code. Traditional QR code information-hiding strategies usually embed information directly into the black-and-white modules of the QR code. However, this strategy has very limited embedding capacity and is constrained by the version of the QR code. Even when using the highest version of the QR code, its capacity for embedding information still struggles to meet the high-capacity requirements for secret image embedding. Moreover, such methods tend to degrade the inherent error-correction capability of the QR code during embedding, reducing the QR code’s robustness itself. Therefore, this algorithm chooses to embed the share image directly into the pixel values of the QR code image, utilizing the pixel information of the QR code itself to store the share image information, thus achieving share image embedding. During the embedding process, this scheme preserves the most significant bit (MSB) of the QR code image pixels, ensuring that the QR code still maintains visual significance and readability after the share image is embedded.
To address these issues, this scheme proposes a robust secret image sharing strategy based on QR codes, aiming to achieve the lossless reconstruction of secret information and to ensure that the secret image can be reconstructed under noisy environments.
3.2. Proposed Scheme
This section presents the design details of the proposed scheme. Figure 2 illustrates the overall workflow of the algorithm. In the sharing phase shown in Figure 2, the G4/G16 sharing strategy represents the compression-based sharing method proposed in this paper. It compresses an input 8-bit grayscale image and distributes it into n share images, each with a pixel bit length of 3. The image inpainting algorithm depicted in the reconstruction phase of Figure 2 is designed to further improve the quality of the preliminary reconstructed image. This algorithm takes the preliminary reconstructed image and a mask image (MASK) as the input parameters. The MASK records the error positions in the preliminary reconstructed image. By leveraging the error location information provided by the MASK, the image inpainting algorithm can accurately correct the erroneous regions to obtain the final reconstructed image.
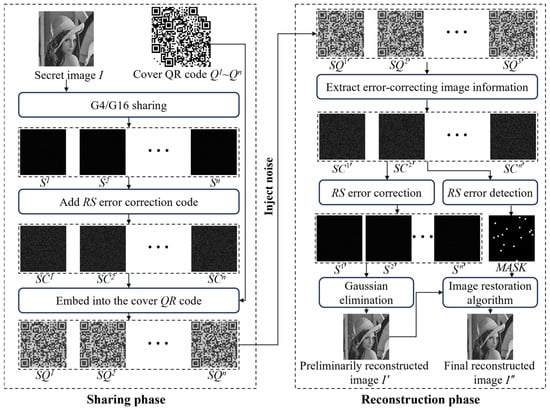
Figure 2.
The flowchart of the proposed scheme.
Table 1 lists the key symbols used in this paper along with their definitions.

Table 1.
Key symbols in the article.
3.2.1. G4/G16 Secret Image Sharing Strategies
Traditional (k, n) threshold secret sharing schemes divide a secret into n shares using a polynomial function, and at least k shares are required to successfully reconstruct the secret. However, the pixel values generated by the polynomial function are 8 bits in size, which are the same as standard image pixel values. As a result, shares generated using traditional threshold sharing strategies have no extra space for adding error-correction codes, nor can they be effectively combined with QR code carriers for meaningful sharing. Therefore, it is essential to compress the bit length of the share pixels so that there is enough space to add redundant check information. In our research, we find that the maximum bit length of the polynomial output is directly related to the modulus used: the larger the modulus, the longer the maximum output bit length. Based on this property, we replace the original modulus of 251 in the polynomial function with a larger modulus. At the same time, by adjusting the pixel grouping strategy and increasing the number of coefficients in the polynomial used to embed secret pixels, we can input more pixel data into each polynomial, thereby obtaining compressed share information. Of course, this strategy may sacrifice some flexibility in secret sharing. For example, if we choose to embed the secret into the first three coefficients of the polynomial, the scheme must ensure that the total number of participants and the threshold . Otherwise, the secret information cannot be fully embedded. This strategy also affects the distribution of pixel values in the resulting share images.
The G4 and G16 sharing strategies proposed in this algorithm achieve the compression of the share image’s bit length by adjusting the modulus of the polynomial, the number of embeddable coefficients, and the partitioning of the secret image. The G4 sharing strategy, specifically, groups four secret image pixels together, with a group size of , and sets the modulus M to 4093. At this point, the maximum bit length of the polynomial function’s calculation result is 12 bits. Then, the four secret image pixels are embedded into the three polynomial coefficients . Since each coefficient can store a maximum value of M, the three coefficients can store a maximum bit length of 36 bits. The total bit length of the four secret image pixels’ bitstream is 32 bits. Considering that directly embedding the bits could cause an individual coefficient’s value to exceed 4093, which would result in precision loss, this algorithm decides to first concatenate the four secret image pixels into 32-bit binary data, denoted as BI. The 32-bit binary data BI is then converted into a 3-digit M-ary number, with each digit represented as E0, E1, and E2, where , , and . Additionally, let denote the maximum bit range within the polynomial coefficient that can be used to embed E2. It is calculated by the formula , where bitlen is a function that returns the bit length of the input data, and 1 << 32 means shifting the number 1 to the left by 32 bits. After computation, is obtained. Therefore, the polynomial function for the sharing strategy is given by Equation (3).
where represents a random number with a binary length of . Based on Equation (3), the bit length of the polynomial calculation result is 12. Since this method groups four secret image pixels together and embeds them into the polynomial coefficients, the final result of the polynomial calculation is divided into four equal parts, which results in a compressed share group. This compressed share group contains four shares, each with a bit length of three. At this point, we have successfully compressed the bit length of the share information. We start with four secret image pixels, each with a bit length of eight, and obtain four share image pixels, each with a bit length of three. Compared to traditional methods, this approach achieves a 62.5% reduction in the bit length of the share image. The limitation of this method is that it only supports threshold sharing with . When , the number of possible pixel values in the share image is limited to , which is eight possibilities. Figure 3 illustrates the specific process of generating three shadow information groups from a secret information group using the G4 sharing strategy under a (3, 3) threshold scheme.
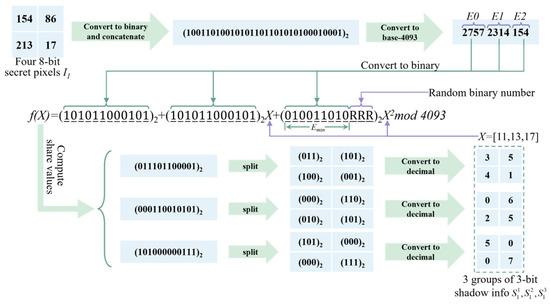
Figure 3.
Example of dividing a secret information group into three shadow information groups using the G4 strategy under a (3, 3) threshold scheme.
G16 sharing is an extension of G4 sharing, addressing the issue of the limited number of pixel values in the share image while further enhancing the algorithm’s noise resistance. G16 sharing means selecting 16 secret image pixels as one group for sharing, with a group size of . The modulus is denoted as , and the maximum bit length of the polynomial calculation result corresponding to G16 sharing is 48 bits. Similar to the G4 sharing strategy, the polynomial calculation result is first converted to binary and then transformed into a 3-digit M-ary number, with each digit represented as E0, E1, and E2. The minimum bit length that can be embedded into the coefficient in E2, denoted as , is calculated, and it is determined that . Thus, the polynomial for G16 sharing is given by Equation (4).
where represents a random number with a binary length of , and the number of possible values for the share image pixel is , which is 32768 possible values. In summary, G4 and G16 sharing achieve the compression of the bit length of a single share image pixel from the original 8 bits down to 3 bits, given that .
3.2.2. Sharing Procedure Based on QR Code
Figure 4 illustrates the basic process of generating share groups from secret information groups under the condition of and . In the sharing example shown in Figure 4, the sharing scheme is used.
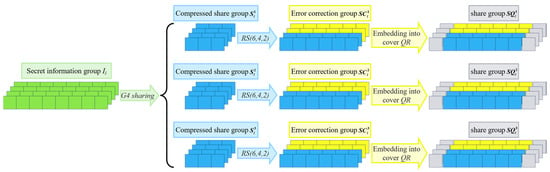
Figure 4.
The design concept of the (3, 3) threshold sharing phase: the green part represents the secret image information, the blue part represents the share information, the yellow part represents the error-correction information, and the gray part represents the carrier QR code information.
At the beginning of the sharing phase, the scheme first groups the secret image. The group size is related to the sharing strategy chosen by the algorithm. In this case, the G4 sharing strategy is selected, and the group size is . Figure 4 shows the sharing process of the l-th secret information group . First, the secret information group is substituted into the G4 sharing strategy, generating three compressed share groups, , , , with each piece of information in the compressed share groups having a bit length of 3. Next, equal-length error-correction information is added to each piece of information in the compressed share groups to generate the corresponding error-correction groups , , , with each piece of information in the error-correction groups having a bit length of 3. Finally, each piece of information from the three error-correction groups is embedded into the 2nd- to 6th-bit positions of the corresponding carrier QR code pixel groups , , and , resulting in the generation of three share groups, , , and . During the embedding process, the proposed method retains the first bit of the carrier QR code’s pixel, thus preserving part of the visual integrity of the carrier QR code. As a result, the share images generated by this method remain valid QR codes that can still be successfully decoded by standard QR code scanners. Furthermore, the last bit of the carrier QR code is also preserved, enabling the share images to be fully resistant to LSB-flipping noise. Further details of the algorithm are provided in Algorithm 1.
| Algorithm 1: Sharing Algorithm ( Sharing) |
| Input: Secret image size of ; carrier QR codes size of ; threshold ; number of participants ; identity authentication information . Output: share images . |
| Step 1: The secret image is divided into multiple secret information groups of size , with the total number of groups denoted as , i.e., . Similarly, each of the carrier QR codes is partitioned into groups of the same size , resulting in a total number of carrier groups also equal to . Step 2: Set . Step 3: Data Preprocessing. Let denote the bitwise concatenation of and . Define the modulus as . Convert the secret information group into its binary representation, denoted as , where . Subsequently, convert into a 3-digit base- representation, with each digit denoted as , , , where , , and . Let the minimum bit length that can be embedded into the embeddable coefficient in E2 be denoted as , where . Step 4: Generation of Compressed Share Groups , where , . First, generate a set of random coefficients , and set , , and . Let denote a random number with a bit length of . Then, substitute into the following polynomial function: Step 5: Generate the error-correction groups from the compressed share groups. For the -th compressed share group, pairwise concatenate its four pieces of information to obtain two 6-bit-length data segments, denoted as and , where and . Subsequently, input and into the to produce two 6-bit-length error-correction codes and . Finally, , , , and constitute the -th error-correction group, denoted as , , , and , respectively. In this step, . Step 6: Embed the error-correction group information into the carrier QR codes. Let denote the -th piece of information in the -th share group of the -th share image. Define , , , and , where . Step 7: Increment by 1 and repeat Step 3 to Step 6 until all secret information groups have been processed. Step 8: Output the share images . |
Algorithm 1 illustrates the sharing process based on the sharing strategy. To perform sharing based on the sharing strategy, one only needs to replace the modulus in Algorithm 1 with 281474976710597, change the group size to , and adjust the error-correction coding size to . Compared to sharing, sharing enables the share images to achieve higher noise resistance and improved lossless reconstruction capability. However, when the noise density is excessively high, sharing may slightly outperform in terms of noise robustness. Therefore, the choice between the two strategies can be made depending on the specific application requirements.
3.2.3. Reconstruction Procedure Based on QR Code
Figure 5 illustrates the basic process of reconstructing the secret information group from the share groups under the conditions and in this algorithm. The image reconstruction process mainly consists of two stages. The first stage is the reconstruction of the secret image. The second stage is the image restoration process. During the reconstruction in the first stage, the algorithm can reconstruct the secret image under basic noise conditions by leveraging the error-correction capability of the RS codes. However, in environments with strong noise, some local areas may still fail to be reconstructed. Therefore, this stage introduces an image restoration algorithm [21] to further repair the unreconstructed regions of the image, thereby improving the integrity and visual quality of the reconstructed image. Figure 6 illustrates an example of reconstructing a secret information group and its corresponding error mask using three share groups under a (3, 3) threshold scheme.
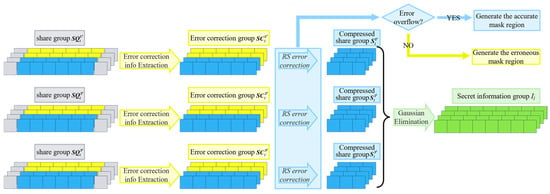
Figure 5.
The process flow of the (3, 3) threshold reconstruction phase. The green regions represent the secret image information, the blue regions denote the share information, the yellow regions correspond to the error-correction information, and the gray regions indicate the carrier QR code information.
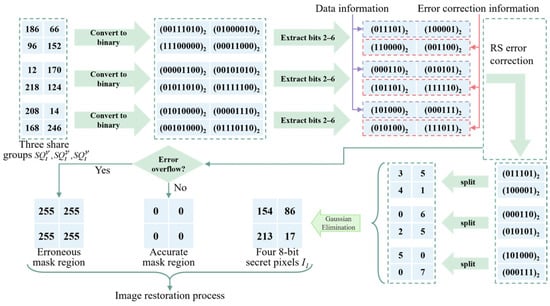
Figure 6.
Example of reconstructing a secret information group and its corresponding error mask using three share groups under a (3, 3) threshold scheme.
The image restoration algorithm relies on an error mask, which records the locations of erroneous pixels. However, due to the inherent uncertainty of the secret image during the reconstruction process, the positions of erroneous pixels in the reconstructed secret image are generally unpredictable. Consequently, obtaining an accurate error mask without introducing additional redundant data is nearly infeasible. Considering that the RS code employed in the sharing phase of this algorithm possesses not only error-correcting capabilities but also error-detecting capabilities, with the latter being twice that of the former, this paper proposes an error region marking mechanism based on the error-detecting ability of RS codes to indirectly infer the possible locations of errors within the image. Nonetheless, RS codes cannot precisely locate individual erroneous pixels; their error-detection capability only indicates whether an error has occurred within a segment of the RS code. Therefore, this mechanism partitions the image into multiple groups, each corresponding in size to one RS code segment. By leveraging the error-detection functionality of RS codes at the group level, the error mask expands from pinpointing exact pixel positions to marking error regions. Finally, the reconstructed image along with the error mask recording the error regions is input into the image restoration algorithm. The size of an RS code segment corresponds directly to the chosen sharing strategy: for the G4 sharing strategy, the RS code segment size is 4; for the G16 sharing strategy, the segment size is 16. The detailed reconstruction process is presented in Algorithm 2.
| Algorithm 2: Reconstruction Algorithm (G4 Sharing) |
| Input: share images , each of size , and authentication information . Output: Secret image . |
| Step 1: Partition each of the t share images into multiple share groups of size . The total number of share groups is denoted as , where . Define as the error mask of size , initialized with all zeros. Similarly, divide into groups of size , where denotes the -th group of mask information. Step 2: Set . Step 3: Extracting Error-Correction Groups from t Share Groups. Let denote the -th element of the -th share group in the -th share image, and denote the -th element of the -th error-correction group in the -th error-correction image. Define: , , , , where . Accordingly, the t error-correction groups can be obtained. Step 4: Decode the error-correction groups using RS coding. For the -th error-correction group, directly input the four 6-bit elements into the RS decoder. Denote the decoded data as and , both of which have a bit length of 6. Simultaneously, use RS decoding to record whether an overflow error has occurred in the i-th group. Subsequently, split and into four compressed share elements of 3 bits each. Let denote the -th element in the -th compressed share group of the -th compressed share image, i.e., define: , , , , where . After decoding all groups, determine whether any error-correction group has encountered an overflow. If none has, proceed to Step 6. Step 5: Set all values in to 255 to indicate that an error has occurred in the corresponding region. Step 6: All compressed share groups are input into the Gaussian elimination algorithm to obtain a 32-bit binary sequence, denoted as . This sequence is then equally divided into four 8-bit segments, yielding four secret pixels denoted as . Here, represents the -th group of secret information, i.e., . Step 7: Repeat Steps 3 through 6 until , incrementing by 1 in each iteration. Step 8: Input the error mask and the reconstructed secret image into the image inpainting algorithm to obtain the final reconstructed secret image , in which the erroneous regions have been corrected. Step 9: Output the final secret image . |
In the reconstruction process of this algorithm, different sharing strategies yield slightly different reconstruction results. Due to the smaller group size in the sharing strategy, the probability of error-correction failure is higher when noise affects the reconstruction process, and it is more prone to error-detection mistakes. However, because of the smaller group size, the quality of error region restoration is finer in terms of detail. On the other hand, the algorithm uses larger group sizes, resulting in a lower probability of error-correction failure and fewer error-detection mistakes. However, the quality of error region restoration is not as detailed as with the strategy. Overall, the image reconstructed using the sharing strategy has a significantly better quality compared to the strategy.
4. Experimentational Results and Analysis
4.1. Simulation Experiment
In this experimental section, the proposed scheme selects the image “cameraman” as the secret image, sets the sharing threshold to (3, 4), the group size to , the authentication information as [111,171,177,191], the carrier QR code version as 5, and the error-correction level as 3. This simulation experiment primarily aims to demonstrate the feasibility of the proposed algorithm and ensure its correct operation. Figure 7 presents the experimental results of this study. Images , , , and represent the carrier QR code images, while , , , and correspond to the four generated share images. Figure 7j illustrates the reconstructed image data when the secret image is reconstructed with the participation of k or more qualified participants. In contrast, Figure 7k shows the reconstruction result when fewer than k participants are involved in the reconstruction process, where the secret image cannot be successfully restored. These results clearly indicate that the proposed scheme can only reconstruct the secret image when the required number of shares is present, thus validating its effectiveness in achieving the (k, n) threshold property. Furthermore, the experiment confirms that the proposed algorithm is fully executable and demonstrates practical feasibility.

Figure 7.
Figure 7 shows the experimental results of our algorithm under the (3, 4) setting. (a) Secret image; (b–e) carrier QR codes; (f–i) share images; (j) secret image reconstructed from three share images (f–h); (k) secret image reconstructed from two share images (f,g).
Not only is the proposed algorithm executable, but it also supports the lossless reconstruction of secret images. In traditional P-SIS algorithms, all computations are performed under modulo 251 or 257. Regardless of the modulus chosen, such operations inevitably introduce some degree of distortion to the reconstructed image. In contrast, our algorithm overcomes this limitation through polynomial optimization and pixel planning strategies, ensuring the preservation of image quality. To quantitatively demonstrate the lossless reconstruction capability, we compare our method with the traditional P-SIS algorithm using two common image quality metrics: PSNR (Peak Signal-to-Noise Ratio) and SSIM (Structural Similarity Index). The PSNR measures the similarity between two images, with higher values indicating greater similarity. Its theoretical range is from 0 to infinity (Inf). The SSIM evaluates the similarities in terms of brightness, contrast, and structure, ranging from 0 to 1, where values closer to 1 indicate higher similarity. In the experiments, the traditional P-SIS algorithm achieves a PSNR of 82.1548 and SSIM of 0.9999, which already indicate near-lossless reconstruction. However, our proposed method achieves a PSNR of ∞ and SSIM of 1, meaning it perfectly reconstructs the secret image without any loss. These results confirm that while traditional methods approach losslessness, our method achieves it in the strictest theoretical sense.
4.2. Security Analysis
In terms of security, the proposed algorithm also demonstrates strong performance. According to the (k, n) secret sharing strategy, at least k participants are required to successfully reconstruct the secret. Suppose an attacker has already compromised shares and attempts to recover the final share through brute force. In this case, if the secret image has dimensions , and the G4 sharing strategy is employed, the probability of successfully brute-forcing a single share group is only , while the probability of recovering the entire share image is negligible, as low as . If the G16 sharing strategy is adopted, the probability of successfully compromising the entire share image is reduced even further, to only . It is important to note that this probability reflects merely the chance of recovering a single share image. If the attacker possesses fewer than share images, the probability of reconstructing the secret will decrease exponentially. Even if an attacker obtains more than k shared fragments, they will still need to acquire additional critical parameters from the sharing process, such as the pixel partitioning scheme, the embedding region configuration, and the modulus settings, to successfully launch an attack. Therefore, the proposed scheme maintains a high level of security during the reconstruction phase. Moreover, during the secret sharing phase, this scheme employs QR codes as the carriers. Compared to the original noise images, QR code images have visual meaning, and thus the shares are less likely to be detected by attackers during transmission. In contrast, noise images lack inherent meaning and are more prone to arouse attackers’ suspicion and potential attacks during transmission. Therefore, due to the meaningful carrier information in the sharing phase, this scheme reduces the probability of being attacked and indirectly enhances security compared to the traditional P-SIS algorithm.
4.3. Anti-Noise Experiment
In this section, the robustness of the proposed scheme against noise is evaluated by applying four types of individual noise and one type of mixed noise. All experiments are conducted using a (3, 3) threshold sharing strategy based on the G16 scheme. The group size is set to , the identity authentication information is [11,13,17], and all carrier QR codes are of version 5 with an error-correction level of 3.
4.3.1. Resistance to Different Types of Noises
In this experiment, four types of noise with varying noise densities are introduced into the share images generated by the proposed scheme. This is done to evaluate the noise robustness of the share images under different noise conditions. The noise types selected in this experiment are Gaussian noise, salt-and-pepper noise, LSB-flipping noise, and JPEG image compression noise. Among them, Gaussian noise refers to noise whose probability density function follows a Gaussian distribution, which usually occurs during the acquisition and transmission of signals and data. The intensity of Gaussian noise is usually measured by its standard deviation and noise density : the higher the standard deviation , the stronger the noise intensity; the larger the noise density , the wider the coverage of the noise. Salt-and-pepper noise damages image pixel information by adding completely white or completely black pixels to the image, and its noise intensity is mainly measured by the noise density : the greater the value of , the stronger the noise intensity. LSB-flipping noise refers to noise added by flipping the least-significant bit values of image pixels. Its noise intensity is similar to that of salt-and-pepper noise and is also measured by the noise density : the higher the density , the stronger the noise intensity. JPEG image compression noise is caused by compressing images using JPEG compression technology, which leads to partial loss of pixel information. Unlike the previous three types of noise, JPEG noise does not involve the concept of noise density; instead, it uses image quality as the parameter to measure noise intensity. A lower image quality indicates a higher compression rate and thus higher noise intensity; a higher image quality indicates a lower compression rate and thus lower noise intensity.
In the experiment, the images “Lena,” “Pepper,” “Baboon,” and “Cameraman” are used as the secret images, each with a size of 128 × 128. The traditional P-SIS scheme is employed as the control group, using the same experimental parameters and noise settings. The experimental results are shown in Figure 8. There are four groups in total. In each group, represents the original image, denotes the third carrier QR code, refers to the third share image, and indicates the third share image that has been subjected to a noise attack. represent the pixel positions in the third share image that are affected by noise; in the image, white dots indicate that the corresponding position in is attacked by noise, while black dots indicate that it is not. represents the reconstructed secret image from the noisy share images , , and using our proposed method, whereas refers to the secret image reconstructed from the first to the third share images using the traditional P-SIS algorithm. Among the four sets of data: Figure 8(a1–g1) illustrate the experimental results of the secret image under the Gaussian noise attack with a noise density of 0.10, and a mean and standard deviation of 0 and 0.5, respectively. Figure 8(a2–g2) show the results under the salt-and-pepper noise attack with a noise density of 0.10. Figure 8(a3–g3) present the results under the JPEG compression noise with a compression quality factor of 99. Figure 8(a4–g4) demonstrate the results under the LSB-flipping noise attack with a noise density of 0.50. The experimental results shown in Figure 8 demonstrate that the proposed scheme exhibits strong robustness against various types of noise. Moreover, as observed from Figure 8(f1–f4) and Figure 8(g1–g4), the reconstructed images generated by the proposed algorithm are of significantly higher quality compared to those produced by the traditional P-SIS algorithm. The images reconstructed using our method are almost indistinguishable from the original, while those reconstructed by the traditional P-SIS algorithm show noticeable differences and suffer from severe image degradation. The experiment demonstrates that the proposed algorithm is capable of resisting four types of noise attacks. In particular, with respect to LSB-flipping noise, the proposed algorithm can fully withstand this type of interference, achieving the lossless reconstruction of the secret image under any noise density of LSB-flipping attacks.

Figure 8.
Figure 8 illustrates the experimental process under Gaussian noise, salt-and-pepper noise, JPEG compression noise, and LSB-flipping noise attacks.
To further demonstrate the noise robustness of the proposed algorithm, this experiment also provides a quantitative evaluation of its anti-noise performance. Specifically, the Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) are employed to assess the quality of the reconstructed images under four different types of noise attacks. For each calculation of the PSNR and SSIM, five independent experiments are conducted, and the average of the five results is taken as the final value. In this experiment, the image is considered to be losslessly reconstructed when the PSNR reaches 100. For Gaussian noise, salt-and-pepper noise, and LSB-flipping noise, the proposed scheme conducts anti-noise experiments by varying the noise density in the range of [0, 0.3], with an increment of 0.01. For JPEG compression noise, the compression quality of the image is varied from 100 to 70, with a step size of 1. The detailed experimental results are shown in Figure 9.
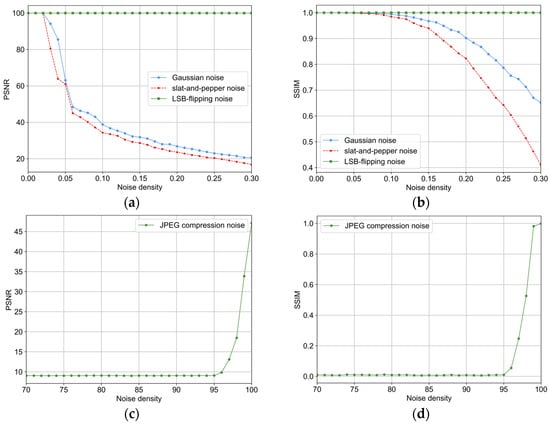
Figure 9.
PSNR and SSIM values of the reconstructed images under four different types of noise attacks using the proposed algorithm. (a) PSNR under Gaussian, Salt-and-Pepper, and LSB noise; (b) SSIM under Gaussian, Salt-and-Pepper, and LSB noise; (c) PSNR under JPEG compression noise; (d) SSIM under JPEG compression noise.
According to Figure 9a,b, it can be concluded that for Gaussian noise attacks, when the noise density , the proposed algorithm is capable of losslessly reconstructing the image. When , the PSNR of the reconstructed images remains above 40, indicating excellent image quality with almost no visual difference from the original. When the noise density , the PSNR drops below 30 for the first time, with and . This indicates that starting from this noise level, the quality of the reconstructed images begins to degrade significantly, and visual distortion may become apparent. For salt-and-pepper noise attacks, when the noise density , the proposed algorithm can achieve lossless image reconstruction. When the noise density , the reconstructed image quality remains excellent; when , the reconstructed image quality is considered good; when , the quality degrades with noticeable distortion; and when , the image quality becomes unacceptable with severe distortion. For LSB-flipping noise, regardless of the noise density applied, the PSNR of the reconstructed image remains at 100, indicating that the proposed algorithm achieves lossless reconstruction against this type of noise. According to Figure 9c,d, in the case of JPEG compression noise, the image reconstruction quality is excellent only when the compression quality is 100, with and . When the compression quality is 99, the reconstructed image quality is still good and visually close to the original, though slight distortions may be observed, with and . However, when the JPEG compression quality drops below 98, the quality of the reconstructed image becomes unacceptable. Overall, the proposed algorithm demonstrates the strongest robustness against LSB-flipping noise, achieving lossless reconstruction under any noise density. It performs well against Gaussian noise and salt-and-pepper noise as well. Although the reconstruction performance under JPEG compression noise is comparatively weaker, the algorithm still maintains resistance to a certain degree of JPEG compression quality degradation.
4.3.2. Resistance to Combined Noise
This section focuses on evaluating the proposed algorithm’s ability to resist mixed noise attacks. The experimental settings are consistent with those in Section 4.3.1. Three types of noise, namely Gaussian noise, salt-and-pepper noise, and LSB-flipping noise, are combined and simultaneously applied to the images to simulate a more complex attack scenario. The traditional P-SIS scheme is used as a baseline for comparison to assess the robustness of the proposed method against combined noise. The experimental results are shown in Figure 10. The original images used in this experiment are the Lena image and the Barbara image, both with a size of 128 × 128. The density of the combined noise is set to 0.045. Figure 10(a1,a2) show the original image; Figure 10(b1,b2) show the cover QR code; Figure 10(c1,c2) show the share image ; and Figure 10(d1,d2) show , which is after adding the combined noise. Figure 10(e1,e2) indicate the pixel locations where and differ. Figure 10(f1,f2) present the reconstructed image obtained by our proposed algorithm using the noisy share images , , and . Figure 10(g1,g2) show the reconstructed image by the traditional P-SIS algorithm using the first, second, and third share images. The experimental results demonstrate that under combined noise attacks, the images reconstructed by our proposed algorithm exhibit a significantly better visual quality compared to those reconstructed by the traditional P-SIS algorithm. In terms of PSNR and SSIM metrics, the reconstructed images by our algorithm achieve a and , while the traditional algorithm achieves a and an . Therefore, based on these quantitative metrics, our algorithm outperforms the traditional algorithm by a substantial margin.

Figure 10.
Figure 10 shows the experimental results against mixed noise with a noise density of 0.045. The mixed noise consists of Gaussian noise, salt-and-pepper noise, and LSB-flipping noise.
To better investigate the noise resistance of our algorithm against mixed noise, the noise density range of the mixed noise is set from 0.00 to 0.30, with the algorithm executed at intervals of 0.01 noise density. For each run, the PSNR and SSIM metrics of the reconstructed images are calculated. Each measurement is repeated five times, and the average of these five results is taken as the final value. Experimental parameters remain unchanged, and the traditional P-SIS algorithm is used as the control group for comparison. The experimental results shown in Figure 11 indicate that when the noise density , our algorithm can achieve lossless reconstruction. When the noise density is in the range of , the PSNR of our algorithm remains above 40 and the SSIM above 0.99, meaning the reconstructed images have a very high quality, almost indistinguishable from the original. For noise densities within , the PSNR stays above 30 and SSIM above 0.95, still ensuring a good image quality. However, when the noise density is within , the reconstructed image quality becomes poor. Finally, when the noise density , the reconstructed images suffer from severe distortion and the quality drops significantly. In contrast, the traditional algorithm can only reconstruct high-quality images when the noise density is zero. Once the noise density , the PSNR of images reconstructed by the traditional P-SIS algorithm falls below 20, indicating that the traditional P-SIS algorithm lacks any effective ability to resist mixed noise. In summary, our algorithm demonstrates a significant capability to withstand mixed noise attacks, and it far surpasses the traditional P-SIS algorithm in terms of robustness against mixed noise.
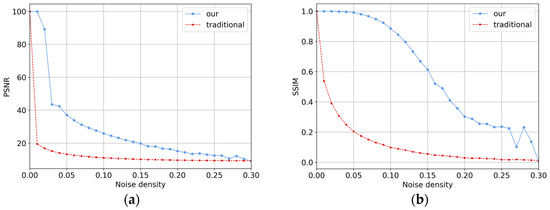
Figure 11.
Experimental results of resisting mixed noise with different noise densities. (a) PSNR under Mixed Noise; (b) SSIM under Mixed Noise.
4.4. Comparison
4.4.1. Comparison with Luo et al.
Luo et al. [18] proposed a robust secret sharing scheme based on the P-SIS approach by embedding RS error-correction codes into the share images using a cyclic displacement strategy. Their algorithm demonstrated remarkable noise resistance. In this experiment, our proposed scheme is compared with Luo et al.’s method in terms of robustness against salt-and-pepper noise and JPEG image compression noise. Both schemes are evaluated under identical experimental parameters, and the comparison is based on the quantitative metrics of the PSNR and SSIM to assess their noise resistance capabilities.
Figure 12 presents the quantitative evaluation results of the proposed scheme and Luo et al.’s method under salt-and-pepper noise attacks. In their study, Luo et al. designed multiple embedding strategies based on the range of Reed–Solomon (RS) codes. For a fair comparison, this work selects the two most effective strategies from their paper. The comparative data used here take the maximum values between the two strategies proposed by Luo et al. for each noise density. As shown in Figure 12a,b, the image reconstruction quality of the proposed algorithm significantly outperforms Luo et al.’s strategies in terms of both the PSNR and SSIM metrics. In Luo et al.’s method, the PSNR drops below 40 when the noise density is at , and further drops below 30 at . In contrast, the PSNR of the proposed method remains above 40 until , and only drops below 30 at . Accordingly, within the high-quality reconstruction interval (), Luo et al.’s valid range is [0, 0.04], while the proposed scheme achieves [0, 0.08], resulting in a 100% improvement. In the lossless reconstruction interval (), Luo et al.’s method supports lossless reconstruction at , whereas the proposed method extends this to , doubling the effective range. Within the good-quality reconstruction interval (), Luo et al.’s method covers [0, 0.06], while the proposed method covers [0, 0.13], representing an approximate 116% improvement. These experimental results demonstrate that although Luo et al.’s method offers a certain degree of noise resistance, the proposed method achieves significantly superior robustness against salt-and-pepper noise.
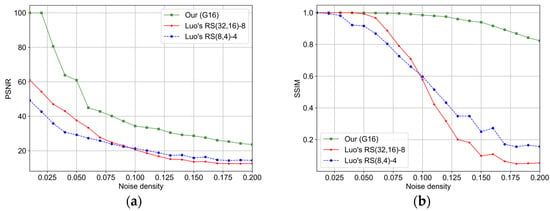
Figure 12.
Comparison of PSNR and SSIM between the proposed method and Luo’s method under salt-and-pepper noise attack. (a) PSNR of under Salt-and-Pepper noise; (b) SSIM of under Salt-and-Pepper noise.
Figure 13 presents the quantitative results of our method and those of Luo et al. under JPEG compression noise attacks. When the image compression quality is 100, the PSNR and SSIM of Luo et al.’s method are 37.63 and 0.9999, respectively, while our method achieves a PSNR of 47.14 and SSIM of 0.9991, representing a 25.27% improvement in the PSNR and a slight decrease of 0.08% in the SSIM. When the compression quality is 99, Luo et al.’s method yields a and , failing to reconstruct a high-quality image, whereas our method still maintains a high reconstruction quality with a PSNR of 33.87 and SSIM of 0.9821. As the compression quality drops below 99, the image reconstruction performance of both methods deteriorates rapidly. However, the proposed method consistently outperforms Luo et al.’s approach in terms of quantitative metrics.
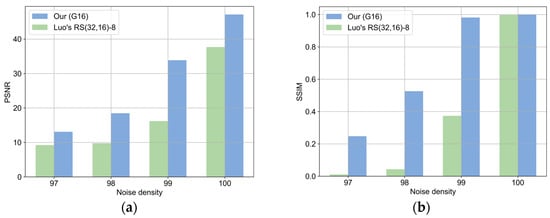
Figure 13.
Comparison of PSNR and SSIM between the proposed method and Luo’s method under JPEG compression noise attack. (a) PSNR under JPEG compression noise; (b) SSIM under JPEG compression noise.
Based on the above experimental data, although the method proposed by Luo et al. demonstrates a certain level of noise resistance, the noise robustness of the proposed scheme significantly surpasses the best performance achieved by Luo et al.’s method across all experimental settings.
4.4.2. Comparison with Other Works
This section presents a comparison between the proposed algorithm and other existing algorithms in terms of several key features. Table 2 illustrates the comparison results. In terms of noise resistance, most existing algorithms exhibit a very limited capability: images cannot be successfully reconstructed under high noise density attacks. However, based on the experimental results presented in Section 4.3 and Section 4.4.1, the proposed algorithm demonstrates significantly superior noise resilience, supporting a much wider range of noise densities than other approaches. In addition to the strength against noise, the variety of noise types that an algorithm can handle is also an important indicator of its robustness. The proposed method is capable of resisting multiple types of noise, including but not limited to Gaussian noise, salt-and-pepper noise, LSB-flipping noise, JPEG compression noise, and mixed noise. These results further confirm the strong robustness of the proposed scheme.

Table 2.
Comparison of features with other algorithms.
Lossless reconstruction capability is also an important indicator to evaluate the noise resistance of an algorithm. Stronger lossless reconstruction means that when data are subjected to noise attacks, loss, or tampering, the algorithm can restore the original data more accurately. Currently, most algorithms have limited lossless reconstruction capabilities. Luo et al.’s algorithm improves this capability by combining RS codes with an integer programming model and pixel block construction methods. Their algorithm can probabilistically achieve the lossless reconstruction of secret images under salt-and-pepper noise attacks with a noise density . In contrast, our proposed algorithm further optimizes the noise resistance by improving the size of RS codes and pixel block construction. It can guarantee the lossless reconstruction of secret images under salt-and-pepper noise attacks with a noise density . Compared with Luo’s method, the lossless reconstruction capability has been improved by 100%.
No pixel expansion is a very important primary metric in secret sharing schemes. It means that the share images do not increase additional storage or transmission overhead. Based on optimized sharing mechanisms and embedding strategies, most current algorithms can achieve no pixel expansion.
The final comparison metric of our algorithm is meaningful sharing. Conventional secret sharing schemes usually generate share images that appear as purely random noise, which are meaningless visually. Meaningful images refer to share images that are visually recognizable or contain certain visual information, without affecting the reconstruction of the secret information. Meaningful share images generally imply lower suspicion and less likelihood of being attacked, thus providing enhanced security. Currently, most algorithms do not achieve meaningful share images. Our algorithm improves the traditional polynomial interpolation function, compresses the secret information size, and embeds it into a cover QR code. This allows our scheme to use the QR code as a carrier to realize meaningful sharing. Moreover, our share images neither affect the reconstruction of the secret information nor impair the readability of the QR code.
4.5. Execution Time Analysis
This section investigates the impact of secret image size, sharing strategy, and various (k, n) threshold settings on the execution efficiency of the algorithm. The experiments were conducted on a general-purpose computing platform equipped with an AMD Ryzen 9 7945HX processor, 16 GB of memory, and the Windows 11 operating system. The algorithm was implemented using Python 3. Lena images with sizes of 128 × 128 and 256 × 256 were used as secret inputs. Three threshold settings were tested: (3, 3), (4, 5), and (7, 10), in order to evaluate performances across different parameter combinations. Each test was repeated five times, and the average runtime was recorded. Table 3 and Table 4 show the algorithm’s execution time under the G4 and G16 sharing strategies, respectively, for different image sizes and threshold settings. Overall, increasing the image size is one of the most direct factors affecting execution time. When the sharing strategy and threshold values are held constant, larger images result in significantly longer runtimes. This effect becomes more pronounced when higher threshold values are used. The (k, n) threshold values also have a notable influence on execution time. With the image size and sharing strategy fixed, increasing the value of n means more shares need to be generated and processed, which leads to a longer computation time. Moreover, the sharing strategy itself plays an important role in determining performance. Under the same image size and threshold settings, the algorithm using the G16 strategy consistently runs faster than the one using the G4 strategy during both the sharing and reconstruction phases. This indicates that the structural design of G16 leads to better computational efficiency. The improvement is especially evident in the sharing phase, where G16 exhibits a more significant performance advantage.

Table 3.
Execution time of the program under G4 strategy with different secret image sizes and (k, n) thresholds.

Table 4.
Execution time of the program under G16 strategy with different secret image sizes and (k, n) thresholds.
5. Summary
This paper proposes a robust secret image sharing algorithm based on QR codes, aiming to address the insufficient noise resistance of traditional secret sharing schemes in noisy environments. By optimizing polynomial computation methods and improving pixel allocation strategies to compress the length of secret information, and by integrating Reed–Solomon (RS) codes, the proposed algorithm significantly enhances the noise resistance and lossless reconstruction capabilities of secret sharing schemes. Compared to existing approaches, the proposed algorithm exhibits superior performance in resisting noise. When the salt-and-pepper noise density , the algorithm can achieve the lossless reconstruction of the secret image. Even when the noise density , it still ensures high-quality reconstruction. Furthermore, the algorithm effectively resists various types of noise, including Gaussian noise, JPEG compression noise, LSB-flipping noise, and mixed noise. In addition, the algorithm avoids the problem of pixel expansion and enables the meaningful sharing of secret content. These advantages advance the research into noise-resilient secret sharing. However, several areas still require further investigation, such as addressing the limited flexibility of the current algorithm, particularly the constraint that the threshold value k must be greater than or equal to 3, and exploring more powerful error-correction codes to further enhance the algorithm’s resistance to noise.
Author Contributions
Conceptualization, P.H. and C.C.; methodology, P.H.; software, C.C.; validation, P.H., C.C. and X.W.; formal analysis, P.H. and C.C.; investigation, X.W.; resources, P.H.; writing—original draft preparation, P.H., C.C. and X.W.; writing—review and editing, P.H. and C.C.; visualization, X.W.; supervision, P.H.; project administration, P.H.; funding acquisition, P.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded in part by the Natural Science Foundation of Fujian Province (Grant Number: 2022J011235), and Xiamen Overseas Students’ Program (Grant Number: [2023] 169-1).
Data Availability Statement
Data is contained within the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
References
- Parihar, B.; Rawat, A.S.; Deshmukh, M. A survey on counting-based secret sharing schemes for resource-constrained environments: Techniques, security, challenges, and future directions. J. Supercomput. 2024, 80, 17633–17687. [Google Scholar] [CrossRef]
- Salman, L.A.; Hashim, A.T.; Hasan, A.M. Selective medical image encryption using polynomial-based secret image sharing and chaotic map. Int. J. Saf. Secur. Eng. 2022, 12, 357–369. [Google Scholar] [CrossRef]
- Xiong, L.; Han, X.; Yang, C.N. CP-PSIS: CRT and polynomial-based progressive secret image sharing. Signal Process. 2021, 185, 108064. [Google Scholar] [CrossRef]
- Prashanti, G.; Bhat, M.N. Cheating identifiable polynomial based secret sharing scheme for audio and image. Multimed. Tools Appl. 2024, 83, 403–423. [Google Scholar] [CrossRef]
- Gao, K.; Horng, J.H.; Chang, C.C.; Chang, C.C. Linguistic secret sharing via ambiguous token selection for IOT security. Electronics 2024, 13, 4216. [Google Scholar] [CrossRef]
- Huang, J.; Cui, Q.; Zhou, Z.; Yu, K.; Yang, C.N.; Choo, K.K.R. Encrypted domain secret medical-image sharing with secure outsourcing computation in IoT environment. IEEE Internet Things J. 2023, 11, 2382–2393. [Google Scholar] [CrossRef]
- Alwan, A.H.; Hashim, A.T.; Ali, S.A. Partial encryption scheme of medical images based on DWT, secret image sharing and hyperchaotic system. Trait. Signal 2024, 41, 1807. [Google Scholar] [CrossRef]
- Zhou, Z.; Wan, Y.; Cui, Q.; Yu, K.; Mumtaz, S.; Yang, C.N.; Guizani, M. Blockchain-based secure and efficient secret image sharing with outsourcing computation in wireless networks. IEEE Trans. Wirel. Commun. 2023, 23, 423–435. [Google Scholar] [CrossRef]
- Sarkar, P.; Nag, A.; Singh, J.P. Blockchain-based authenticable (k, n) multi-secret image sharing scheme. J. Electron. Imaging 2023, 32, 053019. [Google Scholar] [CrossRef]
- Yan, X.; Li, L.; Chen, J.; Sun, L. Public key based bidirectional shadow image authentication without pixel expansion in image secret sharing. Front. Inf. Technol. Electron. Eng. 2023, 24, 88–103. [Google Scholar] [CrossRef]
- Attasena, V.; Darmont, J.; Harbi, N. Secret sharing for cloud data security: A survey. VLDB J. 2017, 26, 657–681. [Google Scholar] [CrossRef]
- Sun, Y.; Lu, Y.; Yan, X.; Liu, L.; Li, L. Robust secret image sharing scheme against noise in shadow images. IEEE Access 2021, 9, 23284–23300. [Google Scholar] [CrossRef]
- Zhou, Z.; Su, Y.; Li, J.; Yu, K.; Wu, Q.M.J.; Fu, Z.; Shi, Y. Secret-to-image reversible transformation for generative steganography. IEEE Trans. Dependable Secur. Comput. 2022, 20, 4118–4134. [Google Scholar] [CrossRef]
- Cheraghchi, M. Nearly optimal robust secret sharing. Des. Codes Cryptogr. 2019, 87, 1777–1796. [Google Scholar] [CrossRef]
- Luo, S.; Liu, Y.; Yan, X.; Yu, Y. Secret image sharing scheme with lossless recovery and high efficiency. Signal Process. 2023, 206, 108931. [Google Scholar] [CrossRef]
- Yan, X.; Liu, L.; Li, L.; Lu, Y. Robust secret image sharing resistant to noise in shares. ACM Trans. Multimed. Comput. Commun. Appl. 2021, 17, 1–22. [Google Scholar] [CrossRef]
- Liu, X.B.; Koh, S.N.; Wu, X.W.; Chui, C.C. Reconstructing a linear scrambler with improved detection capability and in the presence of noise. IEEE Trans. Inf. Forensics Secur. 2011, 7, 208–218. [Google Scholar] [CrossRef]
- Luo, S.; Liu, Y.; Yan, X.; Sun, Y. Robust secret image sharing scheme with improved anti-noise capability. Signal Process. 2024, 219, 109423. [Google Scholar] [CrossRef]
- Sklar, B. Reed-Solomon Codes. 2001, pp. 1–33. Available online: http://hscc.cs.nthu.edu.tw/~sheujp/lecture_note/rs.pdf (accessed on 15 August 2025).
- Cox, R. Qart Codes. Available online: http://research.swtch.com/qart (accessed on 15 August 2025).
- Maduskar, D.; Dube, N. Navier–stokes-based image inpainting for restoration of missing data due to clouds. In Innovations in Computational Intelligence and Computer Vision, Proceedings of the ICICV 2020, Jaipur, India, 17–19 January 2020; Springer: Singapore, 2021; pp. 497–505. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).