Delayed Star Subgradient Methods for Constrained Nondifferentiable Quasi-Convex Optimization

Abstract

In this work, we consider the problem of minimizing a quasi-convex function over a nonempty closed convex constrained set. In order to approximate a solution of the considered problem, we propose delayed star subgradient methods. The main feature of the proposed methods is that it allows us to use the stale star subgradients when updating the next iteration rather than computing the new star subgradient in every iteration. We subsequently investigate the convergence results of sequences generated by the proposed methods. Finally, we present some numerical experiments on the Cobb–Douglas production efficiency problem to illustrate the effectiveness of the proposed method.

1. Introduction

In this work, we consider the quasi-convex optimization problem:

$$\begin{array}{c}\hfill \begin{array}{c}\mathrm{minimize}\hspace{1em}\hspace{1em}f\left(\mathbf{x}\right)\hfill \\ {\displaystyle \mathrm{subject}\mathrm{to}\hspace{1em}\hspace{1em}\mathbf{x}\in X,}\hfill \end{array}\end{array}$$

(1)

where the objective function $f:{\mathbb{R}}^n\to \mathbb{R}$ is quasi-convex continuous (possibly) and nondifferentiable, and the constrained set X is nonempty closed and convex. Throughout this work, we will denote the set of all optimal solutions and the optimal value of the problem (1) as $X^{*}:={\mathrm{argmin}}_{\mathbf{x}\in X}f\left(\mathbf{x}\right)$ and $f^{*}:={min}_{\mathbf{x}\in X}f\left(\mathbf{x}\right)$, respectively. We also assume that $X^{*}\ne \varnothing$.

The problem (1) not only forms a fundamental setting for optimization as every convex function is quasi-convex but also generalizes to several practical situations in many fields such as economics, engineering, and others. An important special setting is the problem of minimizing the ratios of two functions [1] (Lemma 4), [2] (Theorem 2.3.8), for example, optimizing the ratio of outputs and inputs for the highest-quality productivity assessments in economics, such as debt-to-equity ratio analysis in corporate financial planning, inventory-to-sales analysis in production planning, and nurse–patient ratio analysis in hospital planning. This kind of problem is known as fractional programming [3,4,5]. As mentioned above, various kinds of iterative methods have been developed to solve the quasi-convex optimization problem (1); see [1,6,7,8,9,10,11,12,13,14] and references therein.

If the function f is convex, it is well-known that the classical method to deal with the constrained convex optimization problem is the projected subgradient method: for an initial point ${\mathbf{x}}_0\in X,$ compute

$$\begin{array}{c}\hfill {\mathbf{x}}_{k+1}:=P_X({\mathbf{x}}_k-{\alpha }_k\tilde{\nabla }f\left({\mathbf{x}}_k\right)),\hspace{1em}\forall k\in {\mathbb{N}}_0,\end{array}$$

where $\tilde{\nabla }f\left({\mathbf{x}}_k\right)\in \{\mathbf{g}\in {\mathbb{R}}^n:⟨\mathbf{g},\mathbf{y}-\mathbf{x}⟩\le f\left(\mathbf{y}\right)-f\left(\mathbf{x}\right)\mathrm{for}\mathrm{all}\mathbf{y}\in {\mathbb{R}}^n\}$ is the Fenchel subgradient of f at ${\mathbf{x}}_k.$ Because of the simplicity, this method has been continuously developed in the literature, see for instance [8,15]. However, for the quasi-convex case, it should be noted that the Fenchel subgradient may not exist, in general. In this situation, we need a more general subgradient concept, which is the so-called star subgradient proposed in [16,17]. By utilizing the notion of a star subgradient, Kiwiel [1] proposed the star subgradient method to solve the constrained quasi-convex optimization problem (1): for an initial point ${\mathbf{x}}_0\in X,$

$$\begin{array}{c}\hfill {\mathbf{x}}_{k+1}:=P_X\left({\mathbf{x}}_k-{\alpha }_k{\displaystyle \frac{{\tilde{\nabla }}^{\star }f\left({\mathbf{x}}_k\right)}{\parallel {\tilde{\nabla }}^{\star }f\left({\mathbf{x}}_k\right)\parallel }}\right),\hspace{1em}\forall k\in {\mathbb{N}}_0,\end{array}$$

(2)

where ${\tilde{\nabla }}^{\star }f\left({\mathbf{x}}_k\right)\in {\partial }^{\star }f\left({\mathbf{x}}_k\right)\backslash \left\{\mathbf{0}\right\}$ is the nonzero star subgradient of f at ${\mathbf{x}}_k$. After that, Hu et al. [6] proposed an inexact version of the star-subgradient method by considering the approximated star subgradient with the presence of noises. By imposing the Hölder condition, they presented the convergence results in various aspects for both constant and diminishing step sizes. Subsequently, several methods have been investigated for solving more general problem settings, for instance, a conditional star subgradient method [8], a stochastic star subgradient method [7], and an incremental star subgradient method [9].

As we can notice, the above-mentioned methods require computing the star subgradient in every single iteration; however, there are some practical situations such as large-scale problems in which the exact star subgradients may be computationally expensive. This shortcoming can be overcome by using the idea of delayed subgradients in which we can retrieve stale subgradients instead of spending time computing a new subgradient in every iteration. This approach is not only useful for dealing with excessive computation but also for handling communication delays in networked systems. Note that various convex methods with delayed gradient or even subgradient updates are developed and studied, for instance, stochastic gradient descent [18,19], incremental type methods [20,21,22,23], distributed type methods [24,25,26], and references therein.

To the best of our knowledge, there is no report about the star subgradient method with delayed updates to solve the problem (1). To fill this gap, in this work, we propose two delayed star subgradient methods (in short, DSSMs) based on the ideas of the star subgradient method (2) and the delayed subgradient updates, called DSSM-I and DSSM-II, respectively. We investigate the convergence properties of the proposed methods in both objective values and iterations, including proving finite convergence.

This paper is organized as follows: Section 2 provides the essential notations, definitions, and facts utilized in this work. Section 3 contains the proposed methods, including their convergence results. This section is divided into two subsections. In Section 4, we then apply DSSM-I to the Cobb–Douglas production efficiency problem. Finally, we provide the summary in Section 5.

2. Preliminaries

This section contains important symbols, definitions, and tools utilized in this work. Throughout this paper, let $\mathbb{R}$ be the set of all real numbers, ${\mathbb{N}}_0$ the set of all non-negative integers, and $\mathbb{N}$ the set of all positive integers. We denote with ${\mathbb{R}}^n$ a Euclidean space with an inner product $⟨·,·⟩$ and an induced norm $\parallel ·\parallel$. We denote the unit sphere by the set $\mathcal{S}:=\{\mathbf{z}\in {\mathbb{R}}^n:\parallel \mathbf{z}\parallel =1\}$ and the open ball centered at the $\mathbf{x}\in {\mathbb{R}}^n$ with radius $\delta >0$ by the set $\mathcal{B}(\mathbf{x};\delta ):=\{\mathbf{z}\in {\mathbb{R}}^n:\parallel \mathbf{z}-\mathbf{x}\parallel <\delta \}$.

Let $X\subset {\mathbb{R}}^n$ be a nonempty set. The symbol $\mathrm{cl}\left(X\right)$ is the closure of X. The distance (function) between $\mathbf{y}\in {\mathbb{R}}^n$ and X is the function $\mathrm{dist}:{\mathbb{R}}^n\to \mathbb{R}$ defined by

$$\mathrm{dist}(\mathbf{y},X):=\underset{\mathbf{x}\in X}{inf}\parallel \mathbf{y}-\mathbf{x}\parallel .$$

The metric projection of $\mathbf{y}\in {\mathbb{R}}^n$ onto X is the point $P_X\left(y\right)\in X$ such that $\parallel P_X\left(\mathbf{y}\right)-\mathbf{y}\parallel \le \parallel \mathbf{x}-\mathbf{y}\parallel$ for all $\mathbf{x}\in X.$ Note that the metric projection $P_X\left(\mathbf{y}\right)$ exists and is unique for all $\mathbf{y}\in {\mathbb{R}}^n$ whenever X is nonempty, closed, and convex [27] (Theorem 1.2.3). The metric projection onto a nonempty closed convex set X has a nonexpansive property, i.e., $\parallel P_X\left(\mathbf{x}\right)-P_X\left(\mathbf{y}\right)\parallel \le \parallel \mathbf{x}-\mathbf{y}\parallel$ for all $\mathbf{x},\mathbf{y}\in {\mathbb{R}}^n$ [27] (Theorem 2.2.21).

Let $f:{\mathbb{R}}^n\to \mathbb{R}$ be a function, and let $\alpha \in \mathbb{R}$. The strictly sublevel and sublevel set of f corresponding to $\alpha$ are defined by

$$S_{f,\alpha }^{<}:=\{\mathbf{x}\in {\mathbb{R}}^n:f\left(\mathbf{x}\right)<\alpha \}\mathrm{and}{S}_{f,\alpha }^{\le }:=\{\mathbf{x}\in {\mathbb{R}}^n:f\left(\mathbf{x}\right)\le \alpha \},$$

respectively. The function f is called upper semicontinuous on ${\mathbb{R}}^n$ if $S_{f,\alpha }^{<}$ is an open set for all $\alpha \in \mathbb{R}.$ The function f is called lower semicontinuous on ${\mathbb{R}}^n$ if $S_{f,\alpha }^{\le }$ is a closed set for all $\alpha \in \mathbb{R}.$ The function f is continuous on ${\mathbb{R}}^n$ if it is both upper semicontinuous and lower semicontinuous on ${\mathbb{R}}^n$. The function f is called quasi-convex on ${\mathbb{R}}^n$ if $S_{f,\alpha }^{\le }$ is convex for all $\alpha \in \mathbb{R}.$

For any $\mathbf{x}\in {\mathbb{R}}^n,$ the star subdifferential [16,17] of f at $\mathbf{x}$ is the set

$${\partial }^{\star }f\left(\mathbf{x}\right):=\left\{\mathbf{g}\in {\mathbb{R}}^n:⟨\mathbf{g},\mathbf{y}-\mathbf{x}⟩\le 0\mathrm{for}\mathrm{all}\mathbf{y}\in S_{f,f\left(\mathbf{x}\right)}^{<}\right\}.$$

The element $\mathbf{g}\in {\partial }^{\star }f\left(\mathbf{x}\right)$ is called the star subgradient of f at $\mathbf{x}$, and it is denoted by ${\tilde{\nabla }}^{\star }f\left(\mathbf{x}\right).$ It is obvious that $\mathbf{0}\in {\partial }^{\star }f\left(\mathbf{x}\right)$ for all $\mathbf{x}\in {\mathbb{R}}^n$. The following fact provides the basic properties of the star subgradient, which can be found in [16] (Proposition 30) and [6] (Lemma 2.1).

Fact 1. 

Let $f:{\mathbb{R}}^n\to \mathbb{R}$ be a quasi-convex, and let $\mathbf{x}\in {\mathbb{R}}^n.$ Then the following statements hold:

(i)

${\partial }^{\star }f\left(\mathbf{x}\right)\backslash \left\{\mathbf{0}\right\}$ is a nonempty set;

(ii)

${\partial }^{\star }f\left(\mathbf{x}\right)$ is a closed, convex cone.

Next, we will recall the definition and properties of the quasi-Fejer monotone sequence. Let X be a nonempty subset of ${\mathbb{R}}^n$. The sequence ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }\subset {\mathbb{R}}^n$ is said to be quasi-Fejer monotone with respect to X if for any $\mathbf{x}\in X,$ there exists a sequence ${\left\{{\zeta }_k\right\}}_{k=0}^{\infty }\subset (0,\infty )$ such that

$$\sum _{k=0}^{\infty }{\zeta }_k<\infty \mathrm{and}\parallel {\mathbf{x}}_{k+1}{-\mathbf{x}\parallel }^2\le {\parallel {\mathbf{x}}_k-\mathbf{x}\parallel }^2+{\zeta }_k\mathrm{for}\mathrm{all}k\in {\mathbb{N}}_0.$$

Fact 2 

([28]). (Theorem 5.33) Let $X\subset {\mathbb{R}}^n$ be a nonempty set and ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ be a sequence in ${\mathbb{R}}^n$. If the sequence ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ is quasi-Fejer monotone with respect to X, then ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ is bounded and ${lim}_{k\to \infty }\parallel {\mathbf{x}}_k-\mathbf{x}\parallel$ exists for all $\mathbf{x}\in X.$

Finally, we provide the lemma, which is used in the next section.

Lemma 1 

([29]). (Lemma 2.1) Let ${\left\{a_k\right\}}_{k=0}^{\infty }$ be a scalar sequence, and let ${\left\{b_k\right\}}_{k=0}^{\infty }$ be a positive real number sequence such that ${lim}_{k\to \infty }{\sum }_{i=0}^k{b}_i=\infty .$ If ${lim}_{k\to \infty }{a}_k=0$, then ${lim}_{k\to \infty }{\displaystyle \frac{{\sum }_{i=0}^k{a}_i{b}_i}{{\sum }_{i=0}^k{b}_i}}=0$.

3. Algorithms and Convergence Results

In this section, we introduce two delayed star subgradient methods (DSSM-I and DSSM-II) to solve Problem (1) and subsequently investigate the convergence properties of the proposed methods. To deal with delayed-type methods, we need the following assumption of the boundedness of the time-varying delays, as stated below.

Assumption 1. 

The sequence of time-varying delays ${\left\{{\tau }_k\right\}}_{k=0}^{\infty }\subset {\mathbb{N}}_0$ is bounded, that is, there exists a non-negative integer τ such that $0\le {\tau }_k\le \tau$ for all $k\in {\mathbb{N}}_0.$

3.1. Delayed Star Subgradient Method I

Now, we are ready to propose the delayed star subgradient method of the first kind which is defined as the following Algorithm 1.

Algorithm 1 Delayed Star Subgradient Method I (DSSM-I)

Initialization: Given a stepsize ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }\subset (0,\infty ),$ the delays ${\left\{{\tau }_k\right\}}_{k=0}^{\infty }\subset {\mathbb{N}}_0$, and initial points ${\mathbf{x}}_0,{\mathbf{x}}_{-1},{\mathbf{x}}_{-2},\dots ,$${\mathbf{x}}_{-\tau }\in X$. Iterative Step: For a current point ${\mathbf{x}}_k\in X$, we compute $${\mathbf{x}}_{k+1}:=P_X({\mathbf{x}}_k-{\alpha }_k{\mathbf{g}}_{k-{\tau }_k}),$$ where ${\mathbf{g}}_{k-{\tau }_k}\in {\partial }^{\star }f\left({\mathbf{x}}_{k-{\tau }_k}\right)\cap \mathcal{S}$ is a unit star subgradient of f at ${\mathbf{x}}_{k-{\tau }_k}$. Update $k:=k+1$.

Throughout this work, to simplify the analysis, we denote ${\mathbf{x}}_0={\mathbf{x}}_{-1}={\mathbf{x}}_{-2}=\dots ={\mathbf{x}}_{-\tau }.$

Remark 1. 

(i) 

Since the function f is quasi-convex, we note that DSSM-I is well defined. In fact, using Fact 1, we have for any $k\in {\mathbb{N}}_0$, ${\partial }^{\star }f\left({\mathbf{x}}_k\right)\backslash \left\{\mathbf{0}\right\}\ne \varnothing$. Hence, we are able to select any point ${\tilde{\nabla }}^{\star }f\left({\mathbf{x}}_k\right)\in {\partial }^{\star }f\left({\mathbf{x}}_k\right)\backslash \left\{\mathbf{0}\right\}$ and subsequently set ${\mathbf{g}}_k:={\displaystyle \frac{{\tilde{\nabla }}^{\star }f\left({\mathbf{x}}_k\right)}{\parallel {\tilde{\nabla }}^{\star }f\left({\mathbf{x}}_k\right)\parallel }}\in {\partial }^{\star }f\left({\mathbf{x}}_k\right)\cap \mathcal{S}$. Moreover, since ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }\subset X,$ it is clear that $f\left({\mathbf{x}}_k\right)\ge f^{*}$ for all $k\in {\mathbb{N}}_0$.

(ii) 

If ${\tau }_k=0$ for all $k\in {\mathbb{N}}_0$, DSSM-I coincides with the star subgradient method (SSM), which was proposed by Kiwiel [1].

Remark 2. 

Note that methods with time-varying delays allow us to use stale information, which is very helpful when the star subgradients are not easily computed. Assumption 1 is typically assumed for analyzing the convergence results of the delayed-type methods, see [18,19,20,24,25,26] and references therein. The presence of the delayed bound τ ensures that we need to update the unit star subgradient of f at ${\mathbf{x}}_{k-{\tau }_k}$ in at least every τ iteration. Some examples of the delayed sequences are as follows:

(i) 

Constant delay [18], that is, ${\tau }_k:=\tau$ for all $k\in {\mathbb{N}}_0$.

(ii) 

Cyclic delay [19,20,24,26] and references therein. The typical form of this type is ${\tau }_k:=kmod(\tau +1)$ for all $k\in {\mathbb{N}}_0$. In this case, the delays ${\tau }_k$ ($k\in {\mathbb{N}}_0$) are chosen with deterministic order from the set $\{0,1,2,\dots ,\tau \}$. This means that we will use stale information over a consistent period of length $\tau +1$ and update the new star subgradient at every $\tau +1$ iteration.

(iii) 

Random delay [25], that is, the delays ${\tau }_k$ ($k\in {\mathbb{N}}_0$) are randomly chosen in the set $\{0,1,2,\dots ,\tau \}$.

Assumption 2. 

The function f satisfies the Hölder condition with order $p>0$ and modulus $L>0$ on X, i.e., $f\left(\mathbf{x}\right)-f^{*}\le L\mathrm{dist}{(\mathbf{x},X^{*})}^p$ for all $\mathbf{x}\in X$.

The Hölder condition assumption is typically assumed when investigating the convergence results of methods for solving quasi-convex optimization problems [6,7,9,10,11,12]. Note that, for the special case of $p=1$, the Hölder condition is nothing else than the Lipschitz condition.

The following lemma provides a useful property of the star subgradient and will play an important role in the convergence analysis. The formal proof is due to Konnov [10] (Proposition 2.1).

Lemma 2. 

Suppose that Assumption 2 holds. Let ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ be a sequence generated by DSSM-I. For any ${\mathbf{x}}^{*}\in X^{*}$ and $k\in {\mathbb{N}}_0$, if ${\mathbf{x}}_k\notin X^{*},$ then

$$f\left({\mathbf{x}}_k\right)-f^{*}\le L{⟨{\mathbf{g}}_k,{\mathbf{x}}_k-{\mathbf{x}}^{*}⟩}^p\hspace{1em}\mathrm{for}\mathrm{all}{\mathbf{g}}_k\in {\partial }^{\star }f\left({\mathbf{x}}_k\right)\cap \mathcal{S}.$$

Next, we will provide some lemma, which are important tools for proving the convergence results of DSSM-I. We first provide the basic inequality relating to the sufficient decreasing property of the generated sequence.

Lemma 3. 

Suppose that Assumption 2 holds. Let ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ be a sequence generated by DSSM-I. For any ${\mathbf{x}}^{*}\in X^{*}$ and $k\in {\mathbb{N}}_0,$ if ${\mathbf{x}}_{k-{\tau }_k}\notin X^{*},$ then

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2\le \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k^2+2{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel -2{\alpha }_k{L}^{-{\displaystyle \frac{1}{p}}}{\left(f\left({\mathbf{x}}_{k-{\tau }_k}\right)-f^{*}\right)}^{{\displaystyle \frac{1}{p}}}.\end{array}$$

Proof. 

Let ${\mathbf{x}}^{*}\in X^{*}$ and $k\in {\mathbb{N}}_0$ be fixed. Suppose that ${\mathbf{x}}_{k-{\tau }_k}\notin X^{*}.$ We note from the definition ${\mathbf{x}}_k$ in DSSM-I that

$$\begin{array}{ccc}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2& =& \parallel P_X({\mathbf{x}}_k-{\alpha }_k{\mathbf{g}}_{k-{\tau }_k})-P_X\left({\mathbf{x}}^{*}\right){\parallel }^2\hfill \\ & \le & \parallel {\mathbf{x}}_k-{\alpha }_k{\mathbf{g}}_{k-{\tau }_k}-{\mathbf{x}}^{*}{\parallel }^2\hfill \\ & =& \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k^2-2{\alpha }_k⟨{\mathbf{g}}_{k-{\tau }_k},{\mathbf{x}}_k-{\mathbf{x}}^{*}⟩\hfill \\ & \le & \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k^2+2{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel -2{\alpha }_k⟨{\mathbf{g}}_{k-{\tau }_k},{\mathbf{x}}_{k-{\tau }_k}-{\mathbf{x}}^{*}⟩\hfill \\ & \le & \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k^2+2{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel -2{\alpha }_k{L}^{-{\displaystyle \frac{1}{p}}}{\left(f\left({\mathbf{x}}_{k-{\tau }_k}\right)-f^{*}\right)}^{{\displaystyle \frac{1}{p}}},\hfill \end{array}$$

where the first inequality follows from the nonexpansiveness of metric projection, and the second one follows from the Cauchy–Schwarz inequality and the fact that $\parallel {\mathbf{g}}_{k-{\tau }_k}\parallel =1$ for all $k\in {\mathbb{N}}_0$, and the last one follows from Lemma 2. This completes the proof. □

Lemma 4. 

Suppose that Assumption 1 holds. Let ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ be a sequence generated by DSSM-I, and let ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }\subset (0,\infty )$ be a nonincreasing sequence with ${lim}_{k\to \infty }{\alpha }_k=0$ and ${\sum }_{k=0}^{\infty }{\alpha }_k=\infty$. Then $\parallel {\mathbf{x}}_{k-{\tau }_k}-{\mathbf{x}}_k\parallel \le (\tau +1){\alpha }_{k-\tau }$ for all $k\ge \tau$ and ${lim}_{k\to \infty }\parallel {\mathbf{x}}_{k-{\tau }_k}-{\mathbf{x}}_k\parallel =0.$

Proof. 

We first note that for each $k\in {\mathbb{N}}_0$

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel =∥\sum _{i=1}^{{\tau }_k}({\mathbf{x}}_{k-i+1}-{\mathbf{x}}_{k-i})∥\le \sum _{i=1}^{{\tau }_k}\parallel {\mathbf{x}}_{k-i+1}-{\mathbf{x}}_{k-i}\parallel \le \sum _{i=0}^{\tau }\parallel {\mathbf{x}}_{k-i+1}-{\mathbf{x}}_{k-i}\parallel \end{array}$$

(3)

and

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}_k\parallel =\parallel P_X({\mathbf{x}}_k-{\alpha }_k{\mathbf{g}}_{k-{\tau }_k})-P_X\left({\mathbf{x}}_k\right)\parallel \le {\alpha }_k\parallel {\mathbf{g}}_{k-{\tau }_k}\parallel ={\alpha }_k.\end{array}$$

(4)

Let $k\in {\mathbb{N}}_0$ be such that $k\ge \tau .$ Combining (3) and (4) together with the nonincreasing of ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }$ yields

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel \le \sum _{i=0}^{\tau }\parallel {\mathbf{x}}_{k-i+1}-{\mathbf{x}}_{k-i}\parallel \le \sum _{i=0}^{\tau }{\alpha }_{k-i}\le \sum _{i=0}^{\tau }{\alpha }_{k-\tau }=(\tau +1){\alpha }_{k-\tau }.\end{array}$$

(5)

Furthermore, since ${lim}_{k\to \infty }{\alpha }_k=0$, we conclude that ${lim}_{k\to \infty }\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel =0.$ The proof is complete. □

Now, we are ready to prove the first convergence result in the sense of the inferior limit of the function values of the generated sequence is equal to the optimal value $f^{*}$.

Theorem 1. 

Suppose that Assumptions 1 and 2 hold. Let ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ be a sequence generated by DSSM-I and ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }$ be a nonincreasing sequence with ${lim}_{k\to \infty }{\alpha }_k=0$ and ${\sum }_{k=0}^{\infty }{\alpha }_k=\infty$. Then, we have ${lim\; inf}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}$.

Proof. 

It is obvious that ${lim\; inf}_{k\to \infty }f\left({\mathbf{x}}_k\right)\ge f^{*}$ since $f\left({\mathbf{x}}_k\right)\ge f^{*}$ for all $k\in {\mathbb{N}}_0,$ so that it is sufficient to prove that ${lim\; inf}_{k\to \infty }f\left({\mathbf{x}}_k\right)\le f^{*}.$ Now, assume to the contrary that ${lim\; inf}_{k\to \infty }f\left({\mathbf{x}}_k\right)>f^{*}.$ Then there exists $ϵ>0$ and $k_1\in {\mathbb{N}}_0$ such that $f\left({\mathbf{x}}_k\right)>f^{*}+ϵ$ for all $k\ge k_1.$ This yields that

$$\begin{array}{c}\hfill f\left({\mathbf{x}}_{k-{\tau }_k}\right)>f^{*}+ϵ\hspace{1em}\mathrm{for}\mathrm{all}k\ge k_1+\tau .\end{array}$$

(6)

On the other hand, since ${lim}_{k\to \infty }{\alpha }_k=0$ and ${lim}_{k\to \infty }\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel =0$ (from Lemma 4), there exists $k_2\in {\mathbb{N}}_0$ such that

$$\begin{array}{c}\hfill {\alpha }_k<\left({\displaystyle \frac{1}{3}}\right){\left({\displaystyle \frac{ϵ}{L}}\right)}^{{\displaystyle \frac{1}{p}}}\mathrm{and}\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel <\left({\displaystyle \frac{1}{3}}\right){\left({\displaystyle \frac{ϵ}{L}}\right)}^{{\displaystyle \frac{1}{p}}}\hspace{1em}\mathrm{for}\mathrm{all}k\ge k_2.\end{array}$$

(7)

Let ${\mathbf{x}}^{*}\in X^{*}$ and let $k\in {\mathbb{N}}_0$ be such that $k\ge N_1:=max\{k_1+\tau ,k_2\}$. Then, we obtain from Lemma 3 together with the relations (6) and (7) that for any $k\ge N_1,$

$$\begin{array}{ccc}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2& <& \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k\left({\displaystyle \frac{1}{3}}\right){\left({\displaystyle \frac{ϵ}{L}}\right)}^{{\displaystyle \frac{1}{p}}}+2{\alpha }_k\left({\displaystyle \frac{1}{3}}\right){\left({\displaystyle \frac{ϵ}{L}}\right)}^{{\displaystyle \frac{1}{p}}}-2{\alpha }_k{\left({\displaystyle \frac{ϵ}{L}}\right)}^{{\displaystyle \frac{1}{p}}}\hfill \\ & =& \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2-{\alpha }_k{\left({\displaystyle \frac{ϵ}{L}}\right)}^{{\displaystyle \frac{1}{p}}},\hfill \end{array}$$

which yields

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2<{\parallel {\mathbf{x}}_{N_1}-{\mathbf{x}}^{*}\parallel }^2-{\left({\displaystyle \frac{ϵ}{L}}\right)}^{{\displaystyle \frac{1}{p}}}\sum _{i=N_1}^k{\alpha }_i.\end{array}$$

(8)

Since ${\sum }_{k=0}^{\infty }{\alpha }_k=\infty$, we have ${\left({\displaystyle \frac{ϵ}{L}}\right)}^{{\displaystyle \frac{1}{p}}}{\sum }_{k=N_1}^{\infty }{\alpha }_k=\infty ,$ and it follows that there exists $N_2\in {\mathbb{N}}_0$ such that

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{ϵ}{L}}\right)}^{{\displaystyle \frac{1}{p}}}\sum _{i=N_1}^k{\alpha }_i>{\parallel {\mathbf{x}}_{N_1}-{\mathbf{x}}^{*}\parallel }^2\hspace{1em}\mathrm{for}\mathrm{all}k\ge N_2.\end{array}$$

(9)

Thus, for any $k\ge N:=max\{N_1,N_2\},$ we obtain from (8) and (9) that

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2<{\parallel {\mathbf{x}}_N-{\mathbf{x}}^{*}\parallel }^2-{\left({\displaystyle \frac{ϵ}{L}}\right)}^{{\displaystyle \frac{1}{p}}}\sum _{i=N}^k{\alpha }_i<0,\end{array}$$

which is a contradiction. Therefore, we can conclude that ${lim\; inf}_{k\to \infty }f\left({\mathbf{x}}_k\right)\le f^{*},$ and hence ${lim\; inf}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}$, as desired. □

Corollary 1. 

Suppose that Assumptions 1 and 2 hold. Let ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ be a sequence generated by DSSM-I, and let ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }$ be a nonincreasing sequence with ${lim}_{k\to \infty }{\alpha }_k=0$ and ${\sum }_{k=0}^{\infty }{\alpha }_k=\infty$. If the sequence ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ is bounded, then there exists a subsequence of ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ that converges to an optimal solution in $X^{*}$.

Proof. 

We first note from the fact that ${lim\; inf}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}$ in Theorem 1 together with the boundedness of the sequence ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ and the continuity of f that there exists a subsequence ${\left\{{\mathbf{x}}_{k_i}\right\}}_{i=0}^{\infty }$ of ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ such that

$$\begin{array}{c}\hfill \underset{i\to \infty }{lim}f\left({\mathbf{x}}_{k_i}\right)=\underset{k\to \infty }{lim\; inf}f\left({\mathbf{x}}_k\right)=f^{*}.\end{array}$$

(10)

Since the sequence ${\left\{{\mathbf{x}}_{k_i}\right\}}_{i=0}^{\infty }$ is also bounded, there exists a subsequence ${\left\{{\mathbf{x}}_{k_{i_j}}\right\}}_{j=0}^{\infty }$ of ${\left\{{\mathbf{x}}_{k_i}\right\}}_{i=0}^{\infty }$ such that ${lim}_{j\to \infty }{\mathbf{x}}_{k_{i_j}}=\overline{\mathbf{x}}\in {\mathbb{R}}^n.$ Again, the continuity of f and using (10) yield

$$f\left(\overline{\mathbf{x}}\right)=\underset{j\to \infty }{lim}f({\mathbf{x}}_{k_{i_j}})=\underset{i\to \infty }{lim}f\left({\mathbf{x}}_{k_i}\right)=f^{*}.$$

Note that since ${\left\{{\mathbf{x}}_{k_{i_j}}\right\}}_{j=0}^{\infty }\subset X$, the closedness of X yields $\overline{\mathbf{x}}\in X,$ which therefore implies that $\overline{\mathbf{x}}$ is an element in $X^{*}$. □

By imposing either the coercivity of the objective function f or the compactness of the constraint X, we can obtain an approximate convergence behavior and some nice convergence results in comparison to the one obtained in Theorem 1.

Theorem 2. 

Suppose that Assumptions 1 and 2 hold. Let ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ be a sequence generated by DSSM-I, and let ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }$ be a nonincreasing sequence with ${lim}_{k\to \infty }{\alpha }_k=0$ and ${\sum }_{k=0}^{\infty }{\alpha }_k=\infty$. If the function f is coercive or the constrained set X is compact, then the following statements hold:

(i)

For any $\sigma >0,$ there exists $N_{\sigma }\in {\mathbb{N}}_0$ such that

$$\begin{array}{c}\hfill \mathrm{dist}({\mathbf{x}}_k,X^{*})\le \rho \left(\sigma \right)+{\displaystyle \frac{(\tau +2){\sigma }^{\frac{1}{p}}}{2\tau +3}}\mathrm{for}\mathrm{all}k\ge N_{\sigma },\end{array}$$

where $\rho \left(\sigma \right):=max\left\{\mathrm{dist}(\mathbf{x},X^{*}):\mathbf{x}\in X\cap S_{f,f^{*}+L\sigma }^{\le }\right\}$;

(ii)

${lim}_{k\to \infty }\mathrm{dist}({\mathbf{x}}_k,X^{*})=0$, and ${lim}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}.$

Proof. 

Let $\sigma >0$ be arbitrary and denote the notation

$$\rho \left(\sigma \right):=max\left\{\mathrm{dist}(\mathbf{x},X^{*}):\mathbf{x}\in X\cap S_{f,f^{*}+L\sigma }^{\le }\right\}.$$

Since the function f is coercive or the constrained set X is compact, we ensure that $X^{*}\ne \varnothing$ which together with $X^{*}\subseteq X\cap S_{f,f^{*}+L\sigma }^{\le }$ yield that $X\cap S_{f,f^{*}+L\sigma }^{\le }\ne \varnothing .$ Moreover, the continuity and quasi-convexity of f, respectively, imply that $S_{f,f^{*}+L\sigma }^{\le }$ is closed and convex, and so the set $X\cap S_{f,f^{*}+L\sigma }^{\le }$ is also closed and convex. Again, with either the compactness of X or the coercivity of f, the intersection $X\cap S_{f,f^{*}+L\sigma }^{\le }$ is bounded, and hence, $X\cap S_{f,f^{*}+L\sigma }^{\le }$ is a compact set, which ensures that $\rho \left(\sigma \right)<\infty .$

$\left(i\right)$ Let ${\mathbf{x}}^{*}\in X^{*}$ be given. Since ${lim}_{k\to \infty }{\alpha }_k=0,$ we also have ${lim}_{k\to \infty }{\alpha }_{k-\tau }=0.$ Consequently, there exists $k_{\sigma }\in {\mathbb{N}}_0$ such that $k_{\sigma }\ge \tau$ and

$$\begin{array}{c}\hfill {\alpha }_{k-\tau }\le {\displaystyle \frac{{\sigma }^{\frac{1}{p}}}{2\tau +3}}\hspace{1em}\mathrm{for}\mathrm{all}k\ge k_{\sigma }.\end{array}$$

(11)

This together with the relation that $\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel \le (\tau +1){\alpha }_{k-\tau }$ which is obtained in Lemma 4 yield that

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel \le {\displaystyle \frac{(\tau +1){\sigma }^{\frac{1}{p}}}{2\tau +3}}\hspace{1em}\mathrm{for}\mathrm{all}k\ge k_{\sigma }.\end{array}$$

(12)

Now, we will show that

$$\begin{array}{c}\hfill \mathrm{dist}({\mathbf{x}}_{k+1},X^{*})\le max\left\{\mathrm{dist}({\mathbf{x}}_k,X^{*}),\rho \left(\sigma \right)+{\displaystyle \frac{(\tau +2){\sigma }^{\frac{1}{p}}}{2\tau +3}}\right\}\hspace{1em}\mathrm{for}\mathrm{all}k\ge k_{\sigma }.\end{array}$$

(13)

Let $k\ge k_{\sigma }$ be fixed. We divide the proof into two cases according to the behavior of $f\left({\mathbf{x}}_{k-{\tau }_k}\right)$.

Case 1: Suppose that $f\left({\mathbf{x}}_{k-{\tau }_k}\right)>f^{*}+L\sigma .$ Then we have ${\mathbf{x}}_{k-{\tau }_k}\notin X^{*}.$ Applying Lemma 3 and the nonincreasing property of the stepsize ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }$, we get

$$\begin{array}{ccc}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2& \le & \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k{\alpha }_{k-\tau }+2{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel -2{\alpha }_k{\sigma }^{{\displaystyle \frac{1}{p}}}.\hfill \end{array}$$

(14)

Substituting the inequalities (11) and (12) in (14) gives

$$\begin{array}{ccc}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2& \le & \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\displaystyle \frac{{\sigma }^{\frac{1}{p}}{\alpha }_k}{2\tau +3}}+{\displaystyle \frac{2(\tau +1){\sigma }^{\frac{1}{p}}{\alpha }_k}{2\tau +3}}-2{\alpha }_k{\sigma }^{{\displaystyle \frac{1}{p}}}\le {\parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}\parallel }^2.\hfill \end{array}$$

By putting ${\mathbf{x}}^{*}=P_{X^{*}}\left({\mathbf{x}}_k\right),$ we obtain $\mathrm{dist}({\mathbf{x}}_{k+1},X^{*})\le \mathrm{dist}({\mathbf{x}}_k,X^{*}).$

Case 2: Suppose that $f\left({\mathbf{x}}_{k-{\tau }_k}\right)\le f^{*}+L\sigma .$ Then we have ${\mathbf{x}}_{k-{\tau }_k}\in X\cap S_{f,f^{*}+L\sigma }^{\le }$ and $\mathrm{dist}({\mathbf{x}}_{k-{\tau }_k},X^{*})\le \rho \left(\sigma \right).$ We note from the definition of ${\mathbf{x}}_{k+1}=P_X({\mathbf{x}}_k-{\alpha }_k{\mathbf{g}}_{k-{\tau }_k})$ the nonexpansiveness of $P_X$ and the nonincreasing property of ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }$ that

$$\parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}\parallel \le \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}\parallel +{\alpha }_k\le \parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel +\parallel {\mathbf{x}}_{k-{\tau }_k}-{\mathbf{x}}^{*}\parallel +{\alpha }_{k-\tau },$$

which together with the inequality (11) and (12) yield

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}\parallel \le \parallel {\mathbf{x}}_{k-{\tau }_k}-{\mathbf{x}}^{*}\parallel +{\displaystyle \frac{(\tau +2){\sigma }^{\frac{1}{p}}}{2\tau +3}}.\end{array}$$

By putting ${\mathbf{x}}^{*}:=P_{X^{*}}\left({\mathbf{x}}_{k-{\tau }_k}\right)$ and invoking $\mathrm{dist}({\mathbf{x}}_{k-{\tau }_k},X^{*})\le \rho \left(\sigma \right),$ we obtain

$$\mathrm{dist}({\mathbf{x}}_{k+1},X^{*})\le \rho \left(\sigma \right)+{\displaystyle \frac{(\tau +2){\sigma }^{\frac{1}{p}}}{2\tau +3}}.$$

Thus, we proved the relation (13). By using the same analogy of Theorem 1, we obtain that ${lim\; inf}_{k\to \infty }f\left({\mathbf{x}}_{k-{\tau }_k}\right)=f^{*}$. Consequently, there exists $k_{\sigma }^{\prime }$ such that $k_{\sigma }^{\prime }\ge k_{\sigma }$ and $f\left({\mathbf{x}}_{k_{\sigma }^{\prime }-{\tau }_{k_{\sigma }^{\prime }}}\right)<f^{*}+L{\sigma }^{{\displaystyle \frac{1}{p}}}.$ Therefore, we obtain from Case 2 that

$$\begin{array}{c}\hfill \mathrm{dist}({\mathbf{x}}_{k_{\sigma }^{\prime }+1},X^{*})\le \rho \left(\sigma \right)+{\displaystyle \frac{(\tau +2){\sigma }^{\frac{1}{p}}}{2\tau +3}}.\end{array}$$

Put $N_{\sigma }:=k_{\sigma }^{\prime }+1$. Suppose that $\mathrm{dist}({\mathbf{x}}_k,X^{*})\le \rho \left(\sigma \right)+{\displaystyle \frac{(\tau +2){\sigma }^{\frac{1}{p}}}{2\tau +3}}$ for all $k\ge N_{\sigma }.$ Invoking (13), we obtain $\mathrm{dist}({\mathbf{x}}_{k+1},X^{*})\le \rho \left(\sigma \right)+{\displaystyle \frac{(\tau +2){\sigma }^{\frac{1}{p}}}{2\tau +3}}$. Hence, we conclude by the strong induction that

$$\begin{array}{c}\hfill \mathrm{dist}({\mathbf{x}}_k,X^{*})\le \rho \left(\sigma \right)+{\displaystyle \frac{(\tau +2){\sigma }^{\frac{1}{p}}}{2\tau +3}}\hspace{1em}\mathrm{for}\mathrm{all}k\ge N_{\sigma }.\end{array}$$

$\left(ii\right)$ For each $r\in \mathbb{N},$ we denote $X_{{\displaystyle \frac{1}{r}}}:=X\cap S_{f,f^{*}+L\left({\displaystyle \frac{1}{r}}\right)}^{<}.$ Observe that ${\left\{X_{{\displaystyle \frac{1}{r}}}\right\}}_{r=1}^{\infty }$ is nonincreasing and ${\bigcap }_{r\in \mathbb{N}}{X}_{{\displaystyle \frac{1}{r}}}=X\cap S_{f,f^{*}}^{\le }=X^{*}.$ Subsequently, ${\left\{\rho \left({\displaystyle \frac{1}{r}}\right)\right\}}_{r\in \mathbb{N}}$ is also nonincreasing and ${inf}_{r\in \mathbb{N}}\rho \left({\displaystyle \frac{1}{r}}\right)={inf}_{r\in \mathbb{N}}{max}_{\mathbf{x}\in X_{{\displaystyle \frac{1}{r}}}}\mathrm{dist}(\mathbf{x},X^{*})={max}_{\mathbf{x}\in X^{*}}\mathrm{dist}(\mathbf{x},X^{*})=0$. Hence, we obtain that ${lim}_{r\to \infty }\rho \left({\displaystyle \frac{1}{r}}\right)=0$.

Now, let $\epsilon >0$ be arbitrary. Since ${lim}_{r\to \infty }\left(\rho \left({\displaystyle \frac{1}{r}}\right)+{\displaystyle \frac{(\tau +2){\left(\frac{1}{r}\right)}^{\frac{1}{p}}}{2\tau +3}}\right)=0,$ there exists $M_{\epsilon }\in \mathbb{N}$ such that

$$\rho \left({\displaystyle \frac{1}{r}}\right)+{\displaystyle \frac{(\tau +2){\left(\frac{1}{r}\right)}^{\frac{1}{p}}}{2\tau +3}}<\epsilon \hspace{1em}\mathrm{for}\mathrm{all}r\ge M_{\epsilon }.$$

Since ${\displaystyle \frac{1}{M_{\epsilon }}}>0$, there exists $N\in {\mathbb{N}}_0$ such that

$$\mathrm{dist}({\mathbf{x}}_k,X^{*})\le \rho \left({\displaystyle \frac{1}{M_{\epsilon }}}\right)+{\displaystyle \frac{(\tau +2){\left(\frac{1}{M_{\epsilon }}\right)}^{\frac{1}{p}}}{2\tau +3}}<\epsilon \hspace{1em}\mathrm{for}\mathrm{all}k\ge N.$$

Hence, we conclude that ${lim}_{k\to \infty }\mathrm{dist}({\mathbf{x}}_k,X^{*})=0$. Furthermore, by Assumption 2, we therefore obtain that ${lim}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}.$ □

Remark 3. 

Under the setting of Theorem 2, we observe that if an optimal solution is unique, that is, $X^{*}=\left\{{\mathbf{x}}^{*}\right\},$ we obtain that ${lim}_{k\to \infty }\parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}\parallel ={lim}_{k\to \infty }\mathrm{dist}({\mathbf{x}}_k,X^{*})=0,$ which means that the generated sequence ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ converges to an unique solution ${\mathbf{x}}^{*}.$

3.2. Delayed Star Subgradient Method II

In order to obtain the convergence of the generated sequence, we need a modified version of DDSM-I which is defined as the following Algorithm 2.

Algorithm 2 Delayed Star Subgradient Method II (DSSM-II)

Initialization: Given a stepsize ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }\subset (0,\infty ),$ the delays ${\left\{{\tau }_k\right\}}_{k=0}^{\infty }\subset {\mathbb{N}}_0$, and initial points ${\mathbf{x}}_0,{\mathbf{x}}_{-1},{\mathbf{x}}_{-2},\dots ,$${\mathbf{x}}_{-\tau }\in X$. Iterative Step: For a current point ${\mathbf{x}}_k\in X$, if $f\left({\mathbf{x}}_k\right)=f^{*},$ we set $${\mathbf{x}}_{k+1}:={\mathbf{x}}_k$$ and then stop. If $f\left({\mathbf{x}}_k\right)>f^{*},$ we compute $${\mathbf{x}}_{k+1}:=P_X({\mathbf{x}}_k-{\alpha }_k{\mathbf{g}}_{k-{\tau }_k}),$$ where ${\mathbf{g}}_{k-{\tau }_k}\in {\partial }^{\star }f\left({\mathbf{x}}_{k-{\tau }_k}\right)\cap \mathcal{S}$ is a unit star subgradient of f at ${\mathbf{x}}_{k-{\tau }_k}$. Update: $k:=k+1$.

Remark 4. 

(i)

If the delays ${\tau }_k=0$ for all $k\in {\mathbb{N}}_0$, DSSM-II is relating to the method proposed by Hu et al. [9] (Algorithm 1) with the special setting of $m=1$.

(ii)

Note that DSSM-II involves evaluating the function value at the current iterate ${\mathbf{x}}_k\in X$ and deciding to update the next iteration ${\mathbf{x}}_{k+1}$. If the function value $f\left({\mathbf{x}}_k\right)$ equals the optimal value $f^{*}$, then no additional calculations are performed, and DSSM-II terminates so that an optimal solution is obtained at the point ${\mathbf{x}}_k$.

Next, we will derive some fundamental properties for the convergence of DSSM-II.

Lemma 5. 

Suppose that Assumption 2 holds. Let ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ be a sequence generated by DSSM-II. For any $k\in {\mathbb{N}}_0$ and ${\mathbf{x}}^{*}\in X^{*}$, if $f\left({\mathbf{x}}_k\right)>f^{*},$ then

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2\le \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k^2+2{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel -2{\alpha }_k{L}^{-{\displaystyle \frac{1}{p}}}{\left(f\left({\mathbf{x}}_{k-{\tau }_k}\right)-f^{*}\right)}^{{\displaystyle \frac{1}{p}}}.\end{array}$$

Proof. 

Let ${\mathbf{x}}^{*}\in X^{*}$ and $k\in {\mathbb{N}}_0$. Suppose that $f\left({\mathbf{x}}_k\right)>f^{*}$. We have from the definition of DSSM-II that ${\mathbf{x}}_{k+1}=P_X({\mathbf{x}}_k-{\alpha }_k{\mathbf{g}}_{k-{\tau }_k})$. Moreover, since $f\left({\mathbf{x}}_k\right)>f^{*},$ we also have $f\left({\mathbf{x}}_{k-{\tau }_k}\right)>f^{*}.$ Thus, by following the proving lines of Lemma 3, we obtain

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2\le \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k^2+2{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel -2{\alpha }_k{L}^{-{\displaystyle \frac{1}{p}}}{\left(f\left({\mathbf{x}}_{k-{\tau }_k}\right)-f^{*}\right)}^{{\displaystyle \frac{1}{p}}},\end{array}$$

as desired. □

Theorem 3. 

Suppose that Assumptions 1 and 2 hold. Let ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ be a sequence generated by DSSM-II, and let ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }\subset (0,\infty )$ be a nonincreasing sequence with ${lim}_{k\to \infty }{\alpha }_k=0$ and ${\sum }_{k=0}^{\infty }{\alpha }_k=\infty$. Then, we have $\parallel {\mathbf{x}}_{k-{\tau }_k}-{\mathbf{x}}_k\parallel \le (\tau +1){\alpha }_{k-\tau }$ for all $k\ge \tau$, ${lim}_{k\to \infty }\parallel {\mathbf{x}}_{k-{\tau }_k}-{\mathbf{x}}_k\parallel =0$, and ${lim\; inf}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}.$

Proof. 

By invoking Lemma 5, we can prove the same analog of Lemma 4 and Theorem 1 to obtain ${lim\; inf}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}.$ □

Theorem 4. 

Suppose that Assumptions 1 and 2 hold. Let ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ be a sequence generated by DSSM-II, and let ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }\subset (0,\infty )$ be a nonincreasing sequence with ${\sum }_{k=0}^{\infty }{\alpha }_k=\infty$ and ${\sum }_{k=0}^{\infty }{\alpha }_k^2<\infty .$ Then the sequence ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ converges to an optimal solution in $X^{*}$ and, moreover, ${lim}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}.$

Proof. 

If there exists $K\in {\mathbb{N}}_0$ such that $f\left({\mathbf{x}}_K\right)=f^{*}$, we have that ${\mathbf{x}}_K$ is an optimal solution and ${\mathbf{x}}_k={\mathbf{x}}_K$ for all $k\ge K.$ Consequently, we obtain ${lim}_{k\to \infty }{\mathbf{x}}_k={\mathbf{x}}_K\in X^{*}$ and ${lim}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}$ as required.

On the other hand, we suppose that $f\left({\mathbf{x}}_k\right)>f^{*}$ for all $k\in {\mathbb{N}}_0.$ Let $k\in {\mathbb{N}}_0$ and let ${\mathbf{x}}^{*}\in X^{*}.$ We note from Lemma 5 that

$$\begin{array}{ccc}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2& \le & \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k^2+2{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel -2{\alpha }_k{L}^{-{\displaystyle \frac{1}{p}}}{\left(f\left({\mathbf{x}}_{k-{\tau }_k}\right)-f^{*}\right)}^{{\displaystyle \frac{1}{p}}}\hfill \\ & \le & \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k^2+2{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel .\hfill \end{array}$$

Let us admit from the inequalities (3) and (4) that $\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel \le {\sum }_{i=0}^{\tau }\parallel {\mathbf{x}}_{k-i+1}-{\mathbf{x}}_{k-i}\parallel$ and $\parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}_k\parallel \le {\alpha }_k$ for all $k\in {\mathbb{N}}_0.$ Thus, for a fixed $N\in {\mathbb{N}}_0$, we have

$$\begin{array}{ccc}\hfill \sum _{k=0}^N{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel & \le & \sum _{k=0}^N{\alpha }_k\sum _{i=0}^{\tau }\parallel {\mathbf{x}}_{k-i+1}-{\mathbf{x}}_{k-i}\parallel \hfill \\ & =& \sum _{i=0}^{\tau }\sum _{k=-i}^{N-i}{\alpha }_{k+i}\parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}_k\parallel \le \sum _{i=0}^{\tau }\sum _{k=0}^N{\alpha }_{k+i}\parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}_k\parallel \le \sum _{i=0}^{\tau }\sum _{k=0}^N{\alpha }_{k+i}{\alpha }_k,\hfill \end{array}$$

which together with the nonincreasing property of ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }$ implies

$$\begin{array}{c}\hfill \sum _{k=0}^N{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel \le \sum _{i=0}^{\tau }\sum _{k=0}^N{\alpha }_k^2=(\tau +1)\sum _{k=0}^N{\alpha }_k^2.\end{array}$$

(15)

By approaching $N\to \infty$ in (15) and using the assumption that ${\sum }_{k=0}^{\infty }{\alpha }_k^2<\infty$, we obtain that ${\sum }_{k=0}^{\infty }{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel <\infty$, and so

$$\sum _{k=0}^{\infty }\left({\alpha }_k^2+2{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel \right)<\infty .$$

Therefore, the sequence ${\left\{x_k\right\}}_{k=0}^{\infty }$ is quasi-Fejer monotone. By applying Fact 2, we obtain that the sequence ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ is bounded and ${lim}_{k\to \infty }\parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}\parallel$ exists.

Since the sequence ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ is bounded and ${lim\; inf}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}$ (Theorem 3), there exists a subsequence ${\left\{{\mathbf{x}}_{k_i}\right\}}_{i=0}^{\infty }$ of ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ such that

$$\begin{array}{c}\hfill \underset{i\to \infty }{lim}f\left({\mathbf{x}}_{k_i}\right)=\underset{k\to \infty }{lim\; inf}f\left({\mathbf{x}}_k\right)=f^{*}.\end{array}$$

Since ${\left\{{\mathbf{x}}_{k_i}\right\}}_{i=0}^{\infty }$ is also bounded, there exists a subsequence ${\left\{{\mathbf{x}}_{k_{i_j}}\right\}}_{j=0}^{\infty }$ of ${\left\{{\mathbf{x}}_{k_i}\right\}}_{i=0}^{\infty }$ such that ${lim}_{j\to \infty }{\mathbf{x}}_{k_{i_j}}=\overline{\mathbf{x}}\in {\mathbb{R}}^n$. Thus, the continuity of f yields

$$\begin{array}{c}\hfill f\left(\overline{\mathbf{x}}\right)=\underset{j\to \infty }{lim}f({\mathbf{x}}_{k_{i_j}})=\underset{i\to \infty }{lim}f\left({\mathbf{x}}_{k_i}\right)=f^{*}.\end{array}$$

Moreover, the closeness of X implies $\overline{\mathbf{x}}\in X$, and hence we obtain that $\overline{\mathbf{x}}\in X^{*}.$ Since ${lim}_{k\to \infty }\parallel {\mathbf{x}}_k-\overline{\mathbf{x}}\parallel$ exists and ${lim}_{j\to \infty }\parallel {\mathbf{x}}_{k_{i_j}}-\overline{\mathbf{x}}\parallel =0$, we conclude that ${lim}_{k\to \infty }\parallel {\mathbf{x}}_k-\overline{\mathbf{x}}\parallel =0$. Moreover, invoking the continuity of f, we also have that ${lim}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}.$ The proof is complete. □

We end the convergence analysis of DSSM-II by investigating the finite convergence of the generated sequence as the following theorem.

Theorem 5. 

Suppose that Assumptions 1 and 2 hold and $\mathcal{B}({\mathbf{x}}^{*};\delta )\subset X^{*}$ for some $\delta >0.$ Let ${\left\{{\mathbf{x}}_k\right\}}_{k=0}^{\infty }$ be a sequence generated by DSSM-II. If one of the following statements holds:

(i) 

${\alpha }_k=\alpha \in \left(0,{\displaystyle \frac{2\delta }{2\tau +3}}\right)$ for all $k\in {\mathbb{N}}_0;$

(ii) 

${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }$ is nonincreasing with ${lim}_{k\to \infty }{\alpha }_k=0$ and ${\sum }_{k=0}^{\infty }{\alpha }_k=\infty$,

then there exists $K\in {\mathbb{N}}_0$ such that ${\mathbf{x}}_K\in X^{*}$.

Proof. 

We suppose by contradiction that ${\mathbf{x}}_k\notin X^{*}$ for all $k\in {\mathbb{N}}_0$. This implies ${\mathbf{x}}_{k-{\tau }_k}\notin X^{*}$ for all $k\in {\mathbb{N}}_0$. Note that $\parallel {\mathbf{x}}^{*}+\delta {\mathbf{g}}_{k-{\tau }_k}-{\mathbf{x}}^{*}\parallel \le \delta$, which implies that ${\mathbf{x}}^{*}+\delta {\mathbf{g}}_{k-{\tau }_k}\in \mathcal{B}({\mathbf{x}}^{*};\delta )\subset X^{*}.$ Since ${\mathbf{x}}_{k-{\tau }_k}\notin X^{*}$, we have $f({\mathbf{x}}^{*}+\delta {\mathbf{g}}_{k-{\tau }_k})<f\left({\mathbf{x}}_{k-{\tau }_k}\right).$ Thus, by the definition of the star subgradient of f at ${\mathbf{x}}_{k-{\tau }_k}$, we obtain that

$$\begin{array}{c}\hfill ⟨{\mathbf{g}}_{k-{\tau }_k},{\mathbf{x}}^{*}+\delta {\mathbf{g}}_{k-{\tau }_k}-{\mathbf{x}}_{k-{\tau }_k}⟩\le 0,\end{array}$$

which yields

$$\begin{array}{c}\hfill ⟨{\mathbf{g}}_{k-{\tau }_k},{\mathbf{x}}_{k-{\tau }_k}-{\mathbf{x}}^{*}⟩\ge \delta .\end{array}$$

(16)

On the other hand, since ${\mathbf{x}}_k\notin X^{*},$ we have from the definition of DSSM-II that ${\mathbf{x}}_{k+1}=P_X({\mathbf{x}}_k-{\alpha }_k{\mathbf{g}}_{k-{\tau }_k})$, and the nonexpansive property of $P_X$ implies that

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2\le \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k^2+2{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel -2{\alpha }_k⟨{\mathbf{g}}_{k-{\tau }_k},{\mathbf{x}}_{k-{\tau }_k}-{\mathbf{x}}^{*}⟩,\end{array}$$

which combining (16), leads to

$$\begin{array}{c}\hfill \parallel {\mathbf{x}}_{k+1}-{\mathbf{x}}^{*}{\parallel }^2\le \parallel {\mathbf{x}}_k-{\mathbf{x}}^{*}{\parallel }^2+{\alpha }_k^2+2{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel -2{\alpha }_k\delta .\end{array}$$

(17)

Let N be a fixed non-negative integer. By summing up (17) from $k=0$ to $k=N$, we have

$$\begin{array}{c}\hfill 0\le \parallel {\mathbf{x}}_0-{\mathbf{x}}^{*}{\parallel }^2+\sum _{k=0}^N{\alpha }_k^2+2\sum _{k=0}^N{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel -2\delta \sum _{k=0}^N{\alpha }_k,\end{array}$$

which implies

$$\begin{array}{c}\hfill \delta \le {\displaystyle \frac{\parallel {\mathbf{x}}_0-{\mathbf{x}}^{*}{\parallel }^2}{2{\sum }_{k=0}^N{\alpha }_k}}+{\displaystyle \frac{{\sum }_{k=0}^N{\alpha }_k^2}{2{\sum }_{k=0}^N{\alpha }_k}}+{\displaystyle \frac{{\sum }_{k=0}^N{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel }{{\sum }_{k=0}^N{\alpha }_k}}.\end{array}$$

(18)

Based on the conditions (i) and (ii), we will divide our consideration into two cases.

Case 1: Assume that ${\alpha }_k=\alpha \in (0,{\displaystyle \frac{2\delta }{2\tau +3}})$ for all $k\in {\mathbb{N}}_0.$

Let us note from (15) that

$$\begin{array}{c}\hfill \sum _{k=0}^N{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel \le \sum _{i=0}^{\tau }\sum _{k=0}^N{\alpha }_k^2=(\tau +1)(N+1){\alpha }^2.\end{array}$$

Thus, we have

$$\begin{array}{ccc}& & \underset{N\to \infty }{lim}\left({\displaystyle \frac{\parallel {\mathbf{x}}_0-{\mathbf{x}}^{*}{\parallel }^2}{2{\sum }_{k=0}^N{\alpha }_k}}+{\displaystyle \frac{{\sum }_{k=0}^N{\alpha }_k^2}{2{\sum }_{k=0}^N{\alpha }_k}}+{\displaystyle \frac{{\sum }_{k=0}^N{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel }{{\sum }_{k=0}^N{\alpha }_k}}\right)\hfill \\ & \le & \underset{N\to \infty }{lim}\left({\displaystyle \frac{\parallel {\mathbf{x}}_0-{\mathbf{x}}^{*}{\parallel }^2}{2(N+1)\alpha }}+{\displaystyle \frac{\alpha }{2}}+(\tau +1)\alpha \right)\hfill \\ & =& {\displaystyle \frac{(2\tau +3)\alpha }{2}}<\delta ,\hfill \end{array}$$

which is a contradiction to the inequality (18).

Case 2: Assume that ${\left\{{\alpha }_k\right\}}_{k=0}^{\infty }$ is a nonincreasing sequence with ${lim}_{k\to \infty }{\alpha }_k=0$ and ${\sum }_{k=0}^{\infty }{\alpha }_k=\infty$. We obtain from Theorem 3 that ${lim}_{k\to \infty }\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel =0$. Thus, we finally obtain from the fact that ${lim}_{k\to \infty }{\alpha }_k=0$ and ${\sum }_{k=0}^{\infty }{\alpha }_k=\infty$ and ${lim}_{k\to \infty }\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel =0$ with Lemma 1 that

$$\begin{array}{c}\hfill \underset{N\to \infty }{lim}\left({\displaystyle \frac{\parallel {\mathbf{x}}_0-{\mathbf{x}}^{*}{\parallel }^2}{2{\sum }_{k=0}^N{\alpha }_k}}+{\displaystyle \frac{{\sum }_{k=0}^N{\alpha }_k^2}{2{\sum }_{k=0}^N{\alpha }_k}}+{\displaystyle \frac{{\sum }_{k=0}^N{\alpha }_k\parallel {\mathbf{x}}_k-{\mathbf{x}}_{k-{\tau }_k}\parallel }{{\sum }_{n=0}^N{\alpha }_k}}\right)=0,\end{array}$$

which also contradicts to the inequality (18). □

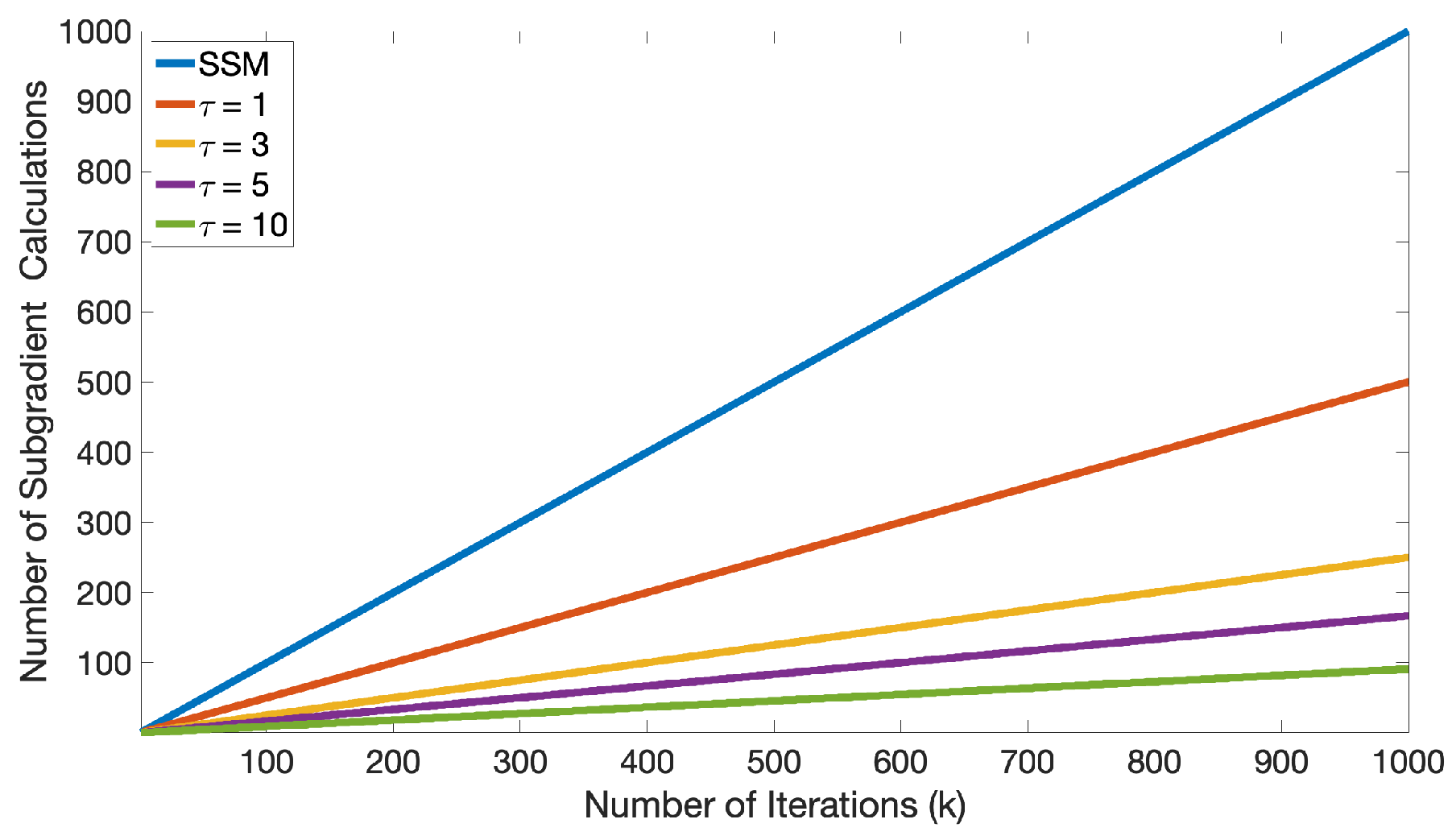
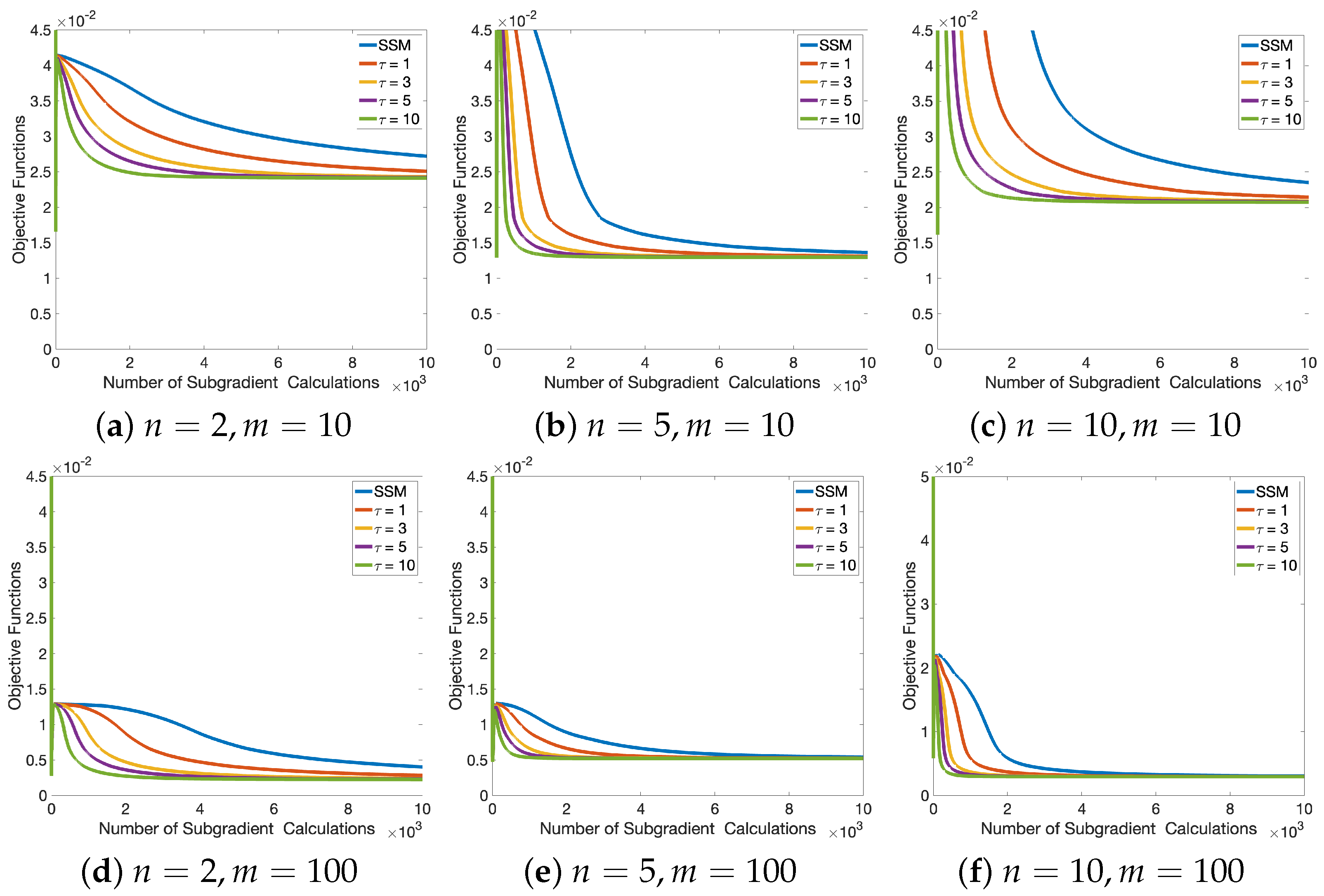
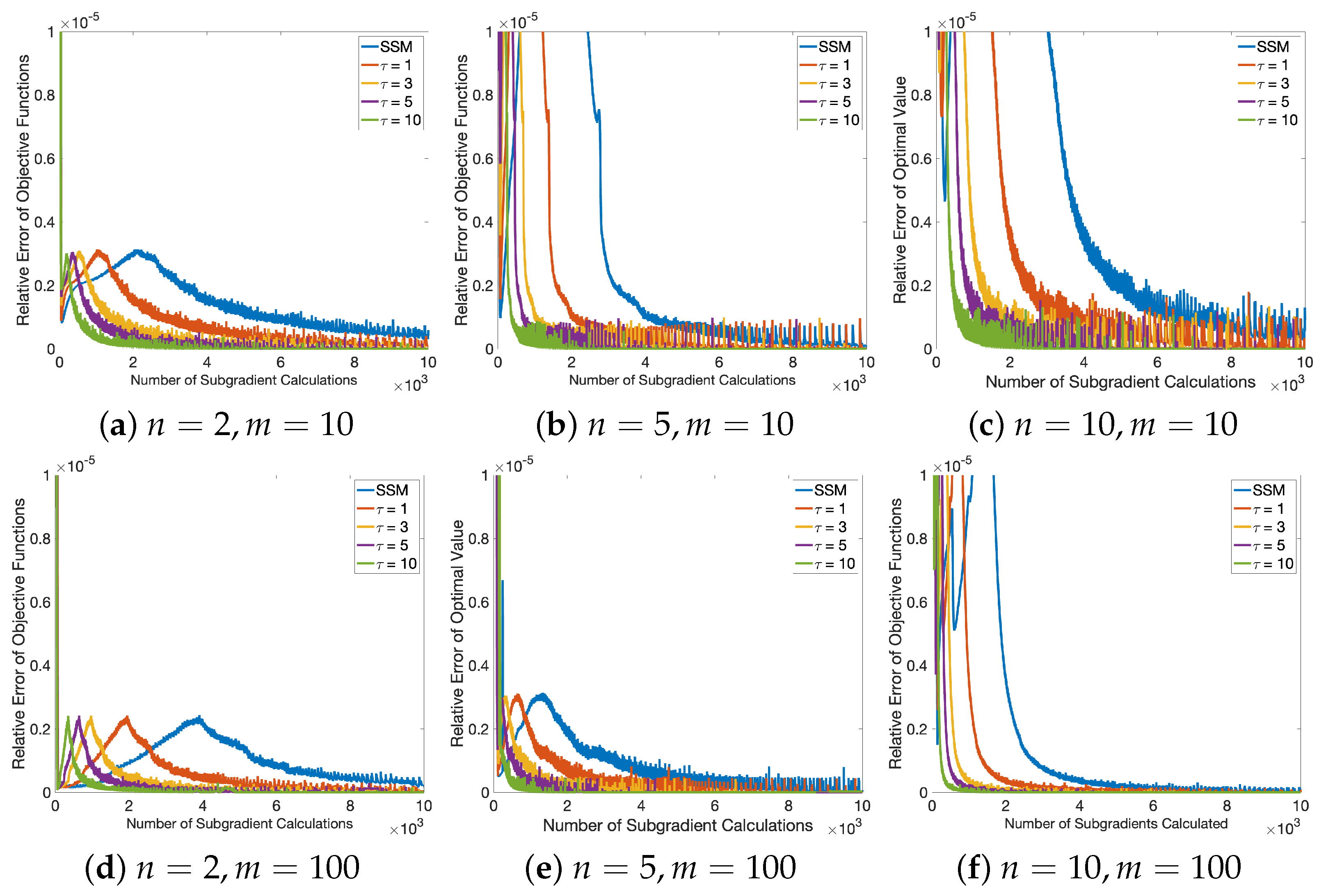
4. Numerical Experiments

In this section, we present experimental results when we apply DSSM-I to solve the Cobb–Douglas production efficiency problem. We performed all experiments on MATLAB (R2023b) on a MacBook Air 13.3-inch with Apple M1 chip processor and 8GB memory.

The Cobb–Douglas production efficiency problem [3,6,12] aims to maximize the ratio of the total profit represented by the Cobb–Douglas product function and the total cost represented by the linear function on the product factor subject to the funding level limitations constraint. More precisely, let $a_0,c_0>0$ and let $a_j,b_{ij},c_j,p_i\ge 0$ for all $j=1,2,\dots ,n$ and $i=1,2,\dots ,m,$ and the Cobb–Douglas production efficiency problem is defined by

$$\begin{array}{c}\hfill \begin{array}{cc}\mathrm{maximize}\hspace{1em}\hfill & f\left(\mathbf{x}\right):={\displaystyle \frac{a_0{\prod }_{j=1}^n{x}_j^{a_j}}{{\sum }_{j=1}^n{c}_j{x}_j+c_0}}\hfill \\ \mathrm{subject}\mathrm{to}\hspace{1em}\hfill & \sum _{j=1}^n{b}_{ij}{x}_j\ge p_i,i=1,2,\dots ,m\hfill \\ & x_j\ge 0,j=1,2,\dots ,n,\hfill \end{array}\end{array}$$

(19)

where ${\sum }_{j=1}^n{a}_j=1.$ Here, $\mathbf{x}:=(x_1,x_2,\dots ,x_n)\in {\mathbb{R}}^n$ when $x_j$ is the j-th product factor $(j=1,2,\dots ,n)$, and for each $i=1,2,\dots ,m$, $p_i$ is the profit to be obtained from project i, and $b_{ij}$ is the support of product factor j to project i to achieve $p_i$. According to the literature [6,12], we know that the Cobb–Douglas production efficiency problem (19) is a quasi-convex optimization problem. Note that the function f is continuous and quasi-concave [4] (Theorem 2.5.1), satisfying the Hölder condition on ${\mathbb{R}}^n$ [12] (Appendix B), and the constraint set $C:={\bigcap }_{i=1}^m\{\mathbf{x}\in {\mathbb{R}}^n:⟨{\mathbf{b}}_i,\mathbf{x}⟩\ge p_i\}\cap {[0,\infty )}^n$ is the nonempty closed convex set, where ${\mathbf{b}}_i:={(b_{i1},\dots ,b_{in})}^T$ is a vector in ${\mathbb{R}}^n$. Therefore, we can apply DSSM-I to solve the problem (19). However, since the exact optimal solution to problem (19) is not known, we are unable to apply DSSM-II to solve it. To ensure the boundedness of the constrained set, we set the constrained set to be the set $D:=\{\mathbf{x}\in {\mathbb{R}}^n:⟨{\mathbf{b}}_i,\mathbf{x}⟩\ge p_i\}\cap {[0.001,100]}^n$ which is a subset of C. Thus, the established convergence result from Theorem 2 guarantees that ${lim}_{k\to \infty }f\left({\mathbf{x}}_k\right)=f^{*}.$ It is worth noting that the computational procedure of the metric projection onto the constrained set D is not an easy task since there is no explicit form of $P_D$ in general. To deal with the situation, we utilized the classical Halpern iteration by performing the following inner loop: for arbitrary initial point ${\mathbf{u}}_l\in {\mathbb{R}}^n$ and a sequence ${\left\{{\lambda }_l\right\}}_{l=0}^{\infty }\subseteq (0,1)$ such that ${lim}_{l\to \infty }{\lambda }_l=0,{\sum }_{l=0}^{\infty }{\lambda }_l=\infty ,\mathrm{and}{\sum }_{l=1}^{\infty }|{\lambda }_{l+1}-{\lambda }_l|<\infty ,$ we compute

$${\mathbf{u}}_{l+1}:={\lambda }_l({\mathbf{x}}_k-{\alpha }_k{\mathbf{g}}_{k-{\tau }_k})+(1-{\lambda }_l)P_{D_{m+1}}{P}_{D_m}{P}_{D_{m-1}}\cdots P_{D_1}{\mathbf{u}}_l\mathrm{for}\mathrm{all}l\ge 1,$$

where $D_{m+1}={[0.001,100]}^n$, $D_i:=\{\mathbf{x}\in {\mathbb{R}}^n:⟨{\mathbf{b}}_i,\mathbf{x}⟩\ge p_i\}$ for all $i=1,2,\dots ,m.$ Then the sequence ${\left\{{\mathbf{u}}_l\right\}}_{l=0}^{\infty }$ converges to the unique point $P_D({\mathbf{x}}_k-{\alpha }_k{\mathbf{g}}_{k-{\tau }_k})$, see [28] (Theorem 30.1) for further details. In our experiment, we put the inner initial point ${\mathbf{u}}_0$ as the vector whose all coordinates are 1 and set ${\lambda }_l:={\displaystyle \frac{1}{l+2}}$ for all $l\in {\mathbb{N}}_0.$ We use the stopping criterion ${\displaystyle \frac{\parallel {\mathbf{u}}_{l+1}-{\mathbf{u}}_l\parallel }{\parallel {\mathbf{u}}_l\parallel +1}}\le {10}^{-6}$ for the inner loop.

To perform the numerical experiments, we randomly set the parameter $a_j,b_{ij}\in (0,1),a_0,c_0,c_j\in (0,10),\mathrm{and}{p}_i\in \left(0,{\displaystyle \frac{n}{2}}\right).$ We choose the stepsize and time-varying delays to be ${\alpha }_k:={\displaystyle \frac{1}{k+1}}$ and ${\tau }_k:=kmod\left(\tau +1\right)$ for all $k\in {\mathbb{N}}_0,$ respectively. We put the initial point ${\mathbf{x}}_0$ as the vector whose all coordinates are 1. To explain the influence of the delay bound $\tau$, we perform Algorithm DSSM-I for delay bounds $\tau =0,1,3,5,$ and 10 for various sizes of the problem n and m. Note that DSSM-I with $\tau =0$ is nothing else than the star subgradient method (SSM) proposed by Kiwiel [1]. Figure 1 illustrates the number of subgradient calculations performed by SSM and DSSM-I with the delay strategies ${\tau }_k:=kmod(\tau +1)$ for all $k\in {\mathbb{N}}_0$.

Figure 1. Behaviors of a number of subgradint calculations for various delays bounds $\tau$ versus number of iterations.

The average results of the 10 random data sets are presented in Figure 2 and Figure 3 below.

Figure 2. Behaviors of objective function values for various delays bounds $\tau$ and problem sizes n and m.

Figure 3. Behavior of relative errors for various delay bounds $\tau$ and problem sizes n and m.

It can be observed from Figure 2 that, overall, all the results show a similar pattern as they approach the (approximated) optimal value as supported by Theorem 2. For each subfigure, we notice that the result of $\tau =10$ seems stable and decreases faster than other $\tau$.

Next, we plot the relative errors of the objective functions values in the same setting as above in Figure 3.

It can be seen from Figure 3 that all results seem to decrease and stabilize. More precisely, the graph exhibits fluctuations that are alternating decreases and increases in small periods. These fluctuations gradually diminish and vanish to stabilize. Again, this behavior satisfies the convergence result of DSSM-I, and we notice that the results with $\tau =10$ seems to decrease rapidly to 0 compared to other values of $\tau$.

5. Conclusions

In this work, we proposed the so-called projected star subgradient methods with delayed subgradient updates, namely DSSM-I and DSSM-II, for solving the constrained quasi-convex optimization problem. For DSSM-I, we proved that there exists a subsequence of the generated sequence that converges to an optimal solution provided that the boundedness of the generated sequence is imposed. Furthermore, under the compactness or the coercive assumption with the diminishing step size, we proved that the distance between the sequence and the optimal solution set $X^{*}$ converges to zero, resulting in the convergence of the objective function values to the optimal value. For the modified version as DSSM-II and without requiring the compactness or coercive assumptions, we proved that the generated sequence converges to an optimal solution. We also established the finite convergence provided that the interior of the optimal solution set $X^{*}$ is nonempty. Finally, we applied DSSM-I to solve the Cobb–Douglas production efficiency problem. It is worth noting that the proposed methods can reduce the computational costs of star subgradients by allowing the method to retrieve stale data instead. It is noted that since we could not indicate the precise upper bound on the number of times the star subgradient could be reused, the open problem with this topic still remains. Moreover, one can notice that we require the closed-form expression of the metric projection onto the constraint set X and overcome this obstacle by solving the sub-problem to approximate $P_X$ at each iteration. This also motivated us to consider a future direction that involves a method that does not require solving a sub-problem.