DRFAN: A Lightweight Hybrid Attention Network for High-Fidelity Image Super-Resolution in Visual Inspection Applications

Abstract

Single-image super-resolution (SISR) plays a critical role in enhancing visual quality for real-world applications, including industrial inspection and embedded vision systems. While deep learning-based approaches have made significant progress in SR, existing lightweight SR models often fail to accurately reconstruct high-frequency textures, especially under complex degradation scenarios, resulting in blurry edges and structural artifacts. To address this challenge, we propose a Dense Residual Fused Attention Network (DRFAN), a novel lightweight hybrid architecture designed to enhance high-frequency texture recovery in challenging degradation conditions. Moreover, by coupling convolutional layers and attention mechanisms through gated interaction modules, the DRFAN enhances local details and global dependencies with linear computational complexity, enabling the efficient utilization of multi-level spatial information while effectively alleviating the loss of high-frequency texture details. To evaluate its effectiveness, we conducted ×4 super-resolution experiments on five public benchmarks. The DRFAN achieves the best performance among all compared lightweight models. Visual comparisons show that the DRFAN restores more accurate geometric structures, with up to +1.2 dB/+0.0281 SSIM gain over SwinIR-S on Urban100 samples. Additionally, on a domain-specific rice grain dataset, the DRFAN outperforms SwinIR-S by +0.19 dB in PSNR and +0.0015 in SSIM, restoring clearer textures and grain boundaries essential for industrial quality inspection. The proposed method provides a compelling balance between model complexity and image reconstruction fidelity, making it well-suited for deployment in resource-constrained visual systems and industrial applications.

1. Introduction

Single-image super-resolution (SISR) [1], a pivotal task in low-level computer vision, focuses on reconstructing high-resolution images from their degraded low-resolution counterparts by restoring missing texture details and improving visual fidelity. However, the inherent diversity in image styles and content often leads to varying degrees of information degradation during reconstruction, particularly in preserving and enhancing intricate spatial features. The proliferation of deep learning techniques has driven significant advancements in this domain, with numerous advanced SR approaches being developed to address these reconstruction challenges.

Convolutional neural networks (CNNs) [2,3,4,5,6,7,8,9,10] are the earliest deep learning architectures widely adopted in image processing. The CNN-based method has the characteristics of inductive bias, including localized receptive fields, translation invariance, and hierarchical spatial representations. It can achieve robust performance even with limited training data. CNN-based SISR models excel in capturing local features through these intrinsic properties and weight-sharing mechanisms, thereby notably improving texture reconstruction in degraded images. Despite these strengths, they also inherit the limitation of CNNs in capturing long-range dependencies, resulting in insufficient modeling of distant feature relationships and inability to better enhance the overall image details.

Transformer [11] is celebrated for its robust capacity to model long-range dependencies and has progressively emerged as a prominent research focus in computer vision. Transformer-based SISR models [12,13,14,15,16] address the inherent limitation of CNNs in capturing global dependencies by leveraging the self-attention mechanism to capture global dependencies and model interactions across distant spatial positions. However, the quadratic computational complexity O(N²) associated with the self-attention mechanism necessitates considerably higher computational resources, particularly hindering the processing of high-resolution images. To mitigate this challenge, researchers have introduced a window-based self-attention mechanism [17]. This approach divides the input image into multiple local windows for parallel computation to alleviate the complexity, while the incorporation of sliding window attention further augments the global modeling capacity. Despite the fact that sliding window strategies further enhance inter-window communication, it remains insufficient for comprehensively modeling long-range dependencies, ultimately detracting from the quality of image reconstruction, especially in preserving fine-grained structural coherence.

To overcome these challenges, researchers have progressively investigated several innovative mechanisms, such as linear attention [18] and Mamba [19]. Linear attention reformulates traditional self-attention by linearly decomposing the dot-product operations between query (Q) and key (K) features, effectively reducing computational complexity from O(N²) to O(N). While this approach mitigates computational overhead, it compromises the model’s capacity to capture comprehensive global contextual dependencies, resulting in unstable performance across diverse tasks and data distributions. Mamba, an architecture derived from state space models [20,21,22], integrates the complementary strengths of recurrent neural networks [23,24] and convolutional neural networks. This hybridization preserves its ability to model long-range dependencies while achieving substantial computational efficiency gains. However, its multi-directional scanning strategy is limited in non-autoregressive tasks, and issues such as local pixel forgetting and channel redundancy impede its pixel-level accuracy in image super-resolution. The Mamba-like linear attention (MLLA) model [25] addresses these limitations by establishing a theoretical bridge between Mamba and linear attention, effectively combining the parallel processing efficiency of linear attention with the adaptive feature selection capability of SSM. Operating at linear complexity O(N), MLLA selectively prioritizes critical detail features during reconstruction. Crucially, it circumvents the recursive computation demands of SSM’s forget gates, thereby eliminating a key bottleneck in high-resolution image processing. This framework represents a paradigm shift, balancing computational tractability with enhanced reconstruction precision.

In order to solve the problem of image artifacts and contour blurring in the high-frequency detail reconstruction of existing lightweight methods in complex degraded scenes, this study proposes a novel hybrid architecture lightweight SR network designed to enhance texture detail reconstruction while maintaining a low parameter count. The Dense Residual Fused Attention Network (DRFAN) integrates the Mamba-like linear attention (MLLA) module and Grid Attention Block (GAB) to synergize global contextual modeling with localized feature refinement. Furthermore, it employs dense residual connections to mitigate spatial information loss and channel redundancy in deep networks. Compared with mainstream lightweight models, the DRFAN achieves substantial improvements in reconstructing fine-grained details under constrained parameter budgets. The primary contributions of this paper are as follows:

• We propose the DRFAN, a novel lightweight SISR framework that innovatively integrates the MLLA module and GAB into a unified hybrid architecture. This design enables dynamic multi-scale feature selection through parallel processing mechanisms, reduces channel redundancy, and establishes cross-layer global context modeling pathways, ensuring robust global representation capabilities.
• We introduce the GAB module to extend pixel interaction beyond local regions via a hierarchical interaction strategy. By leveraging structural similarity priors between image patches, it optimizes spatial information aggregation efficiency, significantly enhancing the reconstruction of high-frequency textures and fine-grained details.
• We design a tightly coupled residual framework to synergize the advantages of convolutional local feature extraction, the long-range dependency modeling capability of self-attention, and the efficient computational characteristics of Mamba. This complementary feature fusion mechanism achieves the coordinated optimization of these three core operations.
• Experimental results on multiple benchmark SR datasets demonstrate that the DRFAN shows significant advantages in SISR tasks and industrial inspection scenarios, offering an efficient and reliable solution for practical applications.

To address the limitations of existing lightweight super-resolution methods in reconstructing high-frequency textures under complex degradation, this study proposes several key innovations. First, we introduce the DRFAN, a hybrid architecture that tightly couples convolutional operations, Mamba-like linear attention, and a Grid Attention Block within a dense residual framework. Second, we replace traditional Multi-Layer Perception layers in attention modules with Spatial Gated Feedforward Networks (SGFNs), enhancing spatial modeling capacity and reducing channel redundancy. Third, through the complementary fusion of local, global, and sequential features, our design enables dynamic multi-scale feature selection with strong generalization capabilities. These innovations collectively advance both the theoretical framework and practical deployment feasibility for high-fidelity and efficient image super-resolution.

The remainder of this paper is organized as follows: Section 2 reviews related works in lightweight and hybrid SR networks. Section 3 details the architecture of the proposed DRFAN model. Section 4 presents experimental setup, evaluation metrics, and both quantitative and qualitative results. Section 5 discusses the model’s characteristics, limitations, and application scenarios. Section 6 concludes this study and outlines potential future work.

2. Related Work

2.1. Lightweight Single-Architecture Super-Resolution Network

In recent years, numerous studies have prioritized developing SR models that balance performance and efficiency under such resource-constrained conditions. Conventional approaches typically adopt single-architecture networks, which rely on monolithic architectures (CNN or Transformer) and attempt to achieve lightweight designs through architectural refinements and component-level innovations.

In the early stages of research, scholars focused on lightweight design strategies for convolutional neural networks. SRCNN [3] is the first CNN-based framework for single-image super-resolution. FSRCNN [4] eliminated preprocessing-stage interpolation by operating directly on low-resolution inputs, significantly accelerating training. VDSR [5] and EDSR [6] both drew on the principles of residual learning to accelerate model convergence and enhance training efficiency. The emergence of attention mechanisms has partially alleviated the CNN’s receptive field limitations. RCAN [26] enhanced feature representation by integrating residual channel attention. HAN [27] combined layer-wise and channel–spatial attention to comprehensively model inter-feature dependencies, achieving notable performance gains. With the rise of vision Transformers [28], researchers have begun integrating Transformer-based global modeling into lightweight SISR designs. SwinIR [12] combined local feature modeling with global attention via a sliding-window mechanism, reducing complexity while enhancing reconstruction fidelity.

While single-architecture SR networks offer simplicity and ease of optimization, relying on a singular technical approach can expose inherent limitations. These shortcomings have paved the way for the development of hybrid architectures.

2.2. Lightweight Hybrid Architecture Super-Resolution Network

Hybrid architectures synergize multiple technical approaches. They employ strategies that integrate local feature extraction with global dependency modeling, achieving performance breakthroughs under lightweight constraints.

Early hybrid frameworks predominantly adopted CNN backbones augmented with attention modules to enhance feature selectivity. For example, CBAM [29] fused channel and spatial attention mechanisms to prioritize critical information in feature maps. SAN [30] introduced second-order channel attention and non-locally enhanced residual groups to concurrently capture long-range dependencies and local textures. LatticeNet [31] drew inspiration from lattice filter theory, proposing lattice blocks with multi-scale attention to amplify feature discriminability. As researchers began to recognize the limitations of Transformers, researchers increasingly explore hybrid architectures combining CNNs and Transformers. ESRT [14] reduced the computational complexity of self-attention by using group-wise attention, which limited attention computation within local feature groups. SAFMN [32] enhanced VIT blocks with a spatial adaptive feature modulation mechanism for dynamic feature selection. The emergence of the Mamba architecture has provided further solutions for SISR tasks. DVMSR [33] integrates Mamba with knowledge distillation to optimize inference speed without sacrificing performance.

In addition, several recent studies explore hybrid frameworks combining Mamba and Transformers to enhance low-level vision tasks. For example, Contrast [34] proposed a dual-branch design integrating SSM and a vision Transformer for image restoration. MatIR [35] introduced a Mamba–Transformer fusion model to balance expressiveness and efficiency. In the SR domain, FAMSR [36] incorporated frequency priors into a Mamba-based network to improve detail recovery in remote sensing images, while MPSI [37] leveraged pixel-wise sequential interaction to enhance positional context modeling. MambaCSR [38] adopted a dual-interleaved scan mechanism with Mamba to handle severe compression artifacts. Although these models do not prioritize lightweight design, they highlight the growing trend of combining convolution, attention, and structured state modeling.

Hybrid architectures now demonstrate clear superiority over single-paradigm approaches, emerging as a focal research area. In this context, we propose a dense residual fusion architecture that effectively combines the advantages of convolutional operations, attention mechanisms, and the Mamba architecture. This framework enables efficient multi-level spatial information fusion and effectively mitigates high-frequency texture degradation.

3. Materials and Methods

The overall structure of the DRFAN is illustrated in Figure 1 and primarily comprises three parts: shallow feature extraction, deep feature extraction, and image reconstruction. Specifically, the deep feature extraction module (referred to as the DRFG network) is composed of multiple Mamba-like linear attention (MLLA) blocks, a Grid Attention Block (GAB) [39], and residual structures. We will elaborate on these methods in the following sections.

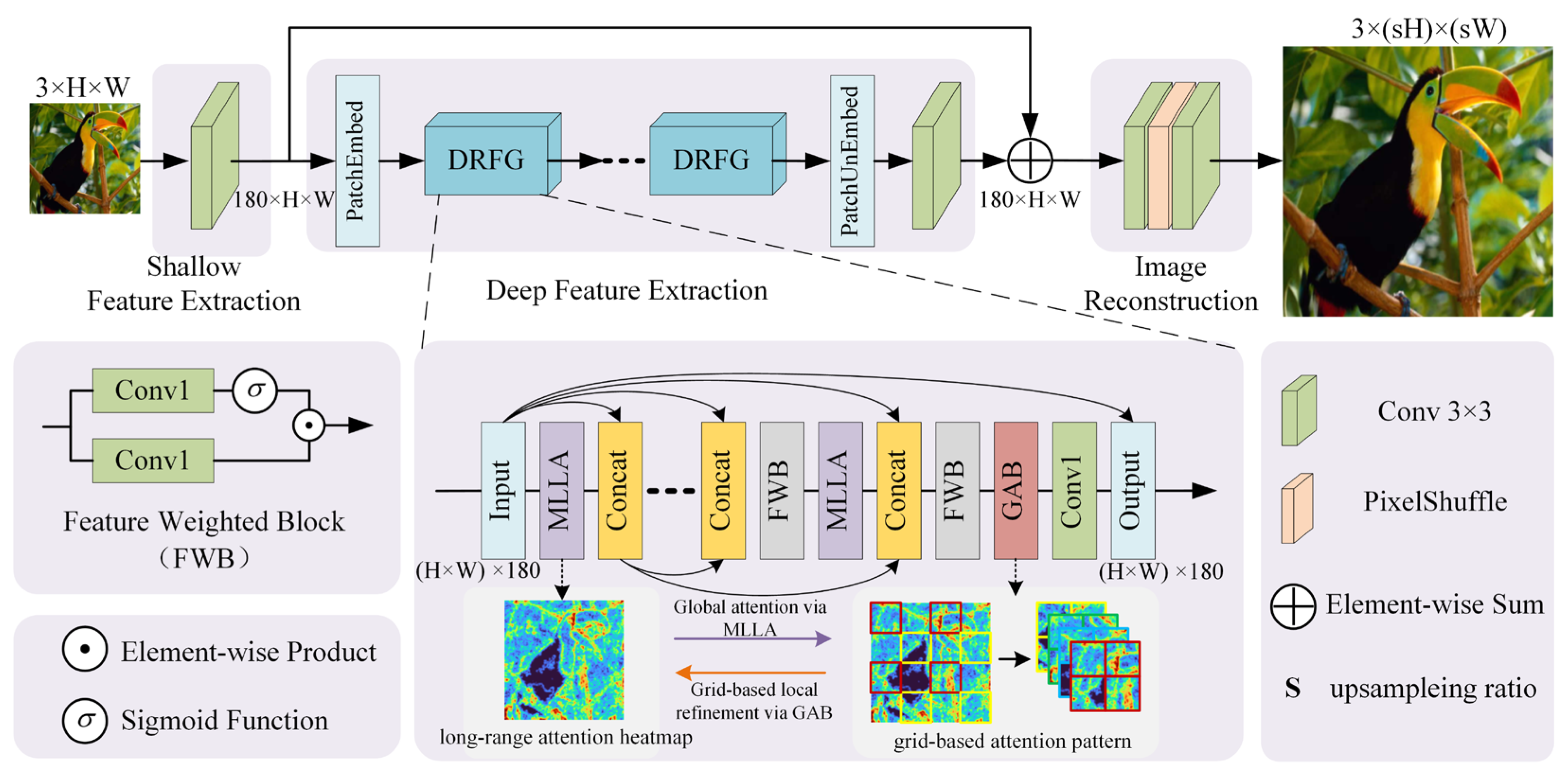
3.1. Overall Architecture

Given a low-resolution image $I_{LR}\in R^{H\times W\times C_{in}}$, $H$, $W$, and $C_{in}$ represent the height, width, and number of channels of the input image, respectively. $I_{LR}$ is processed through a $3\times 3$ convolutional network that extracts basic visual features like edges, textures, and colors, mapping it to a higher-dimensional feature space $F_0\in R^{H\times W\times C}$; it can be formulated as follows:

$$F_0=H_{SF}\left(I_{LR}\right),$$

(1)

where $H_{SF}(·)$ denotes the shallow feature extraction network. $C$ represents the number of channels in the intermediate feature space $F_0$ with $C\gg C_{in}$. Subsequently, $F_0$ is passed to the deep feature extraction network, where it undergoes multiple Dense Residual Fused Blocks to extend the shallow features into global structural and semantic levels, thus enabling the learning of deeper high-level visual features $F_{DF}\in R^{H\times W\times C}$. The Dense Residual Fused Block (DRFG) is composed of several Mamba-like linear attention blocks (MLABs), a Grid Attention Block (GAB) and residual connections. The computation process can be formulated as follows:

$$F_{DF}=H_{DF}\left(F_0\right),$$

(2)

where $H_{DF}(·)$ denotes the deep feature extraction network, composed of N groups of DRFGs and a $3\times 3$ convolutional layer. The computation process of deep feature extraction is formulated as follows:

$$F_i=H_{{DRFB}_i}\left(F_{i-1}\right),i=1,2,\dots ,N,$$

(3)

$$F_{DF}=H_{Conv}\left(F_N\right),$$

(4)

where $H_{{DRFB}_i}(·)$ represents each DRFG. $F_1$, $F_2$, …, $F_i$, as well as $F_{DF}$ are the intermediate features extracted by the network. $H_{Conv}(·)$ denotes a single $3\times 3$ convolutional layer. After aggregating shallow features $F_0$ and deep features $F_{DF}$ via a global residual connection, the super-resolution image $I_{SR}\in R^{H\times W\times C_{in}}$ is reconstructed by an upsampling operation. The reconstruction process can be formalized as follows:

$$I_{SR}=H_{Re}\left(F_0+F_{DF}\right),$$

(5)

where $H_{Re}(·)$ denotes the image reconstruction function, consisting of $3\times 3$ convolution layers and a sub-pixel convolution layer.

3.2. Dense Residual Fused Group (DRFG)

Many studies have demonstrated promising performance in SISR tasks by leveraging dense residual connections. This provides us with a valuable approach. Our approach repeatedly reuses intermediate feature maps across network stages while applying adaptive feature weighting to suppress channel redundancy. This strategy not only expands the effective receptive field but also enhances feature discriminability through hierarchical refinement.

Each DRFG integrates four MLLA modules and one GAB. The MLLA modules dynamically refine the model’s focus through adaptive feature selection, enabling multi-level spatial information extraction via iterative feature reuse. This process progressively expands and enhances the effective receptive field while capturing rich contextual dependencies. Subsequently, the GAB aggregates these multi-scale features while preserving critical high-frequency details. These two modules will be described in detail in subsequent sections. By integrating MLLA, GAB, and dense residual connections, our framework dynamically adapts its focus regions based on global contextual inputs. This enables cross-scale information integration, long-range dependency capture, and the adaptive fusion of global-local features, achieving comprehensive feature extraction essential for high-fidelity super-resolution. For an input feature map M, the computation process of each DRFG is as follows:

$$M_j=F_{MLLA}\left(F_{FWB}\left(\left[F_{MLLA}\left(M\right),\dots ,M_{j-1}\right]\right)\right),j=\mathrm{1,2},\mathrm{3,4},$$

(6)

$$F_{output}=F_{GAB}\left(M_4\right)+M,$$

(7)

where $[·]$ denotes the concatenation of multi-level features from preceding layers. $F_{MLLA}(·)$ and $F_{GAB}(·)$ denotes each MLLA layer and $F_{GAB}(·)$ GAB layer, respectively. Here, M denotes the input feature map to the DRFG block, which is passed via residual connection to later stages (e.g., GAB) to enhance feature continuity and gradient propagation. It is not a tunable parameter, but a reused intermediate representation. $F_{FWB}(·)$ represents a Feature Weighted Block designed to suppress redundant information that accumulates during dense concatenation. It consists of two parallel 1 × 1 convolutional layers, where one branch is followed by a sigmoid activation. Their outputs are fused via element-wise multiplication to produce channel-wise adaptive weights. This effectively learns a relevance score for each channel based on its contribution to the global context. Channels with lower activation are likely to carry redundant or low-utility information and are therefore attenuated by the learned gating weights. This process allows the network to maintain compact and discriminative feature representations throughout the DRFG module.

3.3. Mamba-like Linear Attention (MLLA) Block

3.3.1. Unified SSM Gating and Linear Attention Framework

We draw upon the successful design of the MLLA mechanism, originally applied in image classification, and extend it to SISR, as illustrated in Figure 2. MLLA fundamentally integrates the complementary strengths of linear attention and Selective State Space Models (SSMs), while systematically addressing the limitations of standard self-attention in terms of scalability and temporal modeling.

Linear attention reformulates traditional self-attention by replacing the softmax normalization with linear kernel approximations, reducing the complexity from $O(N²)$ to $O\left(N\right)$. This enables efficient pairwise interaction modeling across long sequences, but lacks mechanisms for adaptive memory control or forgetting.

$$h_i={\tilde{A}}_i⨀h_{i-1}+B_i({∆}_i⨀x_i),$$

(8)

$$y_i=C_i{h}_i/1+D⨀x_i,$$

(9)

where $h_i$ is the internal hidden state at time step $i$; ${\tilde{A}}_i$ acts as a forget gate, regulating how much of the past state $h_{i-1}$ is retained; ${∆}_i$ serves as an input gate, determining the strength of the current input $x_i$; and $D⨀x_i$ provides a residual connection from input to output.

This gated recurrence can be conceptually aligned with the linear attention formulation:

$$S_i=1⨀S_{i-1}+K_i^{\top }\left(1⨀V_i\right),$$

(10)

$$y_i={\displaystyle \frac{Q_i{S}_i}{Q_i{Z}_i}}+0⨀x_i.$$

(11)

In this form, $S_i$ serves as a memory accumulator, similar to the hidden state in Equation (8), and the unnormalized additive accumulation reflects the recursive nature of SSM. However, unlike SSM, linear attention typically lacks forgetting, gating, and residual memory control.

MLLA bridges this gap by embedding the SSM’s gating logic into the linear attention framework. Specifically, the forget gate ${\tilde{A}}_i$ corresponds to a learnable decay that modulates $h_{i-1}$, similar to selective memory decay; the input gate ${∆}_i$ modulates the contribution of the current input $x_i$, enhancing dynamic input selection; the residual connection $D⨀x_i$ preserves low-level features, stabilizing gradient flow. The derivation of MLLA from SSM is shown in Figure 3.

This unified structure enables efficient sequence modeling with explicit mechanisms for structured forgetting and input integration—features absent in traditional linear attention. MLLA thus operates as a gated linear attention method, retaining the scalability of attention while embedding SSM-like memory control, making it particularly suitable for tasks like image super-resolution, where both local recurrence and long-range dependency are essential.

3.3.2. Computational Optimization and Spatial Gating Enhancement

MLLA overcomes Transformer’s computational bottlenecks in long-range dependency modeling by unifying SSMs with linear attention. Through further model optimization, MLLA not only enhances computational efficiency but also preserves strong modeling capabilities, making it suitable for training on large-scale datasets and tackling complex tasks. The computational workflow is formalized as follows:

$$F_1=\sigma \left(\mathcal{L}\left(DwConv\left(x\right)\right)\right),$$

(12)

$$F_2=\sigma \left(\mathcal{L}\left(x\right)\right),$$

(13)

$$F_{atten}=LinearAttention\left(F_1\right),$$

(14)

$$F_{output}=\mathcal{L}\left(F_{atten}\odot F_2\right),$$

(15)

where $x$ and $DwConv(·)$ denote the raw features of the input sequence and depthwise convolution, respectively. $\mathcal{L}(·)$ and $\sigma (·)$ represent the linear transformation and SiLU activation function, respectively. $\odot$ represents the Hadamard (element-wise) product.

We replace the MLP layers in each MLLA module with a Spatial Gated Feedforward Network [40], as illustrated in Figure 3c. The SGFN addresses the limited spatial modeling capacity of conventional feedforward networks by incorporating a spatial gating mechanism that regulates channel-wise information flow. For an input feature $X\in R^{H\times W\times C}$, the SGFN operation is defined as follows:

$$X^{\prime }=\sigma \left(W_p^{1}X\right),\left[X_1^{\prime },X_2^{\prime }\right]=X^{\prime },$$

(16)

$$SGFN\left(X\right)=W_p^2\left(X_1^{\prime }\odot \left(W_d{X}_2^{\prime }\right)\right),$$

(17)

where $W_p^1$ and $W_p^2$ denote the learnable weights of the first and second linear projection layers, respectively. $\sigma$ denotes the GELU activation function. $W_d$ denotes the parameters of the depthwise convolution layer. $X_1^{\prime },X_2^{\prime }\in R^{H\times W\times {\displaystyle \frac{C\prime }{2}}}$, where $C\prime$ denotes the SGFN’s hidden dimension.

Unlike conventional FFNs that apply uniform transformations across spatial dimensions, the SGFN decouples spatial and channel processing. It introduces a spatial gating mechanism and deep convolution to better capture nonlinear spatial information, reducing channel redundancy in fully connected layers, thereby enhancing the model’s expressive capacity. Specifically, the adaptive feature weighting implemented by the SGFN suppresses channel redundancy by applying a depthwise convolution-based gating to one half of the channel-split features. This allows the network to selectively retain informative channels while filtering out less significant ones, especially those that contribute little to spatial structure reconstruction. The remaining channels are directly bypassed and concatenated with the gated features, enabling lightweight yet expressive aggregation.

It is worth noting that our use of the MLLA block represents a domain-level adaptation rather than a direct reuse. Originally designed for image classification and long-sequence modeling, MLLA has not been applied to the SISR task to the best of our knowledge. In this work, we are the first to integrate MLLA into a lightweight super-resolution framework, enabling efficient global context modeling for pixel-level restoration tasks. Furthermore, we introduce an architectural refinement by replacing the conventional MLP component in MLLA with a SGFN. This modification improves spatial feature selectivity and supports more stable attention distribution under high-resolution inputs. Our ablation study in

Table 1. Ablation experiments on SGFN and GAB, with the average PSNR/SSIM evaluated on benchmark datasets under a ×4 scale factor. The best and second-best results are highlighted in red and blue, respectively.

Model	MLP	SGFN	GAB	Params (K)	Set5 PSNR (dB) /SSIM	Set14 PSNR (dB) /SSIM	BSD100 PSNR (dB) /SSIM	Urban100 PSNR (dB) /SSIM	Manga109 PSNR (dB) /SSIM
A	√			1035	32.19/0.8944	28.58/0.7809	27.58/0.7362	25.95/0.7811	30.37/0.9064
B		√		1087	32.30/0.8959	28.67/0.7830	27.61/0.7374	26.14/0.7863	30.62/0.9089
C	√		√	952	32.16/0.8944	28.54/0.7806	27.56/0.7356	25.89/0.7789	30.34/0.9058
D		√	√	1057	32.30/0.8960	28.65/0.7831	27.63/0.7381	26.19/0.7882	30.67/0.9100

shows that the combination of this domain adaptation and structural enhancement leads to consistent improvements in PSNR and SSIM across multiple datasets.

3.4. Grid Attention Block (GAB)

3.4.1. Local Attention Enhancement via GAB

The MLLA module demonstrates notable advantages in capturing global contextual information, yet exhibits relative limitations in processing local features. To address this deficiency, we integrate a self-attention mechanism into each DRFG for local feature enhancement. When Swin Transformer is applied to super-resolution tasks, its reliance on a limited pixel range within local windows hinders its ability to fully leverage the image’s self-similarity for reconstruction. So, we adopt an approach that bolsters long-range dependency modeling by utilizing the Grid Attention Block to expand the pixel interaction range, as illustrated in Figure 4.

Specifically, the input feature map ${\mathrm{F}}_{\mathrm{i}\mathrm{n}}\in {\mathrm{R}}^{\mathrm{H}\times \mathrm{W}\times \mathrm{C}}$ is partitioned into $K^2$ groups based on an interval size $K$, each containing ${\displaystyle \frac{H}{K}}\times {\displaystyle \frac{W}{K}}$ patches. $K$ controls the number of spatial grid partitions, determining the granularity of localized attention. After performing a grid shuffle to rearrange the feature map $F_G\in R^{{\displaystyle \frac{H}{K}}\times {\displaystyle \frac{W}{K}}\times C}$, self-attention is computed within each group. The computation process can be formulated as follows:

$$\widehat{X}=SoftMax\left({\displaystyle \frac{G{K}^{\top }}{d}}+B\right)V,$$

(18)

$$Attention\left(Q,G,\widehat{X}\right)=SoftMax\left({\displaystyle \frac{Q{G}^{\top }}{d}}+B\right)\widehat{X},$$

(19)

where $G\in R^{{\displaystyle \frac{H}{K}}\times {\displaystyle \frac{W}{K}}\times C}$ denotes the global interaction features. $Q,K,V$ are obtained from the feature map $F_G$. $\widehat{X}$ represents intermediate features generated through self-attention computation. The scalar $d$ is a normalization factor used in scaled dot-product attention, following common Transformer practice, and is typically set to the square root of the feature dimension.

The GAB facilitates cross-region similarity modeling for enhanced image reconstruction while employing a post-normalization strategy to improve network training stability. The GAB architecture comprises a grid-MSA layer and an SGFN layer. The computational workflow of GAB is expressed as follows:

$$F_M=LN\left(Grid-MSA\left(F_{in}\right)\right)+F_{in},$$

(20)

$$F_{out}=LN\left(SGFN\left(F_M\right)\right)+F_M,$$

(21)

where $Grid-MSA(·)$ denotes the $\mathrm{G}\mathrm{r}\mathrm{i}\mathrm{d}$ multi-head attention mechanism. $LN(·)$ represents Layer Normalization. Compared with Batch Normalization, Layer Normalization effectively prevents undesirable impacts on image contrast and color characteristics during model training.

3.4.2. Complexity Analysis and Efficiency Optimization

For the quadratic complexity problem existing in GAB, we have carried out some optimization processing operations. And we conducted a computational complexity analysis on Swin Transformer and GAB. The Swin Transformer attention mechanism operates within local windows of size $M\times M$, leading to a complexity of the following:

$${\mathcal{O}}_{swin}=HWC+HW{M}^2.$$

(22)

By contrast, the proposed GAB computes attention over $K^2$ grid groups, each containing ${\displaystyle \frac{H}{K}}\times {\displaystyle \frac{W}{K}}$ tokens. Its computational complexity is as follows:

$${\mathcal{O}}_{GAB}=2HWC+{\displaystyle \frac{H^2{W}^2}{K^2}}.$$

(23)

While GAB enables richer long-range interactions beyond the local window constraints of the Swin Transformer, the quadratic term may raise concerns for high-resolution inputs. To mitigate this, we introduce a Top-k token selection strategy within each group: before applying attention, we select the most salient $k\ll {\displaystyle \frac{H}{K}}\times {\displaystyle \frac{W}{K}}$ tokens based on activation strength. This effectively reduces the complexity to approximately the following:

$${\mathcal{O}}_{Top-kGAB}=HWC+HWk$$

(24)

with $k$ being a small constant, yielding linear complexity with respect to image size, and making GAB applicable to high-resolution super-resolution tasks.

Although the underlying self-attention mechanism in GAB remains conceptually unchanged, we refine its structure by replacing the conventional MLP with SGFN, and further enhance its efficiency through the Top-k token selection scheme. These two enhancements work synergistically: SGFN improves local spatial reasoning, while Top-k attention reduces redundancy and accelerates computation. As confirmed by the ablation experiments in Table 1, GAB alone may slightly degrade performance due to overgeneralized attention, but its effectiveness is fully restored when paired with SGFN and the proposed Top-k optimization, demonstrating the importance of both selective interaction and structural coupling.

4. Experiments

4.1. Datasets

Our model was trained from scratch using the DF2K dataset, comprising two established components: DIV2K [41] and Flickr2K [41]. The DIV2K provides 800 high-quality training images, while Flickr2K contributes 2650 images encompassing broader scene diversity. To generate low-resolution image for training, we implement bicubic downsampling via MATLAB R2022b with scaling factors of ×4. Post-training evaluation was conducted across five benchmark datasets for single-image super-resolution, including Set5 [42], Set14 [43], BSD100 [44], Urban100 [45], and Manga109 [46]. This totals 328 images used in each evaluation experiment.

To further highlight the effectiveness of our model, we also validated it using rice images collected from a real processing environment. This domain-specific collection contains 10 high-resolution rice images, each with a resolution of 4096 × 2160. The dataset comprises images of polished round-grain rice, polished long-grain rice, and semi-polished long-grain rice, among the semi-polished images including some substandard grains such as broken rice and chalky rice. Although the number of images is limited, each image contains hundreds to thousands of densely packed rice grains with significant intra-image diversity. The grains often appear adhered or overlapping, forming complex texture patterns that pose challenges for local structure reconstruction. Unlike public datasets with diverse scenes and backgrounds, this dataset was acquired under controlled conditions (uniform lighting, background, and camera settings), ensuring high consistency while preserving grain-level variability. To facilitate the execution of the SR task, each image was partitioned into LR patches of size 512 × 240, ensuring smooth model operation during testing.

Through experiments on these datasets, we have validated the superior performance of our model across various scenarios.

4.2. Metrics

The evaluation metrics are the peak signal-to-noise ratio (PSNR) and the structural similarity index (SSIM) [47], both computed on the Y channel in the converted YCbCr color space. The PSNR measures the ratio between the image signal and noise, reflecting the level of distortion introduced by image compression. The quality of image reconstruction is assessed by comparing the differences between original and compressed images. The higher PSNR value indicates better reconstruction quality.

The SSIM evaluates the similarity between two images by comparing their luminance, contrast, and structure. Importantly, the SSIM emphasizes the structural information that includes the spatial relationships among pixels, rather than merely the differences in pixel values. SSIM values typically range from 0 to 1, with values closer to 1 indicating greater similarity between the images. Compared to the PSNR, the SSIM better aligns with the human visual perception of image quality.

4.3. Implementation Details

In our proposed model, the deep feature extraction network consists of six Dense Residual Fused Groups. Each DRFG is composed of five MLLA modules, one GAB, and residual connections. The number of heads is set to six, the input channel number C is configured to sixty, the window size used in the GAB is sixteen, and the interaction interval is set to four. All hyperparameters in our framework were selected through a grid search on the DF2K training set. The selection aims to balance performance and efficiency under lightweight constraints. While these settings work well on standard benchmarks, minor adjustments may be necessary when transferring the model to datasets with significantly different image characteristics.

4.4. Training Setting

All experiments were conducted on a single NVIDIA RTX 4080 GPU using PyTorch 2.1.2 as the primary deep learning framework. During training, the model was trained with a patch size of 64 × 64 and a batch size of 32. Data augmentation was performed on the input image patches via random horizontal flipping and rotation. The training process spanned 500K iterations, during which the Adam optimizer was employed to minimize the L1 loss function (β₁ = 0.9, β₂ = 0.999). The initial learning rate was set to 2 × 10⁻⁴ and a multi-step learning scheduler was used, reducing the learning rate by half at 250K, 400K, 450K, and 475K iterations to achieve optimal training performance.

4.5. Ablation Study

To evaluate the effectiveness of individual components in the proposed DRFAN framework, we conduct a series of ablation experiments focusing on three core modules: SGFN, GAB, and the MLLA block. These experiments aim to quantify each module’s contribution to performance and analyze how their interactions influence the model’s overall accuracy and efficiency. All experiments are carried out under the same training settings, using architectures with comparable parameter counts to ensure fair and meaningful comparisons.

We consider four model variants for ablation. Model A: a baseline architecture using MLLA blocks with standard MLPs, without SGFN or GAB; Model B: replaces MLPs in MLLA blocks with SGFN modules, preserving the overall structure; Model C: adds the GAB module to Model A while retaining MLPs; Model D (Proposed): integrates both SGFN and GAB modules into the network.

To further enhance the efficiency of GAB and adapt it to lightweight settings, we incorporate a Top-k token selection strategy within the GAB module. This mechanism allows the model to focus attention computation on the most informative spatial regions, thereby suppressing the quadratic complexity typically associated with attention maps in GAB. The Top-k strategy enables sparse attention with minimal performance loss, aligning with our design goal of achieving a favorable trade-off between accuracy and computational efficiency.

Quantitative results of these four model variants are presented in Table 1, with evaluations conducted on five standard super-resolution benchmarks under a fixed ×4 upscaling factor.

(1)

Efficacy of SGFN Module

As shown in Table 1, Model B consistently outperforms the baseline Model A across all datasets, with only a slight increase in parameter count. The most notable gain is observed on Urban100, where the PSNR improves from 25.95 dB to 26.14 dB and the SSIM improves by 0.0052. This highlights the SGFN’s strength in structured feature generation and its ability to better capture local geometric and textural patterns. The substitution of MLP with the SGFN proves beneficial in dense residual contexts, reducing channel redundancy and enhancing representational capacity.

(2)

Efficacy of GAB Module

The ablation results in Table 1 show that adding the GAB alone (Model C) slightly degrades performance compared to the baseline (Model A), suggesting that the GAB’s effectiveness depends on its integration strategy rather than any inherent flaw. As a grid-based attention mechanism, the GAB introduces patch partitioning and spatial reordering, which may misalign with standard MLP processing, especially under lightweight constraints.

When the GAB is combined with the SGFN (Model D), the network achieves the best overall performance. This improvement stems from the SGFN’s ability to provide structured spatial gating, which complements the GAB by maintaining local consistency and guiding feature fusion after attention redistribution.

These findings highlight that the synergy between the GAB and SGFN is crucial—the SGFN not only stabilizes the attention pathway but also enables the GAB to operate effectively within a lightweight architecture. We have revised the manuscript to reflect this context-dependent relationship more accurately.

(3)

Qualitative Analysis and Error Map Visualization

To visually support the above observations, we present super-resolution results from models A–D on the Urban100 dataset (e.g., img_005 and img_076) in Figure 5. As seen in the visual comparison, Model D yields sharper edges, clearer line structures, and a better preservation of fine textures compared to the other variants.

Additionally, we include error maps in Figure 6 to highlight pixel-wise differences from the ground truth. These maps confirm that Model D minimizes reconstruction errors in structurally complex regions, especially near edges and intersections. In contrast, Models A and C display more dispersed and higher-magnitude error zones. The error maps thus serve as strong visual evidence for the improved accuracy and structure fidelity achieved by combining the SGFN and GAB.

4.6. Benchmark Comparisons on Public Datasets

4.6.1. Quantitative Analysis

To evaluate the effectiveness of our algorithm, we conduct comprehensive ×4 super-resolution comparisons between the DRFAN and other mainstream lightweight super-resolution models (with a total parameter count of less than 2M) on five benchmark test datasets, including SRCNN [3], FSRCNN [4], VDSR [5], EDSR-baseline [6], CARN [7], IMDN [8], RFDN [9], LatticeNet [31], LAPAR-A [48], EMASRN [49], SMSR [50], DeFiAN [51], ShuffleMixer [52], SAFMN [32], DIPNet [53], GASSL-B [54], and DVMSR [33]. Their results are shown in

Table 2. Quantitative comparisons on benchmark datasets under a ×4 scale factor, where the best and second-best results are highlighted in red and blue, respectively. FLOPs is calculated with a 1280 × 720 GT image.

Methods	Params (K)	FLOPs (G)	Set5 PSNR (dB)/ SSIM	Set14 PSNR (dB)/ SSIM	BSD100 PSNR (dB)/ SSIM	Urban100 PSNR (dB)/ SSIM	Manga109 PSNR (dB)/ SSIM
SRCNN [3]	57	52.7	30.48/0.8628	27.49/0.7503	26.90/0.7101	24.52/0.7221	27.66/0.8505
FSRCNN [4]	12	4.6	30.71/0.8657	27.59/0.7535	26.98/0.7150	24.62/0.7280	27.90/0.8517
VDSR [5]	665	612.6	31.35/0.8838	28.01/0.7674	27.29/0.7251	25.18/0.7524	28.83/0.8809
EDSR-baseline [6]	1518	114.0	32.09/0.8938	28.58/0.7813	27.57/0.7357	26.04/0.7849	30.35/0.9067
CARN [7]	1592	90.9	32.13/0.8937	28.60/0.7806	27.58/0.7349	26.07/0.7837	-/-
IMDN [8]	715	40.9	32.21/0.8948	28.58/0.7811	27.56/0.7353	26.04/0.7838	30.45/0.9075
RFDN [9]	550	23.9	32.24/0.8952	28.61/0.7819	27.57/0.7360	26.11/0.7858	30.58/0.9089
LatticeNet [31]	777	43.6	32.18/0.8943	28.61/0.7812	27.57/0.7355	26.14/0.7844	30.54/0.9075
LAPAR-A [48]	659	94.0	32.15/0.8944	28.61/0.7818	27.61/0.7366	26.14/0.7871	30.42/0.9074
EMASRN [49]	546	-	32.17/0.8948	28.57/0.7809	27.55/0.7351	26.01/0.7938	30.41/0.9076
SMSR [50]	1006	57.2	32.12/0.8932	28.55/0.7808	27.55/0.7351	26.11/0.7868	-/-
DeFiAN [51]	1065	12.8	32.16/0.8942	28.63/0.7810	27.58/0.7363	26.10/0.7862	30.59/0.9084
ShuffleMixer [52]	411	28.0	32.21/0.8953	28.66/0.7827	27.61/0.7366	26.08/0.7835	30.65/0.9093
SAFMN [32]	240	14.0	32.18/0.8949	28.60/0.7813	27.58/0.7359	25.97/0.7809	30.43/0.9063
DIPNet [53]	543	72.97	32.20/0.8950	28.58/0.7811	27.59/0.7364	26.16/0.7879	30.53/0.9087
DVMSR [33]	424	19.67	32.19/0.8955	28.61/0.7823	27.58/0.7379	26.03/0.7838	30.48/0.9084
GASSL-B [54]	694	39.9	32.17/0.8950	28.66/0.7835	27.62/0.7377	26.16/0.7888	30.70/0.9100
DRFAN (ours)	1057	65.1	32.30/0.8960	28.65/0.7831	27.63/0.7381	26.19/0.7882	30.67/0.9100

.

The experimental results indicate that our model achieves superior performance across all evaluation metrics, demonstrating particular strength in reconstructing high-frequency details under complex degradation scenarios. Specifically, compared to the runner-up models on the Set5, BSD100, Urban100, and Manga109 test datasets, our model improves PSNR/SSIM by 0.06 dB/0.0005, 0.02 dB/0.0002, 0.03 dB/0.0003, and 0.02 dB/0.0007, respectively.

We further analyze the computational efficiency of the DRFAN by comparing the parameter count and FLOPs with mainstream lightweight super-resolution models, as shown in Table 2. The DRFAN achieves consistently competitive or superior performance across most benchmark datasets, with a relatively moderate computational footprint of 1057K parameters and 65.1G FLOPs. While the DRFAN outperforms models like RFDN (550K, 23.9G) and IMDN (715K, 40.9G) in PSNR and SSIM, it also delivers comparable or better reconstruction quality than highly compact models such as SAFMN (240K, 14.0G) and DVMSR (424K, 19.67G), though at the cost of higher complexity. In particular, although GASSL-B surpasses the DRFAN in PSNR by a narrow margin on Set14 and Manga109, the DRFAN still maintains the best SSIM scores on all five benchmarks. Overall, these results highlight that the DRFAN achieves a favorable trade-off between reconstruction accuracy and computational demand, making it suitable for high-fidelity SR tasks under constrained resources.

4.6.2. Qualitative Experiments

We perform visual comparisons of our method with CARN, IMDN, SwinIR-S, ShuffleMixer, and SAFMN on the Urban100 dataset under a ×4 scaling factor, with detailed visualizations for samples img_011, img_024, and img_092 presented in Figure 7.

In terms of reconstructing image texture details, the advantages of our method are clearly evident across these images. For instance, in the image generated by our algorithm (img_011), the PSNR/SSIM metrics improved by 1.2 dB/0.0281 compared to SwinIR-S. The lines in our result appear notably straighter, whereas those generated by other methods tend to be more distorted. A similar observation can be made for img_024. In the case of img_092, our algorithm achieves PSNR and SSIM improvements of 0.31 and 0.0084 compared to SwinIR-S, respectively. The horizontal and vertical lines by our model are closer to the original image, in contrast to other methods that convert originally vertical lines into slanted ones. These experimental results demonstrate that our model is capable of more comprehensively and accurately restoring high-frequency texture details in complex degradation scenarios, while also effectively suppressing artifacts and distortions.

To further visualize structural reconstruction accuracy, we provide corresponding error maps in Figure 8. These maps show the pixel-wise absolute differences between the predicted SR images and ground truth. As seen in the error maps, the DRFAN produces minimal red zones, especially along edges and fine structures, indicating superior detail restoration with reduced pixel-wise error compared to other methods.

4.6.3. Parameter Analysis

To assess the lightweight nature of our model, We benchmarked the DRFAN against 12 mainstream SR methods on the Urban100 dataset under ×4 scaling. The compared methods include IMDN, RFDN, LatticeNet, LAPAR-A, EMASRN, SMSR, DeFiAN, ShuffleMixer, SAFMN, DIPNet, GASSL-B, and DVMSR. As depicted in Figure 9, the DRFAN achieves the highest PSNR with minimal parameter growth, outperforming existing methods by 0.03–0.22 dB while maintaining a competitive model size.

4.7. Comparative Experiments on Rice Grain Dataset

4.7.1. Quantitative Analysis

To further evaluate the deployability of our model in resource-constrained scenarios, we conducted a quantitative assessment of inference efficiency across all compared lightweight SR models. The comparison models include CARN [7], IMDN [8], SAFMN [32], ShuffleMixer [52], and SwinIR-S [12]. All tests were carried out under a ×4 scale factor using weight files pretrained on public datasets to ensure fairness.

Table 3. Quantitative comparisons on the rice dataset under a ×4 scale factor, with the best and second-best results indicated in red and blue, respectively. FLOPs and inference time are calculated with a 1280 × 720 GT image.

Scale	Methods	Params (K)	PSNR (dB)/SSIM	Inference Time (ms)
×4	CARN [7]	1592	34.91/0.8370	57.7
	IMDN [8]	715	36.54/0.8944	26.0
	SAFMN [32]	240	37.65/0.9122	8.9
	ShuffleMixer [52]	411	37.86/0.9137	17.8
	SwinIR-S [12]	897	37.90/0.9150	31.5
	DRFAN (ours)	1057	38.09/0.9165	41.3

summarizes not only the PSNR/SSIM and FLOPs but also the average inference time (in milliseconds) per 1280 × 720 rice image on a single NVIDIA RTX 4080 GPU.

As shown in Table 3, DRFAN achieves a PSNR of 38.09 dB and an SSIM of 0.9165, surpassing all baseline models in reconstruction accuracy. In terms of computational cost, the DRFAN maintains a reasonable balance with 1057K parameters and 65.1G FLOPs. Its inference time of 41.3 ms is higher than those of ultra-fast models such as SAFMN (8.9 ms) and ShuffleMixer (17.8 ms), but this trade-off yields significantly better reconstruction quality. Compared to SwinIR-S, the DRFAN offers improved accuracy (+0.19 dB PSNR, +0.0015 SSIM), with only a modest increase in runtime (41.3 ms vs. 31.5 ms).

These results demonstrate that the DRFAN achieves a favorable balance between performance and efficiency, making it a promising solution for industrial inspection systems where image fidelity is critical but computational resources may be limited.

4.7.2. Qualitative Experiments

To further validate the reconstruction performance of our model on various rice images, we selected several typical rice samples for visual comparison analysis. As illustrated in Figure 10, our model is capable of restoring the contours of rice grains more clearly while preserving more texture details. In comparison with other lightweight methods, our model exhibits a distinct advantage in reconstructing rice grain details. For example, as shown in Figure 11, the rice grain edges reconstructed by CARN, IMDN, and ShuffleMixer appear rather blurry, whereas our model accurately restores the surface texture of the rice grains, yielding superior overall visual quality. Our model accurately reconstructs surface textures, providing superior visual fidelity. These high-quality reconstructions establish a reliable feature foundation for downstream tasks such as rice variety identification and processing quality inspection.

4.7.3. Statistical Validation

To address the concern of statistical significance with a small sample size, we conducted patch-level significance testing using the Wilcoxon signed-rank test. Each of the 10 high-resolution rice images was partitioned into multiple non-overlapping patches (512 × 240), resulting in a total of 40 low-resolution test samples. We compared the PSNR and SSIM values of our proposed DRFAN model against representative lightweight baselines.

As shown in

Table 4. Statistical significance tests (Wilcoxon signed-rank test) between DRFAN and other models on the rice dataset.

Comparison	Metric	p-Value	Significance (p < 0.01)
DRFAN vs. CARN	PSNR	0	Yes
	SSIM	0.00195	Yes
DRFAN vs. IMDN	PSNR	0	Yes
	SSIM	0.00195	Yes
DRFAN vs. SAFMN	PSNR	0	Yes
	SSIM	0.00195	Yes
DRFAN vs. ShuffleMixer	PSNR	0	Yes
	SSIM	0.00195	Yes
DRFAN vs. SwinIR-S	PSNR	0	Yes
	SSIM	0.00195	Yes

, the p-values for both PSNR and SSIM are less than 0.01 in all comparisons, confirming that the DRFAN’s superiority is statistically significant. This indicates that even with a small dataset, the performance gains of the DRFAN are consistent and reliable, confirming that its superiority in dense-grain texture reconstruction is not incidental.

Additionally, we present box plots in Figure 12 to visualize the distribution of PSNR scores across models. These results validate the robustness of our method in restoring fine-grained textures under industrial conditions, despite the relatively limited number of source images.

5. Discussion

This section reflects on the strengths, challenges, and application prospects of the proposed DRFAN model.

5.1. Efficiency–Accuracy Trade-Off and Linear Complexity Advantage

The DRFAN achieves competitive or superior PSNR and SSIM performance on multiple benchmarks with 1057K parameters and 65.1G FLOPs. Compared to other lightweight models, it demonstrates a strong capability to reconstruct high-frequency details while maintaining a lightweight footprint. The DRFAN leverages the MLLA module to achieve linear computational complexity $O\left(N\right)$. This contrasts with subquadratic Transformer variants such as LongViT and BigBird, which attempt to lower the attention cost to $O\left(NlogN\right)$ or $O\left(N\sqrt{N}\right)$ through window partitioning, local/global token sparsification, or memory token compression. While effective in reducing computational load, these designs often rely on heuristics that may degrade fine-grained texture recovery—especially critical for pixel-level tasks like super-resolution.

The DRFAN’s use of MLLA enables efficient global feature modeling with minimal loss in local detail precision. This design offers a practical balance between computational tractability and visual quality, though we acknowledge that further empirical comparisons with subquadratic Transformers are warranted to more precisely quantify this trade-off under diverse workloads.

5.2. Limitations on Scalability to Higher Magnification

While the DRFAN achieves strong performance under the ×4 super-resolution setting, its current architecture is not explicitly optimized for higher scaling factors such as ×6 or ×8. Preliminary experiments indicate noticeable quality degradation at such magnification levels due to the increasing semantic gap between low-resolution inputs and their high-resolution counterparts. This is a known challenge in SR models, especially under lightweight constraints.

To address this, future extensions of DRFAN may incorporate progressive upscaling strategies, such as cascaded SR stages, or use degradation-aware modules to modulate reconstruction paths adaptively. These methods can help bridge the semantic gap and preserve consistency across extreme scaling conditions.

5.3. Generalization to Motion Blur and Real-World Degradations

The DRFAN is currently trained using bicubic-downsampled data, which do not fully represent real-world degradations such as motion blur, sensor noise, or defocus. When applied to motion-blurred images, the DRFAN exhibits a decline in edge sharpness and structural continuity. This limits its applicability in dynamic or handheld imaging scenarios.

To improve robustness, we plan to incorporate synthetic degradation kernels (e.g., motion blur simulation) and possibly adopt domain adaptation techniques to fine-tune the DRFAN on real degraded images without requiring a paired ground truth. This direction is essential for broader deployment in uncontrolled visual environments.

5.4. Embedded Deployability and Future Evaluation

One of the core motivations behind the DRFAN is its deployability in resource-constrained platforms such as embedded vision systems, mobile devices, and industrial edge modules. With only 1057K parameters and 65.1G FLOPs, the DRFAN meets the general efficiency requirements of embedded hardware. Our current evaluations show that it runs smoothly on high-end GPUs, but deployment on mobile SoCs (e.g., ARM-based NPUs, NVIDIA Jetson, or Huawei Ascend Lite) has not yet been quantitatively benchmarked.

In future work, we plan to evaluate the DRFAN’s runtime latency, power consumption, and memory footprint on embedded platforms. We will then explore optimizations such as quantization, weight pruning, or TensorRT/NPU acceleration for low-precision inference. Finally, we will assess its real-time capability with practical image streams from industrial cameras. These steps will help further validate the DRFAN’s real-world usability and pave the way for integration into automated inspection systems, portable grain analysis terminals, and low-bandwidth visual transmission modules.

5.5. Broader Industrial Applicability and Future Dataset Expansion

While the DRFAN demonstrates strong performance on standard benchmarks and the rice grain dataset, we acknowledge that the current industrial validation is limited to a relatively small and domain-specific dataset. To ensure broader applicability, especially in other manufacturing or quality inspection scenarios, it is necessary to evaluate the DRFAN on additional real-world datasets with higher visual complexity, such as printed circuit board (PCB) defects, fabric flaw detection, or pharmaceutical packaging.

These tasks often involve subtle, high-frequency anomalies embedded within repetitive backgrounds—conditions where super-resolution models must balance texture fidelity with robustness to noise. We plan to expand our evaluations to such datasets in future work. Additionally, to mitigate domain-specific overfitting, we will explore unsupervised domain adaptation and multi-domain training strategies, enabling the model to generalize across varying types of industrial image degradations.

By extending the DRFAN to diverse industrial tasks, we aim to enhance its value as a universal lightweight SR backbone for embedded inspection systems across agriculture, electronics, and manufacturing sectors.

6. Conclusions

This paper proposes the DRFAN, a novel hybrid architecture for single-image super-resolution, comprising three core components: shallow feature extraction, deep feature refinement, and image reconstruction. By integrating the Mamba-like linear attention (MLLA) module and Grid Attention Block (GAB), we synergize the local sensitivity of depthwise convolutions, the long-range dependency modeling of self-attention, and the sequential evolution properties of SSMs through a gated coupling mechanism. A hierarchical grid interaction strategy dynamically allocates weights based on structural similarity priors between image patches, extending the effective receptive field to non-local regions and enhancing texture reconstruction. Experimental results demonstrate that the DRFAN outperforms existing methods on several benchmark datasets, validating its effectiveness in SISR tasks. Additionally, tests in actual rice processing and inspection scenarios show that our method can effectively enhance the contours and texture details of small rice grain targets, confirming its significant engineering application value. In future work, we aim to further improve the scalability of the DRFAN to support higher magnification factors (e.g., ×6, ×8) and enhance its robustness under real-world degradations such as motion blur and sensor noise. Additionally, the proposed lightweight design shows great potential for deployment in edge devices and intelligent agricultural systems, such as real-time rice quality assessment in milling lines or embedded inspection tools in mobile platforms.