Abstract
We present Bayesian Binary Search (BBS), a novel framework that bridges statistical learning theory/probabilistic machine learning and binary search. BBS utilizes probabilistic methods to learn the underlying probability density of the search space. This learned distribution then informs a modified bisection strategy, where the split point is determined by probability density rather than the conventional midpoint. This learning process for search space density estimation can be achieved through various supervised probabilistic machine learning techniques (e.g., Gaussian Process Regression, Bayesian Neural Networks, and Quantile Regression) or unsupervised statistical learning algorithms (e.g., Gaussian Mixture Models, Kernel Density Estimation (KDE), and Maximum Likelihood Estimation (MLE)). Our results demonstrate substantial efficiency improvements using BBS on both synthetic data with diverse distributions and in a real-world scenario involving Bitcoin Lightning Network channel balance probing (3–6% efficiency gain), where BBS is currently in production.
1. Introduction
The concept of organizing data for efficient searching has ancient roots. One of the earliest known examples is the Inakibit-Anu tablet from Babylon (c. 200 BCE), which contained approximately 500 sorted sexagesimal numbers and their reciprocals, facilitating easier searches [1]. Similar sorting techniques were evident in name lists discovered on the Aegean Islands. The Catholicon, a Latin dictionary completed in 1286 CE, marked a significant advance by introducing rules for complete alphabetical classification [1].
The documented modern era of search algorithms began in 1946 when John Mauchly first mentioned binary search during the seminal Moore School Lectures [1]. This was followed by William Wesley Peterson’s introduction of interpolation search in 1957 [2]. A limitation of early binary search algorithms was their restriction to arrays with lengths one less than a power of two. This constraint was overcome in 1960 by Derrick Henry Lehmer, who published a generalized binary search algorithm applicable to arrays of any length [3]. A significant optimization came in 1962 when Hermann Bottenbruch presented an ALGOL 60 implementation of binary search that moved the equality comparison to the end of the process [4]. While this increased the average number of iterations by one, it reduced the number of comparisons per iteration to one, potentially improving efficiency. Further refinements to binary search continued, with A. K. Chandra of Stanford University developing the uniform binary search in 1971 [1]. This variant aimed to provide more consistent performance across different input distributions. In the realm of computational geometry, Bernard Chazelle and Leonidas J. Guibas introduced fractional cascading in 1986 [5]. This technique provided a method to efficiently solve various search problems in geometric contexts, broadening the application of search algorithms beyond simple sorted lists. More recently, hybrid and learning-based approaches have gained attention. For instance, ref. [6] proposed a hybrid search algorithm combining binary search and interpolated search, a theme also explored by [7] with an algorithm that performs interpolation once over a binary search. A newer related trend involves improving the binary search tree data structure using a frequency estimation oracle [8].
The bisection method, a fundamental technique in numerical analysis, shares conceptual similarities with binary search. This method, also known as the interval halving method, binary chopping, or Bolzano’s method, has origins of the bisection method that can be traced back to ancient mathematics. However, its formal description is often attributed to Bolzano’s work in the early 19th century [9]. Bolzano’s theorem, which guarantees the existence of a root in a continuous function that changes sign over an interval, provides the theoretical basis for the bisection method. In the context of root-finding algorithms, ref. [10] provides a comprehensive treatment of the bisection method, discussing its convergence properties and error bounds. They highlight the method’s robustness and guaranteed convergence, albeit at a relatively slow linear rate. Variants of the bisection method have been developed to improve efficiency and applicability. Ref. [11] first introduced probabilistic bisection. Ref. [12] employed interval analysis and bisection to develop reliable methods for finding global optima. These studies demonstrate how bisection principles can be extended beyond simple root-finding to more complex optimization problems.
The connection between bisection and binary search in computer science was explored by [1], who discussed both methods in the context of searching and optimization algorithms. This connection underlies our approach in leveraging probabilistic techniques to enhance binary search. Recent work has focused on adapting bisection methods to handle uncertainty and noise. Ref. [13] introduced a probabilistic bisection algorithm for noisy root-finding problems. Their method, which updates a probability distribution over the root location based on noisy measurements, shares conceptual similarities with our Bayesian Binary Search approach. In the context of stochastic optimization, ref. [14] developed a probabilistic bisection algorithm for binary classification problems. Their work demonstrates how Bayesian updating can be incorporated into the bisection process, providing a precedent for our probabilistic approach to binary search. The bisection method has also found applications in various fields beyond pure mathematics. For instance, ref. [15] discussed the use of parallel bisection methods in scientific computing, highlighting the potential for algorithmic improvements through parallelization.
Probabilistic machine learning, as described by Ghahramani [16], provides a framework for reasoning about uncertainty in data and models. Gaussian Processes (GPs), a cornerstone of many probabilistic machine learning methods, were extensively explored by Rasmussen andWilliams [17]. GPs offer a flexible, non-parametric approach to modeling distributions over functions, making them particularly suitable for tasks involving uncertainty quantification. In recent years, Bayesian deep learning has emerged as a powerful approach to combining the expressiveness of deep neural networks with principled uncertainty quantification. Wang and Yeung [18] provide a comprehensive survey of Bayesian deep learning techniques, discussing various methods for incorporating uncertainty into deep neural networks and their applications in complex, high-dimensional problems. The field of Bayesian Optimization, which shares conceptual similarities with our work, has seen substantial growth. Shahriari et al. [19] provide a comprehensive overview of Bayesian Optimization techniques, highlighting their effectiveness in optimizing expensive-to-evaluate functions. These methods typically use GPs, Bayesian Neural Networks (BNNs) or other probabilistic models to guide the optimization process, analogous to our use of probability density estimates in Bayesian Binary Search.
2. Methodology
2.1. Classical Binary Search/Bisection
Binary search is an efficient algorithm for finding a target value in a defined search space. It repeatedly divides the search interval in half, eliminating half of the remaining space at each step. The algorithm maintains two boundaries, low and high, and computes the midpoint as mid = (low + high)/2. By evaluating the midpoint and comparing it to the target value, it determines which half of the search space to explore next, updating either low or high accordingly. This process continues until the target is found or the search space is exhausted. The efficiency of binary search stems from its ability to halve the potential search space with each iteration, resulting in a logarithmic time complexity.
2.2. Bayesian Binary Search (BBS)
2.2.1. Binary Search as Bayesian Inference
The classical binary search/bisection algorithm can be formally framed within the context of Bayesian inference. Consider a sorted search space represented by the interval . In the absence of prior knowledge about the location of the target value x, we define a uniform prior probability density function (PDF) over this initial interval:
Let denote the search interval at the k-th step of the binary search. At each step, we probe the midpoint . The comparison of with the target value provides an observation which can be one of two outcomes: or (assuming the target is not exactly at ).
We can express the posterior probability density after the k-th probe using conditional probability. Let denote the posterior PDF given the observation at step k.
If the observation is , then the posterior PDF becomes
In this case, the new search interval for the next step is .
If the observation is , then the posterior PDF becomes
Here, the new search interval is .
In both scenarios, the posterior distribution remains uniform over the reduced search interval, with the probability mass concentrated in half of the previous interval. This deterministic update of the probability distribution based on each probe is analogous to Bayesian inference, where the likelihood function effectively assigns zero probability to the half of the search space that is inconsistent with the observation.
Thus, standard binary search can be viewed as a specific instance of Bayesian inference employing a uniform prior and a deterministic observation model that halves the search space at each step. This provides a foundational perspective for understanding how Bayesian Binary Search generalizes this approach by incorporating learned priors and probabilistic probing strategies.
2.2.2. Problem Formulation
Given a search space S and a target value t, our aim is to locate t in S, or produce a specified range for t with a given tolerance. Unlike classical binary search, we assume that the distribution of potential target locations is not uniform across S. We represent this non-uniform distribution using a probability density function (PDF) , where . We formulate the binary search algorithm in two parts: (1) search space density estimation, which produces a PDF that is fed into a (2) modified binary search algorithm that begins at the median of the PDF and bisects in probability density space. BBS is equivalent to basic binary search when the search space PDF estimation process is replaced with the assumption of a uniformly distributed target space. This formulation maps to a binary search problem on a sorted array in the following way: the search space S corresponds to the sorted array, the target value t is the element being searched for, and the PDF p(x) represents the probability of finding the target at each index in the array using interpolation.
2.3. Bayesian Binary Search Framework
In contrast to the uniform prior that is assumed when looking at the classical binary search algorithm from the lens of Bayesian inference, BBS begins with a potentially non-uniform prior distribution, , estimated from data using methods such as Gaussian Process Regression, Bayesian Neural Networks, Quantile Regression, Gaussian Mixture Models, Kernel Density Estimation, or Maximum Likelihood Estimation. This learned prior encapsulates prior knowledge or beliefs about the likely location of the target value.
The subsequent steps in BBS involve probing the search space based on this learned prior (or the evolving posterior distribution derived from it). Each probe and the resulting observation then lead to an update of the posterior distribution using Bayes’ Theorem:
or, more generally, at step k:
This iterative process, starting with a learned prior (Algorithm 1–5), allows BBS to focus its search on regions of higher probability, potentially leading to faster convergence and improved efficiency compared to standard binary search’s assumption of a uniform prior. The posterior update in this case is mathematically equivalent to bisecting in probability density space.
2.4. Proof of Posterior Update Equivalence to Bisection in Probability Density Space with a Non-Uniform Prior
In Bayesian Binary Search (BBS), the prior distribution over the search interval is not necessarily uniform. Let be the prior PDF at the k-th step. The core principle of BBS is to choose a probe location within such that it effectively bisects the probability mass according to the current posterior belief.
At each step, BBS aims to find a probe location that satisfies
where is the posterior PDF after k probes (or the learned prior at ). Assuming the posterior is properly normalized, . Therefore, the probe location is chosen, such that
Now, let us consider the two possible outcomes of the probe at .
2.5. Case 1: Observation
The likelihood function for this observation is
The posterior PDF after this observation is given by Bayes’ Theorem:
This implies that the posterior PDF is non-zero only for :
Since the probe was chosen such that , the posterior PDF over the new interval is proportional to the original posterior and normalized such that the total probability mass in this interval is now 1. The key point is that the probability mass is now concentrated in the interval , which contained exactly half of the total probability mass before the observation.
2.6. Case 2: Observation
The likelihood function for this observation is
The posterior PDF after this observation is
This implies that the posterior PDF is non-zero only for :
Since and , it follows that . Thus, the posterior PDF is now concentrated in the interval , which also contained exactly half of the total probability mass before the observation.
In Bayesian Binary Search, the probe location is strategically chosen at each step to bisect the probability mass of the current posterior distribution. Regardless of whether the target is found to be less than or greater than , the subsequent posterior distribution is concentrated over an interval that contained exactly half of the probability mass of the previous distribution. This demonstrates that the posterior update step in BBS, even with a non-uniform prior, is mathematically equivalent to a bisection in the probability density space, where the “bisection” refers to the halving of the probability mass rather than necessarily the physical midpoint of the search interval.
2.7. Search Space Probability Density Function Estimation
The effectiveness of BBS depends on the accuracy of the PDF estimation. Some methods for estimating can include the following.
2.7.1. Supervised Learning Approaches
- Gaussian Process Regression (GPR): GPR provides a non-parametric way to model the PDF, offering both a mean prediction and uncertainty estimates.
- Bayesian Neural Networks (BNNs): BNNs combine the flexibility of neural networks with Bayesian inference, allowing for uncertainty quantification in the predictions.
- Quantile Regression: Quantile Regression estimates the conditional quantiles of a response variable, providing a more comprehensive view of the relationship between variables across different parts of the distribution, without assuming a particular parametric form for the underlying distribution.
2.7.2. Unsupervised Learning Approaches
- Gaussian Mixture Models (GMMs): GMMs (typically fit using the Expectation-Maximization (EM) algorithm) can model complex, multimodal distributions by representing the PDF as a weighted sum of Gaussian components.
- Kernel Density Estimation (KDE): KDE is a non-parametric method for estimating PDFs, which can capture complex shapes without assuming a specific functional form.
- Maximum Likelihood Estimation (MLE): MLE is a method of estimating the parameters of a probability distribution by maximizing a likelihood function. It can be used to fit various parametric distributions (e.g., normal, exponential, Poisson) to data, providing a PDF that best explains the observed samples according to the chosen distribution family.
2.8. Probabilistic Bisection Step
BBS leverages a probabilistic bisection step. Instead of dividing the search space at the midpoint, BBS divides it at the median of the current PDF. Formally, at each step, we find , such that
After each comparison, we update the PDF based on the result. If the target is found to be in the lower half, we set for and renormalize the PDF. Similarly, if the target is in the upper half, we set for and renormalize. As proven above, this step is mathematically equivalent to the posterior update step when viewing the algorithm from the lens of Bayesian inference.
We evaluate BBS against a basic binary search on both simulated data across several distributions and a real-world example of binary search/bisection of probing channels in the Bitcoin Lightning Network, for which accessing the search space is an expensive operation (time and liquidity) [20]. We further perform a thorough theoretical analysis located in Appendix A.
| Algorithm 1: Bayesian Binary Search |
 |
| Algorithm 2: Estimate Search Space Probability Density Function (PDF) |
 |
| Algorithm 3: FindMedian Function |
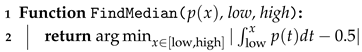 |
| Algorithm 4: UpdatePDF Function |
 |
| Algorithm 5: Sign Function |
 |
3. Experiments
3.1. Experiments on Simulated Data
We evaluated the performance of BBS against binary search on simulated data from several distributions: normal, bimodal, and exponential. The results of the normal distribution experiments are shown below, while the results of the bimodal and exponential distributions can be found in Appendix A. We additionally show experiments for which the estimated search space density function does not match the target search space as measured by Kullback–Leibler (KL) divergence. We demonstrate how BBS performance degrades as the estimated search space density drifts further from the target distribution, and eventually can cause the BBS to perform worse than basic binary search.
3.1.1. Experimental Setup
To evaluate the performance of BBS compared to the standard binary search in the context of normal distributions, we conducted a series of experiments with the following setup.
3.1.2. Distribution Parameters
For the normal distribution experiments, we used the following parameters:
- Mean (): 0;
- Standard Deviation (): 10,000.
3.1.3. Target Value Generation
We generated 1000 target values by sampling from the specified normal distribution. Each target value was obtained by drawing a random sample x from the distribution and applying the floor function to ensure integer targets: .
3.1.4. Search Procedure
For each target value, both search algorithms attempt to locate the target within a specified precision (), set to 8. The search space is initialized based on the properties of the normal distribution:
- Lower Bound (): ;
- Upper Bound (): .
The algorithms iteratively narrow down the search space until the target is found within the acceptable error margin.
3.1.5. Metrics Collected
We collected the following performance metrics:
- Number of Steps: Total iterations required to find each target.
- Bracket Size: The range () at each step of the search.
3.2. Experiments on Lightning Network Channel Probing
Probing a channel in the Lightning Network is the construction of a fake payment to be sent through the network to obtain information on the balance of a channel. If the payment fails, then the balance on that side of the channel is lower than the payment amount; if it succeeds, then the balance is greater than or equal to the payment amount. Typically, it is currently performed using a basic binary search/bisection. The response of a given probe can be viewed as an oracle, which is a continuous and monotonic function, making it suitable for the bisection method as it guarantees that there is only one root of the function.
Each probe is computationally expensive and fundamentally constrained in this domain due to the max HTLC (Hashed Timelock Contract) limit (483 on Lightning Network Daemon (LND), the most popular Lightning Node implementation) on each channel in the Lightning Node software implementation for security purposes. Probes occupying this limit fundamentally constrain network throughput, which could otherwise process real payments. The Lightning Network can potentially be probed millions of times a week, underscoring the importance of designing an algorithm that optimizes efficiency.
To demonstrate the computational complexity of executing probes on the Lightning Network, we probed 1500 channels from our Lightning Node, with an average hop length of 2.26. The probe time average for each channel has a mean of 3.1 s and a standard deviation of 0.7 s. The density estimation step per channel here in comparison (random forest inference and KDE) takes 0.18 s, and only needs to be performed once per channel. The added overhead of density estimation here is significantly outweighed by the probing computational cost and the domain max HTLC constraint.
For search space density estimation in the Lightning Network channel probing experiment, we detail a random forest model to predict the search target (channel balance in this case). We constructed a PDF from the prediction of the random forest using Kernel Density Estimation (KDE) on the predictions of individual predictors (trees) in the ensemble. Alternatively, we could have used Bayesian Neural Networks or a Gaussian Process Regressor (results in Appendix A), but the random forest yielded superior predictive performance in our experiments [21].
3.2.1. Description of Channel Balance Prediction Task
The Lightning Network can be modeled as a directed graph , where V represents the set of nodes and E represents the set of edges. Each node u and each edge have associated features, denoted by for nodes and for edges, which contain specific information about those nodes and edges. Additionally, each edge has a scalar value , representing the pre-allocated balance for transactions from u to v.
Graph G has the constraint that if an edge exists in one direction, it must also exist in the opposite direction, i.e., . The set of two edges between any two nodes is called a channel, denoted as . For simplicity, we represent a channel by the set of its two nodes: . The total capacity of the channel is defined as .
We are provided with the total channel capacities for all channels in the graph, but we only know the individual values for a subset of edges. Note that knowing allows us to determine , since . Therefore, we can focus on predicting .
Moreover, since we are given for all edges, and we know that , we also have that , where . Intuitively, is the proportion of the channel capacity which belongs to the direction. From this, we see that we focus on predicting , and then use it to obtain .
Therefore, our primary task is to predict for all edges where it is not observed.
3.2.2. Data Collection and Preprocessing
The data used in this experiment are a combination of publicly available information from the Lightning Network and crowdsourced information from nodes in the network. A snapshot of the network from 15 December 2023 was used in this experiment. Balance information for each node is represented by its local balance, recorded at one-minute intervals over the preceding hour. These data were converted into a probability density function (PDF) through Kernel Density Estimation. Subsequently, a balance value was sampled from each PDF, serving as the representative local balance for the corresponding channel within the dataset.
3.3. Methodology
The following section outlines the details of our modeling approach.
3.3.1. Modeling
We will predict by learning a parametric function:
where are learnable weights, , , and are the node and edge features, respectively, while is the capacity of the channel. While several choices are possible for , such as multi-layer perceptrons ([22]) or Graph Neural Networks, we focus on random forests for this work given their simplicity and efficacy. In particular, our random forest (RF) model operates on the concatenation of the features of the source and destination nodes as well as the edge features:
The model was trained using a Mean Squared Error loss.
3.3.2. Node Features
- Node Feature FlagsA vector of 0–1 indicating which of the features each node supports. For example, feature flag #19, the wumbo flag.
- Capacity CentralityThe node’s capacity divided by the network’s capacity. This indicates how much of the network’s capacity is incident to a node.
- Fee RatioRatio of the mean cost of a node’s outgoing fees to the mean cost of its incoming fees.
3.3.3. Edge Features
- Time Lock Delta: The number of blocks a relayed payment is locked into an HTLC.
- Min HTLC: The minimum amount this edge will route (denominated in millisats).
- Max HTLC msat: The maximum amount this edge will route (denominated in millisats).
- Fee Rate millimsat: Proportional fee to route a payment along an edge (denominated in millimillisats).
- Fee Base msat: Fixed fee to route a payment along an edge (denominated in millisats).
3.3.4. Positional Encodings
Positional encoding is essential for capturing the structural context of nodes, as graphs lack inherent sequential order. Utilizing eigenvectors of the graph Laplacian matrix as positional encodings provides a robust solution to this challenge. These eigenvectors highlight key structural patterns, enriching node features with information about the overall topology of the graph [23]. By integrating these spectral properties, machine learning models can effectively recognize and utilize global characteristics, enhancing performance in tasks like node classification and community detection.
3.3.5. Concatenated Prediction ML Model
Our model predicts as a function of the concatenation of the features of the source and destination nodes as well as edge features:
3.3.6. Model Training Details and Performance
We set aside of the observed as our test set and as our validation set. The RF model trained for balance prediction has an MAE of 1.08, an R of 0.612, and of 0.365. For the BBS experiments, we use the predictions on the validation set (89 channels). For validation set channels, we feed the predictions of each tree in the ensemble (100) into a Kernel Density Estimation (KDE) process to construct the search space PDF. Using these constructed PDFs, we compare BBS with basic binary search in measuring how many probes it would take to ascertain the balance of a given channel.
4. Discussion
Our experimental results demonstrate the potential of Bayesian Binary Search (BBS) as a promising alternative to classical binary search/bisection, particularly in scenarios where the search space exhibits non-uniform distributions and is costly to access. The performance improvements observed in both simulated environments and real-world applications, such as probing payment channels in the Bitcoin Lightning Network, highlight the promise of BBS (Figure 1 and Figure 2, Table 1 and Table 2). However, it is important to consider these findings in a broader context and acknowledge the limitations and implications of our work. The results observed here are also consistent with some theoretical analysis from [24,25], and the BBS framework provides a novel perspective on how probabilistic machine learning techniques can be used to achieved these efficiencies.
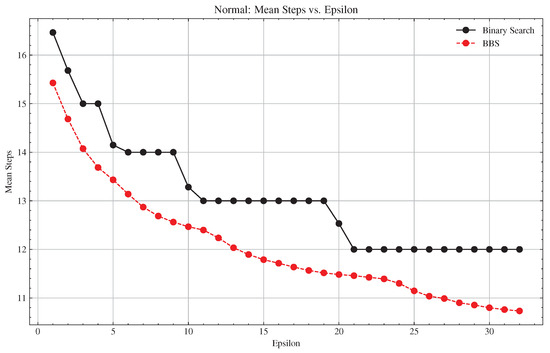
Figure 1.
Normal Distribution: Basic vs. BBS Convergence Comparison.
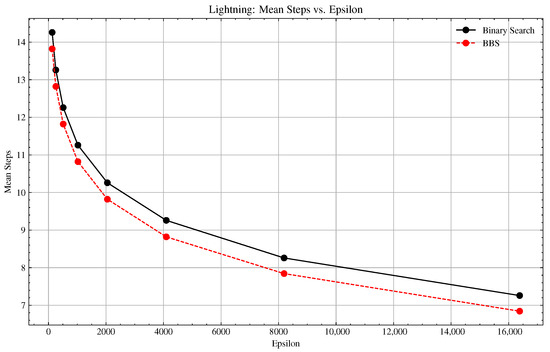
Figure 2.
Lightning Probing Experiment: Basic vs. BBS Convergence Comparison.

Table 1.
.

Table 2.
Lightning Channel Probing Comparison.
4.1. Theoretical Alignment and Performance Gains
The superior performance of BBS over classical binary search in non-uniform distributions aligns with our theoretical expectations. By leveraging probabilistic information about the search space, BBS can make more informed decisions at each step, leading to faster convergence on average. This is particularly evident in our simulated experiments with skewed distributions, where BBS consistently required fewer steps to locate the target. The ability of BBS to adapt to the underlying distribution of the search space represents an advance in the design of search algorithms, and a fusion of search theory and probabilistic machine learning/statistical learning.
4.2. Real-World Application and Implications
In the context of the Bitcoin Lightning Network, the improvement in probing efficiency could have significant practical implications. Faster and more accurate channel capacity discovery can enhance routing algorithms, potentially leading to improved transaction success rates. Crucially, probes in the Lightning Network consume network-wide computational resources, as each probe requires processing by multiple nodes along potential payment routes. By using BBS to enhance probe efficiency, we effectively reduce unnecessary network load, akin to removing spam from the system. This reduction in network overhead could lead to improved overall network performance and scalability.
4.3. Limitations and Challenges
Despite the promising results, several limitations of our study should be acknowledged:
- Computational Overhead: The improved search efficiency of BBS comes at the cost of increased computational complexity, particularly in the PDF estimation step. This overhead may offset the reduction in search steps for certain applications, especially those dealing with small search spaces or requiring extremely fast operation.
- PDF Estimation Accuracy: The performance of BBS is heavily dependent on the accuracy of the PDF estimation. In scenarios where the underlying distribution is highly complex or rapidly changing, the chosen PDF estimation method may struggle to provide accurate probabilities, potentially leading to suboptimal performance.
4.4. Future Research Directions
Our findings open up several exciting avenues for future research:
- Adaptive PDF Estimation: Developing methods to dynamically adjust the PDF estimation technique based on the observed search space characteristics could further improve the robustness and efficiency of BBS.
- Theoretical Bounds: While we provide empirical evidence of BBS’s effectiveness, deriving tighter theoretical bounds on its performance under various distribution types would strengthen its theoretical foundation.
- Application to Other Domains: Exploring the applicability of BBS to other areas such as database indexing, computational biology, or optimization algorithms could reveal new use cases and challenges.
4.5. Conclusions
Bayesian Binary Search represents a significant step towards more adaptive and efficient search algorithms. By incorporating probabilistic information, BBS demonstrates the potential to outperform classical binary search in non-uniform distributions, as evidenced by our experiments in both simulated and real-world scenarios. In the context of the Lightning Network, BBS not only improves search efficiency but also contributes to reducing unnecessary network load, potentially enhancing the overall performance and scalability of the system. The promising results open up new possibilities for optimizing search processes in various domains. As we continue to navigate increasingly complex and data-rich environments, algorithms like BBS that can adapt to the underlying structure of the problem space will become increasingly valuable. Future work in this direction has the potential to not only improve search efficiency but also to deepen our understanding of how probabilistic approaches can enhance fundamental algorithms in computer science and their real-world applications.
Author Contributions
V.S., M.K. and V.D. participated in writing the main manuscript text and execution of experiments. All authors V.S., M.K., V.D., H.R., E.R., J.S. and P.L. reviewed the manuscript and contributed to experimental design. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are grateful to be able to produce this work while being employed/funded for their roles at Stillmark and Amboss Technologies.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Vikash Singh was employed by the company Stillmark. Author Matthew Khanzadeh was indepedently affiliated but employed by Ontra at the time of working on the project. Author Emanuele Rossi was employed by VantAI and an advisor to Amboss Technologies. Authors Vincent Davis, Harrison Rush and Jesse Shrader were employed by the company Amboss Technologies. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A
Appendix A.1. BBS on Imperfect Search Space Density Estimation
The performance of BBS depends on the accuracy of the search space density estimation. To demonstrate the performance of BBS on varying degrees of accuracy in search space density estimation, we run experiments in which the estimated search space probability density function is a given Kullback–Leibler (KL) divergence from the target normal distribution of the search space.
We derive a new normal distribution with a specified KL divergence to a target distribution below:
Given
- Target distribution: ;
- Desired KL divergence: D.
We want to find parameters and for a new distribution , such that
The KL divergence between two normal distributions is given by
For simplicity, let us assume . Then, the equation simplifies to
Solving for ,
We choose the positive solution
Therefore, the parameters of the new distribution are
This ensures that

Table A1.
, = 10, N = 200.
Table A1.
, = 10, N = 200.
| KLD | Percent Decrease | Basic Mean Steps | Bayesian Mean Steps |
|---|---|---|---|
| 0.0 | 9.40% | 10.00 ± 0.00 | 9.06 ± 0.95 |
| 0.05 | 8.85% | 10.00 ± 0.00 | 9.12 ± 1.07 |
| 0.1 | 7.70% | 10.00 ± 0.00 | 9.23 ± 1.12 |
| 0.15 | 6.95% | 10.00 ± 0.00 | 9.30 ± 1.19 |
| 0.2 | 6.35% | 10.00 ± 0.00 | 9.37 ± 1.26 |
| 0.25 | 6.15% | 10.00 ± 0.00 | 9.38 ± 1.34 |
| 0.3 | 4.90% | 10.00 ± 0.00 | 9.51 ± 1.40 |
| 0.35 | 4.35% | 10.00 ± 0.00 | 9.56 ± 1.44 |
| 0.4 | 3.00% | 10.00 ± 0.00 | 9.70 ± 1.42 |
| 0.45 | 2.25% | 10.00 ± 0.00 | 9.78 ± 1.56 |
| 0.5 | 1.20% | 10.00 ± 0.00 | 9.88 ± 1.62 |
| 0.55 | 0.60% | 10.00 ± 0.00 | 9.94 ± 1.65 |
| 0.6 | 0.60% | 10.00 ± 0.00 | 9.94 ± 1.66 |
| 0.65 | −0.20% | 10.00 ± 0.00 | 10.02 ± 1.77 |
| 0.7 | −0.90% | 10.00 ± 0.00 | 10.09 ± 1.80 |
| 0.75 | −1.90% | 10.00 ± 0.00 | 10.19 ± 1.87 |
| 0.8 | −2.75% | 10.00 ± 0.00 | 10.28 ± 1.94 |
| 0.85 | −3.35% | 10.00 ± 0.00 | 10.34 ± 2.00 |
| 0.9 | −4.10% | 10.00 ± 0.00 | 10.41 ± 2.00 |
| 0.95 | −4.85% | 10.00 ± 0.00 | 10.48 ± 2.03 |
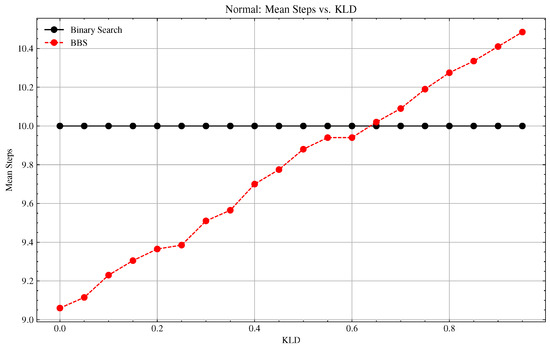
Figure A1.
Basic vs. BBS Convergence with KLD Separation of Estimated Search Space PDF and Actual PDF.

Table A2.
Bimodal Parameters, .
Table A2.
Bimodal Parameters, .
| Percent Decrease | Basic Mean Steps | Bayesian Mean Steps | |
|---|---|---|---|
| 1 | 3.14% | 13.38 ± 0.49 | 12.96 ± 0.99 |
| 2 | 2.38% | 12.58 ± 0.50 | 12.28 ± 0.90 |
| 3 | 2.67% | 12.00 ± 0.00 | 11.68 ± 0.79 |
| 4 | 4.22% | 11.86 ± 0.35 | 11.36 ± 0.72 |
| 5 | 0.36% | 11.00 ± 0.00 | 10.96 ± 0.78 |
| 6 | 2.91% | 11.00 ± 0.00 | 10.68 ± 0.82 |
| 7 | 4.55% | 11.00 ± 0.00 | 10.50 ± 0.74 |
| 8 | 5.27% | 11.00 ± 0.00 | 10.42 ± 0.64 |
| 9 | 1.53% | 10.48 ± 0.50 | 10.32 ± 0.51 |
| 10 | 0.40% | 10.00 ± 0.00 | 9.96 ± 0.78 |
| 11 | 2.80% | 10.00 ± 0.00 | 9.72 ± 0.81 |
| 12 | 3.80% | 10.00 ± 0.00 | 9.62 ± 0.75 |
| 13 | 4.40% | 10.00 ± 0.00 | 9.56 ± 0.76 |
| 14 | 5.00% | 10.00 ± 0.00 | 9.50 ± 0.71 |
| 15 | 5.60% | 10.00 ± 0.00 | 9.44 ± 0.67 |
| 16 | 5.80% | 10.00 ± 0.00 | 9.42 ± 0.64 |
| 17 | 6.40% | 10.00 ± 0.00 | 9.36 ± 0.56 |
| 18 | 6.60% | 10.00 ± 0.00 | 9.34 ± 0.52 |
| 19 | -1.98% | 9.08 ± 0.27 | 9.26 ± 0.56 |
| 20 | 0.00% | 9.00 ± 0.00 | 9.00 ± 0.78 |
| 21 | 1.78% | 9.00 ± 0.00 | 8.84 ± 0.84 |
| 22 | 2.67% | 9.00 ± 0.00 | 8.76 ± 0.74 |
| 23 | 3.78% | 9.00 ± 0.00 | 8.66 ± 0.75 |
| 24 | 4.00% | 9.00 ± 0.00 | 8.64 ± 0.75 |
| 25 | 4.00% | 9.00 ± 0.00 | 8.64 ± 0.75 |
| 26 | 4.44% | 9.00 ± 0.00 | 8.60 ± 0.76 |
| 27 | 4.44% | 9.00 ± 0.00 | 8.60 ± 0.76 |
| 28 | 5.11% | 9.00 ± 0.00 | 8.54 ± 0.76 |
| 29 | 6.00% | 9.00 ± 0.00 | 8.46 ± 0.68 |
| 30 | 6.22% | 9.00 ± 0.00 | 8.44 ± 0.67 |
| 31 | 6.44% | 9.00 ± 0.00 | 8.42 ± 0.64 |
| 32 | 6.67% | 9.00 ± 0.00 | 8.40 ± 0.61 |
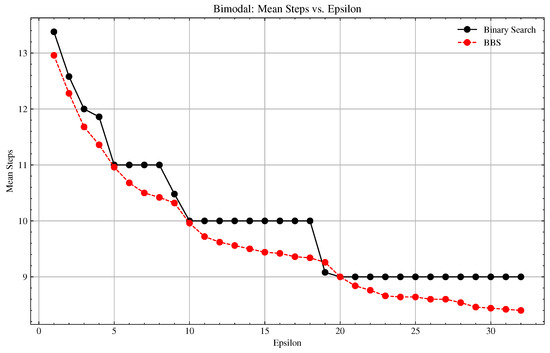
Figure A2.
Bimodal Distribution: Basic vs. BBS Convergence Comparison.

Table A3.
Exponential Parameters, scale = 10,000.
Table A3.
Exponential Parameters, scale = 10,000.
| Percent Decrease | Basic Mean Steps | Bayesian Mean Steps | |
|---|---|---|---|
| 1 | 12.86% | 16.87 ± 0.34 | 14.70 ± 1.41 |
| 2 | 13.03% | 16.00 ± 0.00 | 13.91 ± 1.34 |
| 3 | 14.40% | 15.55 ± 0.50 | 13.31 ± 1.37 |
| 4 | 13.07% | 15.00 ± 0.00 | 13.04 ± 1.33 |
| 5 | 15.10% | 15.00 ± 0.00 | 12.73 ± 1.35 |
| 6 | 17.17% | 15.00 ± 0.00 | 12.43 ± 1.36 |
| 7 | 13.01% | 14.03 ± 0.16 | 12.20 ± 1.37 |
| 8 | 13.75% | 14.00 ± 0.00 | 12.07 ± 1.34 |
| 9 | 14.39% | 14.00 ± 0.00 | 11.98 ± 1.31 |
| 10 | 15.54% | 14.00 ± 0.00 | 11.82 ± 1.34 |
| 11 | 16.89% | 14.00 ± 0.00 | 11.63 ± 1.36 |
| 12 | 18.11% | 14.00 ± 0.00 | 11.46 ± 1.36 |
| 13 | 19.00% | 14.00 ± 0.00 | 11.34 ± 1.35 |
| 14 | 13.83% | 13.05 ± 0.23 | 11.25 ± 1.36 |
| 15 | 14.27% | 13.00 ± 0.00 | 11.14 ± 1.37 |
| 16 | 14.62% | 13.00 ± 0.00 | 11.10 ± 1.37 |
| 17 | 15.00% | 13.00 ± 0.00 | 11.05 ± 1.34 |
| 18 | 15.38% | 13.00 ± 0.00 | 11.00 ± 1.32 |
| 19 | 15.65% | 13.00 ± 0.00 | 10.96 ± 1.32 |
| 20 | 16.42% | 13.00 ± 0.00 | 10.87 ± 1.34 |
| 21 | 17.35% | 13.00 ± 0.00 | 10.74 ± 1.36 |
| 22 | 18.19% | 13.00 ± 0.00 | 10.63 ± 1.36 |
| 23 | 18.50% | 13.00 ± 0.00 | 10.60 ± 1.37 |
| 24 | 19.08% | 13.00 ± 0.00 | 10.52 ± 1.34 |
| 25 | 19.81% | 13.00 ± 0.00 | 10.43 ± 1.35 |
| 26 | 20.15% | 13.00 ± 0.00 | 10.38 ± 1.34 |
| 27 | 20.77% | 13.00 ± 0.00 | 10.30 ± 1.34 |
| 28 | 15.42% | 12.13 ± 0.34 | 10.26 ± 1.36 |
| 29 | 14.92% | 12.00 ± 0.00 | 10.21 ± 1.37 |
| 30 | 15.42% | 12.00 ± 0.00 | 10.15 ± 1.37 |
| 31 | 15.58% | 12.00 ± 0.00 | 10.13 ± 1.37 |
| 32 | 15.75% | 12.00 ± 0.00 | 10.11 ± 1.37 |
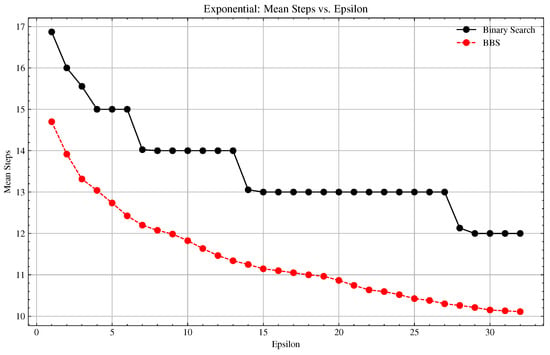
Figure A3.
Exponential Distribution: Basic vs. BBS Convergence Comparison.

Table A4.
Beta Parameters; a = 1, b = 5, scale = 10,000, and n = 500.
Table A4.
Beta Parameters; a = 1, b = 5, scale = 10,000, and n = 500.
| Percent Decrease | Basic Mean Steps | Bayesian Mean Steps | |
|---|---|---|---|
| 1 | 4.26% | 13.25 ± 0.43 | 12.68 ± 0.92 |
| 2 | 4.36% | 12.39 ± 0.49 | 11.85 ± 0.89 |
| 3 | 5.43% | 12.00 ± 0.00 | 11.35 ± 0.79 |
| 4 | 6.20% | 11.62 ± 0.49 | 10.90 ± 0.85 |
| 5 | 4.04% | 11.00 ± 0.00 | 10.56 ± 0.82 |
| 6 | 5.44% | 11.00 ± 0.00 | 10.40 ± 0.76 |
| 7 | 6.67% | 11.00 ± 0.00 | 10.27 ± 0.73 |
| 8 | 9.42% | 11.00 ± 0.00 | 9.96 ± 0.84 |
| 9 | 3.65% | 10.08 ± 0.27 | 9.71 ± 0.85 |
| 10 | 4.24% | 10.00 ± 0.00 | 9.58 ± 0.85 |
| 11 | 5.14% | 10.00 ± 0.00 | 9.49 ± 0.81 |
| 12 | 5.84% | 10.00 ± 0.00 | 9.42 ± 0.77 |
| 13 | 6.28% | 10.00 ± 0.00 | 9.37 ± 0.74 |
| 14 | 6.74% | 10.00 ± 0.00 | 9.33 ± 0.71 |
| 15 | 7.44% | 10.00 ± 0.00 | 9.26 ± 0.72 |
| 16 | 9.50% | 10.00 ± 0.00 | 9.05 ± 0.81 |
| 17 | 11.44% | 10.00 ± 0.00 | 8.86 ± 0.86 |
| 18 | 4.50% | 9.15 ± 0.36 | 8.74 ± 0.86 |
| 19 | 3.80% | 9.00 ± 0.00 | 8.66 ± 0.86 |
| 20 | 4.56% | 9.00 ± 0.00 | 8.59 ± 0.86 |
| 21 | 5.09% | 9.00 ± 0.00 | 8.54 ± 0.83 |
| 22 | 5.64% | 9.00 ± 0.00 | 8.49 ± 0.82 |
| 23 | 5.98% | 9.00 ± 0.00 | 8.46 ± 0.79 |
| 24 | 6.31% | 9.00 ± 0.00 | 8.43 ± 0.77 |
| 25 | 6.53% | 9.00 ± 0.00 | 8.41 ± 0.76 |
| 26 | 6.84% | 9.00 ± 0.00 | 8.38 ± 0.75 |
| 27 | 7.24% | 9.00 ± 0.00 | 8.35 ± 0.72 |
| 28 | 7.47% | 9.00 ± 0.00 | 8.33 ± 0.70 |
| 29 | 7.58% | 9.00 ± 0.00 | 8.32 ± 0.69 |
| 30 | 7.84% | 9.00 ± 0.00 | 8.29 ± 0.68 |
| 31 | 8.36% | 9.00 ± 0.00 | 8.25 ± 0.71 |
| 32 | 10.36% | 9.00 ± 0.00 | 8.07 ± 0.80 |
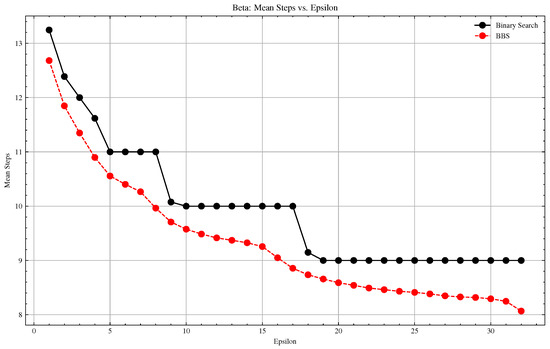
Figure A4.
Beta Distribution: Basic vs. BBS Convergence Comparison.

Table A5.
Lognorm Parameters; s = 1, scale = 10,000, n = 500.
Table A5.
Lognorm Parameters; s = 1, scale = 10,000, n = 500.
| Percent Decrease | Basic Mean Steps | Bayesian Mean Steps | |
|---|---|---|---|
| 1 | 21.08% | 19.53 ± 0.50 | 15.41 ± 1.90 |
| 2 | 22.52% | 18.78 ± 0.41 | 14.55 ± 1.89 |
| 3 | 21.72% | 18.00 ± 0.00 | 14.09 ± 1.86 |
| 4 | 24.10% | 18.00 ± 0.00 | 13.66 ± 1.89 |
| 5 | 23.51% | 17.46 ± 0.50 | 13.36 ± 1.89 |
| 6 | 22.42% | 17.00 ± 0.00 | 13.19 ± 1.85 |
| 7 | 23.78% | 17.00 ± 0.00 | 12.96 ± 1.82 |
| 8 | 25.28% | 17.00 ± 0.00 | 12.70 ± 1.90 |
| 9 | 26.40% | 17.00 ± 0.00 | 12.51 ± 1.91 |
| 10 | 26.44% | 16.85 ± 0.36 | 12.39 ± 1.91 |
| 11 | 23.15% | 16.00 ± 0.00 | 12.30 ± 1.88 |
| 12 | 23.64% | 16.00 ± 0.00 | 12.22 ± 1.86 |
| 13 | 24.19% | 16.00 ± 0.00 | 12.13 ± 1.85 |
| 14 | 24.68% | 16.00 ± 0.00 | 12.05 ± 1.82 |
| 15 | 25.88% | 16.00 ± 0.00 | 11.86 ± 1.87 |
| 16 | 26.69% | 16.00 ± 0.00 | 11.73 ± 1.89 |
| 17 | 27.36% | 16.00 ± 0.00 | 11.62 ± 1.93 |
| 18 | 27.84% | 16.00 ± 0.00 | 11.55 ± 1.93 |
| 19 | 28.34% | 16.00 ± 0.00 | 11.47 ± 1.90 |
| 20 | 28.69% | 16.00 ± 0.00 | 11.41 ± 1.90 |
| 21 | 27.63% | 15.71 ± 0.45 | 11.37 ± 1.90 |
| 22 | 24.44% | 15.00 ± 0.00 | 11.33 ± 1.89 |
| 23 | 24.84% | 15.00 ± 0.00 | 11.27 ± 1.88 |
| 24 | 25.07% | 15.00 ± 0.00 | 11.24 ± 1.87 |
| 25 | 25.37% | 15.00 ± 0.00 | 11.19 ± 1.86 |
| 26 | 25.65% | 15.00 ± 0.00 | 11.15 ± 1.85 |
| 27 | 25.93% | 15.00 ± 0.00 | 11.11 ± 1.84 |
| 28 | 26.09% | 15.00 ± 0.00 | 11.09 ± 1.84 |
| 29 | 26.44% | 15.00 ± 0.00 | 11.03 ± 1.81 |
| 30 | 27.21% | 15.00 ± 0.00 | 10.92 ± 1.85 |
| 31 | 27.95% | 15.00 ± 0.00 | 10.81 ± 1.88 |
| 32 | 28.24% | 15.00 ± 0.00 | 10.76 ± 1.89 |
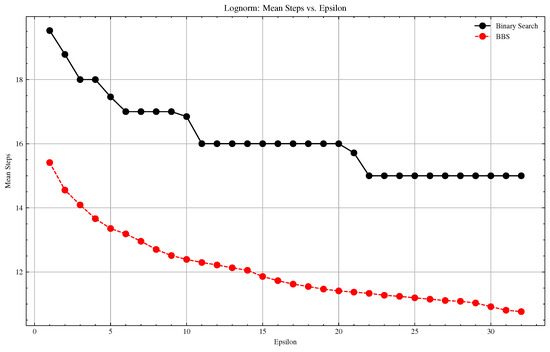
Figure A5.
Lognorm Distribution: Basic vs. BBS Convergence Comparison.
Appendix A.2. Binary Search Tree Visualization Comparison
To visualize the difference between the execution of BBS and standard binary search in a normally distributed search space , , we show binary search trees (BSTs) for basic binary search and BBS over 10,000 iterations of the experiment. We observe a significantly higher percentage of BBS searches terminating at a depth of 2, where all basic searches in this experiment terminate at a depth of 3 or 4. The bracket represents the search interval, and the number below for internal nodes represents the median of that search interval. The number below the bracket for the green leaf nodes represents how many times the search terminated at that leaf.
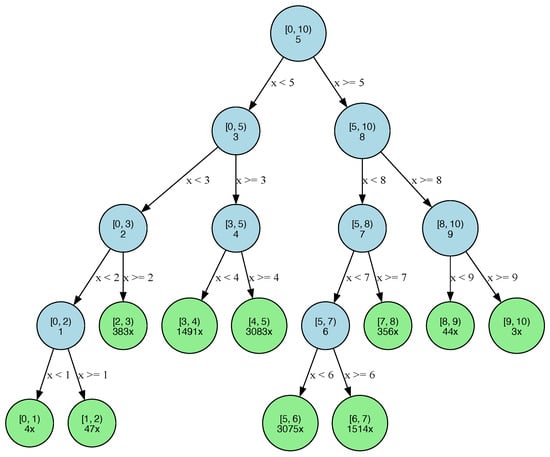
Figure A6.
Binary Search Tree.
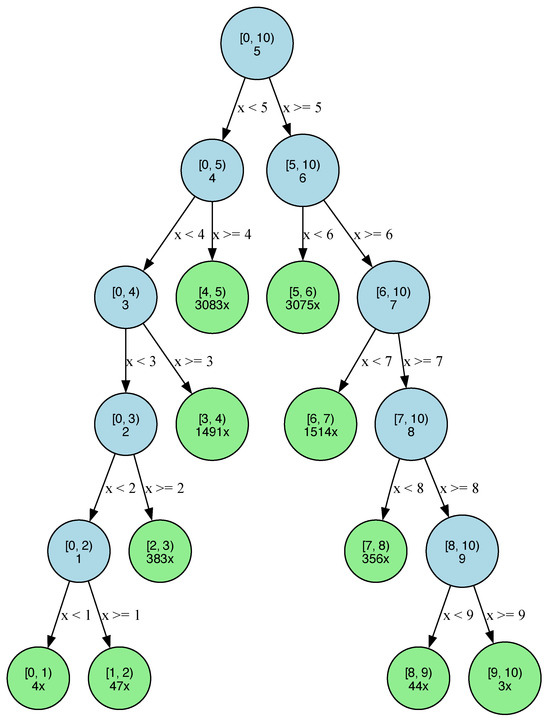
Figure A7.
Bayesian Binary Search Tree.
Theoretical Foundations of Probabilistic Search
The “bisection” algorithm, a strategy where the root is chosen to equalize the total weight of the left and right subtrees as much as possible (Rule II in the paper), relevant to our discussion, was rigorously analyzed in [24].
Mehlhorn’s Theorem 1 provides an upper bound on the weighted path length () of a tree constructed according to Rule II, in terms of the entropy (H) of the frequency distribution:
where is the entropy of the frequency distribution. The value of . This result provides a worst-case guarantee on the performance of the bisection-based tree construction in relation to the inherent uncertainty (entropy) of the data.
Furthermore, Theorem 2 in the paper establishes a lower bound on the weighted path length () of any optimal binary search tree for the same frequency distribution:
This lower bound shows that the performance of any search tree cannot be arbitrarily better than the entropy of the distribution. The fact that the upper bound for the balanced tree (constructed by the bisection-like Rule II) is within a constant factor of this lower bound demonstrates the near-optimality of this simple algorithm.
Recent work by [25] complements these findings by considering the scenario where the prediction of the distribution itself might be imperfect. They present an algorithm with a query complexity of , where is the entropy of the true distribution p, and is the Earth mover’s distance (EMD) between p and the predicted distribution [cite: 8]. This result shows that the search complexity depends not only on the entropy of the true distribution but also on the accuracy of the predicted distribution. Notably, they also provide a lower bound demonstrating that this query complexity is asymptotically tight.
Appendix A.3. Theoretical Analysis: General Convergence Proof and Worst Case for Normal Distribution
Terms:
- Domain/Search Space: , where and ;
- Unknown Target: ;
- Sign Function: ;
- Boundary Conditions: ;
- Tolerance: .
Appendix A.3.1. Proof of Convergence of Bisection Method on Domain Space
Algorithm Description
The bisection method starts with an initial interval such that and . The interval is halved at each step, and the new interval is chosen based on the sign of the function s at the midpoint. This process is repeated until the length of the interval is less than or equal to a specified tolerance , where .
Let the length of the initial interval be . At each iteration, the interval is halved, so after k iterations, the length of the interval becomes
Stopping Condition
The method stops when the length of the interval is less than or equal to , i.e., when
Solving for k, we get
Taking the logarithm (base 2) of both sides,
Thus, the number of iterations k required to achieve the desired tolerance is
Appendix A.3.2. Proof of Convergence of Bisection Method on Probability Density Space
Algorithm Description
Given the same framework of terms as above, in addition to
Bisecting on probability density space is similar to the above method where we bisect on the domain space.
The key difference is that rather than bisecting the domain space with an initial interval of , we will bisect the probability space with an initial interval of , i.e., , where and . Our search space then becomes , and at each iteration, we will cut the percentile interval in half.
Our stopping condition then becomes
Stopping Condition
Define the length of the interval as . At iteration 0, . At iteration 1, the interval could be or , where the length of both ranges is . Because the percentile interval is cut in half at each iteration, we know that the length of the interval at iteration k is . So, at iteration k, the interval is equivalent to . Note that the left or right side of the interval may remain open if remains 0 or remains 1 throughout the duration of the algorithm, respectively.
We can then rewrite our stopping condition of as .
To prove that this algorithm converges, we know that as n approaches ∞, approaches 0. Thus, as n approaches ∞, the length of the interval approaches 0. Therefore, because , we know this algorithm converges.
The rate of convergence depends on the probability distribution function.
The algorithm is described below:
| Algorithm A1: Number of Steps Required for Bayesian Binary Search Convergence |
 |
Appendix A.3.3. Proving Worst-Case Time Complexity of BBS on Normal Distribution
The worst case of BBS on the normal distribution is when the target t approaches the left or right tail of the normal distribution.
The proofs below assume that the target approaches . However, the same methods can be trivially applied to .
Given that the length of the probability interval is at iteration k, if target , then can be found via
After the first iteration, becomes and is repeatedly halved on each subsequent iteration.
At each iteration k, the searchable domain space is reduced by the quantity of the domain space to the right of ).
Subtracting the length of the domain space by the summation of the domain space reduced up to iteration k is equal to the length of the interval in terms of the domain space. Technically, extends to positive infinity for the normal distribution; however, it is canceled out in the proof below. The proof below proves that the summation is equivalent to the simplified expression below it.
Proof by Induction
Let be the statement
for all positive integers n.
Basis step: is true.
Inductive step: Assume is true for some integer . Now, we show that must also be true:
∴ We have shown using the principle of mathematical induction that is true for all positive integers n.
To prove and are the worst cases in terms of time complexity for targets in the normal distribution, we will prove that no other target takes longer to converge.
Theorem A1.
For a standard normal distribution with CDF and quantile function , the number of binary search steps required to achieve convergence within precision ϵ is maximized when the target approaches or .
Proof.
We proceed by establishing several key properties of the quantile function and showing how they determine the convergence behavior of binary search.
Let us first establish our framework. For any target where , the binary search algorithm maintains an interval in probability space, corresponding to the interval in the domain space. □
Lemma A1.
The derivative of the quantile function is strictly increasing in magnitude as increases toward the tails of the distribution.
Proof of Lemma A1.
The derivative of the quantile function can be expressed as
For the standard normal distribution,
Therefore,
Since is monotonic and as or 1, strictly increases as x approaches 0 or 1 starting from .
Now, consider the binary search algorithm at iteration i. The width of the interval in probability space is . Let be any such interval. The corresponding width in domain space is
By the mean value theorem,
for some .
Due to the monotonicity of established in the lemma, this width is maximized when the interval is positioned as close as possible to either 0 or 1.
When the target approaches or ,
- The interval always includes one of the endpoints (0 or 1);
- The domain space interval is therefore maximized at each iteration.
For convergence, we require
The number of steps required to achieve this condition is determined by the width of the interval in domain space. Since this width is maximized when targeting or , these targets require the maximum number of steps for convergence.
More formally, for any target where , let be the number of steps required for convergence. Then,
Therefore, and represent the worst-case scenarios for convergence of the binary search algorithm. □
Appendix A.3.4. Additional Experiments with GPR Density Estimation and Runtime Approximation
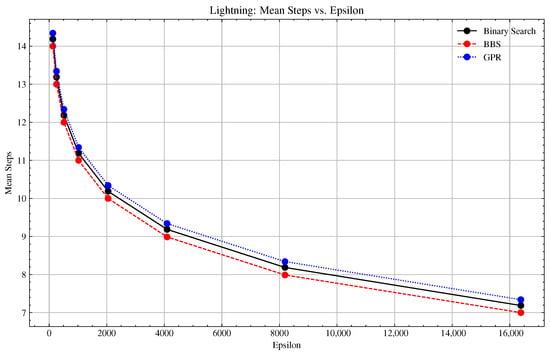
Figure A8.
Lightning Probing Experiment: Basic vs. BBS Convergence Comparison.
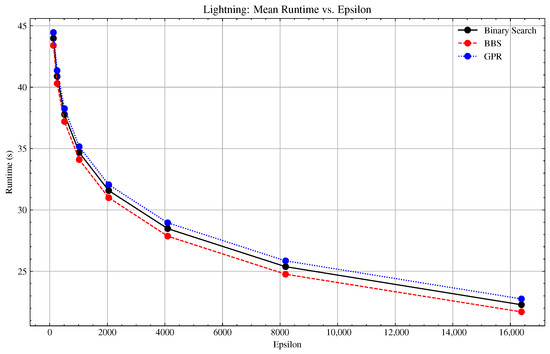
Figure A9.
Lightning Probing Experiment: Basic vs. BBS Convergence Comparison (Runtime).
References
- Knuth, D.E. The Art of Computer Programming: Volume 3: Sorting and Searching; Addison-Wesley Professional: Boston, MA, USA, 1998. [Google Scholar]
- Peterson, W.W. Addressing for random-access storage. IBM J. Res. Dev. 1957, 1, 130–146. [Google Scholar] [CrossRef]
- Lehmer, D.H. Teaching combinatorial tricks to a computer. Proc. Sympos. Appl. Math. 1960, 10, 179–193. [Google Scholar]
- Bottenbruch, H. Structure and use of algol 60. In Symbolic Languages in Data Processing; Gordon and Breach: London, UK, 1962; pp. 121–140. [Google Scholar]
- Chazelle, B.; Guibas, L.J. Fractional cascading: I. A data structuring technique. In Algorithmica; Springer: Berlin/Heidelberg, Germany, 1986; pp. 133–162. [Google Scholar]
- Mohammed, A.S.; Amrahov, Ş.E.; Çelebi, F.V. Interpolated binary search: An efficient hybrid search algorithm on ordered datasets. Eng. Sci. Technol. Int. J. 2021, 24, 1072–1079. [Google Scholar] [CrossRef]
- Lin, J.-L. Interpolation Once Binary Search over a Sorted List. Mathematics 2024, 12, 1394. [Google Scholar] [CrossRef]
- Lin, H.; Luo, T.; Woodruff, D. Learning augmented binary search trees. In International Conference on Machine Learning; PMLR: New York, NY, USA, 2022; pp. 13431–13440. [Google Scholar]
- Russ, S. The Mathematical Works of Bernard Bolzano; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis; Cengage Learning: Boston, MA, USA, 2015. [Google Scholar]
- Horstein, M. Sequential transmission using noiseless feedback. IEEE Trans. Inf. Theory 1963, 9, 136–143. [Google Scholar] [CrossRef]
- Hansen, E.; Walster, G.W. Global optimization using interval analysis: The multi-dimensional case. Comput. Math. Appl. 1991, 21, 173–194. [Google Scholar] [CrossRef]
- Waeber, R.; Frazier, P.I.; Henderson, S.G. A bayesian approach to stochastic root finding. In Proceedings of the 2013 Winter Simulation Conference, Phoenix, AZ, USA, 11–14 December 2011; IEEE: New York, NY, USA, 2013; pp. 4033–4043. [Google Scholar]
- Jedynak, B.; Frazier, P.I.; Sznitman, R. Twenty questions with noise: Bayes optimal policies for entropy loss. J. Appl. Probab. 2012, 49, 114–136. [Google Scholar] [CrossRef]
- Nievergelt, J. Parallel methods for integrating ordinary differential equations. Commun. ACM 1964, 7, 731–733. [Google Scholar] [CrossRef]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452–459. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; MIT Press: Cambridge, UK, 2006. [Google Scholar]
- Wang, H.; Yeung, D.-Y. Towards bayesian deep learning: A framework and some existing methods. IEEE Trans. Knowl. Data Eng. 2016, 28, 3395–3408. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; De Freitas, N. Taking the human out of the loop: A review of bayesian optimization. Proc. IEEE 2015, 104, 148–175. [Google Scholar] [CrossRef]
- Tikhomirov, S.; Pickhardt, R.; Biryukov, A.; Nowostawski, M. Probing channel balances in the lightning network. arXiv 2020, arXiv:2004.00333. [Google Scholar]
- Rossi, E.; Singh, V. Channel balance interpolation in the lightning network via Machine learning. arXiv 2024, arXiv:2405.12087. [Google Scholar]
- Rosenblatt, F. The perceptron—A Perceiving and Recognizing Automaton; Technical Report 85-460-1; Cornell Aeronautical Laboratory: Ithaca, NY, USA, 1957. [Google Scholar]
- Dwivedi, V.P.; Joshi, C.K.; Laurent, T.; Bengio, Y.; Bresson, X. Benchmarking graph neural networks. arXiv 2020, arXiv:2003.00982. [Google Scholar]
- Mehlhorn, K. Nearly optimal binary search trees. Acta Inform. 1975, 5, 287–295. [Google Scholar] [CrossRef]
- Dinitz, M.; Im, S.; Lavastida, T.; Moseley, B.; Niaparast, A.; Vassilvitskii, S. Binary search with distributional predictions. arXiv 2024, arXiv:2411.16030. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).