High-Precision Chip Detection Using YOLO-Based Methods
Abstract
1. Introduction
- We compare the performance of different YOLO versions in detecting debris in images of machining processes;
- A ghost module is introduced into the backbone of the standard YOLOv11 to reduce the computation;
- A dynamic non-maximum suppression algorithm is proposed to enhance the accuracy in identifying small objects—in this case, chips;
- Based on the rising edge signal trigger mechanism, a video-level post-processing algorithm is developed to automatically count the number of chips that fall within the video.
2. Materials and Methods
2.1. Model Architecture
2.1.1. YOLOv11
2.1.2. Ghost Module
2.1.3. GM-YOLOv11
2.2. Dynamic Non-Maximum Suppression (DNMS) Algorithm
2.2.1. Leaving Debris and Left Debris
2.2.2. Box Size Adjustment
2.2.3. Dynamic Non-Maximum Suppression Algorithm
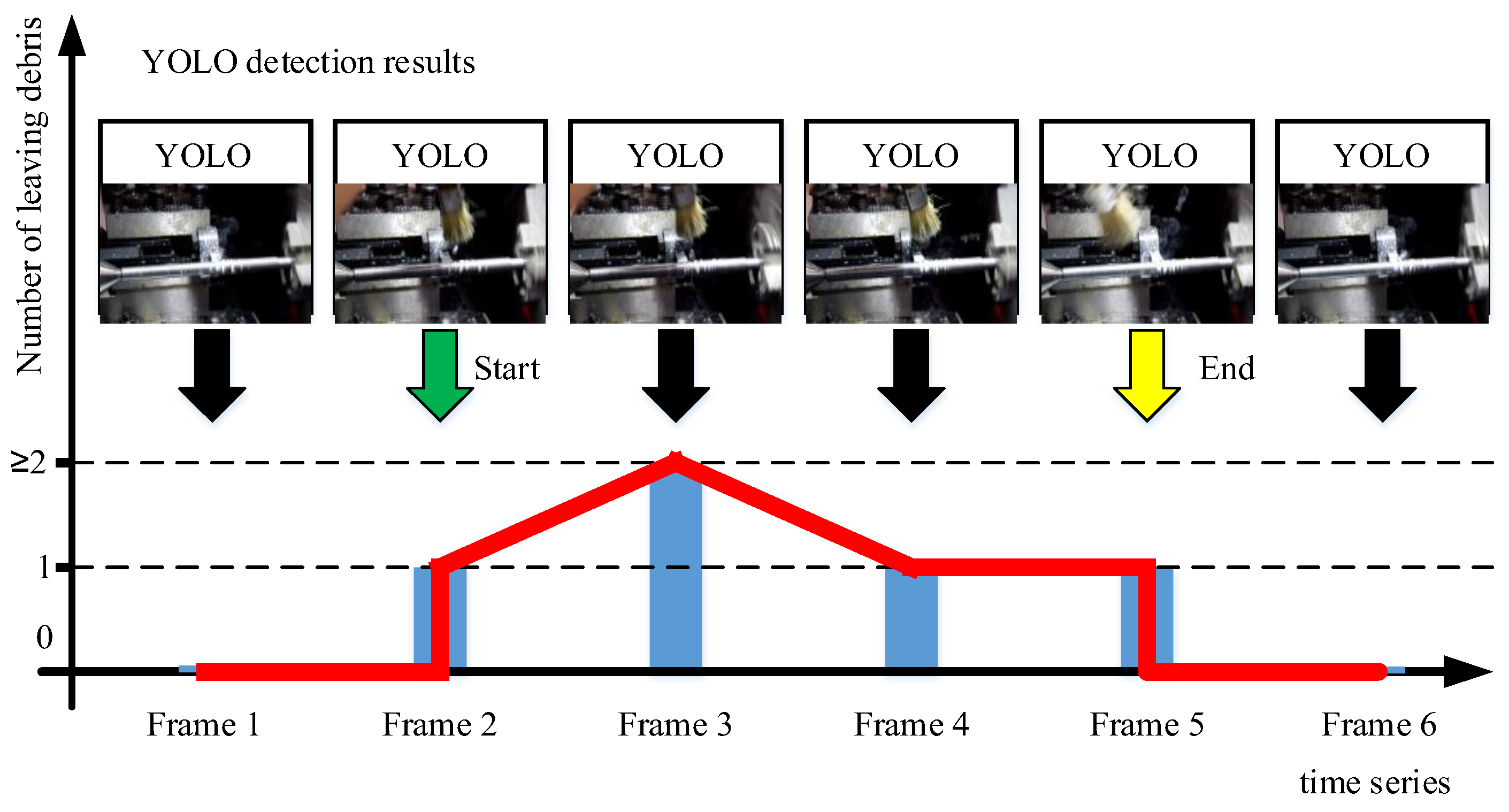
2.3. Video-Level Post-Processing Algorithm (VPPA)
3. Results
3.1. Data Resources
3.2. Performance Indicators
- Precision measures the proportion of correctly detected chip images relative to the total number of images identified as chips (both correct and incorrect). It is formally defined as
- 2.
- Recall measures the proportion of correctly detected chip images relative to the total number of images that should have been detected (including both correctly detected and undetected chips). It is formally defined as
- 3.
- The F1-score is a composite metric for the evaluation of the performance of classification models, defined as the harmonic mean of the precision and recall. It is formally defined as
- 4.
- The average precision (AP) averages the accuracy of the chips in the dataset. The mean average precision (mAP) refers to the average of the AP values for each category. However, the only category in this experiment is pineapple, and the AP is equal to the mAP. The mAP is formally defined as
- 5.
- The FLOPs value quantifies the computational complexity of the algorithm by measuring the number of floating-point operations required during inference. It is formally defined as
- 6.
- Model Size (MS) refers to the size of model and is used to evaluate the complexity of the model.
- 7.
- Frames per second (FPS) is the number of pictures that the model can detect in one second. The calculation formula is
- 8.
- The error proportion is used to evaluate the accuracy of the chip quantity statistics in videos to assess the overall system’s accuracy. It is formally defined as
3.3. Experimental Results
3.3.1. Visualization of the Results
3.3.2. Ghost Module Improvement Experiment
3.3.3. DNMS Improvement Experiment
3.3.4. Results of Video-Level Post-Processing Algorithm
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Section | ID | From | Repeats | Module | Args | Parameter Explanation |
|---|---|---|---|---|---|---|
| Backbone | 0 | −1 | 1 | GhostConv | [64, 3,3,2,2] | Input channels auto-inferred, output 64 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 |
| 1 | −1 | 1 | GhostConv | [128, 3,3,2,2] | Output 128 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 | |
| 2 | −1 | 2 | C3k2 | [256, False, 0.25] | Output 256 channels, no shortcut connection, bottleneck width reduction ratio 0.25 | |
| 3 | −1 | 1 | GhostConv | [256, 3,3,2,2] | Output 256 channels, 3 × 3 kernel, stride 2 | |
| 4 | −1 | 2 | C3k2 | [512, False, 0.25] | Output 512 channels, no shortcut connection, bottleneck width reduction ratio 0.25 | |
| 5 | −1 | 1 | GhostConv | [512, 3,3,2,2] | Output 512 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 | |
| 6 | −1 | 2 | C3k2 | [512, True] | Output 512 channels, with shortcut connection | |
| 7 | −1 | 1 | GhostConv | [1024,3,3,2,2] | Output 1024 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 | |
| 8 | −1 | 2 | C3k2 | [1024, True] | Output 1024 channels, with shortcut connection | |
| 9 | −1 | 1 | SPPF | [1024, 5] | Output 1024 channels, max pooling kernel size 5 × 5 | |
| 10 | −1 | 2 | C2PSA | [1024] | Output 1024 channels | |
| Head | 0 | −1 | 1 | nn.Upsample | [None, 2, “nearest”] | Upsample with scale factor 2, nearest-neighbor interpolation |
| 1 | [−1, 6] | 1 | Concat | [1] | Concatenate current layer with backbone layer 6 along channel dim | |
| 2 | −1 | 2 | C3k2 | [512, False] | Output 512 channels, no shortcut connection | |
| 3 | −1 | 1 | nn.Upsample | [None, 2, “nearest”] | Second 2× upsampling | |
| 4 | [−1, 4] | 1 | Concat | [1] | Concatenate with backbone layer 4 | |
| 5 | −1 | 2 | C3k2 | [256, False] | Output 256 channels, no shortcut connection | |
| 6 | −1 | 1 | Conv | [256, 3, 2] | Output 256 channels, 3 × 3 kernel, stride 2 | |
| 7 | [−1, 13] | 1 | Concat | [1] | Concatenate with head layer 13 | |
| 8 | −1 | 2 | C3k2 | [512, False] | Output 512 channels, no shortcut connection | |
| 9 | −1 | 1 | Conv | [512, 3, 2] | Output 512 channels, 3 × 3 kernel, stride 2 | |
| 10 | [−1, 10] | 1 | Concat | [1] | Concatenate with backbone layer 10 | |
| 11 | −1 | 2 | C3k2 | [1024, True] | Output 1024 channels, with shortcut connection | |
| 12 | [16, 19, 22] | 1 | Detect | [2] | Number of classes is 2 |
| Section | ID | From | Repeats | Module | Args | Parameter Explanation |
|---|---|---|---|---|---|---|
| Backbone | 0 | −1 | 1 | Conv | [64, 3, 2] | Input channels auto-inferred, output 64 channels, 3 × 3 kernel, stride 2 |
| 1 | −1 | 1 | Conv | [128, 3, 2] | Output 128 channels, 3 × 3 kernel, stride 2 | |
| 2 | −1 | 2 | C3k2 | [256, False, 0.25] | Output 256 channels, no shortcut connection, bottleneck width reduction ratio 0.25 | |
| 3 | −1 | 1 | Conv | [256, 3, 2] | Output 256 channels, 3 × 3 kernel, stride 2 | |
| 4 | −1 | 2 | C3k2 | [512, False, 0.25] | Output 512 channels, no shortcut connection, bottleneck width reduction ratio 0.25 | |
| 5 | −1 | 1 | Conv | [512, 3, 2] | Output 512 channels, 3 × 3 kernel, stride 2 | |
| 6 | −1 | 2 | C3k2 | [512, True] | Output 512 channels, with shortcut connection | |
| 7 | −1 | 1 | Conv | [1024, 3, 2] | Output 1024 channels, 3 × 3 kernel, stride 2 | |
| 8 | −1 | 2 | C3k2 | [1024, True] | Output 1024 channels, with shortcut connection | |
| 9 | −1 | 1 | SPPF | [1024, 5] | Output 1024 channels, max pooling kernel size 5 × 5 | |
| 10 | −1 | 2 | C2PSA | [1024] | Output 1024 channels | |
| Head | 0 | −1 | 1 | nn.Upsample | [None, 2, “nearest”] | Upsample with scale factor 2, nearest-neighbor interpolation |
| 1 | [−1, 6] | 1 | Concat | [1] | Concatenate current layer with backbone layer 6 along channel dim | |
| 2 | −1 | 2 | C3k2 | [512, False] | Output 512 channels, no shortcut connection | |
| 3 | −1 | 1 | nn.Upsample | [None, 2, “nearest”] | Second 2× upsampling | |
| 4 | [−1, 4] | 1 | Concat | [1] | Concatenate with backbone layer 4 | |
| 5 | −1 | 2 | C3k2 | [256, False] | Output 256 channels, no shortcut connection | |
| 6 | −1 | 1 | GhostConv | [256, 3,3,2,2] | Output 256 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 | |
| 7 | [−1, 13] | 1 | Concat | [1] | Concatenate with head layer 13 | |
| 8 | −1 | 2 | C3k2 | [512, False] | Output 512 channels, no shortcut connection | |
| 9 | −1 | 1 | GhostConv | [512,3,3,2,2] | Output 512 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 | |
| 10 | [−1, 10] | 1 | Concat | [1] | Concatenate with backbone layer 10 | |
| 11 | −1 | 2 | C3k2 | [1024, True] | Output 1024 channels, with shortcut connection | |
| 12 | [16, 19, 22] | 1 | Detect | [2] | Number of classes is 2 |
| Section | ID | From | Repeats | Module | Args | Parameter Explanation |
|---|---|---|---|---|---|---|
| Backbone | 0 | −1 | 1 | GhostConv | [64, 3,3,2,2] | Input channels auto-inferred, output 64 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 |
| 1 | −1 | 1 | GhostConv | [128, 3,3,2,2] | Output 128 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 | |
| 2 | −1 | 2 | C3k2 | [256, False, 0.25] | Output 256 channels, no shortcut connection, bottleneck width reduction ratio 0.25 | |
| 3 | −1 | 1 | GhostConv | [256, 3,3,2,2] | Output 256 channels, 3 × 3 kernel, stride 2 | |
| 4 | −1 | 2 | C3k2 | [512, False, 0.25] | Output 512 channels, no shortcut connection, bottleneck width reduction ratio 0.25 | |
| 5 | −1 | 1 | GhostConv | [512, 3,3,2,2] | Output 512 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 | |
| 6 | −1 | 2 | C3k2 | [512, True] | Output 512 channels, with shortcut connection | |
| 7 | −1 | 1 | GhostConv | [1024,3,3,2,2] | Output 1024 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 | |
| 8 | −1 | 2 | C3k2 | [1024, True] | Output 1024 channels, with shortcut connection | |
| 9 | −1 | 1 | SPPF | [1024, 5] | Output 1024 channels, max pooling kernel size 5 × 5 | |
| 10 | −1 | 2 | C2PSA | [1024] | Output 1024 channels | |
| Head | 0 | −1 | 1 | nn.Upsample | [None, 2, “nearest”] | Upsample with scale factor 2, nearest-neighbor interpolation |
| 1 | [−1, 6] | 1 | Concat | [1] | Concatenate current layer with backbone layer 6 along channel dim | |
| 2 | −1 | 2 | C3k2 | [512, False] | Output 512 channels, no shortcut connection | |
| 3 | −1 | 1 | nn.Upsample | [None, 2, “nearest”] | Second 2× upsampling | |
| 4 | [−1, 4] | 1 | Concat | [1] | Concatenate with backbone layer 4 | |
| 5 | −1 | 2 | C3k2 | [256, False] | Output 256 channels, no shortcut connection | |
| 6 | −1 | 1 | GhostConv | [256, 3,3,2,2] | Output 256 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 | |
| 7 | [−1, 13] | 1 | Concat | [1] | Concatenate with head layer 13 | |
| 8 | −1 | 2 | C3k2 | [512, False] | Output 512 channels, no shortcut connection | |
| 9 | −1 | 1 | GhostConv | [512,3,3,2,2] | Output 512 channels, 3 × 3 kernel for both primary convolution and linear operation, s = 2, stride 2 | |
| 10 | [−1, 10] | 1 | Concat | [1] | Concatenate with backbone layer 10 | |
| 11 | −1 | 2 | C3k2 | [1024, True] | Output 1024 channels, with shortcut connection | |
| 12 | [16, 19, 22] | 1 | Detect | [2] | Number of classes is 2 |
References
- García Plaza, E.; Núñez López, P.J.; Beamud González, E.M. Multi-Sensor Data Fusion for Real-Time Surface Quality Control in Automated Machining Systems. Sensors 2018, 18, 4381. [Google Scholar] [CrossRef] [PubMed]
- Fowler, N.O.; McCall, D.; Chou, T.-C.; Holmes, J.C.; Hanenson, I.B. Electrocardiographic Changes and Cardiac Arrhythmias in Patients Receiving Psychotropic Drugs. Am. J. Cardiol. 1976, 37, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guo, J.; Wang, D.; Li, S.; Liu, X. Experimental Study on High-Speed Hard Cutting by PCBN Tools with Variable Chamfered Edge. Int. J. Adv. Manuf. Technol. 2018, 97, 4209–4216. [Google Scholar] [CrossRef]
- Cheng, Y.; Guan, R.; Zhou, S.; Zhou, X.; Xue, J.; Zhai, W. Research on Tool Wear and Breakage State Recognition of Heavy Milling 508III Steel Based on ResNet-CBAM. Measurement 2025, 242, 116105. [Google Scholar] [CrossRef]
- Vorontsov, A.L.; Sultan-Zade, N.M.; Albagachiev, A.Y. Development of a New Theory of Cutting 8. Chip-Breaker Design. Russ. Eng. Res. 2008, 28, 786–792. [Google Scholar] [CrossRef]
- Zaidi, S.S.A.; Ansari, M.S.; Aslam, A.; Kanwal, N.; Asghar, M.; Lee, B. A Survey of Modern Deep Learning Based Object Detection Models. Digit. Signal Process. 2022, 126, 103514. [Google Scholar] [CrossRef]
- Pagani, L.; Parenti, P.; Cataldo, S.; Scott, P.J.; Annoni, M. Indirect cutting tool wear classification using deep learning and chip colour analysis. Int. J. Adv. Manuf. Technol. 2020, 111, 1099–1114. [Google Scholar] [CrossRef]
- Rehman, A.U.; Nishat, T.S.R.; Ahmed, M.U.; Begum, S.; Ranjan, A. Chip Analysis for Tool Wear Monitoring in Machining: A Deep Learning Approach. IEEE Access 2024, 12, 112672–112689. [Google Scholar] [CrossRef]
- Chen, S.H.; Lin, Y.Y. Using cutting temperature and chip characteristics with neural network BP and LSTM method to predicting tool life. Int. J. Adv. Manuf. Technol. 2023, 127, 881–897. [Google Scholar] [CrossRef]
- Shen, D.; Chen, X.; Nguyen, M.; Yan, W.Q. Flame Detection Using Deep Learning. In Proceedings of the 2018 4th International Conference on Control, Automation and Robotics (ICCAR), Auckland, New Zealand, 20–23 April 2018; pp. 416–420. [Google Scholar]
- Cai, C.; Wang, B.; Liang, X. A New Family Monitoring Alarm System Based on Improved YOLO Network. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 4269–4274. [Google Scholar]
- Badgujar, C.M.; Poulose, A.; Gan, H. Agricultural Object Detection with You Only Look Once (YOLO) Algorithm: A Bibliometric and Systematic Literature Review. Comput. Electron. Agric. 2024, 223, 109090. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, X.; Zhou, X.; Qian, S.; Yu, J. Defect Detection for Metal Base of TO-Can Packaged Laser Diode Based on Improved YOLO Algorithm. Electronics 2022, 11, 1561. [Google Scholar] [CrossRef]
- Banda, T.; Jauw, V.L.; Farid, A.A.; Wen, N.H.; Xuan, K.C.W.; Lim, C.S. In-process detection of failure modes using YOLOv3-based on-machine vision system in face milling Inconel 718. Int. J. Adv. Manuf. Technol. 2023, 128, 3885–3899. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. Yolov3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. Yolov4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Wang, C.-Y.; Bochkovskiy, A.; Liao, H.-Y.M. YOLOv7: Trainable Bag-of-Freebies Sets New State-of-the-Art for Real-Time Object Detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Online, 27 June 2023; pp. 7464–7475. [Google Scholar]
- Swathi, Y.; Challa, M. YOLOv8: Advancements and Innovations in Object Detection. In Smart Trends in Computing and Communications; Springer Nature: Singapore, 2024; pp. 1–13. [Google Scholar]
- Wang, C.-Y.; Yeh, I.-H.; Mark Liao, H.-Y. YOLOv9: Learning What You Want to Learn Using Programmable Gradient Information. In Computer Vision—ECCV 2024; Springer Nature: Cham, Switzerland, 2024; pp. 1–21. [Google Scholar]
- Kshirsagar, V.; Bhalerao, R.H.; Chaturvedi, M. Modified YOLO Module for Efficient Object Tracking in a Video. IEEE Lat. Am. Trans. 2023, 21, 389–398. [Google Scholar] [CrossRef]
- Doherty, J.; Gardiner, B.; Kerr, E.; Siddique, N. BiFPN-YOLO: One-Stage Object Detection Integrating Bi-Directional Feature Pyramid Networks. Pattern Recognit. 2025, 160, 111209. [Google Scholar] [CrossRef]
- Yan, J.; Zeng, Y.; Lin, J.; Pei, Z.; Fan, J.; Fang, C.; Cai, Y. Enhanced Object Detection in Pediatric Bronchoscopy Images Using YOLO-Based Algorithms with CBAM Attention Mechanism. Heliyon 2024, 10, e32678. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, W.; Zhang, Z.; Lin, X.; Zhao, J.; Chen, M.; Luo, L. YOLO-DD: Improved YOLOv5 for Defect Detection. Comput. Mater. Contin. 2024, 78, 759–780. [Google Scholar] [CrossRef]
- Wang, M.; Fu, B.; Fan, J.; Wang, Y.; Zhang, L.; Xia, C. Sweet Potato Leaf Detection in a Natural Scene Based on Faster R-CNN with a Visual Attention Mechanism and DIoU-NMS. Ecol. Inf. 2023, 73, 101931. [Google Scholar] [CrossRef]
- Xue, C.; Xia, Y.; Wu, M.; Chen, Z.; Cheng, F.; Yun, L. EL-YOLO: An Efficient and Lightweight Low-Altitude Aerial Objects Detector for Onboard Applications. Expert Syst. Appl. 2024, 256, 124848. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, B.; Fan, Y. PPGS-YOLO: A Lightweight Algorithms for Offshore Dense Obstruction Infrared Ship Detection. Infrared Phys. Technol. 2025, 145, 105736. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Tian, Q.; Guo, J.; Xu, C.; Xu, C. GhostNet: More Features from Cheap Operations. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Online, 24 June 2020; pp. 1577–1586. [Google Scholar]
- Wang, H.; Wang, G.; Li, Y.; Zhang, K. YOLO-HV: A Fast YOLOv8-Based Method for Measuring Hemorrhage Volumes. Biomed. Signal Process. Control 2025, 100, 107131. [Google Scholar] [CrossRef]
- Dong, X.; Yan, S.; Duan, C. A Lightweight Vehicles Detection Network Model Based on YOLOv5. Eng. Appl. Artif. Intell. 2022, 113, 104914. [Google Scholar] [CrossRef]
- Rashmi; Chaudhry, R. SD-YOLO-AWDNet: A Hybrid Approach for Smart Object Detection in Challenging Weather for Self-Driving Cars. Expert Syst. Appl. 2024, 256, 124942. [Google Scholar] [CrossRef]
- Cui, M.; Lou, Y.; Ge, Y.; Wang, K. LES-YOLO: A Lightweight Pinecone Detection Algorithm Based on Improved YOLOv4-Tiny Network. Comput. Electron. Agric. 2023, 205, 107613. [Google Scholar] [CrossRef]
- Li, J.; Su, Z.; Geng, J.; Yin, Y. Real-Time Detection of Steel Strip Surface Defects Based on Improved YOLO Detection Network. IFAC-Pap. 2018, 51, 76–81. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, W.; Li, S.; Liu, H.; Hu, Q. YOLO-Ships: Lightweight Ship Object Detection Based on Feature Enhancement. J. Vis. Commun. Image Represent. 2024, 101, 104170. [Google Scholar] [CrossRef]
- Huangfu, Z.; Li, S.; Yan, L. Ghost-YOLO v8: An Attention-Guided Enhanced Small Target Detection Algorithm for Floating Litter on Water Surfaces. Comput. Mater. Contin. 2024, 80, 3713–3731. [Google Scholar] [CrossRef]
- Chen, J.; Chen, H.; Xu, F.; Lin, M.; Zhang, D.; Zhang, L. Real-Time Detection of Mature Table Grapes Using ESP-YOLO Network on Embedded Platforms. Biosyst. Eng. 2024, 246, 122–134. [Google Scholar] [CrossRef]









| Input: output of YOLO net Output: all chips and their locations |
| (1) Find using the standard non-maximum suppression algorithm (2) Adjust the size of according to Equations (7)–(9) (3) Find the bounding box Bdk with the highest score of pd according to Equation (10) (4) Calculate , , as well as ; if , ) , delete bounding box (5) Repeat the sorting and soft threshold operation for the remaining predicted bounding boxes and perform steps (3) and (4) until no more boxes can be deleted |
| Model | Precision (%) | Recall (%) | F1-Score (%) | mAP@0.5 (%) | FLOPs (G) | MS (MB) | FPS |
|---|---|---|---|---|---|---|---|
| YOLOv5n | 92.66 | 92.44 | 92.55 | 91.10 | 7.73 | 1.9 | 116.68 |
| YOLOv8n | 90.22 | 88.72 | 89.46 | 89.53 | 8.75 | 3.2 | 149.02 |
| YOLOv9t | 89.67 | 90.12 | 89.89 | 92.24 | 8.23 | 2 | 73.78 |
| YOLOv10n | 91.14 | 86.66 | 88.84 | 87.05 | 8.57 | 2.3 | 100.2 |
| YOLOv11n | 94.11 | 95.42 | 94.76 | 94.68 | 6.48 | 2.6 | 154.34 |
| GM-YOLOv11-backbone | 93.60 | 94.08 | 93.84 | 93.63 | 5.81 | 2.2 | 167.34 |
| GM-YOLOv11-head | 93.36 | 93.67 | 93.51 | 93.66 | 6.33 | 2.5 | 156.23 |
| GM-YOLOv11 | 93.80 | 93.96 | 93.88 | 93.81 | 5.72 | 2 | 173.41 |
| Literature [29] | 92.27 | 91.69 | 91.98 | 90.12 | 6.44 | 1.7 | 146.34 |
| Literature [28] | 91.22 | 90.63 | 90.92 | 90.29 | 7.84 | 2.8 | 135.26 |
| Regular Parameters α in Equation (10) | Regular Parameters β in Equation (10) | Left Chip Threshold a1 | Leaving Chip Threshold a2 | Recall (%) |
|---|---|---|---|---|
| 0.3 | 0.6 | 0.4 | 0.3 | 96.27 |
| 0.3 | 0.7 | 0.5 | 0.3 | 95.89 |
| 0.4 | 0.7 | 0.5 | 0.4 | 96.38 |
| 0.5 | 0.4 | 0.6 | 0.5 | 95.75 |
| 0.8 | 0.7 | 0.7 | 0.5 | 95.75 |
| 0.9 | 0.6 | 0.7 | 0.6 | 95.86 |
| Model | Precision (%) | Recall (%) | F1-Score (%) | mAP@0.5 (%) |
|---|---|---|---|---|
| YOLOv5n+DNMS | 93.85 | 94.11 | 93.98 | 92.99 |
| YOLOv8n+DNMS | 93.30 | 90.78 | 92.02 | 90.85 |
| YOLOv9t+DNMS | 90.83 | 91.80 | 91.31 | 93.34 |
| YOLOv10n+DNMS | 92.46 | 88.33 | 90.35 | 88.89 |
| YOLOv11n+DNMS | 97.05 | 96.81 | 96.93 | 96.48 |
| GM-YOLOv11-backbone+DNMS | 95.13 | 96.18 | 95.65 | 95.08 |
| GM-YOLOv11-neck+DNMS | 94.81 | 94.37 | 94.59 | 95.01 |
| GM-YOLOv11+DNMS | 97.04 | 96.38 | 96.71 | 95.56 |
| Literature [25] | 92.27 | 91.69 | 91.98 | 90.12 |
| Literature [24] | 91.22 | 90.63 | 90.92 | 90.29 |
| Serial Number | Duration (s) | Actual Number of Crack Chips |
|---|---|---|
| 1 | 36 | 13 |
| 2 | 103 | 47 |
| 3 | 158 | 61 |
| 4 | 210 | 82 |
| 5 | 213 | 79 |
| 6 | 213 | 80 |
| 7 | 51 | 25 |
| 8 | 49 | 18 |
| 9 | 35 | 24 |
| 10 | 28 | 7 |
| Total | 1096 | 436 |
| Model | Error Proportion (%) |
|---|---|
| YOLOv5n+DNMS+VPPA | 11.93 |
| YOLOv8n+DNMS+VPPA | 15.37 |
| YOLOv9t+DNMS+VPPA | 13.07 |
| YOLOv10n+DNMS+VPPA | 13.30 |
| YOLOv11n+DNMS+VPPA | 9.63 |
| GM-YOLOv11-backbone+DNMS+VPPA | 10.55 |
| GM-YOLOv11-neck+DNMS+VPPA | 11.47 |
| GM-YOLOv11+DNMS+VPPA | 9.86 |
| Literature [29] + VPPA | 15.14 |
| Literature [28] + VPPA | 15.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Zhu, J. High-Precision Chip Detection Using YOLO-Based Methods. Algorithms 2025, 18, 448. https://doi.org/10.3390/a18070448
Liu R, Zhu J. High-Precision Chip Detection Using YOLO-Based Methods. Algorithms. 2025; 18(7):448. https://doi.org/10.3390/a18070448
Chicago/Turabian StyleLiu, Ruofei, and Junjiang Zhu. 2025. "High-Precision Chip Detection Using YOLO-Based Methods" Algorithms 18, no. 7: 448. https://doi.org/10.3390/a18070448
APA StyleLiu, R., & Zhu, J. (2025). High-Precision Chip Detection Using YOLO-Based Methods. Algorithms, 18(7), 448. https://doi.org/10.3390/a18070448






