Adaptive Nonlinear Proportional–Integral–Derivative Control of a Continuous Stirred Tank Reactor Process Using a Radial Basis Function Neural Network
Abstract
1. Introduction
- To propose a nonlinear adaptive PID control technique combining the existing nonlinear PID controller and an RBFNN;
- To refine the NPID controller’s gain function to enhance its performance.
2. Problem Statement
2.1. CSTR Process Modeling
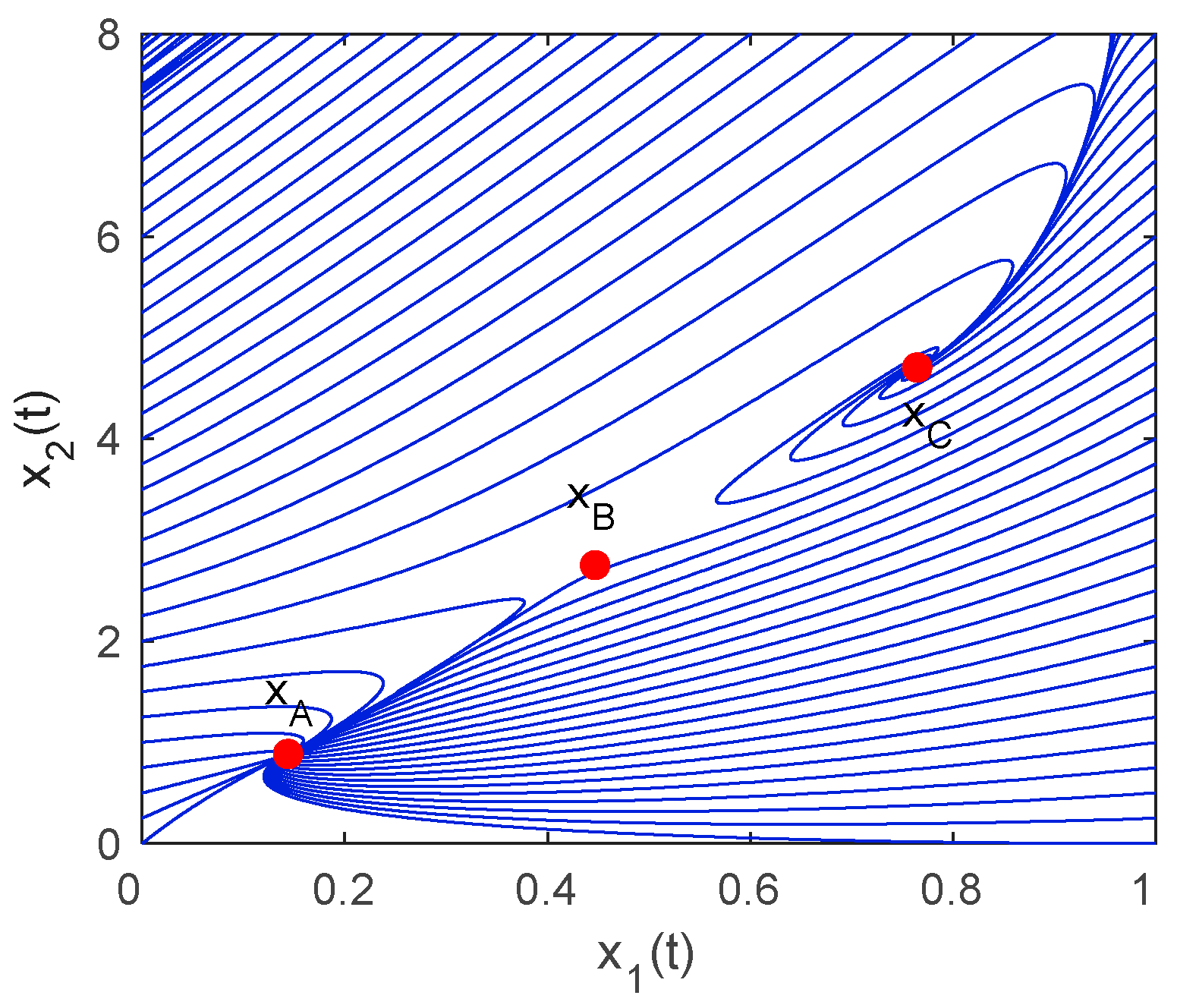
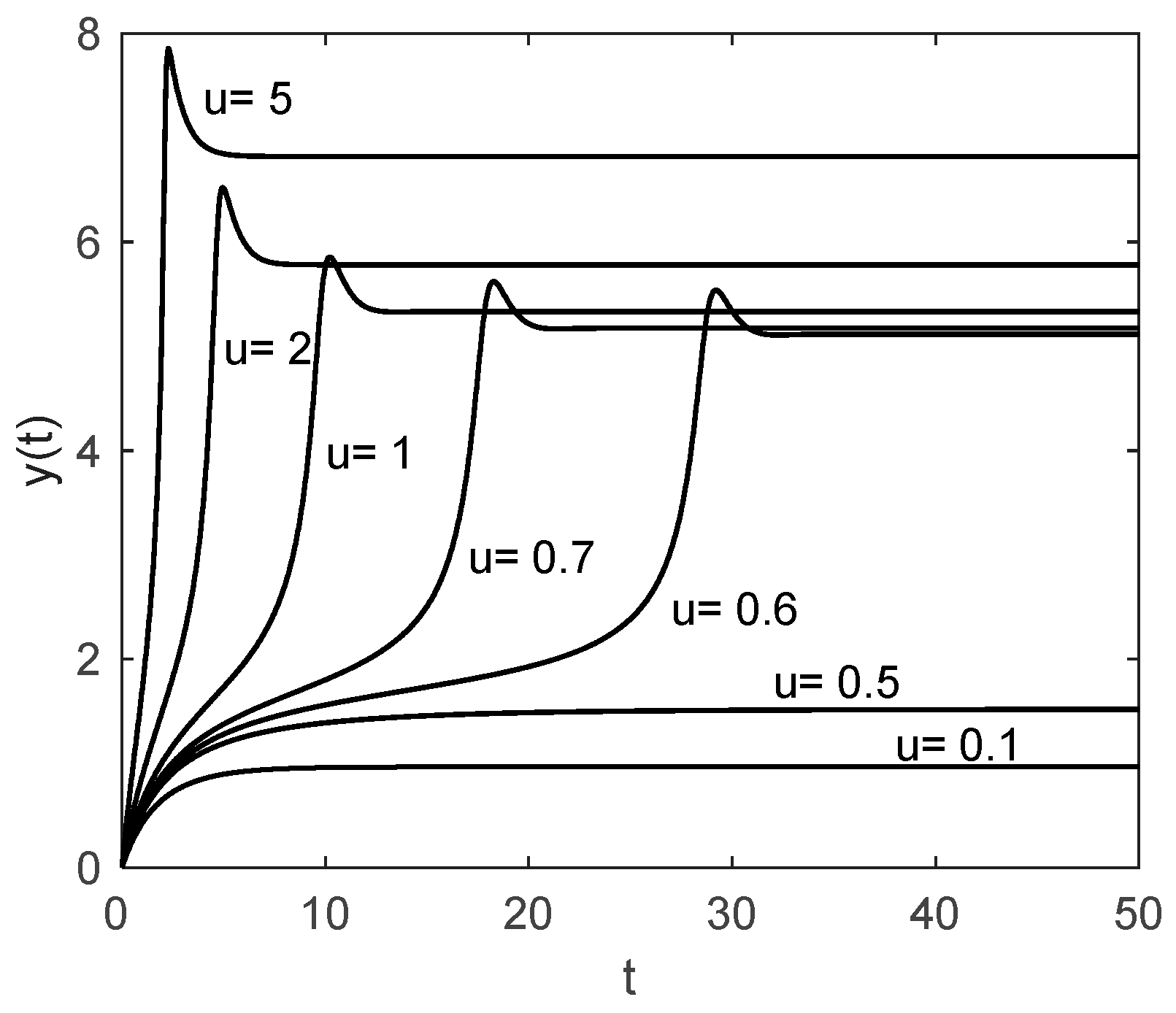
2.2. Process Analysis
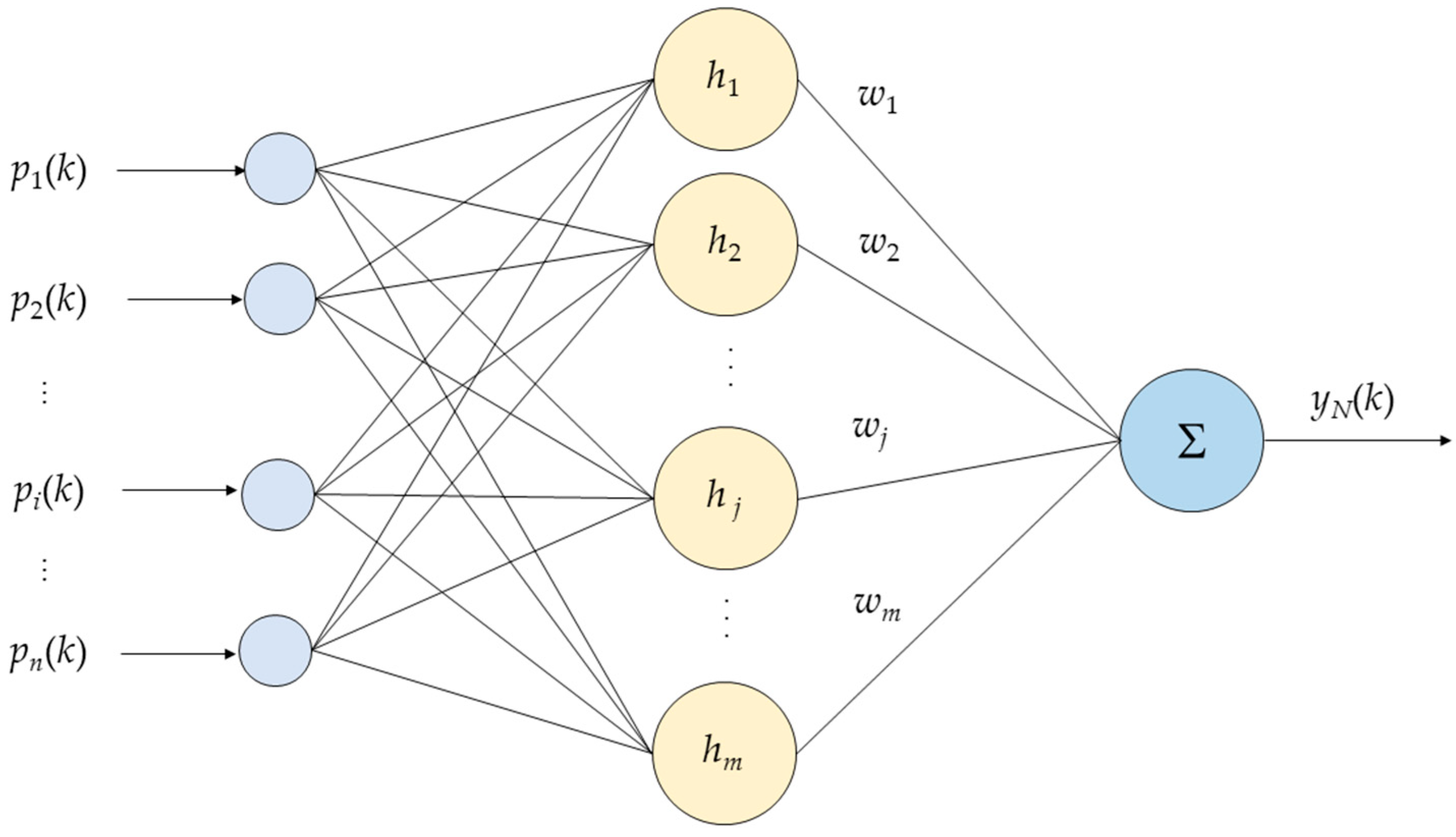
2.3. RBFNN-Based Process Identification
2.3.1. Weight Update
2.3.2. Center Update
2.3.3. Width Update
3. Design of Adaptive Nonlinear PID Controller
3.1. Existing PID Controllers
3.1.1. Linear PID Controller
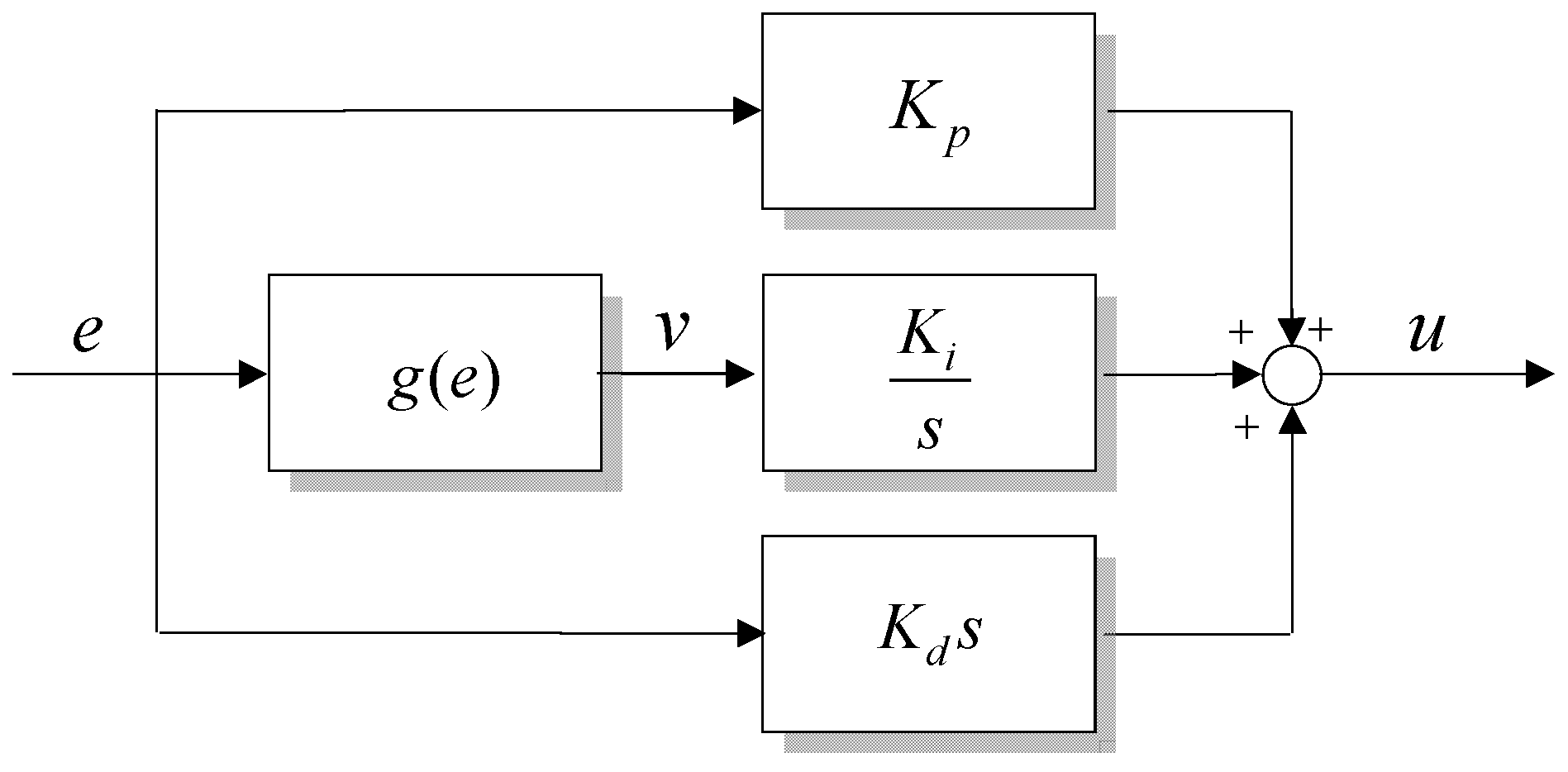
3.1.2. Nonlinear PID Controller
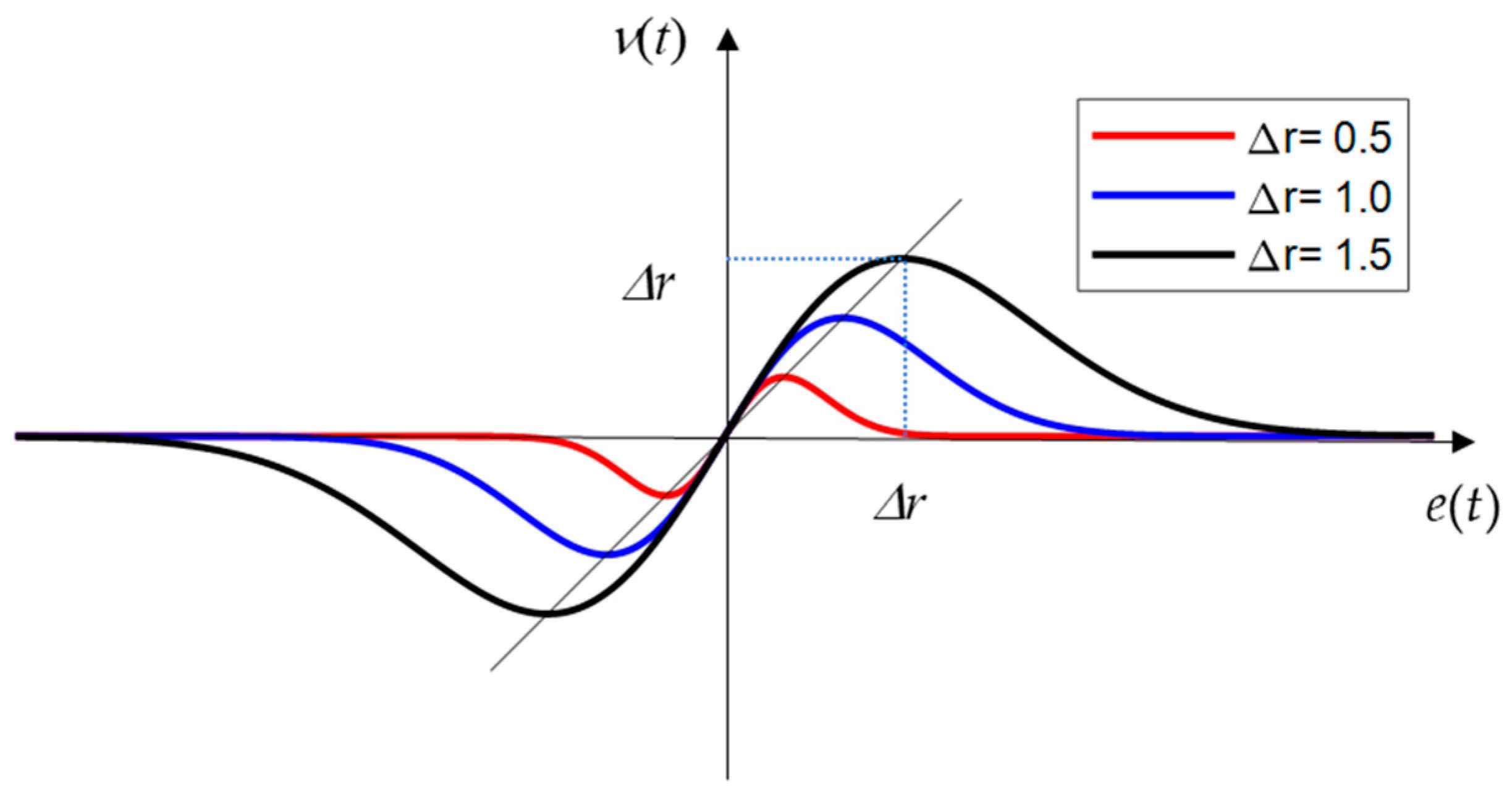
3.2. Enhanced Nonlinear PID Controller
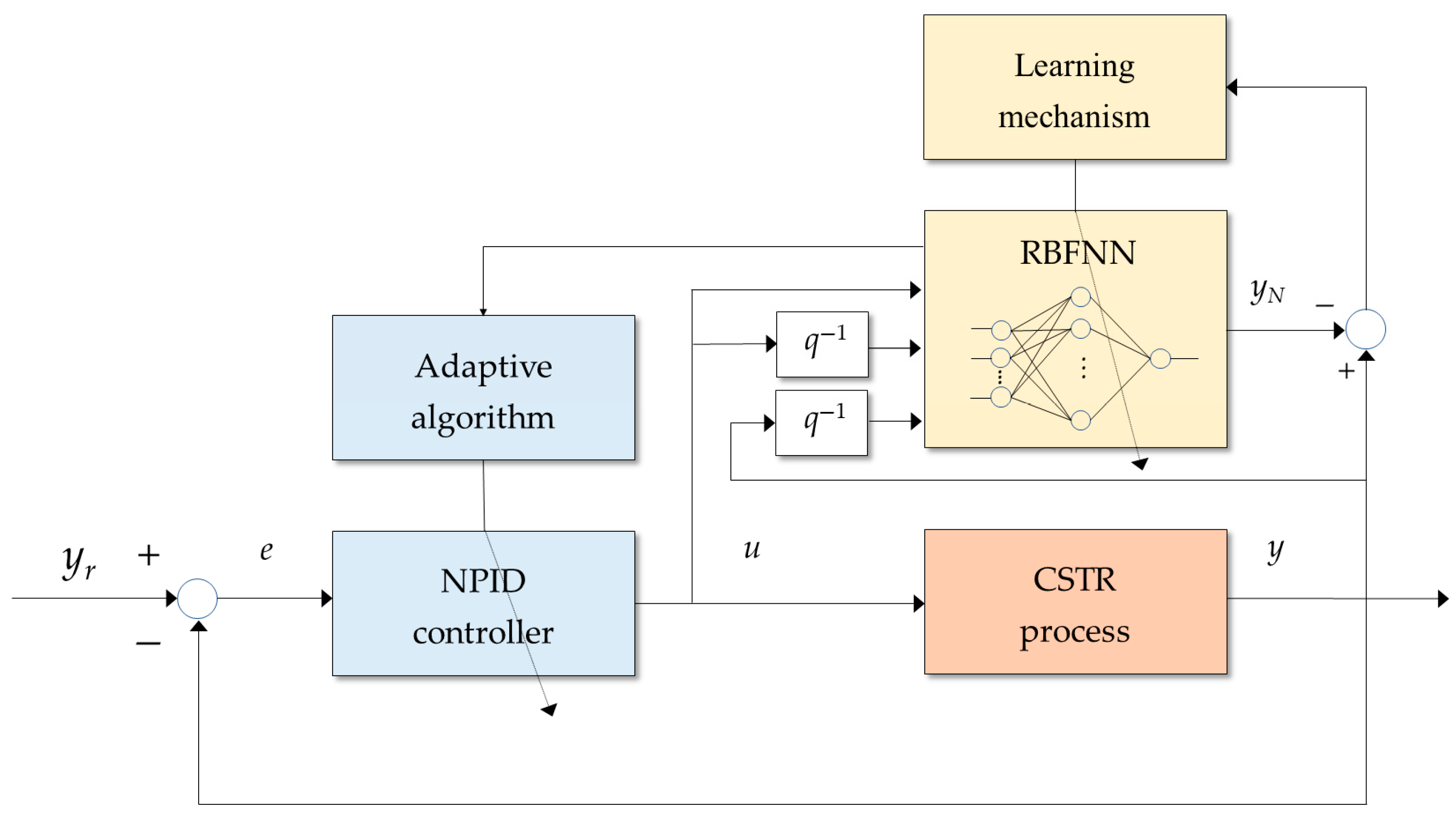
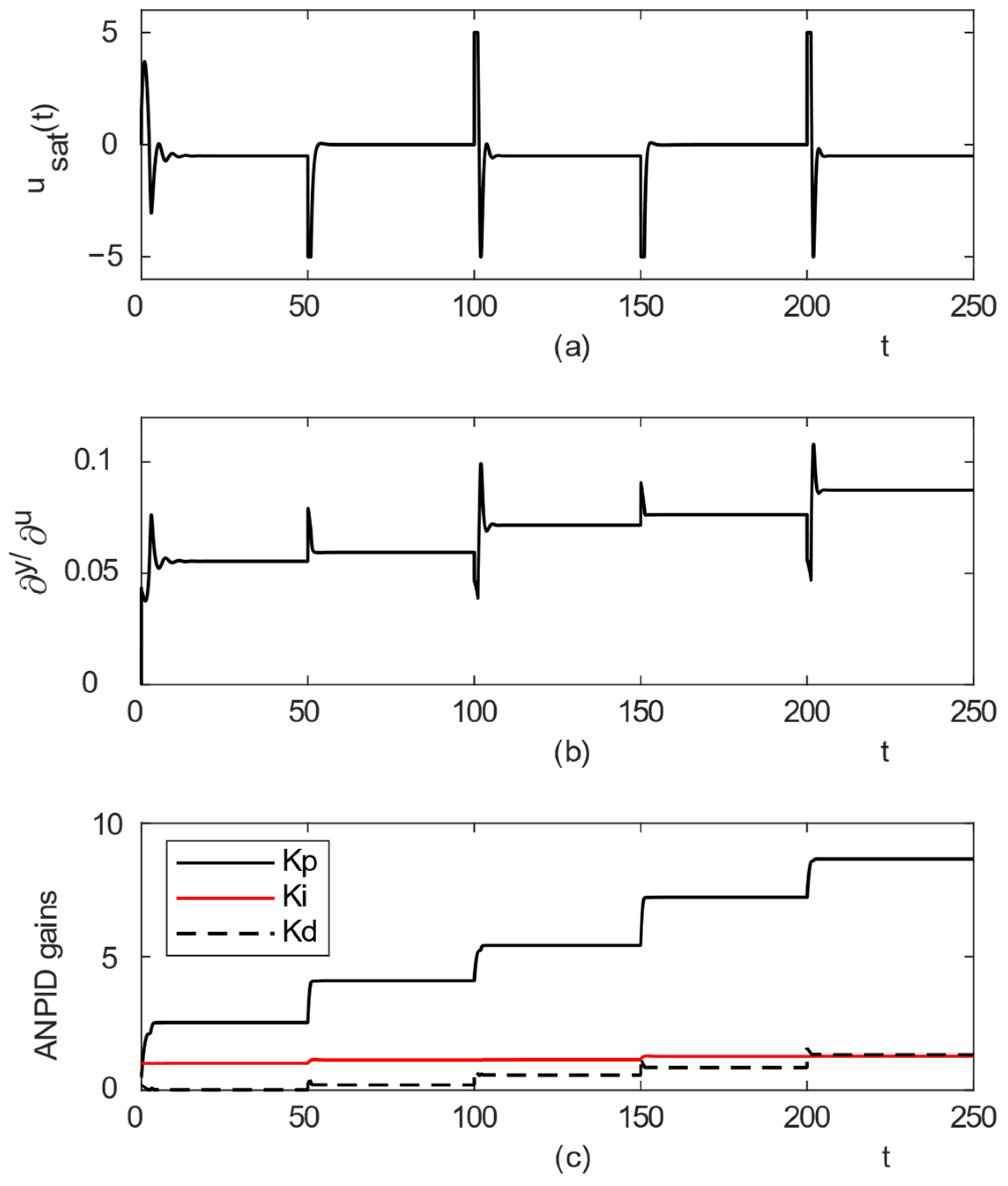
3.3. Proposed Adaptive NPID Controller
| Algorithm 1 The pseudocode representation with RBFNN |
| Step 1: Initialize the adaptive NPID controller gains and RBFNN parameters and set other necessary parameters; Step 2: Set time k = 0; While <Termination condition is not met> do Steps 3–9 Step 3: Update the NPID controller gains using (34)–(40); Step 4: Calculate the NPID control input using (19)–(20) and (25); Step 5: Numerically integrate the CSTR model in (4) to obtain y(k) at the kth instant; Step 6: Calculate the output of the RBFNN using (7) and update its weights, centers and widths using (11), (15) and (17); Step 7: Calculate the Jacobian matrix using (37); Step 8: Update time k = k + 1; Step 9: Output y(k); end |
4. Simulation Results
4.1. Process and Control System Configurations
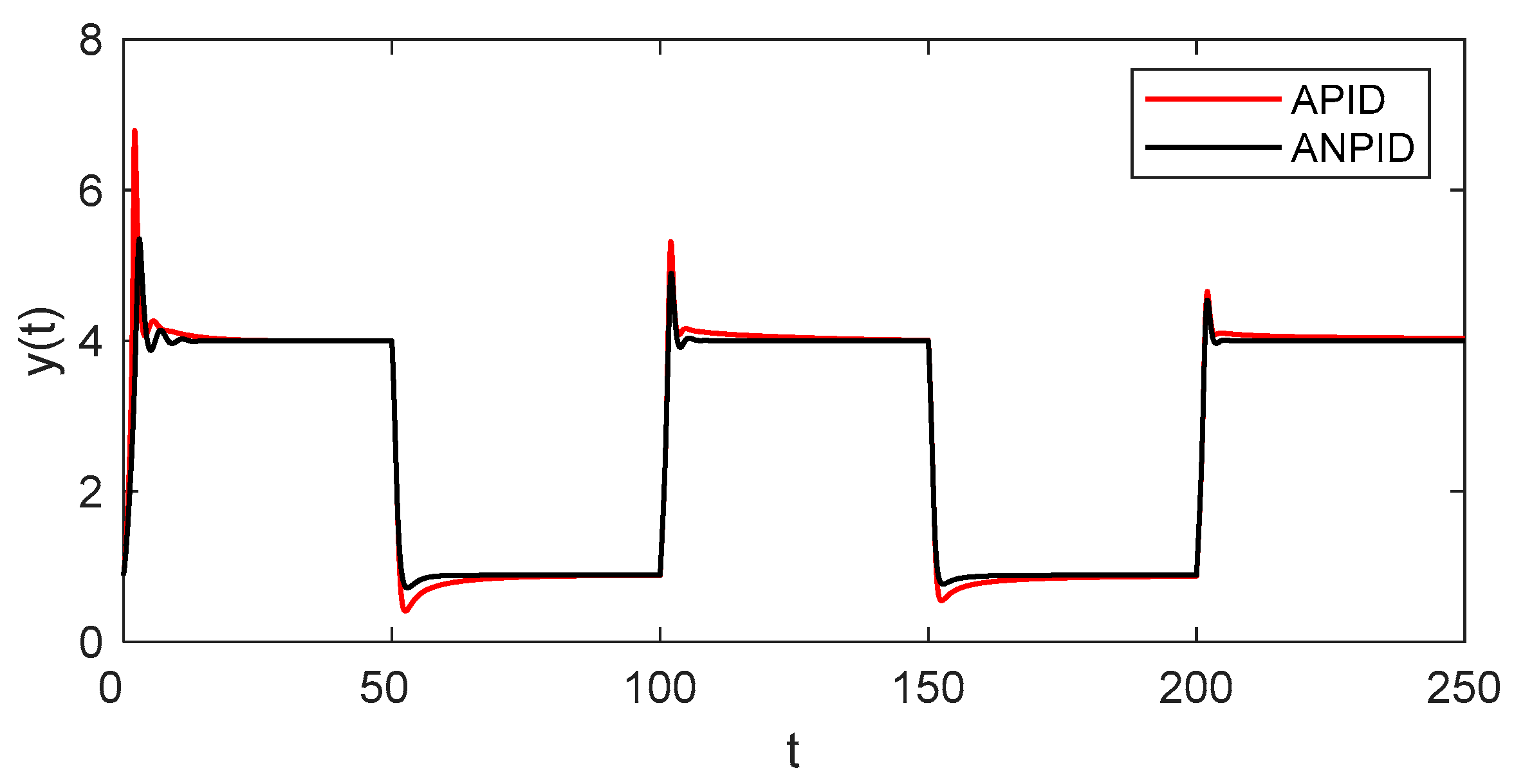
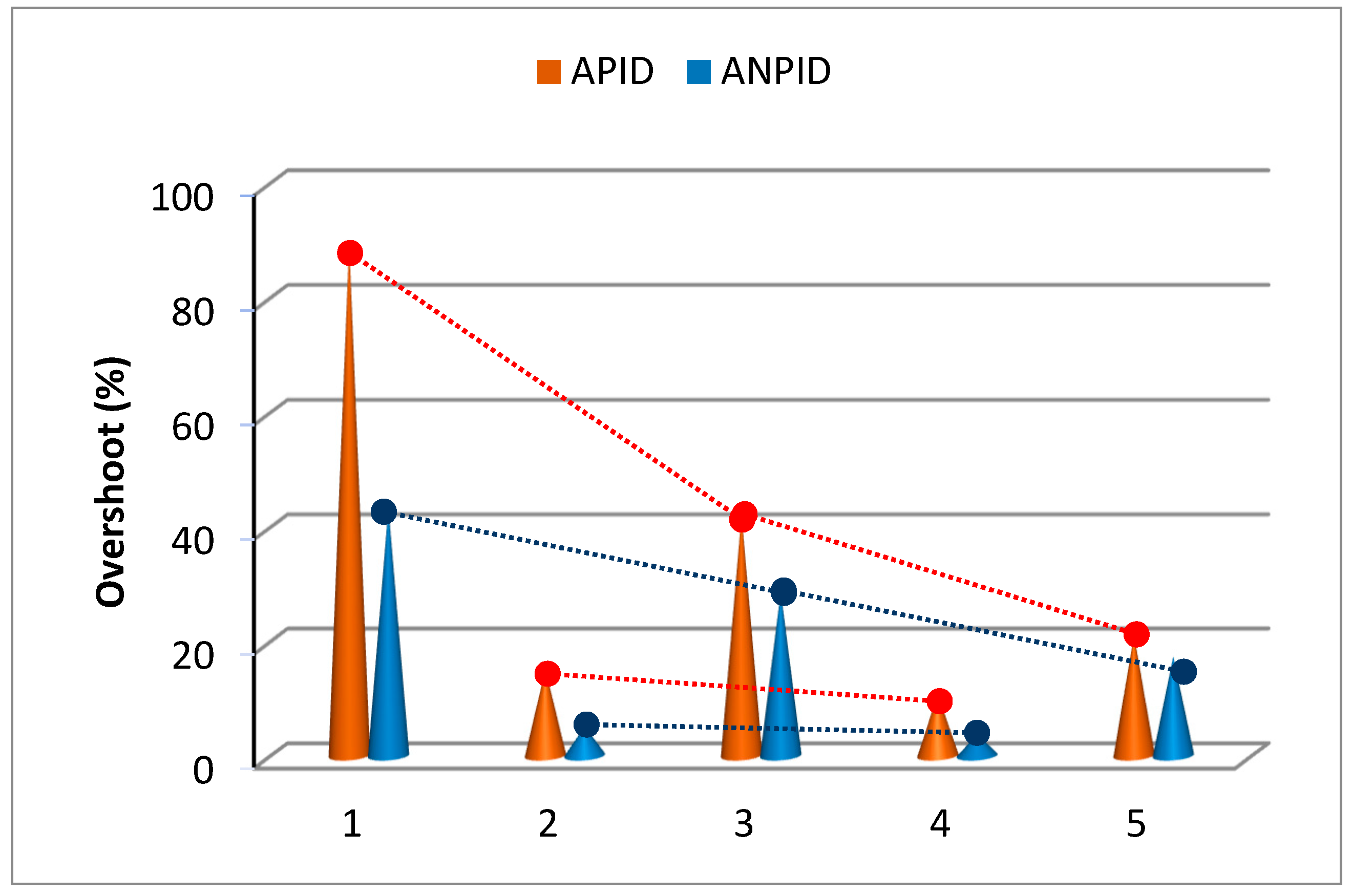
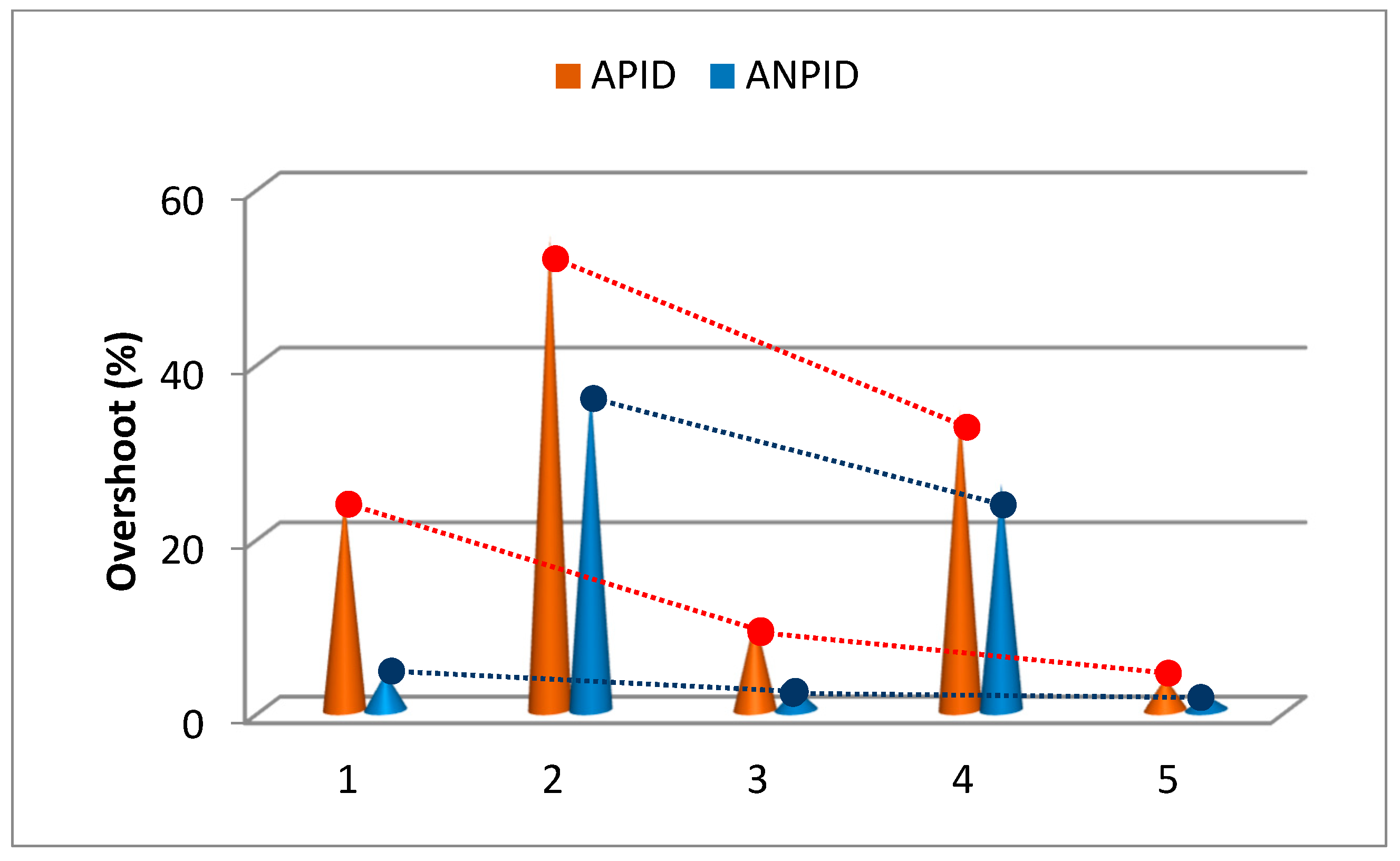
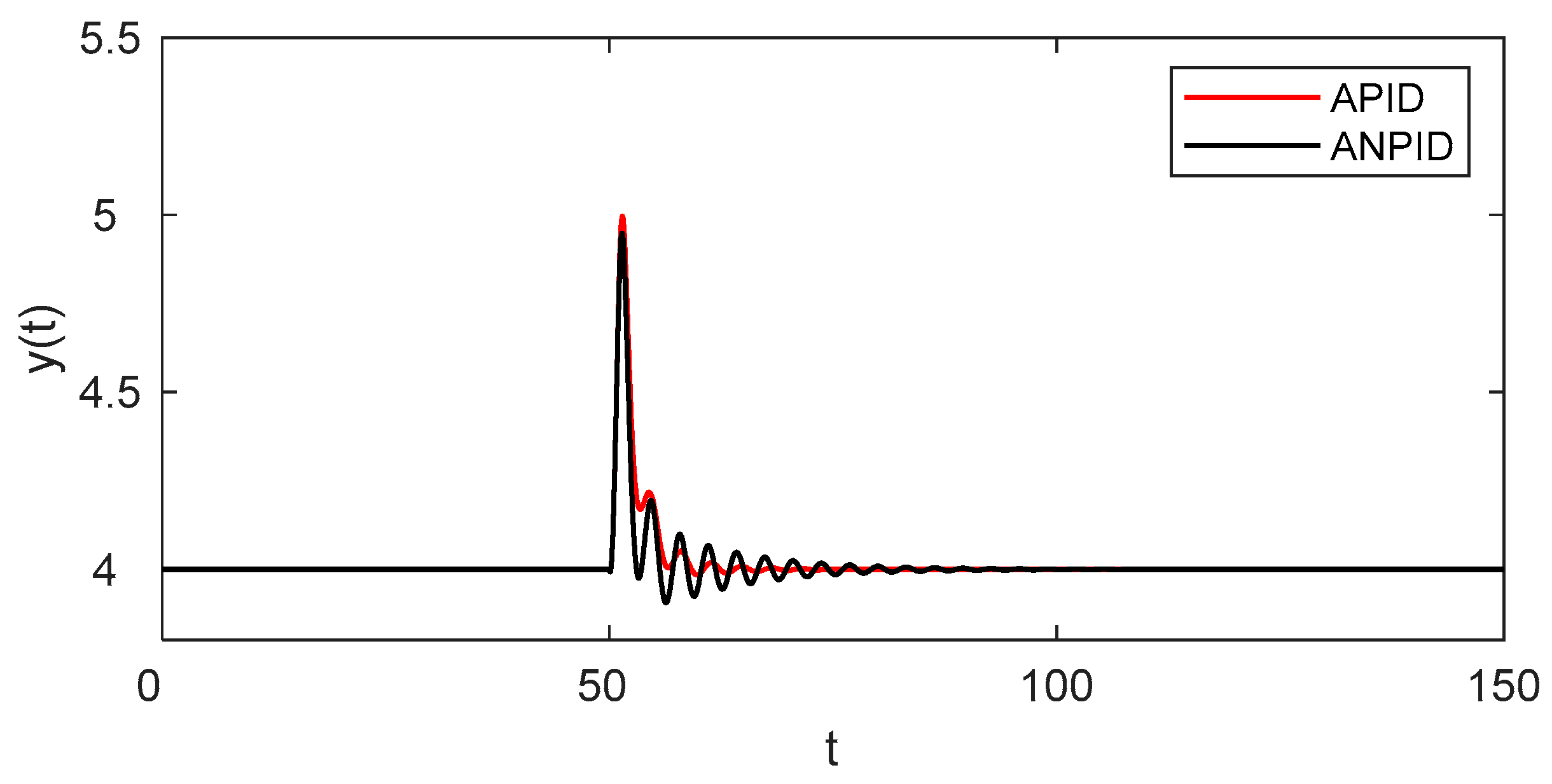
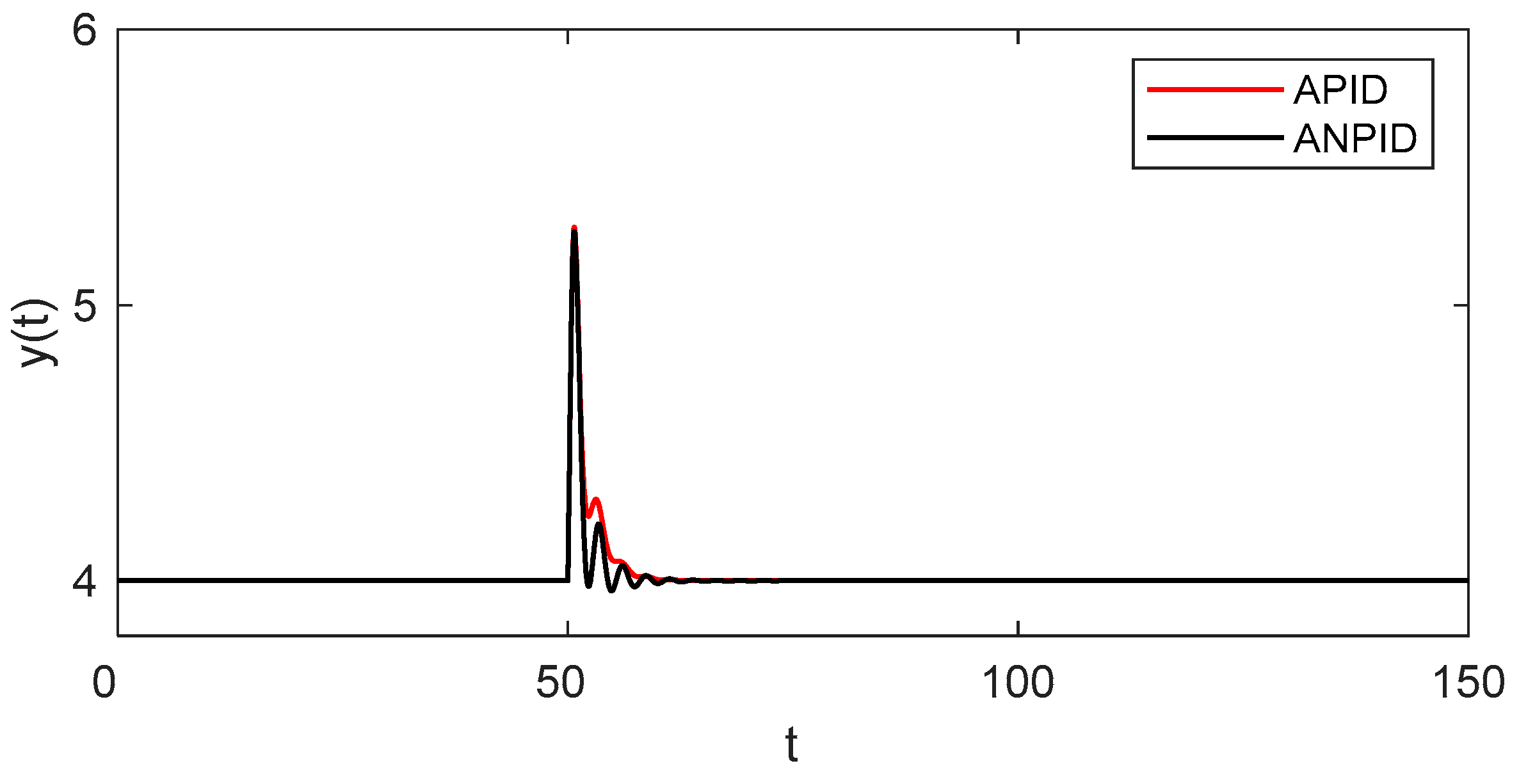
4.2. Setpoint Tracking Performance
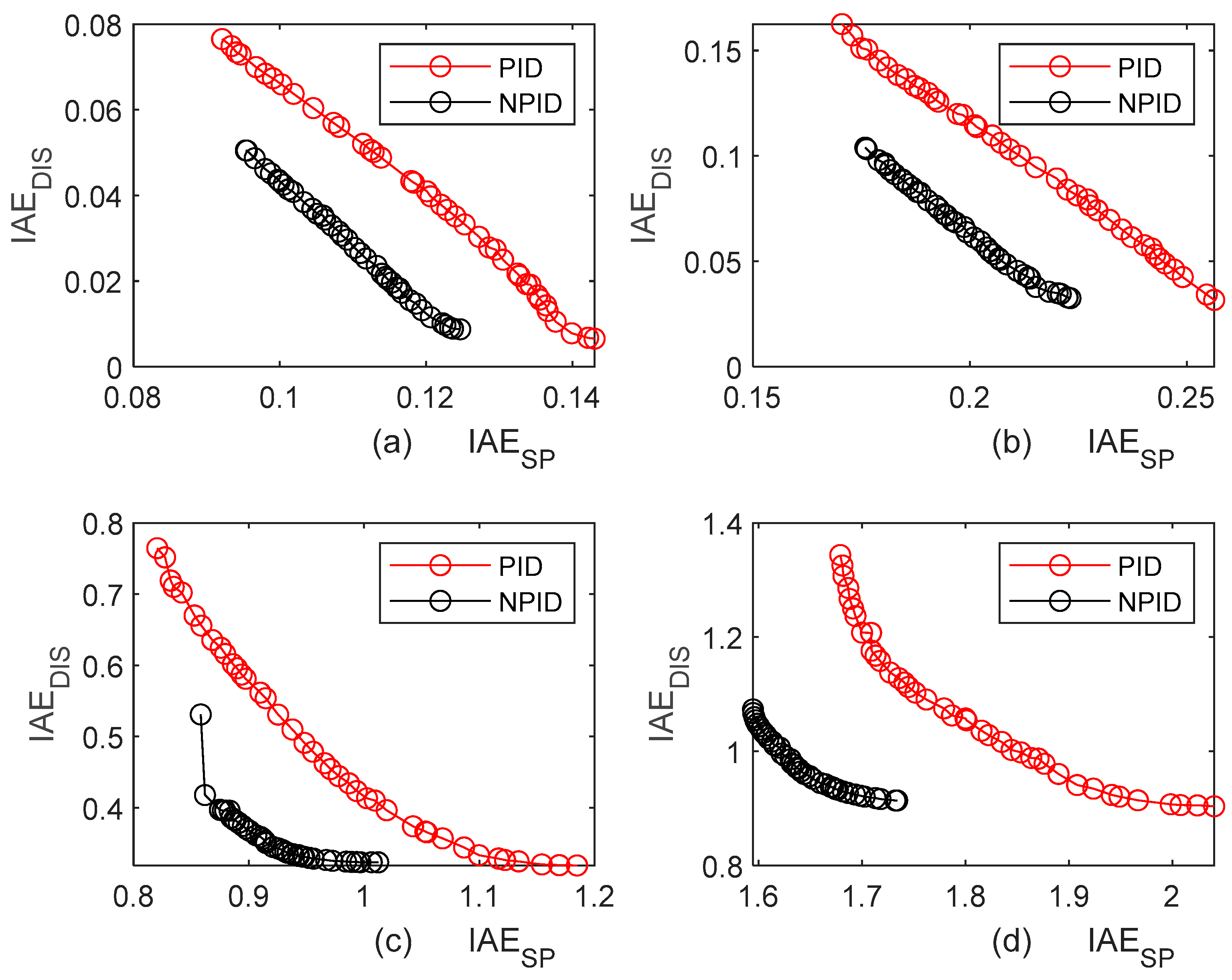
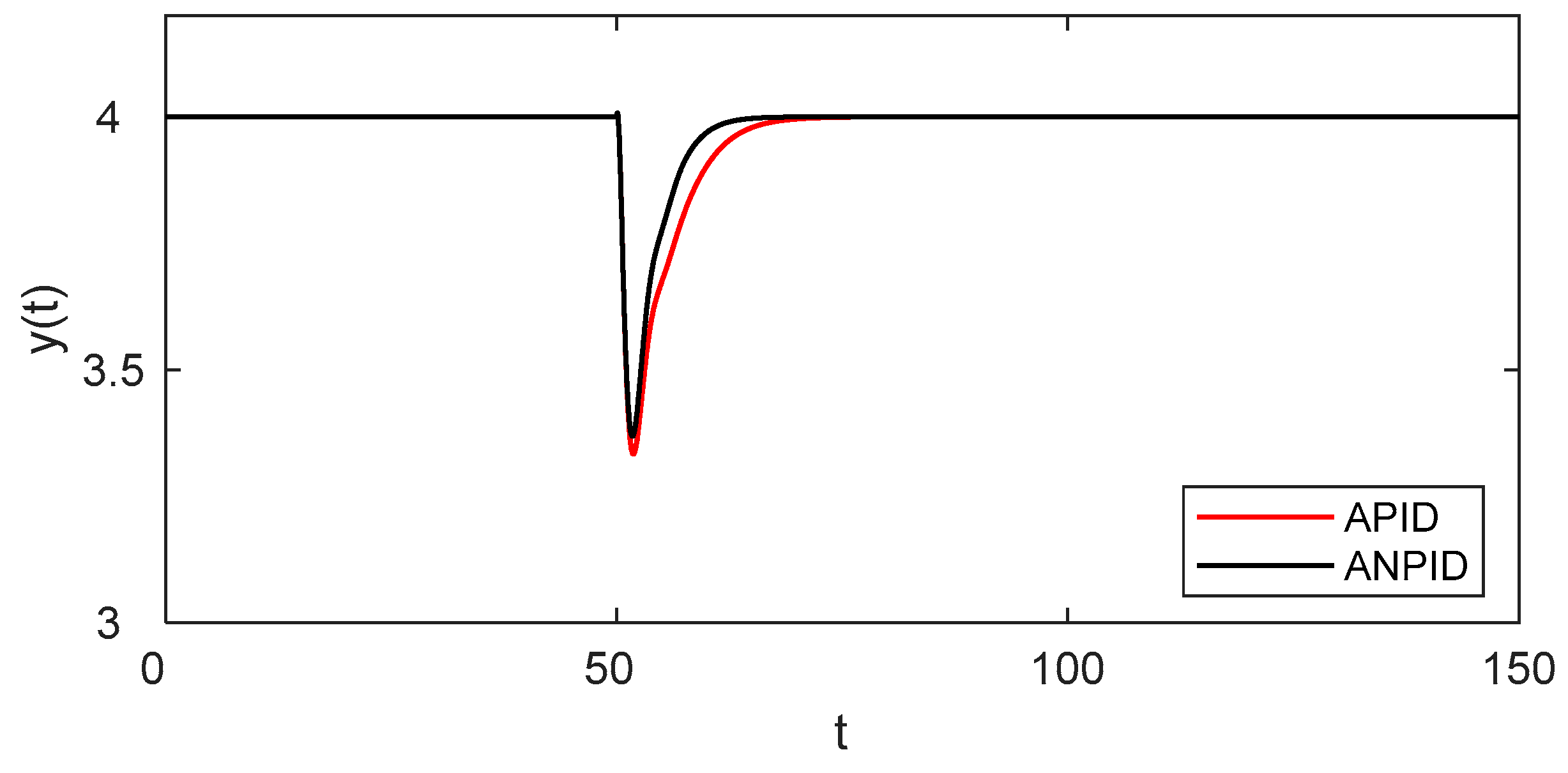
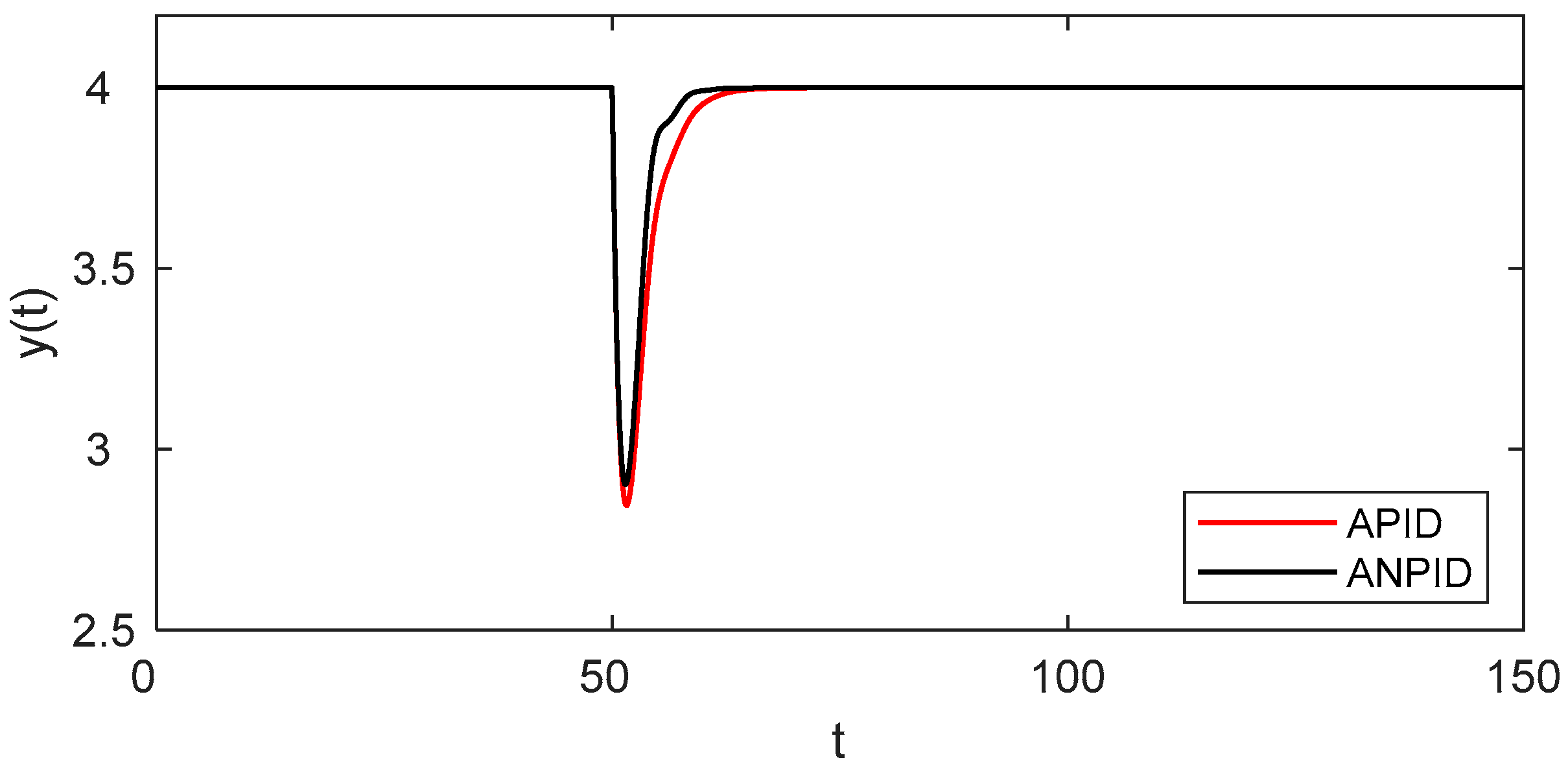
4.3. Disturbance Rejection Performance
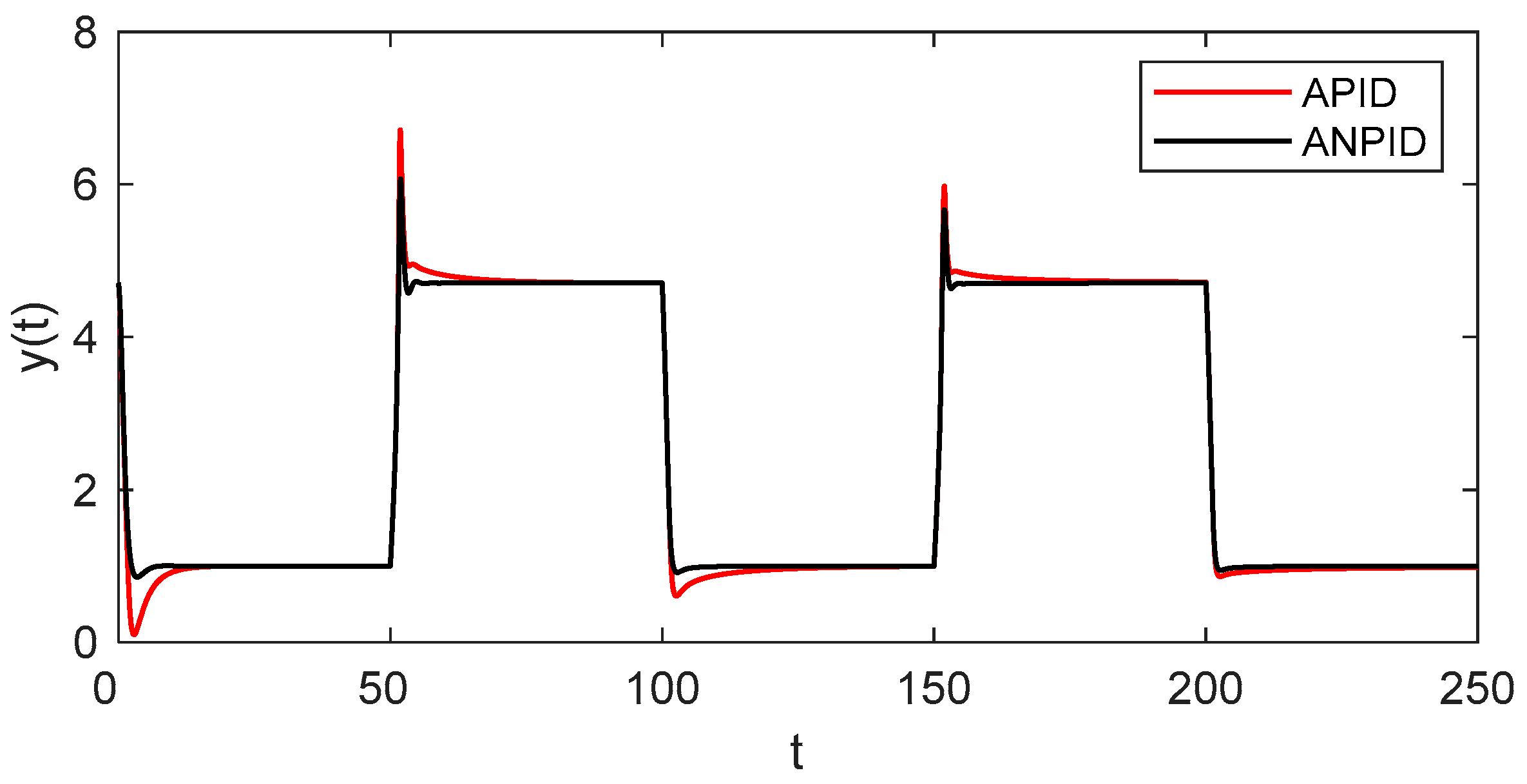
4.4. Robustness to Parameter Variations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luyben, W.L. Chemical Reactor Design and Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Mann, U. Principles of Chemical Reactor Analysis and Design, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Dutta, B.; Kumar Tayal, V. PID Controller Design for Continuous Stirred Tank Reactor (CSTR) Temperature Control. In Innovations in Cyber Physical Systems; Singh, J., Kumar, S., Choudhury, U., Eds.; Lecture Notes in Electrical Engineering, Volume 788; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Jayachitra, A.; Vinodha, R. Genetic Algorithm Based PID Controller Tuning Approach for Continuous Stirred Tank Reactor. Adv. Artif. Intell. 2014, 2014, 791230. [Google Scholar] [CrossRef]
- O’Dwyer, A. Handbook of PI and PID Controller Tuning Rules; Imperial College Press: London, UK, 2009. [Google Scholar]
- Ranjan, A.; Chakraborty, S. Gain-Scheduled Feedback Controller Design for a Nonlinear Continuous Stirred Tank Reactor. In Proceedings of the 2020 International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET), Patna, India, 9–11 July 2020. [Google Scholar] [CrossRef]
- Bingi, K.; Ibrahim, R.; Karsiti, M.N.; Hassan, S.M.; Harindran, V.R. A Comparative Study of 2DOF PID and 2DOF Fractional Order PID Controllers on a Class of Unstable Systems. Arch. Control. Sci. 2018, 28, 635–682. [Google Scholar] [CrossRef]
- Poovarasan, J.; Kayalvizhi, R.; Pongiannan, R.K. Design of Fractional Order PID Controller for a CSTR Process. Int. Ref. J. Eng. Sci. 2014, 3, 8–14. [Google Scholar]
- Wase, M.G.; Gebrekirstos, R.F.; Jin, G.G.; So, G.B. Fuzzy Gain Scheduling of the Fractional-Order PID Controller for a Continuous Stirred-Tank Reactor Process. Processes 2023, 11, 3275. [Google Scholar] [CrossRef]
- Seraji, H. A New Class of Nonlinear PID Controllers. In Proceedings of the 5th IFAC Symposium on Robot Control 1997 (SYROCO ‘97), Nantes, France, 3–5 September 1997; pp. 65–71. [Google Scholar]
- Seraji, H. A New Class of Nonlinear PID Controllers with Robotic Applications. J. Robot. Syst. 1998, 15, 161–181. [Google Scholar] [CrossRef]
- Korkmaz, M.; Aydogdu, O.; Dogan, H. Design and Performance Comparison of Variable Parameter Nonlinear PID Controller and Genetic Algorithm-Based PID Controller. In Proceedings of the 2012 IEEE International Symposium on Innovations in Intelligent Systems and Applications (INISTA), Trabzon, Turkey, 2–4 July 2012; pp. 1–5. [Google Scholar]
- Li, Y.; Guo, G.; Wang, Y. A Nonlinear Control Scheme for Fast Settling in Hard Disk Drives. IEEE Trans. Magn. 2004, 40, 2086–2088. [Google Scholar] [CrossRef]
- So, G.B.; Jin, G.G. Fuzzy-Based Nonlinear PID Controller and Its Application to CSTR. Korean J. Chem. Eng. 2018, 35, 819–825. [Google Scholar] [CrossRef]
- Jin, G.G.; Son, Y.D. Design of a Nonlinear PID Controller and Tuning Rules for First-Order Plus Time Delay Models. Stud. Inform. Control. 2019, 28, 157–166. [Google Scholar] [CrossRef]
- Son, Y.D.; Jin, G.G.; Yetayew, T.T.; Pal, P. New Tuning Formulas for a Nonlinear PID Control Scheme. Int. J. Syst. Assur. Eng. Manag. 2023, 14, 2470–2484. [Google Scholar] [CrossRef]
- Kalita, P.; Barman, J.K. Performance Analysis of Nonlinear Jacketed CSTR Based on Different Control Strategies. J. Electr. Electron. Eng. 2017, 1, 1–7. [Google Scholar]
- Ouyang, M.; Wang, Y.; Wu, F.; Lin, Y. Continuous Reactor Temperature Control with Optimized PID Parameters Based on Improved Sparrow Algorithm. Processes 2023, 11, 1302. [Google Scholar] [CrossRef]
- Maya-Rodriguez, M.C.; Carvajal-Mariscal, I.; López-Muñoz, R.; Lopez-Pacheco, M.A.; Tolentino-Eslava, R. Temperature Control of a Chemical Reactor Based on Neuro-Fuzzy Tuned with a Metaheuristic Technique to Improve Biodiesel Production. Energies 2023, 16, 6187. [Google Scholar] [CrossRef]
- Vojtesek, J.; Dostal, P. Nonlinear versus Ordinary Adaptive Control of Continuous Stirred-Tank Reactor. Sci. World J. 2015, 2015, 389273. [Google Scholar] [CrossRef] [PubMed]
- Anbu, S.; Jaya, N. Design of Model Reference Adaptive Control and Nonlinear PI Controller for Continuous Stirred Tank Reactor. Int. J. Comput. Appl. 2016, 153, 13–16. [Google Scholar] [CrossRef]
- Li, D.; Wang, D.; Gao, Y. Adaptive Neural Control and Modeling for Continuous Stirred Tank Reactor with Delays and Full State Constraints. Complexity 2021, 2021, 9948044. [Google Scholar] [CrossRef]
- Zerari, N.; Chemachema, M. Robust Adaptive Neural Network Prescribed Performance Control for Uncertain CSTR System with Input Nonlinearities and External Disturbance. Neural Comput. Appl. 2020, 32, 10541–10554. [Google Scholar] [CrossRef]
- Shi, X.; Zhao, H.; Fan, Z. Parameter Optimization of Nonlinear PID Controller Using RBF Neural Network for Continuous Stirred Tank Reactor. Meas. Control 2023, 56, 1835–1843. [Google Scholar] [CrossRef]
- Li, D.; Wang, Y.; Liu, Y.-J.; Liu, L. IBLFs-Based Adaptive Fuzzy Control for Continuous Stirred Tank Reactors with Full State Constraints and Actuator Faults. J. Process Control 2023, 124, 14–24. [Google Scholar] [CrossRef]
- Sarjaš, A.; Gleich, D. Event-Triggered Sliding Mode Control For Constrained Networked Control Ssystems. Electron. Energetics 2022, 35, 557–570. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Kumar, N.; Kumar, R. A PSO-optimized novel PID neural network model for temperature control of jacketed CSTR: Design, simulation, and a comparative study. Soft Comput. 2024, 28, 4759–4773. [Google Scholar] [CrossRef]
- Baranilingesan, I.; Deepa, S.N.; Yagambal Jayalaskshmi, N. An Intelligent Neural Network Controller for Non-Linear CSTR Process Control. Iran. J. Chem. Chem. Eng. 2023, 42, 977–988. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Z.; Li, J.; Zhang, W.; Qiu, B. Prescribed Performance Path-Following Control for Rotor-Assisted Vehicles via an Improved Reinforcement Learning Mechanism. IEEE Trans. Neural Netw. Learn. Syst. 2025, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; He, Y.; Zhao, Y.; Jiang, X.; Ren, S. Tunnel construction ventilation frequency-control based on radial basis function neural network. Autom. Constr. 2020, 118, 103293. [Google Scholar] [CrossRef]
- Ray, W.H. Advanced Process Control; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Soukkou, A.; Khellaf, S.; Leulmi, S.; Boudeghdegh, K. Optimal Control of a CSTR Process. Braz. J. Chem. Eng. 2008, 25, 799–812. [Google Scholar] [CrossRef]
- Suo, L.; Ren, J.; Zhao, Z.; Zhai, C. Study on the Nonlinear Dynamics of the Continuous Stirred Tank Reactors. Processes 2020, 8, 1436. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; De Jesús, O. Neural Network Design, 2nd ed.; Martin Hagan; PWS Publishing Co.: Boston, MA, USA, 2014. [Google Scholar]
- Raff, L.; Komanduri, R.; Hagan, M.T.; Bukkapatnam, S. Neural Networks in Chemical Reaction Dynamics; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Srinivas, N.; Deb, K. Multiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
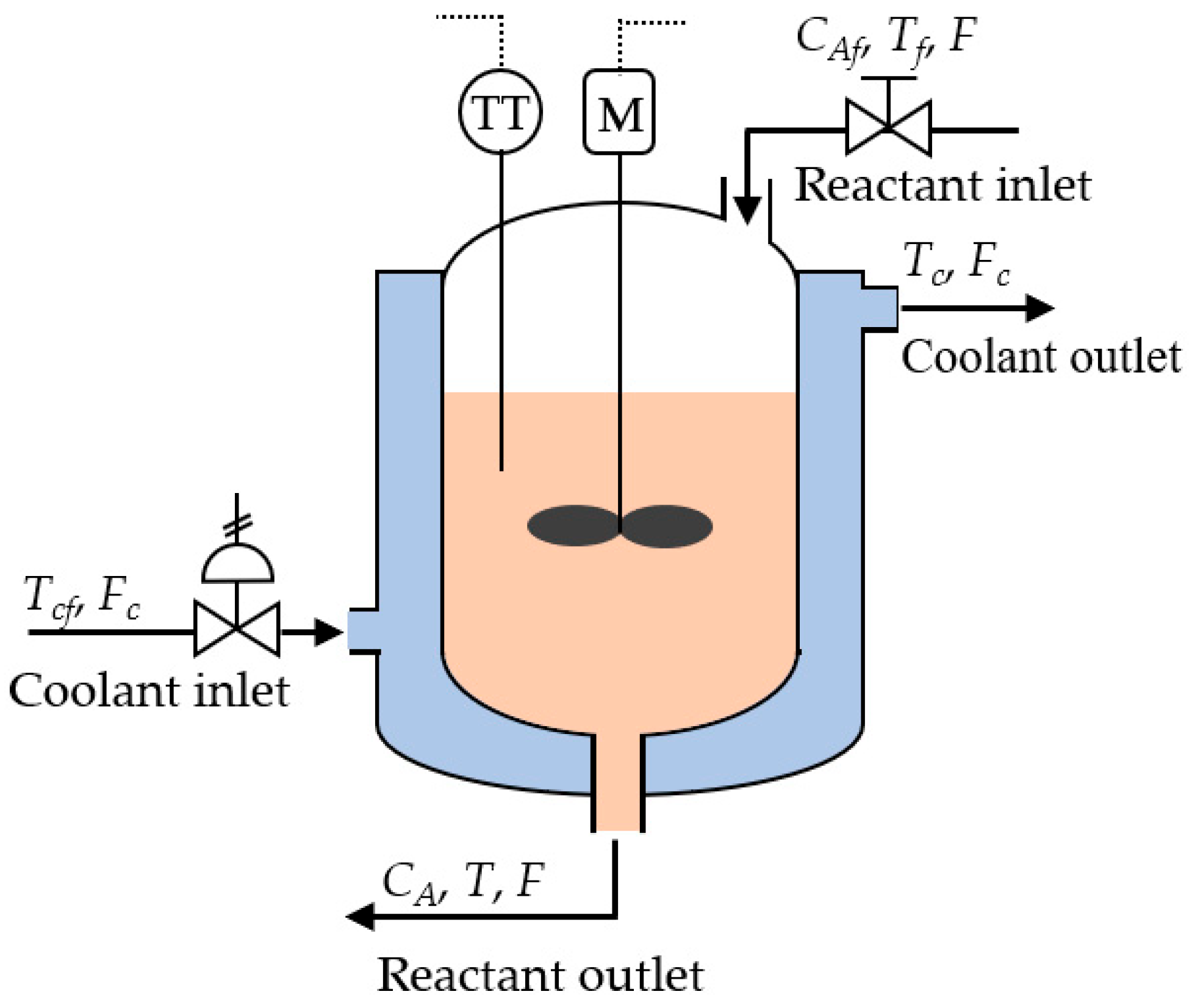
| Parameter | Description |
|---|---|
| CA | Reactant concentration |
| CAf | Reactant inlet concentration |
| T | Reactant temperature |
| Tf | Reactant inlet temperature |
| F | Reactant flow rate |
| Tc | Coolant temperature |
| Tcf | Coolant inlet temperature |
| Fc | Coolant flow rate |
| ρ | Reactant density |
| Cp | Reactant volumetric heat capacity |
| ρj | Coolant density |
| Cpj | Coolant volumetric heat capacity |
| UA | Heat transfer item |
| ΔH | Reaction heat |
| k0 | Reaction rate constant |
| E | Activation energy |
| R | Gas constant |
| V | Reactor volume |
| Vj | Jacket volume |
| τ | Time |
| Controller | yr = 4 → 0.886 | yr = 0.886 → 4 | ||||||
|---|---|---|---|---|---|---|---|---|
| Mp | tr | ts | IAE | Mp | tr | ts | IAE | |
| APID | 10.792 | 1.123 | 6.491 | 5.406 | 21.152 | 1.189 | 2.885 | 5.842 |
| ANPID | 3.755 | 1.203 | 1.565 | 2.867 | 17.416 | 1.213 | 2.730 | 3.265 |
| Controller | yr = 1 → 4.705 | yr = 4.705 → 1 | ||||||
|---|---|---|---|---|---|---|---|---|
| Mp | tr | ts | IAE | Mp | tr | ts | IAE | |
| APID | 34.269 | 1.172 | 2.759 | 6.574 | 3.706 | 1.249 | 1.579 | 5.109 |
| ANPID | 26.004 | 1.188 | 2.475 | 4.252 | 1.660 | 1.270 | 1.633 | 3.383 |
| Controller | d1 = 0 → 0.2, d2 = 0 → 0.2 | d1 = 0 → −0.2, d2 = 0 → −0.2 | ||||
|---|---|---|---|---|---|---|
| Mpeak | trcy | IAE | Mpeak | trcy | IAE | |
| APID | 0.666 | 13.529 | 3.506 | 0.996 | 18.150 | 2.232 |
| ANPID | 0.631 | 9.916 | 2.510 | 0.949 | 14.279 | 2.296 |
| Controller | Da = 0.0864, H = 9.6, β = 0.36 | Da = 0.0576, H = 6.4, β = 0.24 | ||||
|---|---|---|---|---|---|---|
| Mpeak | trcy | IAE | Mpeak | trcy | IAE | |
| APID | 1.283 | 6.147 | 2.306 | 1.155 | 9.401 | 4.686 |
| ANPID | 1.266 | 4.151 | 1.774 | 1.098 | 7.287 | 3.511 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-Y.; Jin, G.-G.; So, G.-B. Adaptive Nonlinear Proportional–Integral–Derivative Control of a Continuous Stirred Tank Reactor Process Using a Radial Basis Function Neural Network. Algorithms 2025, 18, 442. https://doi.org/10.3390/a18070442
Lee J-Y, Jin G-G, So G-B. Adaptive Nonlinear Proportional–Integral–Derivative Control of a Continuous Stirred Tank Reactor Process Using a Radial Basis Function Neural Network. Algorithms. 2025; 18(7):442. https://doi.org/10.3390/a18070442
Chicago/Turabian StyleLee, Joo-Yeon, Gang-Gyoo Jin, and Gun-Baek So. 2025. "Adaptive Nonlinear Proportional–Integral–Derivative Control of a Continuous Stirred Tank Reactor Process Using a Radial Basis Function Neural Network" Algorithms 18, no. 7: 442. https://doi.org/10.3390/a18070442
APA StyleLee, J.-Y., Jin, G.-G., & So, G.-B. (2025). Adaptive Nonlinear Proportional–Integral–Derivative Control of a Continuous Stirred Tank Reactor Process Using a Radial Basis Function Neural Network. Algorithms, 18(7), 442. https://doi.org/10.3390/a18070442






