A Comprehensive Review and Benchmarking of Fairness-Aware Variants of Machine Learning Models
Abstract
1. Introduction
2. Fair Editions of Naive Bayes
2.1. Calders and Verver Fair Variances of Naive Bayes
2.2. Fair Naive Bayes Classifier
2.3. Fairness-Aware Naive Bayes
3. Fair Editions of Decision Trees
3.1. Discrimination-Aware Decision Tree
3.2. Optimal and Fair Decision Trees via Regularization (RegOCT)
3.3. FATT Fairness-Aware Tree Training Method
3.4. Fair and Optimal Decision Trees
3.5. FFTree
3.6. Optimal Fair Decision Trees
3.7. Fair C4.5 Algorithm
3.8. SCAFF Fair Tree Classifier
4. Fair Editions of Logistic Regression
4.1. Prejudice Remover Regularizer
4.2. -Neutral Logistic Regression
Differentially Private and Fair Logistic Regression
4.3. Disparate Impact-Free Logistic Regression
4.4. Constraint Logistic Regression
4.5. Group-Level Logistic Regression
4.6. Maximum Entropy Logistic Regression with Demographic Parity Constraints
5. Fair Editions of Ensemble Models
5.1. AdaFair
5.2. FAIRGBM
5.3. FairXGBoost
5.4. GAFairC: Group AdaBoost with Fairness Constraint
5.5. FAEM: Fairness-Aware Ensemble Model
5.6. FairBoost
5.7. Fair Voting Ensemble Classifier
6. Exponentiated Learning Technique Plus Classical Machine Learning Algorithms
7. Experimental Procedure
7.1. Datasets
7.1.1. Titanic Dataset
7.1.2. Adult Census Dataset
7.1.3. Bank Marketing Dataset
7.1.4. German Credit Dataset
7.1.5. MBA Admission Dataset
7.1.6. Law School Dataset
7.2. Machine Learning Algorithms
- AdaFair: A summary of this algorithm is provided in Section 5.1.
- FairGBM: A summary of this algorithm is provided in Section 5.2.
- Fairlearn-GB: Combines the Exponentiated Gradient technique with a gradient boosting algorithm, implemented using the Fairlearn library.
- Fairlearn-NB: Integrates the Exponentiated Gradient technique with a Naive Bayes classifier via the Fairlearn library.
- Fairlearn-DT: Applies the Exponentiated Gradient technique in conjunction with Decision Trees, utilizing the Fairlearn library.
- Fairlearn-LR: Combines the Exponentiated Gradient technique with Logistic Regression using the Fairlearn library.
- Fair Decision Trees: Summarized in Section 3.8, this algorithm is based on the implementation available in the GitHub repository of [13].
- Fair Random Forest: An extension of the Fair Decision Trees algorithm, also described in Section 3.8 and obtained from the GitHub repository of [13].
- NNB-Parity: Briefly described in Section 2.3, this algorithm is sourced from the GitHub repository of [5].
- NNB-DF: Also detailed in Section 2.3, this algorithm is likewise obtained from the GitHub repository of [5].
- FairBoost: An overview of this algorithm is presented in Section 5.6, based on the work of [29].
- Prejudice Remover Regularizer: Utilized via its implementation in the AI Fairness 360 (AIF360) library.
Model Parameters
7.3. Metrics
- Accuracy Difference: Difference in prediction accuracy across the two different groups. Mathematically expressed as
- Statistical Parity Difference: Difference in rate of positive predictions between groups. Mathematically expressed as
- Equality of Opportunity: Ensures equal true positive rates (TPR) across population groups. Mathematically expressed as
- Equalized Odds: Ensures both equal true positive rates (TPR) and false positive rates (FPR) across groups. Mathematically expressed as
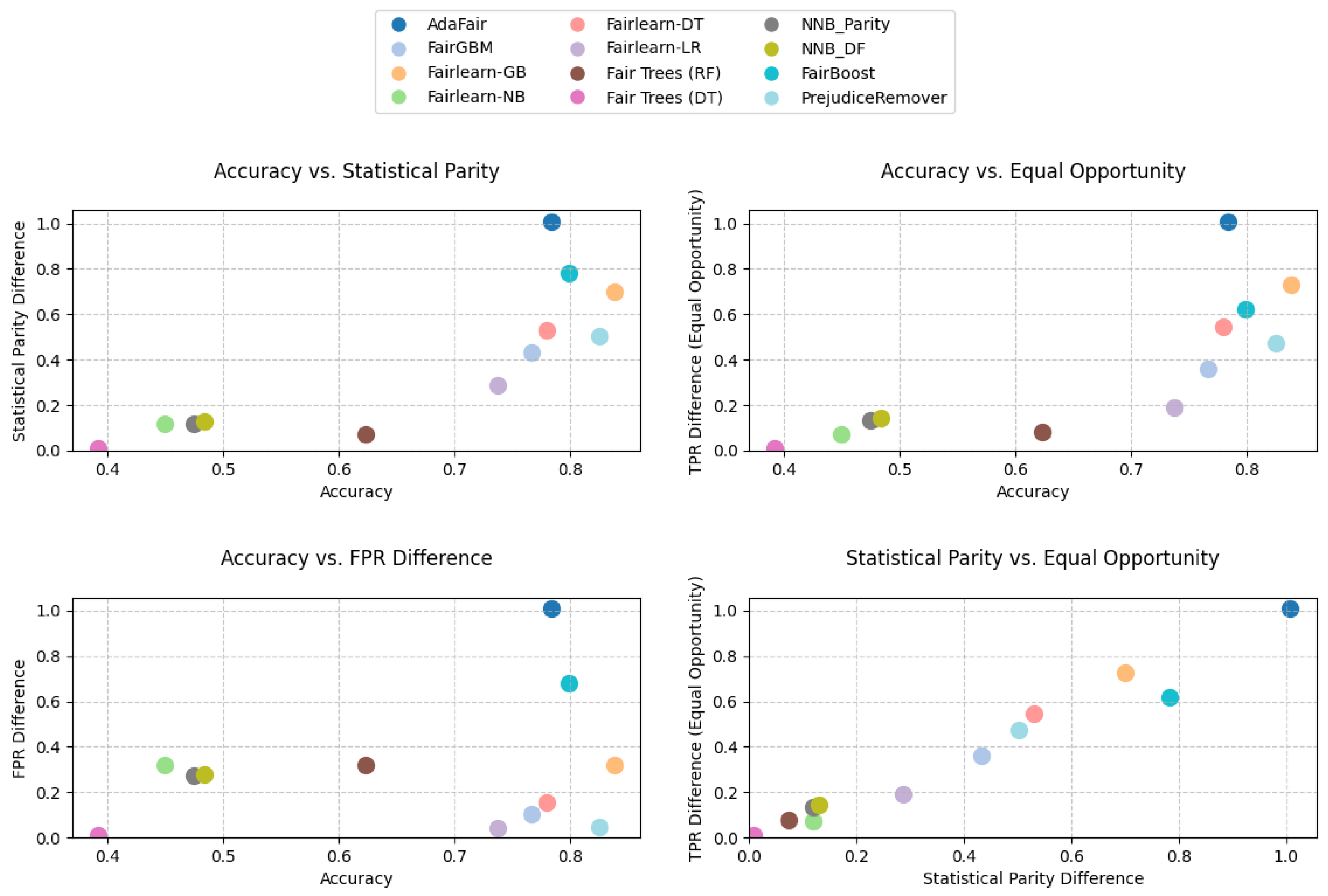
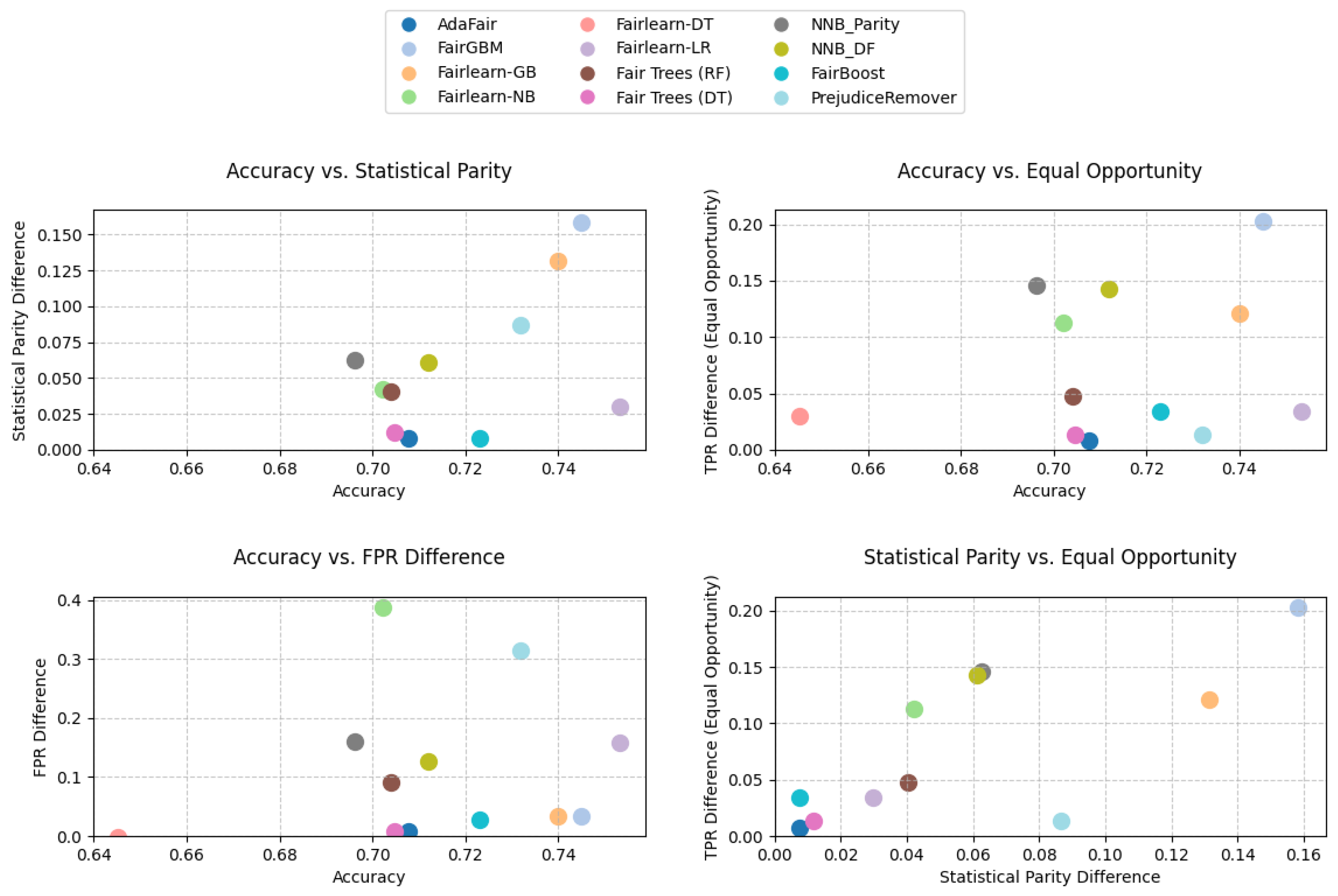
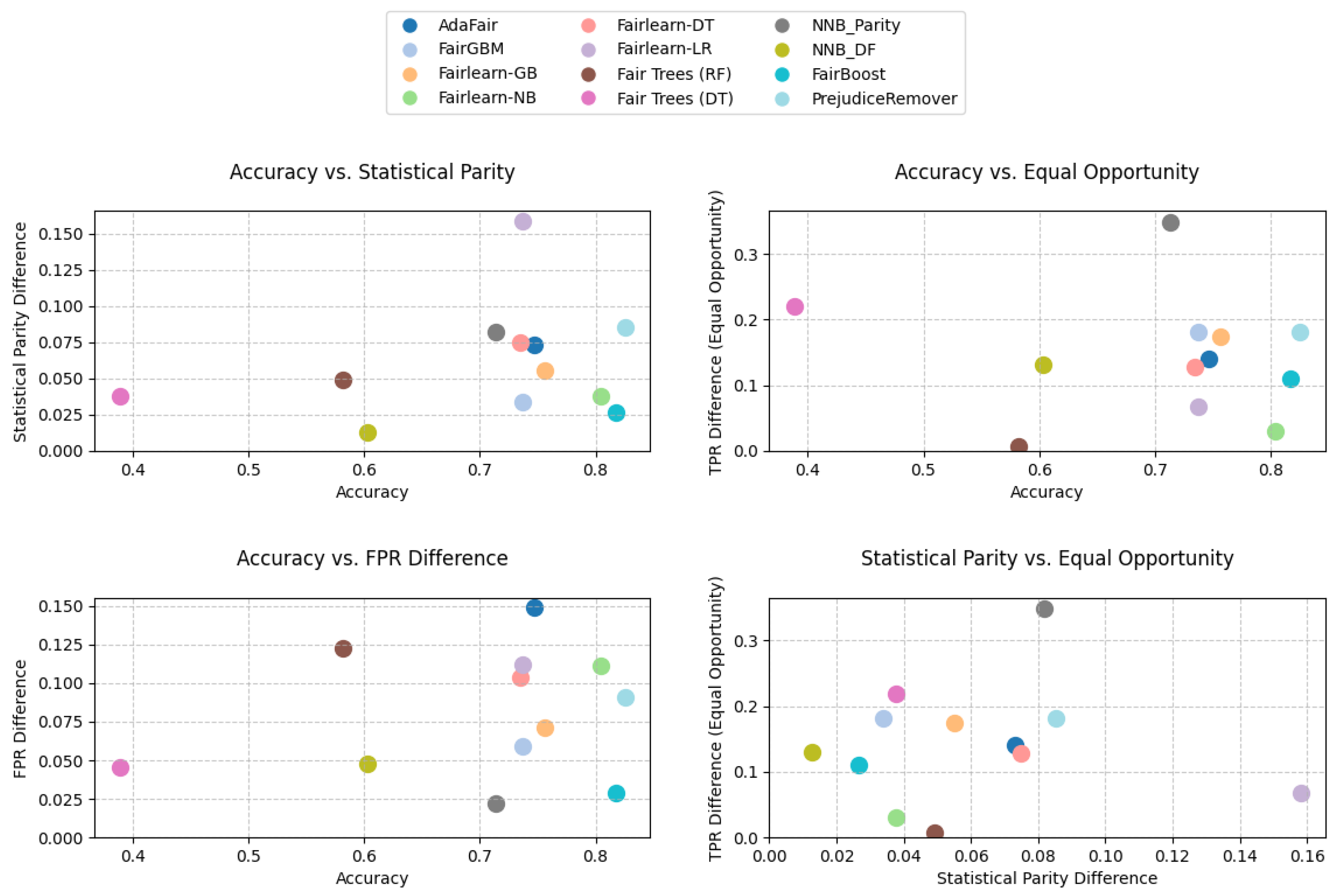
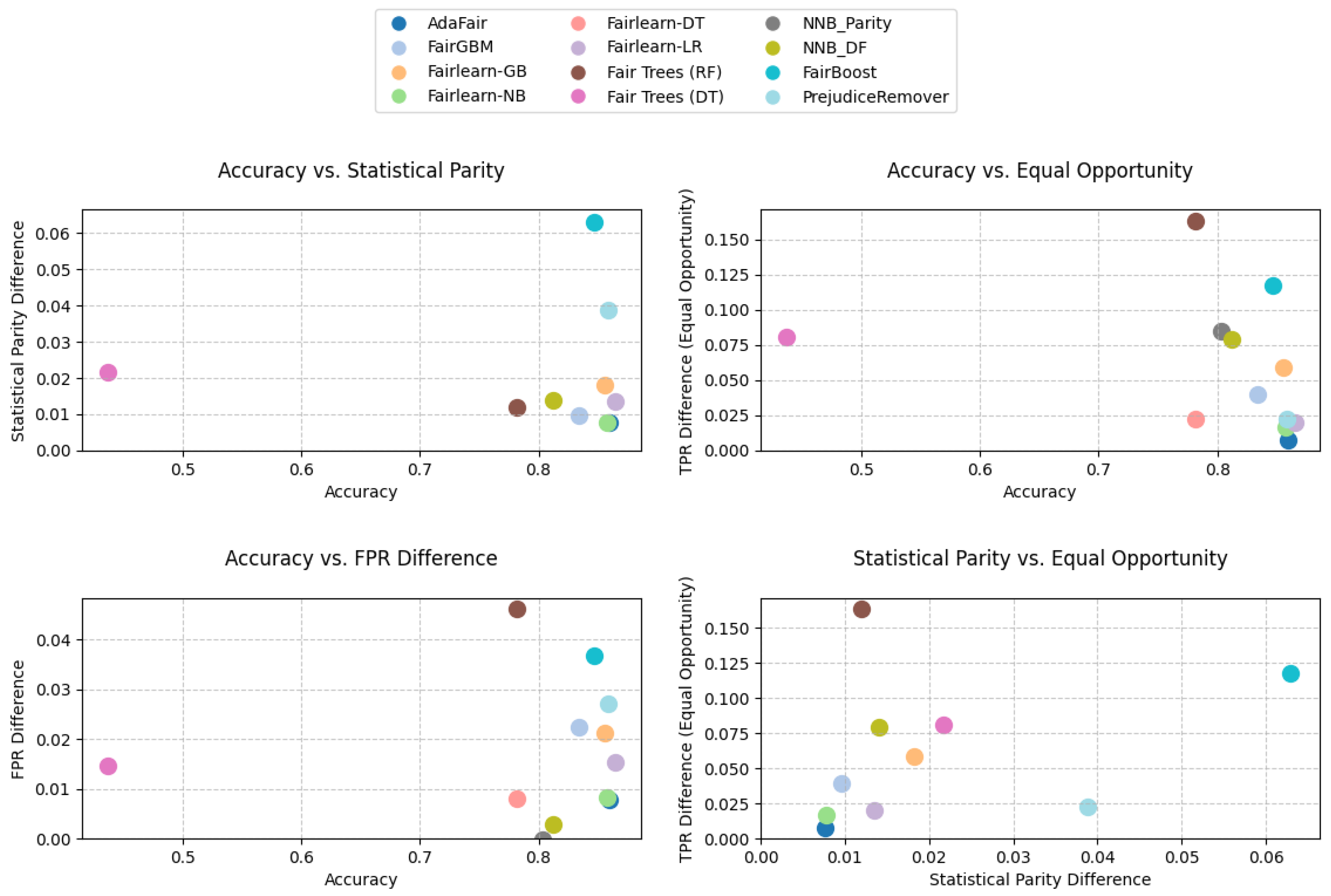
8. Results
8.1. Adult Dataset Results
8.2. BANK Dataset Results
8.3. Titanic Dataset Results
8.4. German Credit Dataset Results
8.5. EAP2024 Dataset Results
8.6. MBA Dataset Results
8.7. LAW Dataset Results
9. Discussion
9.1. Limitations and Hyperparameter Sensitivity
9.2. Do Fairness Models Fulfill Their Goals?
9.3. Evaluation and Selection for Practitioners
9.4. Clarifying Accuracy and Performance Metrics
10. Conclusions
Directions for Future Research
Author Contributions
Funding
Conflicts of Interest
References
- O’Neil, C. Weapons of Math Destruction: How Big Data Increases Inequality and Threatens Democracy; Crown Publishing Group: New York, NY, USA, 2016; ISBN 978-0-553-41881-1. [Google Scholar]
- Raftopoulos, G.; Davrazos, G.; Kotsiantis, S. Evaluating Fairness Strategies in Educational Data Mining: A Comparative Study of Bias Mitigation Techniques. Electronics 2025, 14, 1856. [Google Scholar] [CrossRef]
- Calders, T.; Verwer, S. Three Naive Bayes Approaches for Discrimination-Free Classification. Data Min. Knowl. Disc. 2010, 21, 277–292. [Google Scholar] [CrossRef]
- Choi, Y.; Farnadi, G.; Babaki, B.; Broeck, G.V. den Learning Fair Naive Bayes Classifiers by Discovering and Eliminating Discrimination Patterns. Proc. AAAI Conf. Artif. Intell. 2020, 34, 10077–10084. [Google Scholar] [CrossRef]
- Boulitsakis-Logothetis, S. Fairness-Aware Naive Bayes Classifier for Data with Multiple Sensitive Features. AAAI Spring Symposium: HFIF 23 February 2022. Available online: https://github.com/steliosbl/N-naive-Bayes (accessed on 10 June 2025).
- Kamiran, F.; Calders, T.; Pechenizkiy, M. Discrimination Aware Decision Tree Learning. In Proceedings of the IEEE International Conference on Data Mining, Sydney, NSW, Australia, 13–17 September 2010; pp. 869–874. [Google Scholar]
- Aghaei, S.; Azizi, M.J.; Vayanos, P. Learning Optimal and Fair Decision Trees for Non-Discriminative Decision-Making. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1418–1426. [Google Scholar]
- Ranzato, F.; Urban, C.; Zanella, M. Fair Training of Decision Tree Classifiers. arXiv 2021, arXiv:2101.00909. [Google Scholar] [CrossRef]
- van der Linden, J.; de Weerdt, M.; Demirović, E. Fair and Optimal Decision Trees: A Dynamic Programming Approach. Adv. Neural Inf. Process. Syst. 2022, 35, 38899–38911. [Google Scholar]
- Castelnovo, A.; Cosentini, A.; Malandri, L.; Mercorio, F.; Mezzanzanica, M. FFTree: A Flexible Tree to Handle Multiple Fairness Criteria. Inf. Process. Manag. 2022, 59, 103099. [Google Scholar] [CrossRef]
- Jo, N.; Aghaei, S.; Benson, J.; Gomez, A.; Vayanos, P. Learning Optimal Fair Decision Trees: Trade-Offs Between Interpretability, Fairness, and Accuracy. In Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society, Montreal, QC, Canada, 8–10 August 2023; pp. 181–192. [Google Scholar]
- Bagriacik, M.; Otero, F.E.B. Multiple Fairness Criteria in Decision Tree Learning. Appl. Soft Comput. 2024, 167, 112313. [Google Scholar] [CrossRef]
- Pereira Barata, A.; Takes, F.W.; van den Herik, H.J.; Veenman, C.J. Fair Tree Classifier Using Strong Demographic Parity. Mach. Learn. 2024, 113, 3305–3324. [Google Scholar] [CrossRef]
- Jo, N.; Aghaei, S.; Benson, J.; Gómez, A.; Vayanos, P. Learning optimal fair classification trees. arXiv 2022, arXiv:2201.09932. [Google Scholar]
- Kamishima, T.; Akaho, S.; Asoh, H.; Sakuma, J. Fairness-Aware Classifier with Prejudice Remover Regularizer. In Machine Learning and Knowledge Discovery in Databases, Proceedings of the European Conference, ECML PKDD 2012, Bristol, UK, 24–28 September 2012; Flach, P.A., De Bie, T., Cristianini, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 35–50. [Google Scholar]
- Fukuchi, K.; Kamishima, T.; Sakuma, J. Prediction with Model-Based Neutrality. IEICE Trans. Inf. Syst. 2015, E98.D, 1503–1516. [Google Scholar] [CrossRef]
- Xu, D.; Yuan, S.; Wu, X. Achieving Differential Privacy and Fairness in Logistic Regression. In Proceedings of the Companion Proceedings of the 2019WorldWideWeb Conference, Association for Computing Machinery, San Francisco, CA, USA, 13–17 May 2019; pp. 594–599. [Google Scholar]
- Zafar, M.B.; Valera, I.; Gomez-Rodriguez, M.; Gummadi, K.P. Fairness Constraints: A Flexible Approach for Fair Classification. J. Mach. Learn. Res. 2019, 20, 1–42. [Google Scholar]
- Radovanović, S.; Petrović, A.; Delibašić, B.; Suknović, M. Enforcing Fairness in Logistic Regression Algorithm. In Proceedings of the International Conference on INnovations in Intelligent SysTems and Applications (INISTA), Novi Sad, Serbia, 24–26 August 2020; pp. 1–7. [Google Scholar]
- Elliott, M.; P., D. A Group-Level Learning Approach Using Logistic Regression for Fairer Decisions. In Computer Safety, Reliability, and Security. SAFECOMP 2023 Workshops, Proceedings of the ASSURE, DECSoS, SASSUR, SENSEI, SRToITS, and WAISE, Toulouse, France, 19 September 2023; Guiochet, J., Tonetta, S., Schoitsch, E., Roy, M., Bitsch, F., Eds.; Springer: Cham, Switzerland, 2023; pp. 301–313. [Google Scholar]
- Vancompernolle Vromman, F.; Courtain, S.; Leleux, P.; de Schaetzen, C.; Beghein, E.; Kneip, A.; Saerens, M. Maximum Entropy Logistic Regression for Demographic Parity in Supervised Classification. In Artificial Intelligence and Machine Learning, Proceedings of the 35th Benelux Conference, BNAIC/Benelearn 2023, Delft, The Netherlands, 8–10 November 2023; Oliehoek, F.A., Kok, M., Verwer, S., Eds.; Springer: Cham, Switzerland, 2025; pp. 189–208. [Google Scholar]
- Zhang, J.; Zhang, Z.; Xiao, X.; Yang, Y.; Winslett, M. Functional Mechanism: Regression Analysis under Differential Privacy. Proc. VLDB Endow. 2012, 5, 1364–1375. [Google Scholar] [CrossRef]
- Iosifidis, V.; Ntoutsi, E. AdaFair: Cumulative Fairness Adaptive Boosting. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 781–790. [Google Scholar]
- Iosifidis, V.; Roy, A.; Ntoutsi, E. Parity-Based Cumulative Fairness-Aware Boosting. Knowl. Inf. Syst. 2022, 64, 2737–2770. [Google Scholar] [CrossRef]
- Cruz, A.F.; Belém, C.; Jesus, S.; Bravo, J.; Saleiro, P.; Bizarro, P. FairGBM: Gradient Boosting with Fairness Constraints. arXiv 2023, arXiv:2209.07850. [Google Scholar] [CrossRef]
- Ravichandran, S.; Khurana, D.; Venkatesh, B.; Edakunni, N.U. FairXGBoost: Fairness-Aware Classification in XGBoost. arXiv 2020, arXiv:2009.01442. [Google Scholar]
- Xue, Z. Group AdaBoost with Fairness Constraint. In Proceedings of the SIAM International Conference on Data Mining (SDM), St. Paul Twin Cities, MN, USA, 27–29 April 2023; pp. 865–873. [Google Scholar]
- Zhang, W.; He, F.; Zhang, S. A Novel Fairness-Aware Ensemble Model Based on Hybrid Sampling and Modified Two-Layer Stacking for Fair Classification. Int. J. Mach. Learn. Cyber. 2023, 14, 3883–3896. [Google Scholar] [CrossRef]
- Colakovic, I.; Karakatič, S. FairBoost: Boosting Supervised Learning for Learning on Multiple Sensitive Features. Knowl.-Based Syst. 2023, 280, 110999. [Google Scholar] [CrossRef]
- Monteiro, W.R.; Reynoso-Meza, G. A Proposal of a Fair Voting Ensemble Classifier Using Multi-Objective Optimization. In Systems, Smart Technologies and Innovation for Society, Proceedings of the CITIS’2023, Kyoto, Japan, 14–17 December 2023; Salgado-Guerrero, J.P., Vega-Carrillo, H.R., García-Fernández, G., Robles-Bykbaev, V., Eds.; Springer: Cham, Switzerland, 2024; pp. 50–59. [Google Scholar]
- Agarwal, A.; Beygelzimer, A.; Dudík, M.; Langford, J.; Wallach, H. A Reductions Approach to Fair Classification. arXiv 2018, arXiv:1803.02453. [Google Scholar] [CrossRef]
- Bird, S.; Dudík, M.; Edgar, R.; Horn, B.; Lutz, R.; Milan, V.; Sameki, M.; Wallach, H.; Walker, K. Fairlearn: A Python Toolkit for Assessing and Improving Fairness in AI. 2020. Available online: https://fairlearn.org (accessed on 16 May 2025).
- Titanic Dataset. Available online: https://www.kaggle.com/datasets/yasserh/titanic-dataset (accessed on 8 April 2025).
- Becker, B.; Kohavi, R. Adult Dataset UCI Machine Learning Repository. 1996. Available online: https://archive.ics.uci.edu/dataset/2/adult (accessed on 10 April 2025).
- Moro, S.; Rita, P.; Cortez, P. Bank Marketing, UCI Machine Learning Repository. 2014. Available online: https://archive.ics.uci.edu/dataset/222/bank+marketing (accessed on 10 April 2025).
- Hofmann, H. German Credit Data, UCI Machine Learning Repository. 1994. Available online: https://archive.ics.uci.edu/dataset/144/statlog+german+credit+data (accessed on 10 April 2025).
- MBA Admission Dataset, Class 2025. Available online: https://www.kaggle.com/datasets/taweilo/mba-admission-dataset/data (accessed on 2 October 2024).
- Le Quy, T.; Roy, A.; Iosifidis, V.; Zhang, W.; Ntoutsi, E. A Survey on Datasets for Fairness-Aware Machine Learning. WIREs Data Min. Knowl. Discov. 2022, 12, e1452. [Google Scholar] [CrossRef]
- Harvey, D. Law School Dataset. Available online: https://github.com/damtharvey/law-school-dataset (accessed on 10 April 2025).
- Hort, M.; Chen, Z.; Zhang, J.M.; Harman, M.; Sarro, F. Bias Mitigation for Machine Learning Classifiers: A Comprehensive Survey. ACM J. Responsib. Comput. 2024, 1, 1–52. [Google Scholar] [CrossRef]
- Zhang, W.; Bifet, A.; Zhang, X.; Weiss, J.C.; Nejdl, W. FARF: A Fair and Adaptive Random Forests Classifier. In Advances in Knowledge Discovery and Data Mining, Proceedings of the 25th Pacific-Asia Conference, PAKDD 2021, Virtual Event, 11–14 May 2021; Karlapalem, K., Cheng, H., Ramakrishnan, N., Agrawal, R.K., Reddy, P.K., Srivastava, J., Chakraborty, T., Eds.; Springer: Cham, Switzerland, 2021; pp. 245–256. [Google Scholar]
- Zhang, W.; Ntoutsi, E. FAHT: An Adaptive Fairness-Aware Decision Tree Classifier. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, International Joint Conferences on Artificial Intelligence Organization. Macao, China, 10–16 August 2019; pp. 1480–1486. [Google Scholar]
- Zhang, W.; Bifet, A. FEAT: A Fairness-Enhancing and Concept-Adapting Decision Tree Classifier. In Proceedings of the Discovery Science, 23rd International Conference, Thessaloniki, Greece, 19–21 October 2020; Appice, A., Tsoumakas, G., Manolopoulos, Y., Matwin, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 175–189. [Google Scholar]
- Badar, M.; Fisichella, M.; Iosifidis, V.; Nejdl, W. Discrimination and Class Imbalance Aware Online Naive Bayes. arXiv 2022, arXiv:2211.04812. [Google Scholar] [CrossRef]
- Badar, M.; Fisichella, M. Fair-CMNB: Advancing Fairness-Aware Stream Learning with Naïve Bayes and Multi-Objective Optimization. Big Data Cogn. Comput. 2024, 8, 16. [Google Scholar] [CrossRef]
- Padala, M.; Gujar, S. FNNC: Achieving Fairness through Neural Networks. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, Yokohama, Japan, 7–15 January 2020; pp. 2277–2283. [Google Scholar]
- Datta, A.; Swamidass, S.J. Fair-Net: A Network Architecture For Reducing Performance Disparity Between Identifiable Sub-Populations. In Proceedings of the 14th International Conference on Agents and Artificial Intelligence, Virtual Event, 3–5 February 2022; pp. 645–654. [Google Scholar]
- Mohammadi, K.; Sivaraman, A.; Farnadi, G. FETA: Fairness Enforced Verifying, Training, and Predicting Algorithms for Neural Networks. In Proceedings of the 3rd ACM Conference on Equity and Access in Algorithms, Mechanisms, and Optimization, Boston, MA, USA, 30 October–1 November 2023; pp. 1–11. [Google Scholar]
- Khedr, H.; Shoukry, Y. CertiFair: A Framework for Certified Global Fairness of Neural Networks. Proc. AAAI Conf. Artif. Intell. 2023, 37, 8237–8245. [Google Scholar] [CrossRef]
- Chen, A.; Rossi, R.A.; Park, N.; Trivedi, P.; Wang, Y.; Yu, T.; Kim, S.; Dernoncourt, F.; Ahmed, N.K. Fairness-Aware Graph Neural Networks: A Survey. ACM Trans. Knowl. Discov. Data 2024, 18, 1–23. [Google Scholar] [CrossRef]
- Čutura, L.; Vladimir, K.; Delač, G.; Šilić, M. Fairness in Graph-Based Recommendation: Methods Overview. In Proceedings of the 47th MIPRO ICT and Electronics Convention (MIPRO), Opatija, Croatia, 20–24 May 2024; pp. 850–855. [Google Scholar]



| Method | Key Idea | Fairness Metric(s) | Datasets | Remarks |
|---|---|---|---|---|
| FairBayes I [3]: Probability Mass Adjustment | Modifies P(C|S) and adjusts probability distributions to equalize outcomes between groups while preserving global distribution. | Discrimination Score known as Statistical (Demographic) Parity | Artificial Data, US Census Income (Adult) | Directly reduces discrimination, computationally manageable. |
| FairBayes II [3]: Two-Model Approach | Trains separate Naive Bayes classifiers per sensitive attribute group (2NB) and balances predictions. | – | – | Most effective in balancing fairness and accuracy in practice. |
| FairBayes III [3]: Latent Variable Model | Introduces latent variable L, assumed independent of S, with C derived from L via discrimination; trained using EM algorithm. | – | – | Mathematically rigorous and best in theory but unstable in empirical tests. |
| Fair Naive Bayes Classifier [4] | Efficient branch-and-bound search algorithm to detect discrimination patterns in Naïve Bayes classifiers. | Discrimination Degree | Adult, COMPAS, German Credit | Novel fairness metric, computationally effective |
| Fairness-aware Naive Bayes [5] | Extends FairBayes II (2NB) to multiple sensitive attributes (NNB). | Statistical Parity, Disparate Impact, Differential Fairness | US Census Income (Adult) & Employment Data | NNB-Parity maintains better accuracy but may over-favor non-privileged groups. NNB-DF provides stronger fairness guarantees, but at the cost of a more noticeable accuracy drop. |
| Method | Key Idea | Fairness Metric(s) | Datasets | Remarks |
|---|---|---|---|---|
| Discrimination-Aware Decision Tree [6] | Modifies splitting criterion using IG variants (IGC − IGS, IGC/IGS, IGC + IGS) and applies post-processing relabeling (knapsack optimization). | Statistical Parity | UCI Census Income, Dutch Census 1971, Dutch Census 2001 | IGC + IGS with relabeling achieves best fairness–accuracy trade-off. |
| RegOCT [7] | Mixed Integer Programming (MIP) framework with fairness indices DI and DT. | Disparate Impact (DI), Disparate Treatment (DT) | Adult, Default, Crime | Near-zero discrimination; 1–3% accuracy drop better than Discrimination-Aware Decision Tree computationally demanding. |
| FATT [8] | Genetic optimization using mutation and crossover for fair, single-tree models. | Demographic Parity | Adult, COMPAS, Communities and Crime, German Credit, Heritage Health | Improves fairness by 35–45% with 3.6% accuracy reduction. |
| Fair and Optimal Decision Trees [9] | Dynamic programming with pruning based on fairness bounds to improve scalability. | Bounds Based on Demographic Parity | Adult, Bank Marketing, Communities and Crime, COMPAS, Dutch Census, German Credit, KDD Census, OULAD, Ricci, Student-Mathematics/ Portuguese | Outperforms FairOCT in runtime and scalability. |
| FFTree [10] | Allows user-defined combination of fairness constraints in splitting. Converts unfair nodes to leaves. | Demographic Parity, Predictive Equality, Equal Opportunity, Predictive Parity | Adult, Loan Granting | Select more than one Fairness Metric Maintains accuracy and interpretability with fairness flexibility. |
| Optimal Fair Decision Trees [11] | Flow-based MIO with binary fairness constraints on paths and structure. | Statistical Parity, Conditional Statistical Parity, Equalized Odds | COMPAS, Adult, German Credit | High interpretability and near-perfect fairness 4.2% accuracy trade-off. |
| FAir-C4.5 [12] | Extension of C4.5 with fairness-aware attribute selection: Lexicographic, Constraint-Based, Gain Ratio-Fairness (GRXFR). | Disparate Impact Ratio, Discrimination Score, Consistency, Disparate Treatment | Adult, German Credit, Propublica Recidivism, NYPD SQF CPW, Student Mathematics/Portuguese, Drug Consumption, Ricci, Wine Taste, Bank, Dutch Census, Law School Admission, UFRGS. | 0.5–2% lower accuracy than C4.5 more efficient than FFTree. |
| SCAFF Tree [13] | New splitting criterion (SCAFF) using ROC-AUC and demographic parity. | Demographic Parity | COMPAS, Adult | Achieves higher fairness with 2–4% accuracy reduction outperforms Discrimination-Aware Decision Tree. |
| Method | Main Idea | Fairness Criterion | Datasets | Remarks |
|---|---|---|---|---|
| Prejudice Remover Regularizer [15] | Regularization term to penalize bias using Prejudice Index | Prejudice Index (PI), Normalized PI (NPI) | Adult dataset | Implemented in AIF360 Libary Less Effective than Calder & Verver 2NB |
| -Neutral Logistic Regression [16] | Enforces probabilistic independence between target and sensitive attribute | -Neutrality | Adult, German Credit, Dutch Census, Bank Marketing, Credit Approval | Outperforms 2-NB and Prejudice Remover Regularizer in fairness–accuracy trade-off |
| Differentially Private and Fair Logistic Regression [17] | Combines fairness penalty with differential privacy via noise injection | Group Fairness + -Differential Privacy | Adult, Dutch Census | PFLR better utility than PFLR |
| Disparate Impact-Free Logistic Regression [18] | Adds covariance-based fairness constraint in convex classifiers | Disparate Treatment, Impact, Mistreatment | Synthetic Data, Adult, Bank Marketing, COMPAS, NYPD SQF | Reduces bias by 50–80% with 1–5% accuracy drop |
| Constraint Logistic Regression [19] | Adds equalized odds constraint to [18] method | Disparate Impact, Equalized Odds | Adult, COMPAS | Up to 58% bias reduction, Better Equalized Odds |
| Group-Level Logistic Regression [20] | Ensures group balance via median gradient update across sensitive groups | Implicit Fairness via Group Influence | Adult, OULAD | improves fairness vs. standard LR Less effective than Fairlearn algorithms |
| Max-Entropy LR with Demographic Parity [21] | Maximizes entropy while enforcing fairness constraints on model output | Demographic Parity (via covariance constraint) | Adult, COMPAS, Bank Marketing, German Credit, Law | Includes Fairness-aware Feature Selection algorithm |
| Method | Key Idea | Fairness Metric(s) | Datasets | Remarks |
|---|---|---|---|---|
| AdaFair [23,24] | AdaBoost extension reweighting instances for fairness and accuracy; dynamically optimizes weak learners | Equalized Odds, Statistical Parity, Equal Opportunity | Adult, Bank, COMPAS, KDD Census | AdaFair integrates fairness into the boosting loop |
| FAIRGBM [25] | Adds convex fairness constraints into GBDT via Lagrangian optimization | Equal Opportunity, Equalized Odds | ACS Income, Adult, Account Opening Fraud | FairGBM outperforms similar by achieving high fairness without significant performance loss |
| FairXGBoost [26] | XGBoost with fairness regularizer controlled by hyperparameter to reduce correlation with sensitive attributes | Disparate Impact | Adult, COMPAS, Default, Bank | Each dataset responds differently to tuning |
| GAFairC [27] | AdaBoost with group-aware loss and fairness constraint components: penalty, intensity selection, post-pruning. | Equalized Odds | Bank, KDD, COMPAS, Credit, Adult | GAFairC achieves higher fairness maintaining/improving accuracy More stable across imbalanced datasets. |
| FAEM [28] | Two-stage model: hybrid sampling (ADASYN), followed by two-layer stacking ensemble for fairness-aware predictions | Average Odds Difference, Equal Opportunity Difference, Disparate Impact | German Credit, Adult, Bank, COMPAS | FAEM effectively balances accuracy and fairness, outperforms prior fairness-aware models |
| FairBoost [29] | Based on AdaBoost.SAMME.R; supports multiple sensitive attributes via fairness-aware instance weighting | Demographic Parity, Equalized Odds Difference | Adult, Arrhythmia, Drugs, German Credit | Handles multiple sensitive features |
| Fair Voting Ensemble [30] | Soft voting with separate dynamic weights for privileged/unprivileged groups optimized via RNSGA-II | Counterfactual fairness, Equalized odds (custom based) | COMPAS, Adult, German Credit | Post-Processing fairness approach |
| Model | Accuracy | Acc. Diff | Stat. Parity Diff | TPR Diff | FPR Diff |
|---|---|---|---|---|---|
| AdaFair | |||||
| FairGBM | |||||
| Fairlearn-GB | |||||
| Fairlearn-NB | |||||
| Fairlearn-DT | |||||
| Fairlearn-LR | |||||
| Fair Random Forest | |||||
| Fair Decision Trees | |||||
| NNB-Parity | |||||
| NNB-DF | |||||
| Fairboost | |||||
| Prejudice Remover |
| Model | Accuracy | Acc. Diff | Stat. Parity Diff | TPR Diff | FPR Diff |
|---|---|---|---|---|---|
| AdaFair | |||||
| FairGBM | |||||
| Fairlearn-GB | |||||
| Fairlearn-NB | |||||
| Fairlearn-DT | |||||
| Fairlearn-LR | |||||
| Fair Random Forest | |||||
| Fair Decision Trees | |||||
| NNB-Parity | |||||
| NNB-DF | |||||
| Fairboost | |||||
| Prejudice Remover |
| Model | Accuracy | Acc. Diff | Stat. Parity Diff | TPR Diff | FPR Diff |
|---|---|---|---|---|---|
| AdaFair | |||||
| FairGBM | |||||
| Fairlearn-GB | |||||
| Fairlearn-NB | |||||
| Fairlearn-DT | |||||
| Fairlearn-LR | |||||
| Fair Random Forest | |||||
| Fair Decision Trees | |||||
| NNB-Parity | |||||
| NNB-DF | |||||
| Fairboost | |||||
| Prejudice Remover |
| Model | Accuracy | Acc. Diff | Stat. Parity Diff | TPR Diff | FPR Diff |
|---|---|---|---|---|---|
| AdaFair | |||||
| FairGBM | |||||
| Fairlearn-GB | |||||
| Fairlearn-NB | |||||
| Fairlearn-DT | |||||
| Fairlearn-LR | |||||
| Fair Random Forest | |||||
| Fair Decision Trees | |||||
| NNB-Parity | |||||
| NNB-DF | |||||
| Fairboost | |||||
| Prejudice Remover |
| Model | Accuracy | Acc. Diff | Stat. Parity Diff | TPR Diff | FPR Diff |
|---|---|---|---|---|---|
| AdaFair | |||||
| FairGBM | |||||
| Fairlearn-GB | |||||
| Fairlearn-NB | |||||
| Fairlearn-DT | |||||
| Fairlearn-LR | |||||
| Fair Random Forest | |||||
| Fair Decision Trees | |||||
| NNB-Parity | |||||
| NNB-DF | |||||
| Fairboost | |||||
| Prejudice Remover |
| Model | Accuracy | Acc. Diff | Stat. Parity Diff | TPR Diff | FPR Diff |
|---|---|---|---|---|---|
| AdaFair | |||||
| FairGBM | |||||
| Fairlearn-GB | |||||
| Fairlearn-NB | |||||
| Fairlearn-DT | |||||
| Fairlearn-LR | |||||
| Fair Random Forest | |||||
| Fair Decision Trees | |||||
| NNB-Parity | |||||
| NNB-DF | |||||
| Fairboost | |||||
| Prejudice Remover |
| Model | Accuracy | Acc. Diff | Stat. Parity Diff | TPR Diff | FPR Diff |
|---|---|---|---|---|---|
| AdaFair | |||||
| FairGBM | |||||
| Fairlearn-GB | |||||
| Fairlearn-NB | |||||
| Fairlearn-DT | |||||
| Fairlearn-LR | |||||
| Fair Random Forest | |||||
| Fair Decision Trees | |||||
| NNB-Parity | |||||
| NNB-DF | |||||
| Fairboost | |||||
| Prejudice Remover |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raftopoulos, G.; Fazakis, N.; Davrazos, G.; Kotsiantis, S. A Comprehensive Review and Benchmarking of Fairness-Aware Variants of Machine Learning Models. Algorithms 2025, 18, 435. https://doi.org/10.3390/a18070435
Raftopoulos G, Fazakis N, Davrazos G, Kotsiantis S. A Comprehensive Review and Benchmarking of Fairness-Aware Variants of Machine Learning Models. Algorithms. 2025; 18(7):435. https://doi.org/10.3390/a18070435
Chicago/Turabian StyleRaftopoulos, George, Nikos Fazakis, Gregory Davrazos, and Sotiris Kotsiantis. 2025. "A Comprehensive Review and Benchmarking of Fairness-Aware Variants of Machine Learning Models" Algorithms 18, no. 7: 435. https://doi.org/10.3390/a18070435
APA StyleRaftopoulos, G., Fazakis, N., Davrazos, G., & Kotsiantis, S. (2025). A Comprehensive Review and Benchmarking of Fairness-Aware Variants of Machine Learning Models. Algorithms, 18(7), 435. https://doi.org/10.3390/a18070435








