Assessment of Affordable Real-Time PPP Solutions for Transportation Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model of Multi-GNSS Kinematic RT-PPP
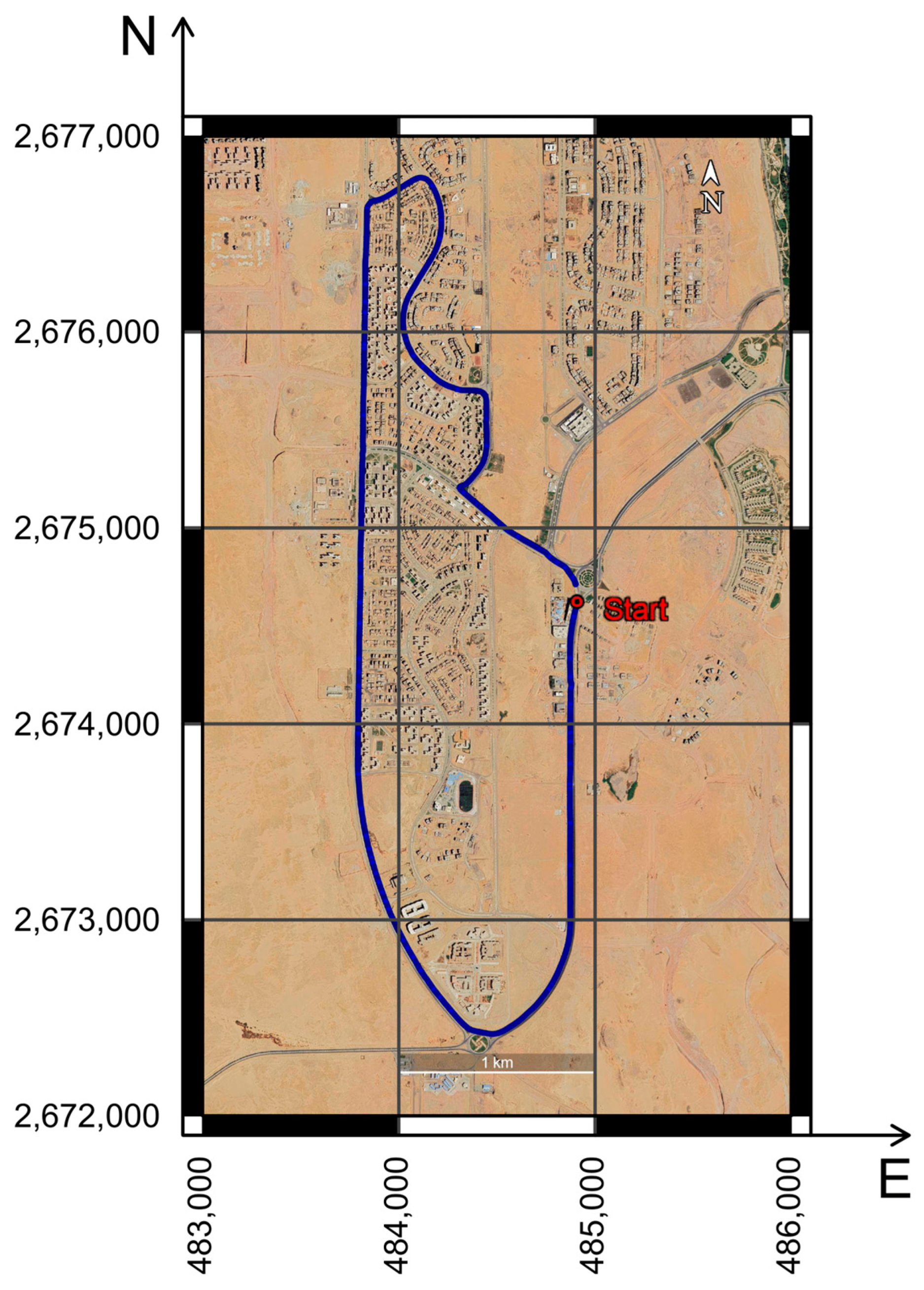
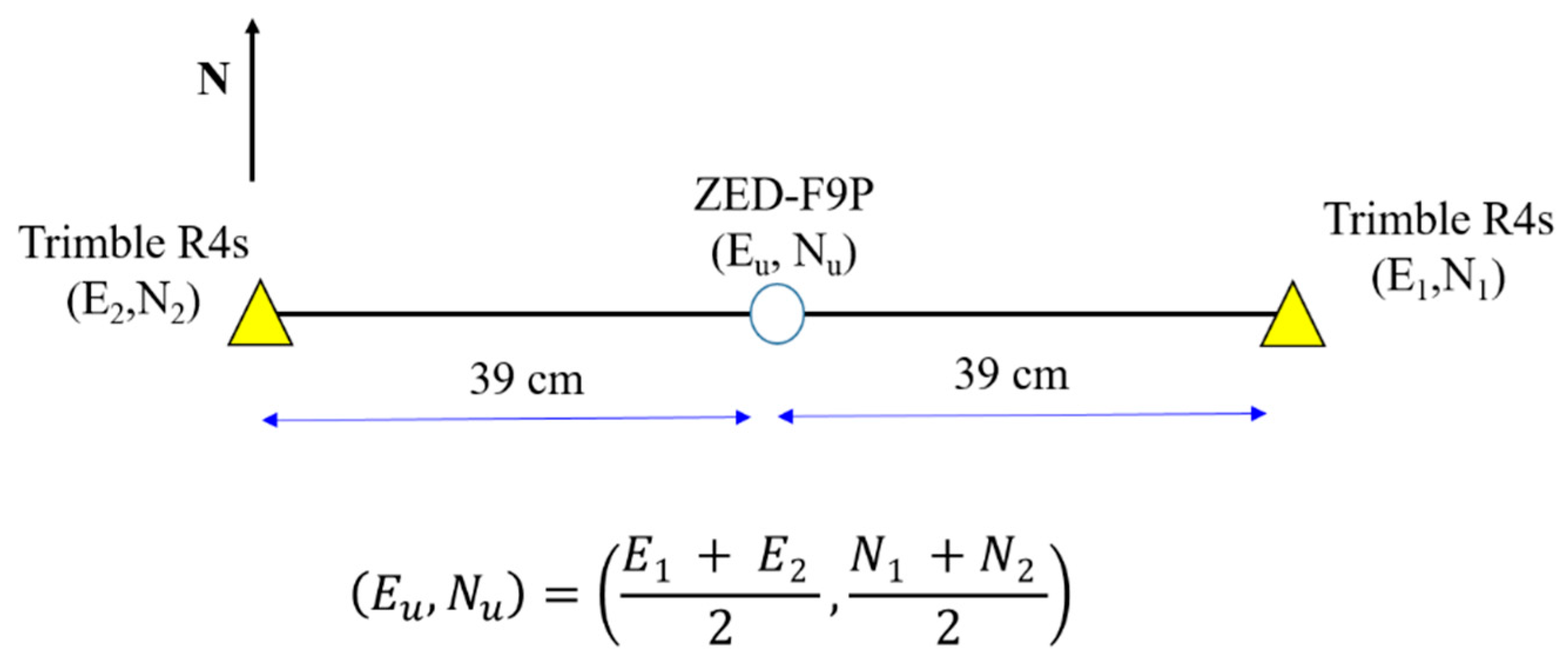
2.2. Kinematic RT-PPP Campaign Setup
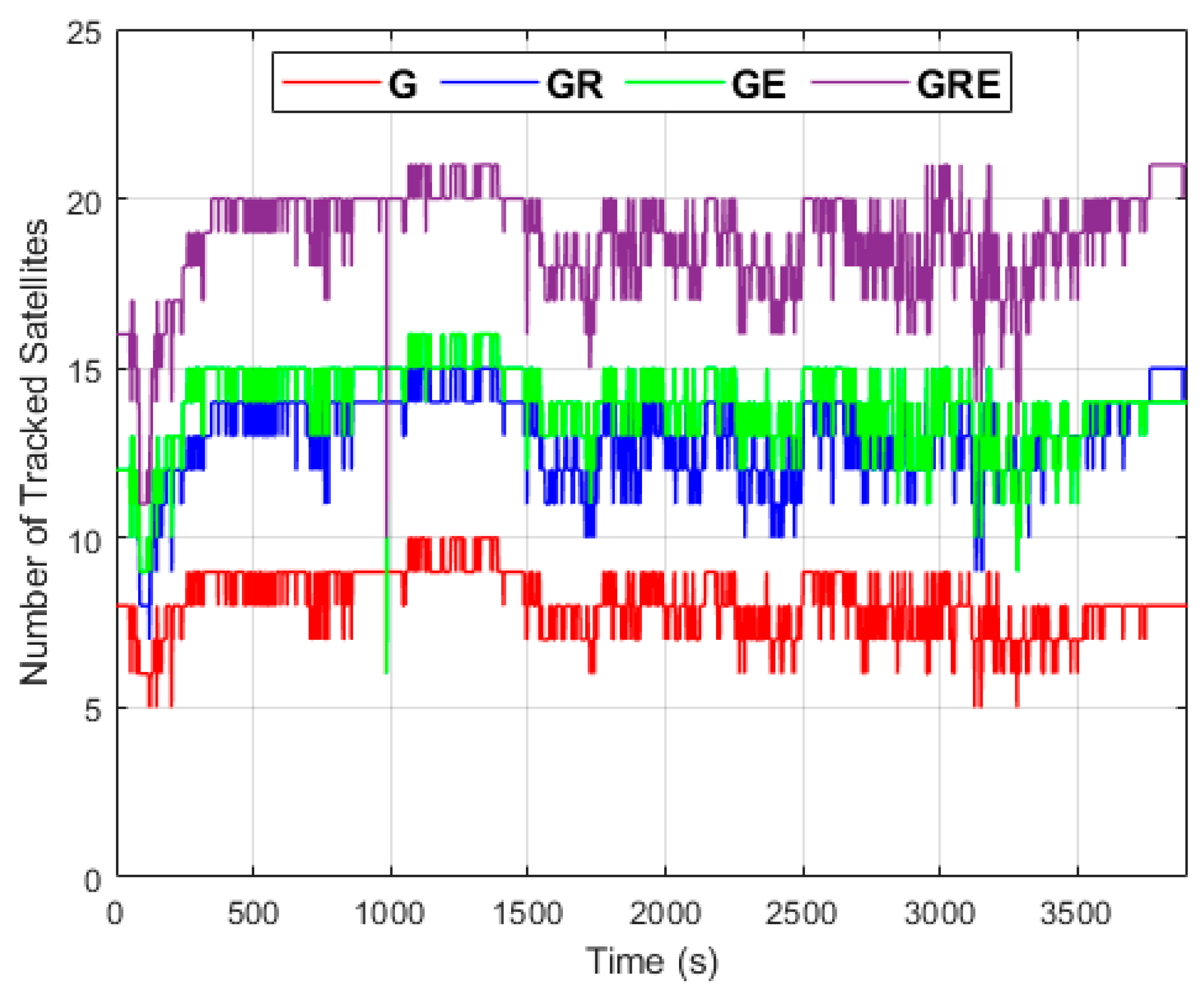
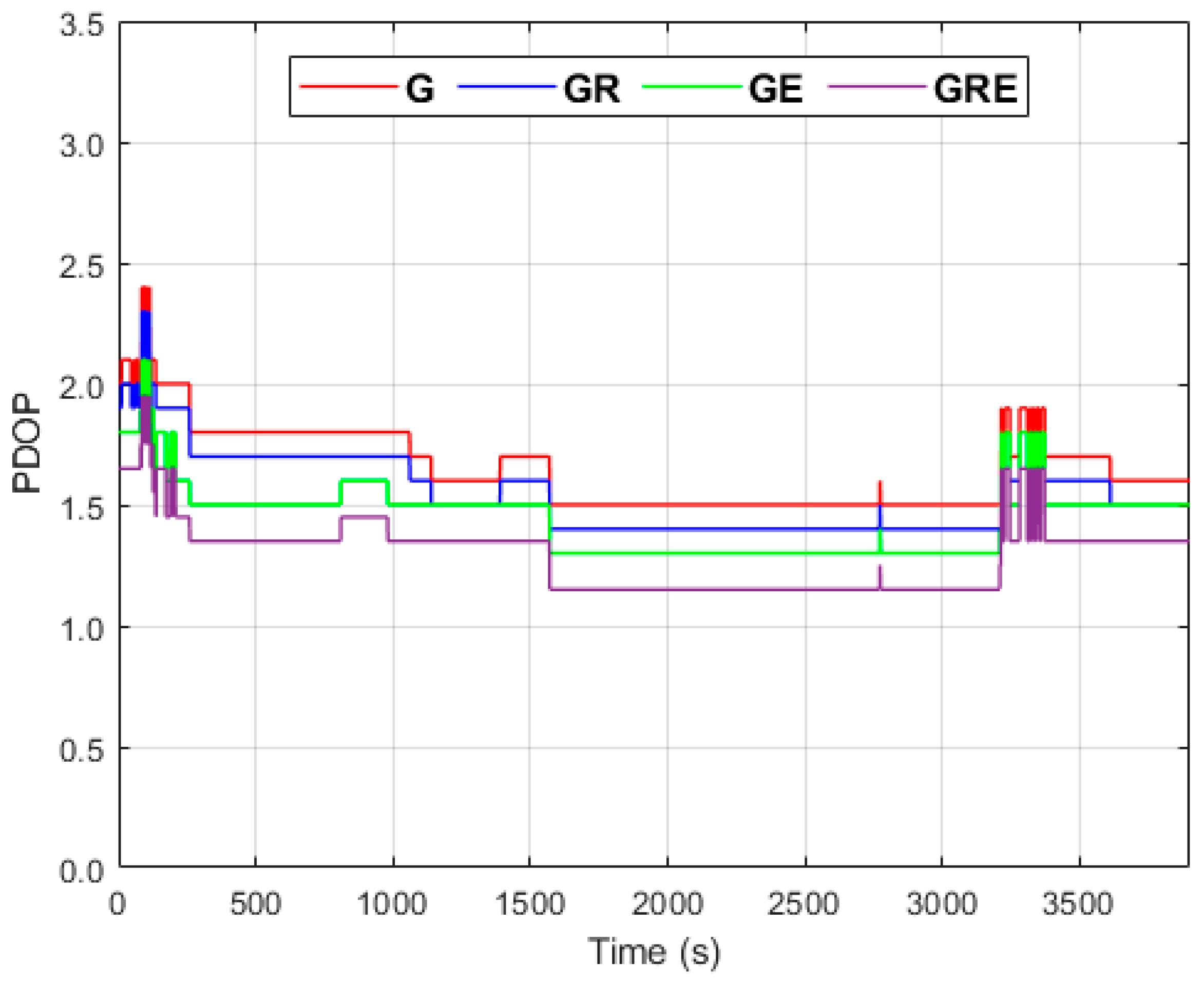
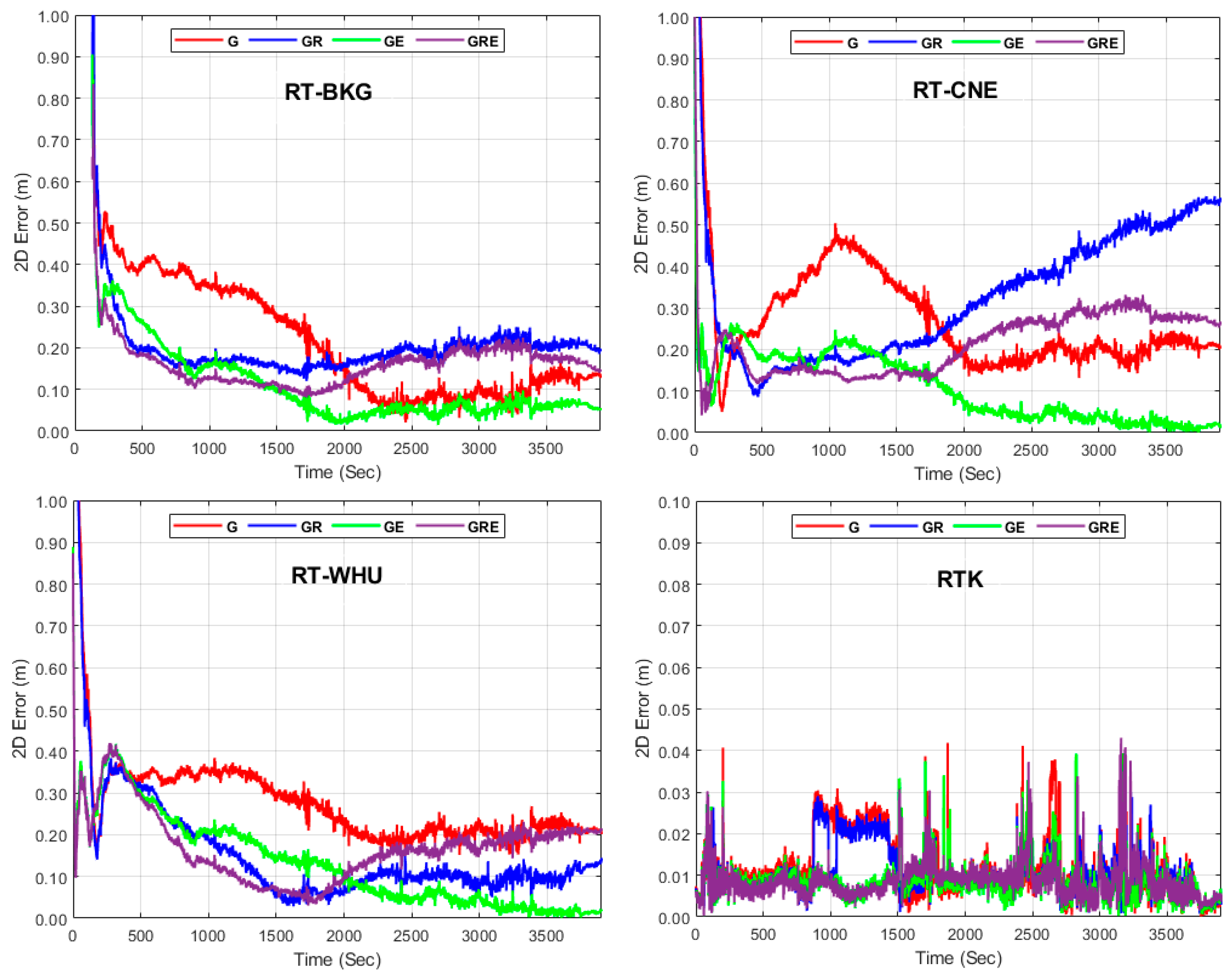
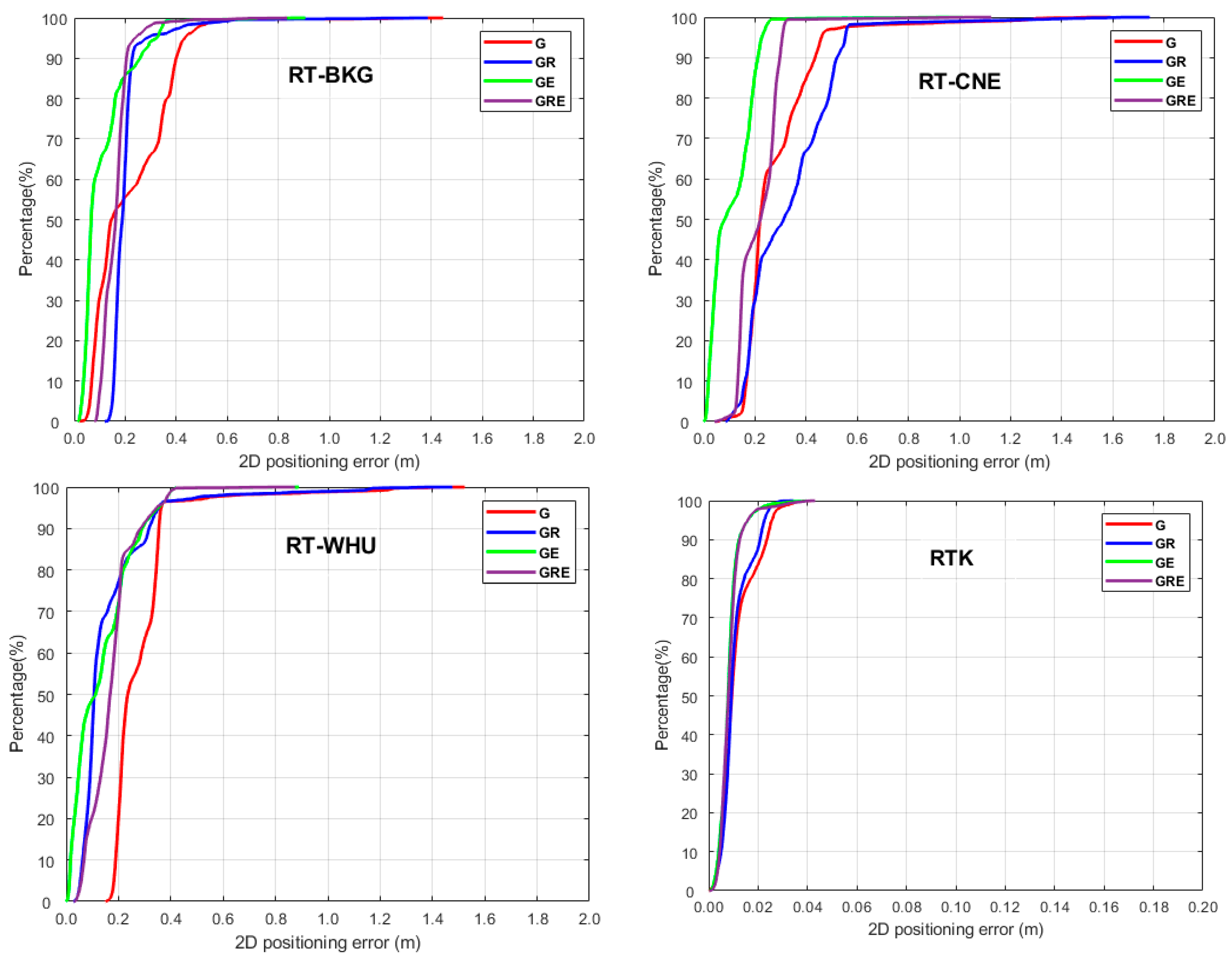
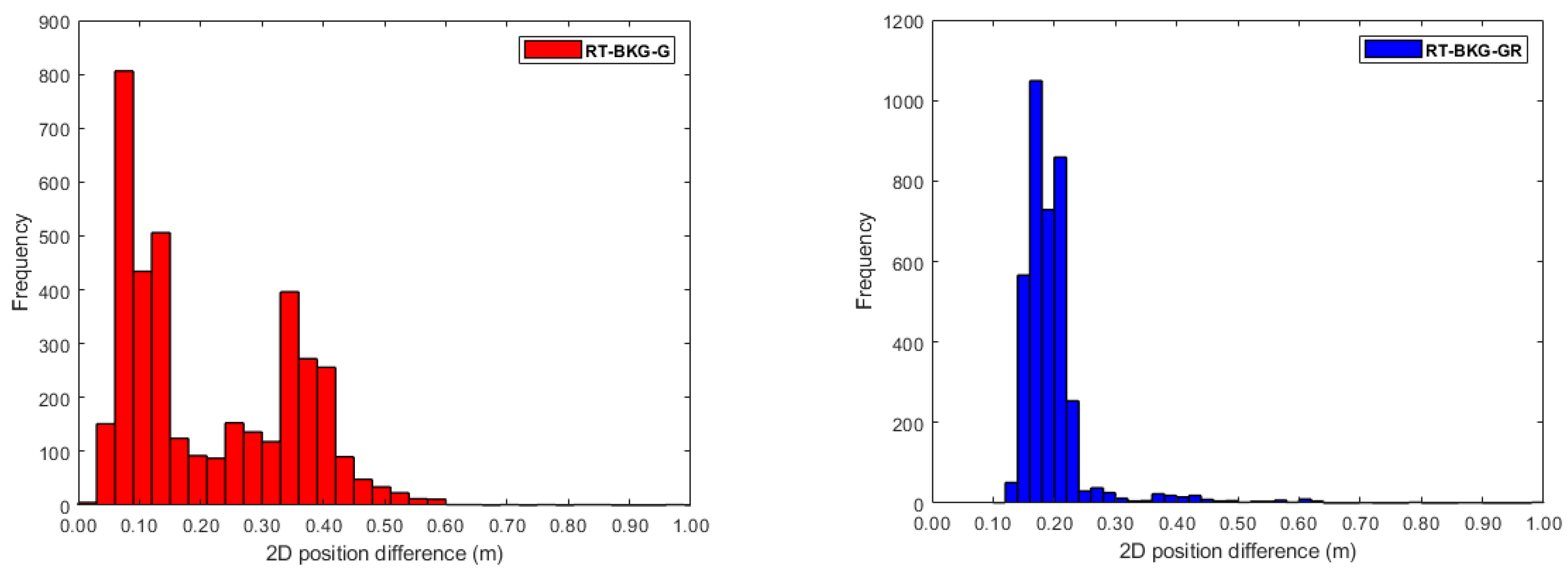
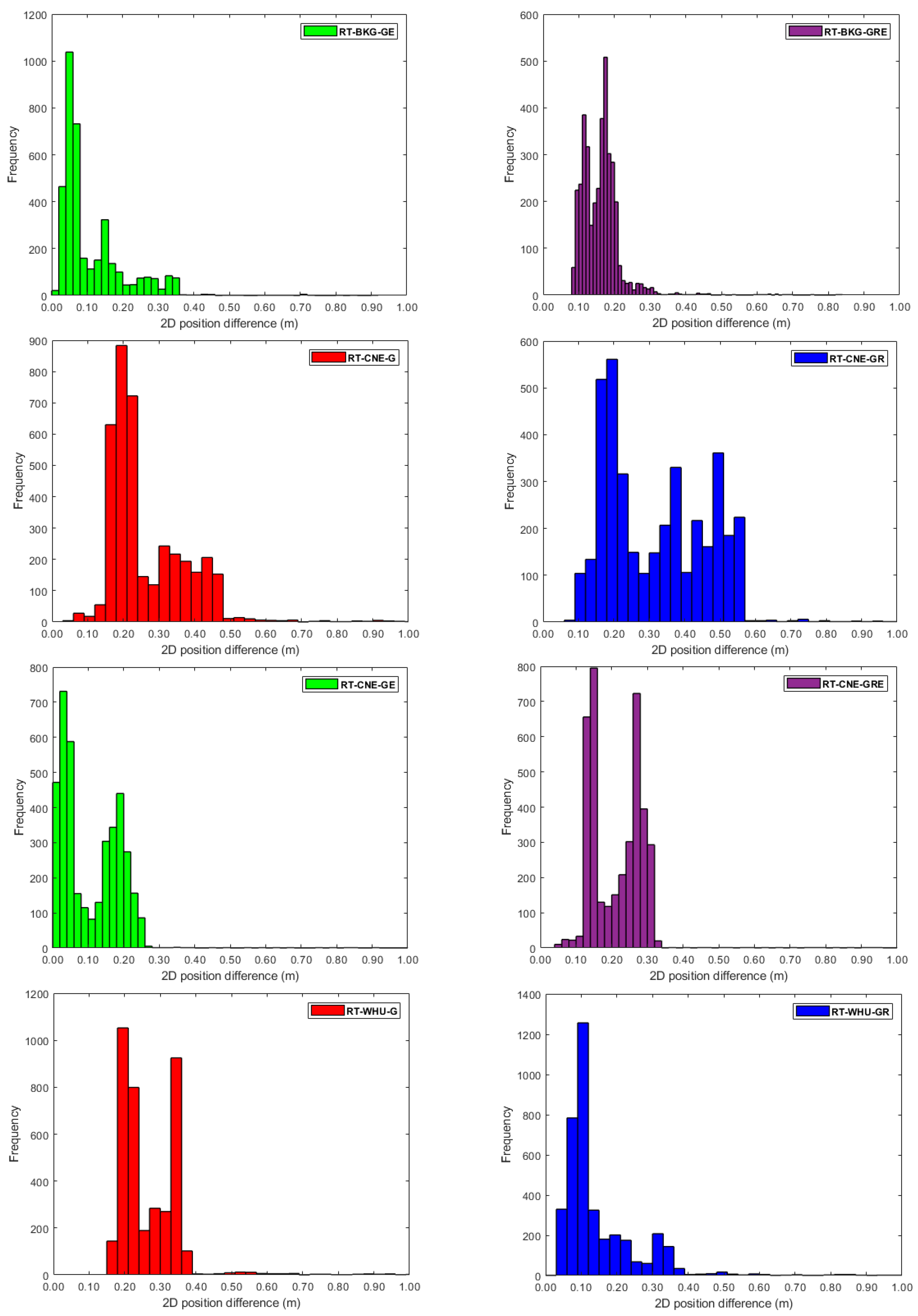
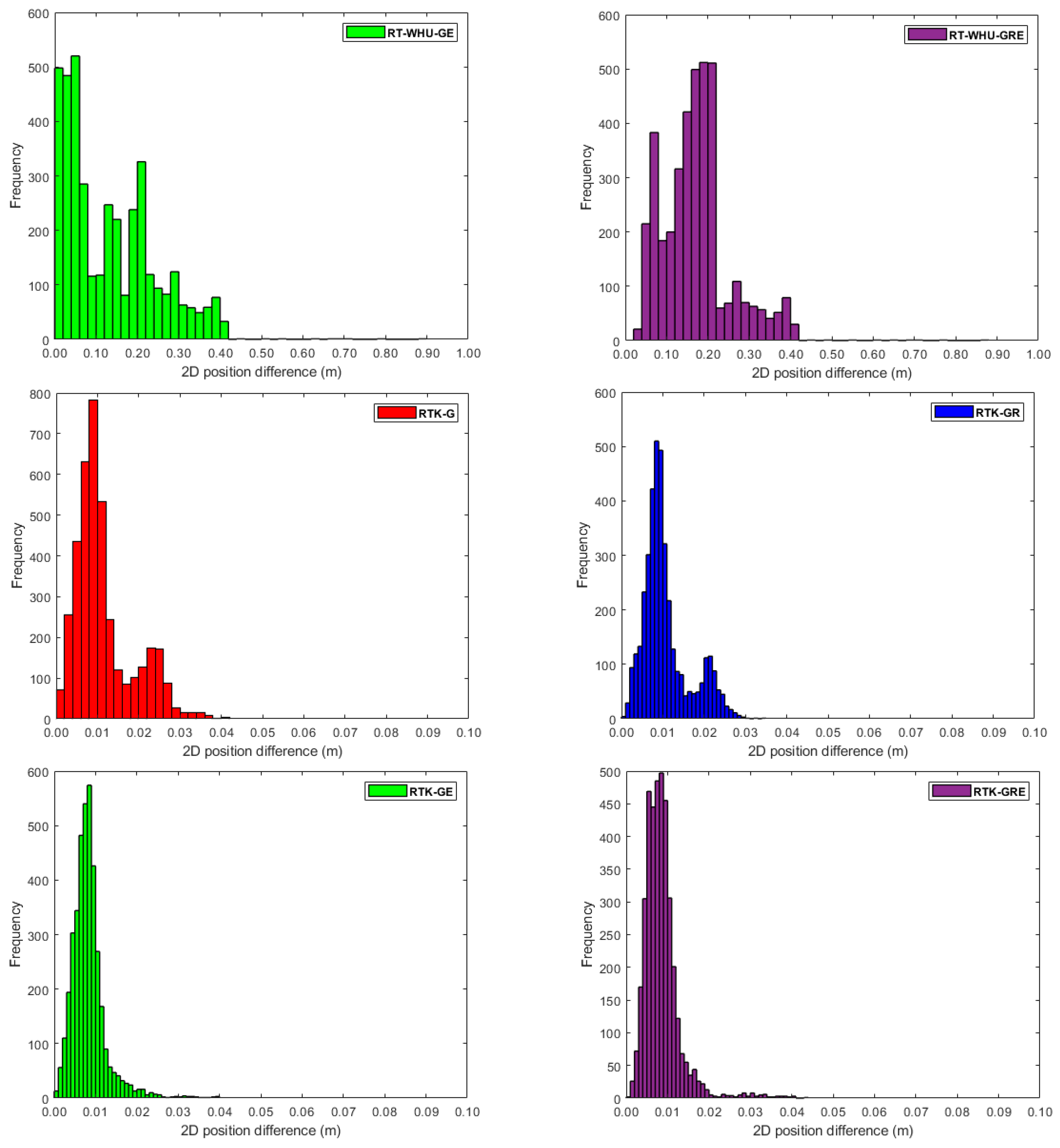
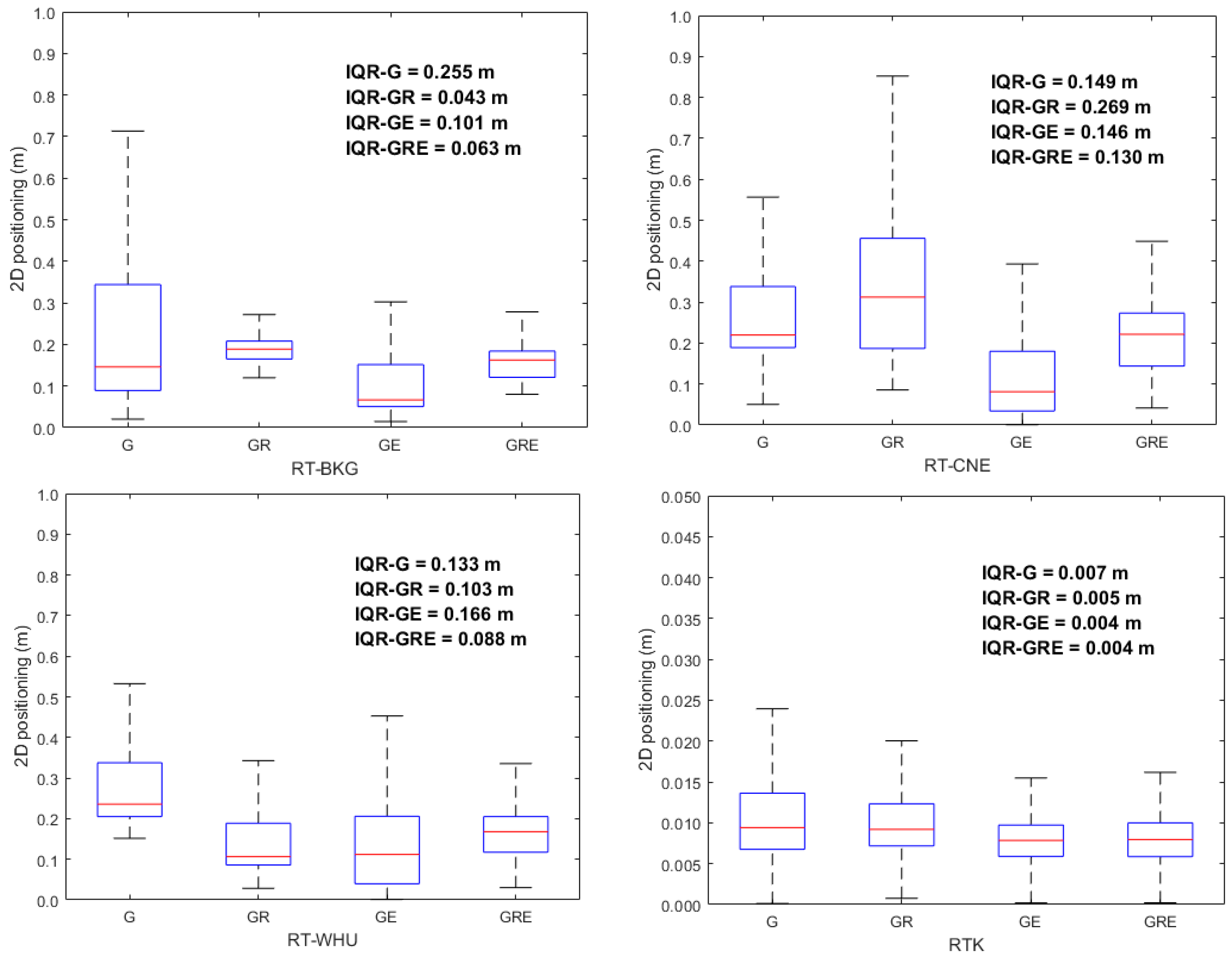
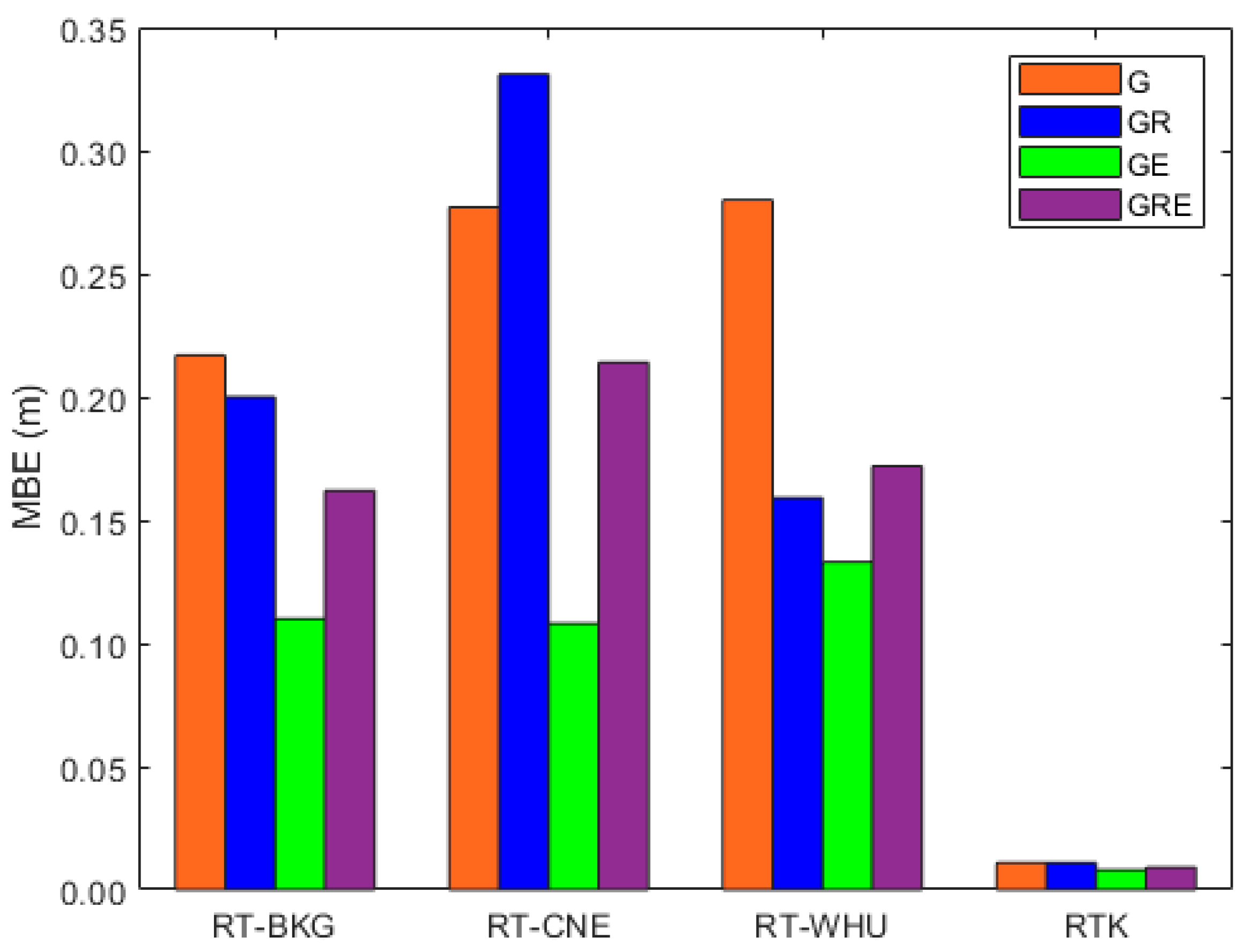
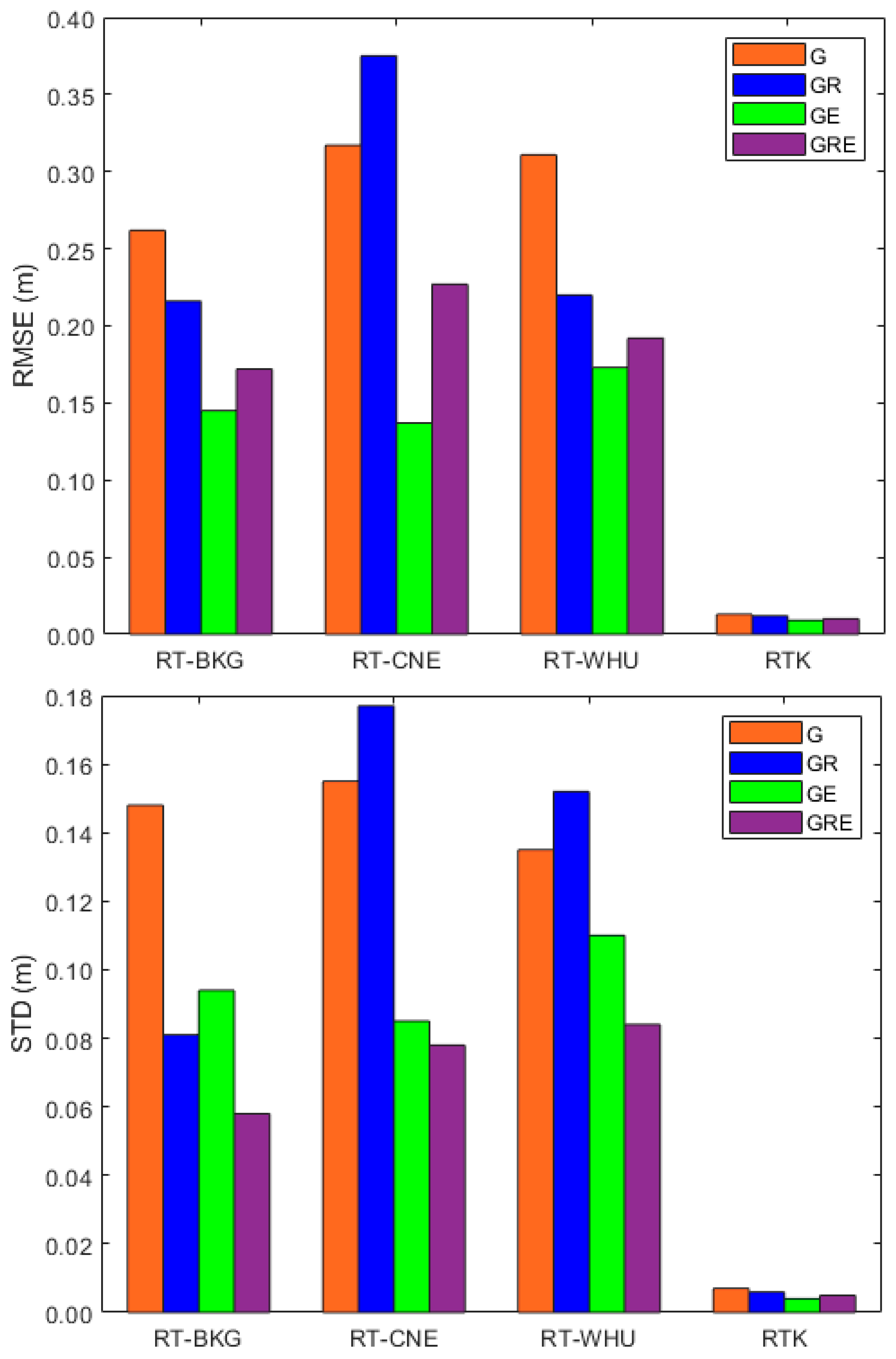
3. Results
4. Discussion
- A one-to-three-decimeter positioning accuracy level can be obtained using the RT-PPP solution, utilizing both the cost-effective ZED-F9P module and satellite orbit and clock correction products from the BKG, CNE, or WHU streams.
- Incorporating GLONASS, Galileo, or both into the GPS RT-PPP solution improves positioning accuracy.
- The BKG and WHU SSR products increase the GPS/GLONASS RT-PPP two-dimensional positioning accuracy by about 18% and 29%, respectively, compared with their counterparts in the GPS RT-PPP solution.
- The enhancement percentages of the GPS/Galileo RT-PPP’s 2D accuracy using orbit and clock products from BKG, CNE, and WHU are around 18%, 57%, and 44%, respectively, compared with their counterparts in the GPS RT-PPP solutions.
- Compared with their counterparts from the GPS RT-PPP solutions, satellite orbit and clock products from the BKG, CNE, and WHU centers enhance the GPS/GLONASS/Galileo RT-PPP positioning accuracy by about 34%, 28%, and 38%, respectively.
- BKG orbit and clock products offer the best solutions for the GPS and GPS/GLONASS/Galileo RT-PPP solutions, while CNE SSR products are superior for the GPS/Galileo RT-PPP solutions, and both BKG and WHU demonstrate similar performance for the GPS/GLONASS RT-PPP solution.
- The GPS-based RT-PPP solutions from the three BKG, CNE, and WHU SSR products require a long time to converge compared with the other solutions, which could be a limitation of our suggested solutions. For this reason, the RT-PPP ambiguity resolution solution will be considered in our future work to improve the convergence time.
- Based on the attained positioning accuracy and compared with the common PPP, RTK, and PPP-RTK solutions, our proposed RT-PPP approach is a cost-effective solution, particularly when compared with the geodetic-grade PPP solution; in addition, its configuration is less complicated than the RTK and PPP-RTK solutions.
- Finally, our processing scenario is based on a suburban context, and continuous SSR corrections are necessary for a successful solution.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- An, X.; Ziebold, R.; Lass, C. PPP-RTK with Rapid Convergence Based on SSR Corrections and Its Application in Transportation. Remote Sens. 2023, 15, 4770. [Google Scholar] [CrossRef]
- Zhang, Q.; Dai, Y.; Zhang, T.; Guo, C.; Niu, X. Road Semantic-Enhanced Land Vehicle Integrated Navigation in GNSS Denied Environments. IEEE Trans. Intell. Transp. Syst. 2024, 25, 20889. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, J.; Guo, M.; Ning, X.; Wang, Y.; Lu, J. Sensor Fusion of GNSS and IMU Data for Robust Localization via Smoothed Error State Kalman Filter. Sensors 2023, 23, 3676. [Google Scholar] [CrossRef]
- Yan, P.; Jiang, J.; Zhang, F.; Xie, D.; Wu, J.; Zhang, C.; Tang, Y.; Liu, J. An improved adaptive Kalman filter for a single frequency gnss/mems-imu/odometer integrated navigation module. Remote Sens. 2021, 13, 4317. [Google Scholar] [CrossRef]
- Xin, S.; Wang, X.; Zhang, J.; Zhou, K.; Chen, Y. A Comparative Study of Factor Graph Optimization-Based and Extended Kalman Filter-Based PPP-B2b/INS Integrated Navigation. Remote Sens. 2023, 15, 5144. [Google Scholar] [CrossRef]
- Wen, W.; Bai, X.; Zhang, G.; Chen, S.; Yuan, F.; Hsu, L.T. Multi-Agent Collaborative GNSS/Camera/INS Integration Aided by Inter-Ranging for Vehicular Navigation in Urban Areas. IEEE Access 2020, 8, 124323–124338. [Google Scholar] [CrossRef]
- Shen, Z.; Li, X.; Wang, X.; Wu, Z.; Li, X.; Zhou, Y.; Li, S. A Novel Factor Graph Framework for Tightly Coupled GNSS/INS Integration with Carrier-Phase Ambiguity Resolution. IEEE Trans. Intell. Transp. Syst. 2024, 10, 13091–13105. [Google Scholar] [CrossRef]
- Shen, Z.; Li, X.; Li, X. Advancing High-Precision Navigation: Leveraging Homogeneous Sensors in Tightly Coupled PPP-RTK/IMU Integration. IEEE Trans. Ind. Electron. 2024, 71, 15100–15110. [Google Scholar] [CrossRef]
- Niu, Z.; Li, G.; Guo, F.; Shuai, Q.; Zhu, B. An Algorithm to Assist the Robust Filter for Tightly Coupled RTK/INS Navigation System. Remote Sens. 2022, 14, 2449. [Google Scholar] [CrossRef]
- Li, X.; Qin, Z.; Shen, Z.; Li, X.; Zhou, Y.; Song, B. A High-Precision Vehicle Navigation System Based on Tightly Coupled PPP-RTK/INS/Odometer Integration. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1855–1866. [Google Scholar] [CrossRef]
- Li, W.; Liu, G.; Cui, X.; Lu, M. Feature-aided RTK/LiDAR/INS integrated positioning system with parallel filters in the ambiguity-position-joint domain for urban environments. Remote Sens. 2021, 13, 2013. [Google Scholar] [CrossRef]
- Kang, M.S.; Ahn, J.H.; Im, J.U.; Won, J.H. Lidar- and V2X-Based Cooperative Localization Technique for Autonomous Driving in a GNSS-Denied Environment. Remote Sens. 2022, 14, 5881. [Google Scholar] [CrossRef]
- Filip, A.; Rispoli, F. Continuity of GNSS as a critical attribute for safety applications in land transport. Sci. Rep. 2024, 14, 11742. [Google Scholar] [CrossRef] [PubMed]
- Baasch, K.N.; Icking, L.; Ruwisch, F.; Schön, S. Coordinate Frames and Transformations in GNSS Ray-Tracing for Autonomous Driving in Urban Areas. Remote Sens. 2023, 15, 180. [Google Scholar] [CrossRef]
- Anand, B.; Senapati, M.; Barsaiyan, V.; Rajalakshmi, P. LiDAR-INS/GNSS-Based Real-Time Ground Removal, Segmentation, and Georeferencing Framework for Smart Transportation. IEEE Trans. Instrum. Meas. 2021, 70, 8504611. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Khodabandeh, A. Review and principles of PPP-RTK methods. J. Geod. 2014, 89, 217–240. [Google Scholar] [CrossRef]
- Novák, A.; Kováčiková, K.; Kandera, B.; Sedláčková, A.N. Global Navigation Satellite Systems Signal Vulnerabilities in Unmanned Aerial Vehicle Operations: Impact of Affordable Software-Defined Radio. Drones 2024, 8, 109. [Google Scholar] [CrossRef]
- Zhu, H.; Xia, L.; Li, Q.; Xia, J.; Cai, Y. IMU-Aided Precise Point Positioning Performance Assessment with Smartphones in GNSS-Degraded Urban Environments. Remote Sens. 2022, 14, 4469. [Google Scholar] [CrossRef]
- Wang, Y.; Qian, C.; Liu, H. WHU-Smartphone: A Large-Scale Multi-Traffic Scene GNSS Dataset of Android Smartphones and a Low-Cost GNSS Module. IEEE Trans. Intell. Transp. Syst. 2024, 25, 17993–18005. [Google Scholar] [CrossRef]
- Vana, S.; Bisnath, S. A modified adaptive factor-based Kalman filter for continuous urban navigation with low-cost sensors. GPS Solut. 2024, 28, 84. [Google Scholar] [CrossRef]
- Vana, S.; Bisnath, S. Low-Cost, Triple-Frequency, Multi-GNSS PPP and MEMS IMU Integration for Continuous Navigation in Simulated Urban Environments. Navig. J. Inst. Navig. 2023, 70, 578. [Google Scholar] [CrossRef]
- Mpimis, T.; Kapsis, T.T.; Gikas, V.; Panagopoulos, A.D. Dynamic Optimal Vehicle Selection for Cooperative Positioning Using Low-Cost GNSS Receivers. IEEE Access 2023, 11, 134146–134154. [Google Scholar] [CrossRef]
- Mahmoud, M.; Abd Rabbou, M.; El Shazly, A. Land Vehicle Navigation Using Low-Cost Integrated Smartphone GNSS Mems and Map Matching Technique. Artif. Satell. 2022, 57, 138–157. [Google Scholar] [CrossRef]
- Han, Z.; Wang, X.; Zhang, J.; Xin, S.; Huang, Q.; Shen, S. An Improved Velocity-Aided Method for Smartphone Single-Frequency Code Positioning in Real-World Driving Scenarios. Remote Sens. 2024, 16, 3988. [Google Scholar] [CrossRef]
- Bae, Y.; Kim, J.; Kim, O.J.; Jeong, H.; Kee, C. GNSS Urban Positioning with Multipath Mitigation Using Duration Time of Time-Differenced Code-Minus-Carrier. IEEE Access 2024, 12, 139724–139741. [Google Scholar] [CrossRef]
- Amalfitano, D.; Cutugno, M.; Robustelli, U.; Pugliano, G. Designing and Testing an IoT Low-Cost PPP-RTK Augmented GNSS Location Device. Sensors 2024, 24, 646. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Park, M.; Bae, Y.; Kim, O.J.; Kim, D.; Kim, B.; Kee, C. A low-cost, high-precision vehicle navigation system for deep urban multipath environment using TDCP measurements. Sensors 2020, 20, 3254. [Google Scholar] [CrossRef] [PubMed]
- Kaczmarek, A.; Rohm, W.; Klingbeil, L.; Tchórzewski, J. Experimental 2D extended Kalman filter sensor fusion for low-cost GNSS/IMU/Odometers precise positioning system. Meas. J. Int. Meas. Confed. 2022, 193, 110963. [Google Scholar] [CrossRef]
- Jagelčák, J.; Kuba, O.; Kubáňová, J.; Kostrzewski, M.; Nader, M. Dynamic Position Accuracy of Low-Cost Global Navigation Satellite System Sensors Applied in Road Transport for Precision and Measurement Reliability. Sustainability 2024, 16, 5556. [Google Scholar] [CrossRef]
- Elsheikh, M.; Abdelfatah, W.; Nourledin, A.; Iqbal, U.; Korenberg, M. Low-cost real-time PPP/INS integration for automated land vehicles. Sensors 2019, 19, 4896. [Google Scholar] [CrossRef]
- Elmezayen, A.; El-Rabbany, A. Ultra-Low-Cost Tightly Coupled Triple-Constellation GNSS PPP/MEMS-Based INS Integration for Land Vehicular Applications. Geomatics 2021, 1, 258–286. [Google Scholar] [CrossRef]
- Barbosa, L.A.; de Oliveira, H.C.; Machado, W.C.; Costa, D.C. A new method for evaluation of the positional error of low-cost devices based on GNSS integrity for transportation applications. Bol. Cienc. Geod. 2022, 28, 1–20. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, H.; Yang, X. A Novel Navigation Method Fusing Multiple Constraint for Low-Cost INS/GNSS Integrated System in Urban Environments. IEEE Trans. Veh. Technol. 2024, 73, 7616–7629. [Google Scholar] [CrossRef]
- Rui, S.; Xiaotong, S.; Qi, C.; Lei, J.; Qi, S. A tightly coupled GNSS RTK/IMU integration with GA-BP neural network for challenging urban navigation. Meas. Sci. Technol. 2024, 35, 086310. [Google Scholar] [CrossRef]
- Falco, G.; Nicola, M.; Pini, M. Positioning based on tightly coupled multiple sensors: A practical implementation and experimental assessment. IEEE Access 2018, 6, 13101–13116. [Google Scholar] [CrossRef]
- Bijjahalli, S.; Sabatini, R. A High-Integrity and Low-Cost Navigation System for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 356–369. [Google Scholar] [CrossRef]
- Barbosa, L.A.; Costa, D.C.; de Oliveira, H.C. Evaluation of low-cost GNSS receivers for speed monitoring. Case Stud. Transp. Policy 2022, 10, 239–247. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, Y.; Chen, J.; Chen, Q.; Xu, K.; Wang, B. Performance Assessment of Multi-GNSS Real-Time Products from Various Analysis Centers. Remote Sens. 2023, 15, 140. [Google Scholar] [CrossRef]
- Wang, A.; Chen, J.; Zhang, Y.; Meng, L.; Wang, B.; Wang, J. Evaluating the impact of CNES real-time ionospheric products on multi-GNSS single-frequency positioning using the IGS real-time service. Adv. Space Res. 2020, 66, 2516–2527. [Google Scholar] [CrossRef]
- Hadas, T.; Hobiger, T. Benefits of using Galileo for real-time GNSS meteorology. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1756–1760. [Google Scholar] [CrossRef]
- Glaner, M.; Weber, R. PPP with integer ambiguity resolution for GPS and Galileo using satellite products from different analysis centers. GPS Solut. 2021, 25, 102. [Google Scholar] [CrossRef]
- Abdelazeem, M.; Çelik, R.N. Evaluation of Triple-Frequency GPS/Galileo/Beidou Kinematic Precise Point Positioning Using Real-Time CNES Products for Maritime Applications. Artif. Satell. 2023, 58, 314–329. [Google Scholar] [CrossRef]
- Abdelazeem, M.; Abazeed, A.; Kamal, H.A.; Mohamed, M.O.A. Towards an Accurate Real-Time Digital Elevation Model Using Various GNSS Techniques. Sensors 2024, 24, 8147. [Google Scholar] [CrossRef]
- Abdelazeem, M. Towards Real-Time Integrated Water Vapor Estimates with Triple-Frequency Galileo Observations and CNES Products. Atmosphere 2024, 15, 1320. [Google Scholar] [CrossRef]
- Yao, W.; Huang, H.; Ma, X.; Zhang, Q.; Yao, Y.; Lin, X.; Zhao, Q.; Huang, Y. Multi-Global Navigation Satellite System (GNSS) real-time tropospheric delay retrieval based on state-space representation (SSR) products from different analysis centers. Ann. Geophys. 2024, 42, 455–472. [Google Scholar] [CrossRef]
- Vidal, M.; Jarrin, P.; Rolland, L.; Nocquet, J.M.; Vergnolle, M.; Sakic, P. Cost-Efficient Multi-GNSS Station with Real-Time Transmission for Geodynamics Applications. Remote Sens. 2024, 16, 991. [Google Scholar] [CrossRef]
- Li, M.; Huang, G.; Wang, L.; Xie, W. BDS/GPS/Galileo Precise Point Positioning Performance Analysis of Android Smartphones Based on Real-Time Stream Data. Remote Sens. 2023, 15, 2983. [Google Scholar] [CrossRef]
- Cui, B.; Wang, J.; Li, P.; Hu, J.; Zuo, X.; Tang, L. Modified ionosphere delay fitting model with atmosphere uncertainty grids for wide-area real-time positioning. Geo-Spat. Inf. Sci. 2025, 1–19. [Google Scholar] [CrossRef]
- Chen, M.; Zhao, L.; Zhai, W.; Lv, Y.; Jin, S. Assessment of the Real-Time and Rapid Precise Point Positioning Performance Using Geodetic and Low-Cost GNSS Receivers. Remote Sens. 2024, 16, 1434. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10. [Google Scholar]
- RTS. Real-Time Satellite Orbit and Orbit Products. Available online: https://igs.org/rts/products/ (accessed on 1 January 2025).
- BRDM. MIXED GNSS BROADCAST EPHEMERIS. Available online: https://cddis.nasa.gov/archive/gnss/data/daily/2024/brdc/ (accessed on 1 January 2025).
- Zhang, Y.; Chen, J.; Gong, X.; Chen, Q. The update of BDS-2 TGD and its impact on positioning. Adv. Space Res. 2020, 65, 2645–2661. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géodésique 1972, 105, 279–298. [Google Scholar] [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. 2006, 111, B02406. [Google Scholar] [CrossRef]

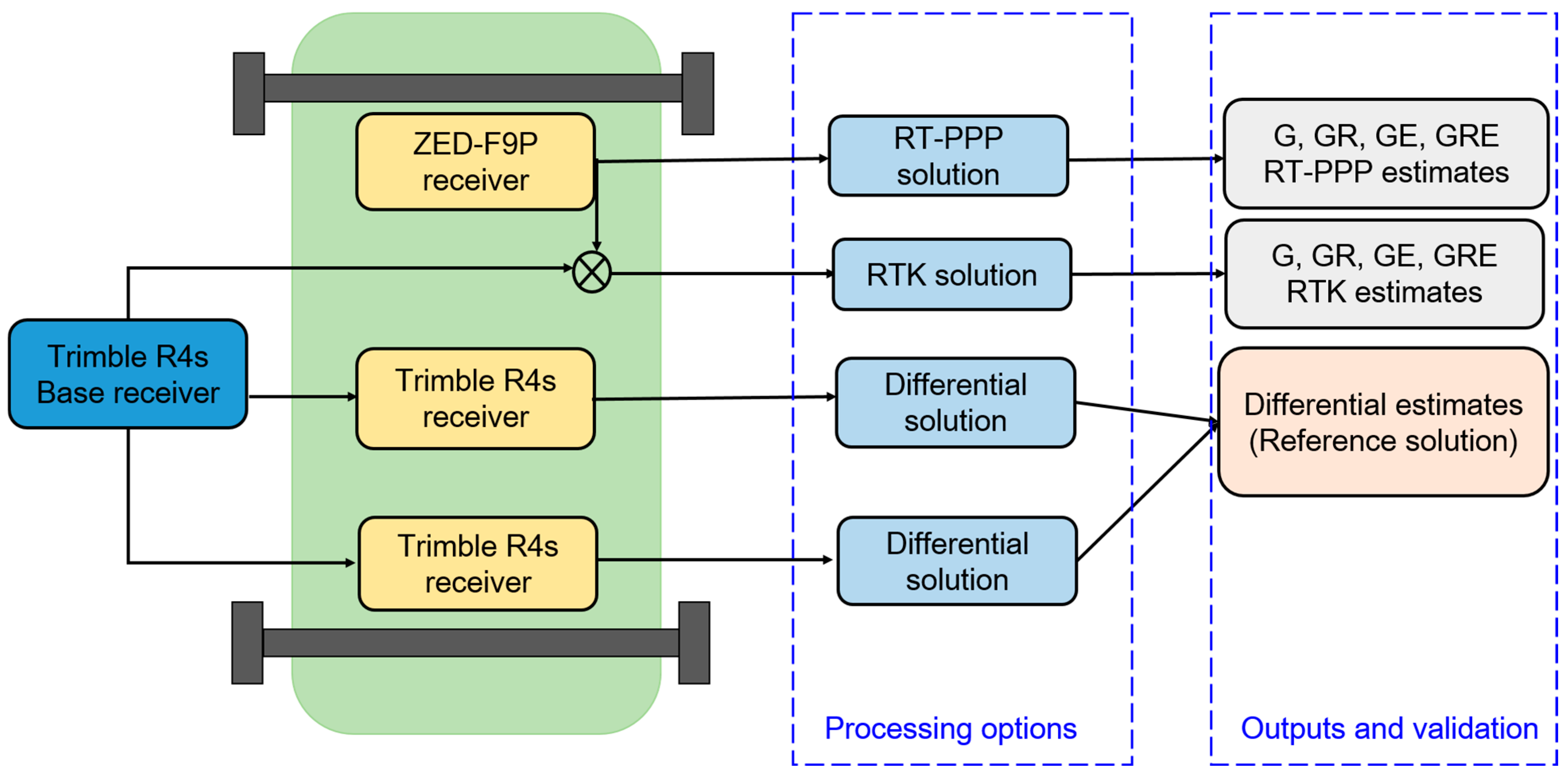
| Parameter | Processing Strategy | ||
|---|---|---|---|
| RT-PPP | RTK | Differential | |
| System | GPS, GLONASS, Galileo | ||
| Frequency | GPS: L1/L2; GLONASS: G1/G2; Galileo: E1/E5b | ||
| Mathematical model | Undifferenced | Differenced | Differenced |
| Observation interval | 1 HZ | ||
| Elevation angle | 10 degrees | ||
| Orbits and clocks | BKG, CNE, WHU | BRDM | IGS-Final |
| Tropospheric modeling | Saastamoinen model + VMF | ||
| Parameter estimation | Kalman filter | ||
| GNSS | RT-PPP | RTK | ||
|---|---|---|---|---|
| BKG | CNE | WHU | ||
| G | RT-BKG-G | RT-CNE-G | RT-WHU-G | RTK-G |
| GR | RT-BKG-GR | RT-CNE-GR | RT-WHU-GR | RTK-GR |
| GE | RT-BKG-GE | RT-CNE-GE | RT-WHU-GE | RTK-GE |
| GRE | RT-BKG-GRE | RT-CNE-GRE | RT-WHU-GRE | RTK-GRE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelazeem, M.; Abazeed, A.; Alsultan, A.; Wahaballa, A.M. Assessment of Affordable Real-Time PPP Solutions for Transportation Applications. Algorithms 2025, 18, 390. https://doi.org/10.3390/a18070390
Abdelazeem M, Abazeed A, Alsultan A, Wahaballa AM. Assessment of Affordable Real-Time PPP Solutions for Transportation Applications. Algorithms. 2025; 18(7):390. https://doi.org/10.3390/a18070390
Chicago/Turabian StyleAbdelazeem, Mohamed, Amgad Abazeed, Abdulmajeed Alsultan, and Amr M. Wahaballa. 2025. "Assessment of Affordable Real-Time PPP Solutions for Transportation Applications" Algorithms 18, no. 7: 390. https://doi.org/10.3390/a18070390
APA StyleAbdelazeem, M., Abazeed, A., Alsultan, A., & Wahaballa, A. M. (2025). Assessment of Affordable Real-Time PPP Solutions for Transportation Applications. Algorithms, 18(7), 390. https://doi.org/10.3390/a18070390







