Algorithmic Techniques for GPU Scheduling: A Comprehensive Survey
Simple Summary
Abstract
1. Introduction
1.1. The History and Evolution of GPUs
1.2. GPU vs. CPU: Similarities and Differences in Architecture and Fundamentals
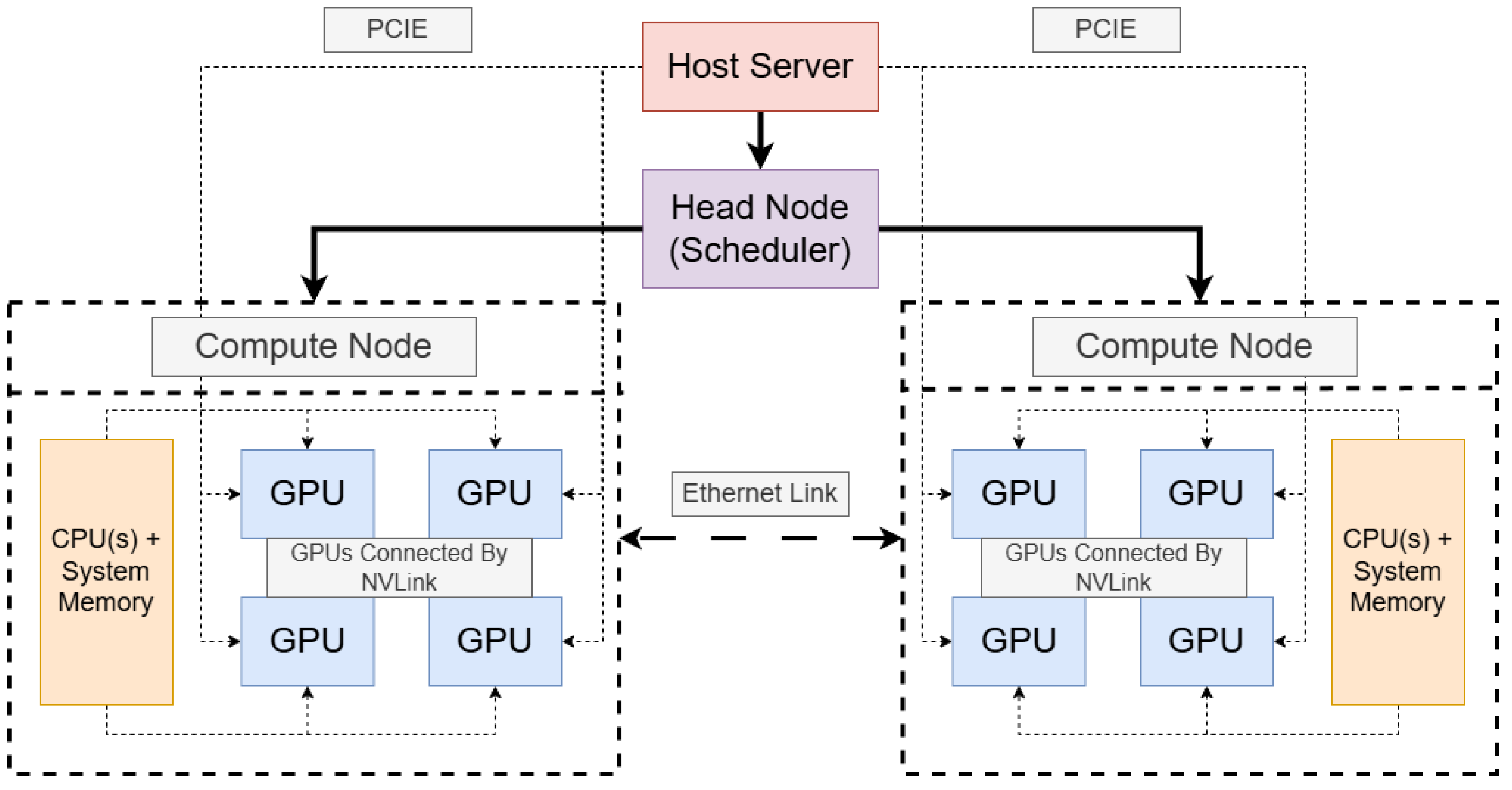
1.3. Cluster Computing and the Necessity of GPU Scheduling Algorithms
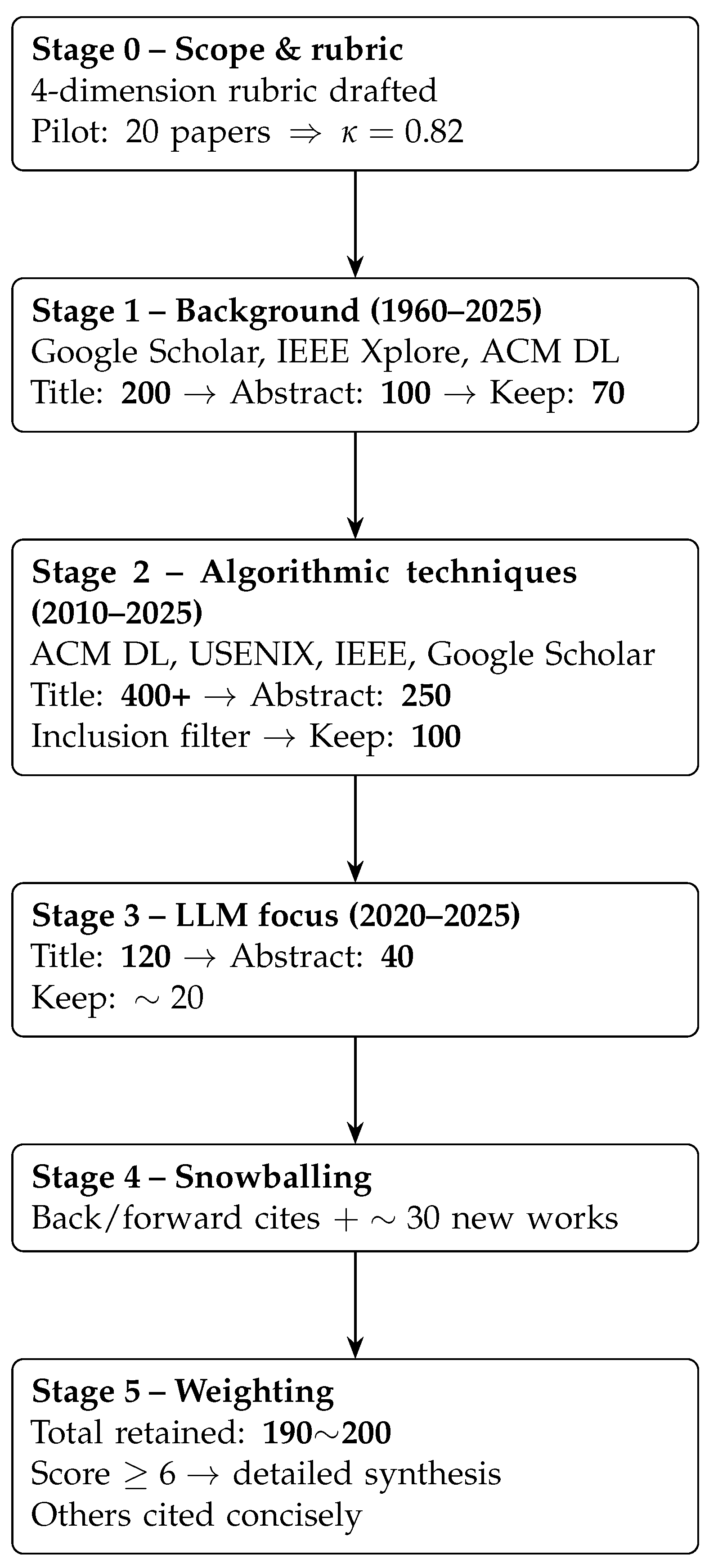
1.4. Survey Methodology
“GPU AND history”, “CPU–GPU architectural comparison”, “cluster topology evolution”, “GPU architecture”.
“GPU” AND “cluster” AND (scheduler OR scheduling) AND (coflow OR multiobjective OR reinforcement OR prediction OR heuristic OR energy-aware OR techniques OR metaheuristic).
“LLM inference” AND “GPU scheduling” AND coflow.
1.5. Limitations of Classical Assumptions
- Alibaba GPU Trace (2021): the 90th percentile job duration is the mean;
- Google Borg Trace (2019): the 90th percentile job duration is approximately the mean.
1.6. Paper Overview
2. Models
2.1. Components of a Model
- GPU demand (which may be fractional or span multiple GPUs),
- estimated runtime ,
- release time (for online arrivals),
- optional priority or weight.
2.2. Categorization of Models
- First-fit: assign each job to the first available GPU or time slot.
- Best-fit: assign each job to the GPU or slot that minimizes leftover capacity.
2.3. Evaluation Metrics and Validation Methods for Scheduling Models
2.4. Choosing a Scheduling Paradigm in Practice
2.5. Comparative Analysis of Models
- Queueing models–Pros: Analytically tractable; provide closed-form performance bounds and optimal policies under stochastic assumptions. Cons: Scale poorly to large systems without relaxation or decomposition; approximations may sacrifice true optimality.
- Optimization models–Pros: Express rich constraints and system heterogeneity; deliver provably optimal schedules within the model’s scope. Cons: Become intractable for large, dynamic workloads without heuristic shortcuts or periodic re-solving; deterministic inputs may not capture runtime variability.
- Heuristic methods–Pros: Extremely fast and scalable; simple to implement and tune for specific workloads; robust in practice. Cons: Lack formal performance guarantees; require careful parameterization to avoid starvation or unfairness.
- Learning-based approaches–Pros: Adapt to workload patterns and capture complex, nonlinear interactions (e.g., resource interference) that fixed rules miss. Cons: Incur training overhead and cold-start penalties; produce opaque policies that demand extensive validation to prevent drift and ensure reliability.
3. Scheduling Algorithms and Their Performance
3.1. Classical Optimization Algorithms
- Continuous relaxation: Replace with , solve the LP, then round the fractional solution.
- List-scheduling rounding: Sort jobs by LP-derived completion times and assign greedily to the earliest available GPU.
3.2. Queueing-Theoretic Approaches
3.3. Learning-Based Adaptive Algorithms
3.4. Comparative Analysis
3.5. Cross-Paradigm Empirical Comparison
3.6. PDE-Driven HPC Workloads
3.7. Summary of Scheduling Algorithms and Their Applicability Concerns
4. Looking Forward: LLM Focus
4.1. Scaling Scheduling for Future GPU Clusters
4.2. Algorithmic Challenges in Large-Scale Training Job Scheduling
4.3. Serving LLMs and Complex Inference Workloads: New Scheduling Frontiers
4.4. Hybrid Scheduling Strategies and Learning-Augmented Algorithms
4.5. Energy Efficiency and Cost-Aware Scheduling
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Abbreviations | Meaning/Context |
| ASIC | Application-Specific Integrated Circuit (fixed-function chip) |
| CPU | Central Processing Unit (general-purpose core) |
| CP-SAT | Constraint Programming—Satisfiability (OR-Tools solver) |
| DL | Deep Learning (neural-network workloads) |
| DP | Dynamic Programming (exact but exponential-time algorithm) |
| DRAM | Dynamic Random-Access Memory (commodity main memory) |
| DRF | Dominant Resource Fairness (a multi-resource fair sharing policy) |
| DVFS | Dynamic Voltage and Frequency Scaling (power-saving knob) |
| FPGA | Field-Programmable Gate Array (reconfigurable device) |
| GPU | Graphics Processing Unit (parallel accelerator) |
| gRPC | Google Remote Procedure Call (GPU resource manager) |
| HBM | High-Bandwidth Memory (stacked on-package DRAM) |
| HPC | High-Performance Computing (science & engineering jobs) |
| ILP | Integer Linear Programming (exact optimization formulation) |
| JCT | Job Completion Time (arrival → finish interval) |
| KV | Key-Value cache in LLMs to store previously computed attention keys and values to avoid redundant calculations |
| LLM | Large Language Model (GPT-class neural networks) |
| MIG | Multi-Instance GPU (NVIDIA partitioning feature) |
| MILP | Mixed-Integer Linear Programming (ILP with continuous variables) |
| ML | Machine Learning (broader umbrella including DL) |
| NUMA | Non-Uniform Memory Access (multi-socket memory topology) |
| NVLink | NVIDIA high-speed point-to-point GPU interconnect (40~60 GB/s per link) |
| NVML | Nvidia Management Library (API for monitoring and managing Nvidia GPUs) |
| NVSwitch | On-node crossbar switch that connects multiple NVLinks |
| PCIe | Peripheral Component Interconnect Express |
| PDE | Partial Differential Equation (scientific HPC workloads) |
| QoS | Quality of Service (aggregate performance target) |
| RAPL | Running Average Power Limit scheduling policy |
| RL | Reinforcement Learning (data-driven scheduling paradigm) |
| SJF | Shortest-Job-First (greedy scheduling heuristic) |
| SLO | Service-Level Objective (numerical QoS target, e.g., p95 latency) |
| SM | Streaming Multiprocessor (GPU core cluster) |
| SMT | Simultaneous Multithreading (CPU core sharing) |
| SRPT | Shortest Remaining Processing Time scheduling policy |
| SSM | Streaming SM (informal shorthand for a single GPU SM) |
| TDP | Thermal Design Power (maximum sustained power a cooling solution is designed to dissipate) |
| TPU | Tensor Processing Unit (Google ASIC for ML) |
| VRAM | Video Random-Access Memory (legacy term for GPU memory) |
Appendix A. Per-Job Energy Consumption Model
References
- Dally, W.J.; Keckler, S.W.; Kirk, D.B. Evolution of the graphics processing unit (GPU). IEEE Micro 2021, 41, 42–51. [Google Scholar] [CrossRef]
- Peddie, J. The History of the GPU-Steps to Invention; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Peddie, J. What is a GPU? In The History of the GPU-Steps to Invention; Springer: Berlin/Heidelberg, Germany, 2023; pp. 333–345. [Google Scholar]
- Cano, A. A survey on graphic processing unit computing for large-scale data mining. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1232. [Google Scholar] [CrossRef]
- Shankar, S. Energy Estimates Across Layers of Computing: From Devices to Large-Scale Applications in Machine Learning for Natural Language Processing, Scientific Computing, and Cryptocurrency Mining. In Proceedings of the 2023 IEEE High Performance Extreme Computing Conference (HPEC), Boston, MA, USA, 25–29 September 2023; pp. 1–6. [Google Scholar]
- Hou, Q.; Qiu, C.; Mu, K.; Qi, Q.; Lu, Y. A cloud gaming system based on NVIDIA GRID GPU. In Proceedings of the 2014 13th International Symposium on Distributed Computing and Applications to Business, Engineering and Science, Xianning, China, 24–27 November 2014; pp. 73–77. [Google Scholar]
- Pathania, A.; Jiao, Q.; Prakash, A.; Mitra, T. Integrated CPU-GPU power management for 3D mobile games. In Proceedings of the 51st Annual Design Automation Conference, San Francisco, CA, USA, 1–5 June 2014; pp. 1–6. [Google Scholar]
- Mills, N.; Mills, E. Taming the energy use of gaming computers. Energy Effic. 2016, 9, 321–338. [Google Scholar] [CrossRef]
- Teske, D. NVIDIA Corporation: A Strategic Audit; University of Nebraska-Lincoln: Lincoln, NE, USA, 2018. [Google Scholar]
- Moya, V.; Gonzalez, C.; Roca, J.; Fernandez, A.; Espasa, R. Shader performance analysis on a modern GPU architecture. In Proceedings of the 38th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO’05), Barcelona, Spain, 12–16 November 2005; pp. 10–364. [Google Scholar]
- Kirk, D. NVIDIA CUDA software and GPU parallel computing architecture. In Proceedings of the International Symposium on Memory Management (ISMM), Montreal, QC, Canada, 21–22 October 2007; Volume 7, pp. 103–104. [Google Scholar]
- Peddie, J. Mobile GPUs. In The History of the GPU-New Developments; Springer: Berlin/Heidelberg, Germany, 2023; pp. 101–185. [Google Scholar]
- Gera, P.; Kim, H.; Kim, H.; Hong, S.; George, V.; Luk, C.K. Performance characterisation and simulation of Intel’s integrated GPU architecture. In Proceedings of the 2018 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), Belfast, UK, 2–4 April 2018; pp. 139–148. [Google Scholar]
- Rajagopalan, G.; Thistle, J.; Polzin, W. The potential of GPU computing for design in RotCFD. In Proceedings of the AHS Technical Meeting on Aeromechanics Design for Transformative Vertical Flight, San Francisco, CA, USA, 16–18 January 2018. [Google Scholar]
- McClanahan, C. History and evolution of GPU architecture. Surv. Pap. 2010, 9, 1–7. [Google Scholar]
- Lee, V.W.; Kim, C.; Chhugani, J.; Deisher, M.; Kim, D.; Nguyen, A.D.; Satish, N.; Smelyanskiy, M.; Chennupaty, S.; Hammarlund, P.; et al. Debunking the 100X GPU vs. CPU myth: An evaluation of throughput computing on CPU and GPU. In Proceedings of the 37th Annual International Symposium on Computer Architecture, Saint-Malo, France, 19–23 June 2010; pp. 451–460. [Google Scholar]
- Bergstrom, L.; Reppy, J. Nested data-parallelism on the GPU. In Proceedings of the 17th ACM SIGPLAN International Conference on Functional Programming, Copenhagen, Denmark, 10–12 September 2012; pp. 247–258. [Google Scholar]
- Thomas, W.; Daruwala, R.D. Performance comparison of CPU and GPU on a discrete heterogeneous architecture. In Proceedings of the 2014 International Conference on Circuits, Systems, Communication and Information Technology Applications (CSCITA), Mumbai, India, 4–5 April 2014; pp. 271–276. [Google Scholar]
- Svedin, M.; Chien, S.W.; Chikafa, G.; Jansson, N.; Podobas, A. Benchmarking the Nvidia GPU lineage: From early K80 to modern A100 with asynchronous memory transfers. In Proceedings of the 11th International Symposium on Highly Efficient Accelerators and Reconfigurable Technologies, Online, 21–23 June 2021; pp. 1–6. [Google Scholar]
- Bhargava, R.; Troester, K. AMD next generation “Zen 4” core and 4th gen AMD EPYC server CPUs. IEEE Micro 2024, 44, 8–17. [Google Scholar] [CrossRef]
- Hill, M.D.; Marty, M.R. Amdahl’s law in the multicore era. Computer 2008, 41, 33–38. [Google Scholar] [CrossRef]
- Rubio, J.; Bilbao, C.; Saez, J.C.; Prieto-Matias, M. Exploiting elasticity via OS-runtime cooperation to improve CPU utilization in multicore systems. In Proceedings of the 2024 32nd Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP), Dublin, Ireland, 20–22 March 2024; pp. 35–43. [Google Scholar]
- Jones, C.; Gartung, P. CMSSW Scaling Limits on Many-Core Machines. arXiv 2023, arXiv:2310.02872. [Google Scholar]
- Gorman, M.; Engineer, S.K.; Jambor, M. Optimizing Linux for AMD EPYC 7002 Series Processors with SUSE Linux Enterprise 15 SP1. In SUSE Best Practices; SUSE: Nuremberg, Germany, 2019. [Google Scholar]
- Fan, Z.; Qiu, F.; Kaufman, A.; Yoakum-Stover, S. GPU cluster for high performance computing. In Proceedings of the SC’04: Proceedings of the 2004 ACM/IEEE Conference on Supercomputing, Pittsburgh, PA, USA, 6–12 November 2004; p. 47. [Google Scholar]
- Kimm, H.; Paik, I.; Kimm, H. Performance comparision of TPU, GPU, CPU on Google colaboratory over distributed deep learning. In Proceedings of the 2021 IEEE 14th International Symposium on Embedded Multicore/Many-Core Systems-on-Chip (MCSoC), Singapore, 20–23 December 2021; pp. 312–319. [Google Scholar]
- Wang, Y.E.; Wei, G.Y.; Brooks, D. Benchmarking TPU, GPU, and CPU platforms for deep learning. arXiv 2019, arXiv:1907.10701. [Google Scholar]
- Narayanan, D.; Shoeybi, M.; Casper, J.; LeGresley, P.; Patwary, M.; Korthikanti, V.; Vainbrand, D.; Kashinkunti, P.; Bernauer, J.; Catanzaro, B.; et al. Efficient large-scale language model training on GPU clusters using megatron-lm. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, St. Louis, MO, USA, 14–19 November 2021; pp. 1–15. [Google Scholar]
- Palacios, J.; Triska, J. A Comparison of Modern GPU and CPU Architectures: And the Common Convergence of Both; Oregon State University: Corvallis, OR, USA, 2011. [Google Scholar]
- Haugen, P.; Myers, I.; Sadler, B.; Whidden, J. A Basic Overview of Commonly Encountered types of Random Access Memory (RAM). Class Notes of Computer Architecture II. Rose-Hulman Institute of Technology, Terre Haute, IN, USA. Available online: https://www.docsity.com/en/docs/basic-types-of-random-access-memory-lecture-notes-ece-332/6874965/ (accessed on 24 April 2025).
- Kato, S.; McThrow, M.; Maltzahn, C.; Brandt, S. Gdev: First-Class GPU Resource Management in the Operating System. In Proceedings of the 2012 USENIX Annual Technical Conference (USENIX ATC 12), Boston, MA, USA, 13–15 June 2012; pp. 401–412. [Google Scholar]
- Kato, S.; Brandt, S.; Ishikawa, Y.; Rajkumar, R. Operating systems challenges for GPU resource management. In Proceedings of the International Workshop on Operating Systems Platforms for Embedded Real-Time Applications, Porto, Portugal, 5 July 2011; pp. 23–32. [Google Scholar]
- Wen, Y.; O’Boyle, M.F. Merge or separate? Multi-job scheduling for OpenCL kernels on CPU/GPU platforms. In Proceedings of the General Purpose GPUs; Association for Computing Machinery: New York, NY, USA, 2017; pp. 22–31. [Google Scholar]
- Tu, C.H.; Lin, T.S. Augmenting operating systems with OpenCL accelerators. ACM Trans. Des. Autom. Electron. Syst. (TODAES) 2019, 24, 1–29. [Google Scholar] [CrossRef]
- Chazapis, A.; Nikolaidis, F.; Marazakis, M.; Bilas, A. Running kubernetes workloads on HPC. In Proceedings of the International Conference on High Performance Computing, Denver, CO, USA, 11–17 November 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 181–192. [Google Scholar]
- Weng, Q.; Yang, L.; Yu, Y.; Wang, W.; Tang, X.; Yang, G.; Zhang, L. Beware of Fragmentation: Scheduling GPU-Sharing Workloads with Fragmentation Gradient Descent. In Proceedings of the 2023 USENIX Annual Technical Conference (USENIX ATC 23), Boston, MA, USA, 10–12 July 2023; pp. 995–1008. [Google Scholar]
- Kenny, J.; Knight, S. Kubernetes for HPC Administration; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2021. [Google Scholar]
- Burns, B.; Grant, B.; Oppenheimer, D.; Brewer, E.; Wilkes, J. Borg, Omega, and Kubernetes: Lessons learned from three container-management systems over a decade. Queue 2016, 14, 70–93. [Google Scholar] [CrossRef]
- Vavilapalli, V.K.; Murthy, A.C.; Douglas, C.; Agarwal, S.; Konar, M.; Evans, R.; Graves, T.; Lowe, J.; Shah, H.; Seth, S.; et al. Apache Hadoop Yarn: Yet another resource negotiator. In Proceedings of the 4th Annual Symposium on Cloud Computing, Seattle, WA, USA, 3–5 November 2013; pp. 1–16. [Google Scholar]
- Kato, S.; Lakshmanan, K.; Rajkumar, R.; Ishikawa, Y. TimeGraph: GPU Scheduling for Real-Time Multi-Tasking Environments. In Proceedings of the 2011 USENIX Annual Technical Conference (USENIX ATC 11), Portland, OR, USA, 15–17 June 2011. [Google Scholar]
- Duato, J.; Pena, A.J.; Silla, F.; Mayo, R.; Quintana-Ortí, E.S. rCUDA: Reducing the number of GPU-based accelerators in high performance clusters. In Proceedings of the 2010 International Conference on High Performance Computing & Simulation, Caen, France, 28 June–2 July 2010; pp. 224–231. [Google Scholar]
- Agrawal, A.; Mueller, S.M.; Fleischer, B.M.; Sun, X.; Wang, N.; Choi, J.; Gopalakrishnan, K. DLFloat: A 16-b floating point format designed for deep learning training and inference. In Proceedings of the 2019 IEEE 26th Symposium on Computer Arithmetic (ARITH), Kyoto, Japan, 10–12 June 2019; pp. 92–95. [Google Scholar]
- Yeung, G.; Borowiec, D.; Friday, A.; Harper, R.; Garraghan, P. Towards GPU utilization prediction for cloud deep learning. In Proceedings of the 12th USENIX Workshop on Hot Topics in Cloud Computing (HotCloud 20), Boston, MA, USA, 13 July 2020. [Google Scholar]
- Jeon, M.; Venkataraman, S.; Phanishayee, A.; Qian, J.; Xiao, W.; Yang, F. Analysis of Large-Scale Multi-Tenant GPU clusters for DNN training workloads. In Proceedings of the 2019 USENIX Annual Technical Conference (USENIX ATC 19), Renton, WA, USA, 10–12 July 2019; pp. 947–960. [Google Scholar]
- Wu, G.; Greathouse, J.L.; Lyashevsky, A.; Jayasena, N.; Chiou, D. GPGPU performance and power estimation using machine learning. In Proceedings of the 2015 IEEE 21st International Symposium on High Performance Computer Architecture (HPCA), Burlingame, CA, USA, 7–11 February 2015; pp. 564–576. [Google Scholar]
- Boutros, A.; Nurvitadhi, E.; Ma, R.; Gribok, S.; Zhao, Z.; Hoe, J.C.; Betz, V.; Langhammer, M. Beyond peak performance: Comparing the real performance of AI-optimized FPGAs and GPUs. In Proceedings of the 2020 International Conference on Field-Programmable technology (ICFPT), Maui, HI, USA, 9–11 December 2020; pp. 10–19. [Google Scholar]
- Nordmark, R.; Olsén, T. A Ray Tracing Implementation Performance Comparison between the CPU and the GPU. Bachelor Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2022. [Google Scholar]
- Sun, Y.; Agostini, N.B.; Dong, S.; Kaeli, D. Summarizing CPU and GPU design trends with product data. arXiv 2019, arXiv:1911.11313. [Google Scholar]
- Li, C.; Sun, Y.; Jin, L.; Xu, L.; Cao, Z.; Fan, P.; Kaeli, D.; Ma, S.; Guo, Y.; Yang, J. Priority-based PCIe scheduling for multi-tenant multi-GPU systems. IEEE Comput. Archit. Lett. 2019, 18, 157–160. [Google Scholar] [CrossRef]
- Chopra, B. Enhancing Machine Learning Performance: The Role of GPU-Based AI Compute Architectures. J. Knowl. Learn. Sci. Technol. 2024, 6386, 29–42. [Google Scholar] [CrossRef]
- Baker, M.; Buyya, R. Cluster computing at a glance. High Perform. Clust. Comput. Archit. Syst. 1999, 1, 12. [Google Scholar]
- Jararweh, Y.; Hariri, S. Power and performance management of GPUs based cluster. Int. J. Cloud Appl. Comput. (IJCAC) 2012, 2, 16–31. [Google Scholar] [CrossRef]
- Wesolowski, L.; Acun, B.; Andrei, V.; Aziz, A.; Dankel, G.; Gregg, C.; Meng, X.; Meurillon, C.; Sheahan, D.; Tian, L.; et al. Datacenter-scale analysis and optimization of GPU machine learning workloads. IEEE Micro 2021, 41, 101–112. [Google Scholar] [CrossRef]
- Kindratenko, V.V.; Enos, J.J.; Shi, G.; Showerman, M.T.; Arnold, G.W.; Stone, J.E.; Phillips, J.C.; Hwu, W.m. GPU clusters for high-performance computing. In Proceedings of the 2009 IEEE International Conference on Cluster Computing and Workshops, New Orleans, LA, USA, 31 August–4 September 2009; pp. 1–8. [Google Scholar]
- Jayaram Subramanya, S.; Arfeen, D.; Lin, S.; Qiao, A.; Jia, Z.; Ganger, G.R. Sia: Heterogeneity-aware, goodput-optimized ML-cluster scheduling. In Proceedings of the 29th Symposium on Operating Systems Principles, Koblenz, Germany, 23–26 October 2023; pp. 642–657. [Google Scholar]
- Xiao, W.; Bhardwaj, R.; Ramjee, R.; Sivathanu, M.; Kwatra, N.; Han, Z.; Patel, P.; Peng, X.; Zhao, H.; Zhang, Q.; et al. Gandiva: Introspective cluster scheduling for deep learning. In Proceedings of the 13th USENIX Symposium on Operating Systems Design and Implementation (OSDI 18), Carlsbad, CA, USA, 8–10 October 2018; pp. 595–610. [Google Scholar]
- Narayanan, D.; Santhanam, K.; Kazhamiaka, F.; Phanishayee, A.; Zaharia, M. Heterogeneity-aware cluster scheduling policies for deep learning workloads. In Proceedings of the 14th USENIX Symposium on Operating Systems Design and Implementation (OSDI 20), Online, 4–6 November 2020; pp. 481–498. [Google Scholar]
- Li, A.; Song, S.L.; Chen, J.; Li, J.; Liu, X.; Tallent, N.R.; Barker, K.J. Evaluating modern GPU interconnect: PCIe, NVLink, NV-SLI, NVSwitch and GPUDirect. IEEE Trans. Parallel Distrib. Syst. 2019, 31, 94–110. [Google Scholar] [CrossRef]
- Kousha, P.; Ramesh, B.; Suresh, K.K.; Chu, C.H.; Jain, A.; Sarkauskas, N.; Subramoni, H.; Panda, D.K. Designing a profiling and visualization tool for scalable and in-depth analysis of high-performance GPU clusters. In Proceedings of the 2019 IEEE 26th International Conference on High Performance Computing, Data, and Analytics (HiPC), Hyderabad, India, 17–20 December 2019; pp. 93–102. [Google Scholar]
- Liao, C.; Sun, M.; Yang, Z.; Xie, J.; Chen, K.; Yuan, B.; Wu, F.; Wang, Z. LoHan: Low-Cost High-Performance Framework to Fine-Tune 100B Model on a Consumer GPU. arXiv 2024, arXiv:2403.06504. [Google Scholar]
- Isaev, M.; McDonald, N.; Vuduc, R. Scaling infrastructure to support multi-trillion parameter LLM training. In Proceedings of the Architecture and System Support for Transformer Models (ASSYST@ ISCA 2023), Oralndo, FL, USA, 17–21 June 2023. [Google Scholar]
- Weng, Q.; Xiao, W.; Yu, Y.; Wang, W.; Wang, C.; He, J.; Li, Y.; Zhang, L.; Lin, W.; Ding, Y. MLaaS in the wild: Workload analysis and scheduling in large-scale heterogeneous GPU clusters. In Proceedings of the 19th USENIX Symposium on Networked Systems Design and Implementation (NSDI 22), Renton, WA, USA, 4–6 April 2022; pp. 945–960. [Google Scholar]
- Kumar, A.; Subramanian, K.; Venkataraman, S.; Akella, A. Doing more by doing less: How structured partial backpropagation improves deep learning clusters. In Proceedings of the 2nd ACM International Workshop on Distributed Machine Learning, Virtual, 7 December 2021; pp. 15–21. [Google Scholar]
- Hu, Q.; Sun, P.; Yan, S.; Wen, Y.; Zhang, T. Characterization and prediction of deep learning workloads in large-scale GPU datacenters. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, St. Louis, MO, USA, 14–19 November 2021; pp. 1–15. [Google Scholar]
- Crankshaw, D.; Wang, X.; Zhou, G.; Franklin, M.J.; Gonzalez, J.E.; Stoica, I. Clipper: A low-latency online prediction serving system. In Proceedings of the 14th USENIX Symposium on Networked Systems Design and Implementation (NSDI 17), Boston, MA, USA, 27–29 March 2017; pp. 613–627. [Google Scholar]
- Peng, Y.; Bao, Y.; Chen, Y.; Wu, C.; Guo, C. Optimus: An efficient dynamic resource scheduler for deep learning clusters. In Proceedings of the Thirteenth EuroSys Conference, Porto, Portugal, 23–26 April 2018; pp. 1–14. [Google Scholar]
- Yu, M.; Tian, Y.; Ji, B.; Wu, C.; Rajan, H.; Liu, J. Gadget: Online resource optimization for scheduling ring-all-reduce learning jobs. In Proceedings of the IEEE INFOCOM 2022-IEEE Conference on Computer Communications, Virtual, 2–5 May 2022; pp. 1569–1578. [Google Scholar]
- Qiao, A.; Choe, S.K.; Subramanya, S.J.; Neiswanger, W.; Ho, Q.; Zhang, H.; Ganger, G.R.; Xing, E.P. Pollux: Co-adaptive cluster scheduling for goodput-optimized deep learning. In Proceedings of the 15th USENIX Symposium on Operating Systems Design and Implementation OSDI 21), Online, 14–16 July 2021. [Google Scholar]
- Zhang, Z.; Zhao, Y.; Liu, J. Octopus: SLO-aware progressive inference serving via deep reinforcement learning in multi-tenant edge cluster. In Proceedings of the International Conference on Service-Oriented Computing, Rome, Italy, 28 November–1 December 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 242–258. [Google Scholar]
- Chaudhary, S.; Ramjee, R.; Sivathanu, M.; Kwatra, N.; Viswanatha, S. Balancing efficiency and fairness in heterogeneous GPU clusters for deep learning. In Proceedings of the Fifteenth European Conference on Computer Systems, Heraklion, Greece, 27–30 April 2020; pp. 1–16. [Google Scholar]
- Pinedo, M.L. Scheduling: Theory, Algorithms, and Systems, 6th ed.; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Shao, J.; Ma, J.; Li, Y.; An, B.; Cao, D. GPU scheduling for short tasks in private cloud. In Proceedings of the 2019 IEEE International Conference on Service-Oriented System Engineering (SOSE), San Francisco, CA, USA, 4–9 April 2019; pp. 215–2155. [Google Scholar]
- Han, M.; Zhang, H.; Chen, R.; Chen, H. Microsecond-scale preemption for concurrent GPU-accelerated DNN inferences. In Proceedings of the 16th USENIX Symposium on Operating Systems Design and Implementation (OSDI 22), Carlsbad, CA, USA, 11–13 July 2022; pp. 539–558. [Google Scholar]
- Gu, J.; Chowdhury, M.; Shin, K.G.; Zhu, Y.; Jeon, M.; Qian, J.; Liu, H.; Guo, C. Tiresias: A GPU cluster manager for distributed deep learning. In Proceedings of the 16th USENIX Symposium on Networked Systems Design and Implementation (NSDI 19), Boston, MA, USA, 26–28 February 2019; pp. 485–500. [Google Scholar]
- Memarzia, P.; Ray, S.; Bhavsar, V.C. The art of efficient in-memory query processing on NUMA systems: A systematic approach. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 781–792. [Google Scholar]
- Vilestad, J. An Evaluation of GPU Virtualization. Degree Thesis, Luleå University of Technology, Luleå, Sweden, 2024. [Google Scholar]
- Amaral, M.; Polo, J.; Carrera, D.; Seelam, S.; Steinder, M. Topology-aware GPU scheduling for learning workloads in cloud environments. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 12–17 November 2017; pp. 1–12. [Google Scholar]
- Zhao, Y.; Liu, Y.; Peng, Y.; Zhu, Y.; Liu, X.; Jin, X. Multi-resource interleaving for deep learning training. In Proceedings of the ACM SIGCOMM 2022 Conference, Amsterdam, The Netherlands, 22–26 August 2022; pp. 428–440. [Google Scholar]
- Mohan, J.; Phanishayee, A.; Kulkarni, J.; Chidambaram, V. Looking beyond GPUs for DNN scheduling on {Multi-Tenant} clusters. In Proceedings of the 16th USENIX Symposium on Operating Systems Design and Implementation (OSDI 22), Carlsbad, CA, USA, 11–13 July 2022; pp. 579–596. [Google Scholar]
- Reuther, A.; Byun, C.; Arcand, W.; Bestor, D.; Bergeron, B.; Hubbell, M.; Jones, M.; Michaleas, P.; Prout, A.; Rosa, A.; et al. Scalable system scheduling for HPC and big data. J. Parallel Distrib. Comput. 2018, 111, 76–92. [Google Scholar] [CrossRef]
- Ye, Z.; Sun, P.; Gao, W.; Zhang, T.; Wang, X.; Yan, S.; Luo, Y. Astraea: A fair deep learning scheduler for multi-tenant GPU clusters. IEEE Trans. Parallel Distrib. Syst. 2021, 33, 2781–2793. [Google Scholar] [CrossRef]
- Mao, H.; Alizadeh, M.; Menache, I.; Kandula, S. Resource management with deep reinforcement learning. In Proceedings of the 15th ACM Workshop on Hot Topics in Networks, Atlanta, GA, USA, 9–10 November 2016; pp. 50–56. [Google Scholar]
- Feitelson, D.G.; Rudolph, L.; Schwiegelshohn, U.; Sevcik, K.C.; Wong, P. Theory and practice in parallel job scheduling. In Proceedings of the Job Scheduling Strategies for Parallel Processing: IPPS’97 Processing Workshop, Geneva, Switzerland, 5 April 1997; Proceedings 3; Springer: Berlin/Heidelberg, Germany, 1997; pp. 1–34. [Google Scholar]
- Gao, W.; Ye, Z.; Sun, P.; Wen, Y.; Zhang, T. Chronus: A novel deadline-aware scheduler for deep learning training jobs. In Proceedings of the ACM Symposium on Cloud Computing, Seattle, WA, USA, 1–4 November 2021; pp. 609–623. [Google Scholar]
- Mahajan, K.; Balasubramanian, A.; Singhvi, A.; Venkataraman, S.; Akella, A.; Phanishayee, A.; Chawla, S. Themis: Fair and efficient GPU cluster scheduling. In Proceedings of the 17th USENIX Symposium on Networked Systems Design and Implementation (NSDI 20), Santa Clara, CA, USA, 25–27 February 2020; pp. 289–304. [Google Scholar]
- Lin, C.Y.; Yeh, T.A.; Chou, J. DRAGON: A Dynamic Scheduling and Scaling Controller for Managing Distributed Deep Learning Jobs in Kubernetes Cluster. In Proceedings of the International Conference on Cloud Computing and Services Science (CLOSER), Heraklion, Greece, 2–4 May 2019; pp. 569–577. [Google Scholar]
- Bian, Z.; Li, S.; Wang, W.; You, Y. Online evolutionary batch size orchestration for scheduling deep learning workloads in GPU clusters. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, St. Louis, MO, USA, 14–19 November 2021; pp. 1–15. [Google Scholar]
- Wang, Q.; Shi, S.; Wang, C.; Chu, X. Communication contention aware scheduling of multiple deep learning training jobs. arXiv 2020, arXiv:2002.10105. [Google Scholar]
- Rajasekaran, S.; Ghobadi, M.; Akella, A. CASSINI: Network-Aware Job Scheduling in Machine Learning Clusters. In Proceedings of the 21st USENIX Symposium on Networked Systems Design and Implementation (NSDI 24), Santa Clara, CA, USA, 16–18 April 2024; pp. 1403–1420. [Google Scholar]
- Yeung, G.; Borowiec, D.; Yang, R.; Friday, A.; Harper, R.; Garraghan, P. Horus: Interference-aware and prediction-based scheduling in deep learning systems. IEEE Trans. Parallel Distrib. Syst. 2021, 33, 88–100. [Google Scholar] [CrossRef]
- Garg, S.; Kothapalli, K.; Purini, S. Share-a-GPU: Providing simple and effective time-sharing on GPUs. In Proceedings of the 2018 IEEE 25th International Conference on High Performance Computing (HiPC), Bengaluru, India, 17–20 December 2018; pp. 294–303. [Google Scholar]
- Kubiak, W.; van de Velde, S. Scheduling deteriorating jobs to minimize makespan. Nav. Res. Logist. (NRL) 1998, 45, 511–523. [Google Scholar] [CrossRef]
- Mokoto, E. Scheduling to minimize the makespan on identical parallel Machines: An LP-based algorithm. Investig. Oper. 1999, 8, 97–107. [Google Scholar]
- Kononov, A.; Gawiejnowicz, S. NP-hard cases in scheduling deteriorating jobs on dedicated machines. J. Oper. Res. Soc. 2001, 52, 708–717. [Google Scholar] [CrossRef]
- Cao, J.; Guan, Y.; Qian, K.; Gao, J.; Xiao, W.; Dong, J.; Fu, B.; Cai, D.; Zhai, E. Crux: GPU-efficient communication scheduling for deep learning training. In Proceedings of the ACM SIGCOMM 2024 Conference, Sydney, Australia, 4–8 August 2024; pp. 1–15. [Google Scholar]
- Zhong, J.; He, B. Kernelet: High-throughput GPU kernel executions with dynamic slicing and scheduling. IEEE Trans. Parallel Distrib. Syst. 2013, 25, 1522–1532. [Google Scholar] [CrossRef]
- Sheng, Y.; Cao, S.; Li, D.; Zhu, B.; Li, Z.; Zhuo, D.; Gonzalez, J.E.; Stoica, I. Fairness in serving large language models. In Proceedings of the 18th USENIX Symposium on Operating Systems Design and Implementation (OSDI 24), Santa Clara, CA, USA, 10–12 July 2024; pp. 965–988. [Google Scholar]
- Ghodsi, A.; Zaharia, M.; Hindman, B.; Konwinski, A.; Shenker, S.; Stoica, I. Dominant resource fairness: Fair allocation of multiple resource types. In Proceedings of the 8th USENIX Symposium on Networked Systems Design and Implementation (NSDI 11), Boston, MA, USA, 30 March–1 April 2011. [Google Scholar]
- Sun, P.; Wen, Y.; Ta, N.B.D.; Yan, S. Towards distributed machine learning in shared clusters: A dynamically-partitioned approach. In Proceedings of the 2017 IEEE International Conference on Smart Computing (SMARTCOMP), Hong Kong, China, 29–31 May 2017; pp. 1–6. [Google Scholar]
- Mei, X.; Chu, X.; Liu, H.; Leung, Y.W.; Li, Z. Energy efficient real-time task scheduling on CPU-GPU hybrid clusters. In Proceedings of the IEEE INFOCOM 2017-IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Guerreiro, J.; Ilic, A.; Roma, N.; Tomas, P. GPGPU power modeling for multi-domain voltage-frequency scaling. In Proceedings of the 2018 IEEE International Symposium on High Performance Computer Architecture (HPCA), Vienna, Austria, 24–28 February 2018; pp. 789–800. [Google Scholar]
- Wang, Q.; Chu, X. GPGPU performance estimation with core and memory frequency scaling. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 2865–2881. [Google Scholar] [CrossRef]
- Ge, R.; Vogt, R.; Majumder, J.; Alam, A.; Burtscher, M.; Zong, Z. Effects of dynamic voltage and frequency scaling on a k20 GPU. In Proceedings of the 2013 42nd International Conference on Parallel Processing, Lyon, France, 1–4 October 2013; pp. 826–833. [Google Scholar]
- Gu, D.; Xie, X.; Huang, G.; Jin, X.; Liu, X. Energy-Efficient GPU Clusters Scheduling for Deep Learning. arXiv 2023, arXiv:2304.06381. [Google Scholar]
- Filippini, F.; Ardagna, D.; Lattuada, M.; Amaldi, E.; Riedl, M.; Materka, K.; Skrzypek, P.; Ciavotta, M.; Magugliani, F.; Cicala, M. ANDREAS: Artificial intelligence traiNing scheDuler foR accElerAted resource clusterS. In Proceedings of the 2021 8th International Conference on Future Internet of Things and Cloud (FiCloud), Rome, Italy, 23–25 August 2021; pp. 388–393. [Google Scholar]
- Sun, J.; Sun, M.; Zhang, Z.; Xie, J.; Shi, Z.; Yang, Z.; Zhang, J.; Wu, F.; Wang, Z. Helios: An efficient out-of-core GNN training system on terabyte-scale graphs with in-memory performance. arXiv 2023, arXiv:2310.00837. [Google Scholar]
- Zhou, Y.; Zeng, W.; Zheng, Q.; Liu, Z.; Chen, J. A Survey on Task Scheduling of CPU-GPU Heterogeneous Cluster. ZTE Commun. 2024, 22, 83. [Google Scholar]
- Zhang, H.; Stafman, L.; Or, A.; Freedman, M.J. Slaq: Quality-driven scheduling for distributed machine learning. In Proceedings of the 2017 Symposium on Cloud Computing, Santa Clara, CA, USA, 25–27 September 2017; pp. 390–404. [Google Scholar]
- Narayanan, D.; Kazhamiaka, F.; Abuzaid, F.; Kraft, P.; Agrawal, A.; Kandula, S.; Boyd, S.; Zaharia, M. Solving large-scale granular resource allocation problems efficiently with pop. In Proceedings of the ACM SIGOPS 28th Symposium on Operating Systems Principles, Virtual, 26–29 October 2021; pp. 521–537. [Google Scholar]
- Tumanov, A.; Zhu, T.; Park, J.W.; Kozuch, M.A.; Harchol-Balter, M.; Ganger, G.R. TetriSched: Global rescheduling with adaptive plan-ahead in dynamic heterogeneous clusters. In Proceedings of the Eleventh European Conference on Computer Systems, London, UK, 18–21 April 2016; pp. 1–16. [Google Scholar]
- Fiat, A.; Woeginger, G.J. Competitive analysis of algorithms. In Online Algorithms: The State of the Art; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–12. [Google Scholar]
- Günther, E.; Maurer, O.; Megow, N.; Wiese, A. A new approach to online scheduling: Approximating the optimal competitive ratio. In Proceedings of the Twenty-Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 6–8 January 2013; pp. 118–128. [Google Scholar]
- Mitzenmacher, M. Scheduling with predictions and the price of misprediction. arXiv 2019, arXiv:1902.00732. [Google Scholar]
- Han, Z.; Tan, H.; Jiang, S.H.C.; Fu, X.; Cao, W.; Lau, F.C. Scheduling placement-sensitive BSP jobs with inaccurate execution time estimation. In Proceedings of the IEEE INFOCOM 2020-IEEE Conference on Computer Communications, Virtual, 6–9 July 2020; pp. 1053–1062. [Google Scholar]
- Mitzenmacher, M.; Shahout, R. Queueing, Predictions, and LLMs: Challenges and Open Problems. arXiv 2025, arXiv:2503.07545. [Google Scholar]
- Gao, W.; Sun, P.; Wen, Y.; Zhang, T. Titan: A scheduler for foundation model fine-tuning workloads. In Proceedings of the 13th Symposium on Cloud Computing, San Francisco, CA, USA, 8–10 November 2022; pp. 348–354. [Google Scholar]
- Zheng, P.; Pan, R.; Khan, T.; Venkataraman, S.; Akella, A. Shockwave: Fair and efficient cluster scheduling for dynamic adaptation in machine learning. In Proceedings of the 20th USENIX Symposium on Networked Systems Design and Implementation (NSDI 23), Boston, WA, USA, 17–19 April 2023; pp. 703–723. [Google Scholar]
- Zheng, H.; Xu, F.; Chen, L.; Zhou, Z.; Liu, F. Cynthia: Cost-efficient cloud resource provisioning for predictable distributed deep neural network training. In Proceedings of the 48th International Conference on Parallel Processing, Kyoto, Japan, 5–8 August 2019; pp. 1–11. [Google Scholar]
- Mu’alem, A.W.; Feitelson, D.G. Utilization, predictability, workloads, and user runtime estimates in scheduling the IBM SP2 with backfilling. IEEE Trans. Parallel Distrib. Syst. 2002, 12, 529–543. [Google Scholar] [CrossRef]
- Goponenko, A.V.; Lamar, K.; Allan, B.A.; Brandt, J.M.; Dechev, D. Job Scheduling for HPC Clusters: Constraint Programming vs. Backfilling Approaches. In Proceedings of the 18th ACM International Conference on Distributed and Event-based Systems, Villeurbanne, France, 24–28 June 2024; pp. 135–146. [Google Scholar]
- Kolker-Hicks, E.; Zhang, D.; Dai, D. A reinforcement learning based backfilling strategy for HPC batch jobs. In Proceedings of the SC’23 Workshops of the International Conference on High Performance Computing, Network, Storage, and Analysis, Denver, CO, USA, 12–17 November 2023; pp. 1316–1323. [Google Scholar]
- Kwok, Y.K.; Ahmad, I. Static scheduling algorithms for allocating directed task graphs to multiprocessors. ACM Comput. Surv. (CSUR) 1999, 31, 406–471. [Google Scholar] [CrossRef]
- Bittencourt, L.F.; Sakellariou, R.; Madeira, E.R. DAG scheduling using a lookahead variant of the heterogeneous earliest finish time algorithm. In Proceedings of the 2010 18th Euromicro Conference on Parallel, Distributed and Network-Based Processing, Pisa, Italy, 17–19 February 2010; pp. 27–34. [Google Scholar]
- Le, T.N.; Sun, X.; Chowdhury, M.; Liu, Z. Allox: Compute allocation in hybrid clusters. In Proceedings of the Fifteenth European Conference on Computer Systems, Heraklion, Greece, 27–30 April 2020; pp. 1–16. [Google Scholar]
- Gu, R.; Chen, Y.; Liu, S.; Dai, H.; Chen, G.; Zhang, K.; Che, Y.; Huang, Y. Liquid: Intelligent resource estimation and network-efficient scheduling for deep learning jobs on distributed GPU clusters. IEEE Trans. Parallel Distrib. Syst. 2021, 33, 2808–2820. [Google Scholar] [CrossRef]
- Guo, J.; Nomura, A.; Barton, R.; Zhang, H.; Matsuoka, S. Machine learning predictions for underestimation of job runtime on HPC system. In Proceedings of the Supercomputing Frontiers: 4th Asian Conference, SCFA 2018, Singapore, 26–29 March 2018; Proceedings 4; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 179–198. [Google Scholar]
- Mao, H.; Schwarzkopf, M.; Venkatakrishnan, S.B.; Meng, Z.; Alizadeh, M. Learning scheduling algorithms for data processing clusters. In Proceedings of the ACM Special Interest Group on Data Communication, Beijing, China, 19–23 August 2019; pp. 270–288. [Google Scholar]
- Zhao, X.; Wu, C. Large-scale machine learning cluster scheduling via multi-agent graph reinforcement learning. IEEE Trans. Netw. Serv. Manag. 2021, 19, 4962–4974. [Google Scholar] [CrossRef]
- Chowdhury, M.; Stoica, I. Efficient coflow scheduling without prior knowledge. ACM SIGCOMM Comput. Commun. Rev. 2015, 45, 393–406. [Google Scholar] [CrossRef]
- Sharma, A.; Bhasi, V.M.; Singh, S.; Kesidis, G.; Kandemir, M.T.; Das, C.R. GPU cluster scheduling for network-sensitive deep learning. arXiv 2024, arXiv:2401.16492. [Google Scholar]
- Gu, D.; Zhao, Y.; Zhong, Y.; Xiong, Y.; Han, Z.; Cheng, P.; Yang, F.; Huang, G.; Jin, X.; Liu, X. ElasticFlow: An elastic serverless training platform for distributed deep learning. In Proceedings of the 28th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Vancouver, BC, Canada, 25–29 March 2023; Volume 2, pp. 266–280. [Google Scholar]
- Even, G.; Halldórsson, M.M.; Kaplan, L.; Ron, D. Scheduling with conflicts: Online and offline algorithms. J. Sched. 2009, 12, 199–224. [Google Scholar] [CrossRef]
- Diaz, C.O.; Pecero, J.E.; Bouvry, P. Scalable, low complexity, and fast greedy scheduling heuristics for highly heterogeneous distributed computing systems. J. Supercomput. 2014, 67, 837–853. [Google Scholar] [CrossRef][Green Version]
- Wei, J.; He, J.; Chen, K.; Zhou, Y.; Tang, Z. Collaborative filtering and deep learning based recommendation system for cold start items. Expert Syst. Appl. 2017, 69, 29–39. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, K.; Yan, X.; Liu, Z.; Cai, Z.; Huang, Y.; Cheng, J.; Yuan, H.; Yu, F. Elastic deep learning in multi-tenant GPU clusters. IEEE Trans. Parallel Distrib. Syst. 2021, 33, 144–158. [Google Scholar] [CrossRef]
- Shukla, D.; Sivathanu, M.; Viswanatha, S.; Gulavani, B.; Nehme, R.; Agrawal, A.; Chen, C.; Kwatra, N.; Ramjee, R.; Sharma, P.; et al. Singularity: Planet-scale, preemptive and elastic scheduling of AI workloads. arXiv 2022, arXiv:2202.07848. [Google Scholar]
- Saxena, V.; Jayaram, K.; Basu, S.; Sabharwal, Y.; Verma, A. Effective elastic scaling of deep learning workloads. In Proceedings of the 2020 28th International Symposium on Modeling, Analysis, and Simulation of Computer and Telecommunication Systems (MASCOTS), Nice, France, 17–19 November 2020; pp. 1–8. [Google Scholar]
- Gujarati, A.; Karimi, R.; Alzayat, S.; Hao, W.; Kaufmann, A.; Vigfusson, Y.; Mace, J. Serving DNNs like clockwork: Performance predictability from the bottom up. In Proceedings of the 14th USENIX Symposium on Operating Systems Design and Implementation (OSDI 20), Online, 4–6 November 2020; pp. 443–462. [Google Scholar]
- Wang, H.; Liu, Z.; Shen, H. Job scheduling for large-scale machine learning clusters. In Proceedings of the 16th International Conference on emerging Networking EXperiments and Technologies, Barcelona, Spain, 1–4 December 2020; pp. 108–120. [Google Scholar]
- Schrage, L. A proof of the optimality of the shortest remaining processing time discipline. Oper. Res. 1968, 16, 687–690. [Google Scholar] [CrossRef]
- Hwang, C.; Kim, T.; Kim, S.; Shin, J.; Park, K. Elastic resource sharing for distributed deep learning. In Proceedings of the 18th USENIX Symposium on Networked Systems Design and Implementation (NSDI 21), Online, 12–14 April 2021; pp. 721–739. [Google Scholar]
- Graham, R.L. Combinatorial scheduling theory. In Mathematics Today Twelve Informal Essays; Springer: Berlin/Heidelberg, Germany, 1978; pp. 183–211. [Google Scholar]
- Han, J.; Rafique, M.M.; Xu, L.; Butt, A.R.; Lim, S.H.; Vazhkudai, S.S. Marble: A multi-GPU aware job scheduler for deep learning on HPC systems. In Proceedings of the 2020 20th IEEE/ACM International Symposium on Cluster, Cloud and Internet Computing (CCGRID), Melbourne, Australia, 11–14 May 2020; pp. 272–281. [Google Scholar]
- Baptiste, P. Polynomial time algorithms for minimizing the weighted number of late jobs on a single machine with equal processing times. J. Sched. 1999, 2, 245–252. [Google Scholar] [CrossRef]
- Liu, C.L.; Layland, J.W. Scheduling algorithms for multiprogramming in a hard-real-time environment. J. ACM (JACM) 1973, 20, 46–61. [Google Scholar] [CrossRef]
- Bao, Y.; Peng, Y.; Wu, C.; Li, Z. Online job scheduling in distributed machine learning clusters. In Proceedings of the IEEE INFOCOM 2018-IEEE Conference on Computer Communications, Honolulu, HI, USA, 15–19 April 2018; pp. 495–503. [Google Scholar]
- Garey, M.R.; Johnson, D.S.; Sethi, R. The complexity of flowshop and jobshop scheduling. Math. Oper. Res. 1976, 1, 117–129. [Google Scholar] [CrossRef]
- Graham, R.L. Bounds for certain multiprocessing anomalies. Bell Syst. Tech. J. 1966, 45, 1563–1581. [Google Scholar] [CrossRef]
- Deng, X.; Liu, H.N.; Long, J.; Xiao, B. Competitive analysis of network load balancing. J. Parallel Distrib. Comput. 1997, 40, 162–172. [Google Scholar] [CrossRef]
- Zhou, R.; Pang, J.; Zhang, Q.; Wu, C.; Jiao, L.; Zhong, Y.; Li, Z. Online scheduling algorithm for heterogeneous distributed machine learning jobs. IEEE Trans. Cloud Comput. 2022, 11, 1514–1529. [Google Scholar] [CrossRef]
- Memeti, S.; Pllana, S.; Binotto, A.; Kołodziej, J.; Brandic, I. Using meta-heuristics and machine learning for software optimization of parallel computing systems: A systematic literature review. Computing 2019, 101, 893–936. [Google Scholar] [CrossRef]
- Yoo, A.B.; Jette, M.A.; Grondona, M. Slurm: Simple Linux utility for resource management. In Proceedings of the Workshop on Job Scheduling Strategies for Parallel Processing, Seattle, WA, USA, 24 June 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 44–60. [Google Scholar]
- Scully, Z.; Grosof, I.; Harchol-Balter, M. Optimal multiserver scheduling with unknown job sizes in heavy traffic. ACM SIGMETRICS Perform. Eval. Rev. 2020, 48, 33–35. [Google Scholar] [CrossRef]
- Rai, I.A.; Urvoy-Keller, G.; Biersack, E.W. Analysis of LAS scheduling for job size distributions with high variance. In Proceedings of the 2003 ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems, Pittsburgh, PA, USA, 17–21 June 2003; pp. 218–228. [Google Scholar]
- Sultana, A.; Chen, L.; Xu, F.; Yuan, X. E-LAS: Design and analysis of completion-time agnostic scheduling for distributed deep learning cluster. In Proceedings of the 49th International Conference on Parallel Processing, Edmonton, AB, Canada, 17–20 August 2020; pp. 1–11. [Google Scholar]
- Menear, K.; Nag, A.; Perr-Sauer, J.; Lunacek, M.; Potter, K.; Duplyakin, D. Mastering HPC runtime prediction: From observing patterns to a methodological approach. In Proceedings of the Practice and Experience in Advanced Research Computing 2023: Computing for the Common Good, Portland, OR, USA, 23–27 July 2023; pp. 75–85. [Google Scholar]
- Luan, Y.; Chen, X.; Zhao, H.; Yang, Z.; Dai, Y. SCHED2: Scheduling Deep Learning Training via Deep Reinforcement Learning. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Big Island, HI, USA, 9–13 December 2019; pp. 1–7. [Google Scholar]
- Qin, H.; Zawad, S.; Zhou, Y.; Yang, L.; Zhao, D.; Yan, F. Swift machine learning model serving scheduling: A region based reinforcement learning approach. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 17–22 November 2019; pp. 1–23. [Google Scholar]
- Peng, Y.; Bao, Y.; Chen, Y.; Wu, C.; Meng, C.; Lin, W. DL2: A deep learning-driven scheduler for deep learning clusters. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 1947–1960. [Google Scholar] [CrossRef]
- Chen, Z.; Quan, W.; Wen, M.; Fang, J.; Yu, J.; Zhang, C.; Luo, L. Deep learning research and development platform: Characterizing and scheduling with QoS guarantees on GPU clusters. IEEE Trans. Parallel Distrib. Syst. 2019, 31, 34–50. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y. Co-scheML: Interference-aware container co-scheduling scheme using machine learning application profiles for GPU clusters. In Proceedings of the 2020 IEEE International Conference on Cluster Computing (CLUSTER), Kobe, Japan, 14–17 September 2020; pp. 104–108. [Google Scholar]
- Duan, J.; Song, Z.; Miao, X.; Xi, X.; Lin, D.; Xu, H.; Zhang, M.; Jia, Z. Parcae: Proactive, Liveput-Optimized DNN Training on Preemptible Instances. In Proceedings of the 21st USENIX Symposium on Networked Systems Design and Implementation (NSDI 24), Santa Clara, CA, USA, 16–18 April 2024; pp. 1121–1139. [Google Scholar]
- Yi, X.; Zhang, S.; Luo, Z.; Long, G.; Diao, L.; Wu, C.; Zheng, Z.; Yang, J.; Lin, W. Optimizing distributed training deployment in heterogeneous GPU clusters. In Proceedings of the 16th International Conference on emerging Networking EXperiments and Technologies, Barcelona, Spain, 1–4 December 2020; pp. 93–107. [Google Scholar]
- Ryu, J.; Eo, J. Network contention-aware cluster scheduling with reinforcement learning. In Proceedings of the 2023 IEEE 29th International Conference on Parallel and Distributed Systems (ICPADS), Danzhou, China, 17–21 December 2023; pp. 2742–2745. [Google Scholar]
- Fan, Y.; Lan, Z.; Childers, T.; Rich, P.; Allcock, W.; Papka, M.E. Deep reinforcement agent for scheduling in HPC. In Proceedings of the 2021 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Virtual, 17–21 May 2021; pp. 807–816. [Google Scholar]
- Hu, Q.; Zhang, M.; Sun, P.; Wen, Y.; Zhang, T. Lucid: A non-intrusive, scalable and interpretable scheduler for deep learning training jobs. In Proceedings of the 28th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Vancouver, BC, Canada, 25–29 March 2023; Volume 2, pp. 457–472. [Google Scholar]
- Zhou, P.; He, X.; Luo, S.; Yu, H.; Sun, G. JPAS: Job-progress-aware flow scheduling for deep learning clusters. J. Netw. Comput. Appl. 2020, 158, 102590. [Google Scholar] [CrossRef]
- Xiao, W.; Ren, S.; Li, Y.; Zhang, Y.; Hou, P.; Li, Z.; Feng, Y.; Lin, W.; Jia, Y. AntMan: Dynamic scaling on GPU clusters for deep learning. In Proceedings of the 14th USENIX Symposium on Operating Systems Design and Implementation (OSDI 20), Online, 4–6 November 2020; pp. 533–548. [Google Scholar]
- Xie, L.; Zhai, J.; Wu, B.; Wang, Y.; Zhang, X.; Sun, P.; Yan, S. Elan: Towards generic and efficient elastic training for deep learning. In Proceedings of the 2020 IEEE 40th International Conference on Distributed Computing Systems (ICDCS), Singapore, 29 November–1 December 2020; pp. 78–88. [Google Scholar]
- Ding, J.; Ma, S.; Dong, L.; Zhang, X.; Huang, S.; Wang, W.; Zheng, N.; Wei, F. Longnet: Scaling transformers to 1,000,000,000 tokens. arXiv 2023, arXiv:2307.02486. [Google Scholar]
- Liu, J.; Wu, Z.; Feng, D.; Zhang, M.; Wu, X.; Yao, X.; Yu, D.; Ma, Y.; Zhao, F.; Dou, D. Heterps: Distributed deep learning with reinforcement learning based scheduling in heterogeneous environments. Future Gener. Comput. Syst. 2023, 148, 106–117. [Google Scholar] [CrossRef]
- Chiang, M.C.; Chou, J. DynamoML: Dynamic Resource Management Operators for Machine Learning Workloads. In Proceedings of the CLOSER, Virtual, 28–30 April 2021; pp. 122–132. [Google Scholar]
- Li, J.; Xu, H.; Zhu, Y.; Liu, Z.; Guo, C.; Wang, C. Lyra: Elastic scheduling for deep learning clusters. In Proceedings of the Eighteenth European Conference on Computer Systems, Rome, Italy, 8–12 May 2023; pp. 835–850. [Google Scholar]
- Albahar, H.; Dongare, S.; Du, Y.; Zhao, N.; Paul, A.K.; Butt, A.R. Schedtune: A heterogeneity-aware GPU scheduler for deep learning. In Proceedings of the 2022 22nd IEEE International Symposium on Cluster, Cloud and Internet Computing (CCGrid), Taormina, Italy, 16–19 May 2022; pp. 695–705. [Google Scholar]
- Robertsson, J.O.; Blanch, J.O.; Nihei, K.; Tromp, J. Numerical Modeling of Seismic Wave Propagation: Gridded Two-Way Wave-Equation Methods; Society of Exploration Geophysicists: Houston, TX, USA, 2012. [Google Scholar]
- Bég, O.A. Numerical methods for multi-physical magnetohydrodynamics. J. Magnetohydrodyn. Plasma Res. 2013, 18, 93. [Google Scholar]
- Yang, J.; Liu, T.; Tang, G.; Hu, T. Modeling seismic wave propagation within complex structures. Appl. Geophys. 2009, 6, 30–41. [Google Scholar] [CrossRef]
- Koch, S.; Weiland, T. Time domain methods for slowly varying fields. In Proceedings of the 2010 URSI International Symposium on Electromagnetic Theory, Berlin, Germany, 16–19 August 2010; pp. 291–294. [Google Scholar]
- Christodoulou, D.; Miao, S. Compressible Flow and Euler’s Equations; International Press: Somerville, MA, USA, 2014; Volume 9. [Google Scholar]
- Guillet, T.; Pakmor, R.; Springel, V.; Chandrashekar, P.; Klingenberg, C. High-order magnetohydrodynamics for astrophysics with an adaptive mesh refinement discontinuous Galerkin scheme. Mon. Not. R. Astron. Soc. 2019, 485, 4209–4246. [Google Scholar] [CrossRef]
- Caddy, R.V.; Schneider, E.E. Cholla-MHD: An exascale-capable magnetohydrodynamic extension to the cholla astrophysical simulation code. Astrophys. J. 2024, 970, 44. [Google Scholar] [CrossRef]
- Müller, E.H.; Scheichl, R.; Vainikko, E. Petascale elliptic solvers for anisotropic PDEs on GPU clusters. arXiv 2014, arXiv:1402.3545. [Google Scholar]
- Xue, W.; Roy, C.J. Multi-GPU performance optimization of a CFD code using OpenACC on different platforms. arXiv 2020, arXiv:2006.02602. [Google Scholar]
- Mariani, G.; Anghel, A.; Jongerius, R.; Dittmann, G. Predicting cloud performance for hpc applications: A user-oriented approach. In Proceedings of the 2017 17th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGRID), Madrid, Spain, 14–17 May 2017; pp. 524–533. [Google Scholar]
- Chan, C.P.; Bachan, J.D.; Kenny, J.P.; Wilke, J.J.; Beckner, V.E.; Almgren, A.S.; Bell, J.B. Topology-aware performance optimization and modeling of adaptive mesh refinement codes for exascale. In Proceedings of the 2016 First International Workshop on Communication Optimizations in HPC (COMHPC), Salt Lake City, UT, USA, 16–18 November 2016; pp. 17–28. [Google Scholar]
- Bender, M.A.; Bunde, D.P.; Demaine, E.D.; Fekete, S.P.; Leung, V.J.; Meijer, H.; Phillips, C.A. Communication-aware processor allocation for supercomputers. In Proceedings of the Workshop on Algorithms and Data Structures, Waterloo, ON, Canada, 15–17 August 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 169–181. [Google Scholar]
- Calore, E.; Gabbana, A.; Schifano, S.F.; Tripiccione, R. Evaluation of DVFS techniques on modern HPC processors and accelerators for energy-aware applications. Concurr. Comput. Pract. Exp. 2017, 29, e4143. [Google Scholar] [CrossRef]
- Narayanan, D.; Santhanam, K.; Phanishayee, A.; Zaharia, M. Accelerating deep learning workloads through efficient multi-model execution. In Proceedings of the NeurIPS Workshop on Systems for Machine Learning, Montreal, QC, Canada, 8 December 2018; Volume 20. [Google Scholar]
- Jayaram, K.; Muthusamy, V.; Dube, P.; Ishakian, V.; Wang, C.; Herta, B.; Boag, S.; Arroyo, D.; Tantawi, A.; Verma, A.; et al. FfDL: A flexible multi-tenant deep learning platform. In Proceedings of the 20th International Middleware Conference, Davis, CA, USA, 9–13 December 2019; pp. 82–95. [Google Scholar]
- Narayanan, D.; Santhanam, K.; Kazhamiaka, F.; Phanishayee, A.; Zaharia, M. Analysis and exploitation of dynamic pricing in the public cloud for ML training. In Proceedings of the VLDB DISPA Workshop 2020, Online, 31 August–4 September 2020. [Google Scholar]
- Wang, S.; Gonzalez, O.J.; Zhou, X.; Williams, T.; Friedman, B.D.; Havemann, M.; Woo, T. An efficient and non-intrusive GPU scheduling framework for deep learning training systems. In Proceedings of the SC20: International Conference for High Performance Computing, Networking, Storage and Analysis, Atlanta, GA, USA, 9–19 November 2020; pp. 1–13. [Google Scholar]
- Yu, P.; Chowdhury, M. Fine-grained GPU sharing primitives for deep learning applications. Proc. Mach. Learn. Syst. 2020, 2, 98–111. [Google Scholar]
- Yang, Z.; Ye, Z.; Fu, T.; Luo, J.; Wei, X.; Luo, Y.; Wang, X.; Wang, Z.; Zhang, T. Tear up the bubble boom: Lessons learned from a deep learning research and development cluster. In Proceedings of the 2022 IEEE 40th International Conference on Computer Design (ICCD), Olympic Valley, CA, USA, 23–26 October 2022; pp. 672–680. [Google Scholar]
- Cui, W.; Zhao, H.; Chen, Q.; Zheng, N.; Leng, J.; Zhao, J.; Song, Z.; Ma, T.; Yang, Y.; Li, C.; et al. Enable simultaneous DNN services based on deterministic operator overlap and precise latency prediction. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, St. Louis, MO, USA, 14–19 November 2021; pp. 1–15. [Google Scholar]
- Zhao, H.; Han, Z.; Yang, Z.; Zhang, Q.; Yang, F.; Zhou, L.; Yang, M.; Lau, F.C.; Wang, Y.; Xiong, Y.; et al. HiveD: Sharing a GPU cluster for deep learning with guarantees. In Proceedings of the 14th USENIX symposium on operating systems design and implementation (OSDI 20), Online, 4–6 November 2020; pp. 515–532. [Google Scholar]
- Jeon, M.; Venkataraman, S.; Qian, J.; Phanishayee, A.; Xiao, W.; Yang, F. Multi-Tenant GPU Clusters for Deep Learning Workloads: Analysis and Implications; Technical Report; Microsoft Research: Redmond, WA, USA, 2018. [Google Scholar]
- Li, W.; Chen, S.; Li, K.; Qi, H.; Xu, R.; Zhang, S. Efficient online scheduling for coflow-aware machine learning clusters. IEEE Trans. Cloud Comput. 2020, 10, 2564–2579. [Google Scholar] [CrossRef]
- Dutta, S.B.; Naghibijouybari, H.; Gupta, A.; Abu-Ghazaleh, N.; Marquez, A.; Barker, K. Spy in the GPU-box: Covert and side channel attacks on multi-GPU systems. In Proceedings of the 50th Annual International Symposium on Computer Architecture, Orlando, FL, USA, 17–21 June 2023; pp. 1–13. [Google Scholar]
- Wang, W.; Ma, S.; Li, B.; Li, B. Coflex: Navigating the fairness-efficiency tradeoff for coflow scheduling. In Proceedings of the IEEE INFOCOM 2017-IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Li, Z.; Shen, H. Co-Scheduler: A coflow-aware data-parallel job scheduler in hybrid electrical/optical datacenter networks. IEEE/ACM Trans. Netw. 2022, 30, 1599–1612. [Google Scholar] [CrossRef]
- Pavlidakis, M.; Vasiliadis, G.; Mavridis, S.; Argyros, A.; Chazapis, A.; Bilas, A. Guardian: Safe GPU Sharing in Multi-Tenant Environments. In Proceedings of the 25th International Middleware Conference, Hong Kong, China, 2–6 December 2024; pp. 313–326. [Google Scholar]
- Zhao, W.; Jayarajan, A.; Pekhimenko, G. Tally: Non-Intrusive Performance Isolation for Concurrent Deep Learning Workloads. In Proceedings of the 30th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Rotterdam, The Netherlands, 30 March–3 April 2025; Volume 1, pp. 1052–1068. [Google Scholar]
- Xue, C.; Cui, W.; Zhao, H.; Chen, Q.; Zhang, S.; Yang, P.; Yang, J.; Li, S.; Guo, M. A codesign of scheduling and parallelization for large model training in heterogeneous clusters. arXiv 2024, arXiv:2403.16125. [Google Scholar]
- Zheng, L.; Li, Z.; Zhang, H.; Zhuang, Y.; Chen, Z.; Huang, Y.; Wang, Y.; Xu, Y.; Zhuo, D.; Xing, E.P.; et al. Alpa: Automating inter-and Intra-Operator parallelism for distributed deep learning. In Proceedings of the 16th USENIX Symposium on Operating Systems Design and Implementation (OSDI 22), Carlsbad, CA, USA, 1–13 July 2022; pp. 559–578. [Google Scholar]
- Athlur, S.; Saran, N.; Sivathanu, M.; Ramjee, R.; Kwatra, N. Varuna: Scalable, low-cost training of massive deep learning models. In Proceedings of the Seventeenth European Conference on Computer Systems, Rennes, France, 5–8 April 2022; pp. 472–487. [Google Scholar]
- Ousterhout, K.; Wendell, P.; Zaharia, M.; Stoica, I. Sparrow: Distributed, low latency scheduling. In Proceedings of the Twenty-Fourth ACM Symposium on Operating Systems Principles, Farmington, PA, USA, 3–6 November 2013; pp. 69–84. [Google Scholar]
- Yuan, B.; He, Y.; Davis, J.; Zhang, T.; Dao, T.; Chen, B.; Liang, P.S.; Re, C.; Zhang, C. Decentralized training of foundation models in heterogeneous environments. Adv. Neural Inf. Process. Syst. 2022, 35, 25464–25477. [Google Scholar]
- Sun, B.; Huang, Z.; Zhao, H.; Xiao, W.; Zhang, X.; Li, Y.; Lin, W. Llumnix: Dynamic scheduling for large language model serving. In Proceedings of the 18th USENIX Symposium on Operating Systems Design and Implementation (OSDI 24), Santa Clara, CA, USA, 10–12 July 2024; pp. 173–191. [Google Scholar]
- Jiang, Z.; Lin, H.; Zhong, Y.; Huang, Q.; Chen, Y.; Zhang, Z.; Peng, Y.; Li, X.; Xie, C.; Nong, S.; et al. {MegaScale}: Scaling large language model training to more than 10,000 GPUs. In Proceedings of the 21st USENIX Symposium on Networked Systems Design and Implementation (NSDI 24), Santa Clara, CA, USA, 16–18 April 2024; pp. 745–760. [Google Scholar]
- Shahout, R.; Malach, E.; Liu, C.; Jiang, W.; Yu, M.; Mitzenmacher, M. Don’t Stop Me Now: Embedding-based Scheduling for LLMs. arXiv 2024, arXiv:2410.01035. [Google Scholar]
- Mei, Y.; Zhuang, Y.; Miao, X.; Yang, J.; Jia, Z.; Vinayak, R. Helix: Serving Large Language Models over Heterogeneous GPUs and Network via Max-Flow. arXiv 2024, arXiv:2406.01566. [Google Scholar]
- Mitzenmacher, M.; Vassilvitskii, S. Algorithms with predictions. Commun. ACM 2022, 65, 33–35. [Google Scholar] [CrossRef]
- Li, Y.; Phanishayee, A.; Murray, D.; Tarnawski, J.; Kim, N.S. Harmony: Overcoming the hurdles of GPU memory capacity to train massive DNN models on commodity servers. arXiv 2022, arXiv:2202.01306. [Google Scholar] [CrossRef]
- Ye, Z.; Gao, W.; Hu, Q.; Sun, P.; Wang, X.; Luo, Y.; Zhang, T.; Wen, Y. Deep learning workload scheduling in G datacenters: A survey. ACM Comput. Surv. 2024, 56, 1–38. [Google Scholar] [CrossRef]
- Chang, Z.; Xiao, S.; He, S.; Yang, S.; Pan, Z.; Li, D. Frenzy: A Memory-Aware Serverless LLM Training System for Heterogeneous GPU Clusters. arXiv 2024, arXiv:2412.14479. [Google Scholar]
- Moussaid, A. Investigating the Impact of Prompt Engineering Techniques on Energy Consumption in Large Language Models. Master’s Thesis, University of L’Aquila, L’Aquila, Italy, 2025. [Google Scholar]
- Yao, C.; Liu, W.; Tang, W.; Hu, S. EAIS: Energy-aware adaptive scheduling for CNN inference on high-performance GPUs. Future Gener. Comput. Syst. 2022, 130, 253–268. [Google Scholar] [CrossRef]
- Khan, O.; Yu, J.; Kim, Y.; Seo, E. Efficient Adaptive Batching of DNN Inference Services for Improved Latency. In Proceedings of the 2024 International Conference on Information Networking (ICOIN), Ho Chi Minh City, Vietnam, 17–19 January 2024; pp. 197–200. [Google Scholar]
- Beltrán, E.T.M.; Pérez, M.Q.; Sánchez, P.M.S.; Bernal, S.L.; Bovet, G.; Pérez, M.G.; Pérez, G.M.; Celdrán, A.H. Decentralized federated learning: Fundamentals, state of the art, frameworks, trends, and challenges. IEEE Commun. Surv. Tutor. 2023, 25, 2983–3013. [Google Scholar] [CrossRef]
- Bharadwaj, S.; Das, S.; Mazumdar, K.; Beckmann, B.M.; Kosonocky, S. Predict; don’t react for enabling efficient fine-grain DVFS in GPUs. In Proceedings of the 28th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Vancouver, BC, Canada, 25–29 March 2023; Volume 4, pp. 253–267. [Google Scholar]
- Albers, S. Energy-efficient algorithms. Commun. ACM 2010, 53, 86–96. [Google Scholar] [CrossRef]
- Han, Y.; Nan, Z.; Zhou, S.; Niu, Z. DVFS-Aware DNN Inference on GPUs: Latency Modeling and Performance Analysis. arXiv 2025, arXiv:2502.06295. [Google Scholar]
- Kakolyris, A.K.; Masouros, D.; Vavaroutsos, P.; Xydis, S.; Soudris, D. SLO-aware GPU Frequency Scaling for Energy Efficient LLM Inference Serving. arXiv 2024, arXiv:2408.05235. [Google Scholar]
| Dimension Evidence Required | Score Range | |
|---|---|---|
| Strong theoretical guarantees | 0–2 | Formal bounds or proofs (e.g., competitive ratio). |
| Hardware realism | 0–2 | Evaluation on clusters with at least 8 GPUs or production-scale traces. |
| Comparative analysis | 0–2 | Benchmarking against standard baselines. |
| Modern DL relevance | 0–2 | Targets large-scale deep learning or LLM workloads. |
| Trait | Typical CPU Cluster | GPU Cluster (A100/H100 era) |
|---|---|---|
| Context switch/preemption | ≈∼s (core) inexpensive, fine-grained | 10 ms∼30 ms (kernel) costly; whole-SM drain required [73,74] |
| Device memory per worker | GB DDR4/5 shared | GB HBM private to each device Placement must avoid OOM even at low utilization. |
| NUMA/socket locality | 1∼4 hop latency tiers per node [75] | Two tiers: NVLink/NVSwitch (200∼900 GB/s) vs. PCIe (32 GB/s, 64 GB/s). Cross-tier traffic quickly dominates runtime [58,76]. |
| Partitioning granularity | Core/SMT thread; OS-level control groups | MIG slices (∼ device) or whole GPU Integer-knapsack bin packing, no fractional share scheduling. |
| Inter-device topology | NUMA DRAM buses and Ethernet/IB | On-node all-to-all (NVSwitch) + inter-node fat-tree IB (NDR/HDR) Topology-aware placement yields up to speed-ups [77]. |
| Power management | Per-core DVFS, RAPL capping | Device-level DVFS; memory clock often fixed Energy models must separate SM vs. HBM power. |
| Objective | Formulation | Definition |
|---|---|---|
| Minimizing average waiting time | Shorten the average time jobs wait in the queue before execution. | |
| Minimizing average completion time | Minimize the average turnaround time between job submission and completion. | |
| Maximizing throughput | Increase the number of jobs completed per unit time. | |
| Maximizing utilization | Maximize the fraction of total time during which GPUs are actively utilized. | |
| Maximizing fairness | Equalize resource allocation by preventing any job j from experiencing excessive slowdown relative to its service time . | |
| Minimizing energy consumption | Reduce the total energy consumed by the GPU cluster during job scheduling. |
| Workload Scenario | Primary Paradigm | Alternative Paradigm | Rationale |
|---|---|---|---|
| Single-tenant training-only, homogeneous cluster, preemptions costly | Greedy heuristic (e.g., SJF + backfill) | Queueing-index (SRPT/PS) | Low job-completion time (JCT) with minimal overhead; preemption avoidance simplifies implementation. |
| Multi-tenant mixed (training + inference), fairness critical, moderate load | DRF-based DP/optimization | Hybrid heuristic + ML-assisted prediction | Provides provable fairness guarantees (e.g., bounded max-slowdown); small throughput trade-off. |
| High load (>75% utilization), variable DAGs, preemption cheap | Reinforcement learning (e.g., Decima) | Hybrid heuristic (HEFT + backfill) | Learns long-horizon dispatch policies to reduce p95 latency; alternative achieves near-optimal makespan with lower engineering cost. |
| Real-time inference with strict SLOs (50∼200 ms), deadline-sensitive | Queueing-index (SRPT/processor-sharing) | Learning-assisted size prediction + PS | Size-based prioritization minimizes tail-latency; if exact sizes are unknown, predictions feed into PS to approach SRPT behavior. |
| Energy-budgeted training under power/carbon caps | MILP-based multi-objective optimization | Hybrid heuristic with DVFS | Precise modeling of time–energy trade-offs; alternative reduces solver latency while achieving near-optimal energy usage. |
| Offline batch scheduling with a fully known job set | Offline MILP or DAG-based optimization | Queueing-theory policies (e.g., with SRPT) | Computes optimal makespan for fixed jobs; when scale is large, queueing models offer analytical insights under stochastic approximations. |
| Unpredictable workloads, heterogeneous GPUs, noisy runtime estimates | Hybrid heuristic + ML prediction | Robust heuristic (backfill with conservative reservations) | ML-predictions guide placement, but the fallback heuristic prevents starvation when prediction error is high. |
| PDE/HPC solvers | Communication-aware MILP | Static bin-packing | Long-lived, tightly coupled jobs with predictable runtimes; performance dominated by NVLink/NVSwitch topology rather than queue dynamics. |
| Paradigm | Representative Algorithms/Workloads | Latency Improvement | Throughput/Utilization | Fairness Impact |
|---|---|---|---|---|
| Greedy heuristics | Tiresias [74] (LAS, training); Gandivafair [70] (time-sharing) | ≈ mean JCT vs. fair baseline; long-job slowdowns mitigated | High GPU utilization via backfilling; heterogeneous GPUs reused via token trading | Maintains long-term fair share |
| Dynamic programming | Lyra [173] (capacity loaning, mixed training + inference) | ∼ queuing/JCT | Up to GPU utilization when borrowing idle inference GPUs | Inference SLOs preserved |
| MILP optimization | Chronus [84] (deadline, training); Dorm/AlloX (fair allocation) | deadline misses; best-effort JCT | Near-optimal utilization; MILP solved in batches (solver overhead acceptable) | Strong DRF-level fairness |
| Queueing theory | LAS priority (Tiresias, training) [74]; dynamic batching model (inference) | ∼ short-job wait; latency vs. batch size analytically predictable | Up to throughput at large batch; short-job throughput boosted | Possible long-job slowdowns if not combined with fairness controls |
| ML-assisted prediction | Helios [106] (runtime/priority); SCHEDTUNE [174] (interference, memory usage) | ≈ average JCT; makespan | GPU-mem utilization; avoids OOM; better packing | Generally fair with tuned safeguards |
| Reinforcement learning | DL2 [159] (supervised, + RL, training); SCHED2 [157] (Q-learning) | average JCT vs. DRF; vs. expert heuristic | jobs/hour; lower fragmentation | Fairness achieved when encoded in reward |
| Hybrid approaches | Pollux [68] (adaptive goodput); AntMan [168] (elastic scaling) | ∼ average JCT | throughput; goodput | Balances efficiency & fairness via policy knobs |
| System | Workload/Testbed | Representative Absolute Metrics |
|---|---|---|
| Tiresias-G, Tiresias-L | 64-GPU ImageNet-style training trace | Average queueing delay: 1005 s (G), 963 s (L); median 39 s/13 s. Small-job JCT: 330 s (G), 300 s (L). Workload makespan: ∼ s vs. s (YARN-CS baseline). |
| Llumnix | LLaMA-7B inference cluster | Live-migration downtime: 20∼30 ms vs. s recompute. P99 first-token latency: up to lower than INFaaS. Up to fewer instances at equal P99 latency. |
| Pollux () | 64-GPU synthetic training workload | Average JCT: h; P99 JCT: 11 h; makespan: 16 h. |
| DL2 | 64-GPU parameter-server testbed | Scheduler latency: s. GPU utilization: (↑ 16% vs. DRF). Scaling overhead: of total training time. |
| Lyra | 15-day simulation (3544 GPU training + 4160 GPU inference) | Average queueing time: 2010 s vs. 3072 s (FIFO). Average JCT: s vs. s. Cluster utilization: vs. . |
| Chronus | 120-GPU Kubernetes prototype | Deadline-miss rate: (≈ vs. prior). Pending time cut from 2105 s to 960 s. Best-effort JCT: up to faster. |
| Helios | 1 GPU + 12 SSD GNN training | Throughput: up to GIDS, Ginex. Saturates PCIe version with 6 SSDs; 91∼ of in-memory throughput on PA dataset. |
| Open Challenge | LLM Training | LLM Inference | Mixed-Tenant Clusters | Edge/IoT | Solution Maturity |
|---|---|---|---|---|---|
| Coflow-aware scheduling | High | Medium | High | Low | Low |
| Secure multi-tenant isolation | Medium | High | High | Medium | Medium |
| Energy-aware DVFS scheduling | Medium | Medium | High | High | High |
| Topology-aware placement for trillion-parameter LLMs | High | Medium | Medium | Low | Medium |
| Cross-objective (carbon/cost/fairness) schedulers | Medium | Low | High | Low | Low |
| Open Problems | Missing Benchmark Signal | Why It Matters |
|---|---|---|
| Coflow-aware scheduling for ultra-fast fabrics | No public trace records per-flow bytes and timing on NVSwitch or InfiniBand-NDR clusters. | Would enable direct evaluation of coflow algorithms on real fabrics, guiding both network stack tuning and scheduler design (see also Parrot’s JCT improvement in Section 3). |
| Secure multi-tenant GPU isolation | No microbenchmark suite reports cache/SM side-channel leakage across MIG or comparable partitions under production drivers. | Establishes the empirical basis for certifying isolation guarantees and designing schedulers that safely colocate untrusted tenants. |
| Energy-aware DVFS under tail-latency SLOs | DVFS studies typically report only median (p50) inference latency; tail latencies (p90–p99) under load remain unmeasured. | Clarifies the true energy–latency trade-off, enabling operators to meet service-level objectives while minimizing power consumption. Appendix A shows that even a cubic power model cannot predict p99 under bursty inference. |
| Topology-aware placement for trillion-parameter LLMs | No open trace logs tensor-parallel bandwidth or collective communication latency beyond 16-GPU slices. | Provides ground truth for placement algorithms to minimize communication hotspots in large-model training. |
| Cross-objective schedulers (cost × carbon × fairness) | Benchmarks lack real-time electricity pricing, carbon intensity, and per-user slowdown metrics in a single trace. | Enables Pareto-optimal scheduler design that balances budget, sustainability, and equity goals. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chab, R.; Li, F.; Setia, S. Algorithmic Techniques for GPU Scheduling: A Comprehensive Survey. Algorithms 2025, 18, 385. https://doi.org/10.3390/a18070385
Chab R, Li F, Setia S. Algorithmic Techniques for GPU Scheduling: A Comprehensive Survey. Algorithms. 2025; 18(7):385. https://doi.org/10.3390/a18070385
Chicago/Turabian StyleChab, Robert, Fei Li, and Sanjeev Setia. 2025. "Algorithmic Techniques for GPU Scheduling: A Comprehensive Survey" Algorithms 18, no. 7: 385. https://doi.org/10.3390/a18070385
APA StyleChab, R., Li, F., & Setia, S. (2025). Algorithmic Techniques for GPU Scheduling: A Comprehensive Survey. Algorithms, 18(7), 385. https://doi.org/10.3390/a18070385






