Substring Counting with Insertions

Abstract

Substring counting is a classical algorithmic problem with numerous solutions that achieve linear time complexity. In this paper, we address a variation of the problem where, given three strings p, t, and s, we are interested in the number of occurrences of p in all strings that would result from inserting t into s at every possible position. Essentially, we are solving several substring counting problems of the same substring p in related strings. We give a detailed description of several conceptually different approaches to solving this problem and conclude with an algorithm that has a linear time complexity. The solution is based on a recent result from the field of substring search in compressed sequences and exploits the periodicity of strings. We also provide a self-contained implementation of the algorithm in C++ and experimentally verify its behavior, chiefly to demonstrate that its running time is linear in the lengths of all three input strings.

1. Introduction

Substring search is one of the classical algorithmic problems, which has a somewhat surprising linear-time solution. However, there is an abundance of algorithms that address the same or similar problems [1]. In this paper, we focus on a new version of the problem, where we are dealing with a changing string in which we are searching for a substring.

We are given strings s, t, and p. We will denote the length of the string s as $\left|s\right|$. If we insert t into s at position k (where $0\le k\le \left|s\right|$), we obtain a new string that is formed by the first k characters of string s, followed by the entire string t and concluded by the remaining $\left|s\right|-k$ characters of s. We want to count the number of occurrences of p as a substring in every string that can be obtained with the insertion of t into s at all possible positions k. We make no assumption regarding the lengths of the input strings. They may be potentially millions of characters long; they may be comparable in length, or some may be much shorter than others. The only constraint is that s and t together should not be shorter than p, as that would make the problem trivial.

For example, if we insert $t=\mathtt{aba}$ into $s=\mathtt{ab}$ at position $k=0$, we get abaab. For insertions at $k=1$ and $k=2$ we get aabab and ababa, respectively. If we are interested in occurrences of $p=\mathtt{aba}$, we will find two when inserting t into s at $k=2$: ababa and ababa (occurrences can of course overlap).

The problem can be solved trivially by employing any substring counting algorithm with a linear time complexity on all $\left|s\right|+1$ strings obtained by inserting t into s. However, we are interested in more efficient solutions that do not have a quadratic time complexity in terms of the length of string s, which we are modifying and searching the substring in.

The paper presents different approaches to solving the problem in the following sections from less to more computationally efficient. Some approaches are improvements of the previous ones while others exploit different properties. We first establish some preliminaries, which are used throughout the rest of the paper. Then we describe a solution with time complexity that is quadratic in terms of the length of the pattern string p but linear in the length of the strings s and t. We achieve this through the use of similarities between the problems of counting the same pattern string p in strings that are a result of inserting t into s in adjacent locations. The following chapter improves this solution with a precomputation that gives us a solution with subquadratic time complexity. Next, we focus on a different, geometric interpretation of a problem, which reorders the computation of solutions to the $\left|s\right|+1$ problems and achieves a time complexity of $O(t+(p+s)logp)$. It is based on reducing the problem to the point location problem, more precisely to rectangle stabbing or dynamic interval stabbing [2,3]. Finally, we present a solution with a linear time complexity $O(s+t+p)$, which is based on a recent result [4] on finding substrings in a compressed text [5].

This paper presents a theoretical result in string processing: a worst-case linear-time algorithm that generalizes the classical string matching problem. Specifically, instead of computing pattern occurrence counts in a single, fixed text, our algorithm efficiently computes such counts across a linear number of systematically modified texts, all within the same asymptotic time bound.

We outline some potential areas of application for the developed algorithms. In bioinformatics, pattern counting is fundamental to genome sequence analysis, where the patterns of interest may correspond to known biological motifs or regulatory elements. The inserted sequences can represent indels or longer structural variants. They could also originate from viruses that are able to insert their genetic material into host chromosomes. In cybersecurity and plagiarism detection, obfuscation techniques often involve the insertion of irrelevant content to evade detection of known signatures. In natural language processing, the insertion of specific phrases or modifiers can be used to detect meaningful linguistic variants. Beyond these applications, the algorithmic techniques presented here may be relevant for developing related algorithms for efficient processing of sequential data.

2. Materials and Methods

2.1. Preliminaries

We will denote the length of the string x by $\left|x\right|$, except in the big O notation $O(·)$ or under the root $\sqrt{·}$, where we will omit the $|·|$ characters. We will use python (https://docs.python.org/3/library/stdtypes.html#typesseq-common, accessed on 18 June 2025) notation for individual characters and substrings. The string x consists of characters $x\left[0\right],\dots ,x\left[\right|x|-1]$; the substring $x[i:j]$ comprises the characters $x\left[i\right],\dots ,x[j-1]$; if i is absent in this notation, we mean $i=0$; if j is absent, we mean $j=\left|x\right|$; if i or j is negative, we should add $\left|x\right|$ to it. Position i in the string x refers to the boundary between characters $x[i-1]$ and $x\left[i\right]$ (position 0 is the left edge of the first character, and position $\left|x\right|$ is the right edge of the last character). The notation $x^{\mathsf{R}}$ will represent the string that we get if we read the characters of the string x from right to left, so $x^{\mathsf{R}}\left[i\right]=x\left[\right|x|-1-i]$; prefixes and suffixes of the strings x and $x^{\mathsf{R}}$ are of course closely related: $x^{\mathsf{R}}[i:]={\left(x\right[:\left|x\right|-i\left]\right)}^{\mathsf{R}}$ and $x^{\mathsf{R}}[:i]={\left(x\right[\left|x\right|.-i:\left]\right)}^{\mathsf{R}}$.

We will frequently make use of prefix tables as we know them from the Knuth–Morris–Pratt algorithm [6]. For a given string x, let ${\mathsf{P}}_x\left[i\right]$ be largest integer $j<i$ such that $x[:j]$ is a suffix of $x[:i]$ the table ${\mathsf{P}}_x$ can be computed in $O\left(x\right)$ time. For strings x and y, we will further define ${\mathsf{P}}_{yx}\left[i\right]$ as the largest integer $j<\left|x\right|$ such that $x[:j]$ is a suffix of $y[:i]$; the table ${\mathsf{P}}_{yx}$ can be computed in $O\left(y\right)$ time by an algorithm very similar to that for ${\mathsf{P}}_x$. In other words, ${\mathsf{P}}_x$ and ${\mathsf{P}}_{yx}$ tell us, for each prefix of x and of y, what is the longest prefix of x that it ends with.

The table ${\mathsf{P}}_{yx}$ is useful, for example, in finding occurrences of the string x as a substring in the string y: these occurrences end at those positions i (recall that position i is the boundary between characters $y[i-1]$ and $y\left[i\right]$) where ${\mathsf{P}}_{yx}[i-1]=\left|x\right|-1$ and $y[i-1]=x[-1]$. This will also be useful to have stored in a table; so let ${\mathsf{O}}_{yx}\left[i\right]=1$ if x appears in y starting at position i (that is, if $y[i:i+|x\left|\right]=x$), otherwise, let ${\mathsf{O}}_{yx}\left[i\right]=0$. Let us further define a table of partial sums: ${Ō}_{yx}\left[i\right]={\sum }_{j=0}^i{\mathsf{O}}_{yx}\left[j\right]$, which therefore counts all occurrences of x as a substring in y at positions 0 to i. All these tables can be calculated in linear time.

Similar to the above precomputation of prefixes, we can also preprocess suffixes; let us define tables ${\mathsf{S}}_x$ and ${\mathsf{S}}_{yx}$ which tell us, for each suffix of x or y, what is the longest suffix of x that it begins with. More precisely, let ${\mathsf{S}}_x\left[i\right]$ be the smallest value $j>i$ such that $x[j:]$ is a prefix of $x[i:]$; and let ${\mathsf{S}}_{yx}\left[i\right]$ be the smallest value $j>0$ such that $x[j:]$ is a prefix of $y[i:]$. Both tables can be computed in linear time by a similar procedure as for ${\mathsf{P}}_x$ and ${\mathsf{P}}_{yx}$, except that we process strings from right to left. (We can also reverse the strings and use the previous procedures for prefix tables; namely ${\mathsf{S}}_x\left[i\right]=\left|x\right|-{\mathsf{P}}_{x^{\mathsf{R}}}\left[\right|x|-i]$ and ${\mathsf{S}}_{yx}\left[i\right]=\left|x\right|-{\mathsf{P}}_{y^{\mathsf{R}}{x}^{\mathsf{R}}}\left[\right|y|-i]$.)

2.2. General Approach

We will successfully solve the problem if we count, for each $k=0,\dots ,\left|s\right|$, the number of occurrences of p in the string $s[:k]ts[k:]$, which arises from inserting t into s at position k. These occurrences can be divided into those that

(I)

lie entirely within $s[:k]$ or entirely within $s[k:]$;

(II)

Lie entirely within t;

(III)

Start within $s[:k]$ and end within t;

(IV)

Start within t and end within $s[k:]$; and

(V)

Start within $s[:k]$ and end within $s[k:]$, and in between extend over the entire t.

• Each of these five types of occurrences will be considered separately and the results added up at the end. Of course, type (II) comes into play only if $\left|p\right|\le \left|t\right|$, and type (V) only if $\left|p\right|\ge \left|t\right|+2$.

(I) Suppose that p appears at position i in s, that is $s[i:i+|p\left|\right]=p$. This occurrence lies entirely within $s[:k]$ if $i+\left|p\right|\le k$, therefore $i\le k-\left|p\right|$; there are a total of ${Ō}_{sp}[k-|p\left|\right]$ such occurrences.

However, if we want the occurrence to lie entirely within $s[k:]$, that means that $i\ge k$; such occurrences can be counted by taking the number of all occurrences of p in s and subtracting those that start at positions from 0 to $k-1$. Thus, we get ${Ō}_{sp}\left[\right|s\left|\right]-{Ō}_{sp}[k-1]$.

(II) The second type consists of all occurrences of p in t, so there are ${Ō}_{tp}\left[\right|t\left|\right]$ of these. We use this result at every k.

(III) The third type consists of occurrences of p that begin within $s[:k]$ and end within t. Suppose that the left j characters of p lie in $s[:k]$ and the rest in t; thus $s[:k]$ ends with $p[:j]$, and t starts with $p[j:]$. We already know that the longest prefix of p appearing at the end of $s[:k]$ is $i:={\mathsf{P}}_{sp}\left[k\right]$ characters long; for the purposes of our discussion, we can therefore replace $s[:k]$ with $p[:i]$.

Let $D\left[i\right]$ be the number of those occurrences of p in $p[:i]t$ that start within the first part, i.e., in $p[:i]$. One possibility is that such an occurrence starts at the beginning of the string (in this case t must start with $p[i:]$); the other option is that it starts a bit later, so that only the first $j<i$ characters of our occurrence lie in $p[:i]$. Therefore $p[:i]$ ends with $p[:j]$; and we already know that the next position j for which this condition is satisfied is $j={\mathsf{P}}_p\left[i\right]$. The table D is prepared in advance with Algorithm 1 (with a linear time complexity), and then at each k, we know that $D\left[{\mathsf{P}}_{sp}\left[k\right]\right]$ occurrences of p start within $s[:k]$ and end within t.

In the above procedure, we need to be able to quickly check whether t starts with $p[i:]$ for a given i. We will use tables ${\mathsf{S}}_p$ and ${\mathsf{S}}_{tp}$ that were prepared in advance. Now $j={\mathsf{S}}_{tp}\left[0\right]$ tells us that $p[j:]$ is the longest suffix of p that occurs at the beginning of t; the second longest such suffix is $p[{\mathsf{S}}_p\left[j\right]:]$, the third $p[{\mathsf{S}}_p\left[{\mathsf{S}}_p\left[j\right]\right]:]$, and so on. We therefore prepare the table E (with Algorithm 2), which tells us, for each possible index j, whether $p[j:]$ occurs at the beginning of t. Hence, the condition “if t starts with $p[i:]$” in our procedure for computing table D can now be checked by looking at the value of $E\left[i\right]$.

Algorithm 1 Computation of the table $D\left[i\right]$—occurrences of p in $p[:i]t$ that start within the first part

$D\left[0\right]:=0$;    for $i:=1$ to $\left|p\right|$:       (*occurrences that have fewer than i characters in $p[:i]$*)       $D\left[i\right]:=D\left[{\mathsf{P}}_p\left[i\right]\right]$;       if t starts with $p[i:]$ then          (*the occurrence of p at the start of $p[:i]t$*)          $D\left[i\right]:=D\left[i\right]+1$;

Algorithm 2 Computation of the table $E\left[j\right]$—does $p[j:]$ occur at the start of t?

for $j:=1$ to $\left|p\right|$ do $E\left[j\right]:=\mathbf{false}$;    $j:={\mathsf{S}}_{tp}\left[0\right]$;    while $j<\left|p\right|$:       $E\left[j\right]:=\mathbf{true}$; $j:={\mathsf{S}}_p\left[j\right]$;

(IV) The fourth type consists of the occurrences of p that start within t and end within $s[k:]$. These can be counted using the same procedure as for (III), except that we reverse all three strings.

(V) We are left with those occurrences of p that start within $s[:k]$, end within $s[k:]$, and contain the entire t in between. This means that $s[:k]$ must end with some prefix of p and we already know that the longest such prefix is $i:={\mathsf{P}}_{sp}\left[k\right]$ characters long; similarly, $s[k:]$ must start with some suffix of p, and the longest such suffix is $\left|p\right|-j$ characters long, where $j:={\mathsf{S}}_{sp}\left[k\right]$. Instead of strings $s[:k]$ and $s[k:]$ we can focus on $p[:i]$ and $p[j:]$ from here on. (These i and j can of course be different for different k, and where relevant we will refer to them as $i_k$ and $j_k$.) We will present several ways of counting the occurrences of p in strings of the form $p[:i] t p[j:]$, from simpler and less efficient to more efficient, but more complicated. Everything we have presented so far regarding types (I) to (IV) had linear time and space complexity, $O(s+t+p)$, so the computational complexity of the solution as a whole depends mainly on how we solve the task for type (V).

2.3. Quadratic Solution

Let $f(i,j)$ be the number of those occurrences of p in the string $p[:i] t p[j:]$ that start within $p[:i]$ and end within $p[j:]$. This function is interesting for $0\le i<\left|p\right|$ and $0<j\le \left|p\right|$ (so that the first and third part, $p[:i]$ and $p[j:]$, are shorter than p). Edge cases are $p(0,j)=p(i,|p\left|\right)=0$, because then the first or third part is empty and therefore p can not overlap with it.

Let us now consider the general case. One occurrence of p in $p[:i] t p[j:]$ may already appear at the beginning of this string; and the rest must begin later, such that within the first part of our string, $p[:i]$, they only have some shorter prefix, say $p[:i^{\prime }]$, which is therefore also a suffix of the string $p[:i]$. The longest such prefix is of length $i^{\prime }:={\mathsf{P}}_p\left[i\right]$; all these later occurrences therefore lie not only within $p[:i] t p[j:]$, but also within $p[:i^{\prime }] t p[:j]$, so there are $f(i^{\prime },j)$ of them. We have thus obtained a recurrence that is the core of Algorithm 3 for calculating all possible values of the function f using dynamic programming.

Algorithm 3 A quadratic dynamic programming solution for counting occurrences of p in $p[:i] t p[j:]$

1    for $i:=1$ to $\left|p\right|-1$ do for $j:=1$ to $\left|p\right|-1$: 2       $f[i,j]:=0$;          (*Does p occur at the start of $p[:i] t p[j:]$?*) 3       if t occurs in p at position i              (i.e., if $p[i:i+|t\left|\right]=t$) then 4           if $i+\left|t\right|<\left|p\right|$ and                $p[j:]$ starts with $p[i+|t|:]$ then 5             $f[i,j]:=1$;         (*Add later occurrences.*) 6       $i^{\prime }:={\mathsf{P}}_p\left[i\right]$; 7       $f[i,j]:=f[i,j]+f[i^{\prime },j]$;

Before the procedure for calculating the function f is actually useful, we still need to consider some important details. We check the condition in line 3 by checking if ${\mathsf{O}}_{pt}\left[i\right]=1$. In line 4 the condition $i+\left|t\right|<\left|p\right|$ checks whether an occurrence of p that started at the beginning of the string $p[:i] t p[j:]$ would even reach $p[j:]$ at the end, because we are only interested in such occurrences—those that lie entirely within $p[:i]t$, have already been considered in under type (III) in Section 2.2. Next, we have to check, in line 4, whether some suffix of p begins with some shorter suffix of p. Recall that the longest $p[j^{\prime }:]$ that occurs at the beginning of the string $p[j:]$ is the one with $j^{\prime }={\mathsf{S}}_p\left[j\right]$; the next is $p[j^{″}:]$ for $j^{″}={\mathsf{S}}_p\left[j^{\prime }\right]$, and so on. In line 4 we are essentially checking whether this sequence of shorter suffixes eventually reaches $p[i+|t|:]$. For this purpose we can use a tree structure, which we will also need later in more efficient solutions. Let us construct a tree $T_{\mathsf{S}}$ in which there is a node for each u from 1 to $\left|p\right|$; the root of the tree is the node $\left|p\right|$ (recall that the number in the suffix notation, such as $p[i:]$, represents the position or index at which this suffix begins; therefore, shorter suffixes have larger indices, and the largest among them is $\left|p\right|$, which represents the empty suffix), and for every $u<\left|p\right|$, let node u be a child of node ${\mathsf{S}}_p\left[u\right]$. Line 4 now actually asks whether node $i+\left|t\right|$ is an ancestor of node j in the tree $T_{\mathsf{S}}$.

This can be checked efficiently if we do a preorder traversal of all nodes in the tree—that is, the order in which we list the root first, then recursively add each of its subtrees (Algorithm 4). For each node u, we remember its position in that order (say ${\sigma }_{\mathsf{S}}\left[u\right]$) and the position of the last of its descendants (say ${\tau }_{\mathsf{S}}\left[u\right]$). Then the descendants of u are exactly those nodes that are located in the order at indices from ${\sigma }_{\mathsf{S}}\left[u\right]$ to ${\tau }_{\mathsf{S}}\left[u\right]$. To check whether some $p[\mathsf{\ell }:]$ is a prefix of $p[j:]$, we only have to check if ${\sigma }_{\mathsf{S}}\left[\mathsf{\ell }\right]\le {\sigma }_{\mathsf{S}}\left[j\right]\le {\tau }_{\mathsf{S}}\left[\mathsf{\ell }\right]$. (Another way to check whether $p[\mathsf{\ell }:]$ is a prefix of $p[j:]$ is with the Z-algorithm ([7], pp. 7–10). For any string w, we can prepare a table ${\mathsf{Z}}_w$ in $O\left(w\right)$ time, where the element ${\mathsf{Z}}_w\left[i\right]$ (for $i=0,\dots ,\left|w\right|$) tells us the length of the longest common prefix of the strings w and $w[i:]$. The question we are interested in—i.e., whether $p[\mathsf{\ell }:]$ is a prefix of $p[j:]$—is equivalent to asking whether $p[\mathsf{\ell }:]=p[j:j+|p|-\mathsf{\ell }]$, which is equivalent to $p^{\mathsf{R}}[:|p|-\mathsf{\ell }]=p^{\mathsf{R}}[\mathsf{\ell }-j:|p|-j]$, and hence to the question whether $p^{\mathsf{R}}$ and $p^{\mathsf{R}}[\mathsf{\ell }-j:]$ match in the first $\left|p\right|-\mathsf{\ell }$ characters, i.e., whether ${\mathsf{Z}}_{p^{\mathsf{R}}}[\mathsf{\ell }-j]\ge \left|p\right|-\mathsf{\ell }$. However, for our purposes the tree-based solution is more useful than the one using the Z-algorithm, as we will later use the tree in solutions with a lower time complexity than the quadratic one that we are describing now.)

Our procedure so far (Algorithm 3) has computed $f(i,j)$ by checking whether p occurs at the beginning of $p[:i] t p[j:]$ and handling subsequent occurrences via $f(i^{\prime },j)$ for $i^{\prime }={\mathsf{P}}_p\left[i\right]$. Of course, we could also go the other way: we would first check whether p occurs at the end (instead of the beginning) of $p[:i] t p[j:]$ and then add earlier occurrences via $f(i,j^{\prime })$ for $j^{\prime }={\mathsf{S}}_p\left[j\right]$. To check if p occurs at the end of $p[:i] t p[j:]$, we should first check whether t occurs in p at indices from $j-\left|t\right|$ to j (with the same table as before in line 3), and then we would be interested in whether $p[:i]$ ends with $p[:j-|t\left|\right]$. Here, it would be helpful to construct a tree $T_{\mathsf{P}}$, which would have one node for each u from 0 to $\left|p\right|-1$; node 0 would be the root, and for every $u>0$, the node u would be a child of node ${\mathsf{P}}_p\left[u\right]$. Using the procedure Preorder on this tree would give us tables ${\sigma }_{\mathsf{P}}$ and ${\tau }_{\mathsf{P}}$. We should then check whether $j-\left|t\right|$ is an ancestor of node i in the tree.

Algorithm 4 Tree traversal for determining the ancestor–descendant relationships

procedure Traverse (tree T, node u,       tables $\sigma$ and $\tau$, index i):    $i:=i+1$; $\sigma \left[u\right]:=i$;    for every child v of node u in tree T:       $i:=$ Traverse(T, v, σ, τ, i);    $\tau \left[u\right]:=i$; return i;

procedure Preorder(input: tree T;       output: tables $\sigma$ and $\tau$):    let $\sigma$ and $\tau$ be tables with indices from 1 to $\left|p\right|$;    Traverse(T, root of T, σ, τ, 0);    return $\sigma ,\tau$; main call: ${\sigma }_{\mathsf{S}},{\tau }_{\mathsf{S}}:=$ Preorder(TS);

Thus, we see that we can compute $f(i,j)$ quickly, in $O\left(1\right)$ time, either from $f({\mathsf{P}}_p\left[i\right],j)$ or from $f(i,{\mathsf{S}}_p\left[j\right])$; both ways will come in handy later.

Our current procedure for computing the function f would take $O\left(p\right)$ time to prepare trees $T_{\mathsf{P}}$ and $T_{\mathsf{S}}$ and tables ${\sigma }_{\mathsf{P}}$, ${\sigma }_{\mathsf{S}}$, ${\tau }_{\mathsf{P}}$ and ${\tau }_{\mathsf{S}}$, followed by $O\left(p^2\right)$ time to calculate the value of $f(i,j)$ for all possible pairs $(i,j)$. This solution has a time complexity of $O(s+t+p^2)$.

2.4. Distinguished Nodes

We do not really need the values of $f(i,j)$, which we calculated in the quadratic solution, for all pairs $(i,j)$, but only for one such pair $(i_k,j_k)$ for each k (i.e., each possible position where t can be inserted into s), which is only $O\left(s\right)$ values and not all $O\left(p^2\right)$. We will show how to compute those values of the function f that we really need, without computing all the others.

Let us traverse the tree $T_{\mathsf{P}}$ from the bottom up (from leaves towards the root) and compute the sizes of the subtrees; whenever we encounter a node u with its subtree (let us call it $T_u$; it consists of u and all its descendants) of size at least $\sqrt{p}$ nodes, we mark u as a distinguished node and cut off the subtree $T_u$. Cutting it off means we will not count the nodes in it when we consider subtrees of u’s ancestors higher up in the tree. When we finally obtain to the root, we mark it as well, regardless of how many nodes are still left in the tree at that time. Algorithm 5 calculates, for each node u, its nearest marked ancestor $M\left[u\right]$; if u itself is marked, then $M\left[u\right]=u$.

Now we have at most $\sqrt{p}$ marked nodes (because every time we marked a node, we also cut off least $\sqrt{p}$ nodes from the tree, and the number of all nodes is $\left|p\right|$); and each node is less than $\sqrt{p}$ steps away from its nearest marked ancestor (if it were $\sqrt{p}$ or more steps away, some lower-lying ancestor of this node would have a subtree with at least $\sqrt{p}$ nodes, and would therefore get marked and its subtree cut off).

Algorithm 5 Marking distinguished nodes

procedure Mark(u):    (*Variable N counts the number of nodes in $T_u$ reachable through unmarked descendants.*)    $N:=1$;    for every child v of node u:       $N:=N+$ Mark(v);    if $N\ge \sqrt{p}$ or $u=0$    then M[u]: = u $;\mathbf{return}0$;     (*Mark u.*)    else M[u]: = −1; return N;   (*Unmarked u.*)

main call:    Mark(0);   (*Start at the root—node 0.*)    (*Pass the information about the nearest marked ancestor down the tree to all unmarked nodes.       (from parents to children)*)    for u: = 1 to |p| − 1 do       if M[u] < 0 then M[u]: = M[Pp[u]];

We know that $f(i,|p\left|\right)=0$ for every i. For each marked i, we can compute all values of $f(i,j)$ for $1\le j<\left|p\right|$ from $f(i,|p\left|\right)$; since there are at most $\sqrt{p}$ marked nodes, this takes $O\left(p\sqrt{p}\right)$ time. Let us describe how we can answer each of the $O\left(s\right)$ queries $(i_k,j_k)$ that we are interested in. The nearest marked ancestor of node $i_k$ is $M\left[i_k\right]$; since it is marked, we already know $f(M\left[i_k\right],j)$ for all j, i.e., also for $j=j_k$, and since $i_k$ lies in the tree $T_{\mathsf{P}}$ at most $O\left(\sqrt{p}\right)$ steps below node $M\left[i_k\right]$, we can calculate $f(i_k,j_k)$ from $f(M\left[i_k\right],j_k)$ in at most $O\left(\sqrt{p}\right)$ steps. Since we have to do this for each query, it takes overall $O\left(s\sqrt{p}\right)$ time. To save space, we can solve queries in groups according to $M\left[i_k\right]$; after we process all queries that share the same node $M\left[i_k\right]$, we can forget the results $f(M\left[i_k\right],j)$. Algorithm 6 presents the pseudocode of this approach to counting the occurrences of type (V).

Algorithm 6 Rearranging queries

(*Group queries $(i_k,j_k)$ based on the nearest marked ancestor.*) for $u:=0$ to $\left|p\right|-1$ do    if $M\left[u\right]=u$ then $L\left[u\right]:=$ empty list; for $k:=1$ to $\left|s\right|-1$ do add k to $L\left[M\left[i_k\right]\right]$; (*Process marked nodes u.*) for $u:=0$ to $\left|p\right|-1$ do if $M\left[u\right]=u$:    (*Compute $f(u,j)$ for all j as $F\left[j\right]$.*)    $F\left[\right|p\left|\right]:=0$;    for $j:=\left|p\right|-1$ downto 1 do       in $F\left[j\right]$ store $f(u,j)$ that is computed from $f(u,{\mathsf{S}}_p\left[j\right])$, which is stored in $F\left[{\mathsf{S}}_p\left[j\right]\right]$;    (*Answer queries $(i_k,j_k)$, where u is the nearest marked ancestor of $i_k$.*)    for each k in $L\left[u\right]$:       (*Prepare the path in the tree from $i_k$ to its ancestor u.*)       $S:=$ empty stack; $i:=i_k$;       while $i\ne u$: push i to S and assign $i:={\mathsf{P}}_p\left[i\right]$;       (*Compute $f(i,j_k)$ for all nodes i on the path from u to $i_k$.*)       $r:=F\left[j_k\right]$; (*i.e., $f(u,j_k)$*)       while S not empty:          $i:=$ node popped from S;          from $f({\mathsf{P}}_p\left[i\right],j_k)$, currently stored in r, compute $f(i,j_k)$ and store it in r;       (*r is now equal to $f(i_k,j_k)$, i.e., the answer to query k, which is the number of occurrences of         p in $s[:k]t s[k:]$ that start within $s[:k]$ and end within $s[k:]$.*)

Everything we did to count the occurrences of types (I) to (IV) had a linear time complexity in terms of the length of the input strings, so the overall time complexity of this solution is $O(t+(p+s)\sqrt{p})$ with an $O(s+t+p)$ space complexity. (Note that this time complexity can be worse than the quadratic solution in cases where $\left|s\right|\gg \left|p\right|\sqrt{p}$.)

2.5. Geometric Interpretation

We want to count those occurrences of p in $p[:i] t p[j:]$ that start within $p[:i]$ and end within $p[j:]$ (Figure 1). Such an occurrence is therefore of the form $p=p[:\mathsf{\ell }] t p[\mathsf{\ell }+|t|:]$, where $0<\mathsf{\ell }\le i$, $j\le \mathsf{\ell }+\left|t\right|<\left|p\right|$, and the following three conditions apply: (a) $p[:\mathsf{\ell }]$ must be a suffix of $p[:i]$, (b) $p[\mathsf{\ell }+|t|:]$ must be a prefix of $p[j:]$, and (c) t must appear in p as a substring starting at index ℓ, i.e., $t=p[\mathsf{\ell }:\mathsf{\ell }+|t\left|\right]$.

Figure 1. The alignment of string p as an occurrence in $p[:i] t p[j:]$.

To check (c), we prepare the table ${\mathsf{O}}_{pt}$ in advance and check whether ${\mathsf{O}}_{pt}\left[\mathsf{\ell }\right]=1$.

Let us now consider the condition (a), i.e., that $p[:\mathsf{\ell }]$ must be a suffix of $p[:i]$. We know that the longest prefix of p that is also a suffix of $p[:i]$ is ${\mathsf{P}}_p\left[i\right]$ characters long; the second longest is ${\mathsf{P}}_p\left[{\mathsf{P}}_p\left[i\right]\right]$ characters long, and so on. The condition that $p[:\mathsf{\ell }]$ must be a suffix of $p[:i]$ essentially asks whether ℓ occurs somewhere in the sequence $i,{\mathsf{P}}_p\left[i\right],{\mathsf{P}}_p\left[{\mathsf{P}}_p\left[i\right]\right],\dots$. This is equivalent to asking whether ℓ is an ancestor of i in the tree $T_{\mathsf{P}}$, which, as we have already seen, can be checked with the condition ${\sigma }_{\mathsf{P}}\left[\mathsf{\ell }\right]\le {\sigma }_{\mathsf{P}}\left[i\right]\le {\tau }_{\mathsf{P}}\left[\mathsf{\ell }\right]$.

Similar reasoning holds for condition (b), i.e., that $p[\mathsf{\ell }+|t|:]$ must be a prefix of $p[j:]$, except that now instead of the table ${\mathsf{P}}_p$ and the tree $T_{\mathsf{P}}$ we use the table ${\mathsf{S}}_p$ and the tree $T_{\mathsf{S}}$. The condition (b) asks whether $\mathsf{\ell }+\left|t\right|$ is an ancestor of j in the tree $T_{\mathsf{S}}$, which can be checked with ${\sigma }_{\mathsf{S}}[\mathsf{\ell }+|t\left|\right]\le {\sigma }_{\mathsf{S}}\left[j\right]\le {\tau }_{\mathsf{S}}[\mathsf{\ell }+|t\left|\right]$.

The two inequalities we have thus obtained,

$${\sigma }_{\mathsf{P}}\left[\mathsf{\ell }\right]\le {\sigma }_{\mathsf{P}}\left[i\right]\le {\tau }_{\mathsf{P}}\left[\mathsf{\ell }\right]\mathrm{and}{\sigma }_{\mathsf{S}}[\mathsf{\ell }+|t\left|\right]\le {\sigma }_{\mathsf{S}}\left[j\right]\le {\tau }_{\mathsf{S}}[\mathsf{\ell }+|t\left|\right],$$

have a geometric interpretation which will prove useful: if we think of ${\sigma }_{\mathsf{P}}\left[i\right]$ and ${\sigma }_{\mathsf{S}}\left[j\right]$ as the x- and y-coordinates, respectively, of a point on the two-dimensional plane, then the two inequalities require the x-coordinate to lie on a certain range and the y-coordinate to lie within a certain other range; in other words, the point must lie within a certain rectangle.

Recall that i and j depend on the position k where the string t has been inserted into s; therefore, to avoid confusion, we will now denote them by $i_k$ and $j_k$. We will refer to the point from the previous paragraph as $Q_k:=({\sigma }_{\mathsf{P}}\left[i_k\right],{\sigma }_{\mathsf{S}}\left[j_k\right])$, and to the rectangle as $R_{\mathsf{\ell }}:=[{\sigma }_{\mathsf{P}}\left[\mathsf{\ell }\right],{\tau }_{\mathsf{P}}\left[\mathsf{\ell }\right]]\times [{\sigma }_{\mathsf{S}}[\mathsf{\ell }+|t\left|\right],{\tau }_{\mathsf{S}}[\mathsf{\ell }+|t\left|\right]]$. Thus, we now see that p occurs in $s[:k] t s[k:]$ such that the occurrence of t at position ℓ of p aligns with the occurrence of t at position k of $s[:k] t s[k:]$ if and only if $Q_k$ lies in $R_{\mathsf{\ell }}$. Actually we are not interested in whether a match occurs for a particular k and ℓ, but in how many occurrences there are for a particular k; in other words, for each k (from 1 to $\left|s\right|-1$) we want to know how many rectangles $R_{\mathsf{\ell }}$ contain the point $Q_k$. Here ℓ ranges over all positions where t appears as a substring in p (i.e., where $p[\mathsf{\ell }:\mathsf{\ell }+|t\left|\right]=t$ or, equivalently, ${\mathsf{O}}_{pt}\left[\mathsf{\ell }\right]=1$); by limiting ourselves to such ℓ, we also take care of condition (c). Thus, we have $O\left(s\right)$ points and $O\left(p\right)$ rectangles, and for each point we are interested in how many of the rectangles contain it.

We have thus reduced our string-searching problem to a geometrical problem, which turns out to be useful because the latter problem can be solved efficiently using a well-known computational geometry approach called a plane sweep [8]. Imagine moving a vertical line across the plane from left to right (x-coordinates—i.e., the values from the ${\sigma }_{\mathsf{P}}$ table—go from 1 to $\left|p\right|$) and let us maintain some data structure with information about which y-coordinate intervals are covered by those rectangles that are present at the current x-coordinate. When we reach the left edge of a rectangle during the plane sweep, we must insert it into this data structure, and when we reach its right edge, we remove it from the data structure. Because the y-coordinates (i.e., the values from the ${\sigma }_{\mathsf{S}}$ table) in our case also take values from 1 to $\left|p\right|$, a suitable data structure is, for example, the Fenwick tree [9]. Imagine a table h in which the element $h\left[y\right]$ stores the difference between the number of rectangles (from those present at the current x-coordinate) that have their lower edge at y, and those that have their upper edge at $y-1$. Then the sum ${\sum }_{z=0}^{y}h\left[y\right]$ is equal to the number of rectangles that (at the current x) cover the point $(x,y)$. The Fenwick tree allows us to compute such sums in $O(logp)$ time and also make updates of the tree with the same time complexity, when any of the values $h\left[y\right]$ changes. Algorithm 7 describes this plane sweep with pseudocode.

Algorithm 7 Plane sweep

let F be a Fenwick tree with all values $h\left[y\right]$ initialized to 0;    for $x:=1$ to $\left|p\right|$:       for every rectangle $R_{\mathsf{\ell }}=[x_1,x_2]\times [y_1,y_2]$ with the left edge at $x_1=x$:          increase $h\left[y_1\right]$ and decrease $h[y_2+1]$ in F by 1;       for every point $Q_k=(x_k,y_k)$ with $x_k=x$:          compute the sum $h\left[1\right]+\dots +h\left[y_k\right]$ in F, i.e., the number of occurrences of          p in $s[:k] t s[k:]$ that start within $s[:k]$ and end within $s[k:]$;       for every rectangle $R_{\mathsf{\ell }}=[x_1,x_2]\times [y_1,y_2]$ with the right edge at $x_2=x$:          decrease $h\left[y_1\right]$ and increase $h[y_2+1]$ in F by 1;

We have to prepare in advance, for every coordinate x, a list of rectangles that have their left edge at x, a list of rectangles that have right edge at x, and a list of points $Q_k$ with this x-coordinate. Preparing these lists takes $O(p+s)$ time; each operation on F takes $O(logp)$ time, and these operations are $O\left(p\right)$ insertions of rectangles, $O\left(p\right)$ deletions and $O\left(s\right)$ sum queries. If we add everything we have seen in dealing with types (I) to (IV) in Section 2.2, the total time complexity of our solution is $O(t+(p+s)logp)$. Instead of using the Fenwick tree, we could use the square root decomposition on the table h (where we divide the table h into approximately $\sqrt{p}$ blocks with $\sqrt{p}$ elements each and we maintain the sum of each block), but the time complexity would increase to $O(t+(p+s)\sqrt{p})$.

2.6. Linear-Time Solution

We will first review a recently published algorithm by Ganardi and Gawrychowski [10] (hereinafter: GG), which we can adapt for solving our problem with a linear time complexity. The algorithm we need is in ([10], Theorem 3.2); we will only need to adjust it a little so that it counts the occurrences of p instead of just checking whether any occurrence exists at all. Intuitively, this algorithm is based on the following observations: if a string of the form $utv$ (where $u=p[:i]$ is a prefix of p and $v=p[j:]$ is a suffix of p) contains an occurrence of p which begins within u and ends within v, this occurrence of p must have a sufficiently long overlap with at least one of the strings u, t and v. All these three strings are substrings of p, and if p overlaps heavily with one of its substrings, it necessarily follows that the overlapping part of the string must be periodic, and any additional occurrences of p in $utv$ can only be found by shifting p by an integer number of these periods. The number of occurrences can thus be calculated without having to deal with each occurrence individually. The details of this, however, are somewhat more complicated and we will present them in the rest of this section.

In the following, we will come across some basic concepts related to the periodicity of strings ([11], Chapter 8). We will say that the string x is periodic with a period of length d if $0<d<\left|x\right|$ and if $x\left[i\right]=x[i-d]$ for each i in the range $d\le i<\left|x\right|$; in other words, if $x[:-d]=x[d:]$, i.e., if some string of length $\left|x\right|-d$ is both a prefix and a suffix of x. The prefix $x[:d]$ is called a period of x; if there is no risk of confusion, we will also use the term period for its length d.

A string x can have periods of different lengths; we will refer to the shortest period of x as its base period. If some period of x is at most $\left|x\right|/2$ characters long, then its length is a multiple of the base period. (This can be proven by contradiction. Suppose this were not always true; consider any such x that has a base period y and also some longer period z, where $0<\left|y\right|<\left|z\right|\le \left|x\right|/2$ and for which $\left|z\right|$ is not a multiple of $\left|y\right|$. Then $\left|z\right|$ is of the form $k\left|y\right|+r$ for some $k\ge 1$ and some r from the range $0<r<\left|y\right|$. Define $y_1=y[:r]$ and $y_2=y[r:]$; thus $y=y_1{y}_2$ and $z=y^k{y}_1$. Let us look at the first $\left|y\right|+\left|z\right|=(k+1)\left|y\right|+r$ characters of the string x; since y is a period of x, this prefix has the form $y^{k+1}{y}_1=y^k{y}_1{y}_2{y}_1$; and since z is a period of x, this prefix has the form $zy=y^k{y}_1{y}_1{y}_2$; but it is the same prefix both times, so the last $\left|y\right|$ characters of this prefix must be the same: $y_2{y}_1=y_1{y}_2$. This means that if we concatenate several copies of the strings $y_1$ and $y_2$ together, it does not matter in what order we do it; so $y^{\mathsf{\ell }}={\left(y_1{y}_2\right)}^{\mathsf{\ell }}=y_1^{\mathsf{\ell }}{y}_2^{\mathsf{\ell }}$. Now consider $\mathsf{\ell }\ge \left|x\right|/|y_1|$; since x has a period y and $\left|x\right|\le |y^{\mathsf{\ell }}|$, x is a prefix of $y^{\mathsf{\ell }}=y_1^{\mathsf{\ell }}{y}_2^{\mathsf{\ell }}$, and since $\left|x\right|\le |y_1^{\mathsf{\ell }}|$, x is also a prefix of $y_1^{\mathsf{\ell }}$; therefore, x has a period $y_1$, which is in contradiction with the initial assumption that y is the base (i.e., shortest) period of x.)

It follows from the definition of periodicity that if y is both a prefix and a suffix of x (and if $0<\left|y\right|<\left|x\right|$), then x is periodic with a period of length $\left|x\right|-\left|y\right|$. (If, in addition, $\left|y\right|>\left|x\right|/2$ also holds, so that occurrences of the string y at the beginning and end of the string x overlap, y is also periodic with a period of this length.) This period $\left|x\right|-\left|y\right|$ is the shorter and the longer y is, so we obtain the base period at the longest y that is both a prefix and a suffix of the string x. If instead of x we consider only its prefix $x[:i]$, we know that the longest y that is both a prefix and a suffix of $x[:i]$ is ${\mathsf{P}}_x\left[i\right]$ characters long; therefore, $x[:i]$ has a base period $i-{\mathsf{P}}_x\left[i\right]$ (if ${\mathsf{P}}_x\left[i\right]=0$, this formula gives the base period i, which of course means that $x[:i]$ is not periodic at all.

Let lcp$(i,j)$ be the length of the longest common prefix of $p[i:]$ and $p[j:]$, i.e., of two suffixes of p. We can compute this in $O\left(1\right)$ time if we have preprocessed the string p to build its suffix tree and some auxiliary tables (in $O\left(p\right)$ time). Each suffix of p corresponds to a node in its suffix tree; the longest common prefix of two suffixes is obtained by finding the lowest common ancestor of the corresponding nodes, which is a classic problem and can be answered in constant time with linear preprocessing time [12,13]. To build a suffix tree in linear time, one can use, for example, Ukkonen’s algorithm [14], or first construct a suffix array (e.g., using the DC3 algorithm of Kärkkäinen et al. [15,16]) and its corresponding longest-common-prefix array [17], and then use these two arrays to construct the suffix tree (this latter approach is what we used in our implementation). We can similarly compute the longest common suffix of two prefixes of p, which will be useful later.

Suppose that x and y are two substrings of p, e.g., $x=p[i_x:i_x+|x\left|\right]$ and $y=p[i_y:i_y+|y\left|\right]$, and that we would like to check whether x appears as a substring in y starting at position k; then (provided that $k+\left|x\right|\le \left|y\right|$) we only need to check whether lcp$(i_x,i_y+k)\ge \left|x\right|$; if that is true, x really appears there ($x=y[k:k+|x\left|\right]$), otherwise the value of the function lcp tells us after how many characters the first mismatch occurs. We can further generalize this: if $x,u,t,v$ are substrings of p and we are interested in whether x appears as a substring in $utv$ starting at position k, we need to perform at most three calls to the lcp function: first, for the part where x overlaps with u; if no mismatch is observed there, we check the area where x overlaps with t; if everything matches there too, we check the area where x overlaps with v.

Let us begin with a rough outline of the GG algorithm (Algorithm 8). Recall that we would like to solve $\left|s\right|-1$ problems of the form “how many occurrences of p are there in the string $utv$ that start within u and end in v?”, where u is some prefix of p, and v is some suffix of p. (To be more precise: for each position k from the range $0<k<\left|s\right|$ we are interested in occurrences of p in the string $s[:k] t s[k:]$, where, as we have seen, we can limit ourselves to the string $p[:i_k] t p[j_k:]$ with $i_k={\mathsf{P}}_{sp}\left[k\right]$ and $j_k={\mathsf{S}}_{sp}\left[k\right]$.) Assume, of course, that $\left|p\right|\ge \left|t\right|+2$ and that t appears at least once as a substring in p (which can be checked with the table ${\mathsf{O}}_{pt}$), because otherwise the occurrences we are looking for cannot exist at all. Since the strings p and t are the same in all our queries, we will list only u and v as the arguments of the GG function. Regarding the loop 1–3, we note that it will have to be executed at most twice, since u starts as a prefix of p, i.e., it is shorter than $\left|p\right|$; it is at least halved in each iteration of the loop, therefore it will be shorter than $\left|p\right|/4$ after at most two halvings. In step 2, we rely on the fact that the occurrences of p we are looking for overlap significantly with u (by at least one half of the latter); we will look at the details in Section 2.6.1. In step 3, we want to discover for some substring of p (namely the right half of the current u, which was a prefix of p) how long is the longest suffix of this substring that is also a prefix of p; we do not know how to do this in $O\left(1\right)$ time, but we can solve $O\left(s\right)$ such problems as a batch in $O(s+p)$ time, which is good enough for our purposes, since we know that we will have to execute the GG algorithm for $O\left(s\right)$ pairs $(u,v)$. (For details of this step, see Section 2.6.3.) Steps 4–6 are just a mirror image of steps 1–3 and the same considerations apply to them; that loop also makes at most two iterations. (Furthermore, note that steps 3 and 6 ensure that no occurrence of p is counted more than once: for example, those counted in step 2 all start within the left half of u, and this is immediately cut off in step 3, so these occurrences do not appear again, e.g., in step 5). In step 7, we then know that u and v are shorter than $\left|p\right|/4$; if $utv$ is longer than p, then t must be at least $\left|p\right|/2$ characters long and we can make use of this when counting occurrences of p in $utv$; we will look at the details in Section 2.6.2. As we will see, steps 2 and 7 each take $O\left(1\right)$ time; the GG algorithm can therefore be executed $O\left(s\right)$ times in $O(s+p)$ time, and $O(s+t+p)$ time is spent on preprocessing the data, so we have a solution with a linear time complexity.

Algorithm 8 Adjustment of the GG algorithm

algorithm GG(u, v): input: two strings, u (a prefix of p) and v (a suffix of p); output: the number of occurrences of p in $utv$ that start               within u and end within v; 1    while $\left|u\right|\ge \left|p\right|/4$: 2       count occurrences of p in $utv$ that start within the left half of u         (at positions $\iota \le \left|u\right|/2$) and end within v; 3       $u:=$ the longest suffix of the current u that is               shorter than $\left|u\right|/2$ and is also a prefix of p; 4    while $\left|v\right|\ge \left|p\right|/4$: 5       count occurrences of p in $utv$ that start within u and end within the right half of v         (at most $\left|v\right|/2$ characters before the end of v); 6       $v:=$ the longest prefix of the current v that is               shorter than $\left|v\right|/2$ and is also a suffix of p; 7    count all occurrences of p in the current string $utv$;

2.6.1. Counting Early and Late Occurrences

Let us now consider step 2 of Algorithm 8 in more detail. The main idea will be as follows: we will find the base period of the string u; calculate how far this period extends from the beginning of strings $utv$ and p; and discuss various cases of alignment with respect to the lengths of these periodic parts.

We are, then, interested in occurrences of p in $utv$ that begin at some position $\iota \le \left|u\right|/2$. Since u is also a prefix of p, the occurrence of u at the beginning of p overlaps by at least one half with that at the beginning of $utv$ (Figure 2). So u’s suffix of length $\left|u\right|-\iota$ is also its prefix; therefore, u has a period of length $\iota$; and since the length of this period is at most $\left|u\right|/2$, it must be a multiple of the base period. Let us denote the base period by d (represented by the arcs under the strings in Figure 2); recall that it can be computed as $\left|u\right|-{\mathsf{P}}_p\left[\right|u\left|\right]$. We need to consider only positions of the form $\iota =\alpha d$ for integer $\alpha$; the lower bound for $\alpha$ is obtained from the conditions $\iota \ge 0$ and $\iota +\left|p\right|>\left|ut\right|$ (so that the occurrence of p ends within v and not sooner), and the upper bound from the conditions $\iota \le \left|u\right|/2$ (so that the occurrence of p begins within the first half of u) and $\iota +\left|p\right|\le \left|utv\right|$ (so that the occurrence of p does not extend beyond the end of $utv$). Let us call these bounds ${\alpha }_{\min }$ and ${\alpha }_{\max }$. If ${\alpha }_{\min }>{\alpha }_{\max }$, we can immediately conclude that no appropriate occurrence of p exists.

Figure 2. The periodicity of u when p occurs in the first half.

The string u is a prefix of p and has a base period d; perhaps there exists a longer prefix of p with this period; let $p[:\kappa ]$ be the longest such prefix. We obtain it by finding the longest common prefix of the strings p and $p[d:]$, i.e., $\kappa =d +$ lcp(0,d). Let $\lambda$ be the length of the longest common prefix of the strings $p[:\kappa ]$ and $\left(utv\right)[{\alpha }_{\max }d:]$ (in other words, we are interested in whether $p[:\kappa ]$ appears in $utv$ starting at ${\alpha }_{\max }d$; we already know that there is certainly no mismatch with u, so at most two calls of lcp are enough to check whether everything matches with t and v or find where the first mismatch occurs). Then we know that the string $\left(utv\right)[:{\alpha }_{\max }d+\lambda ]$ is periodic with the same period of length d as $p[:\kappa ]$ and u. An example is shown in Figure 3.

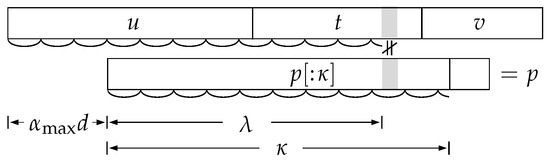
Figure 3. The reach of the base period d at the beginnings of the sequences $utv$ and p.

(1) If $\lambda =\kappa =\left|p\right|$, we have found a suitable occurrence of p, and since $utv$ has a period of d until the end of this occurrence, this means that if we were now to shift p in steps of d characters to the left and then compare it with the same part of $utv$, we would see exactly the same substring in $utv$ after each such shift as before, i.e., we would also find occurrences of p in all these places. In this case, all $\alpha$ from ${\alpha }_{\min }$ to ${\alpha }_{\max }$ are suitable, so we have found ${\alpha }_{\max }-{\alpha }_{\min }+1$ occurrences.

(2) If $\lambda =\kappa <\left|p\right|$, we have found an occurrence of $p[:\kappa ]$ in $utv$ starting at ${\alpha }_{\max }d$. This occurrence of $p[:\kappa ]$ may or may not continue into an occurrence of the entire p; this can be checked with at most two more calls of lcp. As for possible occurrences further to the left, i.e., starting at $\alpha d$ for some $\alpha <{\alpha }_{\max }$: in such an occurrence, $p\left[\kappa \right]$ should match with the character $\left(utv\right)[\alpha d+\kappa ]$, which is still in the periodic part of $utv$ ($\alpha d+\kappa <{\alpha }_{\max }d+\lambda$), i.e., it is equal to the character d places further to the left, which in turn must be equal to the character $p[\kappa -d]$. So $p\left[\kappa \right]$ and $p[\kappa -d]$ should be the same, but they certainly are not, because then the periodic prefix of p (with period d) would be at least $\kappa +1$ characters long, not just $\kappa$ characters. Thus, we see that for $\alpha <{\alpha }_{\max }$ there is definitely a mismatch and p does not occur there.

(3) If $\lambda <\kappa$, we have a mismatch between $p\left[\lambda \right]$ and $\left(utv\right)[{\alpha }_{\max }d+\lambda ]$. We did not find an occurrence of p at ${\alpha }_{\max }d$, but what about $\alpha d$ for smaller values of $\alpha$? If we now move p left in steps of d, the same character of the string $utv$ will have to match $p[\lambda +d]$, $p[\lambda +2d]$, and so on. As long as these indices are smaller than $\kappa$, all these characters are equal to the character $p\left[\lambda \right]$, since this part of p is periodic with period d; therefore, a mismatch will occur for them as well. In general, if p starts at $\alpha d$, the character $\left(utv\right)[{\alpha }_{\max }d+\lambda ]$ will have to match $p[({\alpha }_{\max }-\alpha )d+\lambda ]$; a necessary condition to avoid the aforementioned mismatch is therefore $({\alpha }_{\max }-\alpha )d+\lambda \ge \kappa$ or $\alpha \le {\alpha }_{\max }-\lceil (\kappa -\lambda )/d\rceil$. Thus, we have obtained a new, tighter upper bound for $\alpha$, which we will call ${\alpha }_{\max }^{\prime }$. For $\alpha \le {\alpha }_{\max }^{\prime }$, the string $p[:\kappa ]$ lies entirely within the periodic part of the string $utv$, i.e., within $\left(utv\right)[:{\alpha }_{\max }d+\lambda ]$.

(3.1) If ${\alpha }_{\max }^{\prime }<{\alpha }_{\min }$, we know that there is no possible $\alpha$ and we will not find an occurrence of p here.

(3.2) Otherwise, if $\kappa =\left|p\right|$, we see that for $\alpha \le {\alpha }_{\max }^{\prime }$, the string p (if it starts at position $\alpha d$ in $utv$) lies entirely within the periodic part of $utv$; since $\kappa =\left|p\right|$ means that p is itself entirely periodic with the same period of length d, we can conclude that, for each $\alpha$ (from ${\alpha }_{\min }$ to ${\alpha }_{\max }^{\prime }$), p matches completely with the corresponding part of $utv$; thus there are ${\alpha }_{\max }^{\prime }-{\alpha }_{\min }+1$ occurrences.

(3.3) However, if $\kappa <\left|p\right|$, we can reason very similarly as in case (2). At $\alpha ={\alpha }_{\max }^{\prime }$ we have an occurrence of $p[:\kappa ]$, which may or may not be extended to an occurrence of the whole p; we check this with at most two calls of lcp. At $\alpha ={\alpha }_{\max }^{\prime }$ the string $p[:\kappa ]$ lies entirely within the periodic part of the string $utv$; if we then decrease $\alpha$ and thus shift p to the left by d or a multiple of d characters, then $p\left[\kappa \right]$ will certainly also fall within the periodic part of the string $utv$. In order for the entire p to occur at such a position, among other things, $p\left[\kappa \right]$ and $p[\kappa -d]$ would have to match with the corresponding characters of the string $utv$, but since these two characters are both in the periodic part of the string $utv$, they are equal, while the characters $p\left[\kappa \right]$ and $p[\kappa -d]$ are not equal (because $p[:\kappa ]$ is the longest prefix of p with period d); therefore, a mismatch will definitely occur for every $\alpha <{\alpha }_{\max }^{\prime }$ and p does not appear there. Step 2 of the GG algorithm can therefore be summarized by Algorithm 9.

Algorithm 9 Occurrences of p in $utv$ that start within the left half of u and end within v.

${\alpha }_{\min }:=\max \{0,1+\lfloor (\left|u\right|+\left|t\right|-\left|p\right|)/d\rfloor \}$;    ${\alpha }_{\max }:=\lfloor \min \left\{\right|u|/2,|utv|-|p\left|\right\}/d\rfloor$;    if ${\alpha }_{\max }<{\alpha }_{\min }$ then return 0;    $\kappa :=$ length of the longest prefix of p with a period d;    $\lambda :=$ length of the longest common prefix of $p[:\kappa ]$ and $\left(utv\right)[{\alpha }_{\max }d:]$;    if $\lambda =\kappa$:       if $\kappa =\left|p\right|$ then return ${\alpha }_{\max }-{\alpha }_{\min }+1$       else if p is a prefix of $\left(utv\right)[{\alpha }_{\max }d:]$ then return 1       else return 0;    else:       ${\alpha }_{\max }^{\prime }:={\alpha }_{\max }-\lceil (\kappa -\lambda )/d\rceil$;       if ${\alpha }_{\max }^{\prime }<{\alpha }_{\min }$ then return 0       else if $\kappa =\left|p\right|$ then return ${\alpha }_{\max }^{\prime }-{\alpha }_{\min }+1$       else if p is a prefix of $\left(utv\right)[{\alpha }_{\max }^{\prime }d:]$ then return 1       else return 0;

2.6.2. Counting the Remaining Occurrences

Now let us consider step 7 of Algorithm 8. At that point in the GG algorithm, we have already truncated u and v so that they are shorter than $\left|p\right|/4$. If $\left|u\right|=0$ or $\left|v\right|=0$ or $\left|utv\right|<\left|p\right|$, we can immediately conclude that there are no relevant occurrences of p. We can assume that $\left|t\right|>\left|p\right|/2$, as otherwise the string $utv$ would certainly be shorter than $\left|p\right|$.

We are interested in such occurrences of p in $utv$ that start within u and end within v; such an occurrence also covers the entire t in the middle. Candidates for a suitable occurrence of p in $utv$ are therefore present only where t appears in p (more precisely: the fact that t occurs in p starting at ℓ is a necessary condition for p to appear in $utv$ starting at $\left|u\right|-\mathsf{\ell }$). We compute in advance (using the table ${\mathsf{O}}_{pt}$) the index of the first and (if it exists) second occurrence of t as a substring in p; let us call them ${\mathsf{\ell }}_1$ and ${\mathsf{\ell }}_2$. If there was just one occurrence of t in p, then there is also just one candidate for the occurrence of p in $utv$ and with two more calls of lcp we can check whether p really occurs there (i.e., whether $p[:{\mathsf{\ell }}_1]$ is a suffix of u and $p[{\mathsf{\ell }}_1+|t|:]$ is a prefix of v).

Now suppose that there are at least two occurrences of t in p. Let us consider some occurrence of p in $utv$ (of course one that starts within u and ends within v); the string t in $utv$ matches one of the occurrences of t in p; let ℓ be the position where this occurrence of t in p begins (Figure 4). There are at most $\left|u\right|$ characters to the left of this occurrence of t in p (otherwise p would already extend beyond the left edge of $utv$), and there are at most $\left|v\right|$ characters to the right of it (otherwise p would extend beyond the right edge of $utv$). Therefore, no other occurrence of t in p can begin more than $\left|u\right|$ characters to the left of ℓ or more than $\left|v\right|$ characters to the right of ℓ. If another occurrence of t in p begins at position ${\mathsf{\ell }}^{\prime }$, then $|\mathsf{\ell }-{\mathsf{\ell }}^{\prime }|\le max\{\left|u\right|,\left|v\right|\}<|p|/4$.

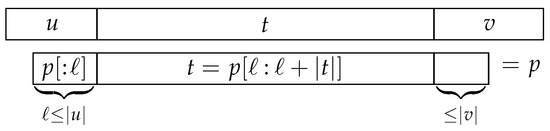
Figure 4. The alignment of string t with string p at an occurrence of p in $utv$.

Since no occurrence of t in p is very far from ℓ, it follows that the first two occurrences of t in p (i.e., those at ${\mathsf{\ell }}_1$ and ${\mathsf{\ell }}_2$) cannot be very far from each other. We can verify this as follows: (1) if the occurrence of t in p at ℓ was exactly the first occurrence of t in p (i.e., if $\mathsf{\ell }={\mathsf{\ell }}_1$), it follows that ${\mathsf{\ell }}_2$ is greater than $\mathsf{\ell }={\mathsf{\ell }}_1$ by at most $\left|v\right|$, so ${\mathsf{\ell }}_2-{\mathsf{\ell }}_1\le \left|v\right|<\left|p\right|/4$; (2) if the occurrence of t in p at ℓ was not the first occurrence of t in p, but the second or some later one (that is, if $\mathsf{\ell }\ge {\mathsf{\ell }}_2$), it follows that ${\mathsf{\ell }}_1$ and ${\mathsf{\ell }}_2$ are both less than or equal to ℓ, but by at most $\left|u\right|$, so again ${\mathsf{\ell }}_2-{\mathsf{\ell }}_1\le \left|u\right|<\left|p\right|/4$.

We see that if p occurs in $utv$ (starting within u and ending within v), the first two occurrences of t in p are less than $\left|p\right|/4$ apart. So, we can start by computing $d:={\mathsf{\ell }}_2-{\mathsf{\ell }}_1$ and if $d\ge \left|p\right|/4$, we can immediately conclude that we will not find, in $utv$, any occurrences of p that start within u and end within v.

Otherwise, we know henceforth that $d<\left|p\right|/4<\left|t\right|/2$, so the first two occurrences of t in p overlap by more than half; the overlapping part is, therefore, both a prefix and a suffix of t, say $t=t_1{t}_2=t_2{t}_3$ for $|t_1|=|t_3|=d$ and $|t_2|>|t|/2$; so t is periodic with a period of length $d<\left|t\right|/2$. Now suppose that t has some shorter period $d^{\prime }$. If $0\le \iota <\left|t\right|-d^{\prime }$, the characters $p[{\mathsf{\ell }}_1+\iota ]$ and $p[{\mathsf{\ell }}_1+d^{\prime }+\iota ]$ both lie in the first occurrence of t in p, so they are equal since t has period $d^{\prime }$; if $\left|t\right|-d^{\prime }\le \iota <\left|t\right|$, then both of these characters lie in the second occurrence of t in p and are therefore equal. Since this is true for all $0\le \iota <\left|t\right|$, we have found another intermediate occurrence of t in p starting at ${\mathsf{\ell }}_1+d^{\prime }$, which contradicts the assumption that the second occurrence is the one at ${\mathsf{\ell }}_2$. Thus, d is the shortest period of t.

Consider the first occurrence of t in p, the one starting at ${\mathsf{\ell }}_1$, and see how far left and right of it we could extend t’s period of length d; that is, we need to compute the longest common suffix of the strings $p[:{\mathsf{\ell }}_1]$ and $p[:{\mathsf{\ell }}_1+d]$, and the longest common prefix of the strings $p[{\mathsf{\ell }}_1+|t|-d:]$ and $p[{\mathsf{\ell }}_1+|t|:]$. Now we can imagine p partitioned into $p=p_1{p}_2{p}_3$, where $p_2$ is the maximal substring that contains that occurrence of t and has a period d.

Similarly, in $utv$, let us see how far into u and v the middle part of t could be extended while maintaining periodicity with period d. This requires some caution: t starts with the beginning of the period, so when we extend the middle part from the right end of u leftwards, we must expect the end of the period at the right end of u. So we must compute the longest common suffix of u and something that ends with the end of t’s period, which is not necessarily t itself because its length is not necessarily a multiple of the period length. A similar consideration applies to extending the middle part from the left end of v rightwards. Let $\tau :=\left|t\right|-\left(\right|t|modd)$ be the length of what remains of t if we restrict ourselves only to periods that occur in their entirety. Since $d<\left|t\right|/2$, it follows that $\tau >\left|t\right|/2$, so $\tau$ is longer than $\left|u\right|$ and $\left|v\right|$. If we now find the longest common suffix of the strings u and $t[:\tau ]$ and the longest common prefix of the strings v and $t[-\tau :]$, we will receive what we are looking for, and we do not have to worry about running out of t before u or v. From now on, let us imagine $utv$ in the form $u_1{u}_{2}t{v}_1{v}_2$, where $u_{2}t{v}_1$ is periodic with a period of length d. Figure 5 shows the resulting partition of the strings $utv$ and p.

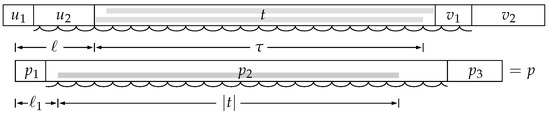
Figure 5. Partition of the strings according to the range of the period of the string t. In t above, $t[:\tau ]$ and $t[-\tau :]$ are marked in gray, which are useful in determining $u_2$ and $v_1$. In the string $p_2$ below, the first occurrence of t in p (starting at ${\mathsf{\ell }}_1$), from which $p_2$ actually grew, is marked in darker gray.

We know that if p appears in $utv$, then the t in $utv$ matches some occurrence of t in p, say the one at ℓ (see Figure 5); if this is not precisely the first occurrence (the one at ${\mathsf{\ell }}_1$), then the first one can start at most $\left|u\right|<\left|t\right|/2$ characters further to the left (otherwise p would extend over the left edge of $utv$ there); both occurrences of t in p (at ${\mathsf{\ell }}_1$ and ℓ) overlap by more than half, so t is periodic with a period of length $\mathsf{\ell }-{\mathsf{\ell }}_1$; this is less than $\left|t\right|/2$, so this period is a multiple of the base period, i.e., d. Thus, we see that only those occurrences of t in p that begin at positions of the form $\mathsf{\ell }={\mathsf{\ell }}_1+\alpha d$ for integer $\alpha$ are relevant.

Furthermore, since the occurrences of t in p at ℓ and at ${\mathsf{\ell }}_1$ overlap by more than half, this overlapping part is longer than d, i.e., the base period of t. In p, the content of this overlapping part, since it lies within the first occurrence of t in p, continues with the period d to the left and right throughout $p_2$, but since this overlapping part also lies within the occurrence of t at ℓ, which matches with t in $utv$, the content of this overlapping part also continues in $utv$ (with the period d) to the left and right throughout $u_{2}t{v}_1$. If we look at what happens in $utv$ where we have the string $p_2$ in p, we see that if $p_2$ extended to the left of $u_2$, we would have a contradiction, because we chose $u_2$ in such a way that a period of length d cannot extend further than the left edge of $u_2$ (if we start from t in $utv$). For a similar reason, $p_2$ cannot extend to the right of $v_1$; it must therefore remain within $u_{2}t{v}_1$.

We said that t starts at $\mathsf{\ell }={\mathsf{\ell }}_1+\alpha d$ in p and matches with t in $utv$; so p starts at $\left|u\right|-\mathsf{\ell }$ in $utv$, and $p_2$ starts at $\left|u\right|-\mathsf{\ell }+|p_1|$ in $utv$. From the condition that $p_2$ must not extend to the left of $u_2$, we get $|u_1|\le |u|-\mathsf{\ell }+|p_1|$, and since it must not extend to the right of $v_1$, we get $\left|u\right|-\mathsf{\ell }+|p_1{p}_2|\le |ut{v}_1|$. In addition, we still expect that p starts within u, so $0\le \left|u\right|-\mathsf{\ell }<\left|u\right|$, and that it ends within v, so $\left|uv\right|<\left|u\right|-\mathsf{\ell }+\left|p\right|\le \left|uvt\right|$. From these inequalities, we can now determine the smallest and largest acceptable value of $\alpha$ (${\alpha }_{\min }$ and ${\alpha }_{\max }$).

If ${\alpha }_{\min }>{\alpha }_{\max }$, we can immediately conclude that there are no relevant occurrences of p. Otherwise, if $p_1$ and $p_3$ are empty strings, then $p=p_2$ and for every $\alpha$ (from ${\alpha }_{\min }$ to ${\alpha }_{\max }$) $p_2$ lies within $u_{2}t{v}_1$, so there are no mismatches; then we have ${\alpha }_{\max }-{\alpha }_{\min }+1$ occurrences.

If $p_3$ is not empty, we can check the case $\alpha ={\alpha }_{\min }$ separately (i.e., we check whether p appears in $utv$ starting at $\left|u\right|-{\mathsf{\ell }}_1-{\alpha }_{\min }d$; we need at most two calls of lcp). What about larger $\alpha$? If we go from ${\alpha }_{\min }$ to some larger $\alpha$, the string p moves by d or a multiple of d characters to the left relative to $utv$; this moves $p\left[\right|p_1{p}_2\left|\right]=p_3\left[0\right]$, (i.e., the first character of the string $p_3$) so far to the left that its corresponding character of $utv$ (with which the first character of the string $p_3$ will have to match if p is to occur at the current position in $utv$) belongs to the periodic part (i.e., $u_{2}t{v}_1$); in addition, recall that (if the new $\alpha$ is still valid at all, i.e., $\le {\alpha }_{\max }$) the string $p_2$ also overlaps with $u_{2}t{v}_1$ by more than one whole period, so the character $p\left[\right|p_1{p}_2|-d]=p_2\left[-d\right]$ is still in such a position that its corresponding character in $utv$ is in the periodic part of $u_{2}t{v}_1$; so here we have two characters in $u_{2}t{v}_1$ that are exactly d places apart, hence they are equal. The first character of $p_3$ cannot be equal to the character d places to the left of it, because otherwise the periodic part of p, i.e., $p_2$, could be expanded even further to the right and this character would not belong to $p_3$ but instead to $p_2$. We see that it is impossible that, in the new position of p, the character $p\left[\right|p_1{p}_2\left|\right]$ and the one d places to the left of it would match with the corresponding characters of $utv$; there will be a mismatch in at least one place, so p can not occur there. Thus, we do not need to consider the case $\alpha >{\alpha }_{\min }$ at all.

The remaining possibility is that $p_3$ is empty, but $p_1$ is not empty. An analogous analysis to the previous paragraph tells us that it is sufficient to check whether p occurs in $utv$ at $\alpha ={\alpha }_{\max }$, and we do not need to consider smaller values of $\alpha$. Thus, step 7 of the GG algorithm can be described with the pseudocode of Algorithm 10.

Algorithm 10 Occurrences of p in the shortened string $utv$.

${\mathsf{\ell }}_1,{\mathsf{\ell }}_2:=$ positions of the first two occurrences of t in p;    if there is only one occurrence then return 1 or 0,       depending on whether p occurs in $utv$ at position $\left|u\right|-{\mathsf{\ell }}_1$ or not;    $d:={\mathsf{\ell }}_2-{\mathsf{\ell }}_1$; if $d\ge \left|p\right|/4$ then return 0;    partition p into $p_1{p}_2{p}_3$, where $p_2$ is the maximal substring that       contains the first occurrence of t in p and has period d;    partition $utv$ into $u_1{u}_{2}t{v}_1{v}_2$, where $u_{2}t{v}_1$ is the maximal substring       containing t between u and v and has period d;    compute ${\alpha }_{\min }$ and ${\alpha }_{\max }$ from the aforementioned inequalities;    if ${\alpha }_{\min }>{\alpha }_{\max }$ then return 0    else if $p_3$ is nonempty then return 1 or 0,       depending on whether p appears in $utv$ at position $\left|u\right|-{\mathsf{\ell }}_1-{\alpha }_{\min }d$ or not    else if $p_1$ is nonempty then return 1 or 0,       depending on whether p appears in $utv$ at position $\left|u\right|-{\mathsf{\ell }}_1-{\alpha }_{\max }d$ or not    else return ${\alpha }_{\max }-{\alpha }_{\min }+1$;

All of these things can be prepared in advance (${\mathsf{\ell }}_1$, ${\mathsf{\ell }}_2$ using the table ${\mathsf{O}}_{pt}$) or computed in $O\left(1\right)$ time (with a small constant number of computations of the longest common prefix or suffix).

2.6.3. Finding the Next Candidate Prefix (or Suffix)

In this subsection we describe step 3 of Algorithm 8 in more detail. The purpose of that step is to answer, in $O(s+p)$ time, up to $\left|s\right|-1$ queries (one for each position k where the string t may be inserted into s) of the form “given a prefix u of p, find the longest suffix of u that is shorter than $\left|u\right|/2$ and is also a prefix of p”. We may describe such a query with a pair $(u_k,b_k)$, where $u_k=\left|u\right|$ is the length of the original prefix and $b_k=\lceil u_k/2\rceil -1$ is the maximum length of the new shorter prefix that we are looking for. Ganardi and Gawrychowski showed that this problem can be reduced to a weighted-ancestor problem in the suffix tree of $p^{\mathsf{R}}$ ([10], Lemma 2.2), for which they then provided a linear-time solution ([10], Section 4). However, this solution is quite complex and in the present subsection we will present a simpler alternative which avoids the need for weighted-ancestor queries.

The longest suffix of $p[:u_k]$ that is also a prefix of p has the length ${\mathsf{P}}_p\left[u_k\right]$, the second longest has the length ${\mathsf{P}}_p\left[{\mathsf{P}}_p\left[u_k\right]\right]$, and so on. We could examine this sequence until we reach an element that is $\le b_k$; that would be the answer to the query $(u_k,b_k)$. We can also imagine this procedure as climbing the tree $T_{\mathsf{P}}$ (first introduced in Section 2.3), starting from the node $u_k$ and proceeding upwards towards the root until we reach a node with the value $\le b_k$. However, we can save time by observing that several of these paths up the tree, for different queries, sometimes meet in the same node and thenceforth always move together.

If several paths reach some node v and do not end there (because the bounds $b_k$ of those queries are $<v$), all these paths will continue into v’s parent $w:={\mathsf{P}}_p\left[v\right]$ and will never separate again, regardless of where in v’s subtree they started. Thus, in a certain sense, we no longer need to distinguish between the nodes w, v, and v’s descendants, as the result of any query with $b_k<v$ is the same regardless of which of these nodes its path begins in. We can imagine these nodes as having merged into one, namely into v’s parent w.

To follow the paths up the tree, we will visit the nodes of the tree in decreasing order, from $\left|p\right|-1$ to 0. Upon reaching node v, we can answer all queries whose bound is exactly $b_k=v$, and then we can merge v with its parent, thereby taking into account the fact that all paths that reach v and do not end there will proceed to v’s parent. For every node w that has not yet been merged with its parent, we maintain a set of all nodes that have already been merged into w; at the start of the procedure, each node forms a singleton set by itself. The pseudocode of this approach is shown in Algorithm 11.

Algorithm 11 Answering a batch of queries $(u_k,b_k)$ in the KMP-tree $T_{\mathsf{P}}$.

1    $F:=\left\{\right\{0\},\{1\},\dots ,\{\left|p\right|-1\left\}\right\}$; 2    for $v:=\left|p\right|-1$ downto 0: 3       for each query $(u_k,b_k)$ having $b_k=v$: 4          the answer to this query is the smallest element of             that member of F which contains $u_k$; 5       merge, in F, the set containing v and the set containing ${\mathsf{P}}_p\left[v\right]$;

The following invariant holds at the start of each iteration of the main loop: F contains one set $A_w$ for each node $w\in \{0,1,\dots ,v\}$, and this set $A_w$ contains w as well as those children of w (in the tree $T_{\mathsf{P}}$) that are greater than v, and all the descendants of those children. In $T_{\mathsf{P}}$ each node has a smaller value than its children, therefore w is the smallest member of $A_w$. If some query has $u_k\in A_w$ and $b_k=v$, this means that $u_k$ is a descendant of w and that all the nodes on the path from $u_k$ to w, except w itself, are greater than v; therefore the path for this query will rise from $u_k$ to w and then stop; thus step 4 of our algorithm is correct in reporting w as the answer to this query. Step 5 ensures that the loop invariant is maintained into the next iteration. Step 3 requires us to sort the queries by $b_k$, which can be achieved in linear time using counting sort.

The time complexity of this algorithm depends on how we implement the union-find data structure F. The traditional implementation using a disjoint-set forest results in a time complexity of $O\left(\right(p+s\left)\alpha \right(p+s,p\left)\right)$ for Algorithm 11 [18], and hence $O(t+(p+s\left)\alpha \right(p+s,p\left)\right)$ for the solution of our problem as a whole. Here $\alpha$ is the inverse Ackermann function, which grows very slowly, making this solution almost linear. However, to obtain a truly linear solution, we can use the slightly more complex static tree set union data structure due to Gabow and Tarjan [19,20], which assumes that the elements are arranged in a tree and that the union operation is always performed between a set containing some node of the tree and the set containing its parent; hence this structure is perfectly suited to our needs. (A minor note to anyone intending to reimplement their approach: ([20], p. 212) uses the macrofind operation in step 7 of find, whereas ([19], p. 248) uses microfind; the latter is correct while the former can lead to an infinite loop. Moreover it may be useful to point out that $\mathit{macrofind}\left(x\right)$ must return, as the “name” of the macroset containing x, not an arbitrary member of that set, but the member which is closest to the root of the tree.) Algorithm 11 then runs in $O(p+s)$ time and our solution as a whole in $O(p+s+t)$ time.

3. Experimental Results and Discussion

We implemented the described solution in C++ as a working example of a solution with a linear time complexity. It is publicly available in an online repository (https://github.com/janezb/insertions, accessed on 16 June 2025). It is a self-contained solution with no external dependencies. Note that the implementation was not optimized for speed so there should be plenty of room for improvements if the actual running time is of importance. All the experiments presented in this section were carried out on a desktop computer with a 3.2 GHz i9-12900K CPU and 64 GB of main memory; the source code was compiled with clang 7.0.0 with all optimizations enabled (-O3).

In this section, we want to demonstrate the linearity of its time complexity and describe the behavior of the algorithm on different inputs that offers further insight into its design. Random data or actual text is unlikely to present an obstacle to any string counting approaches as mismatches occur quickly. This is shown in Table 1, which shows running times in seconds for a reasonably large choice of string lengths $\left|p\right|=200,000$, $\left|s\right|=300,000$, and $\left|t\right|=100,000$. The strings are either randomly generated, substrings (constructed in two ways, on which see the next two paragraphs) of a longer English text, fragments of DNA sequences or of C++ source code, or substrings of a periodic string with a base period of length d (for various values of d). We can see that periodic strings provide the largest obstacle as they force the algorithm to execute all steps. (Defining the strings in this way means that there will be approx. $O\left(\right|s|/d)$ positions k where t may be inserted into s without “disrupting” its period, and for every such k the string t in $s[:k] t s[k:]$ may align with any of the $O\left(\right(\left|p\right|-\left|t\right|)/d)$ occurrences of t in p. Recall that Algorithm 11 starts with u being the longest prefix of p that is a suffix of $s[:k]$; because of the periodicity of p and s, this string u will be at most d characters shorter than p (except if k is close to the beginning of s, but this exception is a small one provided that s is long relative to p), and d (being the length of the period) is small relative to $\left|p\right|$. Hence u is longer than $\left|p\right|/4$, and steps 1–3 of Algorithm 11 get executed. In step 3, after u is cut down by half, it needs to be reduced by no more than d characters in order to become a prefix of p again; hence the loop in steps 1–3 needs to be executed twice (which is the maximum possible amount). The same applies analogously to steps 4–6. Moreover, in step 7, since occurrences of t in p are so frequent (occurring every d characters), none of the checks in the first few lines of Algorithm 10 succeed in terminating it early, and so it has to be executed in full).

Table 1. Running times on various types of strings, with $\left|p\right|=200,000$, $\left|s\right|=300,000$, and $\left|t\right|=100,000$.

Description	Running Time [ms]
	Same Strings	Different Strings
Random binary strings	10.9 ± 0.3	12.2 ± 0.3
English text 1	6.3 ± 0.2	7.4 ± 0.3
English text 2	84.4 ± 3.0	79.9 ± 7.5
DNA sequences	89.8 ± 3.1	82.9 ± 7.0
C++ source code	87.2 ± 3.0	80.7 ± 7.3
Single-letter strings ($d=1$)	121.9 ± 2.0	118.7 ± 3.4
Periodic strings ($d=10$)	120.3 ± 3.7	118.0 ± 3.5
Periodic strings ($d=100$)	131.3 ± 4.4	126.6 ± 3.5
Periodic strings ($d=1000$)	137.5 ± 4.7	134.2 ± 4.3
Periodic strings ($d=4000$)	148.4 ± 3.9	144.6 ± 4.3
Periodic strings ($d=10,000$)	142.2 ± 5.3	140.5 ± 5.2

For “English text 1”, we extracted the letters (converted to lowercase) from an English-language document, resulting in a long string w; we then used the first $\left|s\right|$ characters of w to form the string s, the next $\left|t\right|$ characters to form t, and the next $\left|p\right|$ characters to form p. Since the strings are long, t is not a substring of p and running time is very short, similar to the case of purely random binary strings.

For “English text 2”, we selected p as a random substring (of length $\left|p\right|$) of $w[:|st\left|\right]$, then selected t as a random substring (of length $\left|t\right|$) of p; those parts of $w[:|st\left|\right]$ which did not end up in t were then used to form s. This ensures that t is a substring of p and p does occur (once) in one string of the form $s[:k] t s[k:]$, so that the GG algorithm does need to be executed; but that is the only value of k for which u and v are of nontrivial length; even there, however, they cannot both be longer than $\left|p\right|/4$ since p itself is only twice as long as t. Accordingly, only one of u and v is ever longer than $\left|p\right|/4$, so that only one of the loops 1–3 and 4–6 in Algorithm 8 needs to be executed and some running time is saved by not having to initialize the union-find data structure for the loop that does not need to be executed.

For the “DNA sequences” and “C++ source code” rows in the table, we generated the strings s, t, and p in the same way as for “English text 2”, except that the initial string w was obtained differently. For the DNA sequences, we used as w a DNA sequence of the yeast Saccharomyces cerevisiae (the sequence was obtained from The Saccharomyces Genome Database project (SGD—https://www.yeastgenome.org/, accessed on 18 June 2025) that hosts the data files of the S. cerevisiae strain S288C. More specifically, we used the sequence of chromosome 4 of the release R64-4-1 (http://sgd-archive.yeastgenome.org/sequence/S288C_reference/NCBI_genome_source/chr04.fsa, accessed on 18 June 2025) for C++ source code, and we obtained w by concatenating the files in the include directory of the C++ standard library as distributed with Microsoft Visual Studio. As expected, both of these kinds of strings behave similarly to the English text for the purposes of this experiment.

All reported time measurements in Table 1 are averages and standard deviations over 100 runs (the later experiments in the rest of this section will show averages over 10 runs). For the “same strings” column, the same triple of strings $(s,t,p)$ was used in all the runs, while for the “different strings” column a different triple was generated for each run, according to the rules of the corresponding row (for the “English text 1”, this means that the initial w from which s, t, and p are generated was obtained as a random substring of length $\left|s\right|+\left|t\right|+\left|p\right|$ from a longer sequence of English-language text). Comparing the results in the two columns shows that the measurements are fairly robust both with regard to repeating an experiment on the same test case as well as across different test cases (different triples of strings s, t, p) of the same type.

We will restrict the subsequent analysis to periodic strings with the length of period $d=10$ and further limit the lengths of the input to $\left|t\right|<\left|p\right|\le \left|s\right|+\left|t\right|$. The pattern p should be longer than the inserted string t so that its occurrences can also span the entire inserted string (otherwise Algorithm 8 never gets executed). The pattern p also should not exceed the total length of the string after insertion, i.e., $\left|s\right|+\left|t\right|$.

Figure 6 shows a comparison of the running times of the different solutions presented in this paper: the quadratic-time solution based on dynamic programming (Section 2.3); its $O\left(n\sqrt{n}\right)$ improvement based on distinguished nodes (Section 2.4); the $O(nlogn)$ “geometric” solution based on a plane sweep (Section 2.5); and lastly two variants of the solution based on Algorithm 8: the almost-linear solution where a disjoint-set forest is used in the implementation of Algorithm 11, and the truly linear solution where the static tree set union data structure is used instead.

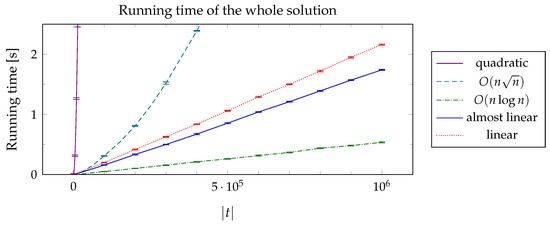
Figure 6. Comparison of the running times of different solutions, for $\left|p\right|=3\left|t\right|$ and $\left|s\right|=5\left|t\right|$.

As expected, the quadratic and the $O\left(n\sqrt{n}\right)$ solutions are the slowest, and their running time grows in accordance with their asymptotic time complexity. For the other three solutions, however, it turns out that their running time in practice is just the opposite of what one might expect given their asymptotical complexity: the $O(nlogn)$ solution is a clear winner in practice, being about three times faster than the almost-linear solution, which in turn is approx. $25\%$ faster than the truly linear solution; moreover, the $O(nlogn)$ solution is much easier to implement. This illustrates the importance, in practice, of the constant factors hidden inside the $O(·)$ notation. Extrapolating the curves from Figure 6 suggests that it would take strings of a quite intractable length, approximately ${10}^{24}$ characters, before the logarithmic factor in the running time of the plane-sweep solution would outweigh the advantage it currently enjoys due to its lower constant factor.

The plane-sweep solution also has the advantage of requiring substantially less memory than the linear solution; in our implementation, the plane-sweep solution required ≈170 bytes of memory per character of p, as compared to ≈390 bytes of the linear solution; and ≈45 bytes of memory per character of s, as compared to ≈176 of the linear solution (though admittedly this latter figure could be reduced to about 80 at the cost of a mild additional inconvenience in the implementation). On the whole, the linear solution consumed about 2.5 to 3 times as much memory as the plane-sweep solution; for example, solving a test case with $\left|t\right|=2·{10}^6$, $\left|p\right|=9·{10}^6$, and $\left|s\right|={10}^7$ required ≈1.83 GB of memory with the plane-sweep solution vs. ≈4.95 GB with the linear solution. Thus, dealing with the strings whose lengths are in the tens of millions is just barely feasible on a typical desktop computer, while lengths in the hundreds of millions would not be feasible.

In Figure 7, we compare the performance of the almost-linear solution (using a disjoint-set forest in Algorithm 11) with the truly linear solution (which uses the static tree set union data structure instead). We show the results for different sizes of the inserted string t, with the other two strings being proportionally longer: $\left|p\right|=3\left|t\right|$, $\left|s\right|=5\left|t\right|$. Both solutions exhibit linear behavior (as expected, considering that the non-linear term in the complexity of the almost-linear solution is the very slowly growing inverse Ackermann’s function) but the almost-linear solution turns out to be faster in practice: with the almost-linear instead of the linear implementation of union-find, Algorithm 11 runs approximately 2.8 times faster and the solution as a whole (of which Algorithm 11 is only a small part) runs approx. 25 % faster. Note that we did not optimize the implementation for speed as we are interested in its asymptotic properties, therefore this comparison might not reflect the true potential of each method (for example, Gabow and Tarjan ([19], p. 249) reported that in some of their experiments, the running time of their static tree set union data structure was only 0.6–0.7 times as long as that of the disjont-set forests). In the remainder of this section, we will report the results of the linear solution.

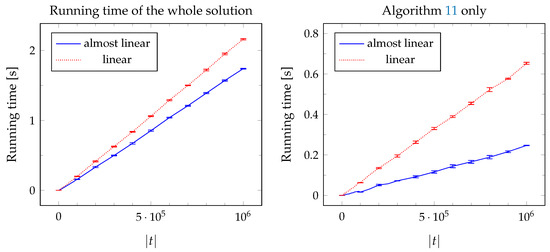
Figure 7. Comparison of the almost-linear union-find data structure with the truly linear one, for $\left|p\right|=3\left|t\right|$ and $\left|s\right|=5\left|t\right|$. The left chart shows the running times of the solution as a whole, the right chart shows only the time spent on Algorithm 11 (including the initialization of the union-find data structure).

We have also analyzed the contribution of each part of the algorithm to its total running time. Here we provide a breakdown for the case of periodic strings ($d=10$) of lengths $\left|s\right|=300,000$, $\left|t\right|=1,000,000$, and $\left|p\right|=\left|t\right|+\left|s\right|/2$, thus at the middle of the “interesting” range of $\left|p\right|$ (i.e., $\left|t\right|<\left|p\right|\le \left|s\right|+\left|t\right|$). Algorithm 8 spends 480 ms in the following ways:

• It spent 263 ms (54.7 %) on preprocessing to support constant-time LCP queries (this includes building suffix trees of p and $p^{\mathsf{R}}$).
• It spendt 17 ms (3.6 %) on counting early and late occurrences of p (steps 2 and 5 of Algorithm 8; described in more detail as Algorithm 9 in Section 2.6.1).
• It spent 133 ms (27.7 %) on processing the ancestor queries (steps 3 and 6 of Algorithm 8; described in more detail as Algorithm 11 in Section 2.6.3). This includes the initialization of the static tree set union data structure.
• It spent 19 ms (3.9 %) on counting the remaining occurrences of p (step 7 of Algorithm 8; described in more detail as Algorithm 10 in Section 2.6.2).
• It spent 48 ms (10.1 %) on everything else: computing the various prefix and suffix tables from the KMP algorithm, counting those occurrences of p in $s[:k] t s[k:]$ that do not span the entire t (i.e., the first four types of occurrences from Section 2.2), and cleanup at the end of the algorithm.

The relative amount of time spent on different parts of the solution remains fairly stable as the length of the pattern p varies (while the strings s and t are kept constant); this is illustrated by the stacked area chart on Figure 8. Major changes only occur when certain parts of the solution can be skipped altogether. For $\left|p\right|<\left|t\right|$, no part of Algorithm 8 needs to be executed and only the “everything else” category remains. For $\left|p\right|>4\left|s\right|$, steps 1–6 of Algorithm 8 do not need to be executed, which also means we do not have to initialize the union-find data structure; we still need to preprocess p to support constant-time LCP queries, however, since these are needed in step 7.

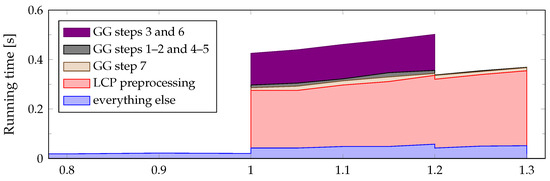
Figure 8. Running time of individual parts of the algorithm, for $\left|s\right|=300,000$, $\left|t\right|=1,000,000$, and various lengths $\left|p\right|$.

The size of the input to our algorithm is defined by three variables—the lengths of the strings p, s, and t. We can show the behavior of the algorithm by fixing one variable to a reasonable value and observing the 3D chart of the running time as a function of the other two variables. In Figure 9, we can observe approximately plane-shaped charts, demonstrating that the running time is linear in the lengths of the input strings.

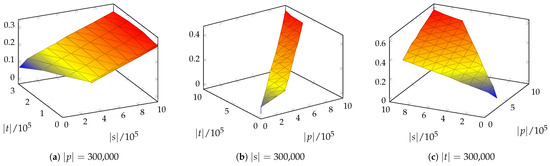
Figure 9. Plots of running times (shown in seconds on the z-axis) when the length of one of the strings s, t, p is fixed at $300,000$ while the length of the other two strings varies. Results are shown only for those combinations of $\left|s\right|$, $\left|t\right|$, $\left|p\right|$ where $\left|t\right|<\left|p\right|\le \left|s\right|+\left|t\right|$ and where all three lengths are ≤${10}^6$.

4. Conclusions

We investigated the problem of computing the number of occurrences of substring p in all possible insertions of string t into string s. We have presented four solutions with different time complexities and based on different techniques. Somewhat surprisingly, the problem can be solved with an algorithm that has linear time complexity $O\left(\right|s|+|t|+|p\left|\right)$ and is based on an adaptation of a recent result from the field of string finding in a compressed text. The algorithm is thoroughly explained. An implementation in C++ of the described solution is publicly available.

We encountered some interesting problems that we were unable to solve. In the geometric solution using a plane sweep, the rectangles are neatly nested in individual dimensions. Projections of rectangles onto coordinate axes are a set of segments, where for every two segments, one is completely contained in the other, or the segments do not intersect. This is an obvious consequence of the fact that each rectangle corresponds to a node or subtree. We have not been able to exploit these properties in our solution.

The second open problem is a simplification of the GG algorithm. The basic result from which our solution is derived was developed for string searching in different concatenations of three substrings of the same string. In our problem, however, we are dealing with inserting one string into all possible places in the other string. As we have shown, we can reduce the problem to searching for a string p in concatenations of a prefix of the string p, the entire string t, and a suffix of the string p. For this specific case, further simplifications may be possible.