Abstract
Machine Learning-assisted metaheuristics is a new and promising research topic, combining the advantages of both method families. Metaheuristics are widely used general problem solvers that can be fine-tuned by prior knowledge about the search space; however, this adaptation can be a very time-consuming and complex task. This paper proposes a hybrid variation of the Hill Climbing method using a Machine Learning model to learn this domain-specific knowledge in advance to help determine the optimal step size of each iteration. A Deep Feedforward Neural Network was trained on the steps of thousands of Hill Climbing runs. This model was used in a novel alternating method (using traditional and Machine Learning-based steps) to predict the optimal step size for each iteration. This hybrid algorithm was compared to the already-known variants. The results show that the novel hybrid method is able to find slightly better results than the original Hill Climbing method, requiring significantly fewer fitness calculations.
1. Introduction
Metaheuristics are powerful optimization methods known for their versatility and adaptability to diverse problem types, ranging from non-linear and non-convex challenges [1] to large-scale, high-dimensional tasks [2]. The stochastic nature of metaheuristics raises innovative solutions, while their scalability and parallelization potential [3] enable efficiency in large computations. Additionally, their simplicity and ease of implementation make them generally applicable, yet they remain flexible enough to incorporate domain-specific heuristics or hybrid approaches for tailored problem-solving. These benefits have made metaheuristics a popular choice across several fields [4]. Although Machine Learning (ML) methods have become increasingly popular in the last decade [5,6], they have been overshadowed in research on metaheuristics.
The principles of different metaheuristic search algorithms are generally straightforward, but these usually have several parameters. This is not a shortcoming that can be eliminated because it gives them their flexibility. For example, these parameters make it possible to find the correct balance between the exploration and exploitation phases, control the speed of convergence, and so on. Even the simplest Hill Climbing (HC) algorithm needs several parameters (staring positions, step size, and number of examined directions) and control functions (fitness calculation and stopping conditions).
These parameters are usually domain-specific and based on the attributes of the search space. Therefore, their setting requires considerable experience or a time-consuming trial-and-error process to achieve the most effective results. The novel idea of our research is to use ML to enhance the already existing metaheuristics to make them capable of learning these parameters themselves. There are several possibilities to build these hybrid methods, for example, to design a Tabu Search [7] using ML to identify the already visited locations or to use ML to define the stopping conditions of the main iteration, answering the question of whether it is worth running further iterations of a local search or whether it is better to restart it from another starting point.
The design of these hybrid methods is very computationally intensive, as a large number of heuristics needs to be run to generate the training database, followed by another resource intensive neural network training; and finally, a lot more benchmark executions are required to ensure reliable evaluation (and this may need to be repeated when testing different ML models). As a preliminary step in this direction, this paper presents the idea of a hybrid ML-assisted HC method capable of determining the appropriate step size dynamically, based on the knowledge extracted from previous runs.
Liu et al. [8] presented a novel method based on variable step size, solving a problem in the domain of tidal energy application with a maximum power tracking control technique for a power generator system. Another example can be the work of Zhang et al. [9], which combines the attributes of individual searches and population-based algorithms. Nolle also presented [10], a novel population-based adaptation scheme with a self-adaptive step size based on the distance of the current position and a randomly selected sample of the population during each iteration. Tanizawa et al. have multiple papers on the topic of the HC method using a random step size [11,12].
These domain-based methods can be very efficient, but they all need the knowledge of the attributes of the search space. In the case of complex problems, it can be very challenging to find the appropriate adaptations. The novel idea of this paper is that this domain-specific knowledge can be extracted via ML.
This paper presents some details about the HC algorithm and its variants, followed by the novel hybrid approach, detailing the methodology behind generating training data, refining the algorithm, and evaluating its effectiveness. The impact of these modifications is analyzed through a comparative study with existing HC variants, demonstrating key findings and performance improvements. The results provide insight into the strengths and limitations of the proposed method, ultimately shaping the conclusions of this work.
2. Materials and Methods
2.1. Steepest Ascent Hill Climbing
HC is one of the most widely used optimization algorithms [13,14,15]. The algorithm aims to maximize or minimize an objective function. This paper assumes a minimization problem; therefore, the goal of the algorithm is to find the location of the S search space, where the value of the f fitness function (also known as cost function) is minimal. The method is quite simple compared to the other metaheuristics and is as follows: It maintains the position of one candidate solution (p). After a random initialization, an iterative process tries to improve the position of p. This is carried out by evaluating the neighboring solutions and moving to the one that provides a better outcome for the objective function. The process continues until no better neighbors are found.
The base idea has several variants, like Stochastic Hill Climbing and Steepest Ascent Hill Climbing. Algorithm 1 presents the main steps of the latter.
- Selecting a random starting point from the entire search space (S). This will be the position of the candidate solution (p).
- Evaluating the neighborhood of p. These are the x points of the S search space, where the distance between the p and x points () equals to . The steepest ascent variant of the method selects the best candidate (q) solution from this neighborhood.
- If the q position represents a better solution than the previously presumed best solution (p), then p moves to the q position, and the iteration restarts.
- If the q position does not represent a better solution than p, it means that the algorithm is stuck in a local minima. The result of the function is the p itself. It is recommended to start an entire new search from another random starting point.
As it is known, the algorithm has several limitations, especially for large search spaces. In general, it is not the right tool to explore the whole search space; it is more applicable to exploit the best candidate in a smaller area. To compensate for this disadvantage, it is fast enough to start the search from different random points consecutively. However, the general opinion is that Hill Climbing is a typical local search method.
| Algorithm 1 Hill Climbing Steepest Ascent algorithm |
|
2.2. The Role of the Parameter
Thanks to its simplicity, the number of parameters is relatively small compared to other metaheuristics. One critical parameter is the step size (), which has a massive impact on the results of the algorithm. The disadvantages of using overly small values are as follows:
- Slower convergence: The search process becomes overly cautious, taking very small steps. This can make convergence to an optimal solution much slower, increasing computational time and making it practically impossible to find the global optimum.
- Becoming stuck in local optima: Small steps may prevent the algorithm from escaping local optima. This can be extremely problematic in the case of noisy data, where the perturbation of data leads to a lot of locally optimal locations.
- Reduced exploration: The algorithm may not adequately explore the solution space, missing out on potentially better solutions that lie further away.
On the other hand, excessively large values also have several disadvantages as follows:
- Reduced precision: The most easily imaginable effect is that by using an excessively large step size, the algorithm simply steps over (or stops before) the ideal point and fails to approach it sufficiently. A special variant of this case is when the HC method oscillates around the optimal location.
- Reduced exploitation: In complex search spaces with many peaks and valleys, large steps might miss small, promising regions of improvement. The algorithm may be able to explore the whole search space, but it is not applicable for exploiting the possibilities of potential areas to reveal the highest quality results.
As is visible, using the right value is crucial in balancing exploration and exploitation in the HC algorithm. Moreover, this value has an effect on the convergence speed and the resistance against noise.
2.3. Strategies for Determination
2.3.1. Fixed Size Strategy
The most straightforward way is to handle as a constant value. It seems easy to set this value as an input parameter of the HC method. This method is quite simple but raises several issues [16].
First of all, it is hard to determine the ideal value in advance. This depends on the problem, the attributes of the search space, the availability of resources, and the requested quality of final solutions. It is usually based on several trial-and-error experiments, but it usually cannot be satisfactory because of the first issue.
As a second issue, it is not guaranteed that the same value will be optimal at the beginning and end of the search. It is common at the beginning of any metaheuristic search to strengthen the exploration behavior, having a relatively large step size in this case. After several iterations, the algorithm should continuously and gradually switch to the exploitation phase, which requires smaller step sizes.
Besides the number of iterations, it is also important to look at the number of fitness calculations. For many optimization problems, the fitness function is quite complex, and its evaluation takes up most of the optimization time. For this reason, it is more important to keep the number of fitness calculations lower than the number of iterations.
The number of fitness calculations is computed as follows:
where is the number of iterations, and is the number of directions the method checks around the current position.
2.3.2. Brute Force Strategy
Another strategy might be to play it safe, even as that may incur a great cost. The use of the Brute Force (BF) method implies accepting that it is not possible to simply determine the correct value. Instead, a discrete list (E) of possible values is defined, and the algorithm checks all of these in every iteration to find the optimal step size.
This method has several benefits, as it uses a dynamic implementation compared to the previous static one [10]. It is not necessary to set the correct value in advance. It is enough to determine it in run-time according to the attributes of the search space and the actual given position. It also has the benefit of automatically switching between the exploration and exploitation phases. The algorithm can progress quickly at the beginning of the search and be more cautious in the latter phases. This behavior can lead to fast and high-quality results.
The obvious disadvantage of this method is the high computation cost. Depending on the size of the list of potential values (), the number of fitness calculations is computed as follows:
2.3.3. Gradient Descent Method
A similar method is the gradient descent algorithm [17]. It uses a dynamic step size variable based on the derivative (or gradient in multi-dimensional cases) of the search space at the current positions. The main idea is based on the fact that the derivative of the fitness function at a local minimum is zero. This is because a local minimum is a point where the slope of the function changes direction, and the derivative at that point becomes zero. This leads to the assumption that positions with large derivatives (large slopes of the fitness function) are far from the global optimum; therefore, it is worth using large step sizes from here. On the contrary, small derivatives lead to small step sizes.
This method can be very well applicable to several problems, but it is not as widely usable as the traditional HC method; the fitness function must be differentiable and have some mathematical properties to work with gradient descent. Due to these limitations, this is considered a separate method and will not be discussed in this article.
2.3.4. Domain-Specific Methods
The proposed methods are generally applicable to any problem and search space. The properties of the search space and the implementation of the fitness function can be problem-specific; the general HC idea will work using either the fix or the Brute Force method. However, there may be better determination strategies based on more knowledge about the search space.
Based on the attributes of the search space, it is possible to change the fixed step size to a dynamic one. The value can be a function of the actual fitness value, the number of iterations, etc. These methods are based on the assumption that the random starting position is far away from the global optimum and has a high fitness value; therefore, it is worth using a large step size at the beginning. As the HC algorithm follows a path of monotonically lowering fitness values, it is worth decreasing the step size to fine-tune the optimal position. This method has several advantages but requires proper mapping from the known information (last , current fitness, and iteration count) to the next value.
2.4. ML-Assisted Metaheuristics
There have been several attempts to combine metaheuristics and ML models. Based on the comprehensive reviews of the area [18,19], these methods can be categorized into one of the following classes:
- Metamodeling: The ML model is used to replace the calculation-intensive fitness function to give fast predictions [20,21].
- Initialization: Instead of starting the metaheuristics from random locations, the initialization of the algorithm is based on the predictions of a ML model [22,23].
- Domain-specific variants: These methods are usually designed to solve a given problem and not as a general problem solving strategy [24,25,26].
In recent years, some specific algorithms with a general purpose have also appeared; for example, the work of Özcan et al. [27], who combined the chaotic hiking algorithm with Machine Learning. It is also common to use metaheuristics to train or fine-tune the hyperparameters of ML models [28,29].
3. Methodology
3.1. Machine Learning-Assisted Hill Climbing Algorithm
The novel method proposed is based on the assumption that domain-specific knowledge about the search space can help the HC method (especially the determination of the distance of each iteration). Algorithm 2 presents the idea of the Machine Learning-assisted Hill Climbing method. The algorithm has the following modifications:
- The additional parameter presents a neural network trained on the specific S search space. Its training is discussed in Section 3.4.
- The additional L queue contains the domain-specific information gathered by the current run of the HC algorithm.
- Line 7 appears as the prediction of the neural network is used to determine the next value. The prediction is based on the already existing information stored by L.
- This variant assumes a simple Feedforward Neural Network (FNN) with a fixed sized input (). The detailed architecture and the training of the FNN are described in Section 3.2, Section 3.3 and Section 3.4. The neural network is not able to predict before the necessary information has been collected; therefore, the algorithm uses the same steps as the original HC for the first few iterations.
- At the end of each iteration, the current fitness value and values are stored in L (line 10). It is enough to store only the information of the last few iterations, based on the input size (line 8).
| Algorithm 2 Machine Learning assisted Hill Climbing Steepest Ascent algorithm |
|
The presented algorithm uses a fixed step size. However, it is obviously possible for any of the already known methods to be used to handle the first few iterations (for example, the BF method). It is also possible to design an alternating version of the algorithm, making some steps based on the BF method, after following some steps based on the prediction of the FNN, and switching back to the BF method for a while.
3.2. Creating the Machine Learning Model
The whole idea is based on the domain-specific knowledge learned by the FNN. Therefore, it makes no sense to create a general ML model to serve all possible problems. On the contrary, it is necessary to train the neural network on a given search space to make it capable of accurate value predictions.
This training needs a training database which is easy to produce. It is possible to run several HC algorithms from random starting points of the search space. The BF method always determines the best value for a given location. The objective of the ML model is to build a function capable of predicting the best values based on the already known values. These are as follows:
- The iteration number (i).
- The current location.
- The fitness value of the current location.
- The current value (size of the previous step).
- Historically, the last k of these values, where
- –
- ;
- –
- ;
- –
- .
To ensure the generalization of the model, the method presented in this paper does not use the p values, it only uses the current (and last k) fitness and values.
3.3. Generating the Training Data
The evaluation is based on the Rosenbrock function, which is a non-convex function forming a valley used by several papers to perform tests for metaheuristics. Because of its shape, finding a good direction is trivial; however, finding the optimal step size is hard. Therefore, the fitness function is defined as follows:
The standard parameters (, ) have been used; therefore, the global minimum is at the , and the value of the function is here.
The training dataset is generated by the execution of 20,000 HC algorithms from random starting positions. As a constraint, the starting positions are chosen randomly from a predefined area around the global optimum.
The training database generator algorithm is based on HC using the BF method for determination, where the set of possible step sizes is as follows:
The number of possible directions () was four, as follows:
According to the BF method, the algorithm examines all values and all directions, and it chooses the best move for all iterations. In total, 11 different values were tested, with 4 directions for each case, so choosing the best move requires 44 fitness calculations. This is quite computationally intensive but gives the most accurate dataset for training. The HC algorithm has been extended with some monitoring operations as follows: it continuously saves the fitness value of the current p position and the best size from this location for each iteration. As visible from Table 1, all HC runs could reach a good fitness value; however, the standard deviation of the required steps is very high.

Table 1.
Attributes of the training database.
3.4. Building the Machine Learning Model
A simple dense Deep Feedforward Neural Network was used for the study. Based on some preliminary tests, the architecture was defined as follows:
- Input layer— number of input neurons.
- Hidden layer—500 dense neurons, using sigmoid activation.
- Hidden layer—500 dense neurons, using sigmoid activation.
- Hidden layer—500 dense neurons, using sigmoid activation.
- Output layer—1 output neuron using sigmoid activation.
The input layer is fed by the following vector: , where i is the number of the iteration, is the fitness of the position of the j-th iteration, and is the chosen value at the -th iteration.
The output is the prediction of the best value for the i-th iteration. As the value can vary over a wide range (in this case, between and 10), it was normalized by the following function:
A training dataset is built on the synthetic dataset presented in Section 3.3. The first iterations of all HC executions were skipped, and after that, vectors containing the given input data format were built for each subsequent iteration. The training dataset consists of 392 M records. The chosen depth (k) value was 5.
The network is trained using the Adam optimizer with a learning rate of 0.001 for 500 epochs. The entire database has been used for training, with no risk of over-fitting due to the massive size of the database (compared to the small capacity of the network). Using synthetically generated data without any noise also helps to avoid over-fitting.
The limitation of the ML model trained in this way is that it is expected to work efficiently only in the search space used to generate the training database. This is the price to pay for replacing the otherwise general HC metaheuristic with a domain-specific HC algorithm, which is, in turn, expected to perform better in this narrower context.
To evaluate the novel method proposed, the assembled hybrid ML-HC algorithm was examined in depth. The built-in FNN model itself was only evaluated with some preliminary tests. This resulted in the choice of three hidden layers. As can be seen in Figure 1, with one hidden layer, the network was not able to achieve good predictions, with two and three hidden layers; the networks showed similar results (slightly to the advantage of three); and with the introduction of the fourth layer, the network training slowed down considerably.
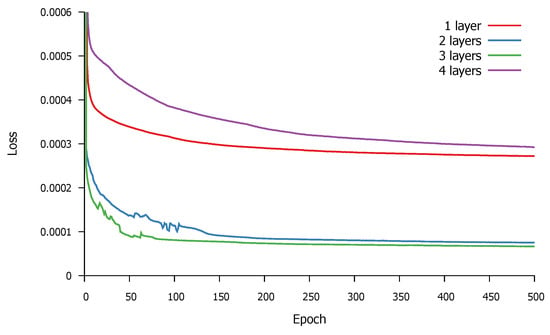
Figure 1.
Loss by epoch for different numbers of hidden layers.
Since the training of different network architectures required a lot of resources and time, finding the perfect architecture and optimizing the training hyperparameters are outside the scope of this paper. Obviously, there may be better architectures (for example, recurrent neural networks), and the size of the network may be smaller. But this network was eligible for the goal of this paper—to prove that it is possible to predict the value based on the data of previous steps—and this method can make the HC algorithm more efficient. A future research topic that can be considered is finding the appropriate ML model for this purpose.
4. Results
4.1. ML-Based Step Count
The original idea of the ML-based hybrid method was to use the BF method to set the value for the first k steps and switch to the ML-based estimation for further steps. In practice, however, this simple solution did not always work. For an understanding of this, it is worth noting that the step size usually decreases continually during the execution of a HC algorithm. At the beginning of the search, the exploration phase has the advantage of high values, but later, it is better to decrease this value for the exploitation phase. This phenomenon is visible in the training database as follows: smaller fitness and inputs usually lead to small predictions (meaning both the absolute values and the changes in the fitness and ). In rare cases, this causes an erroneous loop as follows: (a) as it is just a prediction, the ML model sometimes underestimates the step size; (b) small prediction leads to a small step size and a resultant small fitness change; and (c) based on these small values, the ML model tends to predict more smaller step sizes and so on. In practice, this manifests as the algorithm starting to take smaller and smaller steps at some undefined point, slowing down the convergence.
An algorithm representing alternating behavior has been developed to avoid this loop. This variant starts with the BF method for the first k iterations and switches to the alternating mode. In this mode, it performs l steps using the ML predictions, and after these, one step is carried out using the BF method. If the ML prediction cannot give a better position, it immediately tries one Brute Force step. If this also fails, the algorithm is stuck in a local minima. If not, the search will continue with ML-based predictions.
To find the optimal number of ML steps, an experiment was carried out using different values, containing small l values (1…10) and large ones (20, 50, 100, 200, 500, 1000, and 5000). Based on 20,000 Hybrid ML-HC executions, the results show (Table 2) that the optimal number is 5. However, the achieved best fitness values are very similar, and there are huge differences in the number of iterations, which will be discussed later.

Table 2.
Best fitness values for different numbers of ML steps (l value).
The HC runs for this and subsequent tests were completely independent of the database used to teach the neural network.
4.2. Comparison to Already Existing Methods
Based on the results of the previous section, it can be seen that the alternating method works well, as increasing the number of ML steps (therefore decreasing the ratio of BF steps) does not degrade the final fitness. However, the question of how the novel method performs compared to the existing ones is still open.
Table 3 presents the results of different methods according to the best fitness achieved. As is clearly visible, the fixed step size-based methods were not able to find the global optimum. Decreasing the step size can solve this problem, but it also leads to very slow convergence and high computational costs (Section 4.3); therefore, these are not applicable in practice. The BF and Hybrid solutions could achieve much better results.

Table 3.
Best fitness values for different step size determination methods.
4.3. Comparison of Iteration Counts
In the case of a constant value, a smaller step size causes more steps (iterations of the main HC loop). Comparing the fitness and step count columns of Table 4 makes it obvious that this method has several disadvantages. The configuration needs a similar iteration count to the BF and Hybrid methods, but the fitness is significantly worse. Lowering the fixed step size leads to better results, but the iteration count also grows out of control. This paper does not contain results for smaller values because it was impossible to run all the necessary tests within an acceptable time. The BF and Hybrid solutions also show better performance in this area.

Table 4.
Fitness and step count results for different step size determination methods.
4.4. Comparison of the Fitness Calculation Counts
In the neighborhood check, the BF method has to check number of directions using number of step sizes, which needs fitness function calls. The ML-based method needs only fitness calculations in each iteration (similar to the fixed step size-based methods).
In the case of the hybrid alternating method, the number of fitness function calls depends on the number of BF- and ML-based steps. The ratio of these is based on the properties of the search space; therefore, it cannot be determined in advance. The more ML-based steps are taken during the search, the fewer fitness calculations are needed.
Table 5 shows the average of fitness calculations needed by the different methods. In the case of the fixed step size-based method, this correlates to the number of steps; therefore, smaller values lead to higher computation demands. From this point of view, the BF method is in competition with the fixed step size methods; however, it is worth noting that it was able to find significantly better final solutions.

Table 5.
Fitness and step count results for different step size determination methods.
5. Discussion
In developing the Hybrid ML-HC algorithm, the first question was how many steps to allow the ML model before switching back to the BF method. The first experiments were aimed at determining this. The results show that the number of iterations is significantly affected by this parameter, but this has minimal influence on the best fitness values achieved (Figure 2). The best results were obtained with the algorithm using five ML steps; therefore, this variant was further investigated.
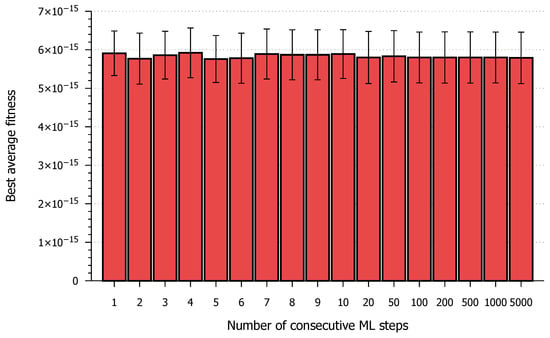
Figure 2.
Average best fitness values for different numbers of ML steps (l value).
When comparing the different methods for determining , it was immediately obvious that solutions using fixed step sizes are not efficient (Figure 3). It is more interesting to compare the standard BF and the novel Hybrid ML-BF methods (Figure 4). As is visible, the new method has achieved basically the same results, sometimes even outperforming the original (although this advantage is not significant). The main strategy of the BF method is that it always chooses the best step size; therefore, it was surprising that the Hybrid method was able to find better results. The reason for this may be that the BF method uses a set of predefined step sizes, and one of these has to be chosen. The ML model was trained on these data, but the model was able to interpolate and extrapolate; therefore, it can suggest better step sizes than in the given predefined set.
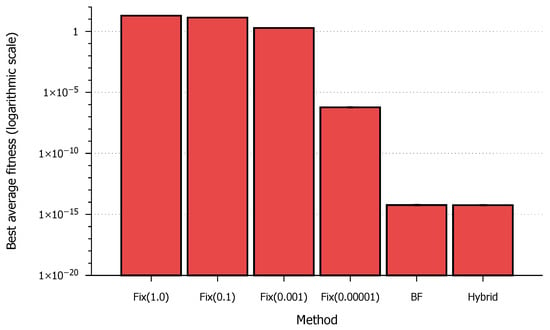
Figure 3.
Average best fitness values for different methods.
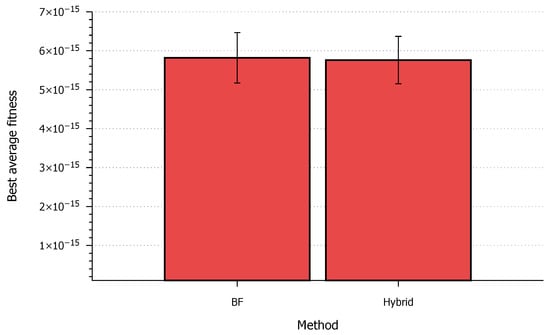
Figure 4.
Best fitness values for the best two methods.
In the next analysis, we examined the number of iterations performed by the different methods. Decreasing the fixed step size yields better results, but the iteration count can become unmanageable. Comparing the BF and Hybrid methods (Figure 5), it is visible that the Hybrid method slightly outperforms the BF method; however, the difference is also not significant. In summary, the novel method can achieve similar results with a similar number of steps.
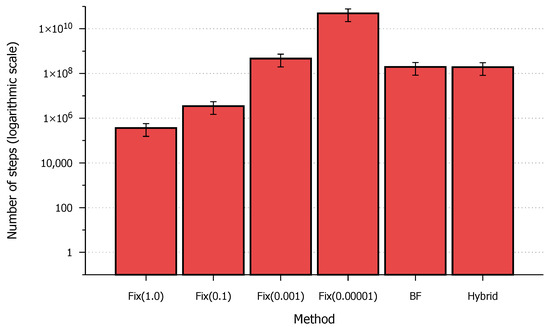
Figure 5.
Comparison of step counts for different methods.
The BF and Hybrid methods outperformed the fixed step size-based methods, both in speed (iteration count) and accuracy (best fitness achieved). These two look very similar in both aspects; however, there is a considerable difference between the number of fitness calculations. The number of iterations performed by the methods is the same, but it is worth taking into account that the computation demand of one iteration is very different. As is visible from Figure 6, the number of fitness calculations is significantly lower for the ML-assisted method.
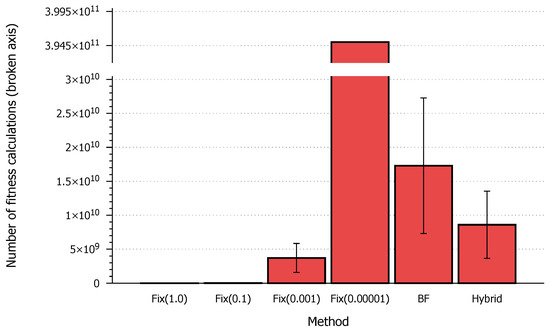
Figure 6.
Comparison of fitness calculation counts for different methods.
6. Conclusions
This paper aimed to develop a novel hybrid HC method using a ML model and BF method to determine the optimal step size of each iteration. This required the modification of the original HC algorithm and building a domain-specific ML model. The model was trained on the information gathered from the best steps of 20,000 BF-based HC runs.
As the results show, the fix-step size has several disadvantages. It is a matter of choice whether to have high-quality results or low computational demands, but both of them are unreachable. The BF method was able to achieve significantly better results, but it needed a moderate number of iterations. The novel hybrid method gives slightly better results using slightly fewer steps.
Taking into account the number of fitness calculations, the results appear more promising. Using the alternating hybrid method (using a maximum of five consecutive ML steps), the same results were achieved using less than half the number of fitness calculations. Considering that fitness calculation is usually the most expensive operation in metaheuristics, this is a significant improvement.
The results obtained in this way cannot be generalized, and the same ML model is unlikely to be applicable to other search spaces. However, this is an acceptable compromise, since the goal was to implement a more efficient domain-specific search than the existing ones, which does not require precise knowledge of the structure of the search space. Further consideration may be required for comparisons of different ML models and the examination of various additional metaheuristics. It is also essential to test the viability of the proposed solution for other problems of greater complexity and with more dimensions. However, the aim of this article was to only examine the theoretical possibilities in practice, and based on the results, it can be clearly stated that it is worth continuing further studies in the direction of Machine Learning-assisted metaheuristics.
Author Contributions
Conceptualization, S.S. and G.L.; methodology, S.S. and G.L.; software, S.S.; validation, S.S.; writing—original draft preparation, S.S.; writing—review and editing, S.S., G.L. and G.K.; supervision, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
This research used generated data, as presented in the article.
Acknowledgments
The authors would like to thank the “Doctoral School of Applied Informatics and Applied Mathematics” and the “High Performance Computing Research Group” of Óbuda University for their valuable support. The authors would like to thank NVIDIA Corporation for providing the graphics hardware for the experiments. On behalf of the “Development of Machine Learning Aided Metaheuristics” project, we are grateful for the permission to use HUN-REN Cloud [30], which helped us achieve the results published in this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- So, M.K. Posterior mode estimation for nonlinear and non-Gaussian state space models. Stat. Sin. 2003, 13, 255–274. [Google Scholar]
- Wu, J.; Kalyanam, R.; Givan, R. Stochastic enforced hill-climbing. J. Artif. Intell. Res. 2011, 42, 815–850. [Google Scholar]
- O’Neil, M.A.; Burtscher, M. Rethinking the parallelization of random-restart hill climbing: A case study in optimizing a 2-opt TSP solver for GPU execution. In Proceedings of the 8th Workshop on General Purpose Processing Using GPUs, San Francisco, CA, USA, 7 February 2015; pp. 99–108. [Google Scholar]
- Mester, A.; Zombori, D.; Pál, L.; Bánhelyi, B. Efficiency improvement of the global optimization method by local search changes. Acta Polytech. Hung. 2022, 19, 29–42. [Google Scholar] [CrossRef]
- Csóka, M.; Paksi, D.; Czakóová, K. Bolstering Deep Learning with Methods and Platforms for Teaching Programming. Ad Alta J. Interdiscip. Res. 2022, 12, 308. [Google Scholar] [CrossRef]
- Kmet, T.; Kmetova, M.; Végh, L. Neural Networks Simulation of Distributed SEIR System. Mathematics 2023, 11, 2113. [Google Scholar] [CrossRef]
- Gendreau, M. An introduction to tabu search. In Handbook of Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2003; pp. 37–54. [Google Scholar]
- Liu, W.; Yao, X.; Xiao, X.; Salvatore, F.; Yang, J. Improved climbing algorithm with variable step size in tidal energy Application of maximum power tracking control technique for power generation system. J. Phys. Conf. Ser. 2023, 2495, 012031. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Lv, H. A Step-Size Adaptive Hill-Climbing Algorithm for Local Search. In Proceedings of the 2021 4th International Conference on Intelligent Robotics and Control Engineering (IRCE), Lanzhou, China, 18–20 September 2021; pp. 1–4. [Google Scholar]
- Nolle, L. On a hill-climbing algorithm with adaptive step size: Towards a control parameter-less black-box optimisation algorithm. In Proceedings of the Computational Intelligence, Theory and Applications: International Conference 9th Fuzzy Days, Dortmund, Germany, 18–20 September 2006; Proceedings. Springer: Berlin/Heidelberg, Germany, 2006; pp. 587–595. [Google Scholar]
- Tanizawa, K.; Hirose, A. Search Control Algorithm Based on Random Step Size Hill-Climbing Method for Adaptive PMD Compensation. IEICE Trans. Commun. 2009, 92, 2584–2590. [Google Scholar] [CrossRef]
- Tanizawa, K.; Hirose, A. Optimal control of tunable PMD compensator using random step size hill-climbing method. In Proceedings of the National Fiber Optic Engineers Conference. Optica Publishing Group, San Diego, CA, USA, 24–28 February 2008; p. JThA75. [Google Scholar]
- Chinnasamy, S.; Ramachandran, M.; Amudha, M.; Ramu, K. A review on hill climbing optimization methodology. Recent Trends Manag. Commer. 2022, 3, 1–7. [Google Scholar]
- Sazaki, Y.; Satria, H.; Primanita, A.; Apriliansyah, R. Application of the steepest ascent hill climbing algorithm in the preparation of the crossword puzzle board. In Proceedings of the 2018 4th International Conference on Wireless and Telematics (ICWT), Nusa Dua, Bali, Indonesia, 12–13 July 2018; pp. 1–6. [Google Scholar]
- Silvilestari, S. Steepest Ascent Hill Climbing Algorithm To Solve Cases In Puzzle Game 8. IJISTECH Int. J. Inf. Syst. Technol. 2021, 5, 366–370. [Google Scholar] [CrossRef]
- Więckowski, J.; Kizielewicz, B.; Kołodziejczyk, J. Application of hill climbing algorithm in determining the characteristic objects preferences based on the reference set of alternatives. In Proceedings of the Intelligent Decision Technologies: Proceedings of the 12th KES International Conference on Intelligent Decision Technologies (KES-IDT 2020), Virtual, 17–19 June 2020; Springer: Singapore, 2020; pp. 341–351. [Google Scholar]
- Stubbs, R.; Wilson, K.; Rostami, S. Hyper-parameter Optimisation by Restrained Stochastic Hill Climbing. In Proceedings of the Advances in Computational Intelligence Systems: Contributions Presented at the 19th UK Workshop on Computational Intelligence, Portsmouth, UK, 4–6 September 2019; Springer: Cham, Switzerland, 2020; pp. 189–200. [Google Scholar]
- Szénási, S.; Légrádi, G. Machine learning aided metaheuristics: A comprehensive review of hybrid local search methods. Expert Syst. Appl. 2024, 258, 125192. [Google Scholar] [CrossRef]
- Talbi, E.G. Machine learning into metaheuristics: A survey and taxonomy. ACM Comput. Surv. (CSUR) 2021, 54, 1–32. [Google Scholar] [CrossRef]
- Yadav, R.; Tripathi, S.; Asati, S.; Das, M.K. A combined neural network and simulated annealing based inverse technique to optimize the heat source control parameters in heat treatment furnaces. Inverse Probl. Sci. Eng. 2020, 28, 1265–1286. [Google Scholar] [CrossRef]
- Shao, S.; Su, B.; Zhang, Y.; Gao, C.; Zhang, M.; Zhang, H.; Yang, L. Sample design optimization for soil mapping using improved artificial neural networks and simulated annealing. Geoderma 2022, 413, 115749. [Google Scholar] [CrossRef]
- Bouhouch, A.; Bennis, H.; Loqman, C.; El Qadi, A. Neural network and local search to solve binary CSP. Indones. J. Electr. Eng. Comput. Sci. 2018, 10, 1319–1330. [Google Scholar] [CrossRef]
- Shao, X.; Kim, C.S. An Adaptive Job Shop Scheduler Using Multilevel Convolutional Neural Network and Iterative Local Search. IEEE Access 2022, 10, 88079–88092. [Google Scholar] [CrossRef]
- Hudson, B.; Li, Q.; Malencia, M.; Prorok, A. Graph Neural Network Guided Local Search for the Traveling Salesperson Problem. In Proceedings of the International Conference on Learning Representations, Virtual, 25 April 2022. [Google Scholar]
- Bożejko, W.; Gnatowski, A.; Niżyński, T.; Wodecki, M. Tabu search algorithm with neural tabu mechanism for the cyclic job shop problem. In Proceedings of the Artificial Intelligence and Soft Computing: 15th International Conference, ICAISC 2016, Zakopane, Poland, 12–16 June 2016; Proceedings, Part II 15. Springer: Cham, Switzerland, 2016; pp. 409–418. [Google Scholar]
- Sarwar, J.; Khan, S.A.; Azmat, M.; Khan, F. A comparative analysis of feature selection models for spatial analysis of floods using hybrid metaheuristic and machine learning models. Environ. Sci. Pollut. Res. 2024, 31, 33495–33514. [Google Scholar] [CrossRef] [PubMed]
- Özcan, A.R.; Mehta, P.; Sait, S.M.; Gürses, D.; Yildiz, A.R. A new neural network–assisted hybrid chaotic hiking optimization algorithm for optimal design of engineering components. Mater. Test. 2025. [Google Scholar] [CrossRef]
- Dasi, H.; Ying, Z.; Ashab, M.F.B. Proposing hybrid prediction approaches with the integration of machine learning models and metaheuristic algorithms to forecast the cooling and heating load of buildings. Energy 2024, 291, 130297. [Google Scholar] [CrossRef]
- Helforoush, Z.; Sayyad, H. Prediction and classification of obesity risk based on a hybrid metaheuristic machine learning approach. Front. Big Data 2024, 7, 1469981. [Google Scholar] [CrossRef] [PubMed]
- Héder, M.; Rigó, E.; Medgyesi, D.; Lovas, R.; Tenczer, S.; Farkas, A.; Emődi, M.B.; Kadlecsik, J.; Kacsuk, P. The past, present and future of the ELKH cloud. Információs Társadalom Társadalomtudományi Folyóirat 2022, 22, 128–137. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).