Abstract
In this study, we develop a simulation of Contact Graph Routing (CGR) for data communication between Mars, Earth, and relay satellites. Due to the changing of the satellites’ distances to Mars and Earth, respectively, there are specific contact windows between NASA’s Mars rovers and orbiting relay satellites, and specific contact windows between these relay satellites and NASA’s global system of antennas on Earth. The barrier in communication develops delays caused by link propagation, so it needs a Delay Tolerant Network (DTN) for routing networks among the nodes (satellites and antennas), which is the concept of storing and forwarding data whenever the windows are open. We construct an efficient algorithm for CGR, which puts all objects into a general framework of numbered nodes, so that we can easily develop another application of a network with a larger number of nodes. Simulated data are generated randomly to mimic the unpredicted data volumes that are sent from Mars to Earth. We construct some cases involving delivering data for one Martian day, and the simulation performs well in carrying, storing, and forwarding data from Mars to Earth, even though the relay satellites are not able to contact Earth for a period of time.
1. Introduction
The proximity of Mars to our Solar System makes it an obvious target for exploration, but there are numerous more reasons to investigate Mars. Searching for life, learning about the planet’s surface and evolution, and preparing for future human exploration are the three main scientific justifications for exploring Mars [1] Mars, commonly referred to as the Red Planet, may have once been habitable because of evidence that suggests it was warmer, had a thicker atmosphere, and was covered with water. The history of water on Mars piques scientists’ curiosity to know how life might have persisted. Aspects of Mars’ past can be found in its volcanoes, meteoroid impact craters, atmospheric and photochemical effects, and geophysical processes. For future human exploration, we must know the risks before sending astronauts. Uncontained Martian material would inevitably be carried back to Earth by astronauts, either on their bodies or on their equipment. Planning and preparedness for these upcoming operations will be aided by the knowledge of any biohazards present in the dust and soil [1].
Since 1997, NASA has deployed several robotic rovers to Mars in order to investigate the planet’s surface and its geology, and to look for evidence of current or former life. The most prominent rovers on Mars include Sojourner, Spirit, Opportunity, Curiosity, and Perseverance.
Curiosity landed at Gale Crater in August 2012 and focuses on habitability studies, including learning more about Mars’ long-term climate history and determining whether the aforementioned crater has ever had environmental conditions conducive to microbial life.
On 18 February 2021, Perseverance, another rover, landed at the Jezero Crater. Its goals include looking for evidence of ancient microbial life on Mars, gathering soil and rock samples for a possible return to Earth in later missions, and researching the planet’s climate, geology, and potential for supporting future human expeditions.
NASA’s dedicated Mars Exploration Program website [2] offers real-time updates on the rovers’ activities. Both rovers send data from the exploration using UHF Ultra to contact the relay satellites; these data are then forwarded to station receivers in Madrid (Spain), Goldstone (United States), and Canberra (Australia). These form part of NASA’s Deep Space Network (DSN), which is a global network of strong antennas used for communication with spacecraft in deep space or for missions that operate outside of the Moon’s orbit. The DSN is essential for spacecraft navigation, scientific data collection, and communication with interplanetary missions.
As shown in [3], stations on planetary surfaces, orbiters, and deep space relays make up interplanetary communication networks. Traditional Internet protocols like TCP/IP are unsuitable for deep space environments due to their reliance on continuous end-to-end connectivity and low latency. These networks must overcome major propagation delays, limited resources, and node mobility. The rovers ideally transmit as much research and exploration data as possible and as quickly as possible to Earth. The vast distance (143 million miles or 16 min of data transmission) to and from Mars is one of numerous restrictions, though. Additionally, each relay satellite has a unique orbit, resulting in varying communication windows [4,5,6].
The goal is for the rovers to transmit as much of the exploration and research data as they can to Earth as fast as possible. A unique type of computer network architecture known as Disruption/Delay-Tolerant Networking (DTN) addresses the limitations of the TCP/IP suite to satisfy deep space networking needs with sporadic end-to-end connectivity. The store–carry-forward method of data transmission in DTN involves the transfer of bundles (data) between relay nodes as custody. This offers more flexibility for erratic connectivity but calls for more intricate routing schemes, requiring more route calculations and network resource usage.
The development of DTN has a wide range of analyses in Intelligent Transportation Systems, which includes Vehicular Delay-Tolerant Networks, or VDTN. In [7], the basic routing process in DTN is classified according to the methods used to identify destinations and whether or not message replication is employed: One copy as opposed to several copies are forwarded, flooded, and randomly forwarded according to the various kinds of information that are available. The authors surveyed the development of opportunistic forwarding for VDTN, which is based on various forwarding methods, including social-based forwarding, mobility prediction, geographical forwarding, and incentive-based and congestion control.
In the context of deep space communication, DTN is designed to work in scenarios where end-to-end connectivity is not always available and lengthy and erratic delays are common [8]. DTN has demonstrated its effectiveness through innovative techniques that ensure connectivity in challenging terrestrial communication scenarios, such as natural catastrophes. Recent research on the architecture of present and future deep space communication systems, the environmental difficulties associated with deep space communication, different DTN architecture implementations and demonstrations, and the verification of associated routing strategies over the Deep Space Relay network are all covered.
There are many relay satellites in space that are available for our approach. In this paper, we simulate the four most commonly observed by NASA due to their reliable storing and forwarding capabilities. MRO (Mars Reconnaissance Orbiter), TGO (Trace Gas Orbiter), Mars Odyssey, and MAVEN (Mars Atmosphere and Volatile Evolution) are of the LEO orbit type and are not always immediately above the rovers. Their altitudes range from 500 to 2000 km. TGO and MAVEN have non-elliptical orbits, so they represent the furthest and closest points from the surface of Mars, with Mars being the location of the Perseverance and Curiosity rovers. See [9,10] for detailed information.
First proposed in [11], the Contact Graph Routing (CGR) architecture is used in DTN protocols to implement the concepts and methods for routing between ground elements and spacecraft in deep space and near-Earth orbit. Based on [3,12], CGR combines several non-trivial algorithm modifications, time-dynamic scheduling, space operations ideas, and certain graph models.
A contact plan outlining the anticipated resources that the space network will have for data transmission may be used to express the future connectedness of the assets in space networks. These circumstances led to the development of time-evolving abstractions, new graph models, and algorithm modifications for the Contact Graph Routing (CGR) framework [12].
The communication between Mars and Earth begins with Earth contacting the rovers on Mars, which is in the form of commands or requests, for example, asking an instrument to take an image or to resend some data; then, the Mars rovers carry out the commands. Mars and Earth are roughly 54.6 to 401 million kilometers apart. When Earth and Mars are on the same side of the Sun, and Earth is close to its perihelion and Mars is at perihelion, the shortest distance, known as perihelic opposition, occurs. This occurs approximately every 15 to 17 years, and is an extremely uncommon occurrence. When Earth and Mars are on opposite sides of the Sun and both are at or close to their aphelion, or the furthest from the Sun, this is known as Superior Conjunction at Aphelion [13,14].
The protocol used in the communication is the bundle protocol (BP), which is a network-layer protocol in the DTN architecture; instead of assuming continuous connectivity like TCP/IP, it bundles data into “bundles” (similar to packets), stores them when necessary, and forwards them opportunistically—whenever a communication path becomes available. The core concepts behind the bundle protocol are as follows.
- Custody Transfer: A node takes responsibility for forwarding the bundle, improving delivery assurance.
- Late Binding: Enables routing decisions to be made later, once more info is available.
- Opportunistic Forwarding: Uses available contact plans or real-time link availability.
The current standard of bundle protocol is BPv7 (RFC 9171). The maximum packet size that can be sent depends on the capacity of the communication link on the rovers, where each rover can send a maximum of 2 Mbps or 258 Kbytes/s.
Taking what happened in the implementation of the bundle protocol, we look deeper to be able to solve the problem that arose by building an approach to optimize data delivery via the bundle protocol, optimizing the size of the packet, time, and path chosen for data delivery. This paper constructs a simulation for optimized route pairings for data transmission from Mars to Earth, using a contact graph containing nine nodes. In Section 2, the mathematical variables and parameters are defined for the construction of the model in general terms. In Section 3, the main algorithm, Rover–Satellite Routing, and Satellite–Antenna Routing are shown. The results of the simulation are in Section 4, and the Conclusion is in Section 5.
2. Model of CGR
We develop a model of Contact Graph Routing for data transmission from rovers on planet Mars (Curiosity and Perseverance), relay satellites (MRO, TGO, Odyssey, and MAVEN), and DSN antennas (USA, SPAIN, and AUS). As the time reference, we use a Martian day, called a sol, which is slightly longer than an Earth day, at approximately 24 h, 39 min, and 35 s. The proposed model consists of the following five parts:
- Arrangement of the contact graph: determination of the number of nodes being used, possible routing among n nodes, storage capacities of satellites, the observed time per minute in a Martian day, contact window schedule between rovers and satellites, and between satellites and DSN antennas.
- Arrangement of data: generating random data size per minute, distributing data into d packets whose maximum size is 256 Kbytes.
- Routing management for the combination of rover and satellite.
- Routing management for the combination of satellite and DSN antenna.
- Plotting the graph.
To evaluate the performance of the built model, we show that the process of sending data from Mars to Earth is satisfactory through the relay satellite, and also that the data storage is successfully carried out by the relay satellite according to its capacity. The stored data can be shown to be distributed to the antenna on Earth when the contact window is first opened. By using randomly generated data for a Martian day, a given schedule of contact windows, and a particular relay satellite with quite limited storage capacity, we calculate what percentage of the data amount is sent from Mars and successfully sent to Earth.
2.1. Arrangement of the Contact Graph
If we plan to construct a contact graph using rovers on Mars, relay satellites, and DSN antennas on Earth, it means that we define three groups for our CGR: nodes for the group of rovers, nodes for relay satellites, and DSN antennas on Earth. So, we have nodes. Any node in each group connects to any node in the other two groups. No connection exists inside a group. We define a general graph of n nodes first, because this model construction is open to any modification in the number of nodes and the connectivity arrangement among nodes. Later, we make some assumptions to make the contact graph that we aim for.
We use the following formula to find the total number of combinations of any two nodes, defining routes r from the total n nodes without considering the order.
An illustration of all combinations of every two nodes from the total n nodes can be seen in Table 1. It is important to define route labels r so they can be used to identify the pairing of routes. In Column 1 of Table 1, routes , , , up to , are, respectively, labeled as . We define . In Column 2, route is labeled as , as , and so on until route as . We specifically assign as the last label of columns, which is formulated as follows.

Table 1.
All combinations of every two of n nodes.
Note that . These labels are useful for defining a vector ids whose size and contains the last label of all non-empty columns in Table 1.
We generate an access matrix with size in Table 2, which means there are connections. However, there are only a few connections that will be used. The connection is only between a couple of nodes from different groups, which are between Groups 1 and 2, and between Groups 2 and 3. Due to a limitation, there is no connection between Groups 1 and 3. The numbers of available connections between these groups are, respectively, and , so the total number of connections is .

Table 2.
Access matrix among rovers, satellites, and DSN antennas.
We now define nodes 1 and 2 as rovers PR and CR, nodes , and 6 as relay satellites MRO, ODY, TGO, and MVN, respectively, and nodes , and 9 as antennas USA, SPN, and AUS, respectively. So, we need 9 nodes for our Contact Graph Routing. Table 2 shows the access matrix, where its entries indicate the storage capacity of satellites. Using Equation (1), for nodes, we calculate the number of edges (between two nodes) from nine nodes, which is .
Two nodes of the rovers can connect to four nodes of the relay satellites, but they cannot connect directly to the last three nodes of the DSN antennas. The very long distance between Mars and Earth does not allow it. The relay satellites can connect to the DSN antennas. So the size of the generated access matrix is 9, but it is sparse, with only 20 non-zero entries, so we have a contact graph of nine nodes with only 20 edges.
The usage of the access matrix is important for the indexation of matrix x, which is defined as follows.
where p is the number of steps between groups, r is the label of route defined from the combination of nodes, d is the index of the data packet being sent at time t, and is the size of data packet d being sent at time t. We have the values , where step 1 is from a rover in Group 1 to a satellite in Group 2, and step 2 is from a satellite in Group 2 to a DSN antenna in Group 3. Due to the very far distance between satellite and DSN antenna, step 1 and step 2 occur at different times (minutes).
If , then . The vector x will be very helpful for identifying the satellite that collects the stored data from the previous time intervals in Section 2.4.
Values , where is the number of data packets at time t. The value of depends on the randomly chosen data size, which is explained in Section 2.2. Parameter t in Equation (4) is the time in a Martian day, or a sol. The time is in 24 h, so , where . If , the time interval is 00:00 to 00:01. For another example, if , the time interval is 01:59 to 02:00, and so on.
Define the storage capacity of satellite j at time t as follows:
where is the index number of MRO, Odyssey, TGO, and MAVEN, respectively. Consequently, we also have
The contact windows of satellites are not always open and depend on the positions of satellites, whether they happen to close to Mars, Earth, or neither of them. As the input of our algorithm, we need to have the schedule of contact windows, which can be updated based on historical data, or from a preceding approximation of the distances from a rover to a satellite and from a satellite to a DSN antenna. For rover-i and satellite j, we define
Examples of the frequencies and the schedule of contact windows, which are used in the simulation section later, from rovers to satellites are shown in Table 3 and Table 4. For example, we have , for t in , , or , and 0 otherwise.

Table 3.
Contact windows for Perseverance Rover (PR) and Curiosity Rover (CR) with satellites.

Table 4.
A simulated contact window between a rover and a satellite.
For satellite j and antenna-k, we also define
For instance during 00:00–04:50, the DSN antenna in Spain open at for time interval 00:00 to 00:01, for time interval 00:01 to 00:02, until for time interval 04:49 to 04:50.
Due to the very long distance between Mars and Earth, there is a delay time in delivering data. Using the speed of light 299,792 km/s, the shortest travel time, called , to send a signal (One-Way Light Time) at closest approach (∼54.6 million km) is calculated as follows.
This travel time needs additional transfer time based on the data size. For example, if 2 Megabits data are transferred and the transfer rate is 256 kilobits per second (kbps) or 0.256 Mbps, the transfer time is
This additional time is quite small so we do not add this to the travel time for simplicity.
Using the travel time calculation, the average travel time is approximately 12 min. For simplicity, we set the delay time to be the same for all times, but the algorithm facilitates the different delay times in the variable for sending a data packet from rover j to antenna k. A data packet is safely delivered from Mars to Earth if and . In this paper, we set min for simplicity.
2.2. Arrangement of Data
Data size is generated randomly between KB up to KBytes per minute. Due to the link capacity of the rovers, the data should be distributed into packets whose maximum size is 256 KBytes.
where KBytes for all w.
A starting node for delivery is set for each packet. The vector Starts is an -sized vector containing the initial node of each data packet. For , Starts
where PR is Perseverance Rover and CR is Curiosity Rover.
Sending data can be started at the same time, but the route taken needs to be different due to the limited capabilities of the links that are used. The delivery of several data packets can be performed at different times if the link to be taken is already fully occupied, so that all data cannot be passed at the same time.
2.3. Routing Management for the Combination of Rover and Satellite
For and , the data will be sent from rover i to satellite j. The choice of satellite j depends on the following conditions:
- (i)
- The contact window between i and j is open, or ;
- (ii)
- for all w with , and the storage is not full;
- (iii)
- There is any DSN-antenna k, such that .
Condition (ii) means we choose the satellite with the maximum current storage capacity among others. The satellite j may be selected from the second maximum if the first maximum’s storage capacity is exhausted, or from the third maximum if the first and second ones are exhausted, and so on. If all satellites are exhausted, the data will be deleted. Those receiving the data on Earth would notice this sending failure, so they would transmit a new command to the sending rover to create the same data to be sent at a consecutive time. For time , if and , then .
If Condition (iii) cannot be satisfied or for all k, the data are stored to satellite j, satisfying Condition (ii). Sometimes, when there is antenna k and satellite j, such that but ; therefore, for all , so satellite j cannot be chosen.
At minute t, if there are data packets from vth-packet to th-packet stored in satellite j, , then the size of these data packets is written as storsats.
The indices of the non-zero entries of this variable identify the satellite indices that hold data while there is no contact window between satellites and DSN antennas, from the previous minute until time t.
For time and data packets , if , , and , then .
Information of the storing satellite j is put into the variable r, where
where index-i is 1 or 2, depending on the departure rover.
2.4. Routing Management for the Combination of Satellite and DSN Antennas
For and , the data will be sent from satellite j to DSN-atenna k if . There are two situations, as follows.
- and , so data are delivered smoothly from Mars to Earth in the same time.
- When there is only and there are data being stored at satellite j from the previous time interval(s).
The first situation needs to find which j is being considered. If and , we invert Equation (12) as follows:
In the second situation, we cannot use variable , because it does not discriminate between stored and carried-through data. The stored data at time t can be a collection of data from a few minutes before the current time t. We look for all indices j satisfying . The stored data are once more divided into packets with a maximum size of 256 KBytes per packet. The total number of these packets is added to the number of data originally being handled at time t, which is .
2.5. Plotting the Graph
For plotting directed graphs, the variable must be transformed into certain routes in various time intervals. Let us see an example for minute t. Matrix x has zero entries except in the following positions and their representation.
- x means , and x means , so packet-1 is delivered in routes ;
- x means , and x means , so packet-2 is delivered in routes ;
- x means , so packet-3 is delivered in route ;
- x where , so packet-3 is delivered in route .
No. 3 and 4 are deliveries of stored data from the previous minutes.
To plot a directed graph, we must specify two collections of edges. The nodes that indicate routes from a satellite and a rover are collected by frstedges, and the nodes that indicate paths from a satellite and a DSN antenna are collected by scndedges.
First, we collect all the indices of rows and columns of x which have non-zero entries, or one to be specific. Note that the first dimension of x is p, and its second dimension is the route label owned by data packet-1 to data packet-. The resulting information is defined as a matrix Idxmat. So, this matrix has two columns; the first column is the step of p and the accumulated label of the route being considered. From the example in the above paragraphs
Remember that we have r with . Packet-2, in the example, or no.2, has and . The indices become and , respectively, in rows 3 and 4 of the matrix. The accumulated labels of packet-3 have an additional for the labels and , respectively.
To transform them into the original value of a route label between 1 and 36, we first use the command to compute the remainder when the value is divided by 36. Later, they are interpreted as the indices of rovers and satellites using Equation (13), and indices of DSN antennas using the following equation.
Now, let be a vector containing indices of Idxmax in (14) whose first column entry is 1, which means routes between a rover and a satellite. Also, define to be a vector containing indices of Idxmax in (14) whose first column entry is 2, which means routes between a satellite and a DSN antenna. If the size of is greater than the size of , then there are data being sent and stored to some satellites. If the size of is less than the size of , then there are additional routes for delivering stored data. Finally, we put all in frstedges, and all in scndedges. From the example above, we have
and the plot is in Figure 1. It shows that the edges in the left part come from frstedges and the edges on the right part come from scndedges.
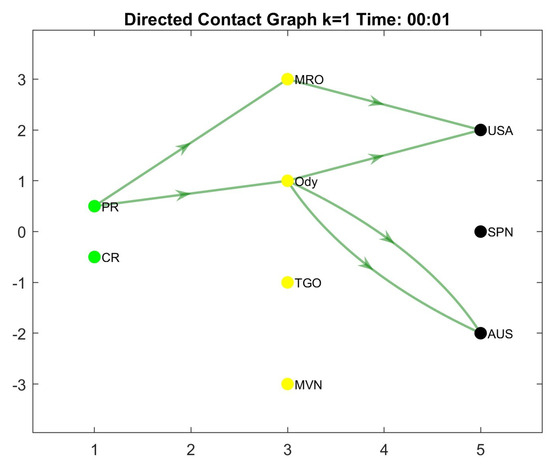
Figure 1.
Plot of the example.
3. Algorithms of the Model
We develop the program using MATLAB R2023b. The main program, procedures RoverSatelliteRouting and SatelliteAntennaRouting, are shown in Algorithms 1, 2, and 3, respectively .
| Algorithm 1 Main Algorithm |
|
| Algorithm 2 Procedure RoverSatelliteRouting |
|
In Algorithm 1 Step 5, we use for evaluating Equation (1), where we look for the number of all possible edges/pairings between two nodes and their dimensions. Steps 8–11 define the variable ids in Equation (3). Every time t, the contact windows of each node are drawn from an external file named ContactWindows, which contains schedules such as in Table 4.
In Algorithm 2 Step 5, we sort the capacity of satellites, based on the access matrix and the contact windows, in descending order. The result is in vector . The index of the satellite whose maximum capacity is , which is chosen as the relay satellite; see Step 10. If this satellite finally has full capacity, its index will be deleted from the variable ; see Step 18. If the capacity is zero, it will begin from satellite 1, which is always zero. This phenomenon is used to check whether there is an index of open satellites still available in the vector or not; see Step 11. If there is an open connection between the chosen satellite and any DSN antenna, then the data will be stored in the satellite; see Step 16. In this procedure, the capacity of the satellite is always checked. If the sum of stored data sizes is greater than the capacity, the latest data sent to the satellite will be deleted. Satellite Odyssey has very limited capacity, so in case 4 of the simulation for one sol, the excess data can be seen as a loss.
Procedure is written in Algorithm 3. This algorithm manages the deliveries of data at a delay time, and of data being stored in satellites due to the nonexistence of open contact windows to all antennas from the previous time. If route is open, or , we save the size data being sent in . Note that it also means that , where route was traveled by the data minutes ago. In Step 25, the stored data are kept again for a longer time due to the nonexistence of open contact windows from a satellite to all antennas.
| Algorithm 3 Satellite–Antenna Routing |
|
4. Simulation Results and Discussion
We simulate contact windows between Mars rovers and satellites and between satellites and DSN antennas on Earth. We simulate three cases to see the performance of the algorithm in the storing, carrying, and forwarding processes due to the timely changes of the contact windows. The simulated storage for each satellite is MRO ( = 20 GB), Odyssey ( 8 MB), TGO ( 16 GB), and Maven ( 16 GB).
We simulate the data delivery for one Martian day. For constructing contact windows of rovers–satellites and satellites–DSN antennas, we need information on the time when the satellite is above the rovers and is within reach of an antenna. Satellites MRO, Odyssey, and TGO typically have 2–6 contact windows per sol for each rover, and MAVEN has 5–6 contact windows per sol. However, the data are unavailable due to the fluctuation of the time interval. We use contact windows using the predicted time when each satellite most frequently overpasses each rover during a day, which is shown in Table 3. In this simulation, we set Table 4 as an example of the detailed contact windows. The DSN antennas are assumed to open to all satellites for certain intervals: 08:56–15:13 (USA), 00:00–04:50 and 22:43–24:00 (Spain), and 15:13–21:31 (Australia).
The simulation results of data deliveries from rovers to satellites are shown in Figure 2. Figure 3 shows the data received by DSN antennas for one Martian day. We demonstrate the performance of our algorithm in four cases.
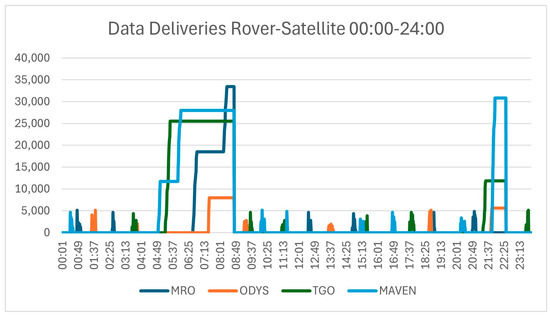
Figure 2.
Data deliveries from rovers.
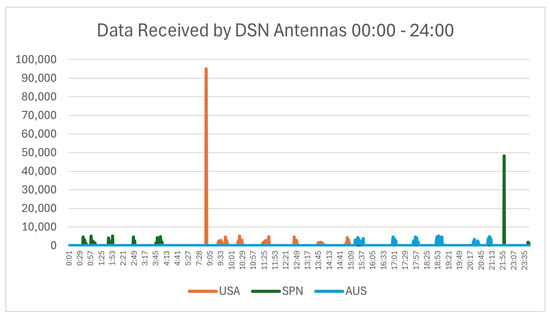
Figure 3.
Data deliveries from Rrovers.
Case 1. We show the deliveries of data from a rover that are delayed by 12 min for their arrival on Earth. Based on Table 4, the first contact window of the day is from 00:25 to 00:34 between the Perseverance Rover (PR) and MAVEN (MVN). In Table 5 and Figure 4a, a data delivery starts at 00:25, containing nine packets with a size of 2304 KBytes. The data are received by the Spain antenna (SPN) at 00:37 due to a delayed time; see Figure 4b. Some data are sent consecutively and received with the same delay. In other contact windows in a whole day, the data can be sent in the expected time based on the expected delay time.

Table 5.
Case 1: Delay on data deliveries.
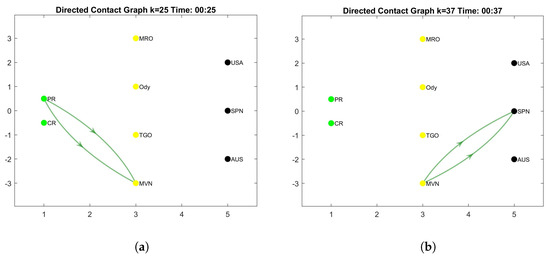
Figure 4.
Case 1: (a) Sending data at 00:25, (b) receiving data at 00:37.
Case 2. Based on the simulated contact windows in Table 4, it is very rare to have data delivery from one rover to two or more satellites at once, because it is very rare that two or more satellites have overlapping contact windows. Neither do the DSN antennas. In this case, the contact windows of Odyssey and TGO overlap. PR has a contact window with ODY during 03:41–03:50. Additionally, CR already has a contact window with TGO during 03:34–03:48. Table 6 shows some data deliveries from PR and CR during 03:41–03:44, and those data are received by SPN during 03:53–03:56. Figure 5 shows the first data packets being sent and received in those time intervals. Data from both satellites are received by a DSN antenna in Spain.

Table 6.
Case 2: Deliveries of data from two rovers.
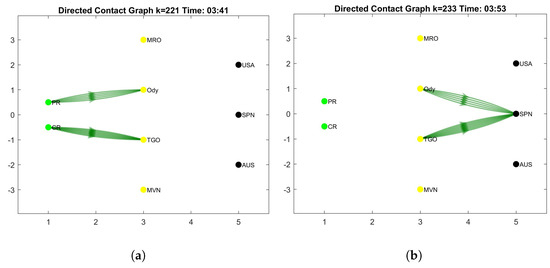
Figure 5.
Case 2: (a) Sending data at 13:41, (b) receiving data at 03:53.
Case 3. During the day, the possibility of a nonexistent contact window for the satellite and DSN antenna is high. If this occurs, data that have already been sent to the satellite should be kept in the satellite’s storage. Based on Table 4, there are nine time intervals of this occurance ranging from 4 to 45 min. In Table 7, the nonexisting contact window occurs frequently, so the accumulated data starting from 04:54 in MVN is kept for more than 4 h. During this time, MVN receives two series of data packets from CR and PR in different times. It also happens to MRO. As shown in Figure 2, all lines during this time have a flat horizontal segment, which indicates no change over the nonexistent contact window. Those lines drop to 0 at 08:44 when all data begin to be transmitted and are received by the DSN antenna in the USA at 08:56.

Table 7.
Case 3: Nonexistent contact windows.
There is a data deletion for deliveries to ODY during 07:29–07:35 due to its limited storage capacity. In this case, the operator of the USA antenna will know after 08:56, so a new request for the lost data is submitted in order to make CR send the data again.
Case 4: An overlap contact window from one rover to two satellites occurs when 21:46–21:58 (PR-ODY) and 21:50–21:58 (PR-MVN). When 21:50–21:58, data from PR should choose between ODY or MVN. The result in Table 8 shows that the data are sent to MVN instead of to ODY because MVN’s storage (16 GB) is bigger than ODY’s storage (8 MB). If it continues to send data to ODY until 21:58, 22,848 KB would be deleted because the ODY’s storage cannot keep data that are larger than 8000KB. Figure 6a shows data sent to ODY, and the destination satellite is switched to MVN in Figure 6b. When there is no available contact window after 45 min, all data are sent to SPN, as seen in Figure 6c.

Table 8.
Case 4: Selection of satellite.
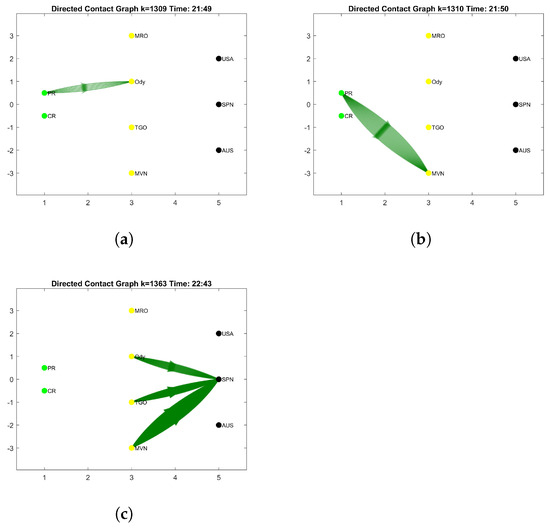
Figure 6.
Case 4: (a) Sending data at 21:49, (b) sending data at 21:50, (c) receiving data at 22:43.
We calculate the percentage of the data that are successfully sent from Mars to Earth. Through running the simulation multiple times, the results show consistently that about 96.4% data is successfully delivered to Earth. The running time of the algorithm is about 8.02 s.
5. Conclusions
In this paper, we construct a simulation of a Contact Graph Routing method for Mars and Earth data communication using two rovers, four relay–store–carry satellites, and three DSN antennas on Earth. Using the assumed window contacts, the successful rate of delivery is very high. However, we are aware that this rate is heavily dependent on the condition of the contact windows. The example in Table 3 shows well-distributed times for the contact windows; therefore, the rate could be worse if the only satellite that is open for connection for a long amount of time is Odyssey, where the rovers would have to deliver their data to this satellite since they have no other choice.
The number of satellites that are used can be increased in the algorithm by increasing the number of middle nodes. If we want to have ten relay satellites, we define nodes 3 up to 12 to be the relay satellites, so in total there are 15 nodes, where there are two initial nodes for the rovers (nodes 1 and 2), and the last three nodes represent the DSN antennas (nodes 13, 14, and 15). There is not much modification needed, except increasing the dimensions of the matrix x and related vectors.
We emphasize that the addition of nodes gives increasing numbers of rovers, satellites, or DSN antennas. The algorithm has utilized the optimized number of groups, which is three. It is not wise to increase this number because the travel time will significantly increase too. More numbers of rovers and satellites with different contact windows could increase the possibility of data delivery more continuously during the day.
The arrangement of satellites to be chosen as a route, or as a path that will be taken by a data packet, is ready to be prioritized in order. In this algorithm, the larger the storage capacity, the more likely it is to be chosen. The order of arrangement can be augmented by adding the probability that the satellite will have a contact window opened shortly or a pre-defined specific time interval.
For future research, we could consider using the CGR method on other forms of DTN, including Vehicular Delay-Tolerant Networks (VDTNs). This would give various potential benefits, such as semi-predictable mobility that improves performance through predictive routing, lower overhead (less flooding in contrast to methods based on epidemics), effective scheduling (forwarding matched contacts to contact availability), and delay awareness (able to give priority to the earliest delivery, which is helpful for data that are time-sensitive). A deep analysis would be needed for this potential development.
Author Contributions
Conceptualization, B.S.; methodology, K.A.S. and N.S.; software, B.S.; validation, B.S., K.A.S. and N.S.; formal analysis, B.S.; investigation, B.S. and N.S.; resources, B.S.; data curation, B.S.; writing—original draft preparation, B.S.; writing—review and editing, B.S. and N.S.; visualization, B.S. and N.S.; supervision, K.A.S.; project administration, B.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Acknowledgments
We thank people we contacted during this research project for their valuable information. We are very grateful for the invaluable inputs from the reviewers.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- ESA. Why Go to Mars? 2019. The Eropean Space Agency. Available online: https://www.esa.int/ScienceExploration/HumanandRoboticExploration/Exploration/WhygotoMars (accessed on 1 December 2024).
- NASA. 2024. Available online: https://eyes.nasa.gov/apps/mrn/#/mars (accessed on 1 December 2024).
- Birrane, E.; Burleigh, S.; Kasch, N. Analysis of the contact graph routing algorithm: Bounding interplanetary paths. Acta Astronaut. 2012, 75, 108–119. [Google Scholar] [CrossRef]
- Herkenhoff, K. Sol 1128: Twenty Minutes to Mars. 2015. Available online: https://science.nasa.gov/blog/msl-update-2442/ (accessed on 1 December 2024).
- Kugler, L. Direct-Dialing Mars? 2024. Available online: https://cacm.acm.org/news/direct-dialing-mars/ (accessed on 1 December 2024).
- Ormston, T. Time Delay Between Mars and Earth. 2012. Available online: https://blogs.esa.int/mex/2012/08/05/time-delay-between-mars-and-earth/ (accessed on 1 December 2024).
- Benamar, N.; Singh, K.D.; Benamar, M.; El Ouadghiri, D.; Bonnin, J.M. Routing protocols in Vehicular Delay Tolerant Networks: A comprehensive survey. Comput. Commun. 2014, 48, 141–158. [Google Scholar] [CrossRef]
- Elewaily, D.I.; Ali, H.A.; Saleh, A.I.; Abdelsalam, M.M. Delay/Disruption-Tolerant Networking-based the Integrated Deep-Space Relay Network: State-of-the-Art. Ad. Hoc. Netw. 2024, 152, 103307. [Google Scholar] [CrossRef]
- NASA. Mars Exploration Program Mars Relay Description for Discovery 2019 Proposals. 2019. Available online: https://discovery.larc.nasa.gov/PDF_FILES/21_Proposers_Guide_To_Mars_Orbiters_-_Discovery_2019_AO_-_Rev_190411b.pdf (accessed on 1 December 2024).
- Zurek, R.; Tamppari, L.; Johnston, M.D.; Murchie, S.; McEwen, A.; Byrne, S.; Seu, R.; Putzig, N.; Kass, D.; Malin, M.; et al. MRO overview: Sixteen years in Mars orbit. Icarus 2024, 419, 116102. [Google Scholar] [CrossRef]
- Burleigh, S.C. Contact Graph Routing: Draft-burleigh-dtnrg-cgr-01. 2010. Available online: https://datatracker.ietf.org/doc/html/draft-burleigh-dtnrg-cgr-01 (accessed on 1 December 2024).
- Fraire, J.A.; De Jonckère, O.; Burleigh, S.C. Routing in the Space Internet: A contact graph routing tutorial. J. Netw. Comput. Appl. 2021, 174, 102884. [Google Scholar] [CrossRef]
- NASA. 2024. Available online: https://science.nasa.gov/mars/facts/#h-size-and-distance (accessed on 1 December 2024).
- Dobrijevic, D. 2025. Available online: https://www.space.com/24701-how-long-does-it-take-to-get-to-mars.html (accessed on 1 December 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).