Abstract
Hybrid quantum–classical (HQC) computing refers to the approach of executing algorithms coherently on both quantum and classical resources. This approach makes the best use of current or near-term quantum computers by sharing the workload with classical high-performance computing. However, HQC algorithms often require a back-and-forth exchange of data between quantum and classical processors, causing system bottlenecks and leading to high latency in applications. The objective of this study is to investigate novel frameworks that unify quantum and reconfigurable resources for HQC and mitigate system bottleneck and latency issues. In this paper, we propose a reconfigurable framework for hybrid quantum–classical computing. The proposed framework integrates field-programmable gate arrays (FPGAs) with quantum processing units (QPUs) for deploying HQC algorithms. The classical subroutines of the algorithms are accelerated on FPGA fabric using a high-throughput processing pipeline, while quantum subroutines are executed on the QPUs. High-level software is used to seamlessly facilitate data exchange between classical and quantum workloads through high-performance channels. To evaluate the proposed framework, an HQC algorithm, namely variational quantum classification, and the MNIST dataset are used as a test case. We present a quantitative comparison of the proposed framework with a state-of-the-art quantum software framework running on a server-grade CPU. The results demonstrate that the FPGA pipeline achieves up to improvement in runtime compared to the CPU baseline.
1. Introduction
Quantum computing continues to generate interest as an emerging technology due to its theoretical ability to tackle unadaptable computational problems that are beyond the capability of traditional computing approaches [1]. Current quantum hardware, termed as noisy-intermediate scale quantum (NISQ) devices, can support intermediate-scale quantum algorithms in the range of 50 to 200 qubits. In the last decade, significant research thrust has been made towards investigating useful algorithms for NISQ hardware, particularly where the quantum processing unit (QPU) can be used as a co-processor along with classical high-performance computing (HPC). Currently, major research efforts worldwide have been launched and/or are ongoing towards realizing QC-HPC integration [2,3,4]. Most of these efforts involve the private sector, national laboratories, and academia developing the theory and software [5] necessary for the integration of QC-HPC. These works focus on two general types of integration: (1) loose integration, where the QPU is physically detached from an HPC system but connected by a network, either on or off premises, and (2) tight integration, where the QPU is located directly on an HPC node. The loose integration model is more practical today and in the near future; however, there are several crucial research challenges involved in developing such quantum–classical integrated systems. Firstly, computational bottlenecks arise in a system with both quantum and classical resources, with QCs having different latencies and I/O time than conventional processors, which have a sequential nature of execution. Secondly, there is a lack of cost-effective heterogeneous platforms facilitating rapid testing, prototyping, and benchmarking of integrated quantum–classical workflows. QC-HPC platforms that are undergoing development are not yet available to researchers, who require a cost-effective platform for developing and benchmarking hybrid quantum–classical applications before deploying them on actual large-scale systems. Thirdly, there is also a lack of unified software environments for deploying algorithms on quantum–classical architectures. In integrated environments, software schedulers are critical for efficient workload distribution and sharing among quantum and classical resources. These challenges have thus far hindered the progress of quantum–classical computing toward demonstrating computational advantage [6].
Reconfigurable computing is a computing paradigm that combines some of the flexibility of software with the high-performance of hardware by processing with cost-effective reconfigurable technology such as field-programmable gate arrays (FPGAs). The principal difference compared to conventional processors is the ability to add custom computational blocks using FPGAs. FPGAs have played critical roles in quantum computing: they are used as control processors to control and measure superconducting quantum processors [7,8]; they are used to develop low-latency scalable architectures for quantum error correction [9]; and they are also used for quantum circuit emulation/simulation [10,11]. Reconfigurable computing and FPGAs can play a critical role in hybrid quantum–classical computing [12] by providing the speed and flexibility needed for tasks like real-time feedback, high-bandwidth post-processing, and implementing optimization kernels, while QPUs handle compute-intensive quantum tasks. For example, variational quantum algorithms (VQAs) often employ hybrid quantum and classical resources. In VQAs, output samples from a quantum circuit are used in a classical feedback loop that optimizes the parameters of the quantum circuit such that some loss function is minimized. Here, the quantum circuit behaves as the model that learns patterns from the data variationally and produces predictions, while classical techniques such as stochastic gradient descent or Bayesian optimization are used for optimization [13].
In this work, we propose a framework that combines reconfigurable processing pipelines with quantum computation for accelerating hybrid quantum–classical (HQC) computing. Keeping in mind the challenges in HQC computing, we propose an FPGA-based solution that offers a cost-effective pathway to address the aforementioned limitations through hardware-level parallelization, customizable interfaces, and data flow architectures. By leveraging low-latency and power-efficient FPGA architectures, this research aims to develop an efficient framework that can significantly reduce the computational burden on traditional processors while enabling seamless integration with quantum processing units (QPUs). We focus on developing specialized FPGA kernels that can streamline iterative tasks in HQC computing, such as parameter optimization for variational quantum classifier circuits [14]. The FPGA kernels communicate with the QPUs through a host that synergizes the workload distribution in a unified software environment. The proposed framework also contains hardware kernels for quantum circuit simulation for cases where quantum processing hardware is unavailable. We use high-level synthesis [15] to accelerate FPGA hardware kernel development and integrate high-level software frameworks such as PYNQ [16] and Qiskit [17] for managing quantum and reconfigurable resources. We demonstrate that the proposed reconfigurable framework can be a cost-effective and user-friendly platform for deploying and testing HQC algorithms by performing quantitative comparison with a server-grade CPU. In this work, we emphasize integration and acceleration at the system level of quantum–classical systems, rather than innovation at the quantum algorithm level. Our contribution lies in designing a general-purpose, FPGA-accelerated framework capable of integrating with QPUs at a high-level of abstraction, to speed up the classical components of hybrid workflows. The use of well-known variational quantum classification serves as a proof-of-concept to validate the performance and feasibility of the proposed framework.
The remainder of the manuscript is organized as follows. Section 2 contains background concepts and discussions of work related to the intersection of HQC computing and reconfigurable computing. Section 3 details the framework proposed and used in this work. The experimental evaluations, results, and analysis are contained in Section 4. Section 5 provides the conclusion and discussion of future work.
2. Background and Related Work
2.1. Quantum Computing Fundamentals
Qubits, or quantum bits, are the basic units of quantum information [18]. Unlike classical bits, which can exist in one of two states (0 or 1), qubits can exist simultaneously in multiple states due to their quantum nature. Superposition [18] refers to the ability of a quantum system, like a qubit, to exist in multiple states at the same time. In the case of a single qubit, this means it can be in a state |0⟩ and |1⟩ or any linear combination of the two, represented as , where and are complex probability amplitudes. The probabilities of measuring the qubit in the |0⟩ or |1⟩ state are determined by the square magnitudes of the probability amplitudes: and . These probabilities add up to 1, which means that the qubit will collapse into one of the two states upon measurement. Entanglement [18] is a unique quantum phenomenon where two or more qubits become interconnected in such a way that the state of one qubit cannot be described independently of the state of the other, even when separated by large distances. This property is key for various applications in quantum communication, cryptography, and quantum computing, allowing for parallel processing and enhanced security protocols [19].
2.2. Quantum Gates
Quantum gates are unitary operations that change the state of qubits. Each quantum gate is associated with a specific matrix that describes its action on the state vector of qubits. A gate that acts on n qubits will be represented by a unitary matrix. We provide a brief description of some notable gates which have been used in this work.
- Hadamard Gate: A single-qubit gate that maps the basis state |0⟩ to and |1⟩ to , thus creating an equal superposition of the two basis states.
- RX, RY, and RZ Rotation Gates: These unitary operators rotate the state vector of a qubit around a given axis by a given angle. The RX gate is one of the rotation operators. It is a single-qubit rotation through angle radians around the x-axis. The RY gate is a single-qubit rotation through angle radians around the y-axis. Similarly, the RZ gate is a single-qubit rotation through angle radians around the z-axis.
- CNOT Gate: A universal two-qubit quantum gate that flips the state of the second qubit, the target qubit, if and only if the first control qubit is in the state |1⟩. A CNOT gate is used to entangle two qubits. Any quantum computation can be performed using only CNOT gates and single-qubit gates. The CNOT gate matrix can be derived from a unitary matrix by flipping the target states based on the control states.
2.3. Quantum Machine Learning
Quantum machine learning (QML) [20] is an interdisciplinary field that merges the principles of quantum mechanics with machine learning techniques to enhance data processing and analysis capabilities. This approach has the potential to outperform classical ML algorithms by utilizing unique properties such as superposition and entanglement. QML in the NISQ era usually incorporates a hybrid approach, integrating quantum computing circuits with traditional machine learning methodologies [21]. This integration has attracted significant research attention as it promises considerable improvements in speed and efficiency for complex computational tasks [22]. A variety of QML algorithms have been proposed to capitalize on quantum computing advantages. The variational quantum classifier (VQC) [23] and quantum support vector machines (QSVM) [24] are notable examples. The VQC algorithm employs parameterized quantum circuits that are trained using classical optimization loops. The circuit parameters are trained using traditional approaches such as stochastic gradient descent, adaptive moment estimation (ADAM), and constrained optimization by linear approximation (COBYLA), significantly enhancing performance for specific tasks [20]. Hybrid QML algorithms have the potential to process large datasets more effectively than their classical counterparts, which is crucial in high-dimensional applications [25].
2.4. Related Work
Numerous ongoing efforts [5] are investigating hybrid quantum–classical applications, and some of the recent and relevant work is discussed here. The work by Giortamis et al. [3] proposed a cloud orchestration framework for quantum–classical applications that run on heterogeneous systems. Here, a high-level and hardware agnostic software environment was developed, which includes a resource estimator and scheduler running on software. A major research effort at Oak Ridge National Laboratory (ORNL) [2] focuses on integrating QPU capabilities into existing HPC workflows. Their framework integrates hardware and software workflows in a synergistic environment for quantum and classical resources, focusing mostly on CPU/GPU heterogeneity. Another multi-institutional collaborative research effort [26] is investigating the possibilities and challenges of QC-HPC for use in materials science. A collaborative effort led by IBM [4] investigated research ideas for quantum-centric supercomputing for use in quantum chemistry and quantum simulations of chemical reactions. The results of their work showed that classical HPC coupled to quantum resources can produce better approximate solutions to quantum simulation problem sizes that are intractable for classical-only or quantum-only systems.
A recent study by Bach et al. [12] introduces a hybrid quantum–classical CNN deployment specifically tailored for FPGA hardware, integrating parameter quantization and a novel quantum layer leveraging Hilbert vector space computations. Despite its success, demonstrated through improved speed and accuracy on the MNIST dataset, the Bach et al. approach remains algorithm-specific, primarily optimized around their unique CNN architecture. This specialization limits its applicability across diverse quantum–classical computing applications. FPGA usage in quantum–classical systems has mostly been restricted to specific tasks, such as qubit control processors [7,8], qubit readout error mitigation [9], and specialized simulation or emulation frameworks [27,28,29]. These specialized frameworks, while effective in achieving considerable speedups over traditional simulators, are typically algorithm-specific [30] and often pose challenges for novice users due to complexities involved with RTL or HLS tools.
In contrast, our proposed research aims to establish a generalized FPGA-based framework capable of accelerating classical subroutines integral to a wide variety of hybrid quantum–classical (HQC) algorithms. Unlike algorithm-specific implementations, our approach emphasizes flexibility, enabling adaptation across different computational tasks by leveraging FPGA characteristics such as high throughput and low latency. Additionally, our unique contribution lies in demonstrating how FPGAs can synergize with quantum processing unit (QPU) accelerators to achieve significant computational advantages. A major research thrust of this effort involves developing a high-level methodology that seamlessly integrates the management of FPGA resources and quantum resources through a unified software stack. Thus, our methodology not only demonstrates FPGA’s potential to accelerate classical computations within quantum–classical workflows but also advances accessibility and usability, paving the way for broader adoption in QC-HPC hybrid systems.
3. Proposed Framework
An overview of the proposed framework is shown in Figure 1. The novel characteristics of the framework are (1) a library of reconfigurable hardware kernels on an FPGA to accelerate quantum–classical algorithms and (2) a unified software stack on the host enabling communication between quantum and reconfigurable resources. The proposed framework can be implemented on any heterogeneous platform containing a host processor connected to a reconfigurable processor or FPGA device. The host contains the main memory where input and output data will be stored. The host code of the hybrid algorithm containing classical and quantum subroutines is executed on the host processor using the unified software stack. The software stack defines the API and functions to control data transfer to/from the QPU and FPGA device during the respective subroutine call. When the quantum subroutine is deployed, the host processor establishes communication with the quantum processing unit (QPU) on the cloud, sends the quantum circuit job to the QPU, and waits for the results. The classical subroutines are deployed on the FPGA’s partial reconfigurable regions (PRRs) as hardware kernels. A hardware kernel manager and memory controller exist as part of the static region (SR) on the FPGA device. The memory controller is responsible for DMA transactions for high-bandwidth data transfer between host and device. We describe in detail the application of this framework for a quantum machine learning and classification problem in the next sections.
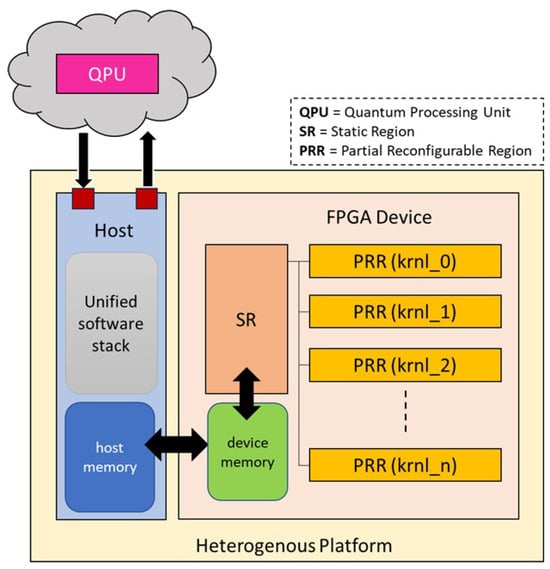
Figure 1.
Reconfigurable framework for hybrid quantum–classical computing.
3.1. Quantum Machine Learning Task
The overview of the quantum machine learning task is shown in Figure 2. This task is split into five stages: data generation, data pre-processing, quantum circuit execution, training, and evaluation. The data generation and pre-processing stages are performed on the host machine CPU and involve functions such as normalization, encoding, feature extraction, and test/train splitting. The details of these functions along with the dataset are elaborated in Section 4.
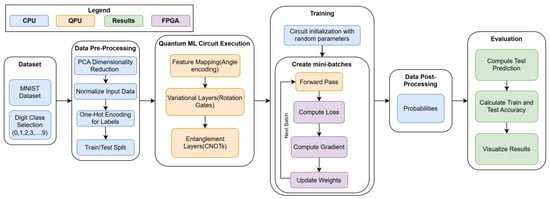
Figure 2.
QML workflow for a quantum machine learning task.
3.1.1. Host Management and Unified Software
Aside from the aforementioned functions, the host also manages the interaction between the QPU and the FPGA accelerator. The host memory management system plays a crucial role, handling the allocation of physically contiguous memory buffers and ensuring proper synchronization between host and FPGA device memory spaces. Additionally, the host carefully manages cache coherency and provides efficient mechanisms for high-bandwidth data transfer to/from the FPGA. Memory management on the host is implemented using a unified buffer allocation system that allocates buffers on the host and device sides, establishing a robust framework for data transfer between the host and FPGA. Several key buffers are allocated: prediction buffers for immediate predictions, extended prediction buffers for batch processing, weight buffers for parameter storage, gradient buffers for optimization computations, and loss buffers for performance tracking. All buffers utilize numpy’s float64 data type to maintain high numerical precision.
Data flow in the host system follows a structured pipeline, beginning with quantum circuit parameter preparation followed by data pre-processing and normalization. The system implements batch processing for training optimization, where each batch of data undergoes quantum circuit simulation before being processed by the FPGA accelerator. Memory synchronization is maintained through and high-level methods which enable ease-of-use, ensuring data coherency between host and FPGA memory spaces.
The host implementation carefully manages the training loop, implementing mini-batch gradient descent optimization. Within each training iteration, the system coordinates data movement between quantum circuit execution on QPU and FPGA acceleration, handles weight updates based on computed gradients, and monitors training progress through loss computation and accuracy metrics. This architecture enables efficient parallel processing of quantum circuit parameters while maintaining the flexibility of quantum circuit execution on the QPU.
3.1.2. Quantum Circuit Generation
After the data pre-processing stage, the prepared data are to be used in the quantum circuit generation stage. In this stage, a trainable, parameterized quantum circuit representing the machine learning model will be constructed using the prepared data as the circuit’s parameters. This quantum circuit is the quantum equivalent of a classical neural network, and the circuit parameters are equivalent to the network’s weights. The circuit architecture is the conventional RealAmplitudes circuit architecture from Qiskit’s circuit library [31], which is tailored for quantum machine learning tasks using real-valued parameters. The circuit structure incorporates an n-qubit system with variational layers. This can be represented by Equation (1), where denotes the final quantum state, represents the i-th variational layer with trainable parameters (for i from 1 to L), is the feature encoding layer for input data x, and is the initial state of the n qubits. The circuit begins with the initial state , representing an n-qubit quantum register initialized to the zero state. The operator is the data encoding unitary, which maps the classical input x into a quantum state. Following this, a sequence of L parameterized unitary operations is applied, where each represents a trainable unitary gate or block with associated parameters . These operations collectively form the variational layers of the quantum model. The composition of these gates yields the final state , which is typically measured to extract information relevant to the task at hand.
The circuit architecture consists of the following:
- Feature mapping layer:
- −
- Initializes qubits with Hadamard (H) gates for superposition.
- −
- Applies RY rotations for data encoding.
- −
- Parameters encode input features into quantum states.
- Real amplitude variational structure:
- −
- Builds on RealAmplitudes design with five variational layers.
- −
- Each layer implements alternating rotation blocks:
- *
- Three-axis rotations (RX, RY, RZ) for single-qubit operations.
- *
- Full entanglement pattern using CNOT gates between adjacent qubits.
- *
- All parameters initialized randomly from normal distribution N(0, 1).
- *
- Comprises (five layers × qubits × three rotations) trainable parameters.
During the circuit creation, we ensure that circuits are created with variational layers limited to five layers and full entanglement scheme, producing a rich quantum feature space and leveraging superposition and entanglement for enhanced pattern recognition. The number of variational layers is limited to avoid issues such as the barren plateau problem [32], where the gradients of the cost function can shrink or vanish exponentially with an increase in the circuit depth or number of qubits. The randomly initialized parameters are optimized during training to learn the classification task while maintaining quantum mechanical properties throughout the computation, allowing the circuit to capture complex data patterns through the multi-layer quantum transformations. Figure 3 represents the quantum circuit. Initial Hadamard gates (H) are shown in the orange boxes at the start of each qubit line; the red boxes represent the parameterized rotation gates (RX, RY, RZ). Each rotation gate displays its initialized random parameter value (e.g., RY = −0.853, RX = −0.626), while the CNOT connections between adjacent qubits show the full entanglement pattern.
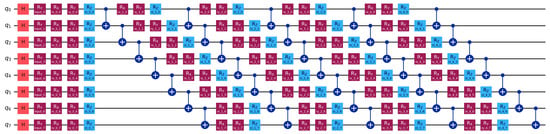
Figure 3.
Parameterized quantum circuit for QML (4 variational layers shown).
3.1.3. Training: Forward Pass Function
In quantum machine learning, the inability to store and utilize the results of intermediate quantum operations on hardware remains a limitation to using classical ML techniques such as backpropagation to compute gradients and update parameters/weights. Most QML algorithms therefore implement a parameter shift rule mechanism [33] that enables the dynamic updating of circuit parameters during the training process. This is achieved through a circuit forward pass function implemented in the training stage (Figure 2), which takes both input data and variational parameters as arguments. This forward pass function executes three critical operations: parameter binding, circuit execution, and probability extraction. Parameter binding combines input features and trainable weights into a unified parameter vector, which is then used to configure the quantum circuit generated in the previous stage. The next step is to execute the circuit, either on a QPU or a simulator. For this work, we have utilized a state vector simulator running on the host CPU for mimicking the QPU operations in our framework. After executing the quantum circuit, the output probabilities need to be calculated. The forward pass function for simulation is defined in the following listing:
- def forward(x, weights, circuit, input_params, weight_params):
- param_values = list(x) + list(weights)
- bound_circuit = circuit.assign_parameters(param_values)
- state = Statevector.from_instruction(bound_circuit)
- return state_to_probs(state.data)
The Statevector.from_instruction method simulates the complete circuit execution, producing a final state vector that encodes the processed information. The state_to_probs function then extracts classification probabilities by computing the squared magnitudes of relevant amplitudes, effectively implementing a quantum measurement process.
3.1.4. Training: Gradient Computation and Loss Function
The gradient computation mechanism implements a stochastic gradient descent approach for parameter optimization, which is designed to handle the complexities of quantum circuit training. This process begins with a forward pass of the circuit using the current weights to establish a baseline prediction and loss value. A matrix of perturbed weight configurations is generated, where each weight is independently perturbed by a small epsilon value, , to maintain numerical stability. This perturbation size is carefully chosen to balance numerical stability with accuracy; too large an epsilon would result in poor gradient estimates, while too small a value could lead to numerical instability due to floating-point arithmetic limitations. A key optimization in this implementation is the batch processing of forward passes for all perturbed configurations, which significantly reduces the computational overhead compared to sequential processing. We also designed a kernel that computes cross-entropy loss values for each perturbed configuration, handling numerical stability through careful epsilon-based adjustments. The final gradient computation approximates partial derivatives through finite differences, calculating (Loss_perturbed − Loss_original)/epsilon for each parameter.
We implement a mini-batch processing strategy in the quantum–classical hybrid learning system that balances computational resources with optimization stability. The system processes data in small batches, where each batch undergoes quantum circuit evolution followed by classical parameter updates (Figure 2). The process begins with shuffling the training data to prevent learning biases, then iterates through the batches, computing the quantum state creation for each sample using the state vector simulator. For each batch, gradients are computed using the stochastic gradient descent (with ) and averaged across the batch samples, providing more stable parameter updates compared to single-sample training. The gradient for each parameter using finite differences can be expressed as
where
- are the circuit parameters.
- is a small perturbation ().
For batch gradient averaging (mini-batch size B),
where represents the loss calculated on the sample of the mini-batch. The forward pass function maps input data to quantum states through parameterized circuit operations, while the loss function with added numerical stability () computes the cross-entropy loss between predicted and actual outputs. The cross-entropy loss for a single data sample with actual label y and predicted probability (from the quantum circuit output) is
where
- is the quantum circuit prediction probability for the positive class (output from the quantum circuit after forward pass).
- is the actual label.
- is a small constant added for numerical stability to avoid .
For a mini-batch of size B, the loss function is averaged over the batch:
This batched approach effectively reduces computational overhead by averaging gradients across multiple samples before updating circuit parameters, while maintaining training stability through consistent gradient estimates. The implementation achieves this by accumulating gradients over each batch.
We implement a processing pipeline on the FPGA, see Figure 4, which consists of multiple kernels performing optimized parameter optimization specifically designed for quantum circuit training. The kernel architectures are structured around efficient gradient computation and weight updates, utilizing high-level synthesis compilers to synthesize C++ descriptions of the kernels to hardware description language. The pipeline employs multiple AXI interfaces for data communication: AXI Master interfaces for high-bandwidth data transfer and AXI-Lite Slave interfaces for managing control and status signals. The kernels perform three critical computations:
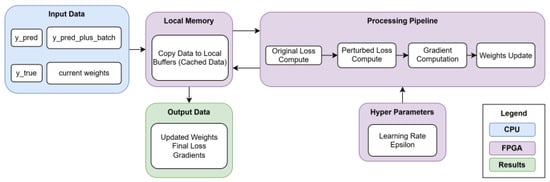
Figure 4.
FPGA pipeline architecture with multiple kernels.
- Loss calculation: Implements parallel cross-entropy loss computation using optimized log-likelihood functions.
- Gradient computation: Accelerates stochastic gradient descent calculations through block processing.
- Weight updates: Performs parallel parameter updates using computed gradients and configurable learning rates.
As illustrated in Figure 4, the Input Data block initiates the process by transferring predicted outputs (predicted probabilities generated by the quantum circuit for the input data), perturbed outputs (model outputs from perturbed forward passes used for gradient estimation), ground-truth labels , and the current circuit parameters from the host memory to the on-board (local) memory. This transfer is optimized using separate LOAD_WEIGHTS and LOAD_BLOCK pipelines for burst transfers and localized access, minimizing latency and improving throughput.
The kernels define the generalized input and output interfaces using HLS pragmas, as shown in Figure 5. Scalar inputs such as the learning rate (used for parameter updates), the stability parameter (used to prevent numerical instability in division and logarithms), the number of qubits , and the number of circuit layers are configured via the AXI-Lite control registers generated by #pragma HLS INTERFACE s_axilite. This interface allows the host processor to dynamically adjust these parameters at runtime, enhancing the flexibility and reusability of the kernel. To avoid an inflexible design, the kernel does not hardcode and , thus supporting various quantum circuit topologies without requiring recompilation.

Figure 5.
HLS pragma interface.
High-bandwidth memory transfers for array inputs, specifically (probabilities from the quantum circuit based on current model weights), (probabilities from the quantum circuit based on perturbed weight configurations), (ground-truth labels), and (current values of model parameters), as well as array outputs including (computed gradients for each parameter), (parameter values after the optimization step), and (computed loss value for the current mini-batch), are achieved using AXI-Master ports specified via #pragma HLS INTERFACE m_axi. This directive allows the host to supply the base addresses of memory buffers, enabling the FPGA to perform direct memory access (DMA) for efficient data movement. This significantly enhances the throughput of data between host and FPGA on-board memory, especially for large batch sizes or complex quantum circuits.
The processing pipeline block is the computational core, where the three critical computations (loss calculation, gradient computation, and weight updates) occur. The initial loss calculation block takes the predicted probability vector and the true label vector as input. It calculates the baseline cross-entropy loss using the negative log-likelihood function , where is the predicted probability, with hardware-optimized logarithmic units and #pragma HLS UNROLL for parallel computation. This hardware optimization, achieved by translating hls::log() into dedicated FPGA logic using techniques like CORDIC and lookup tables, significantly reduces latency and increases throughput compared to CPU-based methods, which is crucial for iterative gradient calculations. The output is the original_loss value.
The perturbed loss is calculated by first slightly altering each weight in the model, generating a new set of predicted outputs stored in . Within the kernel’s perturbed loss compute block, these perturbed predictions are loaded into , and the loss is then computed using the same negative log-likelihood formula as the original loss: . This process leverages #pragma HLS ARRAY_PARTITION and #pragma HLS UNROLL directives for efficient data handling. It determines how changes in individual weights influence the model’s loss. This provides the necessary information for gradient computation and subsequent weight updates during the optimization process.
In the processing pipeline, the gradient computation (accelerating stochastic gradient descent calculations through block processing) and weights update (performing parallel parameter updates using computed gradients and configurable learning rates) stages perform critical calculations. Gradient descent updates the weights by first calculating the gradients using (perturbed_loss − original_loss)/epsilon, see (2) and (3), where original_loss and perturbed_loss are loss values before and after weight perturbation, and epsilon is a small perturbation value. Each gradient, representing the loss function’s slope with respect to the corresponding weight, is then used to update the weights according to (6).
where controls the step size. This pipeline leverages #pragma HLS UNROLL and #pragma HLS ARRAY_PARTITION on weights_local and pred_plus_buffer to parallelize computations across blocks of 16 elements (BLOCK_SIZE) and HLS_PIPELINE II=1 directives to maximize throughput.
The hyper-parameters block supplies the necessary scalar values learning_rate and epsilon, which are interfaced via AXI-Lite. The kernel takes original_loss, perturbed_loss, the current weight , , and epsilon as inputs and outputs the calculated and the updated weight . This process iteratively adjusts weights, optimized for parallel execution and high throughput, to minimize the loss function, effectively accelerating the quantum circuit’s parameter optimization. Finally, the output data block transfers the updated weights, final loss, and gradients back to the host memory. This pipeline-based approach, with targeted HLS optimizations and explicit interface definitions, efficiently utilizes the FPGA’s resources, significantly accelerating the weight optimization process for quantum circuit training.
4. Experimental Results
4.1. Experimental Setup
Our implementation was carried out on the Vitis Unified Platform, using the PYNQ (Python Productivity for Zynq) framework [34] (version 3.0.0), which provides a Python-based environment (version 3.10) for FPGA development. The entire code base was developed and executed through PYNQ’s Jupyter notebook(version 3.4.4) interface, enabling interactive development and real-time result visualization.
The server CPU is a 16-core, 3.0 GHz AMD EPYC 7302P [35] with 128 GB of system memory, and operating with both 32-bit and 64-bit architectures. The CPU configuration includes a substantial cache hierarchy, featuring 512 KiB L1 cache (sixteen instances), 8 MiB L2 cache (sixteen instances), and 128 MiB L3 cache (eight instances). The processor operates at a base frequency of 1500 MHz with a maximum boost frequency of 3000 MHz, utilizing AMD-V virtualization technology. The OS is Ubuntu 18.04 LTS with the Linux 4.15.0-20-generic kernel.
The FPGA device is part of the Alveo U200 (XCU200-2FSGD2104E) [36]. The platform features extensive computational resources, including 1,182K lookup tables (LUTs), 2364K registers, 6840 DSP slices, and 960 UltraRAMs. The memory subsystem provides 64 GB DDR total capacity with a maximum data rate of 2400 MT/s and a total bandwidth of 77 GB/s. Connectivity is facilitated through a PCIe Gen3 x16 interface and dual QSFP28 network interfaces. The processor’s architecture supports advanced security features and mitigations. This robust host configuration, combined with the FPGA resources, creates a powerful platform for accelerating complex computational workloads, particularly in quantum computing applications where both CPU processing power and FPGA acceleration capabilities are crucial. A comparison of the FPGA and CPU resources is given in Table 1.

Table 1.
FPGA accelerator board and CPU resources.
4.2. Dataset Generation and Pre-Processing
The experimental analyzes presented in this study utilize a systematically selected and processed subset of the MNIST dataset [37], specifically focusing on digits ‘0’ and ‘1’ to establish a well-defined binary classification scenario. MNIST is a widely recognized dataset comprising handwritten digit images that are pixels in size, which is extensively employed in image recognition tasks due to its clarity and structured patterns, making it ideal for benchmarking QML algorithms.
4.2.1. Dataset Selection and Initial Processing
We begin by extracting a balanced subset from the MNIST dataset containing only the digits ‘0’ and ‘1’. The decision to select these digits was motivated by their distinct visual patterns, which facilitate clear classification tasks and enable a more robust evaluation of quantum–classical architectures. Formally, the selected dataset is defined as
where n is the total number of extracted samples, each of which is represented initially by 784 pixel intensity values (flattened from a image).
4.2.2. Dimensionality Reduction via Principal Component Analysis (PCA)
Given the computational limitations and architectural requirements of quantum circuits, it is critical to map classical data efficiently into quantum states. To achieve this, we implement principal component analysis (PCA) [38], a linear dimensionality reduction technique designed to preserve maximal variance in the data while reducing feature space dimensionality. PCA transforms original features into a set of linearly uncorrelated principal components (PCs), capturing the most significant data variance.
PCA is performed using the covariance matrix decomposition
Eigen decomposition of the covariance matrix yields principal components:
where are eigenvalues sorted in descending order and are corresponding eigenvectors. For our experiments, PCA reduces the data dimension from 784 to q, where q directly corresponds to the number of qubits used (i.e., ).
4.2.3. Analysis of Variance Distribution
As shown in the left side of Figure 6, the explained variance distribution across principal components follows a characteristic pattern for image data. The first component captures approximately 22% of the total variance, with subsequent components showing diminishing contributions. This distribution reflects the inherent structure of the MNIST digits, where most of the discriminative information is concentrated in a few dominant patterns. The right side of the Figure 6 shows the cumulative explained variance as we add more principal components. With all 11 components, we capture approximately 57% of the total variance in the original 784-dimensional MNIST data. This means that despite reducing the dimensionality by 98.6% (from 784 to 11 dimensions), we preserve more than half of the information content. The graph shows a steep initial increase, with diminishing returns as more components are added, which is characteristic of effective dimensionality reduction. The first five components already capture about 44% of the variance.
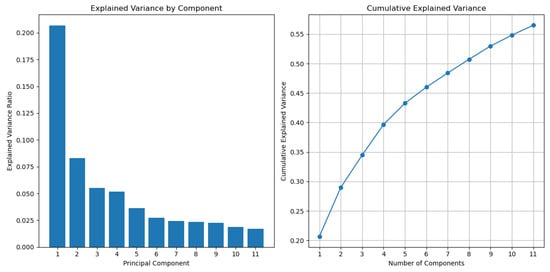
Figure 6.
Explained variance distribution and cumulative explained variance for up to 11 qubits.
Figure 7 visually demonstrates the effect of our PCA transformation on sample digits. The top row shows the original MNIST digits ‘0’ and ‘1’, while the middle row displays their PCA reconstructions using eight principal components. Despite the significant dimensionality reduction, the reconstructed images retain the essential characteristics needed for classification. The bottom row visualizes the first eight principal components (PC 1-8) as spatial patterns. PC 1 clearly captures the fundamental circular structure distinguishing ‘0’ from ‘1’, while subsequent components encode increasingly subtle variations. These visual patterns confirm that our PCA implementation successfully extracts the most discriminative features for quantum encoding.
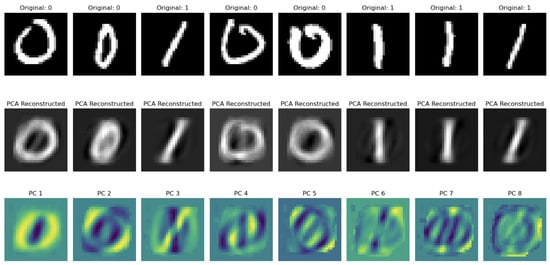
Figure 7.
Original input digits and after PCA extraction.
4.2.4. Quantum-Compatible Data Scaling
To ensure compatibility between classical data and quantum state initialization via rotation gates, data scaling to angles suitable for quantum gate encoding is performed. Each principal component feature is linearly mapped to the range radians, aligning with quantum state preparation protocols utilized in quantum computing:
This scaling procedure ensures efficient and accurate representations of classical data within quantum state vectors.
4.2.5. Binary Label Encoding
Labels are encoded into one-hot vectors to facilitate integration with neural network components in quantum–classical hybrid architectures:
4.2.6. Dataset Splitting
For model training and evaluation, the processed dataset is partitioned into training and test sets using a stratified 80–20 split, maintaining an equal distribution of class labels in both subsets. Stratified sampling preserves class balance and ensures representative training and testing conditions:
A fixed random seed is used to guarantee the reproducibility of the results in repeated experiments. This carefully designed data pre-processing pipeline ensures efficient, quantum-compatible data representation, supporting rigorous evaluation and comparative analysis of quantum–classical hybrid computational architectures.
4.3. Training, Testing, and Validation
The training loop implements a hybrid quantum–classical optimization strategy, iteratively refining quantum circuit parameters to minimize the classification error. For the conducted experiments, a dataset comprising 500 samples was used and pre-processed according to the pipeline described earlier. Each quantum circuit configuration, ranging from eight to fifteen qubits, is trained using a learning rate of 0.01, a batch size of 32, and for a total of two epochs. The circuit initialization involves Hadamard gates, followed by parameterized rotations for encoding the input data. Subsequent quantum layers incorporate parameterized RX, RY, and RZ rotations combined with CNOT gates to facilitate entanglement between neighboring qubits. Quantum circuit simulations during the forward passes are executed using Qiskit’s Statevector simulator, while the FPGA processing pipeline handles gradient calculations and parameter updates. For comparison, a baseline implementation of the gradient calculations and parameter updates were performed on the CPU. Performance metrics such as execution time, accuracy, and FPGA-driven speedup were recorded from the two implementations.
The results in Table 2 demonstrate significant performance gains achieved by integrating FPGA processing for gradient descent and loss calculation with QPU simulations. Columns 2 and 3 in Table 2 represent the timings and accuracy for the baseline implementation on the CPU, while columns 4 and 5 represent the timings and accuracy for the FPGA implementation. As the number of qubits increases, the CPU execution time grows, reaching 3.34 s for 15 qubits, while the FPGA execution time remains consistently low, with a maximum of 0.4 s, as shown in Figure 8. This results in a substantial speedup, increasing from 5.11× for eight qubits to 8.35× for fifteen qubits, highlighting the efficiency of FPGA acceleration, especially for larger computations, as shown in Figure 9. Additionally, the accuracy of the CPU-only approach declines as the number of qubits increases, dropping from 99% for eight qubits to 76% for fifteen qubits. In contrast, the FPGA system maintains higher or comparable accuracy, achieving 99% in multiple cases. These findings indicate that FPGA acceleration not only enhances computational speedup but can also improve accuracy in certain scenarios, making it a powerful tool for hybrid computing environments that demand both efficiency and precision.

Table 2.
Gradient descent and loss calculation results with CPU vs. FPGA execution times and accuracy.
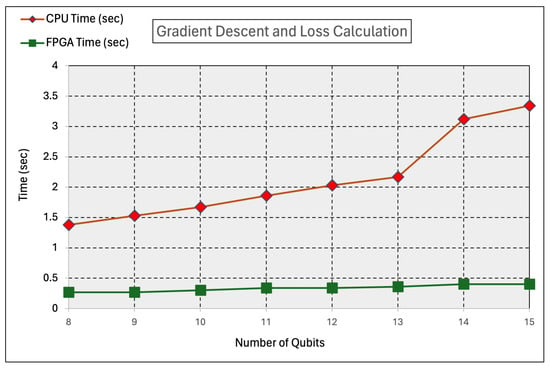
Figure 8.
Execution times for gradient descent and loss calculation (CPU and FPGA).
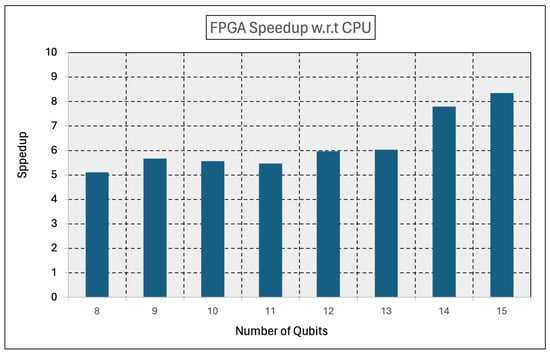
Figure 9.
FPGA speedup with regard to CPU.
4.4. FPGA Resource Utilization
The FPGA resource utilization for the kernel implemented on the Alveo U200 demonstrates efficient resource allocation with minimal hardware overhead (Table 3). The design utilizes 13,515 lookup tables (LUTs) (1.23%) and 12,000 registers (REGs) (0.66%), indicating that small data structures such as intermediate computations and partitioned arrays are stored in registers rather than on-chip memory. The DSP utilization is 71 (0.98%), suggesting arithmetic operations involving multiplications and accumulations. Notably, no block RAM (BRAM) or ultra RAM (URAM) resources are utilized, which indicates that all large data structures, including predictions, weights, gradients, and loss values, are stored in external DDR memory and accessed through AXI interfaces. This design choice minimizes on-chip memory consumption but may introduce latency due to frequent DDR accesses. The low overall resource consumption suggests an optimized implementation, leaving significant room for additional computational tasks or concurrent kernel instantiations. Future enhancements could focus on optimizing memory access patterns, leveraging on-chip BRAM for reduced latency, and increasing DSP utilization to improve computational throughput.

Table 3.
Resource utilizations on XCU200-2FSGD2104E (Alveo U200 board).
4.5. Estimating Speedup for Larger-Scale Quantum Circuits
We used the data points obtained in the range 8–15 qubits to extrapolate the speedup for larger VQC circuits. A polynomial trend line is fitted on the data points using regression and extrapolated up to 50 qubits. The fitted trend line follows the quadratic equation in Equation (14).
The regression trend line estimates a speedup of for 50-qubit circuits, see Figure 10. Therefore, for larger circuits, the benefit of the FPGA processing pipeline becomes even more pronounced as the complexity of parameter optimization increases with the quantum circuit size.
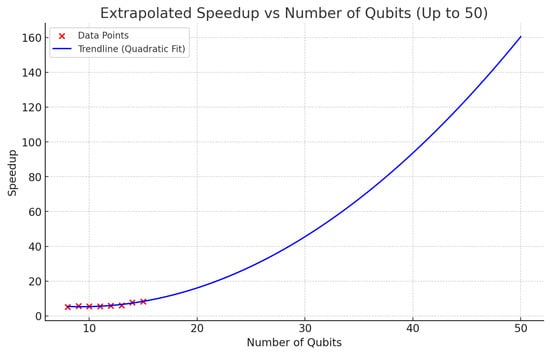
Figure 10.
Projected speedup for larger QML circuits.
While our extrapolation provides a theoretical estimate, the practical evaluation on larger circuits remains an area for future exploration. Based on available hardware specifications, the on-board memory capacity (64GB) could feasibly support simulations of circuits up to 24 qubits, given that each amplitude requires eight bytes for complex number representation. Similarly, although our current experiments used real datasets restricted to 8–15 qubits, larger synthetic datasets could be generated in future studies using techniques such as Gaussian mixture models. These synthetic samples can be projected into higher-dimensional PCA spaces to match the required input dimension for larger quantum circuits. While promising, this dataset generation strategy was not explored in this paper and is left as a direction for future work.
4.6. Complexity Considerations and Algorithm Classes
In addition to the empirical regression, we provide a theoretical perspective on the observed acceleration. For classical computations involved in hybrid quantum–classical loops—such as gradient computation, loss evaluation, and parameter updates—the complexity often scales polynomially with the number of qubits, typically as or depending on the encoding and circuit design [39]. FPGA architectures, with their pipelined and parallelizable data paths, can exploit this structure by reducing the effective time complexity for such operations [40,41]. In contrast, CPU-bound implementations are constrained by sequential bottlenecks and memory latency. As a result, tasks that map well to fixed-point arithmetic, linear algebra primitives or element-wise matrix operations (e.g., parameter-shift gradient evaluations) benefit substantially from FPGA acceleration [33,42]. A general class of algorithms—including variational quantum classifiers, variational quantum eigensolvers (VQEs), and QAOA and QGAN loss modules [43]—fall into this category and represent promising targets for our proposed pipeline.
5. Conclusions and Future Work
In this research, we proposed a generalized FPGA-based framework aimed at accelerating classical computations in hybrid quantum–classical algorithms. By overcoming the limitations of algorithm-specific implementations, our methodology harnesses FPGA’s inherent advantages of high throughput and low latency to effectively support diverse computational scenarios. Furthermore, we introduced a unified high-level framework, integrating classical FPGA and quantum resources, thereby simplifying resource management and improving the accessibility of quantum–classical workflows. We have also investigated a quantitative comparison with a state-of-the-art quantum software framework running on a server-grade CPU, which demonstrated a 8× improvement in runtime when compared to the CPU baseline.
For future work, we envision the development of dedicated FPGA kernels optimized to accelerate quantum circuit simulations. Our preliminary experiments have demonstrated successful simulations of gradient and loss computation up to 15 qubit circuits. However, by leveraging the full available on-board memory, we anticipate the extension of these simulations to handle significantly larger quantum circuits. Given that each state amplitude requires storage for complex numbers (using four bytes each for the real and imaginary components), it is feasible to simulate quantum circuits up to 24 qubits utilizing available on-board memory (64 GB) and other resources. Additionally, we plan to experiment directly with actual quantum processing units (QPUs), such as those provided by IBM, facilitating practical experiments and providing comparisons to hybrid quantum–classical computations. Alongside hardware advancements, we also recognize theoretical challenges in training deep variational quantum circuits, particularly the barren plateau phenomenon [32], that can hinder effective gradient-based optimization. To mitigate this, our current implementation restricts the circuit depth to five layers and incorporates PCA-based input normalization and mini-batch stochastic gradient descent to preserve meaningful gradient flow. Future studies will thus focus on assessing the practical limits and performance improvements achievable through FPGA acceleration in hybrid quantum classical computing. In addition to classification tasks, we envision the extension of the proposed framework to support other key quantum computing applications. Specifically, we plan to implement FPGA-accelerated classical components for VQEs, which are central to quantum chemistry simulations, and for quantum generative models such as quantum Boltzmann machines (QBMs) and quantum generative adversarial networks (QGANs). These extensions would enable the benchmarking of the framework across a broader set of problem classes and provide further evidence of its generality and effectiveness in hybrid quantum–classical workflows. We also plan to explore advanced training strategies such as layer-wise optimization and heuristic parameter initialization, which are promising techniques to further alleviate barren plateau effects and enable more scalable learning in quantum–classical hybrid models.
Author Contributions
Conceptualization, P. and N.M.; methodology, P.; software, P.; validation, P.; formal analysis, N.M.; investigation, P.; resources, N.M.; data curation, P.; writing—original draft preparation, P. and N.M; writing—review and editing, N.M.; visualization, P.; supervision, N.M.; project administration, N.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. The dataset and code-base has not yet been deposited in a public repository but will be made available upon request. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chafii, M.; Bariah, L.; Muhaidat, S.; Debbah, M. Twelve Scientific Challenges for 6G: Rethinking the Foundations of Communications Theory. IEEE Commun. Surv. Tutor. 2023, 25, 868–904. [Google Scholar] [CrossRef]
- Beck, T.; Baroni, A.; Bennink, R.; Buchs, G.; Pérez, E.A.C.; Eisenbach, M.; da Silva, R.F.; Meena, M.G.; Gottiparthi, K.; Groszkowski, P.; et al. Integrating quantum computing resources into scientific HPC ecosystems. Future Gener. Comput. Syst. 2024, 161, 11–25. [Google Scholar] [CrossRef]
- Giortamis, E.; Romão, F.; Tornow, N.; Lugovoy, D.; Bhatotia, P. Orchestrating quantum cloud environments with qonductor. arXiv 2024, arXiv:2408.04312. [Google Scholar]
- Robledo-Moreno, J.; Motta, M.; Haas, H.; Javadi-Abhari, A.; Jurcevic, P.; Kirby, W.; Martiel, S.; Sharma, K.; Sharma, S.; Shirakawa, T.; et al. Chemistry beyond exact solutions on a quantum-centric supercomputer. arXiv 2024, arXiv:2405.05068. [Google Scholar]
- Schulz, M.; Ruefenacht, M.; Kranzlmüller, D.; Schulz, L.B. Accelerating hpc with quantum computing: It is a software challenge too. Comput. Sci. Eng. 2023, 24, 60–64. [Google Scholar] [CrossRef]
- Suchara, M.; Alexeev, Y.; Chong, F.; Finkel, H.; Hoffmann, H.; Larson, J.; Osborn, J.; Smith, G. Hybrid quantum-classical computing architectures. In Proceedings of the 3rd International Workshop on Post-Moore Era Supercomputing, Dallas, TX, USA, 11 November 2018. [Google Scholar]
- Xu, Y.; Huang, G.; Balewski, J.; Naik, R.; Morvan, A.; Mitchell, B.; Nowrouzi, K.; Santiago, D.I.; Siddiqi, I. QubiC: An Open-Source FPGA-Based Control and Measurement System for Superconducting Quantum Information Processors. IEEE Trans. Quantum Eng. 2021, 2, 1–11. [Google Scholar] [CrossRef]
- Yang, Y.; Shen, Z.; Zhu, X.; Wang, Z.; Zhang, G.; Zhou, J.; Jiang, X.; Deng, C.; Liu, S. FPGA-based electronic system for the control and readout of superconducting quantum processors. Rev. Sci. Instruments 2022, 93, 074701. [Google Scholar] [CrossRef]
- Branchini, B.; Conficconi, D.; Sciuto, D.; Santambrogio, M.D. The Hitchhiker’s Guide to FPGA-Accelerated Quantum Error Correction. In Proceedings of the 2023 IEEE International Conference on Quantum Computing and Engineering (QCE), Bellevue, WA, USA, 17–22 September 2023; Volume 02, pp. 338–339. [Google Scholar] [CrossRef]
- Moawad, Y. Architectures and Optimisations for FPGA-Based Simulation of Quantum Circuits. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2025. [Google Scholar]
- Mahmud, N.; El-Araby, E.; Caliga, D. Scaling reconfigurable emulation of quantum algorithms at high precision and high throughput. Quantum Eng. 2019, 1, e19. [Google Scholar] [CrossRef]
- Bach, N.H.; Vu, L.H.; Tran, D.L.; Dao, T.T.; Luu, T.T.H.; Nguyen, D.N. Re-structuring CNN using quantum layer executed on FPGA hardware for classifying 2-D data. In Proceedings of the 2024 9th International Conference on Integrated Circuits, Design, and Verification (ICDV), Hanoi, Vietnam, 6–7 June 2024; pp. 143–147. [Google Scholar] [CrossRef]
- Pushpak, S.N.; Jain, S. An Implementation of Quantum Machine Learning Technique to Determine Insurance Claim Fraud. In Proceedings of the 2022 10th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO), Noida, India, 13–14 October 2022. [Google Scholar]
- Nikoloska, I.; Simeone, O. Training hybrid classical-quantum classifiers via stochastic variational optimization. IEEE Signal Process. Lett. 2022, 29, 977–981. [Google Scholar] [CrossRef]
- Wani, J.; Allamsetty, T.K.; Gherde, R.; Agarwal, V. HLS Implementation of Quantum Shor’s Algorithm Using Matrix Pruning. In Proceedings of the 2022 Second International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 21–22 April 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, E.; Davis, J.J.; Cheung, P.Y. A PYNQ-based framework for rapid CNN prototyping. In Proceedings of the 2018 IEEE 26th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Boulder, CO, USA, 29 April–1 May 2018; p. 223. [Google Scholar]
- IBM Quantum. Qiskit: An Open-Source Framework for Quantum Computing. 2021. Available online: https://zenodo.org/records/8190968 (accessed on 5 April 2025). [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Mavroeidis, V.; Vishi, K.; Zych, M.D.; Jøsang, A. The Impact of Quantum Computing on Present Cryptography. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 405–414. [Google Scholar] [CrossRef]
- Misra, S.; Rani, P. Quantum Machine Learning: A Comprehensive Overview and Analysis. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24–28 June 2024. [Google Scholar]
- Choppakatla, A. Quantum Machine Learning: Bridging the Gap Between Quantum Computing and Artificial Intelligence: An Overview. Int. J. Res. Appl. Sci. Eng. Technol. 2023, 11, 1149–1153. [Google Scholar] [CrossRef]
- Jiang, J.R. A Quick Overview of Quantum Machine Learning. In Proceedings of the 2023 IEEE 5th Eurasia Conference on IOT, Communication and Engineering (ECICE), Yunlin, Taiwan, 27–29 October 2023. [Google Scholar]
- Maheshwari, D.; Sierra-Sosa, D.; Garcia-Zapirain, B. Variational quantum classifier for binary classification: Real vs synthetic dataset. IEEE Access 2021, 10, 3705–3715. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Lloyd, S. Quantum support vector machine for big data classification. Phys. Rev. Lett. 2014, 113, 130503. [Google Scholar] [CrossRef] [PubMed]
- Melnikov, A.; Kordzanganeh, M.; Alodjants, A.; Lee, R. Quantum machine learning: From physics to software engineering. Adv. Phys. X 2023, 8, 2165452. [Google Scholar] [CrossRef]
- Alexeev, Y.; Amsler, M.; Barroca, M.A.; Bassini, S.; Battelle, T.; Camps, D.; Casanova, D.; Choi, Y.J.; Chong, F.T.; Chung, C.; et al. Quantum-centric supercomputing for materials science: A perspective on challenges and future directions. Future Gener. Comput. Syst. 2024, 160, 666–710. [Google Scholar] [CrossRef]
- Suzuki, T.; Miyazaki, T.; Inaritai, T.; Otsuka, T. Quantum AI simulator using a hybrid CPU–FPGA approach. Sci. Rep. 2023, 13, 7735. [Google Scholar] [CrossRef]
- Belfore, L.A. A Scalable FPGA Architecture for Quantum Computing Simulation. arXiv 2024, arXiv:2407.06415. [Google Scholar]
- Pilch, J.; Długopolski, J. An FPGA-based real quantum computer emulator. J. Comput. Electron. 2019, 18, 329–342. [Google Scholar] [CrossRef]
- Bilgin, Y.; Tesfay, S.W.; Ipek, S.; Uğurdağ, H.F.; Durak, K.; Goren, S. PYNQ-based rapid FPGA implementation of quantum key distribution. In Proceedings of the 2021 6th International Conference on Computer Science and Engineering (UBMK), Ankara, Turkey, 15–17 September 2021; pp. 483–488. [Google Scholar]
- Brassard, G.; Hoyer, P.; Mosca, M.; Tapp, A. Quantum amplitude amplification and estimation. Contemp. Math. 2002, 305, 53–74. [Google Scholar]
- McClean, J.R.; Boixo, S.; Smelyanskiy, V.N.; Babbush, R.; Neven, H. Barren plateaus in quantum neural network training landscapes. Nat. Commun. 2018, 9, 4812. [Google Scholar] [CrossRef]
- Wierichs, D.; Izaac, J.; Wang, C.; Lin, C.Y.Y. General parameter-shift rules for quantum gradients. Quantum 2022, 6, 677. [Google Scholar] [CrossRef]
- AMD PYNQ. Available online: https://www.pynq.io/ (accessed on 5 April 2025).
- AMD. AMD EPYC 7302—16-Core—3.0 GHz. Available online: https://www.exxactcorp.com/AMD-100-000000043-E198061333 (accessed on 5 April 2025).
- AMD Alveo™ U200 Data Center Accelerator Card. Available online: https://www.amd.com/en/products/accelerators/alveo/u200/a-u200-a64g-pq-g.html (accessed on 5 April 2025).
- Deng, L. The mnist database of handwritten digit images for machine learning research [best of the web]. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L.; et al. Variational quantum algorithms. Nat. Rev. Phys. 2021, 3, 625–644. [Google Scholar] [CrossRef]
- Waidyasooriya, H.M.; Hariyama, M.; Miyama, M.J.; Ohzeki, M. OpenCL-based design of an FPGA accelerator for quantum annealing simulation. J. Supercomput. 2019, 75, 5019–5039. [Google Scholar] [CrossRef]
- Choi, S.; Lee, K.; Lee, J.J.; Lee, W. Standalone FPGA-Based QAOA Emulator for Weighted-MaxCut on Embedded Devices. arXiv 2025, arXiv:2502.11316. [Google Scholar]
- Efthymiou, S.; Ramos-Calderer, S.; Bravo-Prieto, C.; Pérez-Salinas, A.; García-Martín, D.; Garcia-Saez, A.; Latorre, J.I.; Carrazza, S. Qibo: A framework for quantum simulation with hardware acceleration. Quantum Sci. Technol. 2021, 7, 015018. [Google Scholar] [CrossRef]
- Zoufal, C.; Lucchi, A.; Woerner, S. Quantum Generative Adversarial Networks for learning and loading random distributions. npj Quantum Inf. 2019, 5, 103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).