Abstract
This paper investigates the problem of ensuring the stable operation of multiple high-speed train systems under the threat of False Data Injection (FDI) attacks. Due to the wireless communication characteristics of railway networks, high-speed train systems are particularly vulnerable to FDI attacks, which can compromise the accuracy of train data and disrupt cooperative control strategies. To mitigate this risk, we propose a Distributed Model-Free Adaptive Predictive Control (DMFAPC) scheme, which is data-driven and does not rely on an accurate system model. First, by using a dynamic linearization method, we transform the nonlinear high-speed train system model into a dynamically linearized model. Then, based on the above linearized model, we design a DMFAPC control strategy that ensures bounded train velocity tracking errors even in the presence of FDI attacks. Finally, the stability of the proposed scheme is rigorously analyzed using the contraction mapping method, and simulation results demonstrate that the scheme exhibits excellent robustness and stability under attack conditions.
1. Introduction
In recent years, with the ongoing advancement of global urbanization and rapid national economic growth, high-speed rail has emerged as a widely adopted and rapidly developing mode of transportation worldwide due to its high efficiency, low carbon emissions, and operational safety. The safe and stable operation of high-speed train systems significantly impacts both the national economy and public life. Consequently, enhancing the accuracy, real-time performance, and robustness of control systems during high-speed operation has become a research hotspot [1,2].
In multi-agent systems (MASs), individual agents often operate autonomously and with limited access to global information. However, coordinated behavior at the system level can be achieved through local interactions and information exchange among agents [3,4]. Recent studies have demonstrated that cooperative control strategies based on train-to-train (T2T) communication can effectively facilitate the collaborative operation of multi-high-speed train (MHST) systems, thereby improving network transportation efficiency and ensuring operational safety. This cooperative control framework enables MHSTs to directly share information and coordinate with neighboring trains under specific communication topologies [5,6]. For instance, ref. [7] proposed a finite-time distributed adaptive coordination control method for multi-traction units, ensuring coordination within a limited time. Building on this, ref. [8] designed a distributed adaptive fault-tolerant control strategy with failure-handling capabilities for MAS, and [9] addressed system uncertainties, input saturation, and state constraints by constructing an adaptive cooperative control mechanism. In [10], a distributed learning control method integrating safety constraints was developed to improve both safety and intelligence in train systems, while [11] focused on distributed cooperative fault-tolerant control under actuator faults and input saturation conditions.
Traditional control system designs often rely on accurate mathematical models grounded in physical principles. However, due to the complexity of high-speed rail systems—including strong nonlinearity, interconnection of subsystems, and operational fluctuations—model-based approaches can become cumbersome or infeasible. As complexity increases, model-free techniques have become a more attractive alternative, particularly when operating conditions deviate from quantifiable norms or system parameters vary over time. Model-Free Adaptive Control (MFAC) has emerged as a promising data-driven approach, deriving control laws directly from real-time input–output (I/O) data without requiring explicit system models [12,13,14,15,16]. For example, ref. [17] introduced a model-free adaptive control approach combining disturbance observers and dynamic linearization to enhance robustness against external disturbances. In [18], event-triggered mechanisms and iterative learning control were integrated to address communication constraints in fading channels, achieving resource-efficient adaptive control.
It is worth emphasizing that MFAC, as a representative data-driven method for nonlinear systems, has attracted considerable attention in train control for its effectiveness and practicality. In [19], a resilient data-driven coordination control method for multiple high-speed trains was developed to improve robustness and stability under harsh network conditions such as measurement fading and denial-of-service (DoS) attacks. Similarly, ref. [20] addressed the issue of dynamic topological switching in subway train networks by designing an event-triggered data-driven coordination strategy that reduces communication costs while maintaining coordination performance. Predictive control has received much attention for its ability to improve system performance by optimizing future control inputs and effectively handling physical constraints on inputs and outputs by using system models to predict future outputs based on current and past inputs [21,22,23,24,25]. Ref. [26] proposed a distributionally robust MPC framework with output feedback to enhance control system performance under uncertainty. Ref. [27] developed an adaptive MPC method for cruise control in high-speed trains, incorporating time-varying parameters to improve real-time adaptability and robustness in dynamic conditions such as varying speeds and external disturbances. Combined with the above analysis, we integrate the prediction mechanism into the MFAC framework, which can enable the controller to predict future system behavior and enhance robustness to disturbances and uncertainties.
Model-Free Adaptive Predictive Control (MFAPC), an advanced control methodology that adjusts controller parameters online using real-time input–output data without relying on complete system models, has drawn significant scholarly attention [28,29]. Recent studies have applied MFAPC across various domains to achieve resilient control under challenging conditions. For instance, ref. [30] proposed an event-triggered MFAPC method for the secure operation of multi-area power systems under spoofing attacks. In [31], a robust predictive tracking control strategy was developed for high-speed trains to address quantization errors and DoS attacks. Additionally, ref. [32] introduced a constraint-aware MFAPC strategy for perimeter control and path guidance in multi-area urban traffic systems, achieving traffic flow optimization without accurate models. Based on generalized learning systems, ref. [33] developed an MFAPC method for nonlinear MAS to improve resilience and responsiveness under DoS attacks. For heterogeneous nonlinear MAS, ref. [34] implemented a distributed control framework enabling cooperative behavior without model information. Further extending this approach to MIMO MAS, ref. [35] proposed a distributed robust predictive control scheme to counter deception attacks. In [36], a robust distributed control method with anti-DoS capabilities was designed for multi-area power systems, ensuring coordination and stability under adversarial disruptions.
Meanwhile, the increasing digitalization and networking of high-speed trains have made their open communication systems more vulnerable to cybersecurity threats [37]. To address this, ref. [38] introduced an anti-attack distributed cooperative control strategy based on topological reconfiguration, enhancing resilience through a virtual coupling mechanism. In [39], an event-triggered adaptive control method was developed for bottleneck sections, capable of resisting deception attacks. Furthermore, in ref. [40], aiming at the problem of random topology change and data loss that may occur in high-speed train operation, a security consistency tracking and control method with a data recovery mechanism was constructed. Combining sliding mode control with event-triggered mechanisms, ref. [41] achieved secure and energy-efficient control of high-speed trains under energy constraints and malicious attacks. In summary, this study presents a systematic exploration of distributed control, model-free adaptive predictive control, and cyber-attack defense strategies.
Inspired by the above discussion, we investigate the cooperative control problem of MHSTs under FDI attack. The main contributions of this paper are as follows:
1. A Distributed Model-Free Adaptive Predictive Control (DMFAPC) method is developed for the cooperative control of multiple high-speed trains (MHSTs) under false data injection (FDI) attack conditions. A dynamic linearization approach is introduced to convert the nonlinear train dynamics into a data-driven model, eliminating the need for an accurate system model.
2. Compared to the existing literature [19,20,33,34], this paper investigates the impact of FDI attacks on the performance of MHSTs by combining model-free adaptive algorithms with predictive algorithms to achieve enhanced stability and control performance.
3. Unlike existing model-free adaptive predictive control schemes [23,24,29], this paper proposes a distributed consensus tracking control scheme for MHSTs in the FDI attack environment.
In this paper, some relevant mathematical symbols are defined as shown in Table 1.

Table 1.
Notations and descriptions.
2. Preliminaries and Problem Description
2.1. Preliminaries
Throughout this study, standard notation is employed. Consider a directed graph , where denotes the vertex set, represents the edge set, and indicates the weighted adjacency matrix. An edge exists in if there is a reachable path from agent i to agent j. The neighborhood of agent i is defined as . The adjacency matrix satisfies for all , and if , otherwise . The Laplacian matrix of the graph is defined as , with , and each element .
2.2. Dynamic Model of MHSTs
Employing Newtonian mechanics, a dynamic model for the i-th train has been derived.
Within this model, the fixed sampling interval is denoted by , s denotes the moment, and ℓ denotes the train number. , , and denote the control inputs, train speed, and position, respectively. Furthermore, the model incorporates resistance components, where denotes the intrinsic resistance and denotes supplementary resistance factors.
The intrinsic and supplementary resistances are mathematically expressed through coefficients a, b, and c, which are presently unidentified. Resistance factors related to track conditions, specifically, gradient , curvature , and tunnel effects , are accounted for according to the train’s positional context. Integrating the resistance expressions into the initial dynamic model formulation results in an overall representation involving an unknown nonlinear function .
where, represents an unknown nonlinear function.
The following assumptions are adopted for the operational conditions of the multi-high-speed-train (MHST) system.
Assumption 1.
The nonlinear function with respect to is continuous.
Assumption 2.
Except for a finite number of instances ℓ, the nonlinear function satisfies a generalized Lipschitz condition. Specifically, for any with , and , the following inequality holds:
where is a constant representing the generalized Lipschitz coefficient.
Remark 1.
Assumption 1 is frequently utilized in control scheme design for nonlinear systems. In contrast, Assumption 2 constrains the maximum allowable rate of change in train speed. From an energy perspective, the bounded energy variation available from the traction network inherently restricts the magnitude of speed variations achievable by high-speed trains (HSTs).
Theorem 1
([40]). For the MHST (3) satisfying Assumptions 1 and 2, if holds, then there exists a parameter such that (3) can be converted into the following dynamic linearized model:
where is a variable called the pseudo-partial derivative (PPD), which satisfies . and .
Based on the incremental data model mentioned above, the following forward-step prediction equation can be proposed:
Based on Equation (5), the following N-step forward prediction equation can be further proposed:
Let
where represents the N-step forward prediction vector of the system’s output, and denotes the control input increment. Equation (6) can be simplified as follows:
the parameter specifies the control horizon. Under the condition that for , the prediction model described by Equation (7) can be reformulated accordingly.
where
Equation (8) presented above constitutes an N-step ahead predictive data model for train i.
2.3. False Data Injection Attacks
It is noteworthy that deception attacks in communication links can disrupt the system’s state estimation by injecting falsified state information (such as fabricated position or velocity data). Collaborative communication channels between MHSTs, relying heavily on wide-area wireless transmissions, are particularly vulnerable to these attacks compared to local closed-loop control signals. Furthermore, considering the attacker’s limited capabilities and the necessity of concealing their malicious activities, attack attempts do not always succeed. Hence, this paper employs a success probability to characterize the attacker’s strategy. The measurements received by the controller from the leading train and neighboring vehicles are defined as follows:
the variable denotes the neighboring train speed signal under deception attacks, while indicates the original speed signal. The variable denotes the leading train speed signal under deception attacks, while indicates the original speed signal. and characterize the attacker’s impact on the train system, where and specify whether the attack succeeds or fails, and and are the actual injected deceptive data. Consequently, the expression can quantify both the success rate and the influence of the attacker on the control system. The statistical properties of and are predefined with , , and , , where are constants. Additionally, the unknown deceptive attack data are constrained by cyber-attack energy limitations, satisfying .
2.4. Controller Design
Considering the deception attack mentioned above, the locally distributed output is defined as follows:
Consider the control input criterion function:
where .
Substituting Equation (8) into Equation (11) and setting , the following control rate can be obtained:
where the matrix denotes the estimated value of , while represents a positive weighting parameter.
Therefore, the control input at the current time step is:
where .
2.5. Parameter Estimation Algorithm
This paper employs the dynamic linearization technique to address the nonlinearities present in the MHSTs described in Equation (3). This approach introduces a PPD , which establishes a linear relationship between the increments of input/output data, and effectively captures the system’s overall variation. Additionally, the controller design necessitates the use of as part of its operation. The primary challenge lies in the fact that is time varying. Specifically, we consider the following criterion functions related to the PPD in the same way as in the literature [24]:
where is a weighting factor, and is the estimated value of .
By minimizing the criterion function, we derive the following PPD estimation algorithm:
To enhance the capability of the PPD estimation algorithm (15) in tracking time-varying parameters, a reset mechanism is incorporated as follows:
2.6. PPD Prediction Algorithm
It is important to note that the controller design incorporates not only the current information but also the information at future time steps, where . However, since Equation (18) does not provide a means to calculate future estimates , so there is no direct method to compute the values of in using the system’s input and output data up to time ℓ. Therefore, these values must be predicted based on the previously estimated value sequence . Assume that the estimated values have been obtained using Algorithm (11). Based on this estimation sequence, an autoregressive (AR) model can be constructed for prediction [28].
where, denotes the appropriate order, typically chosen within the range of 2 to 7 [28], and , for , represents the coefficients.
The prediction algorithm is as follows:
where .
Define , which can be expressed as follows:
where .
The proposed DMFAPC scheme is developed by combining the controller algorithms (12) and (13), the PPD estimation algorithm (15), the PPD reset mechanism (16), and the PPD prediction algorithms (18) and (19).
where the parameter represents the step size, while parameters and serve as weighting factors.
Algorithm 1 shows the pseudo-code of the DMFAPC algorithm proposed in this paper, and its structure is shown in Figure 1.
| Algorithm 1 Distributed Model-Free Adaptive Predictive Control Algorithm |
|
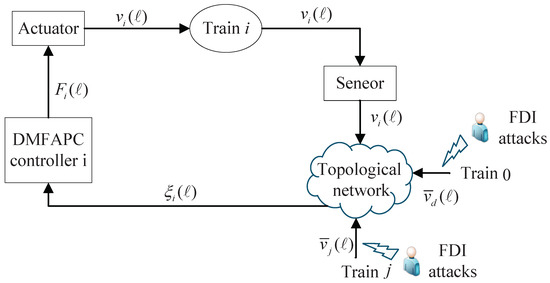
Figure 1.
System block diagram.
3. Stability Analysis
Before proceeding with the stability analysis of MHSTs governed by the MFAPC framework, several fundamental assumptions and supporting lemmas are introduced to facilitate the subsequent theoretical developments.
Assumption 3.
For all and , if , then the sign of remains invariant. Specifically, it holds that or , where z is a small positive constant. Without loss of generality, only the case of is considered in this study.
Assumption 4.
The extended directed communication graph associated with the MHST system is strongly connected. Moreover, only a subset of follower high-speed trains (HSTs) has access to the reference trajectory .
Remark 2.
Assumption 3 implies that the system exhibits a monotonic relationship between the control input and the output, meaning the output does not decrease as the input increases. This behavior reflects a “quasi-linear” characteristic of the system and is consistent with the fundamental premise of model-based control approaches, which typically require the control direction to be known or invariant. Assumption 4, on the other hand, serves as a necessary condition for achieving consensus tracking within multi-agent systems, ensuring that no high-speed train (HST) is isolated from the communication topology of the group.
Lemma 1
([42]). If is an irreducible and time-varying substochastic matrix, in which the diagonal entries are positive, then there exists a set W of all possible , such that
where and , are chosen arbitrarily from W.
Theorem 2.
For an MHST that satisfies Assumptions 1 and 2 but is subject to an FDI attack, a distributed model-free adaptive predictive controller is used and appropriate controller parameters are chosen such that the speed tracking error is bounded, i.e., when
Proof of Theorem 2.
First, we prove that is bounded.
Define . Subtracting from both sides of the estimation algorithm (20) gives
Substituting Equation (4) and taking the absolute value of both sides yields:
Furthermore, since is bounded, we have , where is the upper bound of . Thus, Equation (28) can be rewritten as:
We choose , thus . Then, we can obtain .
From Equation (29), we can have
We can conclude that is bounded, which also implies that is bounded. As a direct result of Algorithms (22) and (23), the PPD prediction values are guaranteed.
Prove that the tracking error is convergent.
Next, we continue to discuss the convergence of . We begin by defining the following vectors:
The distributed error expressed in Equation (10) can be reformulated as follows:
Taking the mathematical expectation yields
Extending the aforementioned equation over the range to , we obtain
where
Rewrite as follows:
Substituting Control Algorithm (24) for (34) yields
Calculating the mathematical expectation, we obtain
where .
Along the same trajectory, (36) is extended to a vector form
where .
By replacing Control Algorithm (24) with (25), we obtain
Applying the norm operation to both sides of Equation (38), we derive
where .
To proceed, it is necessary to establish that the matrix qualifies as an irreducible substochastic matrix. As a preliminary step, we examine the properties of the matrix . Define the matrix as , then
Since is positive semidefinite and , it follows that is positive definite. Consequently, its inverse also possesses positive definiteness. Based on this, the following results can be derived:
Let be a matrix and be the adjoint matrix of . The element is the algebraic cofactor of . Hence, the following relationship holds:
and then
Given that both and remain bounded for all time instants ℓ, it follows that the diagonal entries of the matrix defined in Equation (41) are likewise bounded. Moreover, the corresponding upper bounds do not depend on the specific value of ℓ, indicating time-invariant boundedness of these elements.
As we know, is positive definite matrix; thus, det(C) is a monic polynomial in of degree . Further, and are monic polynomials in of degree and , respectively. Therefore there exists a constant 0 such that the sign of every entry in matrix denoted by Equation (40) is the same as that of for any . Furthermore, there is a positive constant satisfying that
As indicated by Equation (42), all diagonal entries of the matrix are strictly less than one. In addition, since the row sums of the matrix do not exceed one, it follows that the row sums of are also strictly less than one. Consequently, satisfies the criteria for being an irreducible substochastic matrix. Moreover, it is clear that for is bounded. Hence, a positive constant can be identified such that
Substituting accordingly, Equation (39) is transformed into
where .
According to Lemma 1, it can be seen that
where denotes the floor function.
Therefore, the tracking error is convergent. □
4. Numerical Simulation
In this section, a network of four high-speed trains is modeled, and the proposed MFAPC algorithm is implemented within the MATLAB R2019b environment. The communication topology among the MHSTs is depicted in Figure 2, illustrating that information transmission is unidirectional and limited to neighboring train units.

Figure 2.
Directed communication topology of multiple high-speed trains.
It has been established that the duration of the operation will be 2500 s, with a consistent sample interval of one second. The desired speed profile is presented in Figure 3. Below is a list of key parameters provided for the test: AR model order , , forward forecast step .
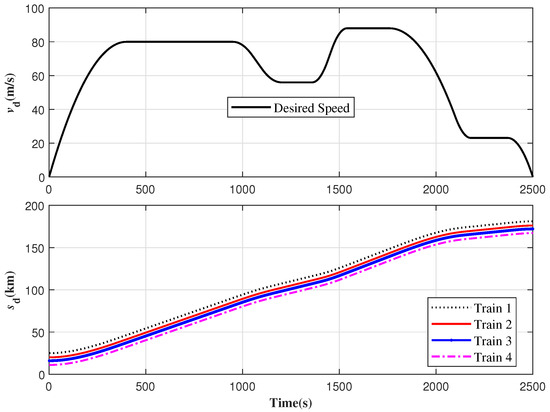
Figure 3.
Reference trajectories for speed and position.
Comprehensive information on the simulation coefficients related to running resistance is provided in refs. [15,19]. It is important to note that these resistance coefficients are employed solely to compute the basic and additional resistances encountered during train operation. This set of coefficients is not exclusive, and alternative values may be used if necessary.
The additional resistance is
The effectiveness of the proposed DMFAPC scheme is evaluated by analyzing the position and velocity tracking errors. The results shown in Figure 4 and Figure 5 indicate that the velocity and the MHSTs can be rapidly stabilized to closely follow the intended trajectory under the proposed DMFACPC algorithm. Thus, the DMFAPC algorithm then has a good control effect.
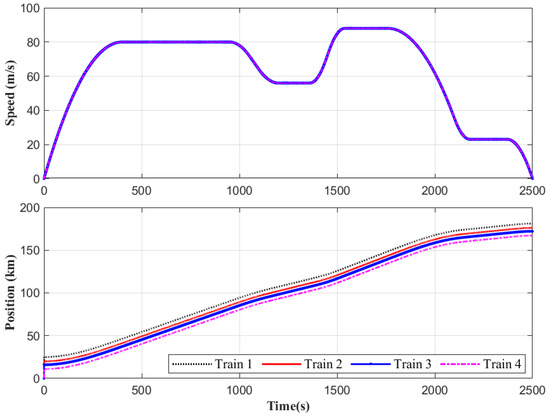
Figure 4.
The speed and position dynamics of the MHSTs under the implementation of the MFAPC scheme.
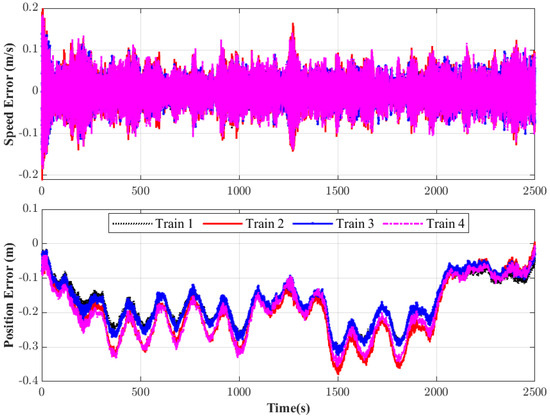
Figure 5.
Tracking errors in speed and position of the MHSTs.
Accordingly, a set of experiments is carried out to examine the trade-off between the false data injection (FDI) attack and the convergence characteristics of . The outcomes corresponding to are presented in Figure 6, whereas those related to are depicted in Figure 7. As illustrated in Figure 6 and Figure 7, the choice of and exerts a notable impact on both the convergence rate and the ultimate convergence bound of . In particular, a larger or a larger tends to undermine the stability of the system.
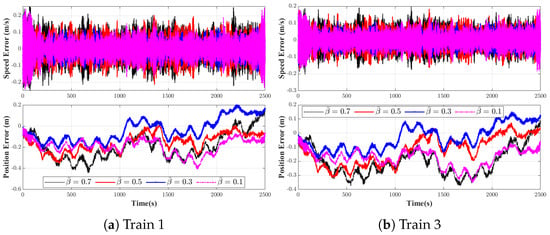
Figure 6.
Investigation of the impact of on the with .
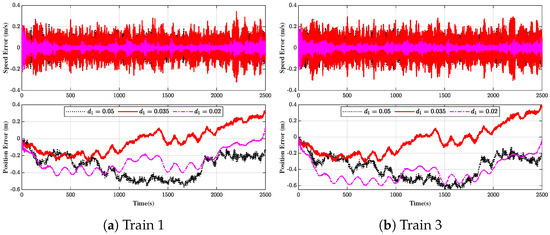
Figure 7.
Investigation of the impact of on the with .
Furthermore, a comparative evaluation of the proposed DMFAPC scheme, the MFAC approach [33], and the conventional PI controller was performed, with the associated error trajectories presented in Figure 8. The results indicate that all three strategies successfully confine the velocity-tracking error to the prescribed interval . Nevertheless, Figure 8 clearly shows that the DMFAPC scheme exhibits faster convergence and superior steady-state accuracy compared with both the MFAC and PI algorithms.
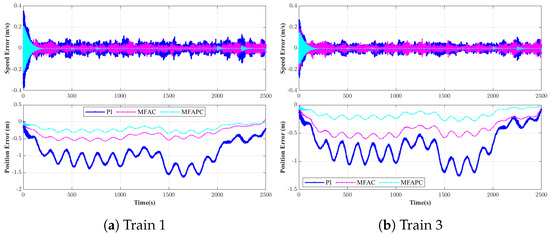
Figure 8.
Comparative performance analysis across various control strategies.
5. Conclusions
This study investigates the cooperative control of multiple high-speed trains under false data injection attacks. A dynamic linearization method is employed to transform the nonlinear high-speed train system into a linear data-driven model. Based on this model, a data-driven DMFAPC scheme is developed, which requires no prior knowledge of the train dynamics. Theoretical analysis demonstrates that the proposed scheme ensures bounded velocity tracking errors among the multiple trains. Finally, simulation results confirm the effectiveness of the proposed DMFAPC approach. However, the proposed approach has some limitations. Firstly because of the reliance on real-time data for model-free control, which may be sensitive to noise and delays in data transmission, especially in case of attacks. Secondly, the parameter tuning process requires empirical tuning, which may increase the complexity of the implementation. Our future work will introduce more advanced attack models to further improve the robustness of the proposed method.
Author Contributions
Conceptualization, B.Z., D.W. and F.W.; methodology, B.Z. and F.W.; software, B.Z. and D.W.; validation, B.Z., D.W. and F.W.; formal analysis, B.Z. and F.W.; investigation, B.Z., D.W. and F.W.; resources, B.Z., D.W. and F.W.; data curation, B.Z.; writing—original draft preparation, B.Z.; writing—review and editing, B.Z., D.W. and F.W.; visualization, B.Z., D.W. and F.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by The Science and Technology Project of Henan Province (Research on data-driven analysis system for high-voltage electrical safety operation status of new energy vehicles, No. 232102241028).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
Due to an error in article production, the incorrect Academic Editor was previously listed. This information has been updated and this change does not affect the scientific content of the article.
References
- Liu, E.; Yang, H.; Cai, G. Optimization for the following operation of a high-speed train under the moving block system. IEEE Trans. Intell. Transp. Syst. 2017, 19, 3406–3413. [Google Scholar]
- Dong, H.; Ning, B.; Cai, B.; Hou, Z. Automatic train control system development and simulation for high-speed railways. IEEE Circuits Syst. Mag. 2010, 10, 6–18. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, H.; Yang, J.; Hou, L.; Yang, D. Event-Triggered Fully Distributed Bipartite Containment Control for Multi-Agent Systems Under DoS Attacks and External Disturbances. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 1–14. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, F. Distributed Hybrid Dynamic Event-Triggered Consensus Control for Nonlinear Multi-Agent Systems. IEEE Trans. Autom. Sci. Eng. 2025, 22, 10470–10483. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, L.; Wang, H.; Tang, T.; Li, K. Robust distributed cruise control of multiple high-speed trains based on disturbance observer. IEEE Trans. Intell. Transp. Syst. 2019, 22, 267–279. [Google Scholar] [CrossRef]
- Tian, Y.; Lin, P. Cooperative control for multiple high-speed trains with constraints and acceleration zone under moving block system. Int. J. Robust Nonlinear Control 2022, 32, 3662–3673. [Google Scholar] [CrossRef]
- Wang, D.; Su, S.; Han, L.; Li, D. Finite-time distributed adaptive coordinated control for multiple traction units of high-speed trains. IEEE Trans. Intell. Transp. Syst. 2024, 25, 8499–8513. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, Q.; Sun, P.; Feng, X. Distributed adaptive fault-tolerant control for high-speed trains using multi-agent system model. IEEE Trans. Veh. Technol. 2023, 73, 3277–3286. [Google Scholar] [CrossRef]
- Guo, Y.; Sun, P.; Wang, Q.; Feng, X. Adaptive cooperative control for multiple high-speed trains with uncertainties, input saturations and state constraints. Control Eng. Pract. 2024, 142, 105768. [Google Scholar] [CrossRef]
- Gao, S.; Song, Q.; Shen, D. Distributed learning control for high-speed trains subject to operation safety constraints. IEEE Trans. Cybern. 2023, 54, 1794–1805. [Google Scholar] [CrossRef]
- Zhu, L.; Li, X.; Huang, D.; Dong, H.; Cai, L. Distributed cooperative fault-tolerant control of high-speed trains with input saturation and actuator faults. IIEEE Trans. Intell. Veh. 2022, 8, 1241–1251. [Google Scholar] [CrossRef]
- Hou, Z.; Chi, R.; Gao, H. An overview of dynamic-linearization-based data-driven control and applications. IEEE Trans. Ind. Electron. 2016, 64, 4076–4090. [Google Scholar] [CrossRef]
- Bu, X.; Hou, Z.; Yu, Q.; Yang, Y. Quantized Data Driven Iterative Learning Control for a Class of Nonlinear Systems with Sensor Saturation. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 5119–5129. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, Q.; Peng, L.; Yu, H. Resource-efficient model-free adaptive platooning control for vehicles with encrypted information. IEEE Trans. Intell. Transp. Syst. 2024, 25, 20006–20016. [Google Scholar] [CrossRef]
- Yu, W.; Wang, R.; Bu, X.; Hou, Z.; Wu, Z. Resilient Model-Free Adaptive Iterative Learning Control for Nonlinear Systems Under Periodic DoS Attacks via a Fading Channel. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4117–4128. [Google Scholar] [CrossRef]
- Bu, X.; Liang, J.; Hou, Z.; Chi, R. Data-driven terminal iterative learning consensus for nonlinear multiagent systems with output saturation. IEEE Trans. Neural Networks Learn. Syst. 2020, 32, 1963–1973. [Google Scholar] [CrossRef]
- Yang, Z.; Hou, M.; Hou, Z.; Jin, S. Disturbance observer dynamic linearization-based model-free adaptive control for discrete-time nonlinear systems. IEEE Trans. Cybern. 2024, 54, 6957–6970. [Google Scholar] [CrossRef]
- Bu, X.; Yu, W.; Yu, Q.; Hou, Z.; Yang, J. Event-triggered model-free adaptive iterative learning control for a class of nonlinear systems over fading channels. IEEE Trans. Cybern. 2021, 52, 9597–9608. [Google Scholar] [CrossRef]
- Yu, W.; Huang, D.; Qin, N. Resilient coordinated data-driven control of multiple high-speed trains under fading measurements and denial-of-service attacks. IEEE Trans. Veh. Technol. 2023, 72, 5690–5701. [Google Scholar] [CrossRef]
- Wang, Q.; Jin, S.; Hou, Z. Data-driven event-triggered cooperative control for multiple subway trains with switching topologies. IEEE Trans. Intell. Transp. Syst. 2021, 23, 14702–14711. [Google Scholar] [CrossRef]
- Mayne, D.Q. Model predictive control: Recent developments and future promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Yuan, S.; Zhu, H.; Li, B.; Liu, Y.; Sun, L. Energy Scheduling of Hydrogen Hybrid UAV Based on Model Predictive Control and Deep Deterministic Policy Gradient Algorithm. Algorithms 2025, 18, 80. [Google Scholar] [CrossRef]
- Jin, L.; Liu, L.; Wang, X.; Shang, M.; Wang, F.-Y. Physical-informed neural network for MPC-based trajectory tracking of vehicles with noise considered. IEEE Trans. Intell. Veh. 2024, 9, 4493–4503. [Google Scholar] [CrossRef]
- Pan, T.; Hou, J.; Jin, X.; Yu, Z.; Zhou, W.; Wang, Z. Distributed Control of Hydrogen-Based Microgrids for the Demand Side: A Multiagent Self-Triggered MPC-Based Strategy. Algorithms 2024, 17, 251. [Google Scholar] [CrossRef]
- Ates, C.; Bicat, D.; Yankov, R.; Arweiler, J.; Koch, R.; Bauer, H.-J. Model predictive evolutionary temperature control via neural-network-based digital twins. Algorithms 2023, 16, 387. [Google Scholar] [CrossRef]
- Li, B.; Guan, T.; Dai, L.; Duan, G.-R. Distributionally robust model predictive control with output feedback. IEEE Trans. Autom. Control 2023, 69, 3270–3277. [Google Scholar] [CrossRef]
- Xu, X.; Peng, J.; Zhang, R.; Chen, B.; Zhou, F.; Yang, Y.; Gao, K.; Huang, Z. Adaptive model predictive control for cruise control of high-speed trains with time-varying parameters. J. Adv. Transp. 2019, 2019, 7261726. [Google Scholar] [CrossRef]
- Hou, Z.; Jin, S. Data-driven model-free adaptive control for a class of MIMO nonlinear discrete-time systems. IEEE Trans. Neural Networks 2011, 22, 2173–2188. [Google Scholar]
- Li, F.; Hou, Z. Event-triggered model-free adaptive predictive control for networked control systems under deception attacks. IEEE Trans. Syst. Man Cybern. Syst. 2023, 54, 1325–1334. [Google Scholar] [CrossRef]
- Bu, X.; Dai, X. Event-triggered model-free adaptive predictive control for multi-area power systems under deception attacks. Energy Rep. 2023, 9, 1812–1825. [Google Scholar] [CrossRef]
- Wang, D.; Wang, F. Model-Free Adaptive Predictive Tracking Control for High-Speed Trains Considering Quantization Effects and Denial-of-Service Attacks. Actuators 2024, 13, 301. [Google Scholar] [CrossRef]
- Hou, Z.; Lei, T. Constrained model free adaptive predictive perimeter control and route guidance for multi-region urban traffic systems. IEEE Trans. Intell. Transp. Syst. 2020, 23, 912–924. [Google Scholar] [CrossRef]
- Xiong, H.; Chen, G.; Ren, H.; Li, H. Broad-Learning-System-Based Model-Free Adaptive Predictive Control for Nonlinear MASs Under DoS Attacks. IEEE/CAA J. Autom. Sin. 2025, 12, 381–393. [Google Scholar] [CrossRef]
- Pan, Z.; Hou, Z.; Chi, R. Distributed model-free adaptive predictive control for heterogeneous nonlinear multi-agent systems. Int. J. Syst. Sci. 2022, 53, 3027–3041. [Google Scholar] [CrossRef]
- Pan, Z.; Chi, R.; Hou, Z. Distributed model-free adaptive predictive control for MIMO multi-agent systems with deception attack. IEEE Trans. Signal Inf. Process. Netw. 2024, 10, 32–47. [Google Scholar] [CrossRef]
- Bu, X.; Dai, X.; Wu, J.; Ni, M. Resilient distributed model-free adaptive predictive control for multiarea power systems under denial of service attack. Asian J. Control 2023, 25, 4567–4580. [Google Scholar] [CrossRef]
- Zhao, H.; Dai, X.; Ding, L.; Cui, D.; Ding, J.; Chai, T. Resilient cooperative control for high-speed trains under denial-of-service attacks. IEEE Trans. Veh. Technol. 2021, 70, 12427–12436. [Google Scholar] [CrossRef]
- Xiao, S.; Ge, X.; Wu, Q. Attack-resilient distributed cooperative control of virtually coupled high-speed trains via topology reconfiguration. IEEE/CAA J. Autom. Sin. 2024, 11, 1066–1068. [Google Scholar] [CrossRef]
- Zhao, H.; Dai, X.W. Event-triggered adaptive control for multiple high-speed trains with deception attacks in bottleneck sections. Inf. Sci. 2021, 547, 470–481. [Google Scholar] [CrossRef]
- Yu, W.; Huang, D.; Wang, X.L.; Dong, H. Data-driven security consensus tracking of multiple high-speed trains under random topologies with data recovery mechanism. IEEE Trans. Control Syst. Technol. 2024, 32, 2298–2309. [Google Scholar] [CrossRef]
- Yu, W.; Huang, D.; Sun, P.; Wang, Q. Sliding mode control for high-speed train via event-triggered strategy under energy-limited deception attacks. IEEE Trans. Veh. Technol. 2023, 73, 1554–1566. [Google Scholar] [CrossRef]
- Yang, S.; Xu, J.; Li, X. Iterative learning control with input sharing for multi-agent consensus tracking. Syst. Control Lett. 2016, 94, 97–106. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).