Abstract
Martensite start (Ms) temperature is a critical parameter in the production of parts and structural steels and plays a vital role in heat treatment processes to achieve desired properties. However, it is often challenging to estimate accurately through experience alone. This study introduces a model that predicts the Ms temperature of medium-carbon steels based on their chemical compositions using the artificial neural network (ANN) method and compares the results with those from previous empirical formulae. The results indicate that the ANN model surpasses conventional methods in predicting the Ms temperature of medium-carbon steel, achieving an average absolute error of −0.93 degrees and −0.097% in mean percentage error. Furthermore, this research provides an accurate method or tool with which to present the quantitative effect of alloying elements on the Ms temperature of medium-carbon steels. This approach is straightforward, visually interpretable, and highly accurate, making it valuable for materials design and prediction of material properties.
1. Introduction
Medium-carbon steels, containing approximately 0.30 wt.% to 0.60 wt.% carbon and 0.60 wt.% to 1.65 wt.% manganese, are extensively used in various structural applications, particularly as load-bearing components [1]. It is widely utilized in large components, forging, and automotive parts due to its balanced ductility and strength, along with good wear resistance [2]. A significant amount of research is being conducted on these steels to explore their performance and enhance their properties [3,4,5].
Martensite start (Ms) temperature is crucial for steels during the manufacturing process, considering the significant impact of phase transformation and heat treatment on the mechanical properties of steel [6]. Consequently, substantial progress has been made in estimating or predicting Ms temperature by numerous researchers through numerical methods over the years [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Many researchers have proposed at least one formula for Ms temperature, based on their research or as an improvement to earlier formulations. From these studies, a generalized linear formula was derived to describe the relationship between the Ms temperature and the chemical composition, as expressed in Equation (1).
Here, y represents the calculated Ms temperature for the target steel. The offset parameter θ is a constant, representing the Ms temperature of steel without any alloying elements—essentially pure iron, derived from extrapolating the Ms temperatures of iron-based alloys as adopted by researchers or from the databases and references they utilized. The weight coefficient for alloying element i, is adjusted iteratively to achieve the best-fit prediction of Ms temperature as a dependent variable. The amount of the alloying element “i” is denoted by .
In essence, each input representing the content of an alloying element is multiplied by its corresponding weight coefficient , and the resulting products are summed and then added to a temperature offset constant “θ”. The output y is the predictive Ms temperature value.
Table S1 in Supplementary Materials presents the calculation formulae for Ms temperature specifically applicable to medium-carbon steels. It includes 21 empirical equations from 17 research studies, spanning from earlier works to more recent investigations. The value of θ varies between 693 K and 834 K across different formulae. Beyond the common linear form, some formulae incorporate unique forms or transformed terms. For instance, Carapella’s formula includes a product formula ∏(1 − ) [29]. Andrews’ formulae [11] feature product terms Σ, and Wang et al.’s formula [26] includes the square roots of product terms Σ, both of which aim to account for the co-action by alloying elements on Ms temperature. Additionally, Lee and Park’s method [25] introduces a chemical composition independent item 11.67(dγ) to reflect the influence of average austenite grain size on Ms temperature. However, as indicated by the researchers, the existing prediction models or empirical formulae for Ms temperature are limited by the types of alloying elements included, the range of chemical composition content, or their inability to align with experimental results when values exceed the established ranges.
Fe-based materials have been widely studied due to their diverse applications in structural and functional materials. For instance, Fe oxides have been explored for memory devices due to their unique electronic properties [30], while Fe-based Heusler alloys have shown great potential for thermoelectric energy conversion [31]. These studies highlight the versatility of Fe-based systems in advanced technologies.
In structural materials, understanding the martensite start (Ms) temperature is crucial as it directly influences the phase transformation behavior, microstructure, and mechanical properties of steels. Precise prediction of Ms temperature is essential for optimizing alloy design and tailoring mechanical performance, particularly in applications requiring a balance between strength and toughness.
In another respect, artificial neural networks (ANN), as a kind of approach to machine learning in artificial intelligence, have found extensive applications in various fields, especially in the era of big data at present. They could provide much more reliable results rather than empirical methods.
This study aims to model the calculation of the Ms temperature using the ANN method and then compare the results with those from the previous empirical formulae suitable for medium-carbon steels. Furthermore, the quantitative effects of alloying elements on Ms temperature will be revealed by the ANN model.
2. Methodology and Experimental Database
The advancement of modern techniques, especially in computer science, has enabled the processing of vast datasets that were once unmanageable. ANN modeling, a machine learning method, is utilized across various research fields, including materials science [32], mechanical engineering [33], architecture [34], medicine [35], and business [36], to estimate predicted values or results, which are difficult to obtain through conventional methods.
In comparison to our prior work on the Ms temperature of high-carbon steels [37], the construction of the ANN model in this study is similar but not identical. A typical neural network, containing several nodes, consists of three layers: input, hidden, and output. Each node in the input layer represents an independent variable value. The hidden layer nodes perform computations, and the output layer nodes calculate the final output as the dependent variable. The parameters for the input and output layers are set according to the project requirements, while others of the model, such as the number of hidden layers, nodes per layer, learning rate, momentum term, and iterations, are determined by the researchers’ expertise and through trial and error across different scenarios.
The ANN modeling process consists of the following steps:
- Collection of data.
The ANN model requires a detailed description of the chemical composition of steel sets (including ten alloying elements—carbon (C), manganese (Mn), silicon (Si), chromium (Cr), nickel (Ni), molybdenum (Mo), vanadium (V), aluminum (Al), tungsten (W) and copper (Cu)—which may vary depending on different cases) and their corresponding experimental Ms temperature values. A reference search yielded a total of 1533 samples that meet the criteria, out of which 313 sets were classified as medium-carbon steel in accordance with the definition, as shown in Table S2 in Supplementary Materials.
- 2.
- Grouping of data.
The dataset, comprising 313 entries, was divided into two groups: training and testing, with the ratio typically ranging from 6:4 to 8:2. Training with a higher portion can increase the model accuracy but the selection of too large a training set may result in overfitting, which limits the model generalizability. Therefore, a ratio of 6:4 was adopted to ensure the model’s broad applicability, assigning sets #1 to #188 for training and the remaining sets #189 to #313 for testing.
- 3.
- Training of ANN.
The training dataset was used to optimize the ANN configuration, minimizing deviations in the untrained test data through a trial-and-error process. The process involved selecting various hidden layers with different numbers of neurons and optimizing the learning rate, momentum term, and number of iterations to achieve the best prediction for unseen data. Figure 1 illustrates the entire process of trial and error for the modeling in different parameters.
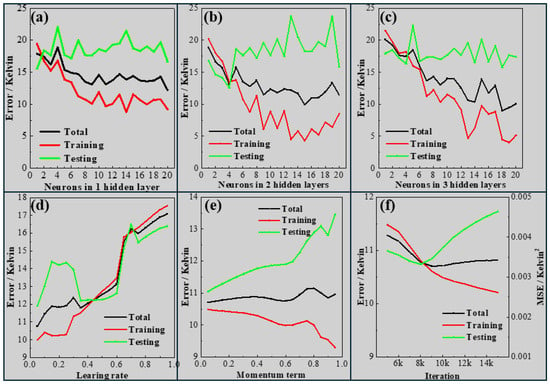
Figure 1.
Effect of various parameters on error for training, testing, and total datasets: (a) Number of neurons in a single hidden layer, (b) Number of neurons in two hidden layers, (c) Number of neurons in three hidden layers, (d) Learning rate, (e) Momentum term, (f) Number of iterations.
The ideal ANN model was achieved under the following conditions: two hidden layers within 4-4 neurons, a learning rate of 0.05, a momentum term of 0.05, and 8000 iterations. With this configuration, the model’s performance on the testing dataset resulted in a mean absolute error (MAE) of 10.74 K, an average absolute error (AAE) of 0.76 K, a mean squared error (MSE) of 0.00189 K2, and a mean percentage error (MPE) of 0.17%. The calculation equations could be easily found in a statistics textbook and are listed below.
in which is the number of different steels for which the Ms temperature is predicted, is the predictive value of the Ms temperature, and is the actual value of the Ms temperature being predicted.
- 4.
- Correlation Analysis.
The Pearson correlation coefficient can be used to express the linear relationships between inputs and output, as shown in the heatmap of Figure 2. The color intensity in each square of the heatmap indicates the strength of the relationship between input and output, facilitating the easy identification of correlations. The values are represented with negative and positive signs to indicate inverse and direct relationships, respectively, on the heatmap. For example, the negative values and darker color intensity for C and Ni with experimental Ms highlight the more significant negative impact of these two elements on the Ms temperature. Similarly, the values close to zero and the very light color intensity for Mo in the heatmap indicate that it has a minimal effect on the Ms temperature.
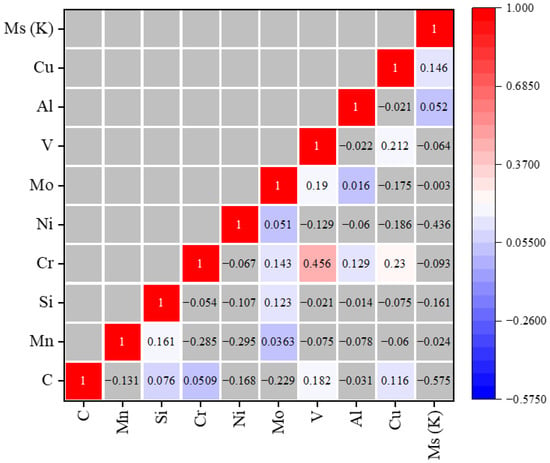
Figure 2.
Colored heatmap illustrating the relationship between input and output variables using the Pearson correlation coefficient. The color gradient in each square represents the degree of correlation strength.
The heatmap analysis illustrates the correlation between alloying elements and their corresponding Ms temperature is not strictly linear, with significant differences. It reveals that there is not a substantial correlation between the elemental composition and the Ms temperature, suggesting a complicated, nonlinear relationship.
- 5.
- Simulation and prediction using the trained ANN model.
A JAVA-based virtual alloy addition system was developed for the ANN model. This system allowed for the straightforward prediction of the Ms temperature by inputting the alloying contents in steel. The graphical user interface (GUI), shown in Figure 3, clearly presents the correlation between the inputs (alloying content) and the output (predicted Ms temperature) in a simple and visual manner. This user interface represents a knowledge discovery in databases (KDD) model developed for predicting the Ms temperature of medium-carbon steels based on alloy compositions. The model is powered by an optimal ANN trained using precise synaptic weights to ensure high accuracy. By inputting the chemical composition of elements such as C, Mn, Si, Cr, Ni, Mo, V, Al, W, and Cu within the specified ranges, the model can predict Ms temperature with remarkable precision. The prediction output is dynamic, allowing for infinite combinations of compositions within the defined input ranges, making it a versatile tool for alloy design and research.
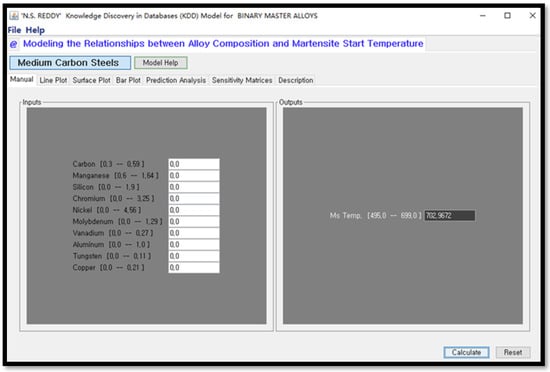
Figure 3.
The graphical user interface of the ANN model.
In addition to predictions, this tool offers advanced functionalities such as one-variable and two-variable sensitivity analysis, enabling users to understand the influence of each element on Ms temperature. It also includes features to compare predicted outputs with training and test datasets to validate the model’s accuracy. A description of the model, including its development methodology and features, is integrated into the interface for user understanding. Furthermore, the tool calculates the index of relative importance (IRI) for alloying elements, providing insight into their contribution to Ms temperature. Overall, this predictive model is a robust and user-friendly tool designed to support alloy development and metallurgical research.
3. Results and Discussion
3.1. Comparisons Among the Predicted Ms Temperature Results
Eight random samples from the testing dataset, detailed in Table 1 with their chemical compositions and corresponding experimental Ms temperatures, are selected to evaluate the efficiency of the ANN model.

Table 1.
Medium-carbon steel sets for predictive result comparisons.
Figure 4 presents the predicted Ms temperature results for these samples using the above-mentioned formulae and the ANN model. The results demonstrate that the ANN model, with an AAE of 6.79 degrees and an MPE of 1.26%, outperforms the alternative methods. The line fitting of the data points yields a Pearson correlation coefficient of 0.97, indicating a high degree of correlation with the actual values. In addition, among the entire set of 313 steel samples, the ANN model achieves an AAE of −0.93 degrees and −0.097% in MPE.
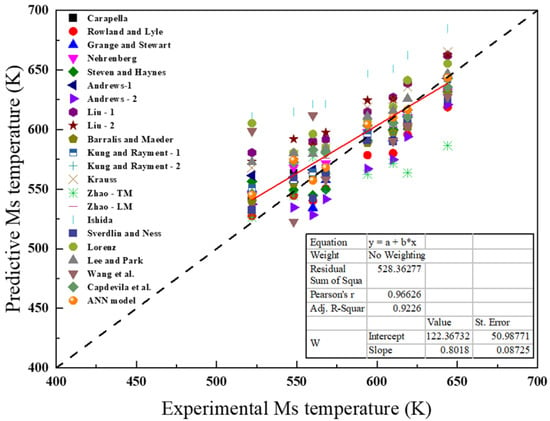
Figure 4.
Graphical representation of the experimental, ANN-predicted, and calculated Ms values using calculation formulas [8,9,10,11,13,15,18,19,22,23,25,26,29,38,39,40,41] selected in this study.
3.2. Quantitative Effect of Individual Alloying Element
The Ms temperature is predominantly influenced by the chemical composition of steels [34,35]. From the alloying elements, Carbon content is recognized as having the most substantial impact on the Ms temperature, as evidenced by the highest weight coefficients in the formulae presented in Table S1 of Supplementary Materials. C is known to significantly lower the Ms temperature by increasing the stability of austenite, while Mn addition is noted for its effectiveness in inhibiting martensitic transformation. The individual effects of alloying elements on Ms temperature have been acknowledged in previous studies; however, a detailed stepwise analysis of their influence remains unexplored, as well as the exact values of each alloying element [23,42].
The incremental quantitative effect of each alloying element on the Ms temperature is determined by utilizing the developed ANN model. We considered steel sample #290, with its chemical composition and experimental Ms temperature detailed in Table 1, i.e., Fe-0.5C-0.73Mn-0.22Si-0.83Cr-0.04Ni-0.41Mo-0.15V-0.07Al and 568 K, respectively. The baseline Ms temperature for pure iron, assuming zero content of all alloying elements, is predicted to be 703.0 K by the ANN model. Subsequently, the corresponding amount of each potential alloying element was incrementally introduced into the ANN model.
This stepwise addition alters the Ms temperature progressively from the initial value for pure iron, as illustrated in Figure 5. Furthermore, through straightforward calculations, it is determined that the Ms temperature of medium-carbon steel sample #290 decreases by 86.5 degrees with the addition of 0.5 wt.% C. Thus, the quantitative effect of C on the Ms temperature of medium-carbon steel #290 is −173 K/wt.%, along with the values of other alloying elements, as shown in Figure 5, after a rough calculation. For this case, alloying element V shows a positive effect on the Ms temperature, whereas C, Mn, Ni, Cr, Mo, Si, and Al have a negative impact (in the order of their effect strength). The calculation process is independent of the sequence in which alloying elements are introduced. Moreover, the results vary from one case to another and could not be applied to a universal value across all situations or for all samples. In short, it can provide substantial advancements in the accuracy of materials design and manufacturing.
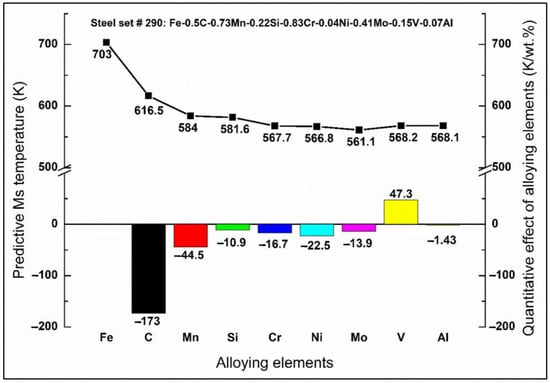
Figure 5.
Stepwise prediction and quantitative effect of alloying elements on Ms temperature for steel set #290.
3.3. Varying Effect of Dual Alloying Elements
Figure 6 illustrates the Ms temperature variations by different dual alloying elements for steel set #290, with color bands highlighting temperature differences. Figure 6a examines the influence of C and Mn on the Ms temperature. It shows that as the amount of C and Mn increases, the Ms temperature decreases regularly, by the evidence of the mostly parallel contour bars. Figure 6b explores the Ms temperature variation by C versus Si. The nearly parallel Si-axis to the contour bars indicates that the effect of C is significantly greater than that of Si. When compared to C and Mn in Figure 6a, it demonstrates a similar Ms temperature-decreasing behavior for Cr and Ni in Figure 6c. Additionally, W, as a strong carbide former, exhibits its ability to increase the Ms temperature, as illustrated in Figure 6d.

Figure 6.
Ms temperature variations of steel set #290 by dual alloying additions predicted by ANN model: (a) C-Mn; (b) C-Si; (c) Cr-Ni; and (d) W-Cu.
4. Conclusions
In summary, the proposed virtual prediction model utilizes the ANN methodology to predict the Ms temperature for medium-carbon steels. The effect of ten potential alloying elements on the Ms temperature is also predicted. The ANN model predictions are in close agreement with experimental Ms temperature values, surpassing previous empirical formulae in accuracy and convenience. For the total 313 samples, the model exhibits an AAE of −0.93 K and an MPE of −0.097%. Notably, the model reveals the quantitative influence of alloying elements on the Ms temperature, marking an unprecedented finding. As previous empirical formulae require complex calculations and are not universally applicable to all alloying additions, the developed ANN model serves as an ideal replacement for these formulae. This model can aid in material design, and its predictive capabilities could be extended to a wide range of material properties in the future.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/a18020116/s1: Table S1: Calculation formulae of Ms temperature for medium-carbon steel; Table S2: Medium-carbon steel set database. References [38,39,40,41] are cited in the Supplementary Materials.
Author Contributions
Conceptualization, N.G.S.R.; methodology, N.G.S.R. and A.K.M.; software, N.G.S.R.; validation, S.-G.K.; formal analysis, X.-S.W. and M.I.; investigation, X.-S.W. and M.I.; resources, N.G.S.R. and A.K.M.; data curation, X.-S.W. and M.I.; writing—original draft preparation, X.-S.W.; writing—review and editing, S.-G.K. and N.G.S.R.; visualization, N.G.S.R.; supervision, N.G.S.R.; project administration, N.G.S.R.; funding acquisition, S.-G.K. and N.G.S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, Further inquiries can be directed to the corresponding author.
Acknowledgments
N.S. Reddy acknowledges YSJ-TV for the inspiration and Y.K.K. for helping with the model GUI development. The authors would like to acknowledge the support from the Engineering Research Institute, Gyeongsang National University.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Ms | Martensite start |
| ANN | Artificial neural network |
| MAE | Mean absolute error |
| AAE | Average absolute error |
| MSE | Mean squared error |
| MPE | Mean percentage error |
| GUI | Graphical user interface |
| KDD | Knowledge discovery in databases |
References
- Wiewiórowska, S.; Muskalski, Z. The Application of Low and Medium Carbon Steel with Multiphase TRIP Structure in Drawing Industry. Procedia Manuf. 2015, 2, 181–185. [Google Scholar] [CrossRef]
- Mohanty, O.N. 13—Forging Grade Steels for Automotives. In Automotive Steels; Rana, R., Singh, S.B., Eds.; Woodhead Publishing: Cambridge, UK, 2017; pp. 413–453. [Google Scholar] [CrossRef]
- Sugimoto, K.-i.; Hojo, T.; Srivastava, A.K. Low and Medium Carbon Advanced High-Strength Forging Steels for Automotive Applications. Metals 2019, 9, 1263. [Google Scholar] [CrossRef]
- Li, S.; Feng, H.; Wang, S.; Gao, J.; Zhao, H.; Wu, H.; Xu, S.; Feng, Q.; Li, H.; Liu, X.; et al. Phase Transformation Behaviors of Medium Carbon Steels Produced by Twin Roll Casting and Compact Strip Production Processes. Materials 2023, 16, 1980. [Google Scholar] [CrossRef] [PubMed]
- Ishtiaq, M.; Inam, A.; Tiwari, S.; Seol, J.B. Microstructural, mechanical, and electrochemical analysis of carbon doped AISI carbon steels. Appl. Microsc. 2022, 52, 10. [Google Scholar] [CrossRef] [PubMed]
- van Bohemen, S.M.C.; Sietsma, J. Kinetics of martensite formation in plain carbon steels: Critical assessment of possible influence of austenite grain boundaries and autocatalysis. Mater. Sci. Technol. 2014, 30, 1024–1033. [Google Scholar] [CrossRef]
- Payson, P. Martensite reactions in alloy steels. Trans. Am. Soc. Met. 1944, 33, 261–280. [Google Scholar]
- Nehrenberg, A. Contribution to discussion on grange and stewart. Trans. Am. Inst. Min. Met. Eng 1946, 167, 494–498. [Google Scholar]
- Grange, R. The temperature range of martensite formation. Trans. Am. Inst. Min. Metall. Eng. 1946, 167, 467–501. [Google Scholar]
- Steven, W. The temperature of martensite and bainite in low-alloy steels. J. Iron Steel Inst. 1956, 183, 349–359. [Google Scholar]
- Andrews, K. Empirical formulae for the calculation of some transformation temperatures. J. Iron Steel Inst. 1965, 203, 721–727. [Google Scholar]
- Van Bohemen, S. Bainite and martensite start temperature calculated with exponential carbon dependence. Mater. Sci. Technol. 2012, 28, 487–495. [Google Scholar] [CrossRef]
- Capdevila, C.; Caballero, F.G.; De Andrés, C.G. Determination of Ms temperature in steels: A Bayesian neural network model. ISIJ Int. 2002, 42, 894–902. [Google Scholar] [CrossRef]
- Jaffe, L.; Hollomon, J. Hardenability and quench cracking. AIME TRANS 1946, 13, 1–8. [Google Scholar]
- Kung, C.; Rayment, J. An Examination of the Validity of Existing Empirical Formulae for the Calculation of Ms Temperature. 1981. Available online: https://escholarship.org/content/qt9mh7k297/qt9mh7k297.pdf (accessed on 13 February 2025).
- Li, C.; Liu, P.; Wang, M. Computation of Ms temperature in carbon equivalence method. J. Liaoning Tech. Univ. Nat. Sci. 1998, 17, 293–295. [Google Scholar]
- Pickering, F. Physical metallurgical development of stainless steels. In Proceedings of the Stainless Steels 84, Goteborg, Sweden, 3–4 September 1984. [Google Scholar]
- Rowland, E.; Lyle, S. The application of Ms points to case depth measurement. Trans. ASM 1946, 37, 27–47. [Google Scholar]
- Sverdlin, A.; Ness, A. The effects of alloying elements on the heat treatment of steel. In Steel Heat Treatment Handbook; CRC Press: Boca Raton, FL, USA, 1997; pp. 45–92. [Google Scholar]
- Trzaska, J. Calculation of critical temperatures by empirical formulae. Arch. Metall. Mater. 2016, 61, 981–986. [Google Scholar] [CrossRef]
- Gramlich, A.; van der Linde, C.; Ackermann, M.; Bleck, W. Effect of molybdenum, aluminium and boron on the phase transformation in 4 wt.–% manganese steels. Results Mater. 2020, 8, 100147. [Google Scholar] [CrossRef]
- Ishida, K. Calculation of the effect of alloying elements on the Ms temperature in steels. J. Alloys Compd. 1995, 220, 126–131. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, Z.; Northwood, D.O.; Liu, Y. A new empirical formula for the calculation of MS temperatures in pure iron and super-low carbon alloy steels. J. Mater. Process. Technol. 2001, 113, 556–562. [Google Scholar] [CrossRef]
- Dogan, A.; Ozer, T. Determination of martensite transformation temperatures associated with Fe-Mn-Si-Ni-Cr-Ce-Ti-N shape memory alloys. Can. Metall. Q. 2005, 44, 555–562. [Google Scholar] [CrossRef]
- Lee, S.-J.; Park, K.-S. Prediction of Martensite Start Temperature in Alloy Steels with Different Grain Sizes. Metall. Mater. Trans. A 2013, 44, 3423–3427. [Google Scholar] [CrossRef]
- Wang, J.; Wolk, P.J.V.d.; Zwaag, S.V.d. Determination of Martensite Start Temperature in Engineering Steels Part I. Empirical Relations Describing the Effect of Steel Chemistry. Mater. Trans. JIM 2000, 41, 761–768. [Google Scholar] [CrossRef]
- Yang, H.-S.; Jang, J.H.; Bhadeshia, H.; Suh, D.-W. Critical assessment: Martensite-start temperature for the γ→ε transformation. Calphad-Comput. Coupling Phase Diagr. Thermochem. 2012, 36, 16–22. [Google Scholar] [CrossRef]
- Peet, M. Prediction of martensite start temperature. Mater. Sci. Technol. 2015, 31, 1370–1375. [Google Scholar] [CrossRef]
- Carapella, L. Computing A” or ms (transformation temperature on quenching) from analysis. Met. Prog. 1944, 46, 108. [Google Scholar]
- Ishibe, T.; Maeda, Y.; Terada, T.; Naruse, N.; Mera, Y.; Kobayashi, E.; Nakamura, Y. Resistive switching memory performance in oxide hetero-nanocrystals with well-controlled interfaces. Sci. Technol. Adv. Mater. 2020, 21, 195–204. [Google Scholar] [CrossRef]
- Garmroudi, F.; Riss, A.; Parzer, M.; Reumann, N.; Müller, H.; Bauer, E.; Khmelevskyi, S.; Podloucky, R.; Mori, T.; Tobita, K.; et al. Boosting the thermoelectric performance of Fe2Val—Type Heusler compounds by band engineering. Phys. Rev. B 2021, 103, 085202. [Google Scholar] [CrossRef]
- Ishtiaq, M.; Tiwari, S.; Panigrahi, B.B.; Seol, J.B.; Reddy, N.S. Neural Network-Based Modeling of the Interplay between Composition, Service Temperature, and Thermal Conductivity in Steels for Engineering Applications. Int. J. Thermophys. 2024, 45, 137. [Google Scholar] [CrossRef]
- Paturi, U.M.R.; Cheruku, S.; Reddy, N.S. The Role of Artificial Neural Networks in Prediction of Mechanical and Tribological Properties of Composites—A Comprehensive Review. Arch. Comput. Methods Eng. 2022, 29, 3109–3149. [Google Scholar] [CrossRef]
- Al-Gahtani, K.S.; Alsugair, A.M.; Alsanabani, N.M.; Alabduljabbar, A.A.; Almohsen, A.S. ANN prediction model of final construction cost at an early stage. J. Asian Archit. Build. Eng. 2024, 1–25. [Google Scholar] [CrossRef]
- Daoud, M.; Mayo, M. A survey of neural network-based cancer prediction models from microarray data. Artif. Intell. Med. 2019, 97, 204–214. [Google Scholar] [CrossRef]
- Tkáč, M.; Verner, R. Artificial neural networks in business: Two decades of research. Appl. Soft Comput. 2016, 38, 788–804. [Google Scholar] [CrossRef]
- Wang, X.-S.; Narayana, P.L.; Maurya, A.K.; Kim, H.-I.; Hur, B.-Y.; Reddy, N.S. Modeling the quantitative effect of alloying elements on the Ms temperature of high carbon steel by artificial neural networks. Mater. Lett. 2021, 291, 129573. [Google Scholar] [CrossRef]
- Zhao, J.-C. Continuous cooling transformations in steels. Mater. Sci. Technol. 1992, 8, 997–1003. [Google Scholar]
- Barralis, J.; Maeder, G. Métallurgie-Tome I: Métallurgie Physique; Collection Scientifique ENSAM; Communication Actives: Paris, France, 1982; p. 270. [Google Scholar]
- Krauss, G. Steels: Heat Treatment and Processing Principles; ASM International: Materials Park, OH, USA, 1990. [Google Scholar]
- Lorenz, U. Anwendung von Werkstoffmodellen auf die Phasenumwandlung und die Austenitkonditionierung von Stählen. Ph.D. Thesis, Institut für Eisenhüttenkunde der RWTH Aachen, Aachen, Germany, 2004. [Google Scholar]
- Capdevila, C.; Caballero, F.G.; García De Andrés, C. Analysis of effect of alloying elements on martensite start temperature of steels. Mater. Sci. Technol. 2003, 19, 581–586. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).