1. Introduction
Among several potential post-Moore technologies,
quantum computing has emerged as a promising candidate, showing significant theoretical speedups in certain workloads compared to classical computers [
1,
2,
3]. As a result, quantum computing has received significant interest from researchers in many diverse fields [
4], including the high-performance-computing (HPC) community. However, executing quantum algorithms on physical devices remains a challenge. Quantum algorithms, once developed, need to be converted into a
quantum circuit compatible with the target device on which it will be executed. This is because physical devices typically support a limited number of
gates, and all circuits executed on them must be expressed using only these gates. The process of converting an input quantum algorithm to a machine’s
native basis gate-set, is termed
quantum compilation or
quantum circuit synthesis. Circuit synthesis is also subject to additional constraints. In a given quantum device, multi-qubit gates may only be applicable between a limited set of qubits [
5], determined by the connectivity or
topology of the qubits. Thus,
routing and
mapping of logical qubits between physical qubits on the machine may be required. Since routing is typically achieved using gates during execution, it becomes desirable to optimize routing to minimize gate overhead.
Moreover, current generation
Noisy Intermediate-Scale Quantum (NISQ) [
6] devices are very susceptible to environmental
noise. The state of qubits can rapidly become corrupted, in a process called
decoherence [
7,
8], causing errors in any running computation. Thus, circuits need to be designed with sufficiently short execution times, measured by circuit
depth, to ensure acceptable fidelity of results. In addition, the application of gates, particularly multi-qubit gates such as CNOT, can also introduce errors [
9]. Therefore, it is beneficial to have circuits with as few gates as possible.
The process of synthesizing a circuit for a target machine, while accounting for the machine-dependent constraints mentioned above, can be shown to be a computationally difficult problem and in some cases intractable [
10]. Analytical methods are, therefore, unsuitable in the general case for all but the smallest qubit counts. Practical state-of-the-art optimizing compilers that seek to address these constraints attempt to produce
approximate results, often using heuristics-based techniques, in order to generate circuits optimized for NISQ device constraints at the cost of some compilation error [
11]. However, one key challenge approximate compilers face when synthesizing quantum circuits for NISQ devices is that the imposed constraints can be in conflict with each other. For example, better approximations may be achieved with longer circuits, increasing risk of decoherence, while shorter depth targets reduce flexibility for the compiler, making it difficult to achieve compilation error targets.
To address this challenge, in this work, we model quantum circuit synthesis for NISQ devices as a
multi-objective optimization (MOO) problem and propose a
genetic-algorithm-based (GA) [
12,
13] synthesis technique. In particular, we leverage the Non-dominated Sorting Genetic Algorithm variant II (NSGA-II) [
14], a MOO-specific GA, for the simultaneous optimization of approximation error, circuit depth and number of CNOT gates in synthesized circuits. GAs are a class of gradient-free optimization techniques inspired by the process of
natural selection and known for their guaranteed convergence [
15], ability to escape local minima and inherent parallelization potential. We also propose a runtime parameter adaptation mechanism leveraging
fuzzy logic [
16] to improve GA efficiency. Fuzzy logic enables us to formulate the GA runtime parameter update mechanism using sophisticated linguistically defined variables and relationships, with the ability to tune how these are interpreted. Our contributions in this work can be summarized as follows:
Propose a GA-based quantum circuit synthesis algorithm which synthesizes machine-compatible circuits from a given unitary.
Leverage existing MOO techniques to optimize multiple synthesis objectives simultaneously, minimizing approximation error, circuit depth and number of gates, specifically multi-qubit gates such as CNOTs.
Propose a fuzzy logic based runtime parameter adaptation method for our GA to improve search efficiency and solution quality.
Accelerate GA implementation through parallelization.
The remaining sections in this paper are structured as follows:
Section 2 presents brief descriptions of necessary background material, while
Section 3 discusses related existing literature.
Section 4 details the proposed algorithm,
Section 5 presents experimental evaluation results and finally,
Section 6 and
Section 7 provide closing discussions, future work directions and conclusions.
2. Background
In this section, we first take a look at key background material needed to understand quantum circuit synthesis. Following that, we present brief introductions to genetic algorithms and fuzzy logic, and refer the interested reader to material for further study.
2.1. Quantum Circuit Basics
Quantum computing is a system of computation which relies on the principles of
quantum mechanics [
17]. In particular, it relies on
superposition [
18], which states that a quantum object can exist in a combination of its possible states simultaneously and
entanglement [
18], which enables quantum objects to become strongly correlated. A
qubit is the fundamental unit of quantum computation and it can exist in a superposition of two basis states
and
, with probability amplitudes that determine measurement outcomes. The state of a single qubit, expressed as a vector
, can be written as a linear combination of the probability amplitudes of its corresponding basis states,
. Similarly, an
n-qubit state can be written as
, where
,
. Operations on qubits are called quantum
gates, and can be mathematically represented by unitary operators or matrices [
19]. An operator is considered unitary if its matrix
U satisfies
, where
is the conjugate transpose. Two quantum operations
U and
V are considered equivalent, up to a global phase
, if
.
Quantum computations evolve a statevector through unitary operations which can be represented as matrix-vector multiplications,
. Multiple quantum operations can be combined into a single unitary operation, where gates applied in series can be modeled as matrix multiplications, while parallel gates are described by Kronecker products. Thus, any circuit can be reduced to a single unitary matrix. In some cases, a unitary operation could also be decomposed into a sequence of smaller individual operations. This property is crucial for quantum compilation. The
circuit model, or
gate model, is a universal framework for quantum computation, representing quantum operations as gates acting on qubits [
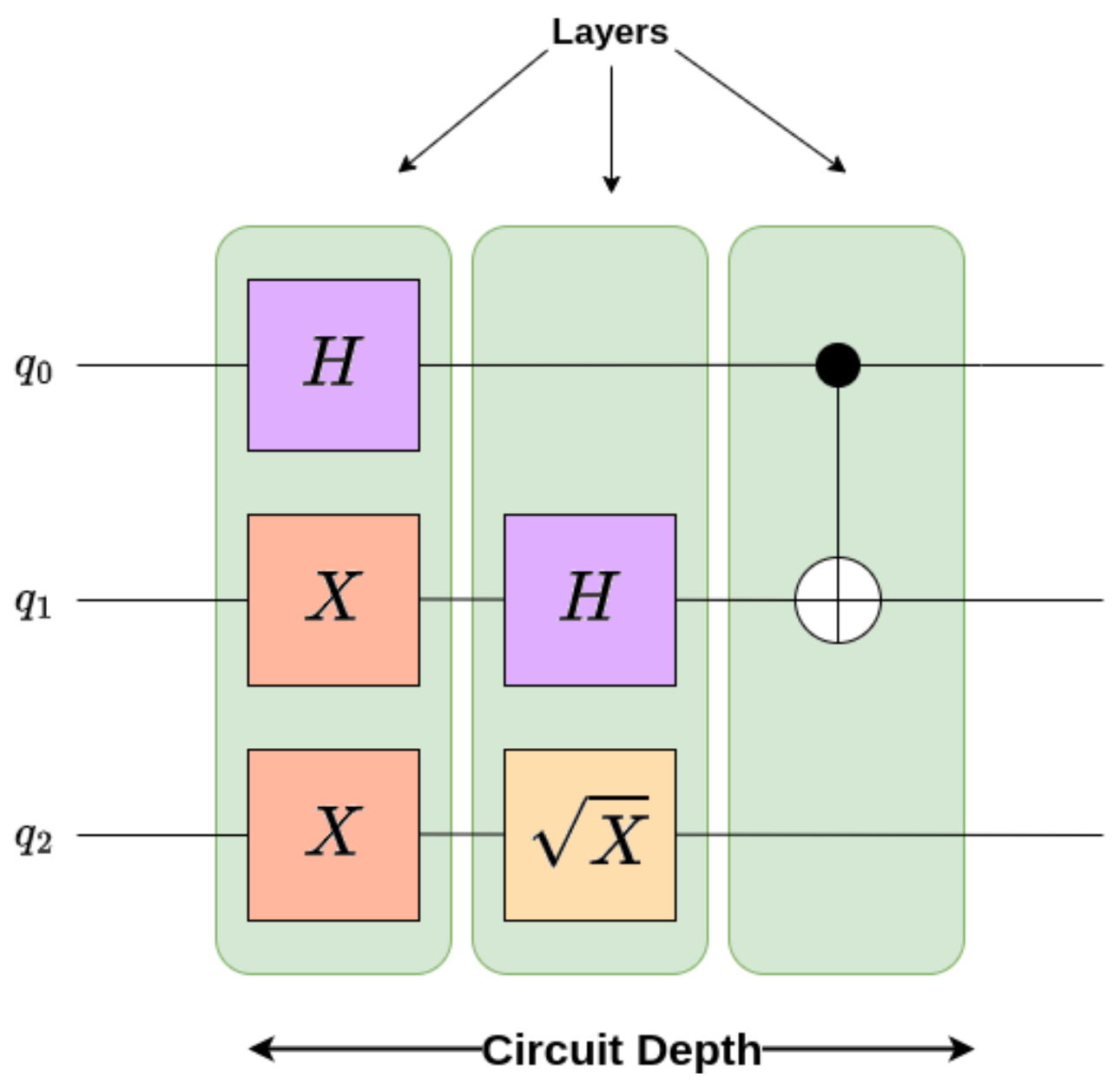
20], with time flowing from left to right. In this model, qubits are depicted as wires, and gates placed on those wires represent quantum operations acting on those qubits. Gates that can be applied in parallel form a
layer. The total number of layers in a circuits is called its
depth, and determines the execution time of the circuit; see
Figure 1.
2.2. Quantum Circuit Compilation and Synthesis
Quantum circuit
compilation, or circuit
synthesis, is the process of converting quantum operations into a circuit compatible with the target device. A finite set of gates, called a
basis gate set, can be used to construct all possible quantum operations [
20]. Quantum devices usually implement such a gate set, referred to as its
native basis gate set. In this work, we specifically refer to the process of converting an input unitary matrix to a machine-compatible circuit as ‘quantum circuit synthesis’. Since connectivity of qubits is required for applying certain gates [
5], the structure of qubit connectivity, called the qubit
topology, is an integral part of quantum compilation. It determines where gates can be applied and if any routing is necessary to move logical qubits to appropriate physical qubits [
5,
21]. However, routing generally requires application of additional gates (e.g., CNOT or SWAP gates [
22]), which can increase the circuit depth and introduce gate errors; see
Figure 2. Since NISQ devices have short decoherence times and high noise sensitivity, it is crucial to reduce the circuit depth and number of gates. Therefore, optimizing compilers for these devices must attempt to minimize the circuit depth, as well as the number of gates. In addition, to minimize the routing overhead, compilers will also attempt to optimize the mapping between logical and physical qubits, attempting to place qubits with higher levels of interaction close to each other, such that fewer routing gates are required; see
Figure 3.
Compilation can be categorized into two types:
exact, which produces a circuit equivalent to the original operation up to a global phase, and
approximate, which approximates the original operation with some error. Exact synthesis techniques generally result in very high circuit depths and gate counts, and generating exact circuits of optimal depth can be computationally unfeasible for anything but the smallest qubit counts. Hence, many modern optimizing compilers trade-off approximation error for reduced circuit depth and gate count. The primary compiler provided by the IBM Qiskit framework [
23] is an example of an exact compiler, while the BQSkit compiler [
11] is an example of an approximate compiler (which can also perform exact compilation).
2.3. Genetic Algorithms
In this section, we take a brief look at GAs, which are search-based, gradient-free, optimization algorithms inspired by the process of
natural selection and
survival of the fittest [
12]. GAs start with a
population of potential solutions, called
members or
individuals. Much like biological life, each individual is characterized by a
chromosome, composed of smaller units called
genes. The genes encode specific characteristics of the overall solution represented by the chromosome. The encoding scheme is therefore essential for the success of the GA and can determine the size of the search space, time to convergence, and overall quality of solutions. A
fitness function is used to evaluate solutions and rank them based on their quality. Fitness functions can be maximizing or minimizing and they can be designed to track single or multiple objectives.
The population undergoes a
reproduction step to produce a new
generation of individuals from the first. There are two processes that are generally used to achieve this—
crossover and
mutation. In the process of crossover, individuals, called
parents, are combined to produce new individuals, called
offspring. Parents are usually chosen with consideration to their relative fitness within the population. For example, individuals with greater fitness can be chosen to try to increase the fitness of the population. However, maintaining population diversity is crucial to prevent premature convergence. To balance these factors, several selection processes exist with various trade-offs. In addition to crossover, a mutation operation is also applied randomly to a subset of the population. This operation causes random modifications to chromosomes and increases the genetic diversity of the population. Here, diversity refers to the chromosomal variation between individuals within a population. This is necessary for the GA to search wide areas within the problem space and escape local minima/maxima [
13,
24].
Once the reproduction step is complete, the survival step determines which individuals in the population will survive and carry on to the next generation. An ideal survival step aims to preserve the most desirable traits and while maintaining diversity. To guarantee that the population will eventually converge to an optimal solution, it is important to implement elitism—a process where the best individuals survive from generation to generation. Survival strategies differentiate GAs from unstructured random search, the latter not utilizing already discovered solutions to search future ones. This step ensures that each generation is progressively more desirable than the last. The iterations (or generations) of evaluation, crossover, mutation, and survival, halt when a specified end criteria is achieved.
2.4. Non-Dominated Sorting Genetic Algorithms (NSGA)
Multi-objective optimization (MOO) problems involve optimizing different, often competing, objectives
simultaneously. These problems typically do not have a single best solution. Instead, they are characterized by a range of
non-dominated or
Pareto optimal solutions. A non-dominated solution is one which cannot be improved in one objective without causing degradation in another. Algorithms targeting MOO problems attempt to produce a set of non-dominated solutions, called a
Pareto front, which characterizes the trade-offs between objectives in the solution space. In a MOO problem instance, the fitness of a solution might be characterized by a vector
where each
is an objective value. A solution with vector
is said to
dominate another solution with vector
if and only if (
1) and (
2) hold true. The number of other solutions which dominate a given solution is sometimes referred to as its
domination level or
rank in the set of solutions. A Pareto front is, therefore, a set of solutions which have a rank of 0.
Due to their flexibility, many GAs have been proposed which attempt to target MOOs [
14,
25,
26,
27,
28,
29]. One such family of algorithms is called the Non-domintated Sorting Genetic Algorithm (NSGA) [
14,
25,
28]. NSGAs operate by performing a
non-dominated sort on the population which ranks solutions with a lower domination level as better. Over time, the GA discards dominated solutions while preserving non-dominated ones, progressing toward the Pareto front of the solution space. In this work, we leverage the NSGA-II [
14] variant for our quantum compiler. We chose this over the newer NSGA-III [
28] because our proposed work targets three objectives, which is within the threshold of NSGA-II, and thus we can avoid the additional processing overhead of NSGA-III without any loss of efficacy.
2.5. Fuzzy Logic
Fuzzy logic is a mathematical framework that extends classical binary logic to handle degrees of truth [
16]. It assigns fractional values between 0 and 1 to variables to indicate its
degree of membership to a given state/category. For example, a
fuzzy variable, with states “HIGH”, “MEDIUM” and “LOW”, could be 80% “HIGH”, 15% “MEDIUM” and 0.5% “LOW”, simultaneously. The degree of membership in one category can be independent of the degree of membership in another. This approach allows us to model uncertainty and overlap in real-world phenomena, similar to human linguistic reasoning [
30]. Fuzzy variables can be combined using the fuzzy equivalents of Boolean operators such as AND and OR (refer to
Table 1), allowing intuitive, linguistically defined, input–output relationships. Numerical input values (
crisp values), are processed into fuzzy variables via
membership functions, which map values to states characterized by degrees of membership to different categories. While these functions, often designed based on expert knowledge, can be arbitrary, they are often triangular, sinusoidal, Gaussian, or trapezoidal, and allow variables to belong to multiple categories simultaneously. The outputs can be
defuzzified using methods such as the centroid method [
31].
3. Related Work
Several exact analytical compilation techniques have been proposed in the current literature [
32,
33,
34,
35], each using different compilation techniques and mathematical frameworks [
36,
37], with different goals and objectives. Many of these have also been incorporated into industry standard compilation frameworks [
38]. Additionally, exact compilation techniques often incorporate staged compilation, where an initial compiled circuit is further optimized using dedicated depth reduction techniques [
39,
40]. However, exact techniques are limited by two prevailing factors. First, exact compilers generate very deep circuits that are unsuitable for NISQ hardware, which have very short decoherence times. Second, attempts to produce optimal depth circuits, while adhering to qubit topologies, quickly become computationally infeasible for all but the smallest of qubit sizes using these methods.
To overcome these limitations, approximate methods trade-off compilation error to produce circuits with reduced depths and/or fewer gates while also trying to be scalable to a higher number of qubits. These compilers use various types of optimization techniques, such as numerical instantiation [
11,
41,
42,
43,
44,
45], SAT-solvers [
46] and other methods [
47]. We refer the interested reader to a detailed survey of many such compilation methods that have been presented in [
48].
GA-based compilation methods are a subcategory of approximate compilation. Several GA-based techniques have been proposed which target circuit compilation, generation, discovery and related tasks. For instance, a simple three-qubit quantum teleportation circuit was evolved using a GA in [
49], while [
50] introduced an encoding scheme to represent quantum circuits as 1-dimensional array chromosomes. Lukac et al. developed a GA-based circuit synthesis technique that analyzes circuit costs in terms of number of gates used and utilizes predetermined quantum operation primitives to generate low-cost quantum circuits [
51]. The Q-PACE framework introduced in [
52] leveraged Genetic Programming (GP) [
53] to evolve optimized quantum circuits, programs, and algorithms. Ruican et al. proposed a software flow for quantum circuit synthesis with runtime adaptation of GA parameters based on operator performance [
54]. Potoček et al. utilized a Non-dominated Sorting Genetic Algorithm (NSGA) for multi-objective circuit synthesis, with objectives of circuit error and cost reduction, incorporating unique genetic operators specifically designed for quantum circuits [
54]. Another novel technique utilized evolutionary methods that leverage quantum computers to produce optimized circuits [
55]. The work in [
56] introduced the use of island GAs [
57], which promote diverse evolution trajectories by running separate, mutually exclusive instances of GAs, occasionally allowing crossover between these instances to enhance the search for optimal solutions. The GA4QCO framework [
58] proposed a comprehensive set of crossover and mutation methods, along with an encoding scheme that represents circuits as 2-dimensional arrays of gates, allowing for a wide range of genetic operations and allows the user to set ad hoc fitness functions. GAs have also been used in tasks adjacent to quantum compilation, such as discovering unitary matrices [
59], optimizing specific algorithms [
60], and minimizing routing overhead in circuits [
61]. Additionally, GA-based techniques for quantum state preparation have been developed to produce efficient circuits that generate desired quantum states, as demonstrated by Creevey et al. in [
62] and the work using the NSGA-II algorithm in [
63].
One more area of research where GAs have seen a lot of interest in is variational quantum circuits. Variational quantum circuits provide an effective and resourceful method for utilizing error-prone NISQ devices to perform optimization, simulation, and machine-learning tasks. Various studies have explored the synthesis and tuning of variational circuits using GAs for different purposes. Some research works have focused on discovering effective ansatzes for use in variational algorithms [
64,
65,
66]. Other studies have concentrated on tuning the free parameters of these circuits to optimize their performance [
67]. Additionally, some works have aimed to compile noise-limiting circuits using GAs [
68].
We now briefly discuss how our work differentiates itself from the existing literature. Our proposed method performs approximate circuit synthesis directly from an arbitrary unitary for a target quantum device, accounting for qubit connectivity. It incorporates and optimizes three compilation objectives simultaneously: approximation error, depth, and gate counts. Our approach leverages the NSGA-II algorithm with modifications, includes qubit mapping strategies and utilizes a nested numerical optimization step to tune parameterized gates. It further enhances the GA through runtime parameter adaptation using a fuzzy logic controller, and is, to our knowledge, the first work to combine fuzzy logic in GA-based circuit synthesis. We also provide parallelization strategies for acceleration of the implementation and perform experimental comparison with industry-standard quantum compilers, making it a comprehensive and unique contribution to the field of GA-based quantum circuit synthesis. Further, by using a GA, our proposed work is also able to avoid many of the limitations of gradient based techniques, such as local minima and unguaranteed convergence. Finally, while our proposed method is able to incorporate several objectives during compilation, and the NSGA technique makes it possible to add more.
4. Materials and Methods
In this section, we discuss the construction of the GA-based circuit synthesizer. We formally describe the problem, followed by an overview of the proposed solution. We then go into details of each component of the GA. Finally, we include some discussions about efforts to accelerate the GA.
4.1. Problem Description
We assume as input a unitary matrix which needs to be synthesized for a specific target device. We also provide as input the native basis gate set B and qubit topology T of the target. Our compiler is then required to synthesize a circuit , with an equivalent unitary , using gates and adhering to topology T for multi-qubit gate placement. Let be the approximation error between and , be the depth of , which is used as a metric for execution time, and be the number of n-qubit gates, used as a metric to estimate gate error. In our work , since we only consider CNOT gates. The goal of the GA-based compiler is to simultaneously minimize , and , possibly with a target threshold for .
We can, therefore, formally define our optimization problem as:
At this point we note that this optimization problem, which includes optimizing both a combinatorial problem (placement of gates in the circuit) and a continuous one (tuning gate parameters), is
non-convex by nature [
47]. It is characterized by a complex solution landscape with multiple local minima. This problem is also non-linear, since it involves non-linear components such as the optimization of parametric gates.
4.2. GA-Based Compiler Overview
To address the problem described above, in this work, we propose a synthesis technique based on NSGA-II, a GA used for MOO problems. In this section, we describe the high level flow of the proposed technique, shown in
Figure 4, and subsequent sections discuss each component of the technique. The compiler begins with an input unitary matrix,
, and starts the compilation process by generating an initial population of randomly generated chromosomes, each of which encode a random quantum circuit. The population size,
, can be specified by the user, but is ideally adjusted to fully utilize available computational resources. The chromosomes are evaluated, using (
6), and the equivalent fitness vector assigned to each chromosome. The population members are then ranked and sorted using the NSGA-II technique and the GA is now ready to begin the main loop.
The first step in the loop is parent selection for producing offspring. In our proposed technique, we keep the population size constant to constrain the design complexity and to reduce the computational burden of having a growing population. Thus, each generation, the compiler produces a fixed number of offspring, also equal to . At the start of a generation, pairs of parents are selected to produce two offspring. Limiting the number of offspring per parent pair to two allows more chromosomes to participate in the crossover process since the total number of offspring in a generation is kept constant. Thus, parent pairs are chosen to produce offspring.
After parent selection, the parents are mutated probabilistically and the mutation rate/probability allows the GA to control the diversity of the population. After mutation, the parents are crossed over, the offspring evaluated for their fitness and merged with the initial population. After the merge, the combined temporary population, of size , is re-ranked and sorted using NSGA-II sorting. If the stopping criteria is met, the best circuit found so far is returned. Otherwise, the bottom half of the population is discarded and the GA moves on to the next generation. However, if runtime parameter adaptation is enabled, the progress statistics and current mutation rates are used to adjust the mutation rate for the next generation using a fuzzy controller.
4.3. Encoding
For a GA-based quantum compiler, encoding involves representing quantum circuits as chromosomes that are compatible with genetic operators. The encoding method used in this work (see
Figure 5) was selected after careful investigation of several different schemes with various trade-offs. To encode a circuit as a chromosome, we represent the circuit as a sequence of
layers, where each layer consists of gates applied in parallel. Within each layer, a qubit is allowed to be part of only one gate, and gate placements that violate this requirement are incompatible with the scheme. Crossover and mutation are allowed at the level of layers as well as gates, and are discussed further in the following sections. However, one important point to note here is that the process of mutation and crossover can result in layers in offspring with incompatible gates. In the case of crossover, if multiple gates are incompatible, one of them is selected at random and the rest are discarded (and replaced with
I gates where appropriate). In the case of mutation, if an incompatible gate is introduced, the new gate is always kept and the old is discarded in order to make the mutation successful.
This scheme also encodes initial qubit mappings and final output qubit mappings. This enables a GA to search across different qubit mapping and routing configurations, in addition to different gate layouts. By nature of being a bottom-up synthesis technique, the GA automatically attempts to discover advantageous mapping and routing scenarios, the latter of which is embedded into the evolved circuit. The input and output mappings also take part in the crossover and mutation process. The encoding scheme is summarized in
Figure 5.
4.4. Crossover
In the proposed method, we utilized three different types of crossover operations. In the first crossover operation, complete layers from each chromosome are selected uniformly at random [
69] to produce an offspring, as shown in
Figure 6a. In the second crossover operation, individual gates from each chromosome are selected uniformly at random, as shown in
Figure 6b. We refer to these crossover operations as
coarse-grained crossover and
fine-grained crossover, respectively. Finally, for the third crossover operation, the input and output qubit mappings are swapped, as shown in
Figure 6c. Further, each of these crossover operations act on two parents and yield two offspring. At runtime, a random crossover operation is chosen out of the three and applied between two parents.
During the crossover step, the parents can be selected based on fitness relative to others in the population in order to pass on their genes. If only chromosomes with the best fitness are chosen as parents, then high
selection pressure [
70] is created. A high selection pressure can speed up convergence by only promoting the best solutions to move forward. However, it can also lead to premature convergence [
70,
71]. On the other hand, low selection pressure is created when chromosomes with both inferior and superior fitness have similar chances of being chosen as parents. In this case, the genetic exploration is better compared to the high selection pressure scenario since more diverse individuals can participate in reproduction, reducing the risk of premature convergence. However, low selection pressure can slow down convergence. To ensure diversity and steady convergence, we use
tournament selection [
70,
72] for parent selection, as described in Algorithm A1 in
Appendix B.1. In this technique,
tournament size number of chromosomes are randomly chosen to compete and the chromosome with the best fitness among the selected cohort is selected to be a parent. This process is repeated until the desired number of parents have been obtained. It is worth noting that selection pressure is directly correlated with tournament size. Smaller tournament sizes result in lower selection pressure due to increased randomness in cohort selection, while larger tournament sizes lead to higher selection pressure, as they increase the likelihood of selecting only the highest-fitness individuals in the cohort.
Tournament selection is a proven selection mechanism that provides a broader selection net while allowing control over the influence of fitness (rank) by adjusting the tournament size. In contrast, purely rank-based selection, where parents are chosen exclusively based on fitness, often leads to repeated selection of a limited number of high-ranking chromosomes, resulting in a saturated population with low diversity. Therefore, tournament selection promotes higher diversity compared to purely rank-based methods. In our tests, we use a tournament size of 2.
4.5. Mutation
Genetic algorithms use mutations to ensure diversity of solutions and, thus, avoid local minima. In this work, we utilize three different mutation schemes,
coarse-grained mutation,
fine-grained mutation, and
mapping mutation, similar to the crossover methods described in
Section 4.4. The first two schemes perform mutation at different levels of granularity. Coarse-grained mutations, as shown in
Figure 7a, are used to introduce mutations at the level of layers and has three variants: layer update, layer addition and layer deletion. The layer update mutation replaces a randomly chosen layer with a randomly generated layer, keeping the depth constant. The layer addition and deletion variants randomly insert or delete a layer, respectively, increasing or decreasing the depth, and can be used to roughly control the average circuit depth of the population. Fine-grained mutations, as shown in
Figure 7b, are used to perform individual gate mutations inside a layer and has two variants: gate removal and gate update. In gate removal, a gate is replaced by an identity gate. On the other hand, gate update replaces a gate with a new randomly selected gate from the input basis gate set. To handle the edge case described in
Section 4.3, where mutation introduces a gate incompatible with other gates in the layer, the original gate is always removed and replaced with the new gate as a policy. Finally, the initial and final mappings also undergo mutation, as shown in
Figure 7c. To perform a mutation on a chromosome, a random mutation out of fine-grained, coarse-grained and mapping mutation schemes is chosen at random. Further, the mutation rate and number of mutations are adjustable parameters to the GA.
4.6. Fitness Evaluation
Fitness functions are key to efficient GAs, as they guide the algorithm toward optimal solutions. While a naive fitness function may be used, which directly models the input problem, fitness functions can be enhanced with additional metrics to enable better search efficiency and faster convergence. Since efficient synthesis of quantum circuits for NISQ devices require simultaneous optimization of multiple objectives, the NSGA-II algorithm proves itself as a suitable candidate. Specifically, it allows the use of different objective metrics without needing to normalize them, assign weights to them or combine them into a single metric. This alleviates many of the issues which appear when trying to combine multiple metrics into a single one (e.g., using Euclidean distance). We discuss some of these issues in
Appendix A for the interested reader.
For a given chromosome, with circuit
and unitary
, the approximation error
, shown in (
3), is based on the Hilbert–Schmidt distance, and is adapted from [
42]. This method is chosen over the more familiar Frobenius distance [
73],
, since the latter is not tolerant of global phase [
42]. The chosen error function generates an error value between 0 and 1, where 0 indicates equivalence of two circuits/unitaries and 1 indicates maximal error. The depth
, and CNOT count
are obtained trivially by counting the number of layers and CNOT gates, respectively. The final fitness vector is therefore as shown in (
6).
4.7. Gate Elimination and Gate Fusion
In many cases, adjacent gates in a circuit can be canceled out, or combined into a single gate. Two consecutive
X gates, for example, could be canceled out or eliminated, see
Figure 8a, while two consecutive rotation gates
and
can be fused into a single gate
; see
Figure 8b. Gate fusions and eliminations often reduce the gate count as well as the number of layers; see
Figure 8c, affecting the fitness of a chromosome. Therefore, in our proposed method, we account for possible gate eliminations and fusions before the evaluation of any objective metrics. We accomplish this by comparing each gate with its right-most neighbor, and applying appropriate eliminations and fusions, which can be user-specified. Since the circuit resulting from one round of elimination and fusion could contain potential for more, the process is performed repeatedly until no more possible eliminations and fusions are found.
4.8. Free Parameter Optimizations
Native basis gate sets often include parameterized gates and a compiler needs to be able to assign optimum values for any such free parameters. In our proposed compiler, we utilize a nested numerical optimization step for tuning free parameters for each chromosome, before assigning final fitness values. The numerical optimizer, obtained from the Python SciPy [
74,
75] library, uses a Broyden–Fletcher–Goldfarb–Shanno (BFGS)-based technique [
76,
77,
78,
79] to find the best set of parameters which minimizes the approximation error
. For a free gate parameter vector
, the optimization is given as:
4.9. NSGA-II Configuration
NSGAs permit multi-objective optimizations with an arbitrary number of objectives and do not require special weighting or combination functions. In this work, we utilize the NSGA-II variation [
14], adapted for quantum compilation. In the basic NSGA-II, the solutions are not concentered near one objective. However, we deliberately bias our solutions towards lower approximation errors, since shallower circuits with less gates might not compensate for lost approximation accuracy. To achieve this, during the sorting step in NSGA-II, the members are sorted on the basis of their rank, then by their approximation errors (our modification) and finally by their crowding distance. The approximation error sorting condition allows the GA to bias towards lower approximation errors rather than trying to balance all objective metrics.
4.10. Runtime Adaptation and Fuzzy Logic
For complex and rough solution spaces, GA convergence can slow down and avoiding local minima may become more challenging. In order to improve search efficiency, GAs can be enhanced using runtime parameter adaptations. These techniques generally try to analyze the current state of the GA parameters, population statistics and improvement trajectory to dynamically adjust parameters for future generations. In our work, we leverage a fuzzy logic controller [
30] to analyze the
update history and current mutation rate and adjust the mutation rate parameter for future generations. Update history is defined as the number of new chromosomes discovered and added to the Pareto front in the last five generations, as a proportion of the total population. Updates are measured with respect to the total population since larger populations would intuitively produce more updates, as a bigger chunk of the solution space is searched each generation. The goal is to guide the GA to increase diversity in the population when updates stagnate, or if the GA already has high mutation rates, to slow down and exploit existing solutions. The update history and current mutation rate are converted into fuzzy variables with three membership categories: LOW, MEDIUM, and HIGH. These variables are processed by the fuzzy inference engine, which outputs a new fuzzified mutation rate value. This value is later defuzzified using the mutation rate’s membership function to obtain a new mutation rate.
Figure 9 gives a brief overview of the fuzzy controller for mutation rate.
Fuzzification uses the membership functions presented in
Figure A2, in
Appendix B.2, to convert crisp values into fuzzy values, while defuzzification uses the centroid method [
31] and the membership function from
Figure A2b specifically to obtain a crisp value from a fuzzy mutation variable. We chose the triangle membership function due to its simplicity of implementation and because it is one of the most widely used functions in literature [
80]. The fuzzy rules, detailed in
Table 2, are designed to address observed evolutionary scenarios: when the GA demonstrates low exploration (few updates and low mutation rates), the system increases mutation rates to enhance solution diversity. Conversely, when the GA demonstrates high exploration (high mutation rates with limited updates), the controller reduces mutation rates to promote exploitation of already discovered chromosomes. The controller also attempts to maintain stable rates when the GA is making consistent progress.
This adaptive mechanism ensures that the genetic algorithm can dynamically balance exploration and exploitation, improving overall search performance. While the membership functions were initially based on informed guesses from experimentation, fuzzy logic’s flexibility allows them to be updated without changing the rule set.
4.11. Additional Runtime Adaptations
When synthesizing circuits, there is usually a trade-off between the circuit depth and approximation error. Deeper circuits allow more configurations and fine-tuned adjustments, making it easier to achieve lower errors while shallower circuits give the compiler less flexibility. In some cases, it may be impossible to achieve a given error threshold without incurring a certain minimum circuit depth. Our testing showed that despite the use of the fuzzy controller, the GA would often plateau at high error values, without any improvement for many generations, indicating premature convergence. Upon closer inspection, it was discovered that the average circuit depth of the population would remain stagnant at a low value. This suggested that the GA was not exploring deeper circuit configurations enough, thereby missing out on lower approximation error opportunities. To address this issue, the dynamic adaptation mechanism also observes the update history over a larger window of 20 generations, and, if the best achieved error has not improved in that duration, it increases the probability of the layer addition mutation type. This biasing helps steer the GA to explore deeper circuits, which may offer much better approximation errors.
4.12. Parallelization and Acceleration of GA
Typically, the fitness function evaluation of individual chromosomes is the most computationally expensive step in a GA. However, since population members can generally be evaluated independently, the fitness evaluation step is also
embarrassingly parallel. This also means that the workload, i.e., the population size can be scaled proportionally with available computational resources. In our work, we leverage the parallel nature of GAs and utilize the Python
multiprocessing library [
81] to distribute chromosomes to separate cores/processes for evaluation, and collect them back for further processing. This method scales linearly with the number of available cores and, thus, bigger population sizes can be evaluated efficiently given more computational resources. However, it is worth mentioning that if the subroutines for function evaluation utilize multiple cores/processes themselves, then the one-to-one ratio of cores to chromosomes will not be guaranteed. Moreover, the communication overhead becomes significant in the cases of larger population size and higher number of cores, and must be accounted for.
The fitness evaluation of a chromosome requires running three subroutines: depth calculation, computation of number of CNOTs, and approximation error calculation. Performance profiling reveals that the last subroutine is the most computationally intensive since it involves free parameter tuning using the BFGS-based numerical optimizer. This optimizer repeatedly calls the approximation error function, until the desired accuracy and convergence conditions are achieved. Calculating the approximation error itself involves three main steps: (a) decoding the chromosome into the equivalent quantum circuit, (b) obtaining the equivalent unitary of the circuit and (c) calculating the approximation error using the formula in (
3). Upon deeper investigation, it was discovered that the second step, obtaining a unitary from a circuit, was the biggest performance bottleneck.
To optimize the first step, we leverage the symbolic variable feature of the IBM Qiskit circuit objects. Specifically, we use symbolic variables for any free parameters in the parameterized gates and cache the circuit decoded from the chromosome. Thus, instead of regenerating the circuit with parameters applied in each iteration, just the free parameter values are supplied before converting to unitary.
To address the next two steps, we use Qiskit API functions to obtain unitary matrices from the circuits which are used to compute the final error value using (
3). To optimize the computation of the error value, we combine the last two steps into one. That is, instead of computing the unitary for a solution circuit, we append the adjoint of our input unitary as a black-box gate to the solution circuit. The final unitary of the resultant circuit is
, which can be obtained using fast Qiskit API functions. From there, we can simply plug this value into (
3) and obtain the final error.
Figure A3 in
Appendix B.3 shows a visual representation of this optimization, where we highlight parts of the optimized and unoptimized functions called repeatedly by the numerical optimizer. However, note that circuits without any parametrized gates do not incur any numerical optimization time penalty. Lastly, since approximation error calculations require
, we calculate this matrix ahead of time and cache it.
5. Results
In this section, we present details about our experimental setup and the results obtained from our evaluations. The computational hardware and software libraries are mentioned, followed by a description of the input dataset used for evaluation. We compare our GA-based method with and without fuzzy logic adaptations against Qiskit and BQSkit, and
Table 3 and
Table 4 summarize the experiments carried out in this work. For clarity, we label GA with fuzzy logic based adaption as GA-F, while GA without fuzzy logic is labeled as just GA.
5.1. Experiment Setup
The KU ITTC HPC cluster was used to run the evaluations, with each compiler provided with 20 CPUs and 8 GB of memory. The compute nodes consisted of AMD Opteron
TM Processor 6274 and 6376 CPUs [
82]. The nodes ran the Rocky Linux 9.4 (Blue Onyx) [
83] operating system, and a Python environment, using version 3.10.9, was set up using Conda (version 24.9.2). The popular scientific Python library SciPy (version 1.11.4) [
74] was utilized for the numerical BFGS-based numerical optimizer, while the SciKit Fuzzy library (version 0.5.0) [
84] was used to implement the fuzzy logic controller. Finally, several libraries from Qiskit (version 1.2.4) [
85] were used to implement the GA-based compiler. It, and BQSkit (version 1.2.0) [
86], were also used for comparison and evaluation of the compiler.
For evaluations, a test suite of random unitary matrices was generated for qubit sizes 2 and 3. These were generated using the
random_unitary [
87] library function from Qiskit, which ensures even distribution of generated unitaries. Five unitaries were generated per qubit size, and we refer to each as a
trial. All experiments were conducted on this test suite, and all compiler comparisons were made based on the outcome of compiling this dataset.
In addition to input matrices, target machines were also provided to the compilers. The target devices used ring-shaped topologies and bidirectional connectivity (i.e., CNOTs available in both direction) were used; see
Figure 10. The basis gate set of
was used for the targets. For the GA,
Table 5 lists the gate elimination and gate fusion policies, noting that during both gate fusion and elimination, the right-most gate gets replaced with the
I gate. All qubits and connections were assumed to be of the same quality.
5.2. GA-Based Compilers vs. Qiskit and BQSkit
We present the results of our comparison of the GA-based compiler with Qiskit and BQSkit. We configured GA with a crossover rate of 1.0 (always occurs) and a mutation rate of 0.1. For the comparison, GA, GA-F and BQSkit were given error threshold targets of 0.1, 0.01 and 0.001 and the results were compared in terms of depth and CNOT count. It is worth mentioning that the compilation techniques used in BQSkit are designed to perform approximate compilation up to a target error threshold, although it is usually also possible to perform exact compilation by setting the error threshold to zero. Thus, we use BQSkit to compare our GAs against existing approximate compilation techniques. Qiskit, on the other hand, uses exact compilers based on analytical methods and does not compile against an error threshold. It always produces unitary preserving circuits [
88], i.e., circuits with effective approximation error of zero. For a fair comparison between Qiskit and the other approximate compilers, we also test GA, GA-F and BQSkit with an extremely low error threshold of
. This is the default error threshold for the BQSkit compiler and is also the default used by the
equiv method of the
Operator class in Qiskit [
89], which is used to check if two operators are equivalent up to a global phase. The Qiskit
transpile function was used for synthesis with the highest optimization level of 3 and the BQSkit
compile function was used with the highest optimization setting of 4. Each compiler was given a 12 h timeout limit per trial.
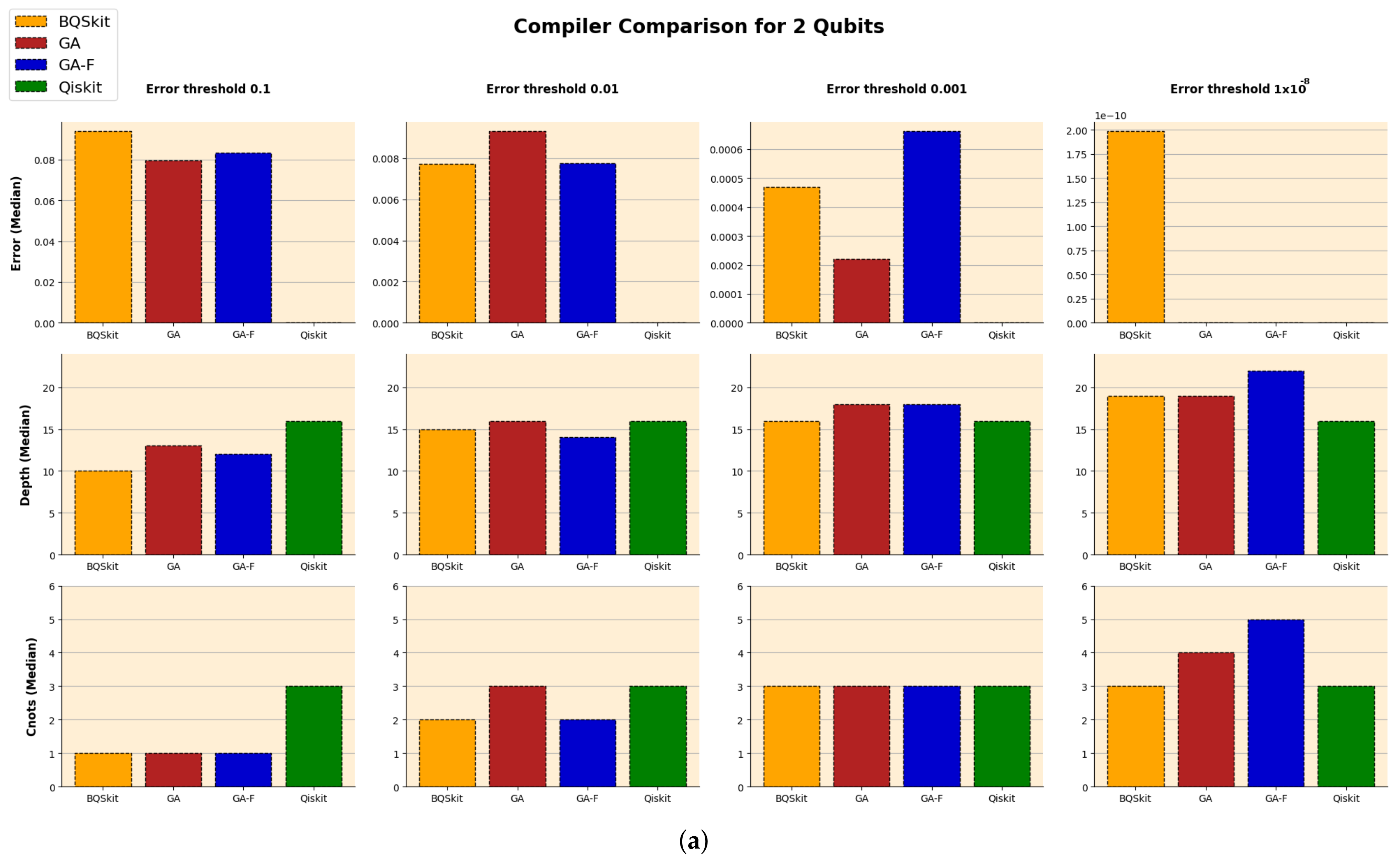
The compilation results are displayed in
Figure 11, showing the median values across five trials for each metric. These show that the GA and GA-F appear to produce results comparable with BQSkit across all metrics across for thresholds of 0.1, 0.01 and 0.001 for 2 qubit unitaries. Furthermore, it able to achieve comparable results with both BQSkit and Qiskit for 2 qubit unitaries with the much more restrictive error threshold of
.
For 3 qubits, however, GA and GA-F are unable to achieve the target error thresholds, indicating that the 12 h limit was not adequate. This can be explained by the fact that moving from 2 qubits to 3 qubits drastically increases the search space, since the number of possible circuits increases exponentially with the number of qubits. Thus, a reasonable conclusion could be that many more generations of the GA and GA-F are needed to converge to an acceptable solution for larger qubit numbers.
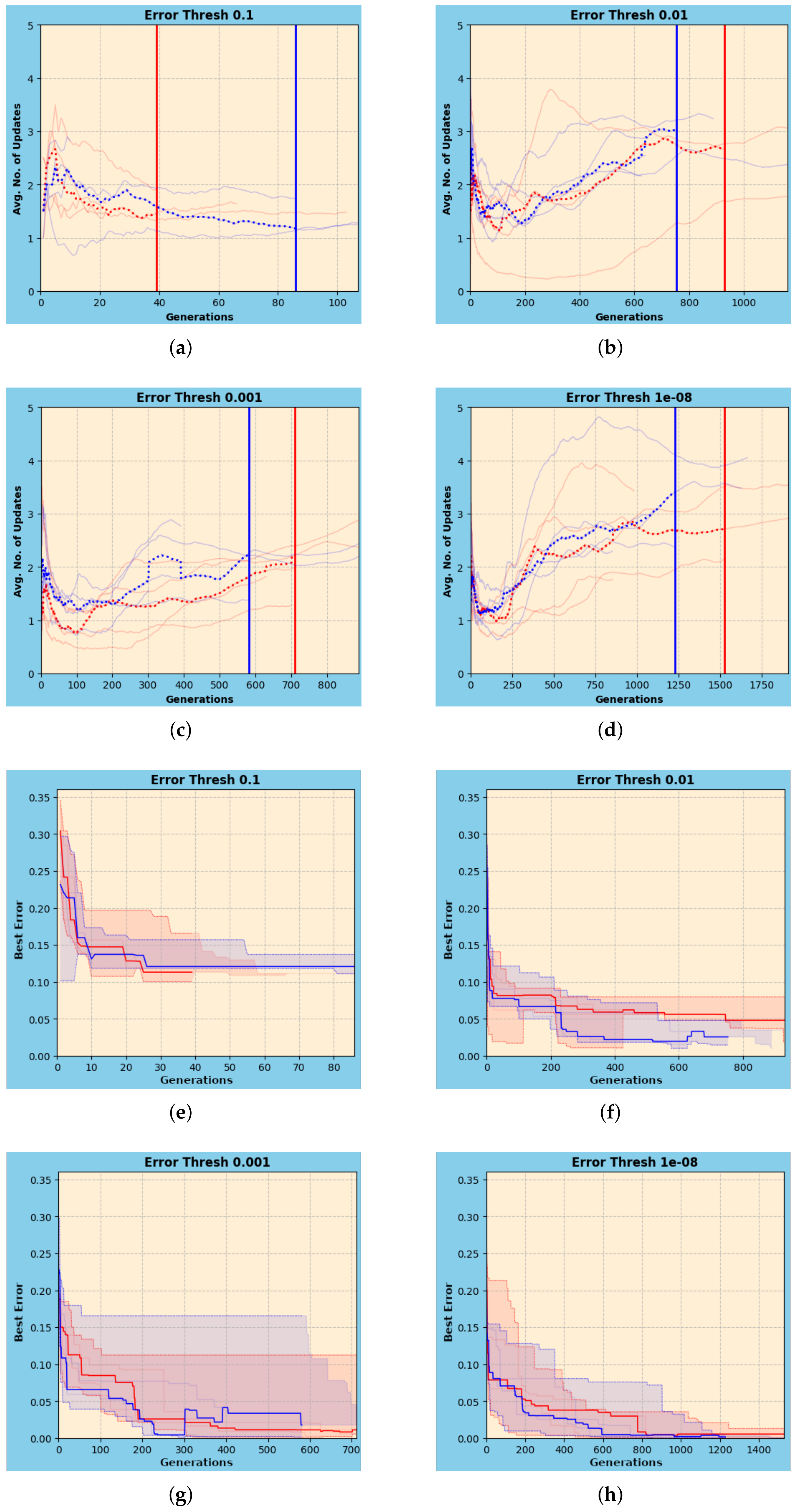
Looking at the runtime characteristics of both GA-based compilers (
Figure 12,
Figure 13 and
Figure 14) provides further evidence of this. In particular, the plots of best error vs. generations for 3 qubits in
Figure 14e–h are missing the sharp drop in error towards the target threshold that we see for 2 qubits in
Figure 13e–h. It indicates that they are struggling to converge to the provided error threshold within the time limit. We can also observe in those figures that the convergence times for GA and GA-F appear to be less than 1000 generations for all but the lowest error threshold when compiling 2 qubit unitaries, whereas for 3 qubits unitaries, they were unable to achieve median errors less than 0.25 even after 1500 generations. Finally,
Figure 13a–d and
Figure 14a–d indicate that the proposed methods are able to maintain slightly higher updates on average for 2 qubits than 3 qubits, although the difference is not much. Overall, this analysis provides additional motivation to accelerate GAs, since running more generations can potentially improve the final solution quality.
At this point we note that error threshold levels for 0.01 and lower, for 3 qubits, are not available for BQSkit due to execution timeout and memory over-utilization. We suspect this is a result of using the highest optimization setting, which incurs a higher compilation time.
5.3. Effect of Runtime Parameter Adaptation
Figure 12 compares GA and GA-F specifically, restricting the plots to only these for clarity. For 2 qubits, both GA and GA-F were able to reach the target error thresholds. We observe that GA-F is able to produce similar median depths and CNOTs for error thresholds of 0.1, 0.001 and 0.001. It performs slightly worse on those metrics for error threshold of
. These observations prompt us to take a deeper look using
Figure 13a–d, which show the cumulative average number of updates each GA-based compiler is able to sustain throughout its progress. It shows that GA-F generally maintains a higher median value for the average number of updates, indicating it is able to find new solutions, which extend the Pareto-front, faster than the regular GA. The graphs also show the median number of generations required for the proposed techniques to hit the error targets and these are marked with vertical lines. We see that, except for the error threshold of 0.1, GA-F is able to achieve convergence earlier.
Figure 13e–h show the progression of the best error achieved over generations. The solid traces plot the median and the shaded areas indicate the region between the maximum and minimum best error values at that generation across trials. We observe that both GA and GA-F progress at similar rates towards convergence in terms of best error for 2 qubits, with GA-F able to achieve slightly faster rates of convergence in some cases.
The results are more mixed and inconclusive for 3 qubits. Neither configuration has a definitive lead in either the average rate of updates or the progress of achieved best error, as can be seen from
Figure 14a–h. Furthermore, since the GAs were not able to achieve the error targets within the given timeout limit, these results are possibly not representative. It is plausible that over a longer number of generations, the GAs would settle into a more stable pattern, perhaps the same as observed for 2 qubit unitaries, but further experimentation is required to confirm.
5.4. Effect of Population Size
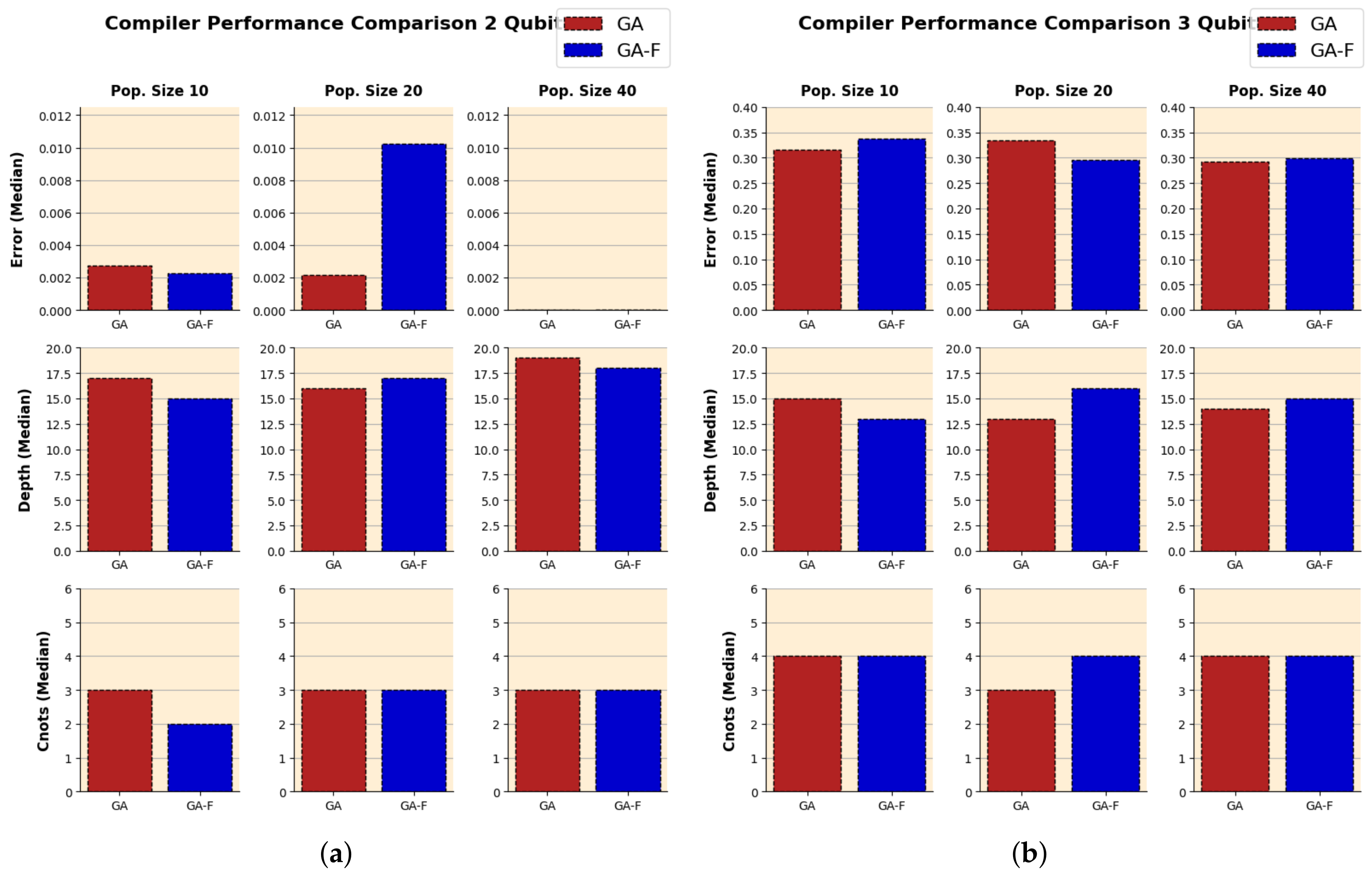
The population size used in a genetic algorithm can affect its performance and the quality of solutions. To observe the effects of population size, we ran GA and GA-F for three different population sizes, 10, 20 and 40. These sizes were chosen with the execution time constraints in mind. For a fair comparison, we limited the number of generations for each compiler to 800 generations, and we repeated the experiments for five trials, excluding results from any trial which was unable to complete the 800 generations in the given time limit.
Figure 15 shows the results for 2 and 3 qubits, respectively, with the median values of metrics plotted.
We can observe that increasing population sizes can sometimes produce slightly better results in terms of approximation error, although there are anomalies and the differences are not significant. There appears to be no noticeable improvements in depth and CNOT across the different population sizes. GA and GA-F perform similarly over the different population sizes. These results, combined with analysis from the previous section, indicate that number of generations has a bigger effect on convergence than the population size, and requires further investigation.
6. Discussion
Our experimental investigations demonstrated that the GA-based compilers are able to produce competitive results for 2 qubits, when compared with industry standard compilers such as BQSkit and Qiskit. However, the investigation was inconclusive for 3 qubits since the compilers were unable to reach error thresholds within the provided time limit. As stated before, going from 2 qubits to 3 qubits dramatically increases the search space. For example, using the five basis gates used in this work, there are possible circuits of depth 1 for 2 qubits. By contrast, there are circuits of depth 1 for 3 qubits. As can be observed, the solution space grows exponentially (roughly about in our case). This effect is made more challenging as the depth of the circuit increases. Thus, it becomes harder for the GA to search this increased solution space. In addition, 3-qubit circuits are likely to have more parameterized gates, resulting in the numerical optimizer taking longer to converge. All of these factors contribute to the extended runtimes of the GAs for 3 qubits in its current form.
Although the provided time limit was insufficient, the experimental data shows that the desired metrics do tend downwards over the generations. It therefore prompts the question of whether increasing the time limit, and/or using a higher population would counteract the increase in search space going from 2 to 3 qubits, and requires further investigation. It also stands to reason that with further performance optimizations or more computational resources, the GA-based compilers might achieve the desired error thresholds within shorter time limits and is also worth studying.
Using runtime parameter adaptations appear to provide noticeable benefits for 2 qubit inputs, as seen in the previous section, in terms of number of new solutions discovered in the Pareto front and convergence speed. However, due to the issues discussed above, their effect on 3-qubit circuits is not apparent. Thus, while further experimentation is required for 3 qubits and beyond, the results for 2-qubit circuits show promise.
Setting the compilation performance aside, the GA-based compilers proposed have additional benefits. Firstly, the GA only requires a unitary matrix as an input, and its performance does not depend on individual circuit structures. Moreover, the multi-objective optimization feature of NSGA enables us to add more compilation objectives easily, at the cost of more computation resources. This can be used to address additional compilation goals such as differentiating gates based on their error rates and reducing the number of high error gates, or weigh connections based on the likelihood of error and reduce the number of CNOTs on such error prone connections. Finally, the results show that the GAs appear to continuously make progress towards better fitnesses (i.e., lower values for metrics), even if slowly.
As for future work, given the versatility of GAs, we believe there is a lot of room for improvement in terms of how the genetic operators of crossover, mutation and non-dominated sorting work. For example, the number of offspring produced from crossover was set at 2, and it is worth investigating if allowing more or less offspring from each parent pair would improve the GA convergence. It would also be interesting to study how the GA responds with a tournament size other than 2. For example, we could investigate if a dynamically adjusted tournament size, to control the selection pressure at runtime, would help with GA convergence. The tournament size and number of offspring together could also be used to control the trade-off between diversity of population and exploitation of solutions. For example, a higher tournament size coupled with higher number of offspring per parent pair would promote only high fitness individuals. This may increase the convergence speed, promoting only the best solutions available, at the cost of a higher risk of premature convergence due to loss of diversity. It would also be worthwhile to investigate the effect of dynamic population sizes, allowing it to grow and shrink. In addition to this, the sequence of mutation and crossover, along with their individual mechanisms, could also be varied to observe their effects on GA performance. Further, tuning the fuzzy logic controller could also be helpful. This could include introducing more input variables and applying more complex rules. It is also to be noted that the process of determining good membership functions is usually done using expert knowledge and domain-specific information, coupled with a significant amount of trial and error [
80]. Therefore, some future effort could be dedicated to identifying better membership functions and related parameters. Overall, the flexibility of GAs allows many avenues for further study and optimization.
In a broader context, quantum computing could play a key role in advancing HPC capabilities, unlocking new research possibilities. However, to achieve this goal, effective execution of quantum algorithms on physical devices must be enabled. To that effect, research into novel and efficient compilation techniques is crucial. Which is why we believe further work on advanced compilation techniques, such as the one proposed here, is of paramount importance and requires careful consideration.
7. Conclusions
Quantum computing promises to open new frontiers to HPC efforts. However, quantum circuit synthesis in the NISQ era involves significant challenges, stemming from constraints such as restricted qubit connectivity (requiring mapping and routing), rapid decoherence of qubits (requiring short circuits) and vulnerability to gate errors (requiring low gate counts). Exact synthesis techniques for optimized circuits are generally intractable, which necessitates approximate synthesis methods which can balance approximation error with other compilation targets. To address these concerns, we proposed a genetic-algorithm-based approximate quantum synthesis technique which conceptualizes quantum compilation as a multi-objective optimization problem. We leverage the Non-dominated Sorting Genetic Algorithm for direct compilation of unitary matrices to targeted quantum hardware. Our compiler synthesizes circuits which conform to machine specific native basis gate sets and qubit topologies, while attempting to minimize approximation error, circuit depth and 2-qubit CNOT gate counts. Furthermore, to augment the GA, we utilize a fuzzy logic based runtime parameter adaptation scheme. This controller dynamically modulates the algorithm’s exploratory and exploitative search behaviors, enabling the GA to better navigate around local minima. Experimental results show promising results for 2 qubits; however, further investigations are required to understand how the method would perform for higher qubit counts.
Author Contributions
Conceptualization, I.I. and E.E.-A.; methodology, I.I., V.J. and E.E.-A.; software, I.I., V.J., S.T., A.N., K.F.E., S.K. and S.O.; validation, I.I., V.J., S.T., A.N., K.F.E., S.K., S.O. and M.C.; formal analysis, I.I. and E.E.-A.; investigation, I.I., V.J., S.T., A.N., K.F.E., S.K., S.O. and M.C.; resources, I.I., V.J., S.T., A.N., K.F.E., S.O., S.K., M.C. and E.E.-A.; data curation, I.I.; writing—original draft preparation, I.I., V.J., S.T., K.F.E., A.N., S.K. and S.O.; writing—review and editing, M.C., K.E.-A., D.K., B.P., M.S. and D.B.; visualization, I.I., S.T., V.J., M.C. and A.N.; supervision, E.E.-A.; project administration, E.E.-A.; funding acquisition, E.E.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to federal collaboration requirements.
Acknowledgments
This research used resources of the Oak Ridge Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC05-00OR22725.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NISQ | Noisy Intermediate-Scale Quantum |
| GA | Genetic algorithm |
| MOO | Multi-objective optimization |
| NSGA | Non-dominated Sorting Genetic Algorithm |
| BFGS | Broyden–Fletcher–Goldfarb–Shanno |
| FPGA | Field Programmable Gate Array |
Appendix A. Fitness Function
Here, we discuss some of the issues with using an Euclidean distance-based method for combining multiple metrics into a single one. To enable proper combination and avoid bias, we need to first rescale all metrics to the same range. While the approximation error function already gives us a value in the range
, the other two metrics also need to be scaled to such a range. The metrics for depth and CNOT could, therefore, be calculated by first measuring them for each circuit and then normalizing them to the range
, using (
A1) and (
A2).
Once normalized, the three values can be combined using the Euclidean distance formula, as shown in (
A3), to obtain the final fitness value of a chromosome, also in the range
.
This method, however, presents several challenges. Firstly, the Euclidean distance-based aggregation implies that in a Cartesian space with the metric axes, all points in a given hypershpere would have the same overall fitness; see
Figure A1. In our testing, this would often cause the population of chromosomes to be saturated with shallow, low gate-count circuits with high approximation error, since it was easier for the GA to remove gates and layers than to optimize for approximation error.
Figure A1.
All points in this hypersphere will have the same fitness of 1.
Figure A1.
All points in this hypersphere will have the same fitness of 1.
This method can also lead to extreme edge cases where circuits with zero (or close to zero) depth and zero CNOTs automatically gain an (unfair) advantage, even though for most cases they would have very low accuracy. For example, for two synthesized circuits
and
, let
,
,
, while
,
,
. Using (
A3), we have
, whereas
, indicating
is roughly twice as better, despite having three times the approximation error! To counteract this issue, weights could be added to each objective, to encourage the GA to find more accurate circuits, without completely disregarding depth and CNOT count. This, however, still does not solve the edge case of zero depth or zero CNOT circuits. Moreover, introducing weights add yet another set of parameters which need tuning, and ascertaining a good ratio between accuracy, depth and gate count is a difficult task.
Euclidean distances can also be affected by the statistical distributions of the metrics. For example, if the standard deviations observed in are small compared to the standard deviations in , the overall fitness value becomes more sensitive to the CNOT count. We observed this when a small change in the number of CNOTs affected the final fitness value much more than changes in approximation error.
Since useful compilations of quantum circuits for NISQ devices require optimizing for multiple objectives, an alternative means of combining the metrics was still needed, which led us to choose the NSGA-II algorithm. It allowed the use of different objective metrics without needing to normalize them, assign weights or combine them into a single metric, alleviating many of the issues of the method discussed here.
Appendix B. Supplemental Information
Appendix B.1. Tournament Selection
The pseudocode for the tournament selection method used in this work is presented below:
Input Parameters:
P: The current population of individuals
n: Number of individuals to select
k: Number of individuals competing in each tournament
| Algorithm A1 Tournament Selection in Genetic Algorithms |
| 1: procedure TournamentSelection() |
| 2: empty list |
| 3: for to n do |
| 4: randomly select n individuals from P |
| 5: individual with best fitness from |
| 6: .append() |
| 7: end for |
| 8: return |
| 9: end procedure |
Appendix B.2. Fuzzy Logic Membership Functions
Figure A2a shows the membership functions for the fuzzy variable
updates, while
Figure A2b shows the membership function for the fuzzy variable
mutation rate, as discussed in
Section 4.10.
Figure A2.
Membership functions for: (a) fuzzy variable updates (b) fuzzy variable mutation rate.
Figure A2.
Membership functions for: (a) fuzzy variable updates (b) fuzzy variable mutation rate.
Appendix B.3. GA Optimization Flows
Figure A3a,b provide a visual description of the approximation error calculation flow for the unoptimized and optimized method.
Figure A3.
Error function calculation flows showing (a) unoptimized and (b) optimized versions.
Figure A3.
Error function calculation flows showing (a) unoptimized and (b) optimized versions.
References
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Aaronson, S.; Arkhipov, A. The computational complexity of linear optics. In Proceedings of the Forty-Third Annual ACM Symposium on Theory of Computing, San Jose, CA, USA, 6–8 June 2011; pp. 333–342. [Google Scholar]
- Bayerstadler, A.; Becquin, G.; Binder, J.; Botter, T.; Ehm, H.; Ehmer, T.; Erdmann, M.; Gaus, N.; Harbach, P.; Hess, M.; et al. Industry quantum computing applications. EPJ Quantum Technol. 2021, 8, 25. [Google Scholar]
- Holmes, A.; Johri, S.; Guerreschi, G.G.; Clarke, J.S.; Matsuura, A.Y. Impact of qubit connectivity on quantum algorithm performance. Quantum Sci. Technol. 2020, 5, 025009. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Zeh, H.D. On the interpretation of measurement in quantum theory. Found. Phys. 1970, 1, 69–76. [Google Scholar]
- Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev. Mod. Phys. 2005, 76, 1267–1305. [Google Scholar] [CrossRef]
- Magesan, E.; Gambetta, J.M.; Johnson, B.R.; Ryan, C.A.; Chow, J.M.; Merkel, S.T.; Da Silva, M.P.; Keefe, G.A.; Rothwell, M.B.; Ohki, T.A.; et al. Efficient measurement of quantum gate error by interleaved randomized benchmarking. Phys. Rev. Lett. 2012, 109, 080505. [Google Scholar] [CrossRef]
- Siraichi, M.Y.; Santos, V.F.d.; Collange, C.; Pereira, F.M.Q. Qubit allocation. In Proceedings of the 2018 International Symposium on Code Generation and Optimization, Vienna Austria, 24–28 February 2018; CGO 2018. pp. 113–125. [Google Scholar] [CrossRef]
- Younis, E.; Iancu, C.C.; Lavrijsen, W.; Davis, M.; Smith, E.; USDOE. Berkeley Quantum Synthesis Toolkit (BQSKit); v1; USDOE: Washington, DC, USA, 2021. [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2015; pp. 19–20. [Google Scholar]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the Parallel Problem Solving from Nature PPSN VI: 6th International Conference, Paris, France, 18–20 September 2000; Proceedings 6. Springer: Berlin/Heidelberg, Germany, 2000; pp. 849–858. [Google Scholar]
- Rudolph, G. Convergence analysis of canonical genetic algorithms. IEEE Trans. Neural Netw. 1994, 5, 96–101. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic. Computer 1988, 21, 83–93. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Williams, C.P. Explorations in Quantum Computing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Rowland, T.; Weisstein, E.W. Unitary Matrix. Available online: https://mathworld.wolfram.com/UnitaryMatrix.html (accessed on 27 February 2025).
- Deutsch, D. Quantum theory, the Church–Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A Math. Phys. Sci. 1985, 400, 97–117. [Google Scholar]
- Chow, J.; Dial, O.; Gambetta, J. IBM Quantum breaks the 100-qubit processor barrier. IBM Res. Blog 2021. Available online: https://www.ibm.com/quantum/blog/127-qubit-quantum-processor-eagle (accessed on 27 February 2025).
- Cowtan, A.; Dilkes, S.; Duncan, R.; Krajenbrink, A.; Simmons, W.; Sivarajah, S. On the qubit routing problem. arXiv 2019, arXiv:1902.08091. [Google Scholar]
- Javadi-Abhari, A.; Treinish, M.; Krsulich, K.; Wood, C.J.; Lishman, J.; Gacon, J.; Martiel, S.; Nation, P.D.; Bishop, L.S.; Cross, A.W.; et al. Quantum computing with Qiskit. arXiv 2024, arXiv:2405.08810. [Google Scholar] [CrossRef]
- Xing, L.n.; Chen, Y.w.; Cai, H.p. An intelligent genetic algorithm designed for global optimization of multi-minima functions. Appl. Math. Comput. 2006, 178, 355–371. [Google Scholar]
- Srinivas, N.; Deb, K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar]
- Qi, Y.; Ma, X.; Liu, F.; Jiao, L.; Sun, J.; Wu, J. MOEA/D with adaptive weight adjustment. Evol. Comput. 2014, 22, 231–264. [Google Scholar]
- Vesikar, Y.; Deb, K.; Blank, J. Reference point based NSGA-III for preferred solutions. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1587–1594. [Google Scholar]
- Tamaki, H.; Kita, H.; Kobayashi, S. Multi-objective optimization by genetic algorithms: A review. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 517–522. [Google Scholar]
- Mamdani, E.H. Application of fuzzy algorithms for control of simple dynamic plant. In Proceedings of the Institution of Electrical Engineers, IET, London, UK, 1 December 1974; Volume 121, pp. 1585–1588. [Google Scholar]
- Hellmann, M. Fuzzy logic introduction. Univ. Rennes 2001, 1. Available online: https://www.researchgate.net/publication/238684924_Fuzzy_Logic_Introduction (accessed on 27 February 2025).
- Tucci, R.R. A rudimentary quantum compiler (2nd ed.). arXiv 1999, arXiv:quant-ph/9902062. [Google Scholar]
- Shende, V.V.; Bullock, S.S.; Markov, I.L. Synthesis of quantum logic circuits. In Proceedings of the 2005 Asia and South Pacific Design Automation Conference, Shanghai, China, 21 January 2005; pp. 272–275. [Google Scholar]
- Khaneja, N.; Glaser, S. Cartan Decomposition of SU (2^ n), Constructive Controllability of Spin systems and Universal Quantum Computing. arXiv 2000, arXiv:quant-ph/0010100. [Google Scholar]
- Iten, R.; Colbeck, R.; Kukuljan, I.; Home, J.; Christandl, M. Quantum circuits for isometries. Phys. Rev. A 2016, 93, 032318. [Google Scholar]
- Barenco, A.; Bennett, C.H.; Cleve, R.; DiVincenzo, D.P.; Margolus, N.; Shor, P.; Sleator, T.; Smolin, J.A.; Weinfurter, H. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457. [Google Scholar] [PubMed]
- Helgason, S. Differential Geometry, Lie Groups, and Symmetric Spaces; Academic Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Qiskit, I. Qiskit SDK: TwoQubitBasisDecomposer. Available online: https://docs.quantum.ibm.com/api/qiskit/qiskit.synthesis.TwoQubitBasisDecomposer (accessed on 27 February 2025).
- Li, G.; Ding, Y.; Xie, Y. Tackling the qubit mapping problem for NISQ-era quantum devices. In Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems, Providence, RI, USA, 13–19 April 2019; pp. 1001–1014. [Google Scholar]
- Wu, X.C.; Davis, M.G.; Chong, F.T.; Iancu, C. Reoptimization of quantum circuits via hierarchical synthesis. In Proceedings of the 2021 International Conference on Rebooting Computing (ICRC), Los Alamitos, CA, USA, 30 November–2 December 2021; pp. 35–46. [Google Scholar]
- Davis, M.G.; Smith, E.; Tudor, A.; Sen, K.; Siddiqi, I.; Iancu, C. Towards optimal topology aware quantum circuit synthesis. In Proceedings of the 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), Denver, CO, USA, 12–16 October 2020; pp. 223–234. [Google Scholar]
- Younis, E.; Sen, K.; Yelick, K.; Iancu, C. Qfast: Conflating search and numerical optimization for scalable quantum circuit synthesis. In Proceedings of the 2021 IEEE International Conference on Quantum Computing and Engineering (QCE), Broomfield, CO, USA, 17–22 October 2021; pp. 232–243. [Google Scholar]
- Patel, T.; Younis, E.; Iancu, C.; de Jong, W.; Tiwari, D. Quest: Systematically approximating quantum circuits for higher output fidelity. In Proceedings of the 27th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Lausanne, Switzerland, 28 February–4 March 2022; pp. 514–528. [Google Scholar]
- Kukliansky, A.; Younis, E.; Cincio, L.; Iancu, C. QFactor: A Domain-Specific Optimizer for Quantum Circuit Instantiation. In Proceedings of the 2023 IEEE International Conference on Quantum Computing and Engineering (QCE), Bellevue, WA, USA, 17–22 September 2023; Volume 1, pp. 814–824. [Google Scholar]
- Liu, J.; Younis, E.; Weiden, M.; Hovland, P.; Kubiatowicz, J.; Iancu, C. Tackling the qubit mapping problem with permutation-aware synthesis. In Proceedings of the 2023 IEEE International Conference on Quantum Computing and Engineering (QCE), Bellevue, WA, USA, 17–22 September 2023; Volume 1, pp. 745–756. [Google Scholar]
- Soeken, M.; Meuli, G.; Schmitt, B.; Mozafari, F.; Riener, H.; De Micheli, G. Boolean satisfiability in quantum compilation. Philos. Trans. R. Soc. A 2020, 378, 20190161. [Google Scholar]
- Madden, L.; Simonetto, A. Best approximate quantum compiling problems. ACM Trans. Quantum Comput. 2022, 3, 1–29. [Google Scholar]
- Kusyk, J.; Saeed, S.M.; Uyar, M.U. Survey on quantum circuit compilation for noisy intermediate-scale quantum computers: Artificial intelligence to heuristics. IEEE Trans. Quantum Eng. 2021, 2, 1–16. [Google Scholar]
- Yabuki, T.; Iba, H. Genetic algorithms for quantum circuit design-evolving a simpler teleportation circuit. In Proceedings of the Late Breaking Papers at the 2000 Genetic and Evolutionary Computation Conference, Las Vegas, NV, USA, 8–12 July 2000; pp. 421–425. [Google Scholar]
- Lukac, M.; Perkowski, M. Evolving quantum circuits using genetic algorithm. In Proceedings of the 2002 NASA/DoD Conference on Evolvable Hardware, Alexandria, VA, USA, 15–18 July 2002; pp. 177–185. [Google Scholar]
- Lukac, M.; Perkowski, M.; Goi, H.; Pivtoraiko, M.; Yu, C.H.; Chung, K.; Jeech, H.; Kim, B.G.; Kim, Y.D. Evolutionary approach to quantum and reversible circuits synthesis. Artif. Intell. Rev. 2003, 20, 361–417. [Google Scholar]
- Massey, P.; Clark, J.A.; Stepney, S. Human-competitive evolution of quantum computing artefacts by genetic programming. Evol. Comput. 2006, 14, 21–40. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Ruican, C.; Udrescu, M.; Prodan, L.; Vladutiu, M. Genetic algorithm based quantum circuit synthesis with adaptive parameters control. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 896–903. [Google Scholar]
- Krylov, G.; Lukac, M. Quantum encoded quantum evolutionary algorithm for the design of quantum circuits. In Proceedings of the 16th ACM International Conference on Computing Frontiers, Alghero, Sardinia, 30 April–2 May 2019; pp. 220–225. [Google Scholar]
- Miranda, F.T.; Balbi, P.P.; Costa, P. Synthesis of quantum circuits with an island genetic algorithm. arXiv 2021, arXiv:2106.03115. [Google Scholar]
- Whitley, D.; Rana, S.; Heckendorn, R.B. Island model genetic algorithms and linearly separable problems. In Proceedings of the Evolutionary Computing: AISB International Workshop, Manchester, UK, 7–8 April 1997; Selected Papers. Springer: Berlin/Heidelberg, Germany, 1997; pp. 109–125. [Google Scholar]
- Sünkel, L.; Martyniuk, D.; Mattern, D.; Jung, J.; Paschke, A. GA4QCO: Genetic algorithm for quantum circuit optimization. arXiv 2023, arXiv:2302.01303. [Google Scholar]
- Bang, J.; Yoo, S. A genetic-algorithm-based method to find unitary transformations for any desired quantum computation and application to a one-bit oracle decision problem. J. Korean Phys. Soc. 2014, 65, 2001–2008. [Google Scholar] [CrossRef]
- Li, R.; Alvarez-Rodriguez, U.; Lamata, L.; Solano, E. Approximate quantum adders with genetic algorithms: An IBM quantum experience. Quantum Meas. Quantum Metrol. 2017, 4, 1–7. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Bandyopadhyay, C.; Mukherjee, A.; Wille, R.; Drechsler, R.; Rahaman, H. Efficient implementation of nearest neighbor quantum circuits using clustering with genetic algorithm. In Proceedings of the 2020 IEEE 50th International Symposium on Multiple-Valued Logic (ISMVL), Miyazaki, Japan, 9–11 November 2020; pp. 40–45. [Google Scholar]
- Creevey, F.M.; Hill, C.D.; Hollenberg, L.C. GASP: A genetic algorithm for state preparation on quantum computers. Sci. Rep. 2023, 13, 11956. [Google Scholar] [CrossRef] [PubMed]
- Rindell, T.; Yenilen, B.; Halonen, N.; Pönni, A.; Tittonen, I.; Raasakka, M. Exploring the optimality of approximate state preparation quantum circuits with a genetic algorithm. Phys. Lett. A 2023, 475, 128860. [Google Scholar] [CrossRef]
- Ding, L.; Spector, L. Evolutionary quantum architecture search for parametrized quantum circuits. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Boston, MA, USA, 9–13 July 2022; pp. 2190–2195. [Google Scholar]
- Ding, L.; Spector, L. Multi-objective evolutionary architecture search for parameterized quantum circuits. Entropy 2023, 25, 93. [Google Scholar] [CrossRef]
- Giovagnoli, A.; Tresp, V.; Ma, Y.; Schubert, M. Qneat: Natural evolution of variational quantum circuit architecture. In Proceedings of the Companion Conference on Genetic and Evolutionary Computation, Lisbon, Portugal, 15–19 July 2023; pp. 647–650. [Google Scholar]
- Acampora, G.; Chiatto, A.; Vitiello, A. Training variational quantum circuits through genetic algorithms. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Huang, Y.; Li, Q.; Hou, X.; Wu, R.; Yung, M.H.; Bayat, A.; Wang, X. Robust resource-efficient quantum variational ansatz through an evolutionary algorithm. Phys. Rev. A 2022, 105, 052414. [Google Scholar] [CrossRef]
- Syswerda, G. Uniform crossover in genetic algorithms. In Proceedings of the ICGA, Fairfax, VA, USA, 1 June 1989; Volume 3. [Google Scholar]
- Miller, B.L.; Goldberg, D.E. Genetic algorithms, tournament selection, and the effects of noise. Complex Syst. 1995, 9, 193–212. [Google Scholar]
- Back, T. Selective pressure in evolutionary algorithms: A characterization of selection mechanisms. In Proceedings of the First IEEE Conference on Evolutionary Computation, IEEE World Congress on Computational Intelligence, Orlando, FL, USA, 27–29 June 1994; pp. 57–62. [Google Scholar]
- Shukla, A.; Pandey, H.M.; Mehrotra, D. Comparative review of selection techniques in genetic algorithm. In Proceedings of the 2015 International Conference on Futuristic Trends on Computational Analysis and Knowledge Management (ABLAZE), Greater Noida, India, 25–27 February 2015; pp. 515–519. [Google Scholar]
- Weisstein, E.W. Frobenius Norm. Available online: https://mathworld.wolfram.com/FrobeniusNorm.html (accessed on 27 February 2025).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 2006. [Google Scholar]
- Broyden, C.G. The convergence of a class of double-rank minimization algorithms 1. general considerations. IMA J. Appl. Math. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Fletcher, R. A new approach to variable metric algorithms. Comput. J. 1970, 13, 317–322. [Google Scholar] [CrossRef]
- Goldfarb, D. A family of variable-metric methods derived by variational means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of quasi-Newton methods for function minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- Sadollah, A. Introductory chapter: Which membership function is appropriate in fuzzy system. In Fuzzy Logic Based in Optimization Methods and Control Systems and Its Applications; IntechOpen: Rijeka, Croatia, 2018; Volume 10. [Google Scholar]
- multiprocessing—Process-Based Parallelism. Available online: https://docs.python.org/3.10/library/multiprocessing.html (accessed on 27 February 2025).
- Cluster Hardware. Available online: https://help.ittc.ku.edu/Cluster_Hardware (accessed on 27 February 2025).
- Release Notes for Rocky Linux 9.4. Available online: https://docs.rockylinux.org/release_notes/9_4 (accessed on 27 February 2025).
- SciKit-Fuzzy. Available online: https://scikit-fuzzy.readthedocs.io/en/latest/overview.html (accessed on 27 February 2025).
- Qiskit. Available online: https://github.com/Qiskit/qiskit/releases/tag/1.2.4 (accessed on 27 February 2025).
- BQSkit. Available online: https://github.com/BQSKit/bqskit/releases/tag/1.2.0 (accessed on 27 February 2025).
- Random Unitary Operator. Available online: https://github.com/Qiskit/qiskit/blob/896d1c8b72888a52a46081a6d1f4de8c56db8aea/qiskit/quantum_info/operators/random.py#L32-L56 (accessed on 27 February 2025).
- TranspileLayout. Available online: https://docs.quantum.ibm.com/api/qiskit/qiskit.transpiler.TranspileLayout (accessed on 27 February 2025).
- Equiv Method for the Operator Class. Available online: https://github.com/Qiskit/qiskit/blob/1263d82877ba5183232db9bac5bc2c61a7da7a26/qiskit/quantum_info/operators/operator.py#L688-L710 (accessed on 27 February 2025).
Figure 1.
Characteristics of a quantum circuit.
Figure 1.
Characteristics of a quantum circuit.
Figure 2.
Routing necessary to make an input circuit compatible with qubit topology.
Figure 2.
Routing necessary to make an input circuit compatible with qubit topology.
Figure 3.
Careful qubit mapping can reduce gates needed for routing.
Figure 3.
Careful qubit mapping can reduce gates needed for routing.
Figure 4.
Overview of GA compiler flow with runtime adaptation.
Figure 4.
Overview of GA compiler flow with runtime adaptation.
Figure 5.
Chromosome encoding scheme, including initial and final qubit mapping.
Figure 5.
Chromosome encoding scheme, including initial and final qubit mapping.
Figure 6.
Three different crossover versions: (a) coarse-grained crossover, (b) fine-grained crossover, (c) mapping crossover.
Figure 6.
Three different crossover versions: (a) coarse-grained crossover, (b) fine-grained crossover, (c) mapping crossover.
Figure 7.
Three different mutation schemes: (a) coarse-grained mutation, (b) fine-grained mutation, (c) mapping mutation.
Figure 7.
Three different mutation schemes: (a) coarse-grained mutation, (b) fine-grained mutation, (c) mapping mutation.
Figure 8.
Example of (a) gate reduction through elimination, (b) gate reduction through gate fusion, (c) depth reduction through elimination and fusion.
Figure 8.
Example of (a) gate reduction through elimination, (b) gate reduction through gate fusion, (c) depth reduction through elimination and fusion.
Figure 9.
Overview of fuzzy controller for GA-based compiler runtime adaptation.
Figure 9.
Overview of fuzzy controller for GA-based compiler runtime adaptation.
Figure 10.
Ring-shaped qubit topologies for 2 and 3 qubit target machines with bidirectional connectivity.
Figure 10.
Ring-shaped qubit topologies for 2 and 3 qubit target machines with bidirectional connectivity.
Figure 11.
Compilation results showing median values of metrics for (a) 2 qubits and (b) 3 qubits.
Figure 11.
Compilation results showing median values of metrics for (a) 2 qubits and (b) 3 qubits.
Figure 12.
Comparison between GA and GA-F (a) 2 qubits and (b) 3 qubits.
Figure 12.
Comparison between GA and GA-F (a) 2 qubits and (b) 3 qubits.
Figure 13.
Comparison between GA-F (blue) and GA (red) for 2 qubits. (a–d) Comparison of cumulative average updates per generation. Vertical line indicates median stop generation. (e–h) Comparison of best error per generation.
Figure 13.
Comparison between GA-F (blue) and GA (red) for 2 qubits. (a–d) Comparison of cumulative average updates per generation. Vertical line indicates median stop generation. (e–h) Comparison of best error per generation.
Figure 14.
Comparison between GA-F (blue) and GA (red) for 3 qubits. (a–d) Comparison of cumulative average updates per generation. Vertical line indicates median stop generation. (e–h) Comparison of best error per generation.
Figure 14.
Comparison between GA-F (blue) and GA (red) for 3 qubits. (a–d) Comparison of cumulative average updates per generation. Vertical line indicates median stop generation. (e–h) Comparison of best error per generation.
Figure 15.
Compilation performance for GA and GA-F across different population sizes. (a) 2 qubits. (b) 3 qubits.
Figure 15.
Compilation performance for GA and GA-F across different population sizes. (a) 2 qubits. (b) 3 qubits.
Table 1.
Fuzzy equivalent of Boolean operators.
Table 1.
Fuzzy equivalent of Boolean operators.
| Boolean Operator | Fuzzy Equivalent |
|---|
| |
| |
| |
Table 2.
Fuzzy rule-set used by the inference engine to guide the GA.
Table 2.
Fuzzy rule-set used by the inference engine to guide the GA.
| Updates | Mutation Rate | New Mutation Rate |
|---|
| Low | Low | Medium |
| Low | Medium | High |
| Low | High | Low |
| Medium | Low | Medium |
| Medium | Medium | High |
| Medium | High | Medium |
| High | Low | Low |
| High | Medium | Medium |
| High | High | High |
Table 3.
Experiments for comparisons between all compilers.
Table 3.
Experiments for comparisons between all compilers.
| Input Size | 2 Qubit Unitary | 3 Qubit Unitary |
|---|
|
Error Thresholds
|
0.1
|
0.01
|
0.001
| |
0.1
|
0.01
|
0.001
| |
|---|
| GA | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| GA-F | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Qiskit | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| BQSkit | ✓ | ✓ | ✓ | ✓ | ✓ | | | |
Table 4.
Experiments for analyzing effects of population size.
Table 4.
Experiments for analyzing effects of population size.
| Input Size | 2 Qubit Unitary | 3 Qubit Unitary |
|---|
|
Population Size
|
10
|
20
|
40
|
10
|
20
|
40
|
|---|
| GA | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| GA-F | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Table 5.
Gate fusion and elimination rules.
Table 5.
Gate fusion and elimination rules.
| Gate 1 | Gate 2 | Action | New Gate on Left-Most Position |
|---|
| X | X | Elimination | I |
| | Elimination | I on both qubits and |
| | Fusion | |
| | Fusion | X |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).