Finite Element Computations on Mobile Devices: Optimization and Numerical Efficiency

Abstract

Smartphones have become increasingly powerful and widespread, enabling complex numerical computations that were once limited to desktop systems. However, implementing high-precision Finite Element Analysis (FEA) on mobile devices remains challenging due to constraints in memory, processing speed, and energy efficiency. This paper presents an optimized algorithmic framework for performing FEA on mobile platforms, focusing on the adaptation of meshing and iterative solver strategies to resource-limited environments. Several iterative solvers for large sparse linear systems are compared, and predefined refined meshing techniques are implemented to balance computational cost and accuracy. A two-dimensional bridge model is used to validate the proposed methods and demonstrate their numerical stability and computational efficiency on smartphones. The results confirm the feasibility of executing reliable FEA directly on mobile hardware, highlighting the potential of portable, low-cost devices as platforms for computational mechanics and algorithmic simulation in engineering and education.

1. Introduction

Over the past two decades, smartphones have profoundly transformed modern life, impacting how people work, learn, and communicate. With continuous advancements in mobile hardware, smartphones have evolved into powerful computing platforms. According to the International Data Corporation (IDC), global smartphone shipments exceeded 1.2 billion units in 2022, whereas personal computer (PC) shipments were approximately 310 million units [1]. In addition, a recent survey by Statista [2] showed that in 2024, mobile devices accounted for more than 62% of global web traffic, reflecting a shift in user behavior towards mobile-first access.

This increase in reach also reflects a growing dependency on smartphones for a range of daily activities beyond basic mobile services. Business Intelligence estimated in-store mobile payments in the USA at $128 billion in 2021 [3]. The accessibility of smartphones and their future potential have led researchers to explore the possibilities of mobile technology in various domains, such as automating construction site monitoring [4]. Despite these impressive developments, the use of smartphones in specialized engineering domains, such as numerical simulation and finite element analysis (FEA), remains relatively limited. A review of current mobile engineering applications reveals that most efforts focus on areas such as Building Information Modeling (BIM), Augmented Reality (AR), data acquisition, and measurement tools. These applications mainly exploit smartphone hardware components—like cameras, sensors, and GPS modules—with computation-heavy tasks usually offloaded to cloud servers [1]. In particular, in the field of engineering simulation and Finite Element Analysis (FEA), most existing mobile applications act primarily as interfaces or gateways to cloud platforms. An illustrative example is Matlab Mobile, which connects users to MathWorks’ cloud infrastructure to perform all processing externally [5].

This reliance on cloud-based solutions can be attributed to several factors, including the historical limitations of mobile hardware and the complexity of numerical computations. Consequently, the smartphone is often treated as an outlet for connection rather than as an autonomous computing unit. While this approach eases local processing requirements, it inherently limits offline access, increases latency, and restricts the level of real-time interactivity.

With the rapid advancement of smartphone hardware capabilities and the global rise in smartphone usage, it becomes increasingly reasonable to consider these devices as viable platforms for lightweight finite element computations. Leveraging mobile hardware for FEA could significantly improve accessibility for field engineers, educators, and students seeking portable simulation tools.

This paper reviews the current state of FEA implementations on mobile platforms, identifies the main scientific and computational challenges, and proposes an optimized algorithmic framework that addresses these limitations through predefined mesh generation, efficient memory management, and lightweight iterative solver techniques. The proposed approach aims to bridge the gap between mobile technology and high-performance numerical computation, demonstrating that smartphones can serve as credible platforms for algorithmic experimentation in computational mechanics.

2. State of the Art: Mobile Applications for Finite Element Analysis (FEA)

The integration of Finite Element Analysis (FEA) capabilities into mobile platforms is an emerging area of research that reflects the ongoing trend toward portability and accessibility in engineering and scientific computation. While traditional FEA tools are designed for desktop and high-performance computing (HPC) environments, advancements in smartphone hardware and mobile software frameworks have opened up opportunities for developing lightweight FEA applications that run directly on mobile devices. These State-of-the-Art aims to explore existing mobile FEA applications, highlight their capabilities, and critically examine their current limitations in terms of performance, autonomy, and usability.

2.1. Existing Mobile Applications for FEA

With the rapid advancement in mobile computing power, several applications have emerged to bring simplified FEA capabilities to smartphones and tablets. However, these applications are often limited in functionality and scope.

2.1.1. Visualization and Post-Processing Tools

Early developments in mobile FEA applications primarily focused on visualization and post-processing. Applications such as Autodesk Viewer, ANSYS Mobile, or COMSOL Client for Android/iOS allow users to view, rotate, and inspect FEA simulation results [6,7,8]. However, the actual computation is still performed on desktops or servers, and the mobile device is used only as a visualization interface. These tools improve collaboration and allow engineers to review simulations in the field, but they do not support on-device model editing, meshing, or solving.

2.1.2. Cloud-Based FEA Solutions

Another important trend is cloud-assisted mobile FEA. In this hybrid model, the mobile app acts as a front-end interface, while the computational tasks are performed on powerful cloud servers. Platforms like CAEplex allow real-time structural analysis directly from a browser or mobile device by offloading the numerical workload to server-side solvers [9]. Similarly, SimScale provides cloud-based FEA and CFD simulation tools for mechanical, thermal, and fluid systems, accessible through any web browser [10]. OnScale Solve also leverages cloud and AI capabilities to provide scalable, multiphysics simulations [11]. While these platforms offer significant benefits, such as reducing the computational burden on mobile devices and enabling high-fidelity analysis without expensive local hardware, they come with important limitations. First, they require a constant and reliable internet connection, which is not always guaranteed in industrial, construction, or field environments. Second, latency issues may arise, especially when uploading large models or downloading high-resolution results. Third, user autonomy is reduced, since simulations are dependent on external servers, and data privacy or security concerns can become critical, particularly for sensitive engineering designs. Lastly, cost and licensing models based on cloud usage can be restrictive for individual researchers or institutions with limited budgets. These disadvantages highlight the need for complementary approaches that support on-device computation, particularly in contexts where mobility, offline access, and autonomy are priorities.

2.1.3. Basic On-Device Simulations

While most mobile FEA applications rely on cloud computing, recent research efforts have begun to explore the feasibility of performing certain computational tasks directly on smartphones. For instance, tools such as QuickFEM demonstrate the potential for running simplified FEA models on mobile devices [12]. Commercial applications like FEA Assistant and FrameDesign support basic static analysis of beams and trusses for simple structures, typically offering minimal user interaction and relying on predefined parameters [13,14]. Similarly, the application developed by B.J. Mac Donald et al. enables users to solve elementary 1D and 2D truss problems on Android platforms [15]. Despite these promising developments, current on-device FEA tools remain limited in both scope and functionality. There is still a lack of open-source or commercial applications capable of performing full-featured FEA directly on mobile hardware. These tools are generally not suited for more complex problems or for offering advanced control over numerical methods. Constraints related to processing power, memory, battery life, and interface usability continue to hinder the development of more robust and autonomous FEA applications on smartphones.

In conclusion, while mobile FEA is not yet a mainstream engineering tool, the state of the art is evolving rapidly. With improvements in smartphone hardware, efficient numerical algorithms, and cloud integration, mobile-based FEA applications are poised to become a practical and innovative component in future engineering workflows—especially in environments where mobility, accessibility, and real-time feedback are critical.

2.2. Research Gap and Motivation

While mobile devices have experienced rapid advances in processing power, memory, and graphics capabilities, the domain of on-device numerical simulation particularly for structural analysis remains significantly underdeveloped. Most finite element analysis (FEA) applications rely on cloud computing and visualization tools, while on-device solutions are still limited. Although several mobile applications have been developed to support FEA on smartphones, these tools remain restricted in scope, functionality, and autonomy. Most are limited to very simplified static problems, offer minimal customization, and lack advanced numerical control. For instance, existing structural applications are very limited: they typically support only small 1D or 2D truss or frame models composed of a limited number of nodes and elements, with fixed mesh sizes and minimal visual feedback. Users generally cannot refine the mesh, visualize the element distribution in detail, or adjust numerical parameters. As highlighted by Khoury et al. [1], most scientific mobile applications focus on data acquisition via embedded sensors (e.g., cameras, accelerometers) or on post-processing tasks such as visualization and result inspection. Very few tools are capable of performing the complete simulation workflow directly on the mobile device without relying on external servers. This gap reveals a clear opportunity: to develop an efficient and lightweight FEA application capable of executing full simulations locally, specifically adapted to the computational and memory constraints of smartphones and tablets. Such a tool would not only extend the capabilities of mobile engineering applications but also offer substantial benefits in educational contexts, remote site analysis, and rapid structural assessment especially in environments with limited connectivity or computational infrastructure. The present work aims to address this challenge by proposing a mobile FEA application dedicated to 2D bridge analysis made of homogeneous materials and based on linear elasticity theory. The solution incorporates a predefined and optimized meshing strategy, efficient data structures for matrix storage, and tailored iterative solvers, all designed to ensure accurate results and acceptable performance within the hardware limits of mobile devices.

3. Scientific and Computational Challenges in Mobile Finite Element Analysis

As previously discussed in our last paper [1], implementing scientific applications on mobile devices involves several challenges. In the case of mobile Finite Element Analysis (FEA) applications, many of these challenges arise from the scientific computations required for simulation. This section focuses on the main scientific challenges related to memory cost and algorithmic precision, which are critical for enabling efficient and accurate FEA on resource-constrained devices such as smartphones and tablets.

3.1. Memory Cost of Algorithms

Scientific algorithms, particularly those used in finite element simulations, often involve large-scale operations that can significantly increase both memory consumption and computational complexity. A primary example is mesh generation, especially when using fine or unstructured meshes, which can consume a substantial amount of memory due to the high number of elements and associated degrees of freedom.

Another critical operation is matrix inversion, which is both computationally expensive and memory-intensive. The computational complexity of direct inversion methods (e.g., Gauss–Jordan or LU decomposition) typically scales as O(n³), while the memory requirement grows as O(n²), since a dense n × n matrix must be entirely stored in memory [16]. Studies such as those by Ataeeshojai et al. and Albreem et al. [17,18] emphasize the challenges of matrix operations even on desktop platforms challenges that are exacerbated on resource-limited mobile devices. The performance of such algorithms depends on both external factors (e.g., hardware architecture, software platform) and internal factors (e.g., algorithmic efficiency in time and memory use). On mobile platforms, where memory and processor power are limited, these issues become even more critical. Research efforts have explored mitigation strategies such as shared memory parallelism [19], which can help reduce execution time and memory usage but are not always feasible on smartphones due to architectural constraints.

3.2. Precision of Algorithms

Many scientific computing algorithms are approximate by nature, particularly those used in optimization and numerical simulation. These approximation algorithms provide results that are acceptably close to the exact solution, with formal guarantees on their deviation from the optimal result. While approximation and iterative methods help reduce memory usage, they can also increase computation time, especially on devices with limited processing capabilities.

The performance of iterative algorithms also depends heavily on the problem context and data structure. For instance, algorithms like the Least Squares Method (LSM) and its variants—including Partial Least Squares (PLS) and Regularized Least Squares (RLS)—show varying behavior based on input size, noise, and data conditioning [20,21]. PLS, for example, is only effective when the number of variables exceeds the number of observations, while RLS performs better with penalty-based regularization. Choosing the right algorithm for a mobile FEA app, therefore, involves balancing accuracy, memory consumption, and runtime—a trade-off that must be tailored to the characteristics of mobile hardware. These challenges are particularly evident in key components of FEA such as mesh generation and matrix solving, where algorithmic choices directly impact computational load and numerical stability. For example, unstructured or overly refined meshes can quickly exhaust memory resources, while poorly chosen solvers can lead to slow convergence or inaccurate results. Addressing these aspects is crucial for ensuring a functional and efficient mobile simulation tool.

4. Case Study: Engineering Application for Finite Element Method

This section presents the practical solutions proposed to address the challenges previously identified in performing Finite Element Analysis (FEA) on mobile devices. To validate these solutions, a dedicated mobile application was developed for the analysis of 2D bridge structures. The app integrates the proposed methods including predefined mesh generation and optimized iterative solvers, to demonstrate their feasibility and effectiveness under real mobile hardware constraints. The mathematical formulations, implementation strategies, and performance evaluations are detailed in the following subsections, followed by an overview of the application’s interface and functionalities.

4.1. Mathematical Model and Implementation of FEM

The finite element method (FEM) involves a series of systematic steps to approximate the behavior of complex structural systems. The application developed follows a classical FEM workflow composed of the following steps:

• Domain Discretization—The structure is subdivided into finite elements connected at nodes.
• Element Stiffness Matrix Calculation—For each element, a local stiffness matrix is derived based on material and geometric properties.
• Assembly of the Global Stiffness Matrix—Using the direct stiffness method, local matrices are assembled into a global matrix.
• Application of Boundary Conditions—Constraints such as supports and applied loads are incorporated.
• System Resolution—The global system of equations [K][U] = [F] is solved.
• Post-processing—The solution is used to compute internal forces, reactions, stresses, and strains.

The linear triangular element is chosen for meshing in the application. The linear triangular element is a two-dimensional finite element. This element can be used for the problems of plane stress or plane strain in elasticity. The linear triangular element is defined by its modulus of elasticity EEE, Poisson’s ratio ν, and thickness t. It consists of three nodes, each with two in-plane degrees of freedom, as illustrated in Figure 1. The global coordinates of the nodes are denoted (Xi, Yi), (Xj, Yj) and (Xm, Ym). The ordering of the nodes is essential: they must be listed in a counter-clockwise direction starting from any chosen node to ensure a positive element area and a consistent formulation.

The corresponding element stiffness matrix can be expressed as follows [22]: where the matrix B^e is:

$$B^e={\displaystyle \frac{1}{\mathrm{d}\mathrm{e}\mathrm{t}\left(J\right)}}\left(\begin{array}{ccc}J22& 0& -J12 \\ 0& -J21& 0\\ -J21& J22& J11\end{array} \begin{array}{ccc}0& -J22+J12& 0 \\ J11& 0& J21-J11\\ -J12& J21-J11& -J22+J12\end{array}\right)$$

And the Jacobien is:

$$J=\left(\begin{array}{c}{\displaystyle \frac{\partial x}{\partial \xi }} {\displaystyle \frac{\partial y}{\partial \xi }}\\ {\displaystyle \frac{\partial x}{\partial \eta }} {\displaystyle \frac{\partial y}{ \partial \eta }}\end{array}\right)=\left(\begin{array}{c}x1-x3\\ x2-x3 \end{array}\begin{array}{c} y1-y3\\ y2-y3 \end{array}\right)= \left(\begin{array}{c}J11\\ J21\end{array} \begin{array}{c}J12\\ J22\end{array}\right)$$

For plane strain, the [D] matrix is given by:

$$D={\displaystyle \frac{E}{1-v^2}}\left(\begin{array}{ccc}1& v& 0 \\ v& 1& 0\\ 0& 0& {\displaystyle \frac{1-v}{2}}\end{array} \right)$$

The global stiffness matrix is obtained through the standard assembly process. The algorithm for assembling the global matrix proceeds as follows:

• Initialize the global stiffness matrix K as a zero matrix of size (2n × 2n), where n is the total number of nodes in the system.
• Loop over all elements in the mesh:
  • Compute the element stiffness matrix Ke using the formulation given above.
  • Identify the global node indices corresponding to the element.
  • Add the local stiffness matrix Ke to the appropriate entries of the global matrix K according to the global node numbering.
• Return the fully assembled global stiffness matrix K.

It is evident that the linear triangular element possesses six degrees of freedom, with two degrees of freedom at each of its three nodes. Consequently, for a structure containing n nodes, the global stiffness matrix K has dimensions 2n × 2n, since each node contributes two degrees of freedom.

Once the global stiffness matrix K is assembled, the structural equilibrium equation takes the form:

[K][U] = [F]

(1)

where U is the global nodal displacement vector and FFF is the global nodal force vector. At this stage, the appropriate boundary conditions are imposed on U and F before solving Equation (1).

In the finite element analysis, both force and displacement boundary conditions were applied to accurately reproduce the structural behavior. The force boundary condition is defined as F = F0, where F0 represents the prescribed nodal forces applied at selected nodes. The components of F0 are specified according to the magnitude and direction of the applied loads, in accordance with the physical characteristics of the problem.

Similarly, the displacement boundary condition is expressed as U = U0, where U0 denotes the prescribed nodal displacements imposed at specific nodes.

Once the unknown displacements and support reactions have been determined by solving Equation (1), the stress and strain fields for each element are computed using:

[ε] = [B][u]

(2)

[σ] = [D][ε]

(3)

where [σ] is the stress vector (size 3 × 1) and [u] is the element displacement vector (size 6 × 1). For each triangular element, the stress vector is written as: {σ} = [σx σy τxy].

4.2. Proposed Solution

The two main challenges lie in the scientific computations themselves, particularly regarding memory usage and numerical precision. These difficulties arise from the large number of elements involved in generating each solution field, as well as the increase in computational cost when the mesh is refined and the number of elements grows.

4.2.1. Predefined and Optimized Meshes

Mesh generation is a fundamental step in Finite Element Analysis (FEA), but it often involves complex algorithms, extensive user input, and large data structures. Many existing mesh generators are part of larger software ecosystems that require developers to learn an entire environment, making them difficult to integrate into lightweight or purpose-driven applications—particularly for users who simply need to mesh a domain quickly and efficiently. Moreover, these general-purpose tools are typically designed for desktop computing and are not optimized for smartphones, which are limited in both memory and processing power. This makes their direct integration into mobile applications impractical.

To address these limitations, we propose a simple and efficient solution: a predefined structured mesh specifically tailored for typical bridge geometries. This approach eliminates the need for real-time meshing, significantly reduces code complexity, and remains fully compatible with the computational constraints of mobile devices, all while maintaining acceptable accuracy.

The proposed meshing strategy is algorithmically efficient. It relies on analytical formulations that directly compute node coordinates and element connectivity using closed-form expressions. This avoids the need for recursive subdivision or graph-based searches, which are typical in general-purpose mesh generators. As a result, the algorithm achieves linear computational complexity and very low memory overhead.

The proposed approach consists of two main steps:

• Initial Node Placement, using a linear distribution to define the mesh structure.
• Fast Mesh Refinement, particularly for triangular meshes (both 3-node and 6-node), in order to obtain accurate and stable results.

This meshing strategy was implemented and tested within the developed mobile FEA application. To validate its performance, the predefined mesh was applied to the analysis of two-dimensional structural domains representing typical bridge configurations. The geometries include rectangular, trapezoidal, and arch-shaped domains, which serve as representative examples to demonstrate the flexibility and robustness of the proposed approach.

For the rectangular-shaped structure, the algorithm presented below is created to generate a structured triangular mesh for finite element analysis (FEA).

The algorithm outputs a 3-node triangular mesh, the x- and y-coordinates of all nodes, and the total number of nodes and elements.

The inputs consist of the rectangular domain dimensions (width and height) and the number of divisions along the x- and y-directions, which determine the desired level of mesh refinement.

The mesh generation procedure used for the rectangular domain is formalized in Algorithm 1.

Algorithm 1. Structured Triangular Mesh Generation for a Rectangular Domain.

Input:       - Domain dimensions (Lx, Ly)       - Number of divisions in x and y directions (Nx, Ny)       - Refinement level (r) Step 1: Initialize Node Coordinates       For i = 0 to Nx:             For j = 0 to Ny:                   x = i * (Lx/Nx)                   y = j * (Ly/Ny)                  Store (x, y) as node[i][j] Step 2: Generate Initial Triangular Mesh       For i = 0 to Nx − 1:             For j = 0 to Ny − 1:                   Triangle 1: (i, j), (i + 1, j), (i + 1, j + 1)                   Triangle 2: (i, j), (i + 1, j + 1), (i, j + 1)                   Store both triangles Step 3: Refine Mesh (Repeat r Times)       For each triangle in mesh:             Compute edge midpoints             Compute triangle centroid             Create 4 new sub-triangles using midpoints and centroid       Replace old triangles with refined ones Output:       - List of node coordinates       - Connectivity of triangular elements

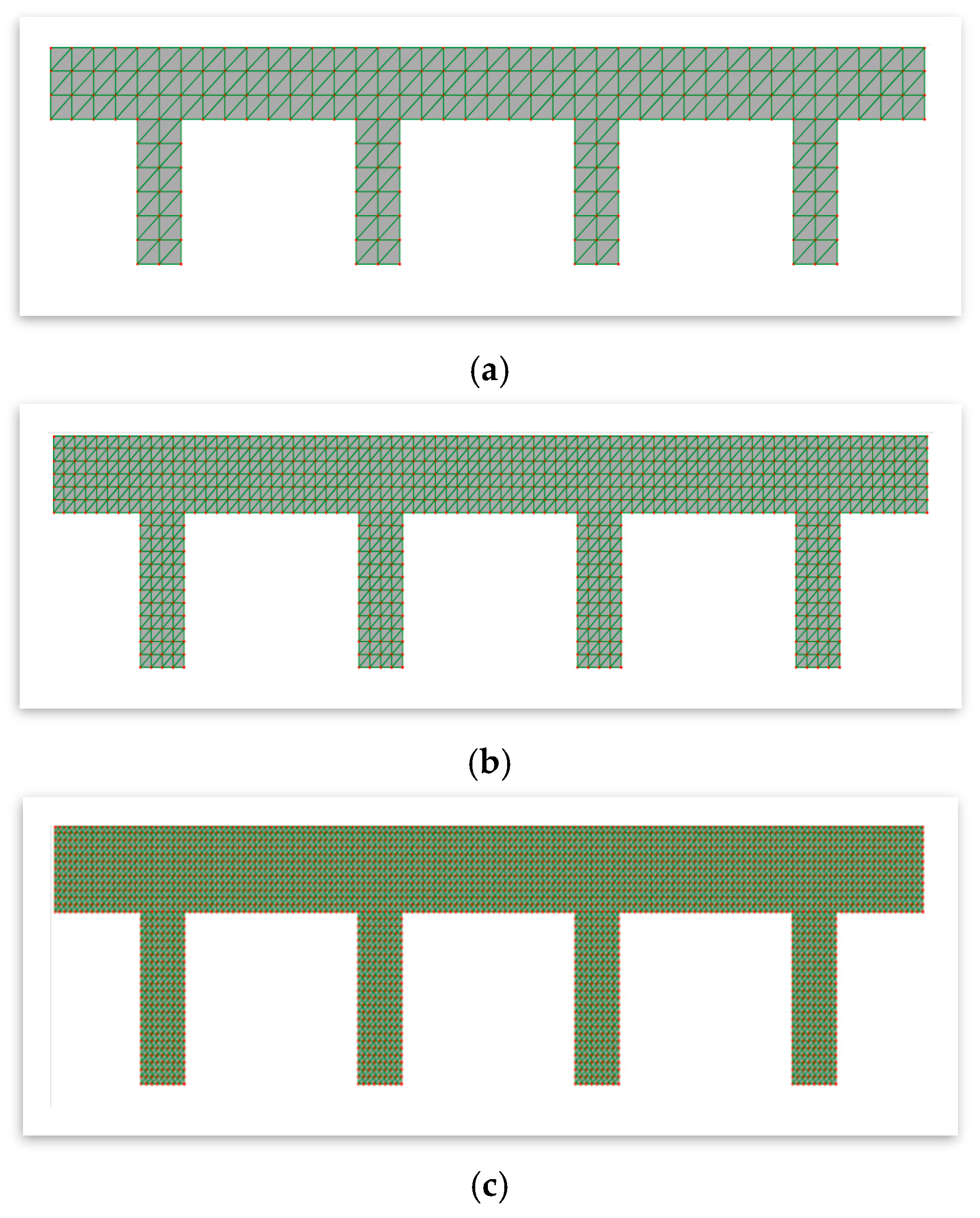
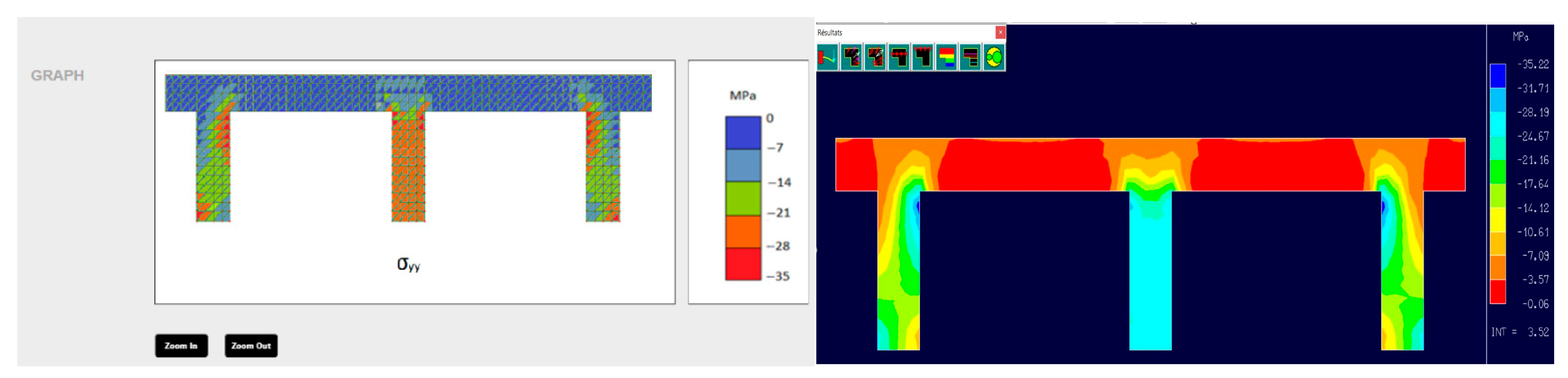
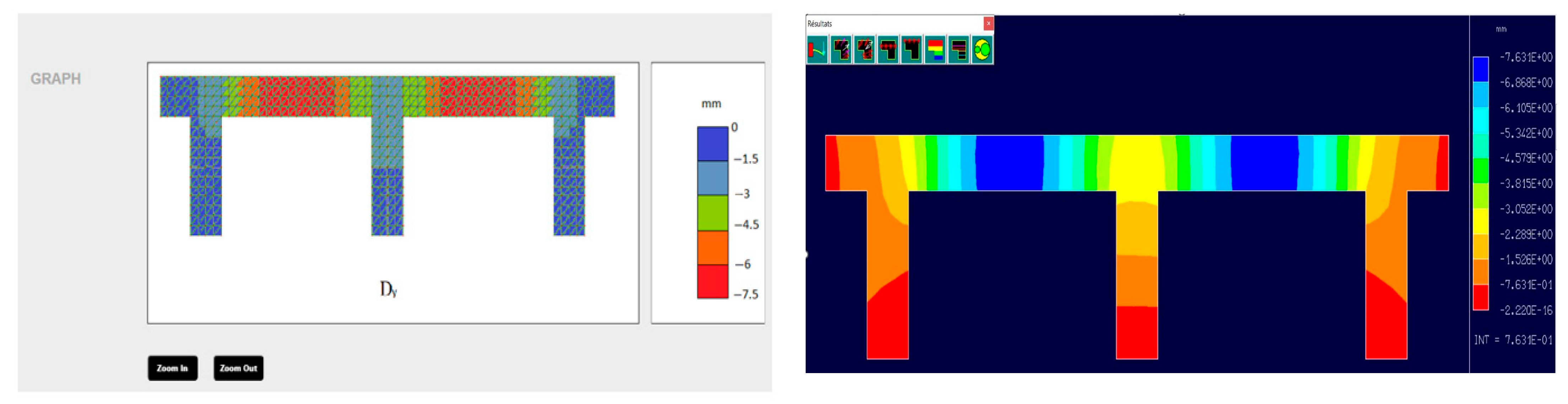
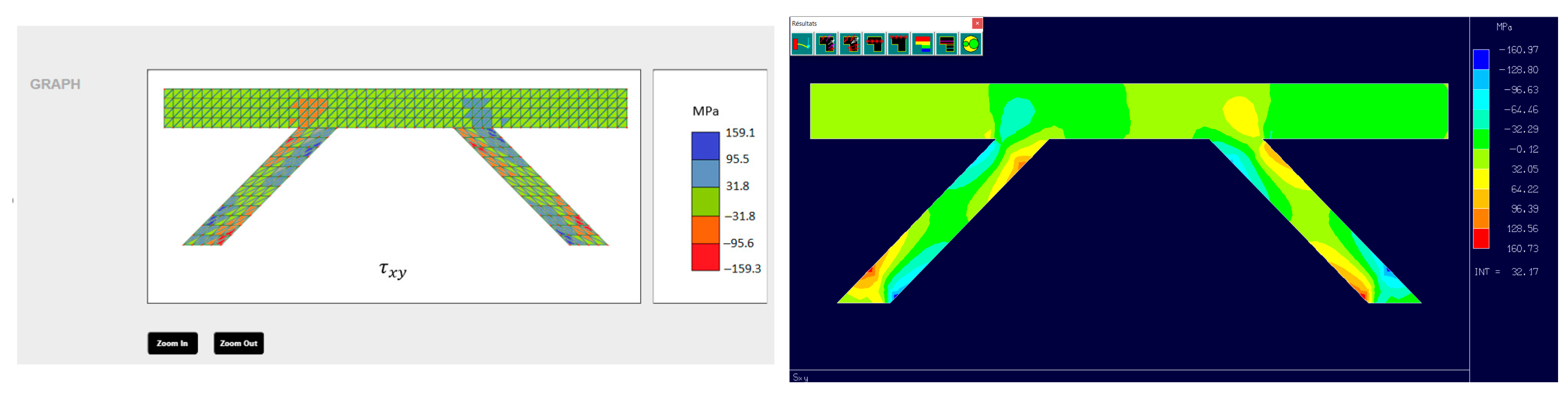
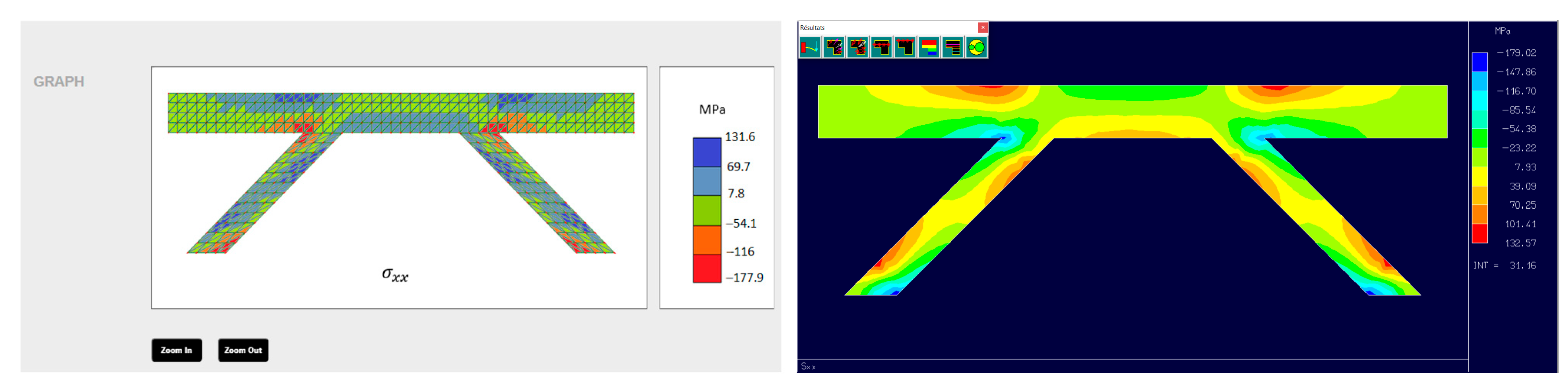
An example of a girder bridge meshed by our application is presented in Figure 2. The bridge has a total length of 40 m and consists of 4 piers, each 2 m thick and 6 m high. The bridge girder is modeled as a rectangular domain of 40 × 3 m.

Using the mesh generator, the domain is discretized with 40 divisions on the x axis and 3 on y-axis. The number of elements is calculated as:

NE = (2NX) × NY = 240

And the number of Nodes is:

NN = (NX + 1) × (NY + 1) = 164

This initial coarse mesh is then refined to generate a finer mesh. The refinement is performed by splitting each triangle into four smaller triangles through edge bisection, allowing for the easy creation of 6-node triangular.

Thus, for the example shown in Figure 2, refining the girder mesh increases the number of elements from 240 to 960 (Figure 2b), and then to 3840 elements (Figure 2c).

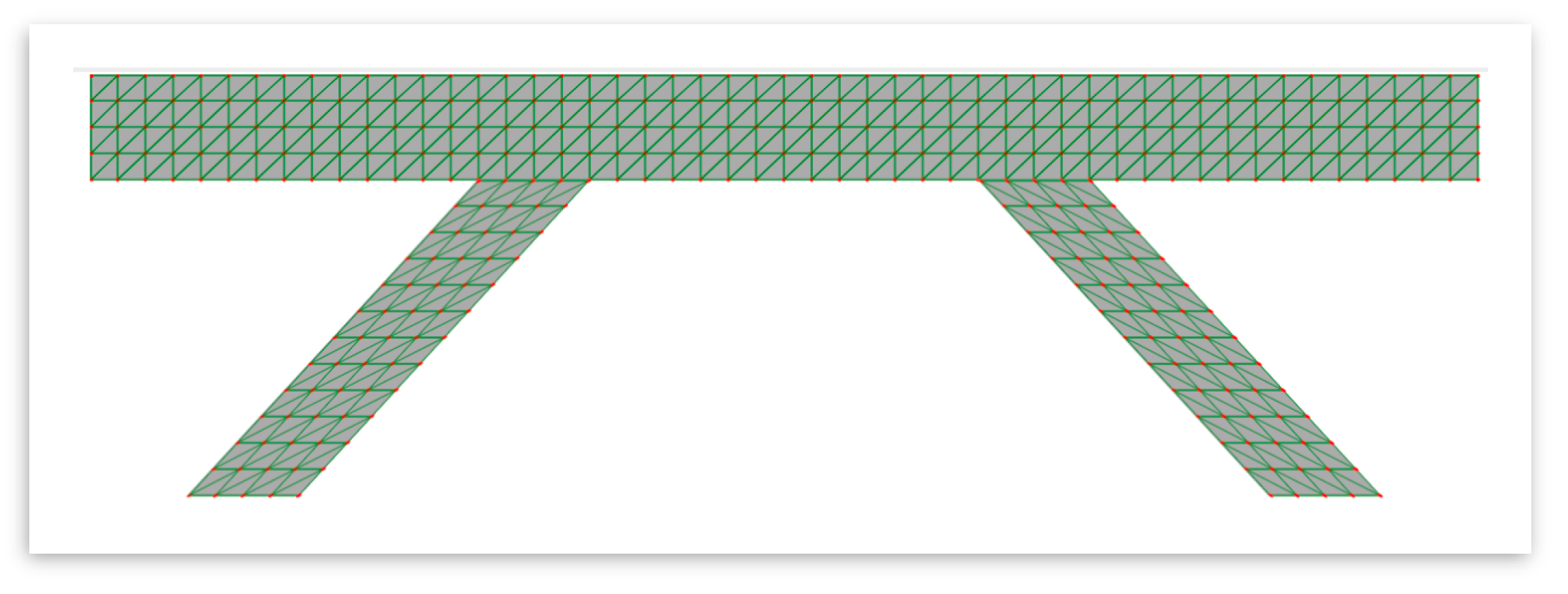
A triangular mesh for the trapezoidal-shaped structure is generated using a geometric transformation matrix. The function context.setTransform (a, b, c, d, e, f), built into Canvas.js, enables the rectangular domain to be efficiently transformed into a trapezoidal one. Figure 3 illustrates the resulting mesh for the trapezoidal portion of the crutch bridge. The mesh for arch-shaped structures is created by distributing nodes uniformly along the arc, using polar coordinates. The number of divisions along the arc defines the refinement level.

The complete node-generation procedure for the arch-shaped domain is formal-ized in Algorithm 2.

Algorithm 2. Node Distribution and Triangular Mesh Generation for Arch-Shaped Domains.

for (let i = 0; i <= numDivisions; i++) {                 const angle = i * angleStep;              const x = centerX + Math.cos(angle) * radius;              const y = centerY + Math.sin(angle) * radius;             drawPoints(x, y);       }

This results in a clean, efficient triangular mesh for the arch geometry, as illustrated in Figure 4.

The predefined mesh strategy adopted in this work is intentionally tailored to simple, parameterized bridge geometries (rectangular, trapezoidal, and arch domains), as it ensures predictable memory usage and avoids the computational overhead of general-purpose mesh generators. However, this approach naturally limits geometric flexibility. In future extensions, adaptive refinement schemes could be integrated—for example, refining elements in regions of high stress gradients or near geometric singularities. Additionally, simple element distortion checks, such as minimum angle or Jacobian-based quality criteria, could be incorporated to prevent poorly shaped triangles during refinement. Such mechanisms would enable the predefined meshes to remain lightweight while improving robustness for more complex or irregular geometries.

Computational Efficiency and Memory Cost on Mobile Device

To assess the performance of the predefined mesh generation algorithm, Performance tests were conducted on a Samsung Galaxy A52 ((Snapdragon 720G, 6 GB RAM; manufactured by Samsung in Suwon, South Korea)), a mid-range smartphone chosen to ensure efficiency on resource-limited hardware. This guarantees that performance would further improve on more powerful devices.

Table 1. Computational cost of mesh generation on a smartphone.

No. of Elements	Memory (KB)	Time (ms)
100	0.197	2.236
500	0.4589	11.321
1500	0.6111	24.658
2500	0.7528	29.254
5000	0.9771	41.110

summarizes the computation time and memory usage for different mesh sizes, ranging from 100 to 5000 triangular elements.

The results demonstrate that the proposed approach maintains both low computational cost and minimal memory usage, even for relatively dense meshes. The memory required to generate 5000 triangular elements does not exceed 1 KB, while the computation time remains below 50 ms, making the meshing process practically instantaneous for the user.

The computational complexity of the algorithm increases approximately linearly with the number of elements (O(n)), confirming its efficiency for real-time applications. Such performance is mainly achieved the fact that both node coordinates and element connectivity are determined using explicit analytical relationships derived from the geometric parameters of the domain. Consequently, the algorithm avoids recursive searches and graph-based data structures typical of generic mesh generators, significantly reducing computational overhead and memory usage. These results confirm that the predefined mesh strategy is well-suited for mobile finite element simulations, ensuring an optimal balance between accuracy, execution time, and resource consumption.

Accuracy Evaluation with Mesh Refinement

Mesh refinement is a well-established strategy in finite element analysis to improve solution accuracy by reducing discretization error. However, finer meshes also increase the computational load during assembly and solving phases, which is particularly critical on mobile devices where memory and processing power are limited. To quantify the accuracy of the proposed mobile solver, three predefined refinement levels—coarse, medium, and refined—were evaluated on the 2D girder bridge case study shown in Figure 2. A high-resolution desktop FEM model was generated using RDM6 with a fine mesh to obtain reference displacement and stress fields. For each refinement level in the mobile application, the corresponding maximum vertical displacement and maximum Von Mises stress were extracted and compared to the reference values. All simulations were performed under the same geometric configuration, boundary conditions, loading setup, and homogeneous material properties to ensure that differences in results arise solely from the mesh resolution. The percentage error was computed using the standard relative deviation formula:

$$Error (\%)={\displaystyle \frac{X_{ref}-X_{mobile} }{X_{ref}}}\times 100$$

Table 2. Accuracy vs. Mesh Refinement for the Mobile Solver.

Mesh Level	Elements	Max Y-Disp. Error (%)	Max Von Mises Error (%)
Coarse	280	2.1	3
Medium	1344	1.4	2
Refined	4992	0.6	0.4

summarizes the error evolution with respect to the number of elements.

As expected from classical finite element theory, increasing mesh density consistently reduces discretization error. The results show that the error decreases systematically with refinement, from approximately 2–3% for the coarse mesh to below 1% for the refined mesh. This quantitative evaluation confirms that the proposed predefined mesh strategy achieves acceptable accuracy while respecting the memory–time constraints of mobile devices.

4.2.2. Efficient Solvers for Linear Systems in Mobile FEA Applications

One of the most computationally intensive phases in the Finite Element Analysis (FEA) process is the resolution of the global linear system of equations, typically expressed as [K]{U} = {F}, where [K] is the global stiffness matrix, {U} is the unknown nodal displacement vector, and {F} is the global force vector. For large meshes with a high number of elements, the resulting system becomes very large and sparse, making direct solvers (based on matrix inversion or factorization) impractical for mobile devices due to their limited memory and processing power. To address this challenge, the proposed application implements and compares several iterative solvers, which are more suitable for constrained environments. Each solver is evaluated based on computation time, memory usage, and solution accuracy. By conducting a series of benchmark tests on representative structural problems, the performance of these algorithms is compared to identify the most efficient and reliable approach for mobile FEA. The goal is to achieve an optimal balance between speed, resource efficiency, and precision, making it feasible to run real-time structural simulations on smartphones and tablets.

Solution Methods

In structural analysis using the Finite Element Method, the resulting global stiffness matrix is typically symmetric, sparse, and positive-definite. These properties allow for the use of specialized iterative solvers that are optimized for such matrix types. To address the computational limitations of mobile platforms, we conducted a focused review of the literature and selected several iterative methods that are known to be efficient for solving this class of linear systems.

The methods implemented and evaluated in our study include: the Conjugate Gradient (CG) method, the Preconditioned Conjugate Gradient (PCG) method with LL^t incomplete factorization, the Gauss-Seidel method, a modified version of Gauss-Seidel known as the One-Dimensional Double Successive Projection Method (1D-DSPM), the Two-Dimensional Double Successive Projection Method (2D-DSPM), the Minimum Residual Method (MINRES), and the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method. These methods were chosen based on their mathematical suitability for sparse and symmetric positive-definite matrices, and their performance as reported in the literature. Each algorithm is briefly described and referenced in the following section.

A.

Conjugate Gradient Method (CG)

The conjugate gradient method derives its name from the fact that it generates a sequence of conjugate (or orthogonal) vectors. The conjugate gradient method (CG) [23] is an iterative method which can be used to solve matrix equations while its coefficient matrix is symmetric and positive definite, since storage for only a limited number of vectors is required [24,25]. CG method has been the subject of considerable interest in recent years because of its efficiency and ability to solve difficult problems. The conjugate gradient method is summarized in Algorithm 3.

Algorithm 3. Conjugate Gradient Method for Symmetric Positive Definite Systems.

$x_0 \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{n} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{g}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{s}, r_{0 }=b-A{ x}_0$ $\mathbf{f}\mathbf{o}\mathbf{r} i=1,2\dots .$ ${\rho }_{i-1 }= {r_{i-1}}^T{r}_{i-1}$ $\mathbf{i}\mathbf{f} i=1$ $p_{i }= r_{i-1}$ $\mathbf{e}\mathbf{l}\mathbf{s}\mathbf{e}$ ${\beta }_{i-1 }= {\displaystyle \frac{{\rho }_{i-1 }}{{\rho }_{i-2 }}}$ ${ p}_{i }= r_{i-1 }+ {\beta }_{i-1 }{p}_{i-1 }$ $\mathbf{e}\mathbf{n}\mathbf{d}\mathbf{i}\mathbf{f}$ ${ q}_i={Ap}_{i }$ ${ \alpha }_i={\displaystyle \frac{{\rho }_{i-1 }}{{{ p}_i}^T{q}_i}}$ ${ x}_i=x_{i-1}+ {\alpha }_i p_i$ ${ r}_i=r_{i-1}- {\alpha }_i q_i$           if    ${\displaystyle \frac{\parallel \mathrm{r}\mathrm{i} \parallel }{\parallel \mathrm{b}\parallel }}<\epsilon$ $\mathbf{then} \mathrm{quit}$     $\mathbf{end}$

where A is a symmetric positive definite matrix, b is the nodal force vector, $x_0$ is the initial value of the solution vector to be determined, $r_0$ is the initial value of the residual vector, ε is a tolerance, and $p_i$ is gradient vectors set, in which arbitrary two vectors are conjugate to each other. It can be noticed that one multiplication of matrix and vector and two vectors inner productions requires to be computed during each iterative procedure in CG algorithm.

B.

Preconditioned conjugate gradient (PCG)

The conjugate gradient algorithm is a widely recognized iterative method for solving sparse, symmetric, and positive definite linear systems. However, as an iterative solver, it is known for its lack of robustness. This drawback can be improved by using preconditioning.

Consider a linear system Ax = b, where A is symmetric and positive definite. It is assumed that a preconditioner M is available and also Symmetric Positive Definite.

A mathematically equal preconditioned system is obtained as follows:

$$M^{-1}AX=M^{-1}b$$

where M = ${\mathrm{L}\mathrm{L}}^{\mathrm{T}}$ and L is the lower triangular matrix. The looking-left column-by-column incomplete factorization procedure is applied and details in [26,27,28].

Replacing the usual Euclidean inner product in the Conjugate Gradient algorithm by the M-inner product, the resulting preconditioned Conjugate Gradient method is obtained, as presented in Algorithm 4 [29]:

Algorithm 4. Preconditioned Conjugate Gradient Method.

$x_0 \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{n} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{g}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{s}, r_{0 }=b-A{ x}_0$ $\mathbf{f}\mathbf{o}\mathbf{r} i=\mathrm{1,2},\dots .$ $\mathbf{s}\mathbf{o}\mathbf{l}\mathbf{v}\mathbf{e} {Mz}_{i-1 }= r_{i-1}$ ${\rho }_{i-1 }= {r_{i-1}}^T{z}_{i-1}$ $\mathbf{i}\mathbf{f} i=1$ $p_{i }= z_{i-1}$ $\mathbf{e}\mathbf{l}\mathbf{s}\mathbf{e}$ ${\beta }_{i-1 }= {\displaystyle \frac{{\rho }_{i-1 }}{{\rho }_{i-2 }}}$ ${ p}_{i }= z_{i-1 }+ {\beta }_{i-1 }{p}_{i-1 }$ $\mathbf{e}\mathbf{n}\mathbf{d}\mathbf{i}\mathbf{f}$ ${ q}_i={Ap}_{i }$ ${ \alpha }_i={\displaystyle \frac{{\rho }_{i-1 }}{{{ p}_i}^T{q}_i}}$ ${ x}_i=x_{i-1}+ {\alpha }_i p_i$ ${ r}_i=r_{i-1}- {\alpha }_i q_i$ if    ${\displaystyle \frac{\parallel \mathrm{r}\mathrm{i} \parallel }{\parallel \mathrm{b}\parallel }}<\epsilon$   $\mathbf{t}\mathbf{h}\mathbf{e}\mathbf{n} \mathrm{q}\mathrm{u}\mathrm{i}\mathrm{t}$     $\mathbf{e}\mathbf{n}\mathbf{d}$

Compared with CG, PCG demands an additional linear system solution during each iteration, and additional memory for storage of the preconditioner while converging faster.

C.

Gauss Seidel Method

The Gauss–Seidel (GS) method is one of the most commonly used iterative techniques for solving large linear systems. It is well established that GS converges for linear systems with a symmetric positive-definite matrix [29]. The iterative scheme of the GS solver can be written as follows:

$${x_i}^{(k+1)}={\displaystyle \frac{1}{a_{ii}}} ( b_i-{\sum }_{j=1}^{i-1}{a}_{ij}{x_j}^{(k+1)}- {\sum }_{j=i+1}^n{a}_{ij}{x_j}^{\left(k\right)} ), i=\mathrm{1,2},\dots ,n.$$

The Gauss–Seidel iterative method is summarized in Algorithm 5.

Algorithm 5. Gauss–Seidel Iterative Method.

${\mathrm{c}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{s}\mathrm{e} \mathrm{a}\mathrm{n} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{g}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{s} x}_0 \mathrm{to} \mathrm{the} \mathrm{solution} \mathrm{of} x$ $\mathbf{f}\mathbf{o}\mathbf{r} k=\mathrm{1,2},\dots .$ $\mathbf{f}\mathbf{o}\mathbf{r} i=\mathrm{1,2},\dots ,n$ $\sigma =0$ $\mathbf{f}\mathbf{o}\mathbf{r} j=\mathrm{1,2},\dots .,i-1$ $\sigma =\sigma +{{a_{i,j}x}_j}^{\left(k\right)}$ $\mathbf{e}\mathbf{n}\mathbf{d}$ $\mathbf{f}\mathbf{o}\mathbf{r} j=i+1,\dots .,n$ $\sigma =\sigma +{{a_{i,j}x}_j}^{(k-1)}$ $\mathbf{e}\mathbf{n}\mathbf{d}$ ${x_i}^{\left(k\right)}={\displaystyle \frac{\left(b_i-\sigma \right)}{a_{i,i}}}$ $\mathbf{e}\mathbf{n}\mathbf{d}$ $\mathbf{e}\mathbf{n}\mathbf{d}$

This method updates each unknown using the most recently computed values, which enhances convergence compared to methods that rely solely on previous iterations. Unlike the Jacobi method—where two full sets of unknowns must be stored, the Gauss–Seidel method requires storing only a single set of unknowns throughout the iterative procedure.

D.

One-dimensional double successive projection method (1D-DSPM) Modified Guass Siedel Method

Ujević [30] introduced a new iterative method for solving linear systems, which can be interpreted as a modification of the classical Gauss–Seidel scheme. In this approach, two components of the approximation vector xk are updated simultaneously at each iteration. Numerical results show that the modified method can converge up to twice as fast as the standard Gauss–Seidel method and provides a more significant reduction in the error.

The formulation of this modified Gauss–Seidel procedure is summarized in Algorithm 6. For a detailed derivation and further theoretical background, the reader is referred to [30].

Algorithm 6. One-Dimensional Double Successive Projection Method (1D-DSPM).

$\mathbf{f}\mathbf{o}\mathbf{r} k=\mathrm{0,1},2,\dots .$ ${ z}_1=x_k$ $\mathbf{f}\mathbf{o}\mathbf{r} i=\mathrm{1,2},\dots .n$ ${ z}_{i+1}=z_i+h_i+{\gamma }_i{q}_i$ $\mathrm{e}\mathrm{n}\mathrm{d} \mathrm{f}\mathrm{o}\mathrm{r} i$ ${ x}_{k+1}=z_{n+1}$ $\mathrm{e}\mathrm{n}\mathrm{d} \mathrm{f}\mathrm{o}\mathrm{r} k$ where ${ h}_i=- {\displaystyle \frac{p_{i }}{a_{ii }}}$ ${ p}_i=\left(a_{i ,}{z}_i\right)-b_{i }$ ${ \gamma }_i=- {\displaystyle \frac{\left(\mathrm{A}{z}_{i }-b,q_{i }\right)+(A{q}_{i },h_{i })}{(A{q}_{i },q_{i })}}$

E.

Two-dimensional double successive projection method (2D-DSPM)

Following Ujević’s modification of the Gauss–Seidel method [30], Jing and Huang [31] introduced an algorithm based on the Two-Dimensional Double Successive Projection Method (2D-DSPM). This algorithm significantly enhances performance by incorporating projection-space adjustment strategies along with a two-step correction procedure [32].

This method has been tested on symmetric sparse matrices and has outperformed both Gauss-Seidel (GS) and Modified Gauss-Seidel (MGS) achieving faster convergence and improved computational efficiency [31,32]. The DSPM method can be expressed in the following iterative form:

Here, $v_{1 }= e_i, v_{2 }= e_j, i\ne j$

$$x_{k+1}=x_k+\alpha v_1+\beta v_2$$

$$\alpha ={\displaystyle \frac{\mathrm{c}{\mathrm{p}}_2-\mathrm{d}{\mathrm{p}}_1}{\mathrm{a}\mathrm{d}-{\mathrm{c}}^2}},\beta ={\displaystyle \frac{\mathrm{c}{\mathrm{p}}_1-\mathrm{a}{\mathrm{p}}_2}{\mathrm{a}\mathrm{d}-{\mathrm{c}}^2}}$$

$$a=〈 A{v}_{1 } , v_{1 }〉 , c=〈 A{v}_{1 } , v_{2 }〉=〈 A{v}_{2 } , v_{1 }〉 , d=〈 A{v}_{2 } , v_2〉$$

$$p_{1 }=〈 A{x}_{k }-b, v_{1 }〉 , p_{2 }=〈 A{x}_{k }-b, v_{2 }〉$$

F.

MINRES

The Minimal Residual Method (MINRES) is a Krylov subspace method for the iterative solution of symmetric linear equation systems. It was proposed by Paige and Saunders in 1975 [16]. Even when A is positive definite, MINRES has been shown to possess several advantageous properties that allow it to be considered a strong alternative to the widely used Conjugate Gradient (CG) method [33,34]. MINRES minimizes the 2-norm of the residual over Krylov subspaces of increasing dimension, rather than minimizing the A-norm of the error as in CG. Additional details can be found in the original work [16] and in standard references [33].

In this study, we use the following MINRES algorithm (Algorithm 7) derived from the MINRES method, which has been demonstrated to be particularly effective for symmetric positive-definite (SPD) matrices [16,33].

Algorithm 7. Minimal Residual Method (MINRES).

$x_0 \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{n} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{g}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{s}, r_0=b ,{ s}_0=A{r}_0,$ ${\rho }_{0 }={r_0}^T{s}_0 , p_{0 }=r_0, { q}_{0 }=s_0$ $\mathbf{f}\mathbf{o}\mathbf{r} i=\mathrm{1,2},\dots .$ ${ q}_{i-1}=A{p}_{i-1}$ ${ \alpha }_i={\displaystyle \frac{{\rho }_{i-1 }}{\Vert { q}_{i-1 }\Vert ^2}}$ $x_i=x_{i-1}+{\alpha }_i p_{i-1}$ ${ r}_i=r_{i-1}-{\alpha }_i q_{i-1}$ ${ s}_i={Ar}_i$ ${ \rho }_{i }={r_i}^T{s}_i$ ${ \beta }_i={\displaystyle \frac{{\rho }_{i }}{{\rho }_{i-1 }}}$ $p_i=r_i+{\beta }_i p_{i-1}$ ${ q}_i=s_i+{\beta }_i q_{i-1}$

G.

BFGS (Broyden–Fletcher–Goldfarb–Shanno)

The BFGS algorithm (Broyden–Fletcher–Goldfarb–Shanno) is an optimization method used to find the minimum of a differentiable function. It is a quasi-Newton method that approximates the Hessian matrix to find the minimum of a function [35]. The algorithm iteratively updates an approximation of the inverse Hessian matrix, making it efficient for solving problems with a large number of variables. The BFGS optimization procedure is summarized in Algorithm 8.

Algorithm 8. BFGS (Broyden–Fletcher–Goldfarb–Shanno) Algorithm.

$x_0 \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{n} \mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{g}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{s},$ $H_{0 }=I$ Initial inverse Hessian approximation (identity matrix) $\mathbf{f}\mathbf{o}\mathbf{r} K=0$ ${ p}_k=-H_{k } \nabla {f(x}_k)$ ${ \alpha }_k=lineSearch ({f,x}_k,$); Perform line search with wolf conditions to find ${ \alpha }_k$ ${ x}_{k+1}=x_k+ {\alpha }_k{ p}_k$ $\mathbf{f}\mathbf{o}\mathbf{r} K=k+1$ ${ d}_k=x_{k+1}- x_k$ ${ y}_k=\nabla {f(x}_{k+1})- \nabla {f(x}_k)$

Update inverse Hessian approximation:

$${ H}_k=H_{k-1 }+ {\displaystyle \frac{y_{k }{y_k}^T}{{y_k}^T{ d}_k}}- {\displaystyle \frac{H_{k-1 }{d}_k{d_k}^T{H}_{k-1 }}{{d_k}^T{H_{k-1 } d}_k}}$$

Numerical Experiments and Results

To evaluate the performance of the seven implemented iterative solvers, we conducted a series of numerical experiments by solving linear systems of increasing size, generated by our finite element mobile application. Each solver was implemented in JavaScript with optimized memory usage strategies, tailored for the constraints of mobile environments.

The experiments were carried out on a Samsung Galaxy A52, a widely available mid-range smartphone featuring a Qualcomm Snapdragon 720G processor (Octa-core CPU), 6 GB RAM, and an Adreno 618 GPU. By selecting a non-high-end device, we aimed to ensure that the application remains functional and efficient even on resource-constrained hardware. This also means that its performance will scale favorably on more advanced smartphones.

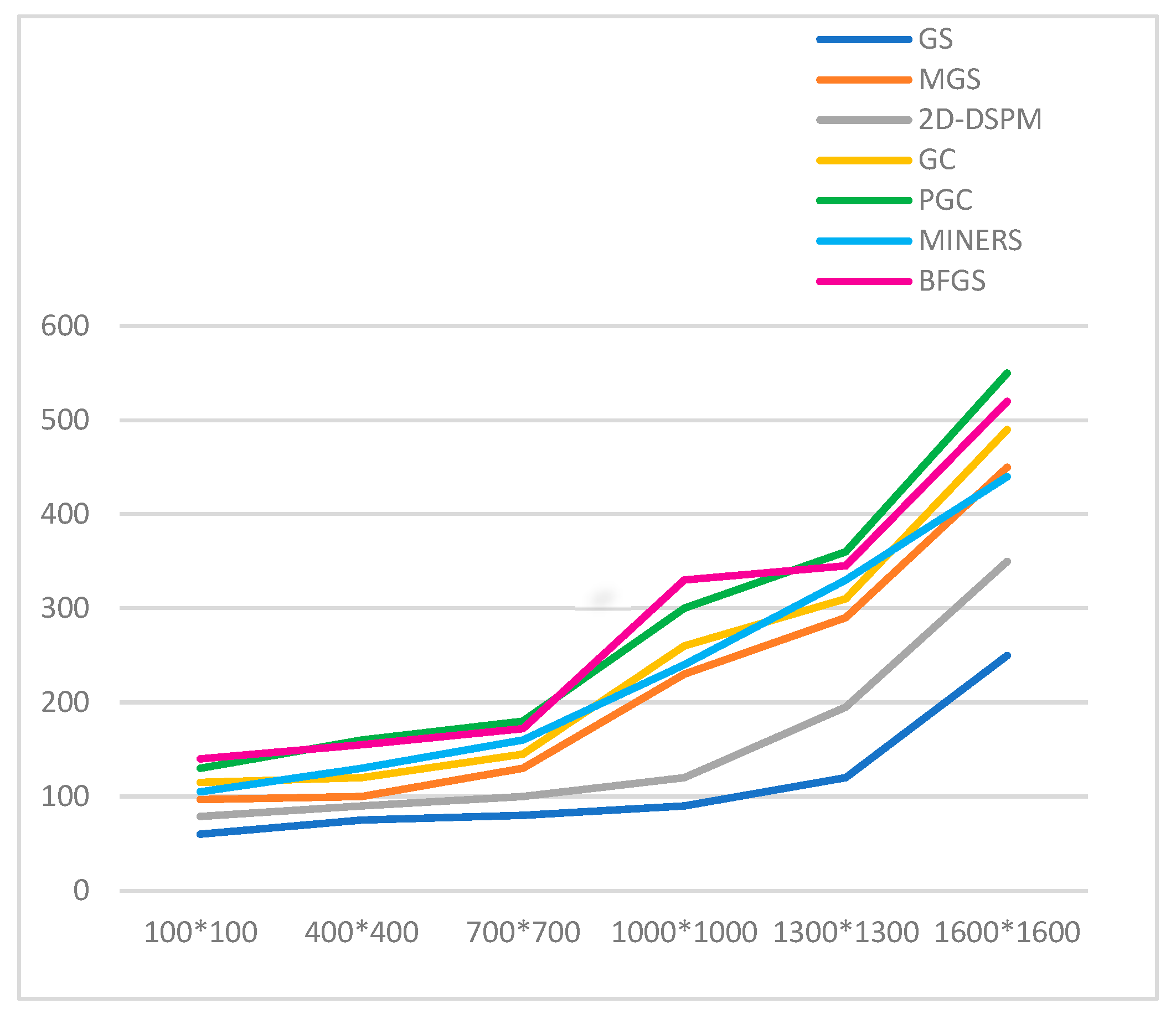
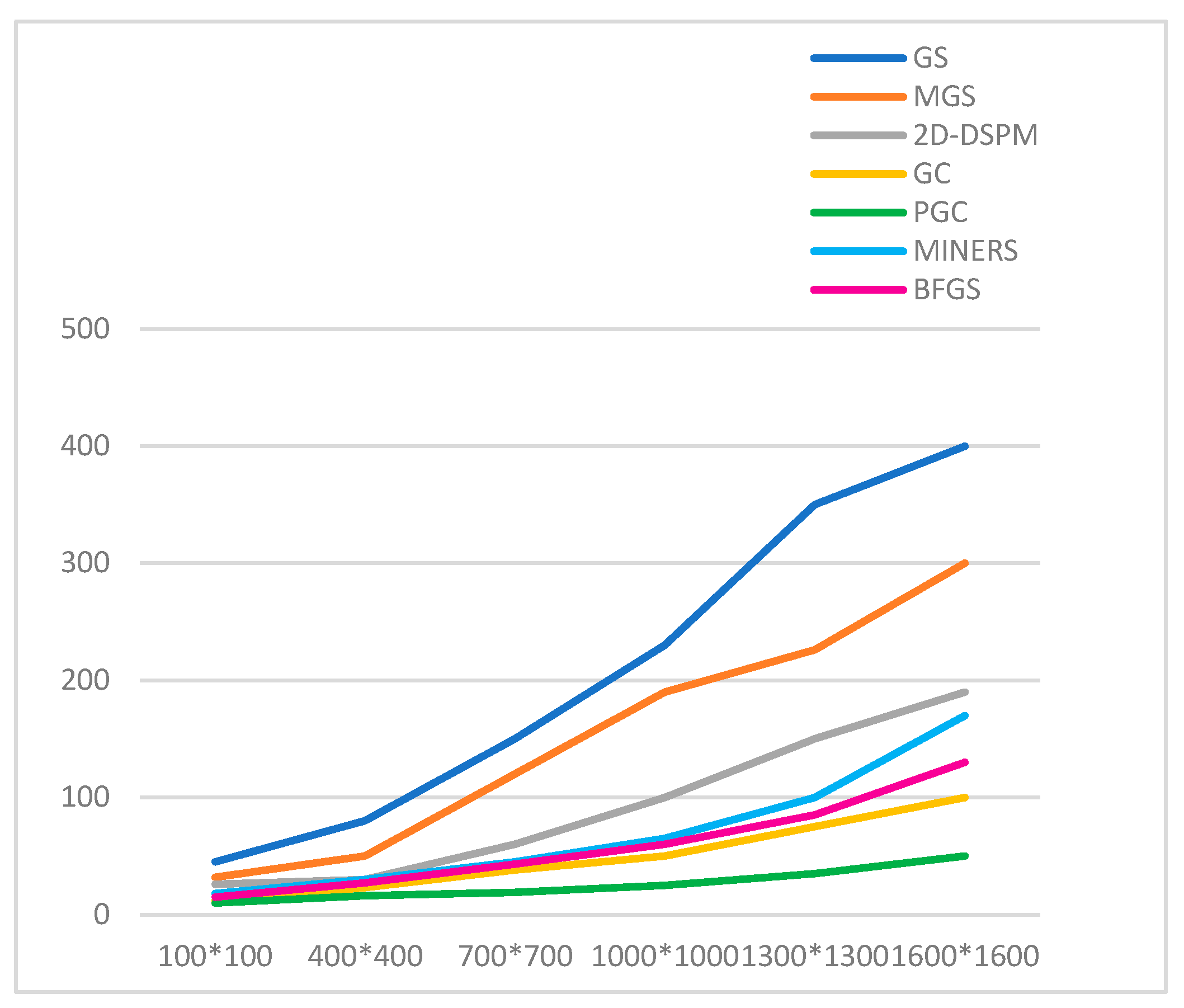
Figure 5 presents the execution time (in seconds) required by seven iterative methods to solve matrices of increasing size, each over a fixed number of 3000 iterations. As expected, execution time increases with matrix size for all methods due to the larger number of unknowns and increased computational workload. Among the tested algorithms, the Gauss-Seidel (GS) method consistently shows the lowest execution time across all matrix sizes, making it the most time-efficient in this fixed-iteration context. However, this does not necessarily imply better convergence or accuracy.

The 2D-DSPM method also demonstrates strong performance, especially for larger matrices, with a moderate and steady increase in computation time, reflecting its efficient iteration strategy.

In contrast, GC, PGC, MINRES, MGS, and BFGS form a group with noticeably higher execution times, particularly beyond matrix sizes of 1000 × 1000. Among these, BFGS and PGC exhibit the highest time costs for the largest matrices (e.g., 1600 × 1600), suggesting greater computational overhead.

In the following tolerance-based experiments (Figure 6 and Figure 7), all iterative solvers use a relative residual tolerance of ${ 10}^{-4}$ (0.01%). This value is particularly suitable for symmetric, well-conditioned structural stiffness matrices, which characterize the 2D linear-elastic bridge problems studied in this work. It also provides an effective balance between numerical accuracy and execution time on resource-constrained mobile devices. In classical FEM workflows, convergence thresholds in the range of ${ 10}^{-3}$ to ${10}^{-4}$ are commonly used for smoother-type algorithms, preconditioning stages, or low-memory iterative solvers [29,36,37]. These values are also consistent with the relaxed convergence criteria recommended by commercial FEM solvers when hardware and memory limitations are present. By selecting a tolerance of ${ 10}^{-4}$, the mobile solver remains aligned with standard FEM practices while enabling real-time execution on mid-range smartphone.

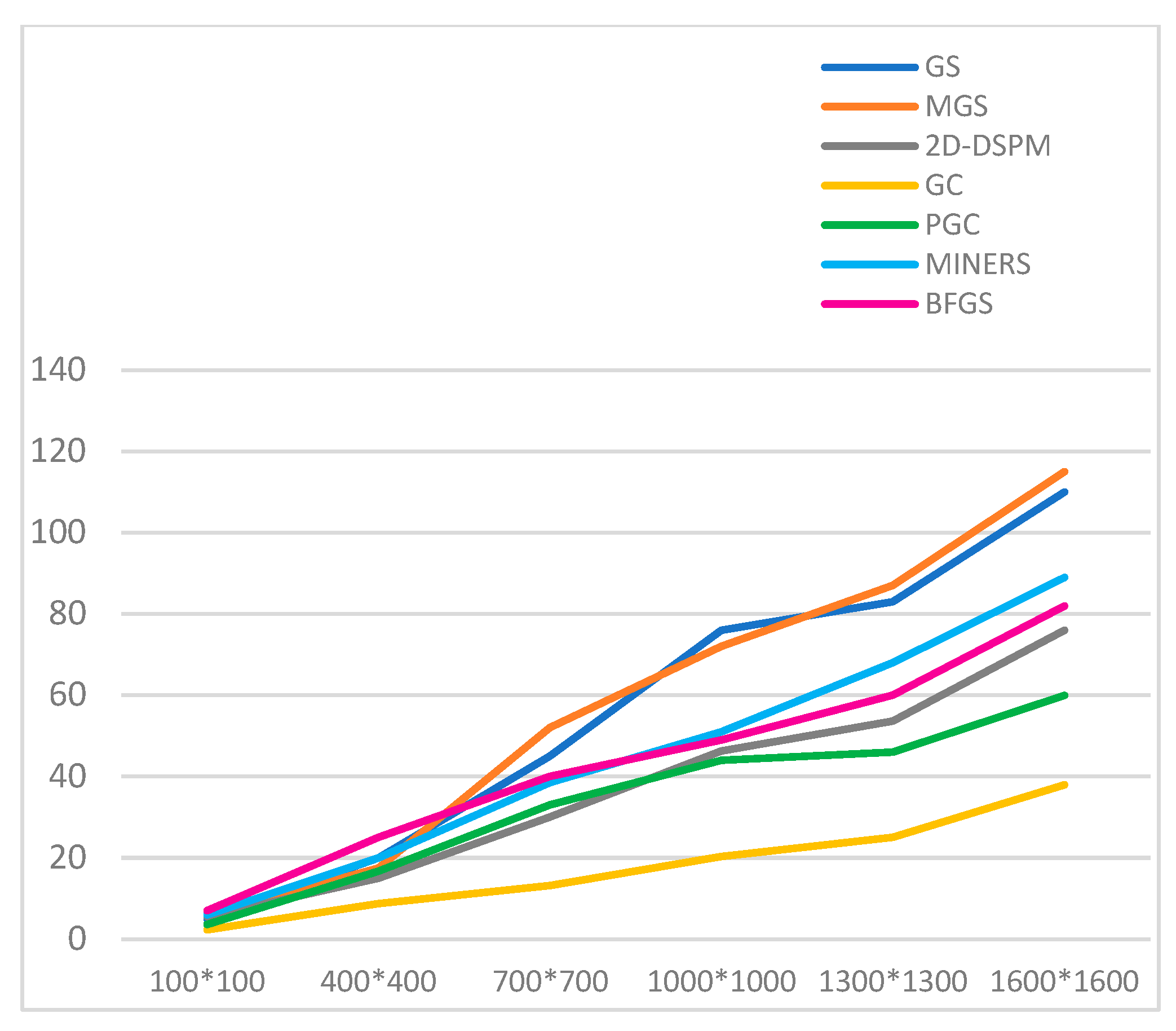
Figure 6 illustrates the average execution times over fifteen simulations of the seven iterative solvers for solving matrices of increasing size, where the stopping criterion is defined by a convergence tolerance of 0.01% as mentioned above. This differs from the previous scenario, which used a fixed number of iterations. Unlike the previous scenario with a fixed number of iterations, this setup allows each method to stop once the desired accuracy is achieved, offering a more realistic comparison of practical efficiency.

The performance varies significantly across the methods, with the Gauss-Seidel (GS) and Modified Gauss-Seidel (MGS) methods demonstrating the longest execution times, especially as the matrix size grows. This trend indicates poor scalability and efficiency in large systems.

The 2D-DSPM and MINERS method shows moderate execution time, outperforming GS and MGS but remaining slower than others methods. In contrast, methods such as GC, BFGS, and especially PGC show superior performance, consistently achieving lower execution times—even for the largest tested matrix (1600 × 1600), with PGC emerging as the fastest method overall.

This suggests that these solvers are more robust and better suited for mobile environments where processing power and memory are limited.

Memory consumption for completing simulations under the same error threshold (0.01%) is shown in Figure 7 for all methods. The Gauss-Seidel (GS) and Modified Gauss-Seidel (MGS) methods exhibit the highest memory usage, which may limit their practicality for larger problems on resource-constrained mobile devices.

At the opposite end, the Conjugate Gradient (GC) method demonstrates remarkably low memory consumption, remaining the most efficient across all matrix sizes. This highlights its suitability for low-memory environments, such as mid-range smartphones. The Preconditioned Conjugate Gradient (PCG) method, while not the most memory-efficient, maintains a relatively stable memory footprint, making it a balanced choice when both execution speed and memory usage are considered.

Convergence Behavior

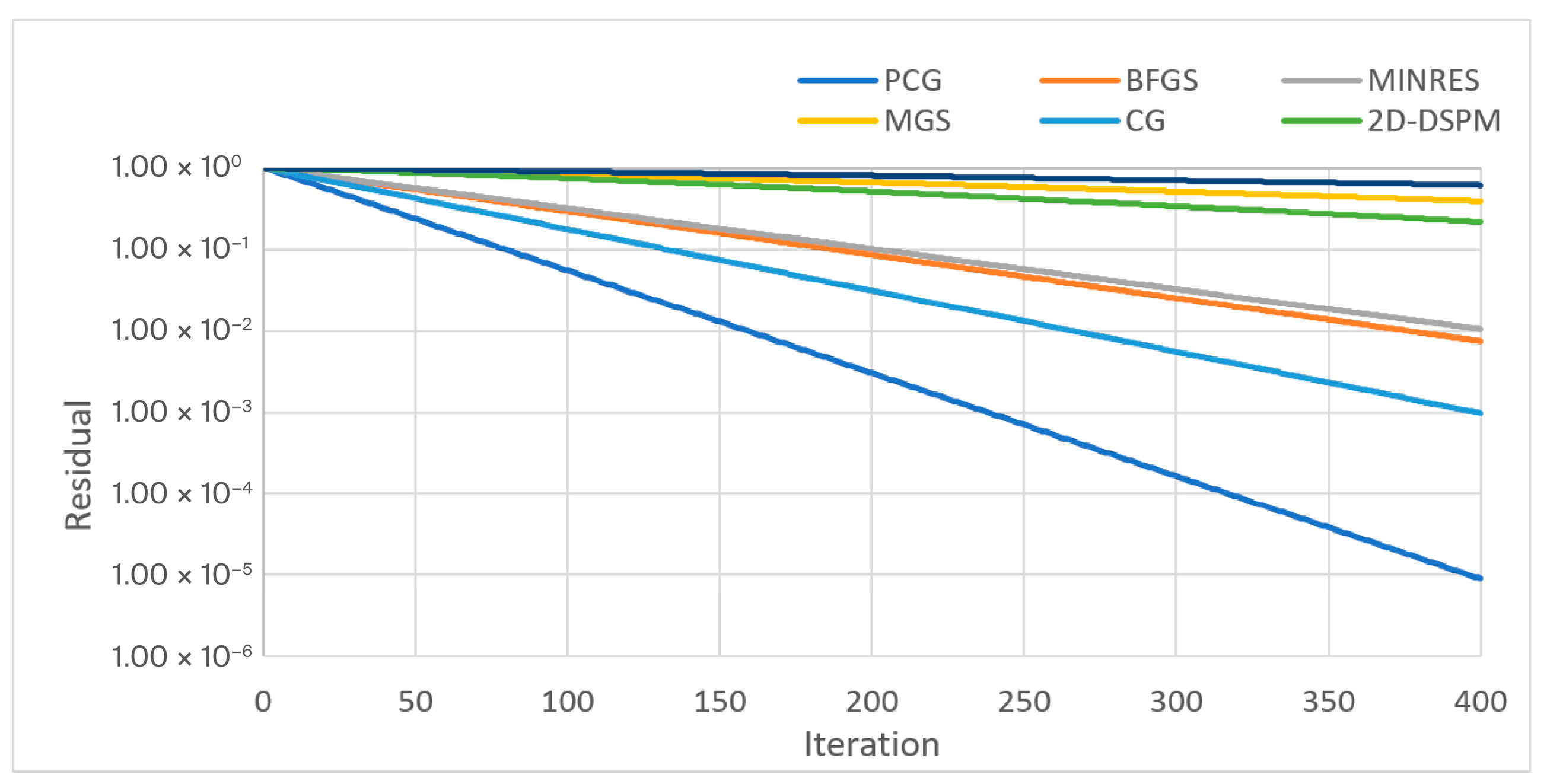
To further strengthen the comparative analysis, we additionally examined the convergence behavior of the iterative solvers. Figure 8 illustrates the evolution of the residual norm as a function of the iteration count for a representative matrix of size 700 × 700. The x-axis is shown on a linear scale, whereas the y-axis uses a logarithmic scale.

The results show that the Krylov-based solvers (CG, PCG) converge rapidly and monotonically, while GS, MGS, and 2D-DSPM require significantly more iterations to reach the same tolerance. This behavior is fully consistent with the execution-time experiments and explains why CG and PCG deliver the best performance under a fixed accuracy threshold.

Discussion

The evaluation of seven iterative solvers under various matrix sizes and stopping criteria reveals that the most suitable method for mobile finite element applications depends on the balance between accuracy, memory usage, and execution time. In our context, where precision is essential and hardware limitations impose strict constraints—particularly on memory—priority is given first to memory efficiency, followed by computational speed.

Our results show that the Conjugate Gradient (CG) method offers the best compromise across these criteria. It maintains consistently low memory consumption across all matrix sizes, which is critical for deployment on mid-range mobile devices. Additionally, it achieves competitive execution times while still satisfying a fixed convergence threshold, making it both practical and robust for real-world mobile applications.

While methods such as PCG and BFGS demonstrate strong speed performance, their higher memory demands reduce their suitability for memory-limited devices. On the other hand, although GS and MGS are simple and initially fast under fixed iterations, they perform poorly in precision-based scenarios and exhibit high memory consumption.

In conclusion, the CG method emerges as the most balanced and scalable choice, offering a favorable trade-off between memory usage and computational efficiency, without compromising accuracy—aligning closely with the priorities of finite element analysis on mobile platforms.

4.3. Application

The mobile application developed in this work is specifically designed to perform finite element analysis (FEA) of two-dimensional bridge structures on smartphones. Its primary goal is to provide a lightweight, accessible, and efficient simulation tool that balances ease of use with computational accuracy making it ideal for both educational and practical engineering contexts.

The application is capable of generating and analyzing various bridge geometries, including girder, crutch, and arcbridges, as illustrated in Figure 9, Figure 10 and Figure 11.

Users can specify geometric parameters such as the length and height of the deck, the number and size of piers, as well as the number and curvature of arches. The interface also allows the selection of material properties, including Young’s modulus and Poisson’s ratio, as well as the definition of boundary conditions such as fixed supports, roller supports, and hinged supports, along with the input of different loading configurations (Figure 11). All data entry and visualization are handled through a user-friendly mobile interface.

One of the key features of the application is its integrated mesh generator, which uses the predefined structured mesh strategy discussed in the previous section. This approach eliminates the need for external meshing tools and is fully optimized for mobile environments. The mesh is automatically generated based on the user’s input, and users can optionally apply mesh refinement to improve the accuracy of the simulation (Figure 12).

Once the model is defined, the application performs a complete finite element analysis (FEA), including, Displacement (deformation) calculations, Stress distribution analysis and Strain evaluation.

The results are displayed directly on the smartphone screen using contour plots and color maps, providing users with an intuitive and immediate visualization of the structural response. This real-time post-processing capability enables users to explore how variations in geometry, material properties, or loading conditions influence the mechanical behavior of the bridge.

To validate the accuracy of the proposed application, we compared its results with those obtained using the RDM6 structural analysis software, version 6.19 (26 November 2018). The test case involves a concrete girder bridge subjected to a uniform linear load of 400 kN/m. The material used in the analysis is concrete, characterized by a Young’s modulus of 30 GPa and a Poisson’s ratio of 0.2. The structure is supported on three piers, each modeled as a simple support restraining vertical displacement.

We present the results for the yy-stress (Figure 13) and the y-displacement (Figure 14). Each figure includes two sets of visualizations: the first obtained from our mobile application, and the second from RDM6.

Regarding yy-stress, the maximum values computed by our application are located at the interior connections between the girder and the two outer piers, as well as along the entire central pier, as shown in red and orange. The maximum yy-stress reaches approximately −35 MPa in these regions. The stress is nearly zero at the mid-span between piers, indicated in blue. The RDM6 results show a similar stress distribution, with maximum values at the same locations (blue region) and minimal stress in the spans (red colors).

For the y-displacement, both methods show that the maximum downward displacement occurs at the mid-span between two piers, represented by the red region in our application and the blue region in RDM6. Our application computes a maximum displacement of approximately −7.5 mm, while the RDM6 software gives −7.62 mm. The close agreement between the two sets of results confirms the reliability and consistency of the proposed mobile application.

In addition, a relative-error check was performed along the entire bridge span for all computed fields (displacement and stresses), and the error remained consistently low across the structure.

A second validation example is presented for the crutch bridge configuration. The same material properties (concrete, E = 30 GPa, ν = 0.2) and a uniform load of 400 kN/m were applied. Figure 15 and Figure 16 show the xx-stress and xy-stress contours obtained from the mobile application together with those produced by RDM6. For this case, the maximum xx-stress computed by the mobile tool ranges from −177.9 MPa to 131.6 MPa, compared to −179.02 MPa to 132.57 MPa in RDM6. Similarly, the maximum xy-stress varies between −159.1 MPa and 159.3 MPa in our application, versus −160.97 MPa and 160.73 MPa in RDM6. The close agreement in both magnitude and spatial distribution demonstrates the reliability of the proposed solver for this additional test case.

5. Conclusions

This work explored the feasibility and potential of performing Finite Element Analysis (FEA) directly on smartphones, focusing on structural engineering applications. The review of existing tools revealed that truly autonomous FEA implementations on mobile platforms remain rare, as most current applications are limited to visualization or rely on constant server connectivity. To address this gap, we proposed an algorithmic framework designed to overcome the principal computational challenges—namely memory constraints, execution time, and numerical precision through the use of predefined optimized meshes and lightweight iterative solvers.

A series of numerical experiments demonstrated that such optimization makes mobile-based FEA both feasible and reliable. Among the tested solvers, the Conjugate Gradient (CG) method achieved the best balance between accuracy, execution time, and memory efficiency, while the predefined meshing approach significantly reduced computational overhead without sacrificing precision. These results confirm that efficient FEA computations can be achieved even on resource-constrained hardware when appropriate algorithmic strategies are employed.

Beyond the technical findings, this study contributes to a research area that remains largely unexplored. Few scientific works have investigated the algorithmic adaptation of finite element computations to mobile devices a field positioned at the intersection of computational mechanics and embedded numerical algorithms. The demonstrated feasibility of smartphone-based simulation opens new perspectives for developing lightweight, accessible, and educational tools, particularly relevant in the context of mobile learning and the digital transformation of engineering education. In addition to the numerical validation and performance analysis presented here, several perspectives naturally emerge. First, although the present study focused on execution time and memory usage—which are strongly linked to energy consumption—no explicit battery profiling or CPU/GPU utilization measurements were conducted. A more detailed energy analysis, using platform-specific profiling tools, is planned as future work to better quantify the power footprint of mobile FEA computations.

Second, several technical extensions can build upon the feasibility demonstrated here. Mobile GPUs and parallel processing could be leveraged to accelerate matrix–vector operations and post-processing tasks, while AI-driven adaptive meshing represents a promising direction for automatically refining regions with high stress gradients. Beyond the linear-elastic 2D formulation considered in this study, future investigations will explore extensions toward composite materials, nonlinear behavior, transient or dynamic analyses, and eventually lightweight 3D geometries. To maintain computational efficiency on mobile hardware when addressing these more demanding problems, the framework will incorporate lightweight numerical strategies such as reduced-order modeling, optimized incremental–iterative procedures, and selective local mesh refinement, all of which help to limit computational growth while preserving accuracy.

Finally, as the application evolves beyond the algorithmic validation phase, user-centered evaluations will be carried out with engineering students and practitioners. These studies focusing on usability metrics such as task-completion time, ease of operation, and perceived intuitiveness will help assess the educational and field applicability of the proposed tool.

Overall, this work provides a solid foundation for the development of more advanced, adaptive, and intelligent mobile FEA environments, capable of supporting both educational use and practical engineering tasks.