The Aho-Corasick Paradigm in Modern Antivirus Engines: A Cornerstone of Signature-Based Malware Detection

Abstract

The Aho-Corasick (AC) algorithm remains one of the most influential developments in deterministic multi-pattern matching due to its ability to recognize multiple strings in linear time within a single data stream. Originally conceived for bibliographic text retrieval, the structure of the algorithm is based on a trie augmented with failure links and output functions, which has proven to be remarkably adaptable across computational domains. This review presents a comprehensive synthesis of the AC algorithm, with details on its theoretical foundations, formal automaton structure, and operational principles, as well as tracing its historical evolution from text-search systems to large-scale malware detection. This work further explores the integration of Aho-Corasick automata within modern antivirus architectures, describing mechanisms of signature compilation, real-time scanning pipelines, and large-scale deployment in contemporary cybersecurity systems. The deterministic structure of the Aho-Corasick automaton provides linear-time pattern recognition relative to input size, while practical performance characteristics reflect memory and architecture constraints in large signature sets. This linear-time property enables predictable and efficient malware detection, where each byte of input induces a constant computational cost. Such deterministic efficiency makes the algorithm ideally suited for real-time antivirus scanning and signature-based threat identification. Thus, nearly fifty years after its inception, AC continues to bridge formal automata theory and modern cybersecurity practice.

1. Introduction

The Aho-Corasick (AC) algorithm, introduced in 1975 at Bell Laboratories by Alfred V. Aho and Margaret J. Corasick, represents one of the most significant advances in computer science for solving the multiple-pattern string matching problem [1]. It was designed to efficiently locate all occurrences of a finite set of strings $P=\left\{p_1,p_2,\dots ,p_n\right\}$ within a text T, which in turn provides a deterministic linear-time performance through the use of a finite-state automaton (FSA), that processes the input in a single pass [1]. The automaton is built from a trie of all patterns and then augmented with failure links, which enable immediate fallback transitions upon mismatches. The design guarantees that each symbol is processed only once [1]. This innovation reduced the time complexity of multi-pattern search to $O(\left|T\right|+\sum \left|p_i\right|+output)$, a bound that would later make it invaluable for real-time data analysis, information retrieval, and security applications [1,2].

The need for such an algorithm arose in the 1970s as text databases and bibliographic systems expanded rapidly, and researchers required fast methods for location of multiple keywords across large datasets [1]. At the time, single-pattern algorithms such as Knuth-Morris-Pratt and Boyer-Moore could handle one query efficiently, but their repeated use across large sets of patterns caused multiplicative computational overhead [2]. The inefficiency of these earlier methods became a critical issue in automated bibliographic search systems and keyword indexing applications, where tens of thousands of terms had to be matched against extensive text corpora [1]. Aho and Corasick proposed a unified structure that merges all patterns into one deterministic automaton. The main design allows for amortization of the match cost across all entries and supports simultaneous pattern recognition in a single traversal of the text [1]. Their experiments demonstrated speed improvements by nearly an order of magnitude when compared to conventional methods, and their approach proved to be the most efficient multi-pattern string matcher of its time [1].

Following its publication, the AC algorithm quickly found utility in areas that required deterministic multi-pattern matching. One of its earliest practical implementations was in the UNIX fgrep utility (Bell Labs, 1979), which performed fixed-string searches by using the AC automaton to efficiently handle multiple literals in file scanning [3]. It soon became standard in information retrieval systems, digital libraries, and computational linguistics, where dictionary-based text parsing and keyword extraction were central tasks [4]. Beyond 1990s, AC had also begun to influence bioinformatics, where it was applied to the detection of nucleotide and protein motifs within large genomic sequences [5]. This cross-domain adaptability highlighted the versatility and the robustness of the algorithm as a general-purpose pattern matcher.

However, its adoption in cybersecurity, specifically in antivirus and intrusion detection systems, was significantly delayed. For nearly two decades after its introduction, hardware limitations made the use of large AC automata impractical for malware signature databases, which could contain tens of thousands of distinct patterns [6]. Early antivirus tools of the 1980s and early 1990s often relied on simpler substring search methods, hash-based indexing, or rolling checksums to detect malicious code [7]. It was only in the late 1990s that the Aho-Corasick algorithm began to see widespread implementation in network intrusion detection systems (NIDS), where the ability to match thousands of attack signatures simultaneously across packet streams was essential for real-time detection [8]. The release of Snort in 1999 marked a pivotal moment: its pattern-matching subsystem used AC as the core of its rule-matching engine, which enabled efficient deep-packet inspection at wire speed [9]. Subsequent studies demonstrated that AC-based approaches could achieve deterministic throughput (i.e., bytes processed per second) with predictable performance across different input sizes, an essential property for high-assurance security applications [10,11].

In early 2000s, the algorithm had become a cornerstone of signature-based malware detection, embedded in open-source security systems such as Snort, Suricata, and ClamAV [8,9]. The roughly twenty-five-year gap between its invention and full-scale adoption in cybersecurity illustrates the historical dependency between theoretical computer science and applied system engineering. Thus, the Aho-Corasick algorithm could only be fully utilized in antivirus and intrusion detection systems after hardware improvements made its deterministic behavior computationally affordable [8,10].

The following decades saw a series of optimizations and architectural variants. The incremental or dynamic Aho-Corasick algorithm, introduced in the mid-1980s, allowed patterns to be added or removed dynamically without the reconstruction of the entire automaton [12]. Much later, Split-AC (i.e., a split of the main automaton into multiple smaller automata, each handling a subset of the pattern space) and memory-optimized implementations addressed the large memory footprint inherent to AC, making it feasible for embedded or high-speed network appliances [10,11].

With the advent of parallel hardware, failure-less and GPU-based variants, collectively known as Parallel Failure-less Aho-Corasick (PFAC); emerged, which allowed for massive concurrent matching operations suitable for deep-packet inspection, DNA analysis, and antivirus scanning [13]. Hardware-level implementations, which include FPGA and ASIC pipelines, further enhanced throughput and achieved multi-gigabit scanning rates while deterministic latency was maintained [14].

Today, the Aho-Corasick algorithm underlies many arrays of systems, from text retrieval and DNA sequencing to network forensics and malware detection [15]. Its enduring relevance in cybersecurity stems from its ability to balance theoretical determinism with practical scalability, qualities that few algorithms have matched. Modern antivirus engines often embed AC within broader frameworks that combine heuristic analysis, statistical models, and machine learning to detect polymorphic and obfuscated threats [15].

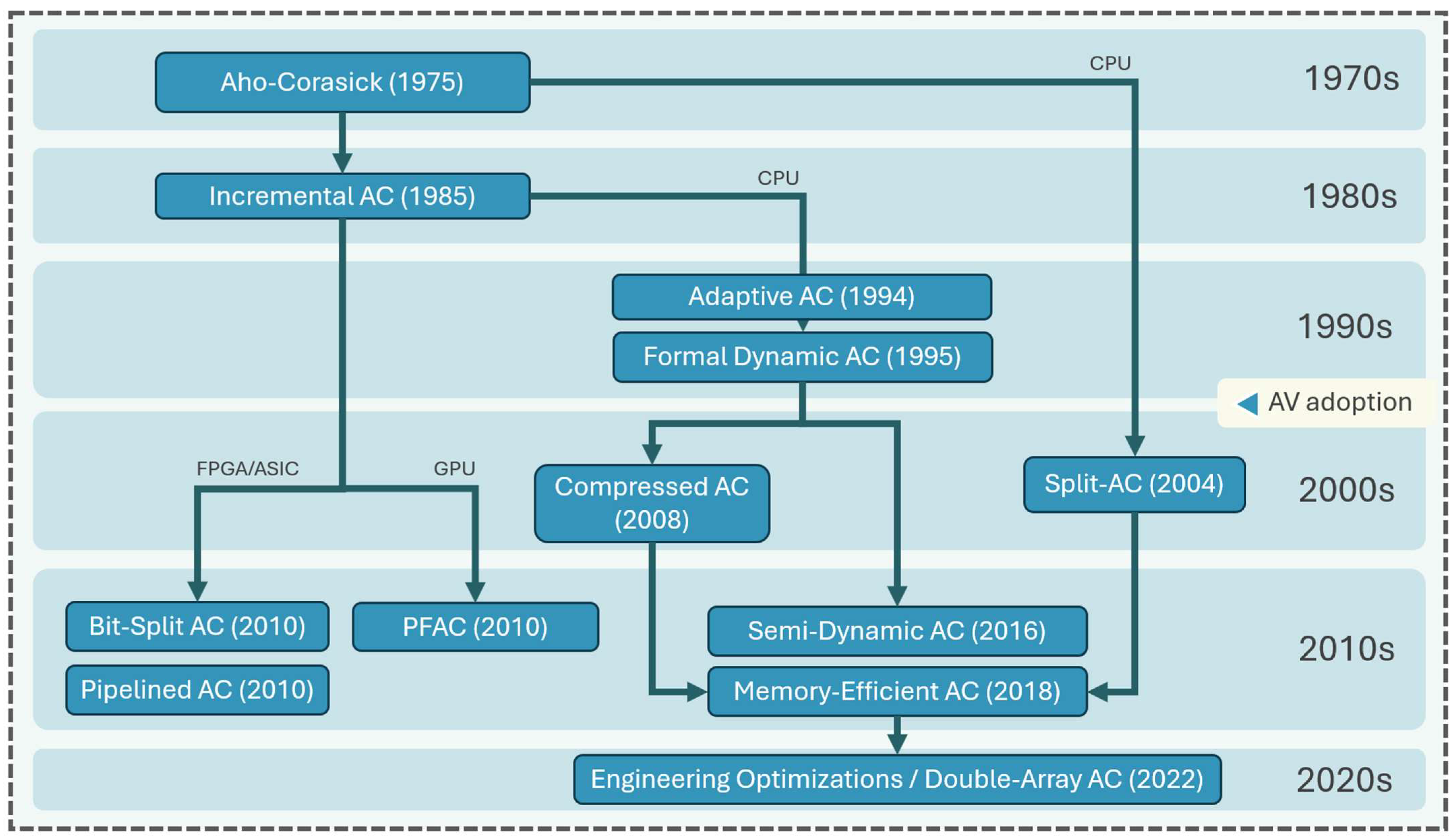
2. Evolution and Optimized Versions

Since its introduction in 1975, the Aho-Corasick (AC) algorithm has evolved to address an increase in computational demands and memory constraints inherent in large-scale pattern matching systems (Figure 1). While the original formulation guarantees linear-time performance, its direct implementation becomes impractical when antivirus databases contain millions of signatures. In order to overcome this issue, several key variants have been developed, including Split-AC, Bit-Split AC, Parallel Failure-less Aho-Corasick (PFAC), and compressed automaton representations, that improve scalability, memory efficiency, and throughput [8,11,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. The Split-AC model was described by Tuck et al. [8], and it divides the global Aho-Corasick automaton into multiple smaller sub-automata, each handling a disjoint subset of patterns. At runtime, a dispatcher dynamically selects which sub-automaton to activate based on prefix matching or hashing. This design improves cache locality and enables parallelization across CPU cores or threads. In antivirus systems, where signature sets often exceed cache capacity, Split-AC minimizes traversal latency and memory contention, and this results in the maintenance of linear throughput even as databases scale.

The Bit-Split AC variant was later proposed for hardware acceleration [14,22]. In this model, input bytes are decomposed into their individual bits, and transitions are evaluated in parallel across logic gates or FPGA slices. This design drastically reduces the size of state transition tables and enables deterministic performance in gigabit-rate data streams, which makes it well-suited for embedded antivirus processors and inline intrusion detection systems. Note that the Bit-Split Aho-Corasick variant, while highly efficient in FPGA and ASIC architectures, exhibits no practical performance advantages for general-purpose processors or mobile devices, as its bit-level parallelism cannot be exploited by standard CPU or GPU instruction pipelines [22].

Furthermore, subsequent advances in GPU-accelerated pattern matching led to the introduction of the Parallel Failure-less Aho-Corasick (PFAC) algorithm [13,24,25]. Thus, by the elimination of the failure link mechanism (i.e., the process by which the automaton follows precomputed fallback transitions after a mismatch to resume matching without a restart from the root) and the assignment of one GPU thread to each byte of the input stream, PFAC transforms the sequential traversal of AC into a massively parallel computation. Although this increases memory requirements, it achieves multi-gigabit per second throughput, which makes it ideal for cloud-scale malware analysis and real-time packet inspection [10,13].

In addition, modern research has focused on compressed automata (i.e., automata whose transition tables are stored in a compact, memory-efficient form without an alteration of their functional behavior) and succinct data structures (i.e., data structures that use space close to the information-theoretic minimum and still allow for constant-time access and updates) for large-scale AC implementations [20,21,28]. Prior work has shown that compressed variants of Aho-Corasick can significantly reduce space requirements. For example, Dimopoulos et al. reported memory savings of up to 75% on FPGA-based AC implementations [11]. Such optimizations enable antivirus engines to load and query large signature sets directly into memory, a previously prohibitive task on constrained systems. These techniques have also been extended into delta-encoded failure links (i.e., failure transitions stored as relative offsets between states rather than absolute pointers to reduce memory consumption) and hierarchical trie compression (i.e., a method that merges common subtrees within the trie to eliminate redundancy and reduce memory usage), which further improve memory locality and reduce cache misses at runtime [4,29,30]. Beyond static optimization, the integration of Aho-Corasick into hybrid intelligent detection pipelines represents a major trend in contemporary antivirus architecture (Figure 2) [31,32]. Here, AC functions as a deterministic pre-filter for known signatures, while heuristic and machine learning layers analyze uncertain or polymorphic samples [15,31,32]. This layered model preserves the speed of deterministic detection and extends coverage to adaptive malware families that traditional pattern matching alone cannot identify [33,34].

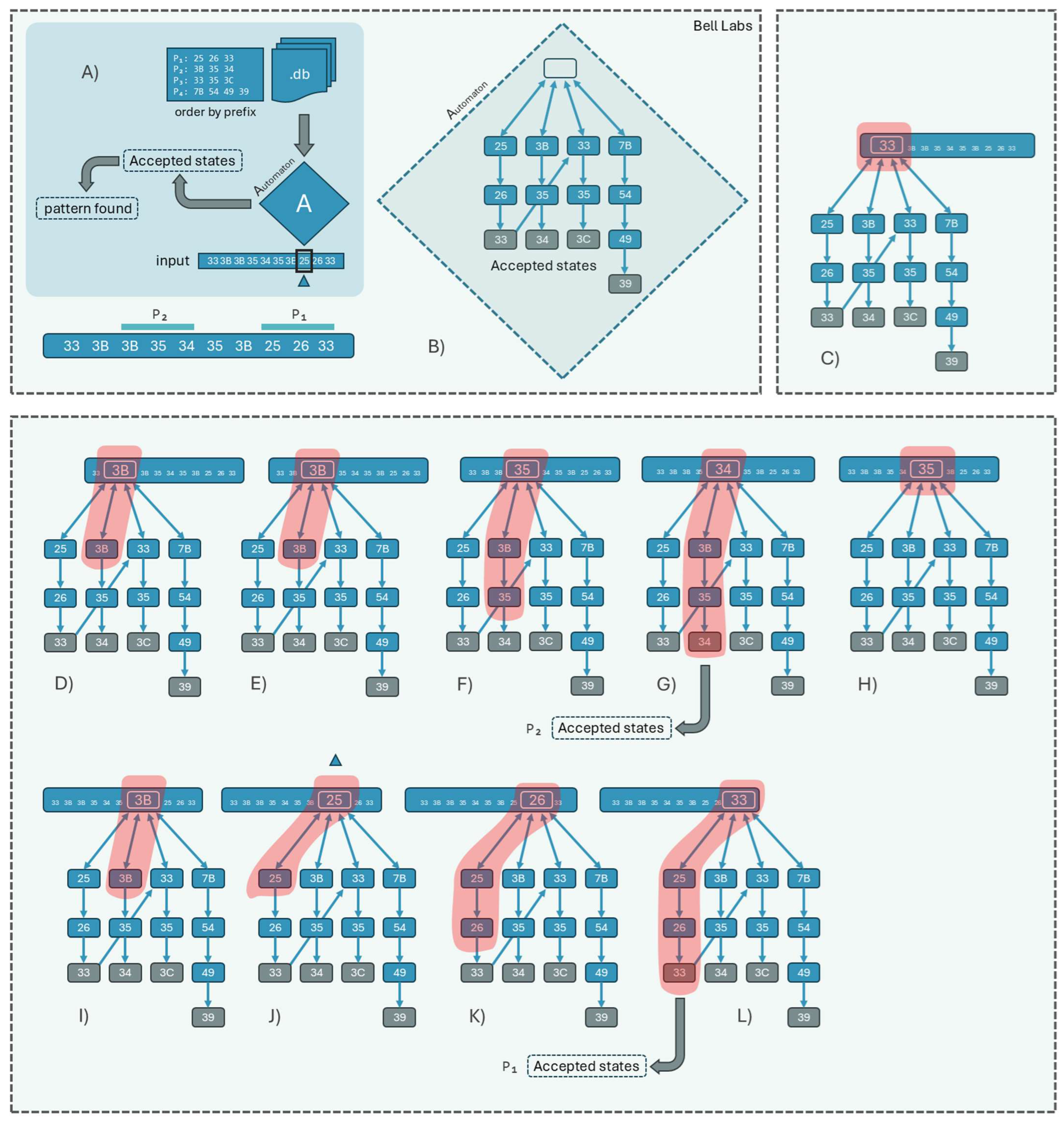
3. Algorithmic Foundations of the Aho-Corasick Automaton

The Aho-Corasick (AC) algorithm operates through the construction and traversal of a deterministic finite-state automaton (FSA) designed to recognize all elements of a finite pattern set $P=\left\{p_1,p_2,\dots ,p_n\right\}$ within an input text $T=\left\{t_1,t_2,\dots ,t_n\right\}$ defined over an alphabet $\Sigma$ [1]. The automaton is derived from a trie in which each node represents a prefix of one or more patterns (Figure 2). The traversal begins at the root state $q_0$, and each directed edge corresponds to a symbol transition labeled by an element $a\in \Sigma$. Once all patterns have been inserted into the trie, additional failure links are introduced. These “failure links” establish fallback transitions that direct the automaton from a state $q$ to the longest proper suffix of the string represented by that state which is also a prefix of another pattern. In the absence of a valid suffix, the link defaults to the root state (Figure 2). This mechanism ensures the continuity of matching after a symbol mismatch, prevents the rescan of already processed characters, and maintains strict linear time behavior. Each state in the automaton is further associated with an output function $O\left(q\right)$ that records all patterns which terminate at that state. While the text is scanned, every symbol $t_j$ from the input sequence is processed exactly once (Figure 2). When the next symbol does not correspond to a defined transition from the current state, the automaton follows the sequence of failure links until a matching transition is identified or the traversal returns to $q_0$. When the symbol is accepted, the state advances to $\delta (q,t_j)$, and if the resulting state has a nonempty output function, all associated patterns are reported as matches ending at the current position. Formally, the overall time complexity of the matching process is $O(m+z)$, where m denotes the length of the input text and z the total number of matches found, while the automaton construction phase requires $O\left(\sum \left|p_i\right|\right)$, operations proportional to the total pattern length [1,2]. Thus, the complete algorithm executes in $O\left(\sum \left|p_i\right|+m+z\right)$, a property that makes it optimal within the class of deterministic multi-pattern matching algorithms, as originally established by Aho and Corasick [1].

From a theoretical perspective, the AC automaton can be interpreted as an augmented deterministic finite automaton with implicit self-repair mechanisms that maintain continuous recognition across the input stream. Unlike nondeterministic or backtracking approaches, it guarantees that every input symbol triggers a constant number of transitions, independent of the number of patterns [1]. This determinism, combined with the distributed cost associated with the construction of shared prefix trees, provides a stable computational framework in which performance scales linearly with the size of the input rather than with the number of signatures. Conceptually, this renders the AC automaton a compact representation of all possible pattern occurrences embedded within a single unified structure [15].

3.1. Formal Description of the Aho-Corasick Algorithm

In order to provide a rigorous understanding of its operation, the Aho-Corasick algorithm can be formally described within the framework of deterministic finite-state automata [1,15]. In this formulation, the matching process is expressed as a set of state transitions driven by the input symbols of the scanned text, with terminal states that correspond to detected patterns (Figure 2). Let:

$$P=\left\{p_1,p_2,\dots ,p_n\right\},$$

be a finite set of patterns over a finite alphabet $\Sigma$, and let:

$$T=t_1,t_2,\dots ,t_m, t_i\in \Sigma$$

be the text to be scanned. The Aho-Corasick automaton is a deterministic finite-state automaton (FSA) defined as:

$$A=\left(Q,\Sigma ,\delta , q_0, F,f,O\right)$$

where $Q$ is the finite set of states (nodes of the trie), $\Sigma$ is the input alphabet, $\delta :Q\times \Sigma \to Q$ is the transition function, $q_0\in Q$ is the initial state, $F\subseteq Q$ is the set of accepting (terminal) states, $f:Q\to Q$ is the failure function that maps each state to the longest proper suffix that is also a prefix in the trie, $O:Q\to 2^P$ is the output function, assigning to each state the set of patterns ending at that state. During automaton construction, for each state $q$ and input symbol $a\in \Sigma$,

$$\delta \left(q,a\right)=\left\{\begin{array}{ll}\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}(q,a)& \mathrm{i}\mathrm{f} a \mathrm{e}\mathrm{x}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{s} \mathrm{i}\mathrm{n} \mathrm{t}\mathrm{r}\mathrm{i}\mathrm{e}\left(q\right)\\ \delta (f\left(q\right),a)& o\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\mathrm{i}\mathrm{f} q{\ne q}_0\\ q_0,& if q=q_0 \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{n}\mathrm{o} \mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{o}\mathrm{n} a\end{array}\right.$$

The failure function $f\left(q\right)$ ensures that after any mismatch, the automaton transitions to the state representing the longest proper suffix of the current input prefix that is also a prefix in the trie. While text T is scanned, the automaton processes each symbol exactly once:

$$q_{i+1}=\delta \left(q,t_i\right), i=1, 2,\dots ,m,$$

and for each reached state $q_i$, the output function is evaluated as: $if O\left(q_i\right)\ne \varnothing$ then report all $p\in q_0$ as matches ending at i. Thus, all pattern occurrences are found in a single pass over the input text (Figure 2). The total time complexity of the Aho-Corasick algorithm is:

$$T_{AC}=O\left(\sum _{i=1}^n\left|p_i\right|+m+z\right),$$

where m denotes the length of the input text T (or the number of symbols processed while the input is scanned), and z represents the total number of pattern matches found. This includes both automaton construction (first term) and text scanning (second and third terms). The space complexity of the algorithm depends on the total number of states and transitions:

$$S_{AC}=O\left(\sum _{i=1}^n\left|p_i\right|·\left|\Sigma \right|\right),$$

where $S_{AC}$ denotes the space complexity of the Aho-Corasick automaton, $p_i$ represents the ith pattern in the set P, $\mid p_i\mid$ is its length, and $\mid \Sigma \mid$ is the size of the input alphabet. This bound represents the theoretical worst case, assuming a dense transition table in which every state maintains outgoing edges for all symbols in $\Sigma$. In practice, only existing transitions are stored, yielding a sparse representation with actual space complexity closer to $O\left(\sum \left|p_i\right|\right)$. Modern antivirus and intrusion–detection engines further reduce memory usage through compressed trie representations, pointer minimization, and delta-encoded failure links, improving cache locality and scalability [11]. Note that $S_{AC}$ can be reduced in optimized variants through sparse transition tables or compressed trie representations. In antivirus systems, where each $p_i$ represents a malware signature encoded as a hexadecimal byte sequence, the automaton A serves as a deterministic recognizer mapping file bytes to signature identifiers. For a data stream $X=x_1,x_2,\dots ,x_L$, a detection occurs whenever,

$$\exists j\in \left[1,L\right],\exists p_k\in P:X\left[j-\left|p_k\right|+1,j \right]=p_k,$$

a condition efficiently realized through the state transitions of A without explicit substring comparison. Note that ∃ denotes the existential quantifier (“there exists”), p_k ∈ P indicates that p_k is a pattern within the finite pattern set P, |p_k| represents the length of pattern p_k, and X [a, b] denotes the substring of the data stream X ranging from position a to b (inclusive). In other words, there exists a position j in the text X, and there exists a pattern p_k in the pattern set P, such that the substring of X ending at j and of length |p_k| equals p_k. Thus, this mathematical property ensures that every byte of the scanned input contributes to a finite number of state transitions, which guarantees bounded computational effort independent of database size.

3.2. Algorithmic Representation and Pseudocode

The procedural form of the Aho-Corasick algorithm is presented in Algorithm 1. The AC-Build phase constructs the finite-state automaton by the insertion of each pattern into the trie and the establishment of failure transitions through breadth-first traversal. The AC-Search phase then performs deterministic traversal of the input sequence, and emits all pattern matches in linear time with respect to the text length and total pattern size. This pseudocode consolidates the theoretical description above into an operational framework suitable for implementation and performance analysis.

Algorithm 1: Aho-Corasick (build + search)

Input:  P = {p1, p2, …, pn}       // patterns over alphabet Σ  T = t1…tm            // text AC-Build(P):  create root q0  for each pattern p in P:   insert p into trie via goto transitions δ(q, a)   mark terminal state with O(q) ← O(q) ∪ {p}  // failure links by BFS  queue ← ∅  for each a ∈ Σ with δ(q0, a) defined:   f( δ(q0, a) ) ← q0   enqueue( δ(q0, a) )  for each a ∈ Σ with δ(q0, a) undefined:   δ(q0, a) ← q0          // optional fallback shortcut  while queue not empty:   v ← dequeue()   for each a ∈ Σ with δ(v, a) defined:    u ← δ(v, a)    x ← f(v)    while δ(x, a) undefined and x ≠ q0:      x ← f(x)    if δ(x, a) defined:     f(u) ← δ(x, a)    else:     f(u) ← q0    O(u) ← O(u) ∪ O( f(u) )      // inherit outputs    enqueue(u)  return automaton (Q, Σ, δ, q0, F, f, O) AC-Search(T):  state ← q0  for each symbol a in T:   while δ(state, a) undefined and state ≠ q0:    state ← f(state)   if δ(state, a) defined:    state ← δ(state, a)   else:    state ← q0   if O(state) ≠ ∅:    report all patterns in O(state) ending at current index

The pseudocode presented above corresponds to a working implementation developed as part of the Scut Antivirus research toolkit (Appendix A). In the implementation, each automaton state is represented by a node structure that contains transition mappings (goto links), failure links, and output lists. These nodes collectively form the trie described in the formal definition. At runtime, input bytes are streamed through this structure in hexadecimal form, which allows the scanner to detect signatures stored in the accompanying database [15]. This direct mapping between formal states and in-memory nodes facilitates efficient traversal, compact storage, and real-time visualization of matching positions (Figure 3). The implementation thus provides an empirical reference that connects the algorithmic formalism to its practical deployment within antivirus engines [35,36].

In practical antivirus systems, each malware signature corresponds to one or more terminal paths within this automaton [15]. While the program executes, file data or memory buffers are streamed sequentially through the automaton, and each transition corresponds to the consumption of a byte represented as a symbol in hexadecimal form (Figure 3). When an accepting state is reached, the engine identifies the associated signature and raises a detection event (Figure 3). The deterministic traversal enables constant-time progression independent of signature count, which prevents the exponential growth in search time characteristic of earlier sequential matching methods [1]. This predictable computational profile is crucial for real-time malware detection, where throughput consistency and latency determinism are essential [8,9,10,11].

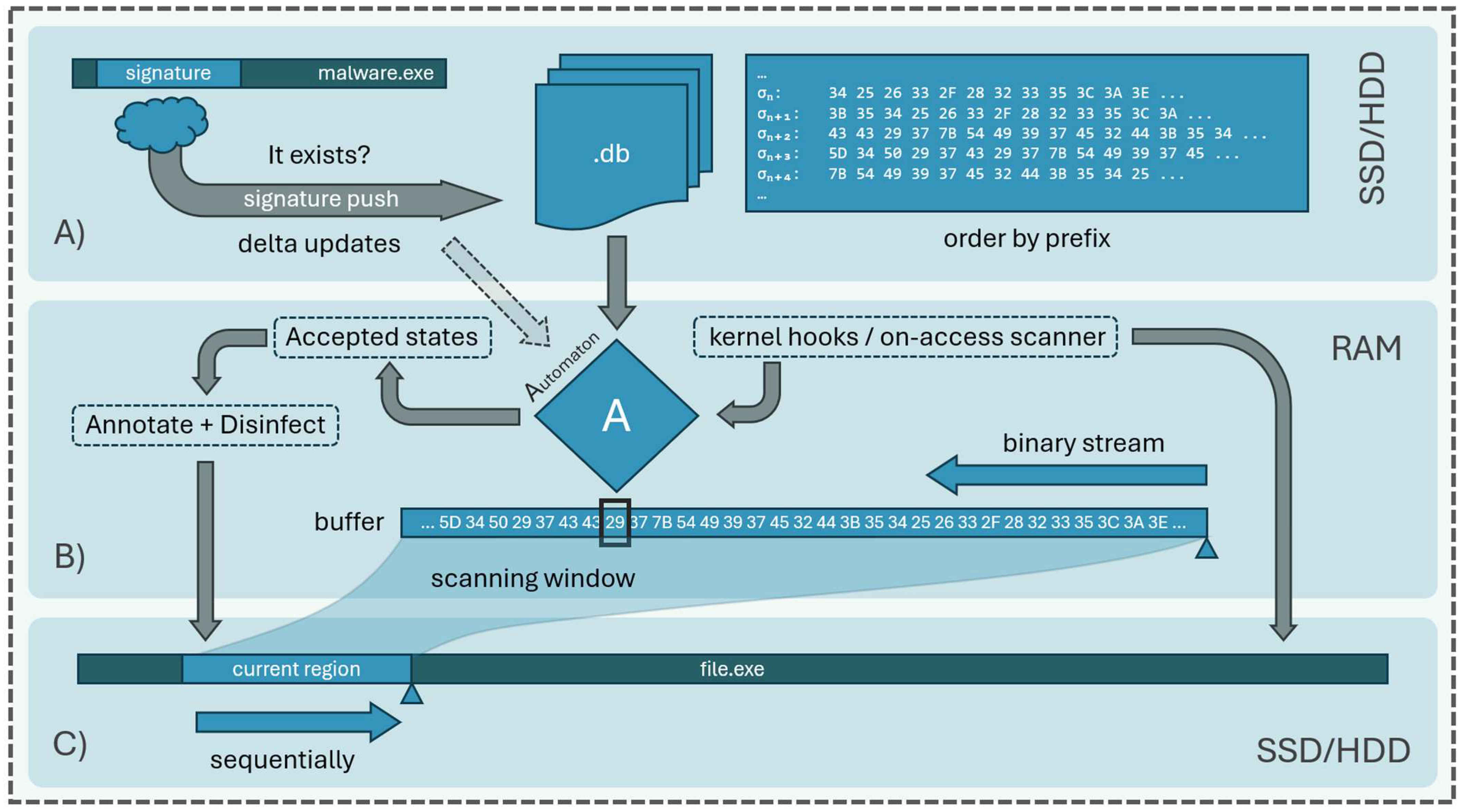
4. Integration in Antivirus Architectures

The Aho-Corasick (AC) algorithm functions as the deterministic core of modern antivirus engines, where it operates as the principal component responsible for pattern recognition across vast collections of malware signatures [15]. The integration of this algorithm into antivirus architectures involves a structured interplay between signature management, scanning pipelines, and real-time monitoring mechanisms that extend from local file systems to network-level analysis (Figure 3) [15]. In a typical antivirus system, signature management begins with the compilation of malware indicators into a structured database [15,37]. Each signature represents a characteristic byte sequence extracted from a malicious executable, macro, or document, and is stored in hexadecimal form [15,37,38]. During database construction, these signatures are preprocessed to remove redundancy, aligned according to shared prefixes, and organized into pattern sets suitable for automaton compilation (Figure 3) [38].

The resulting dataset is then used to build the Aho-Corasick automaton, in which all signatures are merged into a single deterministic state machine [37,38]. This compilation process produces a unified data structure where common subpatterns are stored once, thereby minimizing redundancy without loss of recognition accuracy. Dynamic signature updates, where new malware patterns are inserted or outdated ones removed, require partial reconstruction of affected subtrees or incremental automaton updates (Figure 3A) [39]. In contemporary cloud-connected antivirus platforms, such updates are often performed remotely, with delta-compilation techniques which allow the automaton to be refreshed in memory without a complete rebuild [8,11,15,40]. Although delta-compilation techniques are elegant and allow partial automaton updates, many antivirus systems in practice prefer a full replacement [15]. A new instance builds from the updated database, while the original remains active until swap readiness [15]. This approach eliminates in-place changes and allows for an uninterrupted operation. Nonetheless, once the automaton has been compiled, it becomes the engine of the file scanning pipeline (Figure 3B). When a typical scan is performed, files are read as binary streams and segmented into scanning buffers that are processed sequentially (Figure 3B,C). The AC algorithm traverses each buffer linearly, matching signatures against every byte sequence without a redundant rescan. Each transition through the automaton corresponds to a specific input symbol, which typically represents a hexadecimal byte, and accepting states denote the completion of a signature match (Figure 2). These accepting states correspond to the terminal nodes of signatures embedded in the automaton. Upon reaching such a state, the engine records the match, annotates the corresponding file offset, and forwards this information to higher-level heuristics or disinfection modules (Figure 3B). Because of its deterministic design, the AC-based engine guarantees linear scanning time with respect to input size for a fixed automaton and execution platform. However, throughput (i.e., the amount of information processed per unit of time) and latency remain influenced by memory hierarchy, signature set size, and failure-link traversal costs, especially in cache-constrained environments [9,10,41]. In real-time protection environments, the same automaton operates within memory-resident components that perform continuous monitoring of system events [42]. Known as on-access scanners, these modules intercept file operations through kernel-level hooks or driver interfaces and stream data fragments through the AC engine before the file is executed or read by the operating system [15,42]. Memory-resident scanning extends this principle to volatile regions, with the inspection of loaded processes and modules for known binary sequences that may indicate code injection or self-modifying behavior [15]. The deterministic structure of the Aho-Corasick automaton makes it particularly effective in these contexts, as it can evaluate thousands of signatures per millisecond without any perceptible delay in normal system operation [7,15].

At the network level, the same methodology scales to the inspection of packet payloads. In intrusion detection and intrusion prevention systems, the AC automaton is embedded within network traffic analyzers that scan packet streams for protocol-specific attack signatures [43,44]. Systems such as Snort and Suricata integrate Aho-Corasick as their core rule-matching subsystem, where each rule corresponds to a known exploit pattern or payload fragment [8,9,45]. The automaton traverses reconstructed TCP streams in real time, which allows the detection of malicious payloads across gigabit-speed links [44]. In cloud-integrated antivirus infrastructures, this principle is extended to distributed scanning, where AC automata are deployed in parallel across multiple nodes or virtualized environments [46,47]. Each automaton instance processes a partition of the global signature set, and aggregate results are correlated through centralized detection services [15,47]. This distributed AC framework provides scalable, low-latency malware detection suitable for large network and cloud ecosystems, while it retains the deterministic guarantees of the original algorithm [10,11,13,47]. In parallel, time-aware deep learning models have emerged as a complementary approach in cloud-based intrusion detection systems, which provide enhanced event correlation under temporal constraints [48]. While such models pursue probabilistic reasoning, AC-based methods remain indispensable for deterministic, explainable matching at wire speed. Furthermore, when exact byte positions of AC hits are reported, as proposed in forensic tracing pipelines, they support attribution of data breaches through byte-level signature correlation [49]. Complementary system-level work demonstrates how automata-like reasoning and structured detection workflows continue to inform both real-time OT monitoring [50] and educational modeling of cybersecurity decision trees [51].

5. Comparative Analysis of Algorithmic Variants

Over nearly five decades of study and engineering adaptation, the Aho-Corasick algorithm has evolved into a family of implementations that adjust memory usage, processing rate, and hardware affinity [52]. Each version alters the original deterministic automaton to optimize a specific computational aspect while it retains the linear relation between input size and total runtime [53]. In practical systems, the decisive factors are not only theoretical complexity but also memory hierarchy, cache behavior, and the efficiency of parallel dispatch [52]. In order to present a coherent overview, the principal algorithmic variants are organized by hardware context, namely: CPU-based, GPU-based, and FPGA/ASIC-based realizations [11,22,24,54]. These architectural distinctions are crucial in modern malware scanning engines, where the same automaton must adapt to different computational architectures without loss of detection accuracy (

Table 1. Comparative summary of hardware-specific Aho-Corasick variants. The table outlines the main design principles, operational characteristics, and application domains of representative algorithmic variants optimized for distinct hardware architectures. Each entry highlights the defining computational approach, principal advantages, and key trade-offs in memory use, determinism, and scalability.

Variant	Target Hardware	Key Design Feature	Performance Characteristic	Strengths	Limitations	Typical Applications
Classic AC [1]	CPU	Explicit transition table per symbol	Linear runtime, predictable execution	Simplicity, deterministic scan time	High memory footprint	Antivirus, IDS, text search
Split-AC [11]	CPU (multicore)	Subautomata partitioning	Moderate memory reduction, improved cache locality	Parallelizable, efficient for SIMD	Overhead from partition management	Multi-threaded malware scanners
PFAC [24]	GPU	Failure-less automaton, thread-per-byte mapping	Multi-gigabit data rates	Massive parallelism, ideal for GPUs	Increased memory use	Network inspection, cloud-scale scanning
Bit-Split AC [22]	FPGA/ ASIC	Bit-level transition decomposition	Constant-time propagation	Deterministic timing, sub-µs latency	Not efficient on CPUs or GPUs	Inline packet filtering, cyber-defense hardware

).

5.1. CPU-Oriented Variants

CPU-oriented versions retain the sequential logic of the algorithm while exploiting instruction-level parallelism where possible [11,53]. The classical Aho-Corasick version uses an explicit transition table for every state and alphabet symbol [1]. This approach allows for a deterministic traversal but requires substantial memory for large pattern collections [52]. Its predictable execution makes it ideal for general-purpose processors and embedded systems where simplicity and timing stability are preferred over compact storage [52].

The Split-AC version divides the automaton into smaller subautomata, each responsible for a subset of the pattern space [11]. This partition reduces the transition footprint, improves cache locality, and enables parallel traversal across CPU threads without shared-memory conflicts. Each subautomaton can operate independently, allowing for multiple cores to traverse disjoint pattern partitions simultaneously. Empirical results show moderate memory reduction and better throughput (i.e., data rates) on multi-core processors that support vector instruction sets such as SSE (Streaming SIMD Extensions) or AVX (Advanced Vector Extensions) [13,55,56]. CPU implementations of this class remain dominant in intrusion detection and antivirus software [11,55].

5.2. GPU-Oriented Variants

GPU platforms favor data-parallel formulations. For instance, the Parallel Failure-less Aho-Corasick (PFAC) version removes all failure transitions and assigns every byte position of the input to a separate GPU thread [57]. This transformation converts the automaton traversal from sequential to parallel and allows multi-gigabit data rates in network inspection and large-scale malware analysis [8,57]. The drawback is an increase in memory demand, because the absence of failure compression expands the state table [58,59]. Later studies demonstrate that hierarchical compression and sparse transition encoding (i.e., storing valid state-symbol transitions instead of full tables) reduce the expanded footprint without loss of processing rate [11,58,59]. PFAC therefore represents the most effective model for GPU-based cybersecurity systems where a high data rate is essential and memory capacity is less critical [24,59].

5.3. FPGA and ASIC Variants

In hardware-embedded contexts, the Bit-Split Aho-Corasick version provides deterministic timing through bit-level decomposition of each input byte [22,60]. Every bit of the symbol space passes through a separate combinational path, so the automaton operates as a pipeline of parallel logic units. This structure lowers the dimensionality of state transitions and allows for constant-time propagation, which suits FPGA and ASIC platforms [14]. The automaton can be synthesized directly into physical logic gates, yielding sub-microsecond latency and fixed processing rate regardless of input length. Bit-Split AC performs best in network processors and dedicated cyber-defense circuits that demand predictable, low-latency response [22]. On standard CPUs or GPUs, its bit-parallel structure offers no measurable benefit due to the byte-oriented nature of instruction sets [58]. In the same time frame, Pao et al. (2010) introduced a pipelined hardware implementation of Aho-Corasick (P-AC), targeting memory efficiency and high-throughput matching on FPGA platforms via forward-only traversal and dual-port memory [23]. While architecturally distinct and well-suited for hardware optimization, this variant evolved in parallel to the mainstream AC developments and addressed implementation challenges rather than altering the core automaton model.

5.4. Summary and Architectural Mapping

Each hardware-specific version of Aho-Corasick serves a distinct operational purpose. The classical and Split-AC versions fit CPU architectures that favor sequential determinism with moderate memory trade-offs. PFAC maintains high processing rates on GPUs through the replacement of failure transitions with direct state mappings. Bit-Split AC attains true hardware-level determinism through bit-parallel logic on FPGA or ASIC devices. Together, these versions show the flexibility of the Aho-Corasick model and its ability to align with the physical constraints of modern cybersecurity architectures [8,11,13,14].

6. Practical Example of a Reference Malware Scanner

In order to demonstrate the operational form of the Aho-Corasick automaton in antivirus scanners, an implementation was developed as a reference system (see Supplementary Material). This example illustrates how the automaton can be compiled from a real malware signature set and then applied to binary data streams by using the AC-Build and AC-Search procedures. The proposed scanner processes each byte of the input deterministically and reports all pattern occurrences mapped to their corresponding output states. This supplementary implementation provides a functional representation of the algorithmic model discussed above, bridging the formal pseudocode description with a working antivirus prototype. For a more robust implementation that includes full error handling and input validation, see Appendix A.2.

7. Conclusions

Nearly five decades after its introduction, the Aho-Corasick (AC) algorithm continues to represent one of the most elegant intersections between theoretical computer science and practical cybersecurity engineering. Its deterministic finite-state structure, based on trie construction and failure transitions, provides an asymptotically optimal framework for simultaneous multi-pattern matching; an operation that remains central to malware detection, digital forensics, and intrusion prevention. This review demonstrates that the longevity of AC arises from its theoretical robustness, architectural adaptability, and predictable computational behavior. Initially designed for bibliographic search, its transition into antivirus and intrusion detection systems marked a paradigm shift, which enabled real-time pattern recognition at a scale that no other deterministic algorithm could achieve. Successive optimizations, such as Split-AC, Bit-Split AC, and PFAC, extended its relevance to memory-constrained, parallel, and high-throughput environments, without any alteration of the deterministic core of the algorithm. In the context of antivirus architectures, AC serves as the foundational mechanism for signature-based detection, acting as the deterministic filter preceding heuristic, statistical, and machine learning layers. This integration has transformed AC from a theoretical construct into a cornerstone of practical defense systems, which guarantees that known threats are detected with linear-time precision even in heterogeneous computational settings. From a broader scientific perspective, the persistence of Aho-Corasick across decades of technological evolution underscores the endurance value of automata theory in cybersecurity research. The algorithm exemplifies how formal language models, when implemented with engineering rigor, can sustain their relevance amid rapid hardware and threat landscape transformations. Future research directions lie not in the replacement of AC, but in its augmentation—through the integration of deterministic automata within hybrid analytical frameworks capable of handling polymorphic and behaviorally adaptive malware. Thus, the Aho-Corasick algorithm stands as both a historical milestone and a living framework that bridges symbolic computation and digital defense. Its role in modern antivirus engines reaffirms that the foundation of scalable threat detection remains deeply rooted in deterministic theory, not in transient heuristic trends.